Efficient Retrieval of Music Recordings Using Graph-Based Index Structures
Abstract
:1. Introduction
2. Music Retrieval Application
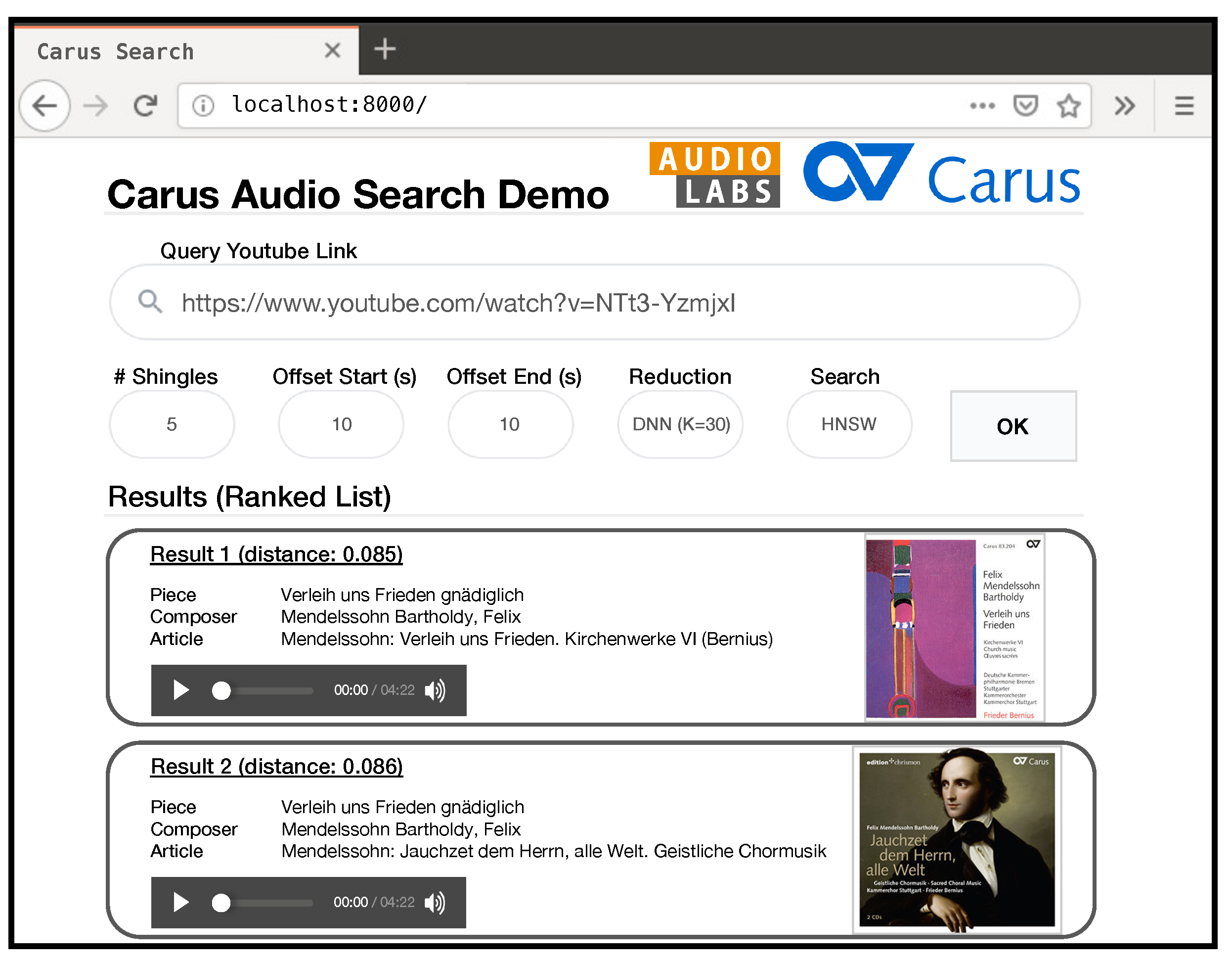
2.1. Motivating Retrieval Scenario
2.2. Cross-Version Retrieval System
2.3. Datasets
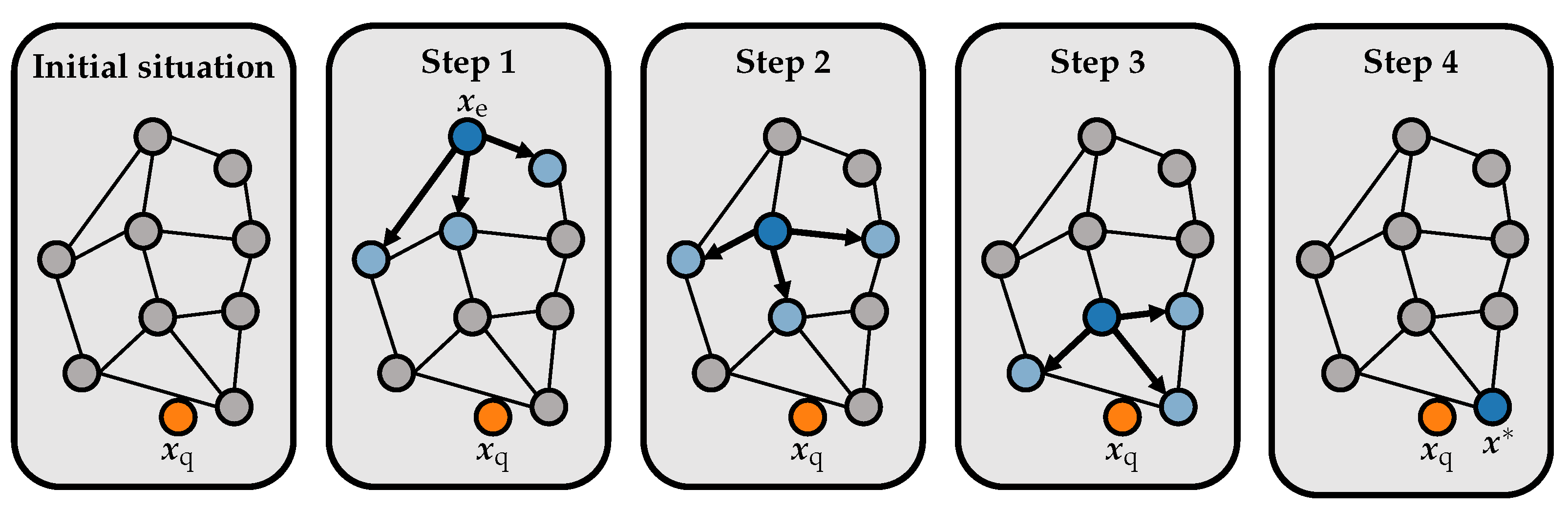
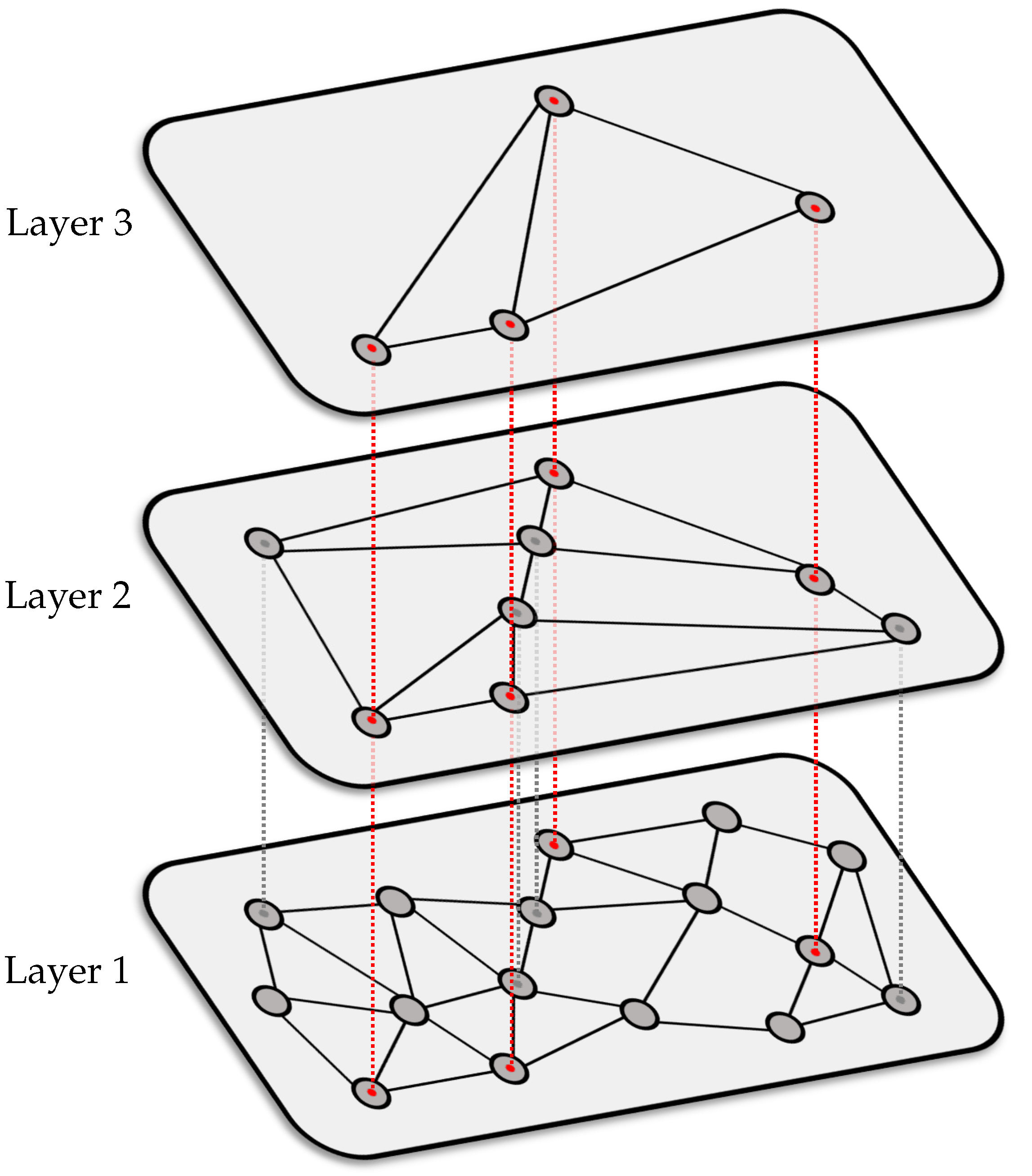
3. Graph-Based Nearest Neighbor Search
3.1. Graph-Based Data Structures
3.2. HNSW Graphs
4. Experiments
4.1. Experimental Setup
4.2. Retrieval Quality
4.3. Feature Computation
4.4. Constructing, Saving, and Loading the Index
4.5. Retrieval Time
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Casey, M.A.; Veltkap, R.; Goto, M.; Leman, M.; Rhodes, C.; Slaney, M. Content-Based Music Information Retrieval: Current Directions and Future Challenges. Proc. IEEE 2008, 96, 668–696. [Google Scholar] [CrossRef] [Green Version]
- Grosche, P.; Müller, M.; Serrà, J. Audio Content-Based Music Retrieval. In Multimodal Music Processing; Müller, M., Goto, M., Schedl, M., Eds.; Dagstuhl Follow-Ups; Schloss Dagstuhl-Leibniz-Zentrum für Informatik: Wadern, Germany, 2012; Volume 3, pp. 157–174. [Google Scholar]
- Typke, R.; Wiering, F.; Veltkamp, R.C. A Survey of Music Information Retrieval Systems. In Proceedings of the International Society for Music Information Retrieval Conference (ISMIR), London, UK, 11–15 September 2005; pp. 153–160. [Google Scholar] [CrossRef]
- Wang, A. The Shazam music recognition service. Commun. ACM 2006, 49, 44–48. [Google Scholar] [CrossRef]
- Wang, A. An Industrial Strength Audio Search Algorithm. In Proceedings of the International Society for Music Information Retrieval Conference (ISMIR), Baltimore, MD, USA, 27–30 October 2003; pp. 7–13. [Google Scholar] [CrossRef]
- Cano, P.; Batlle, E.; Kalker, T.; Haitsma, J. A review of audio fingerprinting. J. VLSI Signal Process. 2005, 41, 271–284. [Google Scholar] [CrossRef] [Green Version]
- Ghias, A.; Logan, J.; Chamberlin, D.; Smith, B.C. Query by humming: Musical information retrieval in an audio database. In Proceedings of the Third ACM International Conference on Multimedia, San Francisco, CA, USA, 5–9 November 1995; pp. 231–236. [Google Scholar] [CrossRef]
- Salamon, J.; Serrà, J.; Gómez, E. Tonal representations for music retrieval: From version identification to query-by-humming. Int. J. Multimed. Inf. Retr. 2013, 2, 45–58. [Google Scholar] [CrossRef] [Green Version]
- Zalkow, F.; Müller, M. Learning Low-Dimensional Embeddings of Audio Shingles for Cross-Version Retrieval of Classical Music. Appl. Sci. 2020, 10, 19. [Google Scholar] [CrossRef] [Green Version]
- Frøkjær, E.; Hertzum, M.; Hornbæk, K. Measuring Usability: Are Effectiveness, Efficiency, and Satisfaction Really Correlated? In Proceedings of the SIGCHI Conference on Human Factors in Computing Systems (CHI), The Hague, The Netherlands, 1–6 April 2000; pp. 345–352. [Google Scholar] [CrossRef]
- Kurth, F.; Müller, M. Efficient Index-Based Audio Matching. IEEE Trans. Audio Speech Lang. Process. 2008, 16, 382–395. [Google Scholar] [CrossRef]
- Bentley, J.L. Multidimensional Binary Search Trees Used for Associative Searching. Commun. ACM 1975, 18, 509–517. [Google Scholar] [CrossRef]
- Friedman, J.H.; Bentley, J.L.; Finkel, R.A. An Algorithm for Finding Best Matches in Logarithmic Expected Time. ACM Trans. Math. Softw. 1977, 3, 209–226. [Google Scholar] [CrossRef]
- Slaney, M.; Casey, M.A. Locality-sensitive hashing for finding nearest neighbors. Signal Process. Mag. IEEE 2008, 25, 128–131. [Google Scholar] [CrossRef]
- Muja, M.; Lowe, D.G. Scalable Nearest Neighbor Algorithms for High Dimensional Data. IEEE Trans. Pattern Anal. Mach. Intell. 2014, 36, 2227–2240. [Google Scholar] [CrossRef]
- Li, W.; Zhang, Y.; Sun, Y.; Wang, W.; Li, M.; Zhang, W.; Lin, X. Approximate Nearest Neighbor Search on High Dimensional Data— Experiments, Analyses, and Improvement. IEEE Trans. Knowl. Data Eng. 2019, 32, 1475–1488. [Google Scholar] [CrossRef]
- Grosche, P.; Müller, M. Toward Characteristic Audio Shingles for Efficient Cross-Version Music Retrieval. In Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP), Kyoto, Japan, 25–30 March 2012; pp. 473–476. [Google Scholar] [CrossRef] [Green Version]
- Miotto, R.; Orio, N. A Music Identification System Based on Chroma Indexing and Statistical Modeling. In Proceedings of the International Society for Music Information Retrieval Conference (ISMIR), Philadelphia, PA, USA, 14–18 September 2008; pp. 301–306. [Google Scholar] [CrossRef]
- Schlüter, J. Learning Binary Codes For Efficient Large-Scale Music Similarity Search. In Proceedings of the International Society for Music Information Retrieval Conference (ISMIR), Curitiba, Brazil, 4–8 November 2013; pp. 581–586. [Google Scholar] [CrossRef]
- Ryynänen, M.; Klapuri, A. Query by humming of MIDI and audio using locality sensitive hashing. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Las Vegas, NV, USA, 30 March–4 April 2008; pp. 2249–2252. [Google Scholar] [CrossRef]
- Reiss, J.; Aucouturier, J.J.; Sandler, M. Efficient Multidimensional Searching Routines. In Proceedings of the International Symposium on Music Information Retrieval (ISMIR), Bloomington, IN, USA, 15–17 October 2001. [Google Scholar] [CrossRef]
- McFee, B.; Lanckriet, G.R.G. Large-scale music similarity search with spatial trees. In Proceedings of the International Society for Music Information Retrieval Conference (ISMIR), Miami, FL, USA, 24–28 October 2011; pp. 55–60. [Google Scholar] [CrossRef]
- Liu, T.; Moore, A.W.; Gray, A.G.; Yang, K. An Investigation of Practical Approximate Nearest Neighbor Algorithms. In Proceedings of the Advances in Neural Information Processing Systems (NIPS), Vancouver, BC, Canada, 13–18 December 2004; pp. 825–832. [Google Scholar]
- Bishop, C.M. Pattern Recognition and Machine Learning; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Malkov, Y.A.; Yashunin, D.A. Efficient and robust approximate nearest neighbor search using Hierarchical Navigable Small World graphs. IEEE Trans. Pattern Anal. Mach. Intell. 2020, 42, 824–836. [Google Scholar] [CrossRef] [Green Version]
- Adewoye, T.; Han, X.; Ruest, N.; Milligan, I.; Fritz, S.; Lin, J. Content-Based Exploration of Archival Images Using Neural Networks. In Proceedings of the Joint Conference on Digital Libraries (JCDL), Virtual Event, Wuhan, China, 1–5 August 2020; pp. 489–490. [Google Scholar] [CrossRef]
- Doras, G.; Peeters, G. A Prototypical Triplet Loss for Cover Detection. In Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP), Barcelona, Spain, 4–8 May 2020; pp. 3797–3801. [Google Scholar] [CrossRef] [Green Version]
- Yesiler, F.; Serrà, J.; Gómez, E. Accurate and Scalable Version Identification Using Musically-Motivated Embeddings. In Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP), Barcelona, Spain, 4–8 May 2020; pp. 21–25. [Google Scholar] [CrossRef] [Green Version]
- Kotsifakos, A.; Kotsifakos, E.E.; Papapetrou, P.; Athitsos, V. Genre Classification of Symbolic Music with SMBGT. In Proceedings of the International Conference on PErvasive Technologies Related to Assistive Environments (PETRA), Rhodes, Greece, 29–31 May 2013. [Google Scholar] [CrossRef]
- McFee, B.; Kim, J.W.; Cartwright, M.; Salamon, J.; Bittner, R.M.; Bello, J.P. Open-Source Practices for Music Signal Processing Research: Recommendations for Transparent, Sustainable, and Reproducible Audio Research. IEEE Signal Process. Mag. 2019, 36, 128–137. [Google Scholar] [CrossRef]
- Gómez, E. Tonal Description of Music Audio Signals. Ph.D. Thesis, Universitat Pompeu Fabra, Barcelona, Spain, 2006. [Google Scholar]
- Müller, M. Fundamentals of Music Processing; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Müller, M. Information Retrieval for Music and Motion; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Müller, M.; Kurth, F.; Clausen, M. Chroma-Based Statistical Audio Features for Audio Matching. In Proceedings of the IEEE Workshop on Applications of Signal Processing (WASPAA), New Paltz, NY, USA, 16–19 October 2005; pp. 275–278. [Google Scholar] [CrossRef]
- Casey, M.A.; Rhodes, C.; Slaney, M. Analysis of Minimum Distances in High-Dimensional Musical Spaces. IEEE Trans. Audio Speech Lang. Process. 2008, 16, 1015–1028. [Google Scholar] [CrossRef] [Green Version]
- Schroff, F.; Kalenichenko, D.; Philbin, J. FaceNet: A Unified Embedding for Face Recognition and Clustering. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 8–10 June 2015; pp. 815–823. [Google Scholar] [CrossRef] [Green Version]
- Marimont, R.B.; Shapiro, M.B. Nearest Neighbour Searches and the Curse of Dimensionality. IMA J. Appl. Math. 1979, 24, 59–70. [Google Scholar] [CrossRef]
- Prokhorenkova, L.; Shekhovtsov, A. Graph-based Nearest Neighbor Search: From Practice to Theory. In Proceedings of the International Conference on Machine Learning (ICML), Vienna, Austria, 12–18 July 2020. [Google Scholar]
- Kriegel, H.; Schubert, E.; Zimek, A. The (black) art of runtime evaluation: Are we comparing algorithms or implementations? Knowl. Inf. Syst. 2017, 52, 341–378. [Google Scholar] [CrossRef]
- Virtanen, P.; Gommers, R.; Oliphant, T.E.; Haberland, M.; Reddy, T.; Cournapeau, D.; Burovski, E.; Peterson, P.; Weckesser, W.; Bright, J.; et al. SciPy 1.0: Fundamental algorithms for scientific computing in Python. Nat. Methods 2020, 17, 261–272. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- McFee, B.; Raffel, C.; Liang, D.; Ellis, D.P.; McVicar, M.; Battenberg, E.; Nieto, O. Librosa: Audio and Music Signal Analysis in Python. In Proceedings of the Python Science Conference, Austin, TX, USA, 6–12 July 2015; pp. 18–25. [Google Scholar] [CrossRef] [Green Version]
- Abadi, M.; Barham, P.; Chen, J.; Chen, Z.; Davis, A.; Dean, J.; Devin, M.; Ghemawat, S.; Irving, G.; Isard, M.; et al. TensorFlow: A System for Large-Scale Machine Learning. In Proceedings of the USENIX Symposium on Operating Systems Design and Implementation (OSDI), Savannah, GA, USA, 2–4 November 2016; pp. 265–283. [Google Scholar]
- Manning, C.D.; Raghavan, P.; Schütze, H. Introduction to Information Retrieval; Cambridge University Press: Cambridge, UK, 2008. [Google Scholar]
- Ram, P.; Sinha, K. Revisiting kd-tree for Nearest Neighbor Search. In Proceedings of the International Conference on Knowledge Discovery & Data Mining (KDD), Anchorage, AK, USA, 4–8 August 2019; pp. 1378–1388. [Google Scholar] [CrossRef]
- García, S.; Derrac, J.; Cano, J.R.; Herrera, F. Prototype Selection for Nearest Neighbor Classification: Taxonomy and Empirical Study. IEEE Trans. Pattern Anal. Mach. Intell. 2012, 34, 417–435. [Google Scholar] [CrossRef] [PubMed]
- Rico-Juan, J.R.; Valero-Mas, J.J.; Calvo-Zaragoza, J. Extensions to Rank-Based Prototype Selection in k-Nearest Neighbour Classification. Appl. Soft Comput. 2019, 85. [Google Scholar] [CrossRef] [Green Version]
- Bustos, B.; Navarro, G.; Chávez, E. Pivot Selection Techniques for Proximity Searching in Metric Spaces. Pattern Recognit. Lett. 2003, 24, 2357–2366. [Google Scholar] [CrossRef] [Green Version]
- Bustos, B.; Morales, N. On the Asymptotic Behavior of Nearest Neighbor Search Using Pivot-Based Indexes. In Proceedings of the International Workshop on Similarity Search and Applications (SISAP), Istanbul, Turkey, 18–19 September 2010; pp. 33–39. [Google Scholar] [CrossRef]
- Brandner, J. Efficient Cross-Version Music Retrieval Using Dimensionality Reduction and Indexing Techniques. Master’s Thesis, Friedrich-Alexander-Universität Erlangen-Nürnberg, Erlangen, Germany, 2019. [Google Scholar]


| # Audio Files | ∑ Duration | ø Duration | Annotations | # Shingles | |
|---|---|---|---|---|---|
| 330 | 16:13:37 | 0:02:57 | ✓ | 52,332 | |
| 7115 | 389:58:03 | 0:03:17 | ✗ | 1,272,386 |
| Step | Performance Measure | Stage | Section |
|---|---|---|---|
| Overall pipeline | Quality (P@1, P@3, P) | Offline & online | Section 4.2 |
| Feature computation | Time (ms) | Offline & online | Section 4.3 |
| Constructing the index | Time (s) | Offline | Section 4.4 |
| Saving the index | Disk space (MB) | Offline | Section 4.4 |
| Loading the index | Time (ms) | Offline | Section 4.4 |
| Retrieval | Time (ms) | Online | Section 4.5 |
| Reduction | K | Search | P@1 | P@3 | P |
|---|---|---|---|---|---|
| — | 240 | Full Search | 1.0000 | 0.9965 | 0.9434 |
| HNSW | 1.0000 | 0.9965 | 0.9434 | ||
| PCA | 30 | Full Search | 1.0000 | 0.9910 | 0.9130 |
| HNSW | 1.0000 | 0.9910 | 0.9130 | ||
| 12 | Full Search | 1.0000 | 0.9679 | 0.8294 | |
| HNSW | 1.0000 | 0.9678 | 0.8294 | ||
| 6 | Full Search | 1.0000 | 0.8937 | 0.7350 | |
| HNSW | 1.0000 | 0.8937 | 0.7350 | ||
| DNN | 30 | Full Search | 1.0000 | 0.9868 | 0.9344 |
| HNSW | 1.0000 | 0.9869 | 0.9345 | ||
| 12 | Full Search | 1.0000 | 0.9757 | 0.8989 | |
| HNSW | 1.0000 | 0.9756 | 0.8989 | ||
| 6 | Full Search | 1.0000 | 0.9236 | 0.8333 | |
| HNSW | 1.0000 | 0.9237 | 0.8333 |
| Step | Time (ms) |
|---|---|
| Audio Loading | 44.8 ± 1.4 |
| Spectral Feature Computation | 1171.5 ± 34.3 |
| CENS Feature Computation | 0.9 ± 0.5 |
| Embedding PCA () | 0.05 ± 0.0 |
| Embedding PCA () | 0.05 ± 0.0 |
| Embedding PCA () | 0.05 ± 0.0 |
| Embedding DNN () | 1.6 ± 0.1 |
| Embedding DNN () | 1.5 ± 0.1 |
| Embedding DNN () | 1.4 ± 0.1 |
| Search | Reduction | K | Construction Time (s) | Save Size (MB) | Load Time (ms) | |||
|---|---|---|---|---|---|---|---|---|
| KD | — | 240 | 0.54 ± 0.0 | 43.03 ± 0.1 | 209.7 | 5161.2 | 131.5 ± 0.4 | 3209.1 ± 25.4 |
| KD | PCA | 30 | 0.06 ± 0.0 | 3.89 ± 0.2 | 27.0 | 664.8 | 17.5 ± 0.3 | 405.1 ± 8.8 |
| KD | PCA | 12 | 0.03 ± 0.0 | 1.66 ± 0.1 | 11.3 | 279.4 | 3.5 ± 0.1 | 167.0 ± 6.9 |
| KD | PCA | 6 | 0.02 ± 0.0 | 0.99 ± 0.1 | 6.1 | 150.9 | 2.1 ± 0.3 | 86.3 ± 2.2 |
| HNSW | — | 240 | 0.65 ± 0.0 | 26.66 ± 0.0 | 53.9 | 1310.9 | 108.1 ± 0.4 | 2680.0 ± 42.8 |
| HNSW | PCA | 30 | 0.51 ± 0.0 | 16.38 ± 0.0 | 9.9 | 241.8 | 85.1 ± 2.1 | 2095.3 ± 6.6 |
| HNSW | PCA | 12 | 0.43 ± 0.0 | 11.58 ± 0.0 | 6.2 | 150.2 | 82.9 ± 0.4 | 2071.5 ± 43.8 |
| HNSW | PCA | 6 | 0.42 ± 0.0 | 10.20 ± 0.0 | 4.9 | 119.6 | 82.6 ± 0.6 | 2049.1 ± 22.8 |
| Reduction | K | Search | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| — | 240 | Full Search | 13.912 | 13.912 | 13.824 | 13.875 | — | — | — | — |
| KD | 0.072 | 23.136 | 24.463 | 25.269 | 771.623 | 775.116 | 770.461 | 772.946 | ||
| HNSW | 0.008 | 0.008 | 0.009 | 0.072 | 0.020 | 0.020 | 0.021 | 0.205 | ||
| PCA | 30 | Full Search | 4.803 | 4.757 | 4.768 | 4.812 | — | — | — | — |
| KD | 0.009 | 0.621 | 1.001 | 2.025 | 36.825 | 48.145 | 66.499 | 88.849 | ||
| HNSW | 0.007 | 0.007 | 0.007 | 0.056 | 0.010 | 0.009 | 0.019 | 0.123 | ||
| PCA | 12 | Full Search | 4.354 | 4.418 | 4.322 | 4.360 | — | — | — | — |
| KD | 0.004 | 0.087 | 0.233 | 0.713 | 0.907 | 1.698 | 4.414 | 10.280 | ||
| HNSW | 0.007 | 0.007 | 0.007 | 0.056 | 0.009 | 0.009 | 0.009 | 0.067 | ||
| PCA | 6 | Full Search | 4.123 | 4.115 | 4.124 | 4.159 | — | — | — | — |
| KD | 0.003 | 0.019 | 0.074 | 0.346 | 0.031 | 0.065 | 0.201 | 0.852 | ||
| HNSW | 0.007 | 0.007 | 0.006 | 0.048 | 0.007 | 0.007 | 0.011 | 0.072 | ||
| DNN | 30 | Full Search | 4.899 | 4.897 | 4.883 | 4.930 | — | — | — | — |
| KD | 0.009 | 0.459 | 1.019 | 2.498 | 30.021 | 46.611 | 75.748 | 117.543 | ||
| HNSW | 0.007 | 0.007 | 0.007 | 0.057 | 0.011 | 0.011 | 0.011 | 0.077 | ||
| DNN | 12 | Full Search | 4.439 | 4.434 | 4.433 | 4.480 | — | — | — | — |
| KD | 0.004 | 0.064 | 0.177 | 0.709 | 0.377 | 0.829 | 2.498 | 7.240 | ||
| HNSW | 0.008 | 0.008 | 0.009 | 0.068 | 0.006 | 0.007 | 0.007 | 0.056 | ||
| DNN | 6 | Full Search | 4.165 | 4.162 | 4.171 | 4.220 | — | — | — | — |
| KD | 0.002 | 0.014 | 0.062 | 0.310 | 0.019 | 0.039 | 0.141 | 0.663 | ||
| HNSW | 0.006 | 0.007 | 0.007 | 0.054 | 0.007 | 0.007 | 0.007 | 0.057 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zalkow, F.; Brandner, J.; Müller, M. Efficient Retrieval of Music Recordings Using Graph-Based Index Structures. Signals 2021, 2, 336-352. https://doi.org/10.3390/signals2020021
Zalkow F, Brandner J, Müller M. Efficient Retrieval of Music Recordings Using Graph-Based Index Structures. Signals. 2021; 2(2):336-352. https://doi.org/10.3390/signals2020021
Chicago/Turabian StyleZalkow, Frank, Julian Brandner, and Meinard Müller. 2021. "Efficient Retrieval of Music Recordings Using Graph-Based Index Structures" Signals 2, no. 2: 336-352. https://doi.org/10.3390/signals2020021
APA StyleZalkow, F., Brandner, J., & Müller, M. (2021). Efficient Retrieval of Music Recordings Using Graph-Based Index Structures. Signals, 2(2), 336-352. https://doi.org/10.3390/signals2020021






