Global Structure-Aware Drum Transcription Based on Self-Attention Mechanisms

Abstract

This paper describes an automatic drum transcription (ADT) method that directly estimates a tatum-level drum score from a music signal in contrast to most conventional ADT methods that estimate the frame-level onset probabilities of drums. To estimate a tatum-level score, we propose a deep transcription model that consists of a frame-level encoder for extracting the latent features from a music signal and a tatum-level decoder for estimating a drum score from the latent features pooled at the tatum level. To capture the global repetitive structure of drum scores, which is difficult to learn with a recurrent neural network (RNN), we introduce a self-attention mechanism with tatum-synchronous positional encoding into the decoder. To mitigate the difficulty of training the self-attention-based model from an insufficient amount of paired data and to improve the musical naturalness of the estimated scores, we propose a regularized training method that uses a global structure-aware masked language (score) model with a self-attention mechanism pretrained from an extensive collection of drum scores. The experimental results showed that the proposed regularized model outperformed the conventional RNN-based model in terms of the tatum-level error rate and the frame-level F-measure, even when only a limited amount of paired data was available so that the non-regularized model underperformed the RNN-based model.

1. Introduction

Automatic drum transcription (ADT) is one of the most important subtasks in automatic music transcription (AMT) because the drum part forms the rhythmic backbone of popular music. In this study, we deal with the three main instruments of the basic drum kit: bass drum (BD), snare drum (SD), and hi-hats (HH). Since these drums produce unpitched impulsive sounds, only the onset times are of interest in ADT. The standard approach to ADT is to estimate the activations (gains) or onset probabilities of each drum from a music spectrogram at the frame level and then to determine the onset frames using an optimal path search algorithm based on some cost function [1]. Although the ultimate goal of ADT is to estimate a human-readable symbolic drum score, few studies have attempted to estimate the onset times of drums quantized at the tatum level. In this paper, the “tatum” is defined as a tick position on the sixteenth-note-level grid (four times finer than the “beat” on the quarter-note-level grid) and the tatum times are assumed to be estimated in advance [2].

Nonnegative matrix factorization (NMF) and deep learning have been used for frame-level ADT [3]. The time-frequency spectrogram of a percussive part, which can be separated from a music spectrogram [4,5], has a low-rank structure because it is composed of repeated drum sounds with varying gains. This has motivated the use of NMF or its convolutional variants for ADT [6,7,8,9,10], where the basis spectra or spectrogram templates of drums are prepared and their frame-level activations are estimated in a semi-supervised manner. The NMF-based approach is a physically reasonable choice, but the supervised DNN-based approach has recently gained much attention because of its superior performance. Comprehensive experimental comparison of DNN- and NMF-based ADT methods have been reported in [3]. Convolutional neural networks (CNNs), for example, have been used for extracting local time-frequency features from an input spectrogram [11,12,13,14,15]. Recurrent neural networks (RNNs) are expected to learn the temporal dynamics inherent in music and have successfully been used, often in combination with CNNs, for estimating the smooth onset probabilities of drum sounds at the frame level [16,17,18]. This approach, however, cannot learn musically meaningful drum patterns on the symbolic domain, and the tatum-level quantization of the estimated onset probabilities in an independent post-processing step often yields musically unnatural drum notes.

To solve this problem, Ishizuka et al. [19] attempted to use the encoder–decoder architecture [20,21] for frame-to-tatum ADT. The model consisted of a CNN-based frame-level encoder for extracting the latent features from a drum-part spectrogram and an RNN-based tatum-level decoder for estimating the onset probabilities of drums from the latent features pooled at the tatum level. This was inspired by the end-to-end approach to automatic speech recognition (ASR), where the encoder acted as an acoustic model to extract the latent features from speech signals and the decoder acted as a language model to estimate the grammatically coherent word sequences [22]. Unlike ASR models, the model used the temporal pooling and had no attention mechanism that connected the frame-level encoder to the tatum-level decoder, i.e., that aligned the frame-level acoustic features with the tatum-level drum notes, because the tatum times were given. Although the tatum-level decoder was capable of learning musically meaningful drum patterns and favored musically natural drum notes as its output, the performance of ADT was limited by the amount of paired data of music signals and drum scores.

Transfer learning [23,24,25] is a way of using external non-paired drum scores for improving the generalization capability of the encoder–decoder model. For example, the encoder–decoder model could be trained in a regularized manner such that the output score was close to the ground-truth drum score and at the same time was preferred by a language model pretrained from an extensive collection of drum scores [19]. More specifically, a repetition-aware bi-gram model and a gated recurrent unit (GRU) model were used as language models for evaluating the probability (musical naturalness) of a drum score. Assuming that drum patterns were repeated with an interval of four beats as was often the case with the 4/4 time signature, the bi-gram model predicted the onset activations at each tatum by referring to those at the tatum four beats ago. The GRU model worked better than the bi-gram model because it had no assumption about the time signature and could learn the sequential dependency of tatum-level onset activations. Although the grammatical knowledge learned by the GRU model was expected to be transferred into the RNN-based decoder, such RNN-based models still could not learn the repetitive structure of drum patterns on the global time scale.

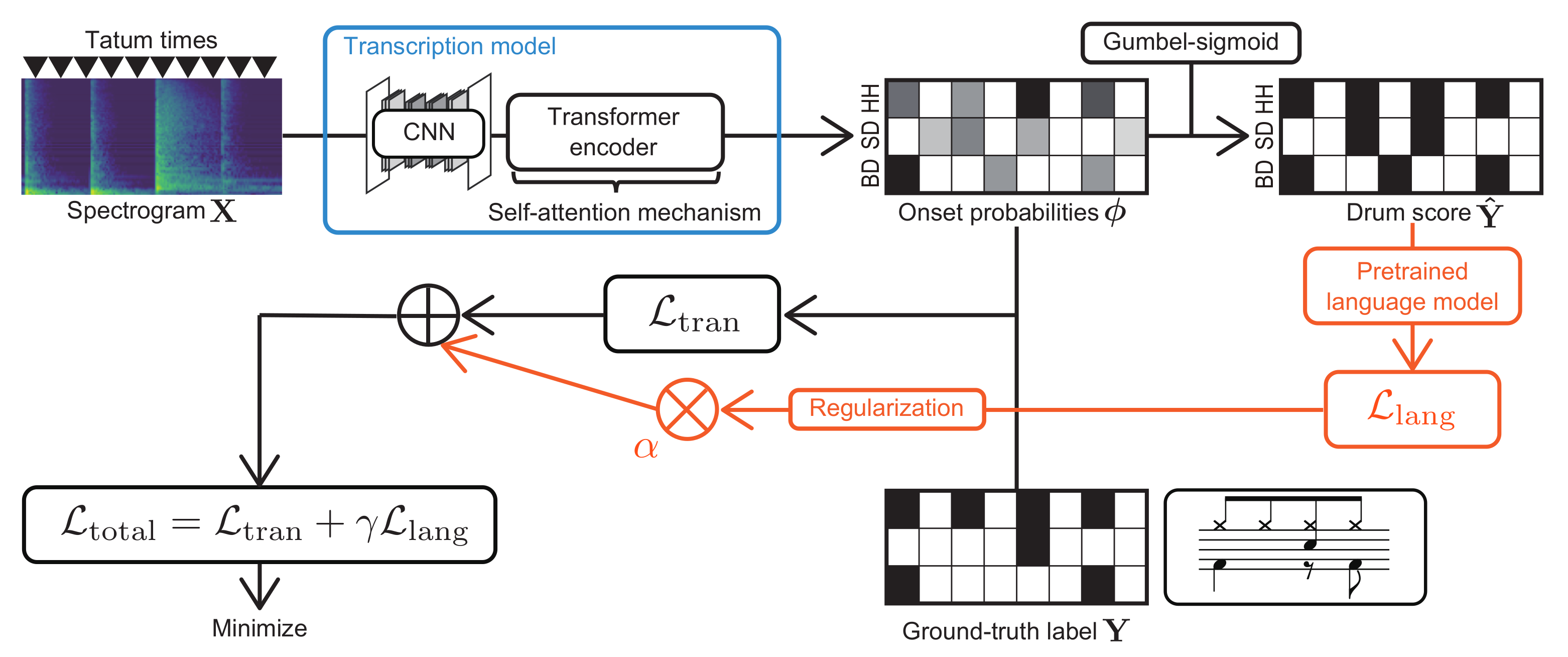
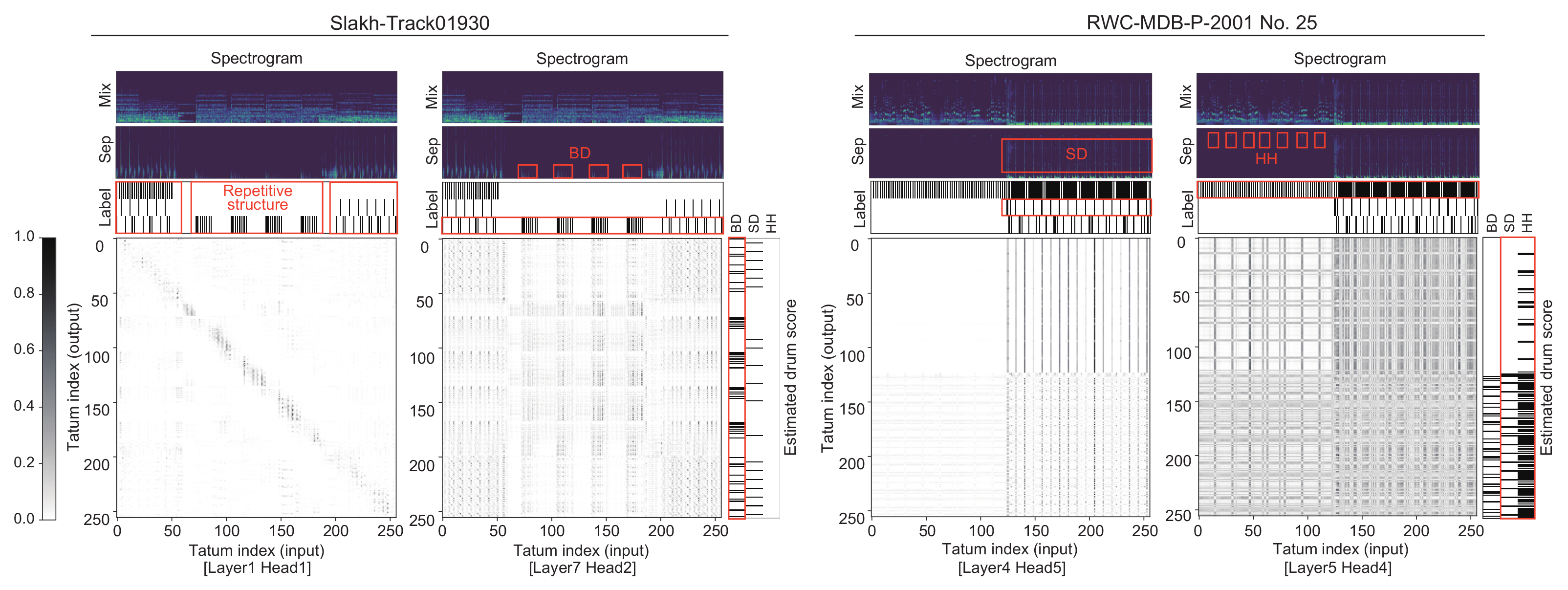
To overcome this limitation, in this paper, we propose a global structure-aware frame-to-tatum ADT method based on an encoder–decoder model with a self-attention mechanism and transfer learning (Figure 1), inspired by the success in sequence-to-sequence tasks such as machine translation and ASR. More specifically, our model involves a tatum-level decoder with a self-attention mechanism, where the architecture of the decoder is similar to that of the encoder of the transformer [26] because the input and output dimensions of the decoder are the same. To consider the temporal regularity of tatums for the self-attention computation, we propose a new type of positional encoding synchronized with the tatum times. Our model is trained in a regularized manner such that the model output (drum score) is preferred by a masked language model (MLM) with a self-attention mechanism that evaluates the pseudo-probability of the drum notes at each tatum based on both the forward and backward contexts. We experimentally validate the effectiveness of the self-attention mechanism used in the decoder and/or the language model and that of the tatum-synchronous positional encoding. We also investigate the computational efficiency of the proposed ADT method and compare it with that of the conventional RNN-based ADT method.

In Section 2 of this paper, we introduce related work on ADT and language modeling. Section 3 describes the proposed method, and Section 4 reports the experimental results. We conclude in Section 5 with a brief summary and mention of future work.

2. Related Work

This section reviews related work on ADT (Section 2.1), global structure-aware language models (Section 2.2), and evaluation metrics for transcribed musical scores (Section 2.3).

2.1. Automatic Drum Transcription (ADT)

Some studies have attempted to use knowledge learned from an extensive collection of unpaired drum scores to improve ADT. A language model can be trained from such data in an unsupervised manner and used to encourage a transcription model to estimate a musically natural drum pattern. Thompson et al. [27] used a template-based language model for classifying audio signals into a limited number of drum patterns with a support vector machine (SVM). Wu et al. [28] proposed a framework of knowledge distillation [29], one way to achieve transfer learning [30], in which an NMF-based teacher model was applied to a DNN-based student model.

Language models have been actively used in the field of ASR. In a classical ASR system consisting of independently trained acoustic and language models, the language model is used in combination with the acoustic model in the decoding stage to generate syntactically and semantically natural word sequences. The implementation of the decoder, however, is highly complicated. In an end-to-end ASR system having no clear distinction of acoustic and language models, only paired data can be used for training an integrated model. Transfer learning is a promising way of making effective use of a language model trained from huge unpaired text data [23]. For example, a pretrained language model is used for softening the target word distribution of paired speech data such that not only ground-truth transcriptions but also their semantically coherent variations are taken into account as target data in the supervised training [25].

A frame-level language model has been used in AMT. Raczyǹski et al. [31] used a deep belief network for modeling transitions of chord symbols and improved the chord recognition method based on NMF. Sigtia et al. [32] used a language model for estimating the most likely chord sequence from the chord posterior probabilities estimated by an RNN-based chord recognition system. As pointed out in [33,34], however, language models can more effectively be formulated at the tatum level for learning musically meaningful structures. Korzeniowski et al. [35] used N-gram as a symbolic language model and improved a DNN-based chord recognition system. Korzeniowski et al. [36] used an RNN-based symbolic language model with a duration model based on the idea that a frame-level language model can only smooth the onset probabilities of chord symbols. Ycart et al. [37] investigated the predictive power of LSTM networks and demonstrated that a long short-term memory (LSTM) working at the level of 16th note timesteps could express musical structures such as note transitions.

A tatum-level language model has also been used in ADT. Ueda et al. [10] proposed a Bayesian approach using a DNN-based language model as a prior of drum scores. Ishizuka et al. [19] proposed a regularized training method with an RNN-based pretrained language model to output musically natural drum patterns. However, these tatum-level language models cannot learn global structures, although the drum parts exhibit repetitive structure in music signals.

2.2. Global Structure-Aware Language Model

The attention mechanism is a core technology for global structure-aware sequence-to-sequence learning. In the standard encoder-decoder architecture, the encoder extracts latent features from an input sequence and the decoder recursively generates a variable number of output symbols one by one while referring to the whole latent features with attention weights [38,39]. In general, the encoder and decoder are implemented as RNNs to consider the sequential dependency of input and output symbols. Instead, the self-attention mechanism that can extract global structure-aware latent features from a single sequence can be incorporated into the encoder and decoder, leading to a non-autoregressive model called the transformer [26] suitable for parallel computation in the training phase.

To represent the ordinal information of input symbols, positional encoding vectors in addition to the input sequence are fed to the self-attention mechanism. Absolute positional encoding vectors are used in a non-recursive sequence-to-sequence model based entirely on CNNs [40]. Predefined trigonometric functions with different frequencies were proposed for representing absolute position information [26]. Sine and cosine functions are expected to implicitly learn the positional relationships of symbols based on the hypothesis that there exists a linear transformation that arbitrarily changes the phase of the trigonometric functions. There are some studies on relative position embeddings [41,42,43].

Recently, various methods for pretraining global structure-aware language models have been proposed. Embeddings from language models (ELMo) [44] is a feature-based pretraining model that combines forward and backward RNNs at the final layer to use bidirectional contexts. However, the forward and backward inferences are separated, and the computation is time-consuming because of the recursive learning process. Generative pretrained transformer (GPT) [45] and bidirectional encoder representations from transformers (BERT) [46] are pretrained models based on fine tuning. GPT is a variant of the transformer trained by preventing the self-attention mechanism from referring to future information. However, the inference is limited to a single direction. BERT can jointly learn bidirectional contexts, and thus, the masked language model (MLM) obtained by BERT is categorized as a bidirectional language model. As the perplexity is difficult to calculate, the pseudo perplexity of inferred word sequences is computed as described in [47].

In music generation, music transformer [48] uses a relative attention mechanism to learn long-term structure along with a new algorithm to reduce the memory requirement. Pop music transformer [49] adopts transformer-XL to leverage longer-range information along with a new data representation that expresses the rhythmic and harmonic structure of music. Transformer variational autoencoder [50] enables joint learning of local representation and global structure based on the hierarchical modeling. Harmony transformer [51] improves chord recognition to integrate chord segmentation with a non-autoregressive decoding method in the framework of musical harmony analysis. In ADT, however, very few studies have focused on learning long-term dependencies, even though a repetitive structure can uniquely be seen in drum patterns.

2.3. Evaluation Metrics for AMT

Most work in AMT have conducted frame-level evaluation for the detected onset times of target musical instruments. Poliner et al. [52] proposed comprehensive two metrics for frame-level piano transcription. The first one is the accuracy rate defined according to Dixon’s work [53]. The second one is the frame-level transcription error score inspired by the evaluation metric used in multiparty speech activity detection.

Some recent studies have focused on tatum- and symbol-level evaluations. Nishikimi et al. [54] used the tatum-level error rate based on the Levenshtein distance in automatic singing transcription. Nakamura et al. [55] conducted symbol-level evaluation for a piano transcription system consisting of multi-pitch detection and rhythm quantization. In the multi-pitch detection stage, an acoustic model estimates note events represented by pitches, onset and offset times (in seconds), and velocities. In the rhythm quantization stage, a metrical HMM with Gaussian noise (noisy metrical HMM) quantizes the note events on a tatum grid, followed by note-value and hand-part estimation. McLeod et al. [56] proposed a quantitative metric called MV2H for both multipitch detection and musical analysis. Similar to Nakamura’s work, this metric aims to evaluate a complete musical score with instrument parts, a time signature and metrical structure, note values, and harmonic information. The MV2H metric is based on the principle that a single error should be penalized once in the evaluation phase. In the context of ADT, in contrast, tatum- and symbol-level metrics have scarcely been investigated.

3. Proposed Method

Our goal is to estimate a drum score $\widehat{\mathbf{Y}}\in {\{0,1\}}^{M\times N}$ from the mel spectrogram of a target musical piece $\mathbf{X}\in {\mathbb{R}}_{+}^{F\times T}$, where M is the number of drum instruments (BD, SD, and HH, i.e., M = 3), N is the number of tatums, F is the number of frequency bins, and T is the number of time frames. We assume that all onset times are located on the tatum-level grid, and the tatum times $\mathbf{B}={\left\{b_n\right\}}_{n=1}^N$, where $1\le b_n\le T$ and $b_n<b_{n+1}$, are estimated in advance.

In Section 3.1, we explain the configuration of the encoder–decoder-based transcription model. Section 3.2 describes the masked language model as a bidirectional language model with the bi-gram- and GRU-based language models as unidirectional language models. The regularization method is explained in Section 3.3.

3.1. Transcription Models

The transcription model is used for estimating the tatum-level onset probabilities $\mathbf{\varphi }\in {[0,1]}^{M\times N}$, where ${\varphi }_{m,n}$ represents the probability that drum m has an onset at tatum n. The drum score $\mathbf{Y}$ is obtained by binarizing $\mathbf{\varphi }$ with a threshold $\delta \in [0,1]$.

The encoder of the transcription model is implemented with a CNN. The mel spectrogram $\mathbf{X}$ is converted to latent features $\mathbf{F}\in {\mathbb{R}}^{D_F\times T}$, where $D_F$ is the feature dimension. The frame-level latent features $\mathbf{F}$ are then summarized into tatum-level latent features $\mathbf{G}\in {\mathbb{R}}^{D_F\times N}$ through a max-pooling layer referring to the tatum times $\mathbf{B}$ as follows:

$$\begin{array}{cc}\hfill G_{d,n}& =\underset{\frac{b_{n-1}+b_n}{2}\le t<\frac{b_n+b_{n+1}}{2}}{max}{F}_{d,t},\hfill \end{array}$$

(1)

where $b_0=b_1$ and $b_{N+1}=b_N$ are introduced for the brief expression.

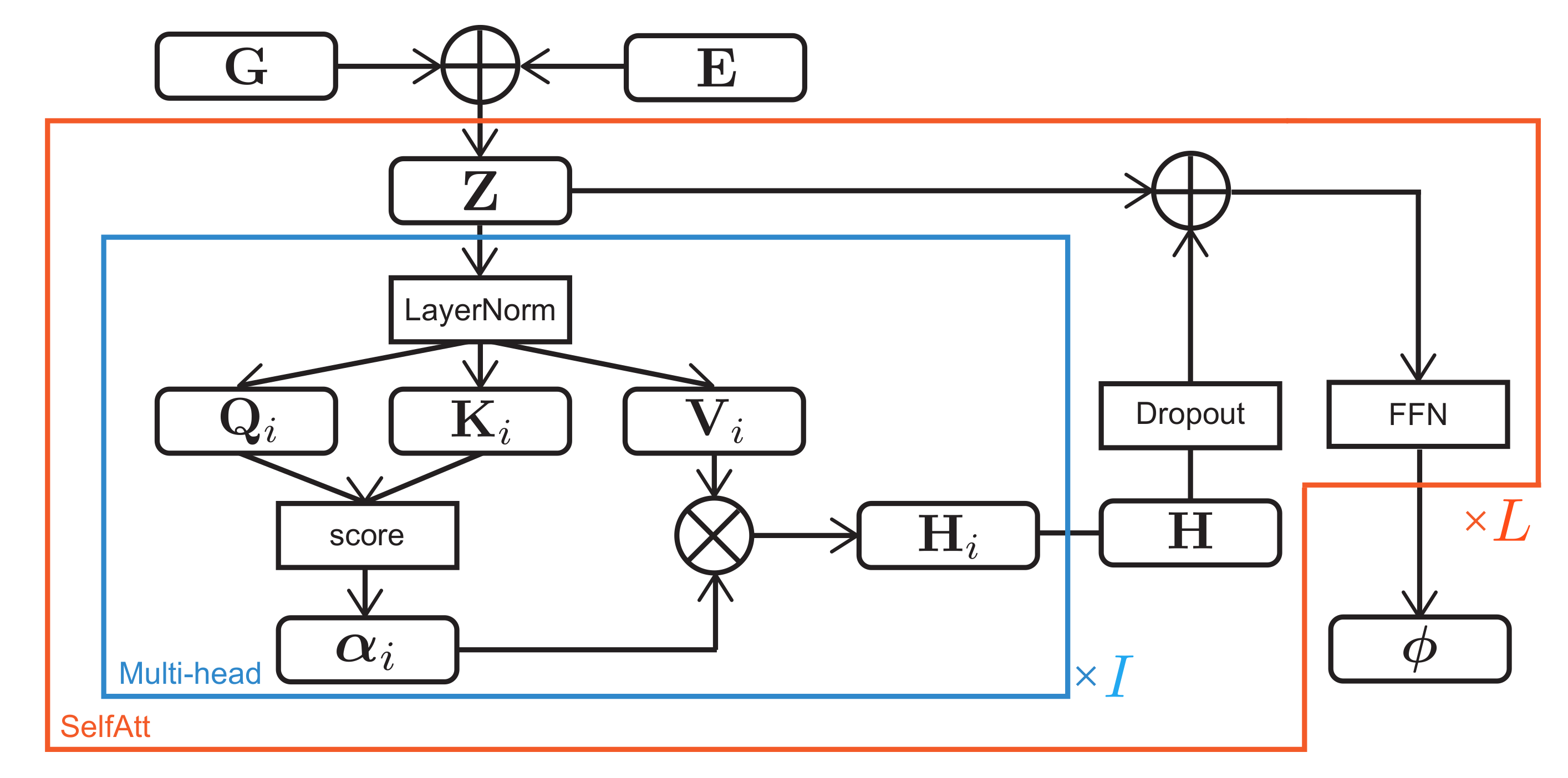
The decoder of the transcription model is implemented with a bidirectional GRU (BiGRU) or a self-attention mechanism (SelfAtt) followed by a fully connected layer. The intermediate features $\mathbf{G}$ are directly converted to the onset probabilities at the tatum level. In the self-attention-based decoder, the onset probabilities are estimated without recursive computation. To learn the sequential dependency and global structure of drum scores, the positional encoding $\mathbf{E}\in {\mathbb{R}}^{D_F\times N}$ are fed into the latent features $\mathbf{G}$ to obtain extended latent features $\mathbf{Z}\in {\mathbb{R}}^{D_F\times N}$. The standard positional encodings proposed in [26] are given by

$$\begin{array}{cc}\hfill E_{d,n}& =\left\{\begin{array}{c}sin\left(\frac{1}{10,{000}^{2d/D_F}}n\right)(d\equiv 0mod2),\hfill \\ cos\left(\frac{1}{10,{000}^{2d/D_F}}n\right)(d\equiv 1mod2),\hfill \end{array}\right.\hfill \end{array}$$

(2)

In this paper, we propose tatum-synchronous positional encodings (denoted SyncPE):

$$\begin{array}{cc}\hfill E_{d,n}& =\left\{\begin{array}{c}sin\left(\frac{\pi }{2+[d/2]}n\right)(d\equiv 0mod2),\hfill \\ cos\left(\frac{\pi }{2+[d/2]}n\right)(d\equiv 1mod2),\hfill \end{array}\right.\hfill \end{array}$$

(3)

where $[·]$ represents the floor function. As shown in Figure 2, the nonlinear stripes patterns appear in the encodings proposed in [26] because the period of the trigonometric functions increases exponentially with respect to the latent feature indices, whereas the proposed tatum-synchronous encodings exhibit the linear stripes patterns.

As shown in Figure 3, the extended features $\mathbf{Z}$ are converted to the onset probabilities $\mathbf{\varphi }$ through a stack of L self-attention mechanisms with I heads [26] and the layer normalization (Pre-Norm) [57] proposed for the simple and stable training of the transformer models [58,59]. For each head i ($1\le i\le I$), let ${\mathbf{Q}}_i\triangleq [{\mathbf{q}}_{i,1},\dots ,{\mathbf{q}}_{i,N}]\in {\mathbb{R}}^{D_K\times N}$, ${\mathbf{K}}_i\triangleq [{\mathbf{k}}_{i,1},\dots ,{\mathbf{k}}_{i,N}]\in {\mathbb{R}}^{D_K\times N}$, and ${\mathbf{V}}_i\triangleq [{\mathbf{v}}_{i,1},\dots ,{\mathbf{v}}_{i,N}]\in {\mathbb{R}}^{D_K\times N}$ be query, key, and value matrices given by

$$\begin{array}{cc}\hfill {\mathbf{Q}}_i& ={\mathbf{W}}_i^{(Q)}\mathrm{LayerNorm}(\mathbf{Z})+{\mathbf{b}}_i^{(Q)},\hfill \end{array}$$

(4)

$$\begin{array}{cc}\hfill {\mathbf{K}}_i& ={\mathbf{W}}_i^{(K)}\mathrm{LayerNorm}(\mathbf{Z})+{\mathbf{b}}_i^{(K)},\hfill \end{array}$$

(5)

$$\begin{array}{cc}\hfill {\mathbf{V}}_i& ={\mathbf{W}}_i^{(V)}\mathrm{LayerNorm}(\mathbf{Z})+{\mathbf{b}}_i^{(V)},\hfill \end{array}$$

(6)

where $D_k$ is the feature dimension of each head ($D_k=\frac{D_F}{I}$ in this paper as in [26]); ${\mathbf{q}}_i\in {\mathbb{R}}^{D_K}$, ${\mathbf{k}}_i\in {\mathbb{R}}^{D_K}$, and ${\mathbf{v}}_i\in {\mathbb{R}}^{D_K}$ are query, key, and value vectors, respectively; ${\mathbf{W}}_i^{(Q)}\in {\mathbb{R}}^{D_K\times D_F}$, ${\mathbf{W}}_i^{(K)}\in {\mathbb{R}}^{D_K\times D_F}$, and ${\mathbf{W}}_i^{(V)}\in {\mathbb{R}}^{D_K\times D_F}$ are weight matrices; and ${\mathbf{b}}_i^{(Q)}\in {\mathbb{R}}^{D_K\times N}$, ${\mathbf{b}}_i^{(K)}\in {\mathbb{R}}^{D_K\times N}$, and ${\mathbf{b}}_i^{(V)}\in {\mathbb{R}}^{D_K\times N}$ are bias vectors. Let $\mathbf{\alpha }\in {\mathbb{R}}^{N\times N}$ be a self-attention matrix consisting of the degrees of self-relevance of the extended latent features $\mathbf{Z}$, which is given by

$$\begin{array}{cc}\hfill e_{i,n,n^{\prime }}& =\frac{{\mathbf{q}}_{i,n}^{\top }{\mathbf{k}}_{i,n^{\prime }}}{\sqrt{D_K}},\hfill \end{array}$$

(7)

$$\begin{array}{cc}\hfill {\alpha }_{i,n,n^{\prime }}& =\frac{exp\left(e_{i,n,n^{\prime }}\right)}{{\sum }_{n^{\prime }=1}^{N}exp\left(e_{i,n,n^{\prime }}\right)},\hfill \end{array}$$

(8)

where ${}^{\top }$ represents the matrix or vector transpose, and n and $n^{\prime }$ represent the feature indices of $\mathbf{Q}$ and $\mathbf{K}$, respectively. Let $\mathbf{H}\triangleq [{\mathbf{H}}_1,\dots ,{\mathbf{H}}_I]\in {\mathbb{R}}^{D_F\times N}$ be a feature matrix obtained by concatenating all the heads, where ${\mathbf{H}}_i\triangleq {\mathbf{V}}_i{\mathbf{\alpha }}_i^{\top }\in {\mathbb{R}}^{D_K\times N}$.

The extended latent features and the extracted features $\mathbf{H}$ with Dropout ($p=0.1$) [60] are then fed into a feed forward network (FFN) with a rectified linear unit (ReLU) as follows:

$$\begin{array}{c}\hfill \mathbf{Z}\leftarrow {\mathbf{W}}_2^{(H)}max\left\{0,{\mathbf{W}}_1^{(H)}\left(\mathrm{Dropout}\left(\mathbf{H}\right)+\mathbf{Z}\right)+{\mathbf{b}}_1^{(H)}\right\}+{\mathbf{b}}_2^{(H)},\end{array}$$

(9)

where ${\mathbf{W}}_1^{(H)}\in {\mathbb{R}}^{D_{\mathrm{FFN}}\times D_F}$ and ${\mathbf{W}}_2^{(H)}\in {\mathbb{R}}^{D_F\times D_{\mathrm{FFN}}}$ are weight matrices, ${\mathbf{b}}_1^{(H)}\in {\mathbb{R}}^{D_{\mathrm{FFN}}\times N}$ and ${\mathbf{b}}_2^{(H)}\in {\mathbb{R}}^{D_F\times N}$ are bias vectors, and $D_{\mathrm{FFN}}$ is the dimension of the output. Equation (4) to Equation (9) are repeated L times with different parameters. The onset probabilities $\mathbf{\varphi }$ are finally calculated as follows:

$$\begin{array}{cc}\hfill \mathbf{\varphi }& =\sigma \left({\mathbf{W}}_3^{(H)}\mathbf{Z}+{\mathbf{b}}_3^{(H)}\right),\hfill \end{array}$$

(10)

where $\sigma (·)$ is a sigmoid function, ${\mathbf{W}}_3^{(H)}\in {\mathbb{R}}^{M\times D_F}$ is a weight matrix, and ${\mathbf{b}}_3^{(H)}\in {\mathbb{R}}^{M\times N}$ is a bias vector.

3.2. Language Models

The language model is used for estimating the generative probability (musical naturalness) of an arbitrary existing drum score $\tilde{\mathbf{Y}}$. For brevity, we assume that only one drum score is used as training data. In practice, a sufficient amount of drum scores are used. In this study, we use unidirectional language models such as the repetition-aware bi-gram model and GRU-based model proposed in [19] and a masked language model (MLM), a bidirectional language model proposed for pretraining in BERT [46] (Figure 4).

The unidirectional language model is trained beforehand in an unsupervised manner such that the following negative log-likelihood ${\mathcal{L}}_{\mathrm{lang}}^{\mathrm{uni}}(\tilde{\mathbf{Y}})$ is minimized:

$$\begin{array}{c}\hfill {\mathcal{L}}_{\mathrm{lang}}^{\mathrm{uni}}(\tilde{\mathbf{Y}})=-logp(\tilde{\mathbf{Y}})=-\sum _{n=1}^{N}logp({\tilde{Y}}_{:,n}|{\tilde{Y}}_{:,1:n-1}),\end{array}$$

(11)

where “$i:j$” represents a set of indices from i to j, and “:” represents all possible indices. In the repetition-aware bi-gram model (top figure in Figure 4), assuming that target musical pieces have the 4/4 time signature, the repetitive structure of a drum score is formulated as follows:

$$\begin{array}{c}\hfill p({\tilde{Y}}_{:,n}|{\tilde{Y}}_{:,1:n-1})=\prod _{m=1}^{M}p({\tilde{Y}}_{m,n}|{\tilde{Y}}_{m,n-16})=\prod _{m=1}^M{\pi }_{{\tilde{Y}}_{m,n-16},{\tilde{Y}}_{m,n}},\end{array}$$

(12)

where ${\pi }_{A,B}(A,B\in \{0,1\})$ represents the transition probability from A to B. Note that this model assumes the independence of the M drums. In the GRU model (middle figure in Figure 4), $p({\tilde{Y}}_{:,n}|{\tilde{Y}}_{:,1:n-1})$ is directly calculated using an RNN.

The MLM is capable of learning the global structure of drum scores (bottom figure in Figure 4). In the training phase, drum activations at randomly selected 15% of tatums in $\tilde{\mathbf{Y}}$ are masked and the MLM is trained such that those activations are predicted as accurately as possible. The loss function ${\mathcal{L}}_{\mathrm{lang}}^{\mathrm{bi}}(\tilde{\mathbf{Y}})$ to be minimized is given by

$$\begin{array}{cc}\hfill \widehat{p}({\tilde{\mathbf{Y}}}_n)& =p({\tilde{Y}}_{:,n}|{\tilde{Y}}_{:,1:n-1},{\tilde{Y}}_{:,n+1:N}),\hfill \end{array}$$

(13)

$${\mathcal{L}}_{\mathrm{lang}}^{\mathrm{bi}}(\tilde{\mathbf{Y}})=-\sum _{n=1}^{N}log\widehat{p}({\tilde{\mathbf{Y}}}_n).$$

(14)

3.3. Regularized Training

To consider the musical naturalness of the estimated score $\widehat{\mathbf{Y}}$ obtained by binarizing $\mathbf{\varphi }$, we use the language model-based regularized training method [19] that minimizes

$${\mathcal{L}}_{\mathrm{total}}={\mathcal{L}}_{\mathrm{tran}}(\mathbf{\varphi }|\mathbf{Y})+\gamma {\mathcal{L}}_{\mathrm{lang}}^{\ast }(\widehat{\mathbf{Y}}),$$

(15)

where $\widehat{\mathbf{Y}}$ is a ground-truth score, $\gamma >0$ is a weighting factor, the symbol * denotes “uni“ or “bi“, and ${\mathcal{L}}_{\mathrm{tran}}(\mathbf{\varphi }|\widehat{\mathbf{Y}})$ is the modified negative log-likelihood given by

$$\begin{array}{cc}\hfill {\mathcal{L}}_{\mathrm{tran}}(\mathbf{\varphi }|\mathbf{Y})& =-\sum _{m=1}^M\sum _{n=1}^N\left\{{\beta }_m{Y}_{m,n}log{\varphi }_{m,n}+(1-Y_{m,n})log(1-{\varphi }_{m,n})\right\},\hfill \end{array}$$

(16)

where ${\beta }_m>0$ is a weighting factor compensating for the imbalance between the numbers of onset and non-onset tatums.

To use backpropagation for optimizing the transcription model, the binary score $\mathbf{Y}$ should be obtained from the soft representation $\mathbf{\varphi }$ in a differentiable manner instead of simply binarizing $\mathbf{\varphi }$ with a threshold. We thus use a differentiable sampler called the Gumbel-sigmoid trick [61], as follows:

$$\begin{array}{cc}\hfill {\eta }_{m,n}^{(k)}& \sim \mathrm{Uniform}(0,1),\hfill \end{array}$$

(17)

$$\begin{array}{cc}\hfill {\psi }_{m,n}^{(k)}& =-log\left\{-log\left({\eta }_{m,n}^{(k)}\right)\right\},\hfill \end{array}$$

(18)

$$\begin{array}{cc}\hfill {\widehat{Y}}_{m,n}& =\sigma \left\{\frac{{\varphi }_{m,n}+{\psi }_{m,n}^{(1)}-{\psi }_{m,n}^{(2)}}{\tau }\right\},\hfill \end{array}$$

(19)

where $k=1,2,$ and $\tau >0$ is a temperature ($\tau$ = 0.2 in this paper). Note that the pretrained language model is used as a fixed regularizer in the training phase and is not used in the prediction phase.

4. Evaluation

This section reports the comparative experiments conducted for evaluating the proposed ADT method and investigates the effectiveness of the self-attention mechanism and that of the MLM-based regularized training.

4.1. Evaluation Data

We used the Slakh2100-split2 (Slakh) [62] and the RWC Popular Music Database (RWC) [63] for evaluation because these datasets include ground-truth beat times. The Slakh dataset contains 2100 musical pieces in which the audio signals were synthesized from the Lakh MIDI dataset [64] using professional-grade virtual instruments, and the RWC dataset contains 100 Japanese popular songs. All music signals were sampled at 44.1 kHz. The onset times of BD, SD, and HH ($M=3$) were extracted as ground-truth data from the synchronized MIDI files provided for these datasets. To make ground-truth drum scores, each onset time was quantized to the closest tatum time (the justification of this approach is discussed in Section 4.4). Only musical pieces in which the drum onset times and tatum times had been annotated correctly as ground-truth data were used for evaluation. For the Slakh dataset, we used 2010 pieces, which were split into 1449, 358, and 203 pieces as training, validation, and test data, respectively. For the RWC dataset, we used 65 songs for 10-fold cross validation, where 15% of training data was used as validation data in each fold. Since here we aim to validate the effectiveness of the language model-based regularized training for self-attention-based transcription models on the same dataset (Slakh or RWC), investigation of the cross-corpus generalization capability (portability) of language models is beyond the scope of the paper and left as future work.

For each music signal, a drum signal was separated with Spleeter [5] and the tatum times were estimated with madmom [2] or given as oracle data. The spectrogram of a music or drum signal was obtained using short-time Fourier transform (STFT) with a Hann window of 2048 points (46 ms) and a shifting interval of 441 points (10 ms). We used mel-spectrograms as input features because they have successfully been used for onset detection [11] and CNN-based ADT [14]. The mel-spectrogram was computed using a mel-filter bank with 80 bands from 20 Hz to 20,000 Hz and normalized so that the maximum volume was 0 db. A stack of music and drum mel-spectrograms was fed into a transcription model.

4.2. Model Configurations

The configurations of the two transcription models (CNN-BiGRU and CNN-SelfAtt(-SyncPE) described in Section 3.1) are shown in Figure 5 and

Table 1. Hyperparameters of the decoders of the two transcription models optimized by Optuna.

	BiGRU			SelfAtt
	Layer	Dim	Size	h	l	${\mathit{D}}_{\mathit{F}}$	${\mathit{D}}_{\mathbf{FFN}}$	Size
Slakh	1	131	573 k	2	8	96	384	1.03 M
RWC	3	98	774 k	8	7	120	480	1.38 M

. The encoders were the same CNN consisting of four convolutional layers with a kernel size of $3\times 3$, and the decoders were based on the BiGRU and the multi-head self-attention mechanism. The influential hyperparameters were automatically determined with a Bayesian optimizer called Optuna [65] for the validation data in the Slakh dataset or with 10-fold cross validation in the RWC dataset under a condition that $D_{\mathrm{FFN}}=4D_{\mathrm{F}}$. As a result, CNN-SelfAtt had about twice as many parameters as CNN-BiGRU. In the training phase, the batch size was set to 10, and the max length was set to 256 for CNN-SelfAtt. We used the AdamW optimizer [66] with an initial learning rate of ${10}^{-3}$. The learning rate of CNN-SelfAtt was changed according to [26], and $warmup\_steps$ was set to 4000. To prevent over-fitting, we used weight regularization ($\lambda ={10}^{-4}$), drop-out just before all of the fully connected layers of CNN-BiGRU ($p=0.2$) and each layer of CNN-SelfAtt ($p=0.1$), and tatum-level SpecAugment [67] for the RWC dataset, where 15% of all tatums were masked in the training phase. The weights of the convolutional and BiGRU layers were initialized based on [68], the fully connected layer was initialized by the sampling from $\mathrm{Uniform}(0,1)$, and the biases were initialized to 0. In the testing phase, the average of the ten parameters before and after the epoch that achieved the smallest loss for the validation data was used in CNN-SelfAtt. The threshold for $\mathbf{\varphi }$ was set to $\delta =0.2$.

The configurations of the three language models (bi-gram, GRU, and MLM(-SyncPE) described in Section 3.2) are shown in

Table 2. Hyperparameters of the three language models optimized by Optuna.

Bi-Gram	GRU			MLM-SyncPE
Size	Layer	Dim	Size	h	l	${\mathit{D}}_{\mathit{F}}$	${\mathit{D}}_{\mathbf{FFN}}$	Size
2	3	64	63 k	4	8	112	448	1.25 M

. Each model was trained with 512 external drum scores of Japanese popular songs and Beatles songs. To investigate the impact of the data size for predictive performance, each model was also trained by using only randomly selected 51 scores. The influential hyperparameters of the neural language models, i.e., the number of layers and the dimension of hidden states in the GRU model and h, l, $D_{\mathrm{F}}$, and $D_{\mathrm{FFN}}$ in the MLM, were automatically determined with Optuna [65] via three-fold cross validation with the 512 scores under a condition that $D_{\mathrm{FFN}}=4D_{\mathrm{F}}$. As a result, the MLM had about twice as many parameters as the GRU model. The bi-gram model was defined by only two parameters ${\pi }_{0,1}$ and ${\pi }_{1,1}$.

4.3. Evaluation Metrics

The performance of ADT was evaluated at the frame and tatum levels. The frame-level F-measure ($\mathcal{F}$) is the harmonic mean of the precision rate $\mathcal{P}$ and the recall rate $\mathcal{R}$:

$$\begin{array}{c}\hfill \mathcal{P}=\frac{N_{\mathrm{C}}}{N_{\mathrm{E}}},\mathcal{R}=\frac{N_{\mathrm{C}}}{N_{\mathrm{G}}},\mathcal{F}=\frac{2\mathcal{R}\mathcal{P}}{\mathcal{R}+\mathcal{P}},\end{array}$$

(20)

where $N_{\mathrm{E}}$, $N_{\mathrm{G}}$, and $N_{\mathrm{C}}$ are the number of estimated onset times, that of ground-truth onset times, and that of correctly-estimated onset times, respectively, and the error tolerance was set to 50 ms. Note that $\mathcal{F}=100\%$ means perfect transcription. For the tatum-level evaluation, we propose a tatum-level error rate (TER) based on the Levenshtein distance. Note that all the estimated drum scores were concatenated and then the frame-level F-measure and TER were computed for the whole dataset. As shown in Figure 6, the TER between a ground-truth score $\mathbf{Y}\triangleq {\mathbf{Y}}_{1:N}\in {\{0,1\}}^{M\times N}$ with N tatums and an estimated score $\widehat{\mathbf{Y}}\triangleq {\widehat{\mathbf{Y}}}_{1:\widehat{N}}\in {\{0,1\}}^{M\times \widehat{N}}$ with $\widehat{N}$ tatums, denoted by $\mathrm{TER}({\mathbf{Y}}_{1:N},{\widehat{\mathbf{Y}}}_{1:\widehat{N}})$, is computed via dynamic programming as follows:

$$\begin{array}{cc}\hfill \mathrm{TER}({\mathbf{Y}}_{1:n+1},{\widehat{\mathbf{Y}}}_{1:\widehat{n}+1})& =\left\{\begin{array}{cc}max(n,\widehat{n})\times M\hfill & (n=0\mathrm{or}\widehat{n}=0),\hfill \\ min\left\{\begin{array}{c}\mathrm{TER}({\mathbf{Y}}_{1:n},{\widehat{\mathbf{Y}}}_{1:\widehat{n}+1})+M\hfill \\ \mathrm{TER}({\mathbf{Y}}_{1:n+1},{\widehat{\mathbf{Y}}}_{1:\widehat{n}})+M\hfill \\ \mathrm{TER}({\mathbf{Y}}_{1:n},{\widehat{\mathbf{Y}}}_{1:\widehat{n}})+S({\mathbf{Y}}_n,{\widehat{\mathbf{Y}}}_{\widehat{n}})\hfill \end{array}\right.\hfill & (\mathrm{otherwise}),\hfill \end{array}\right.\hfill \end{array}$$

(21)

$$\begin{array}{cc}\hfill S({\mathbf{Y}}_n,{\widehat{\mathbf{Y}}}_{\widehat{n}})& =\sum _{m=1}^M|Y_{m,n}-{\widehat{Y}}_{m,\widehat{n}}|,\hfill \end{array}$$

(22)

where $S({\mathbf{Y}}_n,{\widehat{\mathbf{Y}}}_{\widehat{n}})$ represents the sum of the Manhattan distances between the ground-truth activations ${\mathbf{Y}}_n$ at tatum n and the estimated activations ${\widehat{\mathbf{Y}}}_{\widehat{n}}$ at tatum $\widehat{n}$. Note that $\widehat{N}$ might be different from N when the tatum times were estimated with madmom and that $\mathrm{TER}({\mathbf{Y}}_{1:N},{\widehat{\mathbf{Y}}}_{1:\widehat{N}})=0$ does not mean perfect transcription as discussed in Section 4.4. The comprehensive note-level evaluation measures were proposed for AMT [55,56] but were not used in our experiment because ADT focuses on only the onset times of note events.

4.4. Justification of Tatum-Level Drum Transcription

We validated the appropriateness of tatum-level ADT because some kinds of actual onset times cannot be detected in principle under an assumption that the onset times of each drum are exclusively located on the sixteenth-note-level grid. As shown in Figure 7, such undetectable onsets are (doubly) categorized into two groups. If multiple onset times are close to the same tatum time, only one onset time can be detected, i.e., the other onset times are undetectable and categorized into the conflict group. Onset times that are not within 50 ms from the closest tatum times are categorized into the far group. In the tatum-level ADT, the onset times of these groups remain undetected even when $\mathrm{TER}({\mathbf{Y}}_{1:N},{\widehat{\mathbf{Y}}}_{1:\widehat{N}})=0$.

Table 3. Ratio of undetectable onset times.

Dataset	Madmom			Ground-Truth
	conflict	far	conflict ∪ far	conflict	far	conflict ∪ far
Slakh	0.86%	0.16%	1.02%	1.30%	0.35%	1.64%
RWC	0.43%	0.23%	0.65%	1.19%	0.29%	1.48%

shows the ratio of undetectable onset times in each group to the total number of actual onset times when the estimated or ground-truth beat times were used for quantization. The total ratio of undetectable onset times was sufficiently low. This justifies the sixteenth-note-level quantization of onset times, at least for the majority of typical popular songs used in our experiment. Note that our model cannot deal with triplet notes.

Since the tatum times are assumed to be given, we evaluated the beat tracking performance of madmom [2] in the same way as Equation (20). The mir_eval library was used for computing $\mathcal{P}$, $\mathcal{R}$, and $\mathcal{F}$. The F-measure for the 203 pieces of the test data in the Slakh dataset was 92.5% and that for the 65 songs in the RWC dataset was 96.4%.

4.5. Evaluation of Language Modeling

We evaluated the three language models (bi-gram, GRU, and MLM(-SyncPE) described in Section 3.2) in terms of the perplexities for the 203 pieces in the Slakh dataset and the 65 songs in the RWC dataset. The perplexity for a drum score $\tilde{\mathbf{Y}}$ is defined as follows:

$$\begin{array}{cc}\hfill {\mathrm{PPL}}^{\ast }(\tilde{\mathbf{Y}})& =2^{\frac{1}{N}{\mathcal{L}}_{\mathrm{lang}}^{\ast }(\tilde{\mathbf{Y}})},\hfill \end{array}$$

(23)

where “*” denotes “uni” or “bi” and ${\mathcal{L}}_{\mathrm{lang}}^{\mathrm{uni}}(\tilde{\mathbf{Y}})$ and ${\mathcal{L}}_{\mathrm{lang}}^{\mathrm{bi}}(\tilde{\mathbf{Y}})$ are given by Equations (11) and (13), respectively. Since ${\mathcal{L}}_{\mathrm{lang}}^{\mathrm{bi}}(\tilde{\mathbf{Y}})$ based on the MLM does not exactly give the likelihood for $\tilde{\mathbf{Y}}$ because of the bidirectional nature, unlike ${\mathcal{L}}_{\mathrm{lang}}^{\mathrm{uni}}(\tilde{\mathbf{Y}})$ based on the bi-gram or GRU model with the autoregressive nature, ${\mathrm{PPL}}^{\mathrm{bi}}(\tilde{\mathbf{Y}})$ can be only roughly compared with ${\mathrm{PPL}}^{\mathrm{uni}}(\tilde{\mathbf{Y}})$.

As shown in

Table 4. Perplexities obtained by the language models. “MLM” and “MLM-SyncPE” are MLMs with the conventional and proposed tatum-synchronous positional encodings, respectively.

Language Model	Bi-Gram		GRU		MLM		MLM-SyncPE
Dataset Size	51	512	51	512	51	512	51	512
Slakh	1.278	1.265	1.357	1.170	1.180	1.050	1.124	1.049
RWC	1.374	1.369	1.473	1.273	1.289	1.086	1.217	1.085

, the predictive capability of the GRU model was significantly better than that of the bi-gram model based on the strong assumption that drum patterns are repeated with the 4/4 time signature. The MLM using the proposed positional encodings, denoted by MLM-SyncPE, slightly outperformed the MLM using the conventional encodings. The larger the training dataset, the lower (better) the perplexity. The pseudo-perplexity obtained by the MLM was close to 1, meaning that the activations at masked tatums can be predicted accurately from the forward and backward contexts.

4.6. Evaluation of Drum Transcription

We evaluated the two transcription models (CNN-BiGRU and CNN-SelfAtt-SyncPE described in Section 3.1) that were trained with and without the regularization mechanism based on each of the three language models (bi-gram, GRU, and MLM-SyncPE described in Section 3.2). For comparison, we tested the conventional frame-level ADT method based on a CNN-BiGRU model [18] that had the same architecture as our tatum-level CNN-BiGRU model (Figure 5) except that the max-pooling layers were not used. It was trained such that the following frame-level cross entropy was minimized:

$$\begin{array}{cc}\hfill {\mathcal{L}}_{{\mathrm{tran}}^{★}}({\mathbf{\varphi }}^{★}|{\mathbf{Y}}^{★})& =-\sum _{m=1}^M\sum _{t=1}^T\left({\beta }_m^{★}{Y}_{m,t}^{★}log{\varphi }_{m,t}^{★}+(1-Y_{m,t}^{★})log(1-{\varphi }_{m,t}^{★})\right),\hfill \end{array}$$

(24)

where ${\mathbf{\varphi }}^{★},{\mathbf{Y}}^{★}\in {\mathbb{R}}^{M\times T}$ are the estimated onset probabilities and the ground-truth binary activations, respectively, and ${\beta }^{★}>0$ is a weighting factor. For each drum m, a frame t was picked as an onset if

• ${\varphi }_{m,t}^{★}=max\left\{{\varphi }_{m,t-w_1:t+w_2}^{★}\right\}$,
• ${\varphi }_{m,t}^{★}\ge \mathrm{mean}\left\{{\varphi }_{m,t-w_3:t+w_4}^{★}\right\}+\widehat{\delta }$,
• $t-t_{\mathrm{prev}}>w_5$,

where $\widehat{\delta }$ was a threshold, $w_{1:5}$ were interval parameters, and $t_{\mathrm{prev}}$ was the previous onset frame. These were set to $\widehat{\delta }=0.2$, $w_1=w_3=w_5=2$, and $w_2=w_4=0$, as in [18]. The weighting factors $\beta$, $\gamma$, and ${\beta }^{★}$ were optimized for the validation data in the Slakh dataset and by 10-fold cross validation in the RWC dataset, as shown in

Table 5. Weighting factors optimized by Optuna. $m=0$, 1, and 2 represent BD, SD, and HH, respectively.

	CNN-BiGRU									CNN-SelfAtt
	${\mathbf{\beta }}_{\mathbf{0}}^{★}$	${\mathbf{\beta }}_{\mathbf{1}}^{★}$	${\mathbf{\beta }}_{\mathbf{2}}^{★}$	${\mathbf{\beta }}_{\mathbf{0}}$	${\mathbf{\beta }}_{\mathbf{1}}$	${\mathbf{\beta }}_{\mathbf{2}}$	Bi-Gram	GRU	MLM	${\mathbf{\beta }}_{\mathbf{0}}$	${\mathbf{\beta }}_{\mathbf{1}}$	${\mathbf{\beta }}_{\mathbf{2}}$	Bi-Gram	GRU	MLM
							$\mathbf{\gamma }$						$\mathbf{\gamma }$
Slakh	0.67	2.00	1.77	1.07	0.19	0.40	0.10	0.05	0.01	0.62	0.92	0.90	1.02	0.07	1.25
RWC	6.22	8.09	6.48	0.50	0.32	0.71	0.05	0.04	0.26	0.69	0.92	0.55	1.10	0.05	1.31

. To measure the tatum-level transcription performance, the estimated frame-level onset times were quantized at the tatum level with reference to the estimated or ground-truth tatum times.

As shown in

Table 6. Training times per song (s/song), F-measures (%), and TERs obtained by the conventional and proposed methods.

	Decoder		Time	Madmom					Ground-Truth
	+ Language Model			BD	SD	HH	Total	TER	BD	SD	HH	Total	TER
Slakh	BiGRU [18]		55.8	93.6	92.7	71.5	85.9	20.6	93.0	92.5	71.4	85.6	8.4
	BiGRU		15.3	95.6	90.2	75.5	87.1	19.6	95.2	90.2	75.8	87.1	7.2
	+ MLM-SyncPE	(512)	137.0	95.3	90.7	78.4	88.1	19.0	94.7	90.9	77.6	87.8	7.1
	SelfAtt-SyncPE		26.7	95.8	93.1	79.9	89.6	18.7	95.6	92.9	79.5	89.3	6.8
	+ Bi-gram	(512)	15.6	95.8	92.7	80.5	89.7	18.5	95.4	93.1	80.5	89.7	6.3
	+ GRU	(512)	15.7	96.4	93.0	80.5	90.0	18.5	96.1	92.9	80.4	89.8	6.4
	+ MLM-SyncPE	(512)	42.0	96.1	93.2	80.7	90.0	18.5	95.8	93.3	80.9	90.0	6.3
RWC	BiGRU [18]		58.2	86.0	74.0	70.5	76.8	16.7	86.6	74.1	70.9	77.2	12.3
	BiGRU		24.5	86.9	76.2	77.9	80.3	15.2	86.7	76.5	76.9	80.0	11.4
	+ MLM-SyncPE	(512)	130.1	88.0	76.5	79.7	81.4	14.0	88.1	76.5	79.3	81.3	10.3
	SelfAtt-SyncPE		30.5	87.5	76.4	72.6	78.8	17.0	88.0	75.6	72.9	78.8	13.2
	+ Bi-gram	(512)	31.8	86.0	76.5	69.6	77.4	16.8	87.0	76.0	69.6	77.5	12.7
	+ GRU	(512)	24.1	87.6	76.2	73.2	79.0	16.6	87.8	76.3	73.9	79.4	12.5
	+ MLM-SyncPE	(512)	51.6	88.1	74.9	75.4	79.5	16.2	87.9	74.3	71.7	78.0	12.4

, CNN-SelfAtt-SyncPE worked best for the Slakh dataset and CNN-BiGRU with the MLM-SyncPE-based regularization worked best for the RWC dataset in terms of the F-measure and TER. This suggests that a sufficient amount of paired data are required to draw the full potential of the self-attention mechanism. CNN-SelfAtt-SyncPE tended to yield higher or comparable F-measures for BD and SD in the RWC dataset and lower F-measures for HH in both the datasets. This was because percussive sounds in the high-frequency range were not cleanly separated by the Spleeter even with some noises, or SelfAtt-based model had a tendency to detect other instruments similar to HH such as Maracas. The MLM-SyncPE-based regularization made a little improvement for the Slakh dataset because even the non-regularized model worked well on the synthesized dataset with the limited acoustic and timbral variety. In contrast, it significantly outperformed the bi-gram- or GRU-based regularization for the RWC dataset but required much longer training time because every iteration costs $O(C\times N)$, where C represents the batch size. Note that, if enough memory is available, the MLM-based regularization can be calculated in a parallel manner by $O(1)$. CNN-BiGRU with the MLM-based regularization required the longest training time in spite of the highest performance. The frame-level CNN-BiGRU model [18] required much longer training time than our frame-to-tatum model.

4.7. Investigation of Self-Attention Mechanism

We further investigated the behaviors of the self-attention mechanisms used in the transcription and language models. To validate the effectiveness of the proposed tatum-synchronous positional encodings (SyncPE), we compared two versions of the proposed transcription model, denoted by CNN-SelfAtt and CNN-SelfAtt-SyncPE, in terms of the F-measure and TER. As shown in

Table 7. F-measures (%) and TERs obtained by CNN-SelfAtt with the conventional positional encodings and CNN-SelfAtt-SyncPE with the proposed tatum-synchronous positional encodings.

	Decoder		Madmom					Ground-Truth
			BD	SD	HH	Total	TER	BD	SD	HH	Total	TER
Slakh	SelfAtt		96.0	93.1	75.4	88.2	20.0	95.7	92.7	75.7	88.0	7.7
	SelfAtt-SyncPE		95.8	93.1	79.9	89.6	18.7	95.6	92.9	79.5	89.3	6.8
RWC	SelfAtt		87.5	72.0	68.8	76.1	19.2	87.5	72.2	69.1	76.3	15.5
	SelfAtt-SyncPE		87.5	76.4	72.6	78.8	17.0	88.0	75.6	72.9	78.8	13.2

, CNN-SelfAtt-SyncPE always outperformed CNN-SelfAtt by a large margin. To investigate the impact of the data size used for training the transcription models (CNN-BiGRU and CNN-SelfAtt-SyncPE), we compared the performances obtained by using 1/32, 1/16, 1/4, 1/2, and all of the training data in the Slakh or RWC datasets. As shown in Figure 8, CNN-SelfAtt-SyncPE was severely affected by the data size and CNN-BiGRU worked better than CNN-SelfAtt when only a small amount of paired data were available. To investigate the impact of the data size used for training the language models (bi-gram, GRU, and MLM-SyncPE), we compared the performances obtained by CNN-SelfAtt-SyncPE that was regularized with a language model pretrained with 512 or 51 external drum scores. As shown in

Table 8. F-measures (%) and TERs obtained by CNN-SelfAtt-SyncPE regularized by the language models pretrained from 51 or 512 external drum scores.

	Decoder		Madmom					Ground-Truth
	+ Language Model		BD	SD	HH	Total	TER	BD	SD	HH	Total	TER
Slakh	SelfAtt-SyncPE		95.8	93.1	79.9	89.6	18.7	95.6	92.9	79.5	89.3	6.8
	+ Bi-gram	(51)	95.1	93.0	80.5	89.5	18.6	94.9	93.1	80.6	89.5	6.5
	+ GRU	(51)	96.3	92.1	80.0	89.5	18.6	96.1	92.1	79.9	89.3	6.4
	+ MLM-SyncPE	(51)	95.8	93.5	79.9	89.7	19.0	95.8	93.7	79.8	89.8	7.0
	+ Bi-gram	(512)	95.8	92.7	80.5	89.7	18.5	95.4	93.1	80.5	89.7	6.3
	+ GRU	(512)	96.4	93.0	80.5	90.0	18.5	96.1	92.9	80.4	89.8	6.4
	+ MLM-SyncPE	(512)	96.1	93.2	80.7	90.0	18.5	95.8	93.3	80.9	90.0	6.3
RWC	SelfAtt-SyncPE		87.5	76.4	72.6	78.8	17.0	88.0	75.6	72.9	78.8	13.2
	+ Bi-gram	(51)	86.1	76.5	66.8	76.5	17.1	85.7	76.6	67.4	76.6	13.1
	+ GRU	(51)	85.6	73.3	70.2	76.4	19.6	86.7	72.9	71.3	76.9	15.7
	+ MLM-SyncPE	(51)	86.8	75.7	71.5	78.0	17.5	86.9	75.2	72.2	78.1	13.6
	+ Bi-gram	(512)	86.0	76.5	69.6	77.4	16.8	87.0	76.0	69.6	77.5	12.7
	+ GRU	(512)	87.6	76.2	73.2	79.0	16.6	87.8	76.3	73.9	79.4	12.5
	+ MLM-SyncPE	(512)	88.1	74.9	75.4	79.5	16.2	87.9	74.3	71.7	78.0	12.4

, the pretrained language models with a larger number of drum scores achieved higher performances. The effect of the MLM-SyncPE-based regularization severely depends on the data size, whereas the bi-gram model was scarcely affected by the data size.

We confirmed that CNN-SelfAtt-SyncPE with the MLM-SyncPE-based regularization learned the global structures of drum scores through attention matrices and yielded globally coherent drum scores. Figure 9 shows examples of attention matrices. In Slakh-Track01930, both the global structure of drums and the repetitive structure of BD were learned successfully. In RWC-MDB-P-2001 No. 25, the repetitive structures of SD and HH were captured. These examples demonstrate that the attention matrices at each layer and head can capture the different structural characteristics of drums. Figure 10 shows examples of estimated drum scores. In RWC-MDB-P-2001 No. 25, the MLM-SyncPE-based regularization improved ${\mathrm{PPL}}^{\mathrm{bi}}$ (musical unnaturalness) and encouraged CNN-SelfAtt-SyncPE to learn the repetitive structures of BD, SD, and HH. In RWC-MDB-P-2001 No. 40, in contrast, although the MLM-SyncPE-based regularization also improved ${\mathrm{PPL}}^{\mathrm{bi}}$, it yielded an oversimplified score of HH.

5. Conclusions

In this paper, we described a global structure-aware frame-to-tatum ADT method based on self-attention mechanisms. The transcription model consists of a frame-level convolutional encoder for extracting the latent features of music signals and a tatum-level self-attention-based decoder for considering musically meaningful global structure and is trained in a regularized manner based on an pretrained MLM. Experimental results showed that the proposed regularized model outperformed the conventional RNN-based model in terms of the tatum-level error rate and the frame-level F-measure, even when only a limited amount of paired data were available so that the non-regularized model underperformed the RNN-based model. The attention matrices revealed that the self-attention-based model could learn the global and repetitive structure of drums at each layer and head. In future work, we plan to deal with more sophisticated and/or non-regular drum patterns (e.g., fill-ins) played using various kinds of percussive instruments (e.g., cymbals and toms). Considering that beat and downbeat times are closely related to drum patterns, it would be beneficial to integrate beat tracking into ADT in a multi-task learning framework.