Investigating the Benefits of Vector-Based GNSS Receivers for Autonomous Vehicles under Challenging Navigation Environments
Abstract
1. Introduction
2. Literature Review
3. GPS Software-Defined Receiver
4. Receiver Implementation Approaches
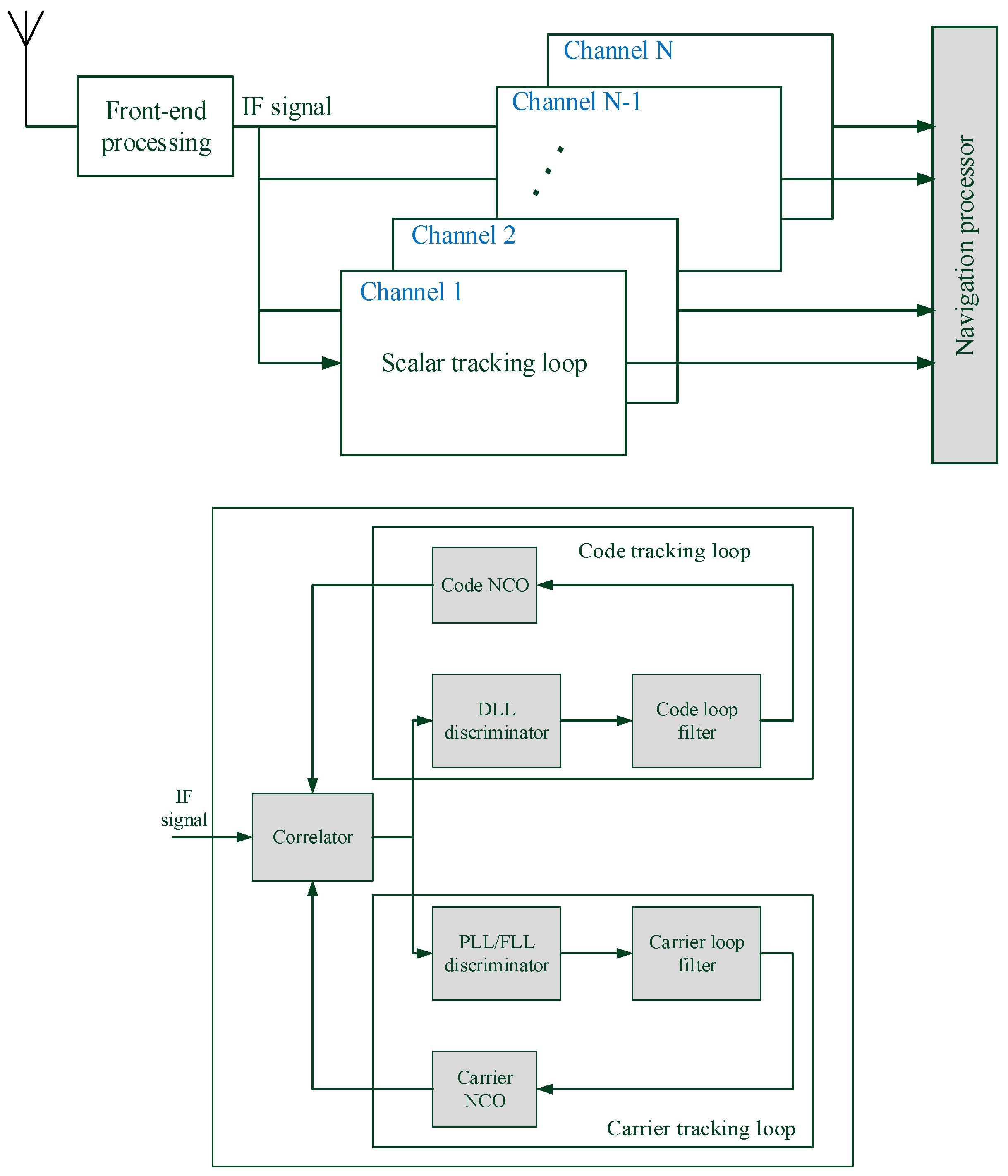
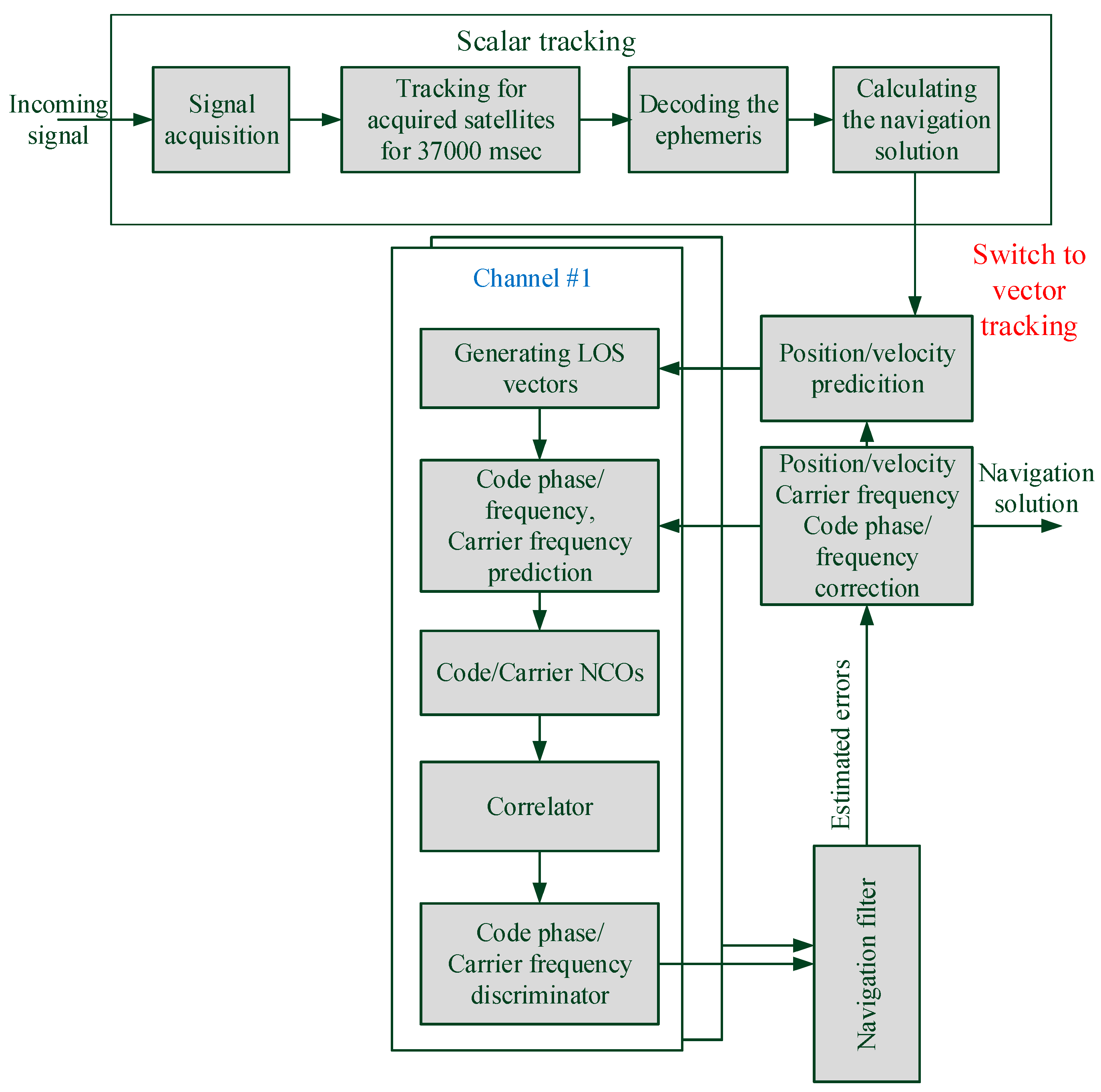
4.1. Scalar Tracking Receiver
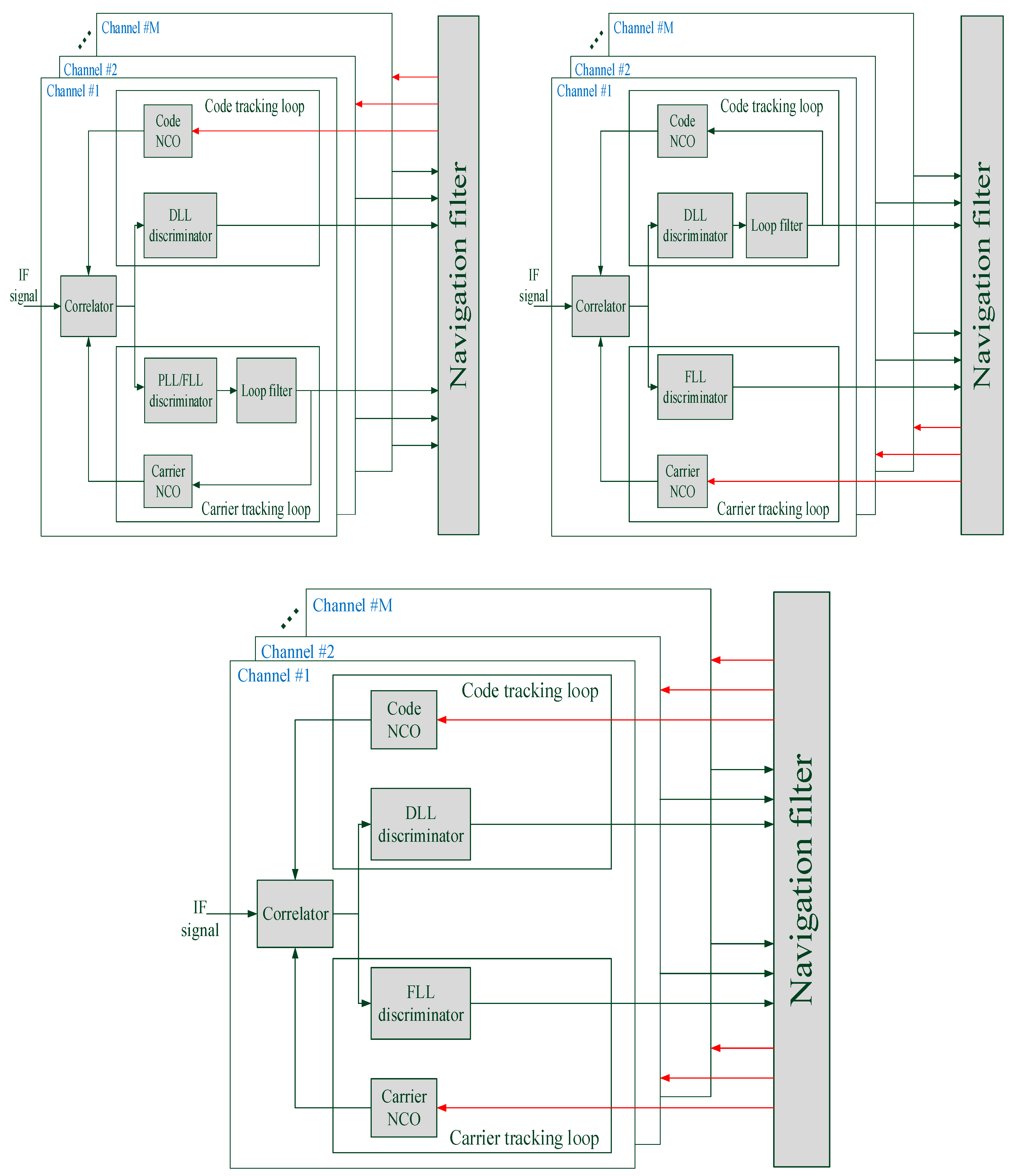
4.2. Vector Tracking Receiver
- Improved tracking performance, as the positioning solution is assisting the tracking,
- Robustness to disturbances such as multipath, high dynamics and degradation in signal strength,
- Some immunity to jamming,
- Bridging momentary outages of one or more satellites.
5. Vector Tracking Loop Architectures
Vector Tracking Module
6. Hardware Experimental Setup
7. Data Collection and Scenario Details
7.1. Static Scenario
- Time of simulation: 2 September 2018 at 12:00:00 p.m.
- Location: Washington Dullus Airport, VA, the United States at 38°57′11.6″ N latitude and 77°27′23.4″ W longitude.
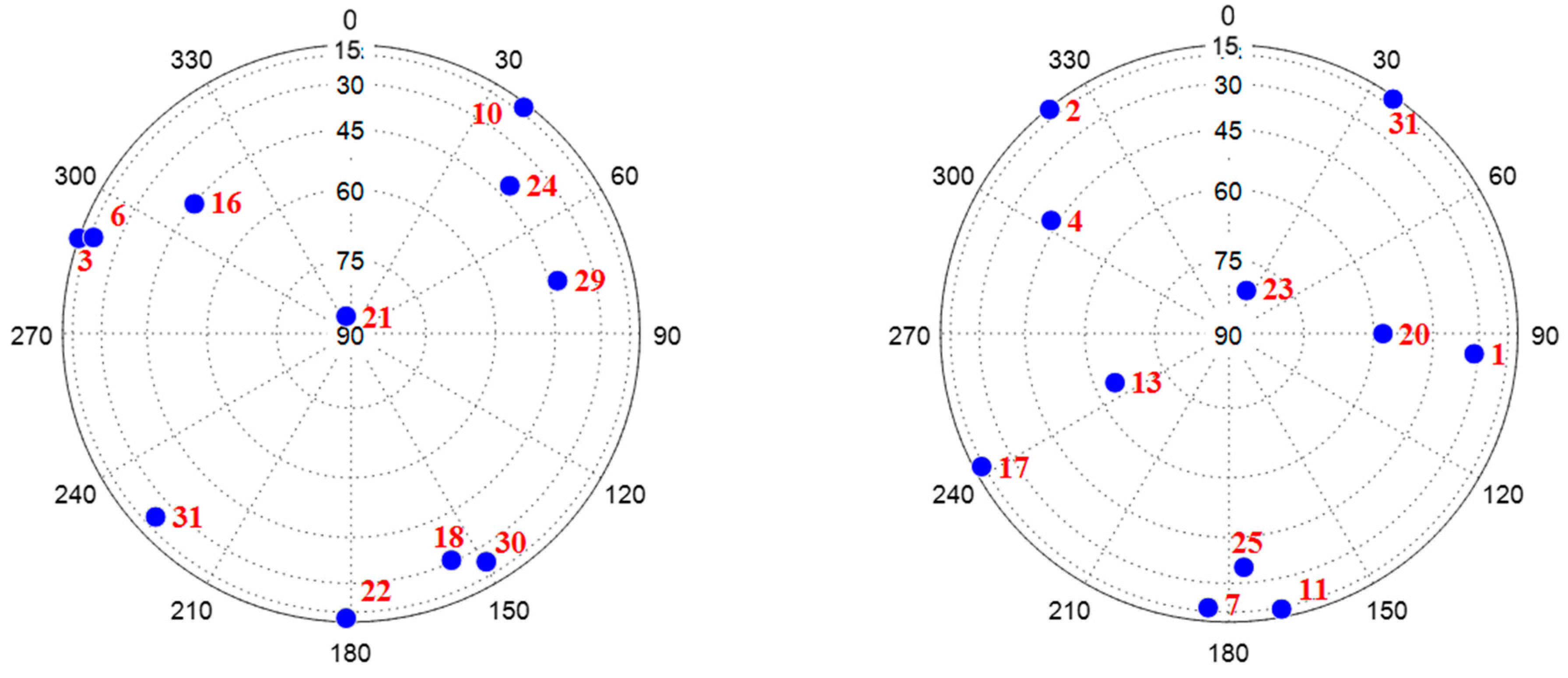
- The number of visible GPS satellites: 11, as shown in Figure 6.
7.2. Dynamic Scenario
- Time of simulation: 16 January 2019 at 12:00:00 p.m.
- Location: Downtown Toronto, ON, Canada with a starting point at 43°39′6.63″ N latitude and 79°22′54.17″ W longitude.
- The number of visible GPS satellites: 11, as shown in Figure 6.
- Duration: 4 min.
- Platform: Land vehicle.
8. Results and Discussion
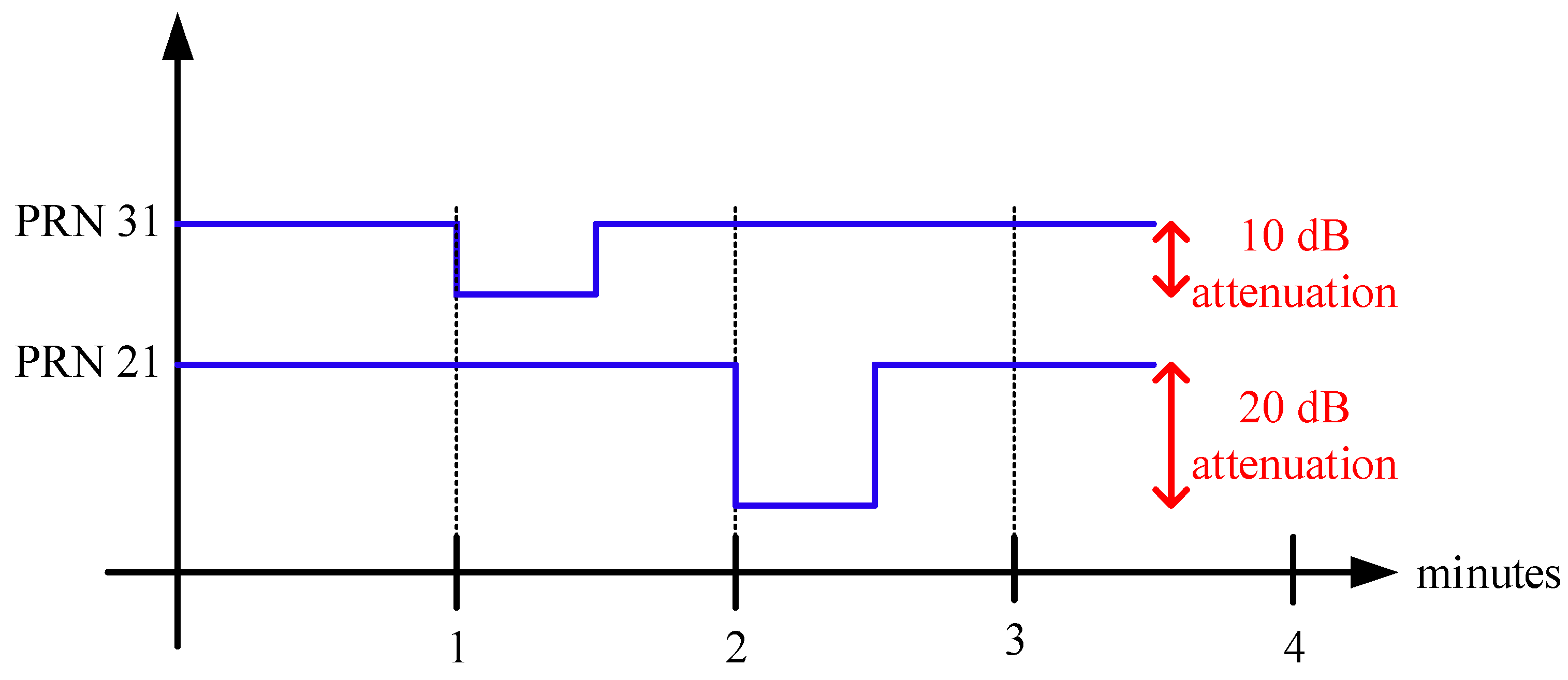
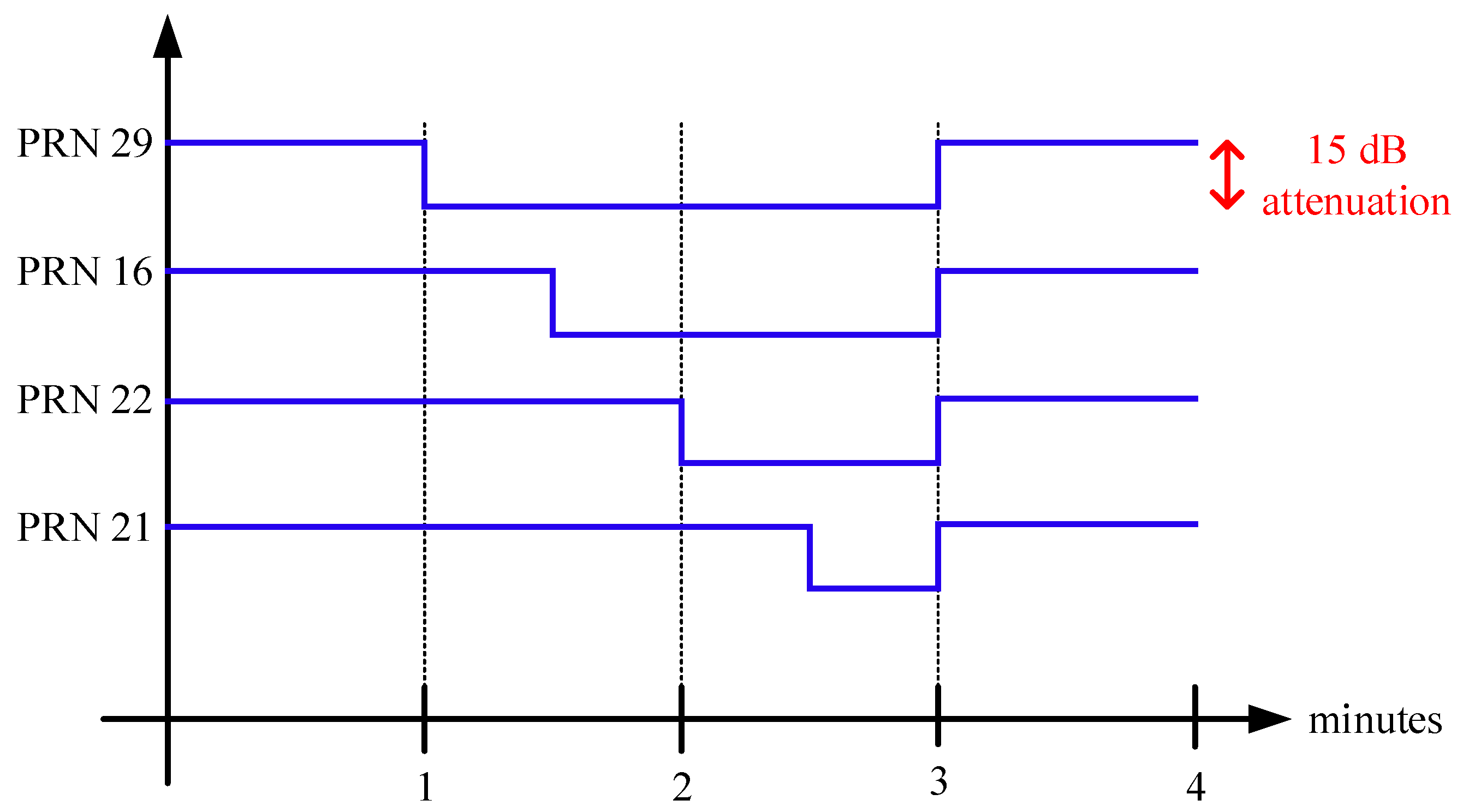
8.1. Static Scenario #1
8.2. Static Scenario #2
8.3. Static Scenario #3
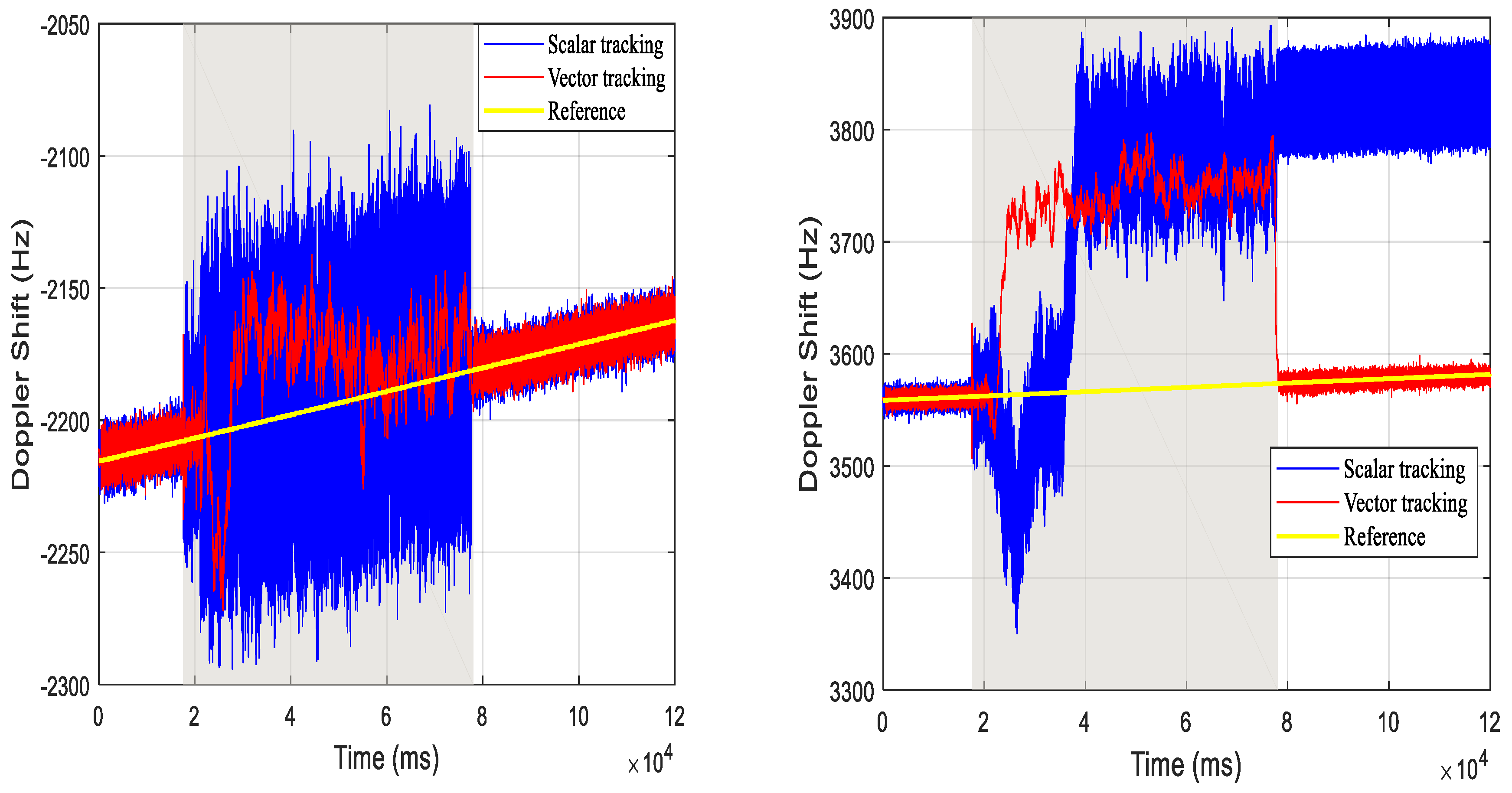
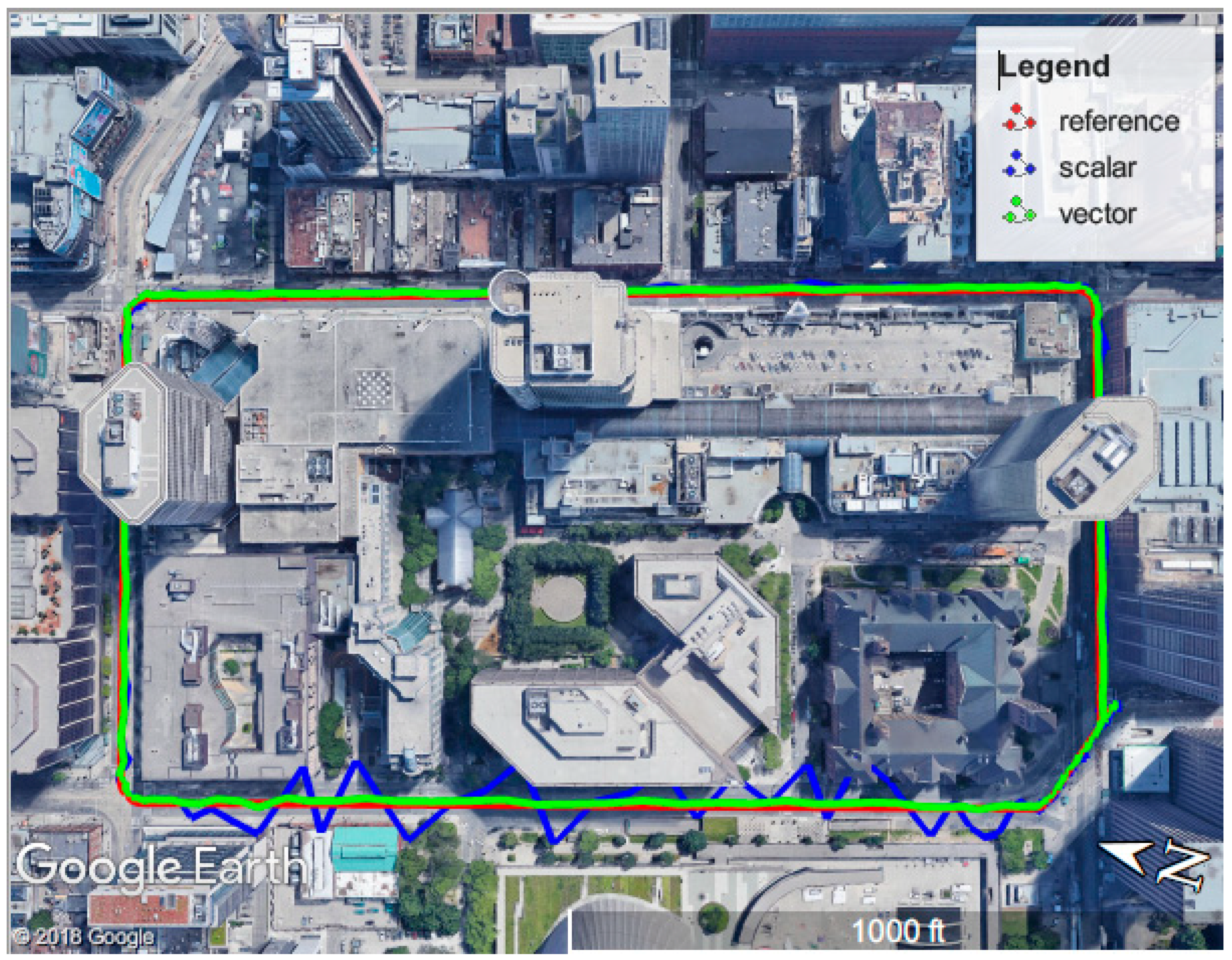
8.4. Dynamic Scenario
9. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Marcus, M. Growing consumer interest in jamming: Spectrum policy implications [Spectrum Policy and Regulatory Issues]. IEEE Wirel. Commun. 2014, 21, 4. [Google Scholar] [CrossRef]
- Elghamrawy, H.; Karaim, M.; Tamazin, M.; Noureldin, A. Experimental Evaluation of the Impact of Different Types of Jamming Signals on Commercial GNSS Receivers. Appl. Sci. 2020, 10, 4240. [Google Scholar] [CrossRef]
- Kuusniemi, H.; Airos, E.; Bhuiyan, M.Z.H.; Kroger, T. GNSS jammers: How vulnerable are consumer grade satellite navigation receivers? Eur. J. Navig. 2012, 10, 14–21. [Google Scholar]
- Tamazin, M. High Resolution Signal Processing Techniques for Enhancing GPS Receiver Performance; Queen’s University: Kingston, ON, Canada, 2015. [Google Scholar]
- Hsu, L.T. Integration of vector tracking loop and multipath mitigation technique and its assessment. In Proceedings of the 26th International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS+ 2013), Nashville, TN, USA, 16–20 September 2013; pp. 3263–3278. [Google Scholar]
- Hsu, L.T.; Groves, P.; Jan, S.S. Assessment of the multipath mitigation effect of vector tracking in an urban environment. In Proceedings of the ION 2013 Pacific PNT Meeting, Honolulu, HI, USA, 23–25 April 2013; pp. 498–509. [Google Scholar]
- Kim, K.-H.; Jee, G.-I.; Im, S.-H. Adaptive vector-tracking loop for low-quality GPS signals. Int. J. Control Autom. Syst. 2011, 9, 709–715. [Google Scholar] [CrossRef]
- Pany, T.; Eissfeller, B. Use of a Vector Delay Lock Loop Receiver for GNSS Signal Power Analysis in Bad Signal Conditions. In Proceedings of the IEEE/ION Position, Location, and Navigation Symposium, Coronado, CA, USA, 25–27 April 2006; pp. 893–903. [Google Scholar]
- Sousa, F.M.G.; Nunes, F.D. Performance comparison of a VDFLL versus VDLL and scalar GNSS receiver architectures in harsh scenarios. In Proceedings of the 2014 7th ESA Workshop on Satellite Navigation Technologies and European Workshop on GNSS Signals and Signal Processing (NAVITEC), Noordwijk, The Netherlands, 3 December 2014; pp. 1–8. [Google Scholar]
- Lin, T.; Abdizadeh, M.; Broumandan, A.; Wang, D.; O’Keefe, K.; Lachapelle, G. Interference suppression for high precision navigation using vector-based GNSS software receivers. In Proceedings of the 24th International Technical Meeting of the Satellite Division of The Institute of Navigation, Portland, OR, USA, 20–23 September 2011; pp. 372–383. [Google Scholar]
- Ko, S.J.; Eissfeller, B.; Won, J.H.; Pany, T. Assessment of vector-trackingloop performance under radio frequency interference environments. In Proceedings of the 25th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS 2012), Nashville, TN, USA, 17–21 September 2012; pp. 2333–2341. [Google Scholar]
- Lashley, M.; Bevly, D.M. Comparison in the performance of the vector delay/frequency lock loop and equivalent scalar tracking loops in dense foliage and urban canyon. In Proceedings of the 24th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS 2011), Portland, OR, USA, 20–23 September 2011; pp. 1786–1803. [Google Scholar]
- Borre, K.; Kudryavtsev, I. Software Defined GNSS Receiver. Procedia Eng. 2015, 104, 9–14. [Google Scholar] [CrossRef][Green Version]
- Lashely, M. Modeling and Performance Analysis of GPS Vector Tracking Algorithms; Auburn University: Auburn, AL, USA, 2009. [Google Scholar]
- Bhattacharyya, S. Performance and Integrity Analysis of the Vector Tracking Architecture of GNSS Receivers; University of Minnesota: Minneapolis, MN, USA, 2012. [Google Scholar]
- Elghamrawy, H. Narrowband jamming mitigation in vector-based GPS software defined receiver. Ph.D. Thesis, Queen’s University, Kingston, ON, Canada, 2019. [Google Scholar]
- Krasovski, S. Vector-Based and Ultra-Tight GPS/INS Receiver Performance in the Presence of Continuous Wave Jamming; University of Calgary: Calgary, AB, USA, 2015. [Google Scholar]
- Li, Q.; Han, Z.; Wang, W.; Wang, X.; Xu, D. Anti-jamming scheme for GPS receiver with vector tracking loop and blind beamformer. Electron. Lett. 2014, 50, 1386–1388. [Google Scholar] [CrossRef]
- Petovello, M.G.; Lachapelle, G. Comparison of vector-based software receiver implementations with application to ultra-tight GPS/INS integration. In Proceedings of the 19th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS 2006), Fort Worth, TX, USA, 26–29 September 2006; pp. 1790–1799. [Google Scholar]
- Zhao, S.; Akos, D. An open source GPS/GNSS vector tracking loop implementation, filter tuning, and results. In Proceedings of the International Technical Meeting of The Institute of Navigation, San Diego, CA, USA, 28–31 January 2019; pp. 1293–1305. [Google Scholar]
- Spirent. Hardware and Software User Manual for Spirent’s GSS6700 Satellite Navigation Simulation Signal Generator; Spirent: Crowley, UK, 2010. [Google Scholar]
- Spirent. SimGEN Software Suite for Spirent Gnss Constellation Simulation Systems; Spirent: Crowley, UK, 2018. [Google Scholar]
- Spirent. User Manual for the Interference Simulation System Using SimGEN, Software for the Spirent Range of Satellite Navigation Simulator Products; Spirent: Crowley, UK, 2014. [Google Scholar]
- NovAtel. Digital GNSS Antenna (Prototype)-DGA NovAtel R&D Project: FireHose, Test Setup and Interface Guide D1708; NovAtel Inc.: Calgary, AB, Canada, 2013. [Google Scholar]






| Parameter | Value | Unit |
|---|---|---|
| Simulated Signal | GPS L1 C/A code | |
| Noise Floor | −130 | dBm |
| Code Length | 1023 | chip |
| Code Frequency | 1.023 | MHz |
| Signal Bandwidth | 2.046 | MHz |
| Parameter | Value | Unit |
|---|---|---|
| Intermediate Frequency (IF) | 0 | Hz |
| Sampling Frequency | 10 | MHz |
| Quantization Bits | 4 | bits |
| Parameter | Value | Unit |
|---|---|---|
| Acquisition Search Space | 14 | kHz |
| Coherent Integration Time | 5 | ms |
| Non-Coherent Integration | 3 | blocks |
| Acquisition Threshold | 2.5 | |
| PLL Damping Ratio | 0.7 | |
| PLL Noise Bandwidth | 25 | Hz |
| DLL Damping Ratio | 0.7 | |
| DLL Noise Bandwidth | 2 | Hz |
| DLL Correlator Spacing | 0.5 | chip |
| Attenuation | Scaler Tracking | Vector Tracking | ||
|---|---|---|---|---|
| 10 dB | 20 dB | 10 dB | 20 dB | |
| Horizontal Position (m) | 4.82 | 33.06 | 2.4 | 2.51 |
| Horizontal Speed (m/s) | 1.58 | 15.46 | 0.03 | 0.05 |
| Up Velocity Component (m/s) | 1.89 | 59.38 | 0.04 | 0.21 |
| Parameter | Scalar Tracking | Vector Tracking |
|---|---|---|
| Horizontal Position (m) | 12.5 | 3.39 |
| Horizontal Speed (m/s) | 5 | 0.15 |
| Up Velocity Component (m/s) | 6.13 | 0.49 |
| Parameter | Value |
|---|---|
| Jamming Signal Type | Swept continuous wave |
| Jamming-to-Signal Ratio | 45 dB |
| Start Frequency | 1575.43 MHz |
| End Frequency | 1575.55 MHz |
| Number of Frequency Hops | 12 |
| Dwell Time | 1 ms |
| Parameter | Scalar Tracking | Vector Tracking |
|---|---|---|
| Horizontal Position (m) | 6.3 | 1.9 |
| Horizontal Speed (m/s) | 1.12 | 0.12 |
| Up Velocity Component (m/s) | 3.88 | 0.05 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Elghamrawy, H.Y.F.; Tamazin, M.; Noureldin, A. Investigating the Benefits of Vector-Based GNSS Receivers for Autonomous Vehicles under Challenging Navigation Environments. Signals 2020, 1, 121-137. https://doi.org/10.3390/signals1020007
Elghamrawy HYF, Tamazin M, Noureldin A. Investigating the Benefits of Vector-Based GNSS Receivers for Autonomous Vehicles under Challenging Navigation Environments. Signals. 2020; 1(2):121-137. https://doi.org/10.3390/signals1020007
Chicago/Turabian StyleElghamrawy, Haidy Y. F., Mohamed Tamazin, and Aboelmagd Noureldin. 2020. "Investigating the Benefits of Vector-Based GNSS Receivers for Autonomous Vehicles under Challenging Navigation Environments" Signals 1, no. 2: 121-137. https://doi.org/10.3390/signals1020007
APA StyleElghamrawy, H. Y. F., Tamazin, M., & Noureldin, A. (2020). Investigating the Benefits of Vector-Based GNSS Receivers for Autonomous Vehicles under Challenging Navigation Environments. Signals, 1(2), 121-137. https://doi.org/10.3390/signals1020007







