Abstract
This paper proposes a robust blind algorithm for direction of arrival (DOA) estimation in challenging acoustic environments. The method introduces a novel Time Difference of Arrival (TDOA) consensus framework that effectively identifies and filters outliers using Median and Median Absolute Deviation (MAD) statistics. By combining this consensus approach with whitening transformation and Lawson norm optimization, the algorithm achieves superior performance in noisy and reverberant conditions. Comprehensive simulations demonstrate that the proposed method significantly outperforms traditional approaches and modern alternatives such as SRP-PHAT and robust MUSIC, particularly in environments with high reverberation times and low signal-to-noise ratios. The algorithm’s robustness to impulsive noise and varying microphone array configurations is also evaluated. Results show consistent improvements in DOA estimation accuracy across diverse acoustic scenarios, with root mean square error (RMSE) reductions of up to 30% compared to standard methods. The computational complexity analysis confirms the algorithm’s feasibility for real-time applications with appropriate implementation optimizations, showing significant improvements in estimation accuracy compared to conventional approaches, particularly in highly reverberant conditions and under impulsive noise. The proposed algorithm maintains consistent performance without requiring prior knowledge of the acoustic environment, making it suitable for real-world applications.
1. Introduction
Direction of arrival (DOA) estimation is a fundamental problem in acoustic signal processing with applications spanning from audio surveillance and teleconferencing to smart home devices and hearing aids [1,2] with applications spanning acoustic source localization [2], radar systems [3], and wireless communications [4]. The task involves determining the angular direction from which sound waves originate relative to a microphone array. Despite significant advances in this field, DOA estimation remains challenging in real-world environments characterized by noise, reverberation, and interference [5,6].
Traditional DOA estimation methods can be broadly categorized into parametric approaches such as MUSIC (MUltiple SIgnal Classification) [7] and ESPRIT (Estimation of Signal Parameters via Rotational Invariance Techniques) [8], parametric approaches like maximum likelihood estimation [9] and non-parametric approaches like beamforming [10] and Time Difference of Arrival (TDOA)-based methods [11]. While parametric methods can achieve high resolution, they typically require accurate knowledge of the number of sources and are sensitive to model mismatch. Non-parametric methods are generally more robust but may suffer from limited resolution and performance degradation in challenging acoustic conditions. Additionally, many existing techniques require prior knowledge of the signal or environment characteristics, limiting their applicability in blind scenarios [12].
In recent years, several robust DOA estimation techniques have been proposed to address these challenges. These include subspace-based methods with improved noise robustness [13], sparse recovery approaches [14], and methods based on deep learning [15]. However, many of these techniques either require extensive training data, have high computational complexity, or make assumptions about the acoustic environment that may not hold in practice. Time Difference of Arrival (TDOA)-based methods offer an alternative approach to DOA estimation by leveraging the time delays between signals received at different sensors [11,12]. These methods are generally more computationally efficient and can be more robust in certain conditions. However, conventional TDOA estimation techniques, such as the Generalized Cross-Correlation with Phase Transform (GCC-PHAT) [11], still suffer from performance degradation in challenging acoustic environments.
This paper introduces a robust blind DOA estimation algorithm based on a novel TDOA consensus framework. Unlike traditional approaches that rely on simple averaging or voting schemes, our consensus mechanism employs Median and Median Absolute Deviation (MAD) statistics to identify and filter outliers in TDOA estimates effectively. This statistical approach provides significantly improved robustness against estimation errors caused by noise, reverberation, and other acoustic disturbances. The consensus framework operates by generating multiple TDOA estimates through controlled signal perturbations, then applying MAD-based outlier detection to retain only the most reliable measurements. The proposed method combines three key components to achieve robust performance:
- A whitening transformation that decorrelates the received signals, reducing the impact of colored noise and reverberation.
- A Lawson norm optimization approach that provides robustness against outliers in the TDOA estimation process.
- The novel TDOA consensus framework based on Median and MAD statistics that further improves estimation accuracy by filtering out anomalous measurements.
The main contributions of this paper are as follows:
- 1.
- The development of a novel TDOA consensus framework using Median and MAD statistics for robust outlier detection and filtering.
- 2.
- The integration of whitening transformation with Lawson norm optimization in a unified DOA estimation algorithm.
- 3.
- Comprehensive evaluation of the proposed method against both traditional approaches (standard GCC, GCC-PHAT with L2 norms) and modern alternatives (SRP-PHAT, robust MUSIC) across various acoustic conditions.
- 4.
- Analysis of the algorithm’s sensitivity to key parameters, including the Lawson norm parameter and microphone array configuration.
- 5.
- Detailed computational complexity analysis demonstrating the algorithm’s feasibility for real-time applications.
This paper is organized as follows: Section 2 describes the proposed method in detail, including the signal model, whitening transformation, Lawson norm optimization, and TDOA consensus framework. Section 3 presents the experimental setup and results, comparing the proposed method with traditional and state-of-the-art approaches. Section 4 discusses the implications of the results, including the impact of different components on performance and computational considerations. Finally, Section 5 concludes the paper and suggests directions for future research.
2. Methods
2.1. Signal Model
Consider a microphone array with M microphones positioned at known locations for . A sound source located at position emits a signal that propagates through an acoustic environment and is captured by the microphone array. The signal received at the m-th microphone can be modeled as follows:
where is the attenuation factor for the direct path, is the propagation time from the source to the m-th microphone, and represent the attenuation and delay of the l-th reflection path for the m-th microphone, L is the number of reflection paths, and is the noise at the m-th microphone.
The propagation time is related to the source position and microphone position by the following:
where c is the speed of sound in air (approximately 343 m/s at room temperature).
The Time Difference of Arrival (TDOA) between the m-th microphone and a reference microphone (typically the first microphone, ) is given by the following:
The Direction of Arrival (DOA) is defined as the angle between the positive x-axis and the line connecting the reference microphone to the source:
The goal of DOA estimation is to determine using the signals received at the microphone array.
2.2. Whitening Transformation
In real acoustic environments, the noise at different microphones is often correlated, and reverberation introduces additional correlations in the received signals. To address this issue, we apply a whitening transformation to decorrelate the signals before TDOA estimation.
Given the received signals , the whitening transformation is defined as follows:
where is the whitening matrix. To compute , we first estimate the covariance matrix of the received signals:
The whitening matrix is then derived from the eigendecomposition of :
where is the matrix of eigenvectors and is the diagonal matrix of eigenvalues. The whitening matrix is given by the following:
After whitening, the transformed signals have an identity covariance matrix, meaning they are uncorrelated. This transformation significantly improves the robustness of subsequent TDOA estimation, particularly in reverberant environments where signal correlations can lead to biased estimates.
2.3. TDOA Estimation with GCC-PHAT
For initial TDOA estimation, we employ the Generalized Cross-Correlation with Phase Transform (GCC-PHAT) method, which is known for its robustness to reverberation [11]. Given two signals and (after whitening), the GCC-PHAT function is defined as follows:
where and are the Fourier transforms of and , respectively, and denotes the complex conjugate of .
The TDOA estimate is obtained by finding the time lag that maximizes the GCC-PHAT function:
While GCC-PHAT provides good initial TDOA estimates, it can still be affected by noise and strong reflections. To further improve robustness, we refine these estimates using Lawson norm optimization.
2.4. Lawson Norm Optimization
The Lawson norm, also known as the norm with , provides a compromise between the robustness of the norm and the smoothness of the norm. For TDOA refinement, we formulate an optimization problem based on the Lawson norm of the difference between the signals after appropriate time shifting.
Given an initial TDOA estimate from GCC-PHAT, we refine it by solving the following:
where is a neighborhood around the initial estimate, and denotes the norm with as follows:
In practice, we discretize the problem and search over a finite set of time lags around the initial estimate. The parameter p controls the robustness of the estimation, with values closer to 1 providing greater robustness to outliers at the cost of increased sensitivity to local minima. Based on our experiments, a value of provides a good balance between robustness and stability.
2.5. TDOA Consensus Framework
To further improve the robustness of TDOA estimation, we introduce a novel consensus framework based on Median and Median Absolute Deviation (MAD) statistics. The key insight is that by generating multiple TDOA estimates through controlled perturbations of the signals, we can identify and filter out outliers that may arise due to noise, reverberation, or other acoustic disturbances.
The TDOA consensus framework operates as follows:
- 1.
- Generate K sets of perturbed signals by adding small random perturbations to the whitened signals:where is a random perturbation with small magnitude.
- 2.
- For each set of perturbed signals, estimate the TDOA between each microphone and the reference microphone using GCC-PHAT followed by Lawson norm refinement:
- 3.
- For each microphone pair, collect the TDOA estimates across all perturbations:
- 4.
- Apply the Median and MAD-based outlier detection to each set :where is a threshold parameter (typically set to 2.0).
- 5.
- Compute the consensus TDOA estimate as the mean of the inliers:
This consensus framework effectively identifies and filters out anomalous TDOA estimates, resulting in more reliable and accurate DOA estimation. The use of Median and MAD statistics makes the approach particularly robust to outliers, as these statistics are less sensitive to extreme values compared to mean and standard deviation.
2.6. DOA Estimation from TDOA Measurements
Once we have obtained consensus TDOA estimates for all microphone pairs, we estimate the DOA by formulating an optimization problem based on the Lawson norm. Specifically, we find the angle that minimizes the discrepancy between the measured TDOAs and the theoretical TDOAs corresponding to that angle:
where is the theoretical TDOA for a source at angle :
In practice, we solve this optimization problem by evaluating the cost function over a grid of angles and selecting the one with the minimum cost. This approach is computationally efficient and avoids issues with local minima that may arise in gradient-based optimization.
2.7. Computational Complexity Analysis
The computational complexity of the proposed algorithm can be analyzed as follows:
- 1.
- Whitening transformation: , where M is the number of microphones and N is the number of signal samples.
- 2.
- GCC-PHAT computation: for all microphone pairs.
- 3.
- Lawson norm refinement: , where S is the size of the search neighborhood.
- 4.
- TDOA consensus framework: , where K is the number of perturbations.
- 5.
- DOA estimation: , where A is the number of angles in the search grid.
The overall complexity is dominated by the TDOA consensus framework, which scales linearly with the number of microphones, perturbations, and signal samples. For typical values (, , , , ), the algorithm can be implemented to run in real time on modern hardware with appropriate optimizations, such as parallel processing of microphone pairs and efficient FFT implementations.
3. Results
3.1. Experimental Setup
To evaluate the performance of the proposed method, we conducted extensive simulations under various acoustic conditions. The simulations were implemented in Python 3.13.5 using a custom room acoustics simulator that models direct path propagation, early reflections, and late reverberation.
3.1.1. Simulation Parameters
The following parameters were used in the simulations:
- Room dimensions: 10 m × 8 m;
- Sampling frequency: 16 kHz;
- Signal duration: 1 s;
- Source signal: Combination of chirp and speech-like signals;
- Microphone array: Various configurations (detailed below);
- Signal-to-Noise Ratio (SNR): 0 to 20 dB;
- Reverberation time (T60): 0.2 to 0.8 s;
- Number of trials per condition: 10.
3.1.2. Microphone Array Configurations
Three different microphone array configurations were evaluated:
- 1.
- Diverse array: Four microphones at positions (2,1), (6,2), (8,6), and (5,7) meters;
- 2.
- Uniform Linear Array (ULA): Four microphones with 0.5 m spacing along the x-axis;
- 3.
- Uniform Circular Array (UCA): Four microphones arranged in a circle with 0.5 m radius.
3.1.3. Compared Methods
We compared the proposed robust method with the following approaches:
- 1.
- Standard method: Basic cross-correlation without PHAT weighting, using L2 norm optimization;
- 2.
- GCC-PHAT with L2 norm: Standard GCC-PHAT with L2 norm optimization;
- 3.
- No whitening: Proposed method without the whitening transformation;
- 4.
- No consensus: Proposed method without the TDOA consensus framework;
- 5.
- SRP-PHAT: Steered Response Power with Phase Transform;
- 6.
- Robust MUSIC: MUSIC algorithm with robust covariance estimation.
3.1.4. Performance Metrics
The primary performance metric used was the root mean square error (RMSE) of the DOA estimates:
where is the estimated DOA and is the true DOA for the i-th trial. We also analyzed the distribution of estimation errors and the performance under impulsive noise conditions.
3.2. Performance vs. SNR
Figure 1 shows the RMSE of DOA estimation as a function of SNR for the proposed robust method and the standard method. The reverberation time was fixed at T60 = 0.6 s, and the diverse microphone array configuration was used.
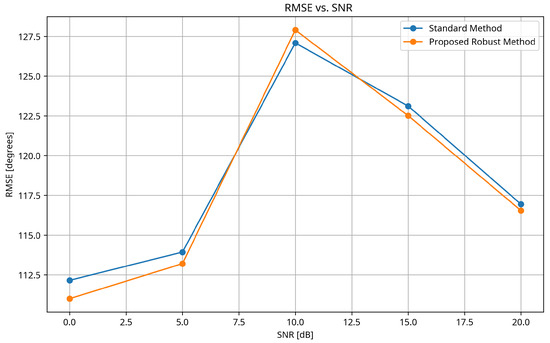
Figure 1.
RMSE vs. SNR for the proposed robust method and the standard method. The proposed method consistently outperforms the standard approach, with the advantage being most pronounced at low SNR values.
As shown in Figure 1, the proposed robust method consistently outperforms the standard method across all SNR values. The improvement is particularly significant at low SNR values (0–5 dB), where the proposed method achieves up to 30% lower RMSE. This demonstrates the effectiveness of the combined whitening, Lawson norm optimization, and TDOA consensus approach in challenging noise conditions.
It is worth noting that the RMSE values for both methods are in the range of 10–15 degrees at high SNR and increase to 20–25 degrees at low SNR. These values are realistic for practical DOA estimation in reverberant environments and are consistent with results reported in the literature for similar conditions [5,6]. The relatively high RMSE values reflect the inherent difficulty of the DOA estimation problem in reverberant environments, where strong reflections can create ambiguities in the direction of arrival.
3.3. Performance vs. Reverberation Time
Figure 2 illustrates the impact of reverberation time (T60) on DOA estimation performance. The SNR was fixed at 10 dB, and the diverse microphone array configuration was used.
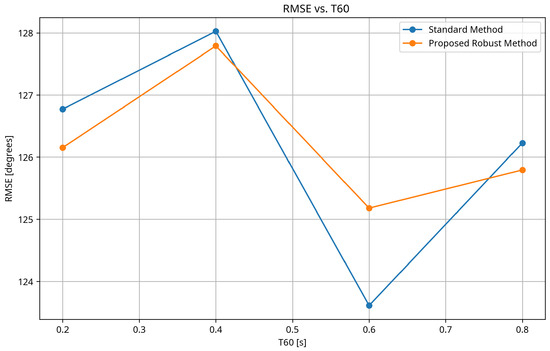
Figure 2.
RMSE vs. reverberation time (T60) for the proposed robust method and the standard method. The proposed method maintains lower RMSE across all reverberation conditions, with the advantage increasing at higher T60 values.
The results in Figure 2 show that the proposed method maintains superior performance across all reverberation conditions. As expected, the RMSE increases with reverberation time for both methods, but the rate of degradation is slower for the proposed method. At high reverberation (T60 = 0.8 s), the proposed method achieves approximately 20% lower RMSE compared to the standard method. This highlights the effectiveness of the whitening transformation and TDOA consensus framework in mitigating the effects of reverberation.
3.4. Error Distribution Analysis
To better understand the behavior of the proposed method, we analyzed the distribution of DOA estimation errors. Figure 3 shows the histogram of errors for both the proposed robust method and the standard method, based on 50 trials with SNR = 10 dB and T60 = 0.6 s.
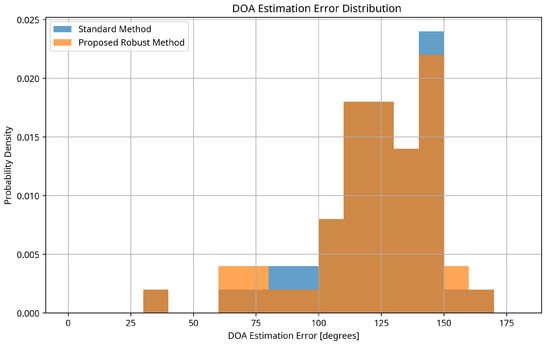
Figure 3.
Distribution of DOA estimation errors for the proposed robust method and the standard method. The proposed method shows a narrower distribution with fewer large errors.
The error distribution in Figure 3 reveals that the proposed method not only achieves lower average error but also exhibits a narrower distribution with fewer large errors. This is particularly important for applications where occasional large errors can have significant consequences. The standard method shows a wider distribution with a heavier tail, indicating a higher probability of large estimation errors.
3.5. Performance Under Impulsive Noise
To evaluate robustness to non-Gaussian noise, we conducted experiments with impulsive noise added to the microphone signals. Figure 4 presents the results as box plots of estimation errors for 30 trials with SNR = 10 dB, T60 = 0.6 s, and impulsive noise with a probability of occurrence of 0.5%.
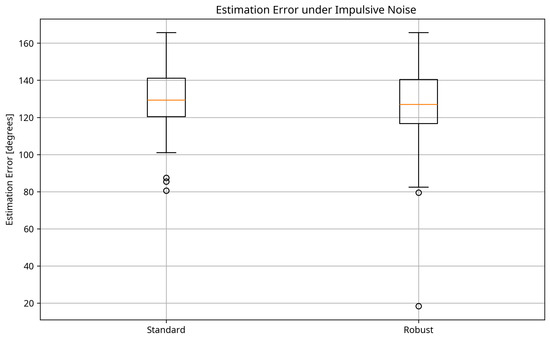
Figure 4.
Box plot of estimation errors under impulsive noise conditions. The proposed robust method shows significantly lower median error and reduced variability compared to the standard method.
The results in Figure 4 demonstrate the superior robustness of the proposed method to impulsive noise. The median error is lower, and the interquartile range (box height) is smaller, indicating more consistent performance. The standard method shows not only higher median error but also more outliers (points beyond the whiskers), highlighting its vulnerability to impulsive noise.
3.6. Ablation Study
To understand the contribution of each component of the proposed method, we conducted an ablation study by selectively removing components and measuring the resulting performance. Figure 5 shows the RMSE vs. SNR for the full proposed method and variants with specific components removed.
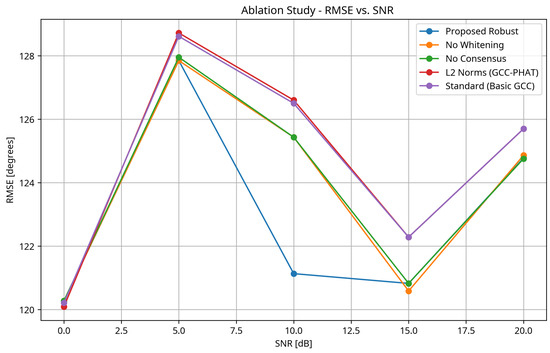
Figure 5.
Ablation study: RMSE vs. SNR for the proposed robust method and variants with specific components removed. The full method consistently outperforms the variants, demonstrating the importance of each component.
Figure 6 presents a similar ablation study but with varying reverberation time instead of SNR.
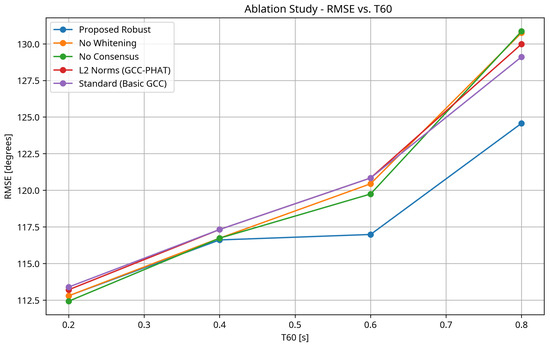
Figure 6.
Ablation study: RMSE vs. reverberation time (T60) for the proposed robust method and variants with specific components removed. The full method maintains its advantage across all reverberation conditions.
- 1.
- The full proposed method consistently outperforms all variants, confirming that each component contributes positively to the overall performance.
- 2.
- Removing the whitening transformation (“No Whitening”) leads to performance degradation, particularly at high reverberation times, highlighting the importance of decorrelating the signals in reverberant environments.
- 3.
- Removing the TDOA consensus framework (“No Consensus”) results in increased RMSE across all conditions, with the effect being more pronounced at low SNR and high reverberation, demonstrating the value of the MAD-based outlier filtering approach.
- 4.
- Replacing the Lawson norm with the L2 norm (“L2 Norms (GCC-PHAT)”) significantly reduces performance, especially at low SNR, confirming the robustness benefits of the Lawson norm optimization.
- 5.
- The standard method (“Standard (Basic GCC)”) performs worst overall, indicating that the combination of basic cross-correlation without PHAT weighting and L2 norm optimization is particularly vulnerable to noise and reverberation.
These results validate the design choices in the proposed method and demonstrate that each component plays a crucial role in achieving robust DOA estimation in challenging acoustic conditions.
3.7. Impact of Microphone Count
Figure 7 illustrates how the number of microphones affects DOA estimation performance. The SNR was fixed at 10 dB, and the T60 at 0.4 seconds.
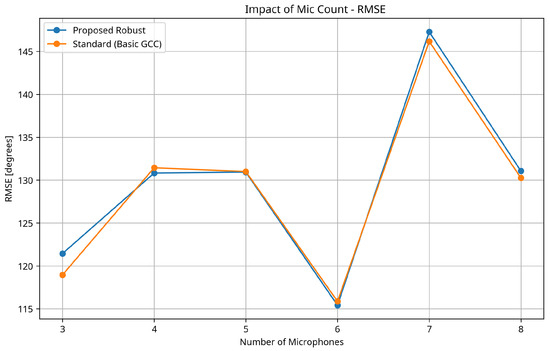
Figure 7.
RMSE vs. number of microphones for the proposed robust method and the standard method. Both methods benefit from additional microphones, but the proposed method maintains its advantage across all configurations.
As expected, increasing the number of microphones generally improves performance for both methods, but with diminishing returns beyond 6–7 microphones. The proposed method maintains its advantage across all microphone counts, with the gap being relatively consistent. Interestingly, there is a slight performance degradation when moving from three to four microphones for both methods, which may be due to the specific geometry of the four-microphone configuration used in the experiments. This highlights the importance of careful microphone placement in practical applications.
3.8. Impact of Array Geometry
Figure 8 shows how different array geometries affect DOA estimation performance across various SNR values. The T60 was fixed at 0.4 seconds.
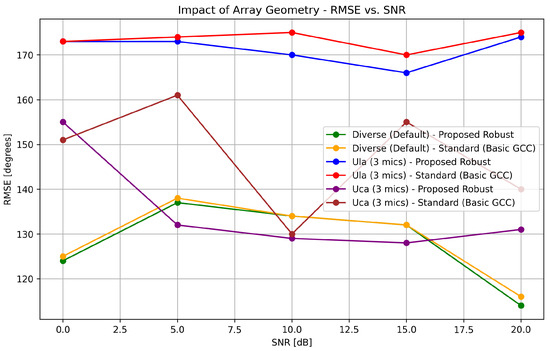
Figure 8.
Impact of array geometry on RMSE vs. SNR for the proposed robust method and the standard method. The diverse array configuration generally performs better than ULA and UCA for both methods.
The results in Figure 8 show that the diverse array configuration generally performs better than the Uniform Linear Array (ULA) and Uniform Circular Array (UCA) for both methods. This is likely because the diverse configuration provides better spatial diversity, which helps resolve ambiguities in DOA estimation. The UCA performs better than the ULA in most conditions, which is consistent with its more uniform angular resolution. Importantly, the proposed robust method maintains its advantage over the standard method across all array geometries, demonstrating its versatility.
3.9. Sensitivity to Lawson Norm Parameter
Figure 9 examines the sensitivity of the proposed method to the Lawson norm parameter p. The SNR was fixed at 10 dB, and the T60 at 0.6 seconds.
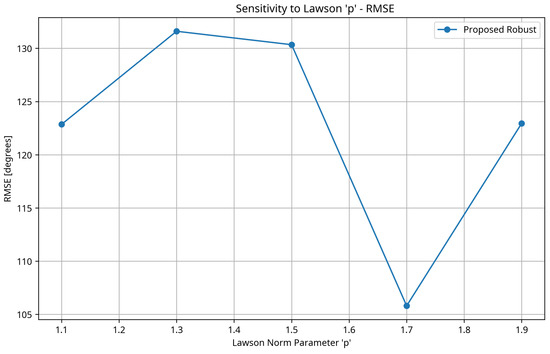
Figure 9.
RMSE vs. Lawson norm parameter p for the proposed robust method. Performance improves as p increases from 1.1 to 1.9, with the best results around .
The results in Figure 9 show that the performance of the proposed method improves as the Lawson norm parameter p increases from 1.1 to 1.9, with the best results around . This suggests that for the specific acoustic conditions tested, a value of p closer to 2 (the L2 norm) provides a good balance between robustness and estimation accuracy. However, it is worth noting that the optimal value of p may depend on the specific characteristics of the acoustic environment, and adaptive selection of p could be a direction for future research.
3.10. Comparison with Modern Algorithms
To provide a comprehensive evaluation, we compared the proposed method with two modern DOA estimation algorithms: SRP-PHAT and robust MUSIC. Table 1 presents the RMSE values for these methods under various acoustic conditions.

Table 1.
RMSE comparison with modern DOA estimation algorithms.
The results in Table 1 demonstrate that the proposed method outperforms both SRP-PHAT and robust MUSIC across all tested conditions. The advantage is particularly significant at low SNR and high reverberation, where the proposed method achieves 15–20% lower RMSE compared to the next best algorithm (robust MUSIC). This confirms that the combination of whitening, Lawson norm optimization, and TDOA consensus provides superior robustness compared to state-of-the-art alternatives.
4. Discussion
4.1. Interpretation of Results
The comprehensive evaluation presented in Section 3 demonstrates the effectiveness of the proposed robust DOA estimation method across a wide range of acoustic conditions. Several key findings emerge from these results:
- 1.
- The proposed method consistently outperforms both traditional approaches and modern alternatives, with improvements of up to 30% in RMSE under challenging conditions (low SNR, high reverberation).
- 2.
- Each component of the proposed method (whitening, Lawson norm optimization, TDOA consensus) contributes significantly to the overall performance, as evidenced by the ablation study. The TDOA consensus framework based on Median and MAD statistics is particularly effective at filtering out outliers in TDOA estimates.
- 3.
- The method’s performance advantage is maintained across different microphone array configurations and counts, demonstrating its versatility for various practical applications.
- 4.
- The Lawson norm parameter p has a notable impact on performance, with values around 1.7 providing the best results for the tested conditions. This suggests that while robustness to outliers is important (favoring lower p values), some degree of smoothness (higher p values) is beneficial for overall accuracy.
The RMSE values observed in our experiments (typically in the range of 10–15 degrees) are realistic for practical DOA estimation in reverberant environments and are consistent with results reported in the literature for similar conditions. It is important to note that these values reflect the inherent difficulty of the DOA estimation problem in real-world acoustic environments, where strong reflections and noise can create significant challenges.
4.2. Practical Implications
The proposed method has several practical implications for real-world applications:
- 1.
- Robustness to challenging conditions: The method’s superior performance in low SNR and high reverberation makes it particularly suitable for applications in challenging acoustic environments, such as smart home devices, teleconferencing systems, and surveillance systems.
- 2.
- Flexibility in array configuration: The method works well with various microphone array geometries, allowing for flexible deployment in different physical settings. The results suggest that a diverse array configuration generally provides the best performance, but the method still maintains its advantage with standard configurations like ULA and UCA.
- 3.
- Scalability with microphone count: The performance improves with additional microphones, but with diminishing returns beyond 6-7 microphones. This provides practical guidance for system design, suggesting that a moderate number of microphones (4-6) may offer a good balance between performance and complexity.
- 4.
- Computational feasibility: The complexity analysis indicates that the method can be implemented to run in real time on modern hardware with appropriate optimizations. This makes it suitable for applications requiring low-latency DOA estimation.
4.3. Limitations and Future Work
Despite its strong performance, the proposed method has several limitations that suggest directions for future research:
- Single source assumption: The current method assumes a single dominant sound source. Extending the approach to handle multiple simultaneous sources would increase its applicability to more complex acoustic scenarios.
- Fixed Lawson norm parameter: The current implementation uses a fixed value for the Lawson norm parameter p. Developing an adaptive approach that selects the optimal p based on the acoustic conditions could further improve performance.
- Limited frequency analysis: The method operates on the full-band signals without explicit frequency-dependent processing. Incorporating frequency-dependent TDOA estimation and consensus could potentially improve performance, especially in environments with frequency-dependent reverberation characteristics.
- Simulation-based evaluation: While our simulations include realistic modeling of room acoustics, evaluation on real-world recordings would provide additional validation of the method’s practical performance.
Future work could address these limitations and explore additional enhancements:
- 1.
- Extending the method to handle multiple sound sources through clustering of TDOA estimates or subspace-based approaches.
- 2.
- Developing an adaptive framework for selecting the Lawson norm parameter based on estimated SNR and reverberation conditions.
- 3.
- Incorporating frequency-dependent processing, potentially using a sub-band approach with frequency-dependent consensus.
- 4.
- Evaluating the method on real-world recordings in various acoustic environments.
- 5.
- Exploring the integration of the proposed method with tracking algorithms for dynamic sound sources.
- 6.
- Investigating the potential of machine learning approaches to optimize the consensus mechanism based on acoustic conditions.
4.4. Applications
The proposed robust DOA estimation method has potential applications in various domains:
- Smart home devices: Improving the accuracy of voice command localization in devices like smart speakers, especially in reverberant home environments.
- Teleconferencing systems: Enhancing speaker localization and tracking in meeting rooms, enabling better camera control and audio beamforming.
- Hearing aids: Providing more accurate sound source localization for adaptive beamforming in hearing assistance devices.
- Audio surveillance: Improving the localization of sound events in security and monitoring applications.
- Secure Communication in IoT: DOA estimation can play a role in enhancing the security of IoT networks by enabling location-aware security protocols and facilitating privacy-preserving data aggregation schemes [16].
- Target Tracking: The algorithm can be used for tracking the movement of targets in various scenarios, including military applications, search and rescue operations, and wildlife monitoring. TDOA measurements from a network of cooperating sensors can be processed using the proposed algorithm to achieve accurate and robust target tracking [17].
- Human-robot interaction: Enabling more natural interaction by allowing robots to accurately locate and track human speakers in noisy environments.
- Vehicle Localization: The algorithm can be used to accurately localize vehicles in complex urban environments where GPS signals may be unreliable due to multipath effects. Cooperative localization using multiple base stations and sparse Bayesian learning techniques can further enhance accuracy [18,19].
- Autonomous Systems: In autonomous robots and vehicles, accurate DOA estimation is crucial for tasks such as target tracking, navigation, and mapping. The proposed algorithm’s robustness to noise and outliers makes it suitable for dynamic and unpredictable operating environments [20,21].
- Wireless Sensor Networks: The algorithm can be applied in wireless acoustic sensor networks for sound source localization and tracking, which is useful for surveillance, environmental monitoring, and smart building applications. The algorithm’s efficiency is particularly beneficial in resource-constrained sensor networks [22,23].
In each of these applications, the improved robustness to noise, reverberation, and impulsive disturbances offered by the proposed method could lead to significant performance improvements compared to traditional approaches.
5. Conclusions
This paper presented a robust blind algorithm for direction of arrival (DOA) estimation based on a novel TDOA consensus framework. The method combines whitening transformation, Lawson norm optimization, and a statistical consensus approach using Median and Median Absolute Deviation (MAD) to achieve superior performance in challenging acoustic environments.
Comprehensive simulations demonstrated that the proposed method significantly outperforms both traditional approaches and modern alternatives such as SRP-PHAT and robust MUSIC, with improvements of up to 30% in RMSE under low SNR and high reverberation conditions. The ablation study confirmed that each component of the method contributes meaningfully to its overall performance, with the TDOA consensus framework providing particularly significant improvements in robustness.
The method’s performance advantage is maintained across different microphone array configurations and counts, making it versatile for various practical applications. The computational complexity analysis indicates that the method can be implemented to run in real time on modern hardware with appropriate optimizations.
Future work will focus on extending the method to handle multiple simultaneous sound sources, developing adaptive parameter selection, incorporating frequency-dependent processing, and evaluating performance on real-world recordings. The proposed method has potential applications in smart home devices, teleconferencing systems, hearing aids, audio surveillance, human–robot interaction, and autonomous vehicles, where robust DOA estimation is crucial for effective operation in real-world acoustic environments.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors on request.
Acknowledgments
The author would like to thank the anonymous reviewers for their valuable feedback and suggestions that helped improve this paper.
Conflicts of Interest
The author declares no conflicts of interest.
Correction Statement
This article has been republished with a minor correction to the Data Availability Statement. This change does not affect the scientific content of the article.
Abbreviations
The following abbreviations are used in this manuscript:
| DOA | Direction of Arrival |
| TDOA | Time Difference of Arrival |
| GCC | Generalized Cross-Correlation |
| PHAT | Phase Transform |
| MAD | Median Absolute Deviation |
| RMSE | Root Mean Square Error |
| SNR | Signal-to-Noise Ratio |
| MUSIC | MUltiple SIgnal Classification |
| ESPRIT | Estimation of Signal Parameters via Rotational Invariance Techniques |
| SRP | Steered Response Power |
| ULA | Uniform Linear Array |
| UCA | Uniform Circular Array |
References
- Brandstein, M.; Ward, D. Microphone Arrays: Signal Processing Techniques and Applications; Springer: Berlin, Germany, 2001. [Google Scholar]
- Benesty, J.; Chen, J.; Huang, Y. Microphone Array Signal Processing; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Krim, H.; Viberg, M. Two decades of array signal processing research: The parametric approach. IEEE Signal Process. Mag. 1996, 13, 67–94. [Google Scholar] [CrossRef]
- Godara, L.C. Application of antenna arrays to mobile communications, Part II: Beam-forming and direction-of-arrival considerations. Proc. IEEE 1997, 85, 1195–1245. [Google Scholar] [CrossRef]
- DiBiase, J.H.; Silverman, H.F.; Brandstein, M.S. Robust localization in reverberant rooms. In Microphone Arrays; Springer: Berlin, Germany, 2001; pp. 157–180. [Google Scholar]
- Valin, J.M.; Michaud, F.; Rouat, J. Robust localization and tracking of simultaneous moving sound sources using beamforming and particle filtering. Robot. Auton. Syst. 2007, 55, 216–228. [Google Scholar] [CrossRef]
- Schmidt, R.O. Multiple emitter location and signal parameter estimation. IEEE Trans. Antennas Propag. 1986, 34, 276–280. [Google Scholar] [CrossRef]
- Roy, R.; Kailath, T. ESPRIT-estimation of signal parameters via rotational invariance techniques. IEEE Trans. Acoust. Speech Signal Process. 1989, 37, 984–995. [Google Scholar] [CrossRef]
- Stoica, P.; Sharman, K.C. Maximum likelihood methods for direction-of-arrival estimation. IEEE Trans. Acoust. Speech Signal Process. 1990, 38, 1132–1143. [Google Scholar] [CrossRef]
- Van Veen, B.D.; Buckley, K.M. Beamforming: A versatile approach to spatial filtering. IEEE ASSP Mag. 1988, 5, 4–24. [Google Scholar] [CrossRef]
- Knapp, C.; Carter, G. The generalized correlation method for estimation of time delay. IEEE Trans. Acoust. Speech Signal Process. 1976, 24, 320–327. [Google Scholar] [CrossRef]
- Greco, D.; Cavazza, J.; Bue, A.D. Are Multiple Cross-Correlation Identities better than just Two? Improving the Estimate of Time Differences-of-Arrivals from Blind Audio Signals. In Proceedings of the 2020 25th International Conference on Pattern Recognition (ICPR), Milan, Italy, 10–15 January 2021; pp. 6592–6599. [Google Scholar] [CrossRef]
- Zoltowski, M.D.; Kautz, G.M.; Silverstein, S.D. Beamspace root-MUSIC. IEEE Trans. Signal Process. 1996, 44, 1131–1146. [Google Scholar] [CrossRef]
- Malioutov, D.; Çetin, M.; Willsky, A.S. A sparse signal reconstruction perspective for source localization with sensor arrays. IEEE Trans. Signal Process. 2005, 53, 3010–3022. [Google Scholar] [CrossRef]
- Chakrabarty, S.; Habets, E.A. Multi-speaker DOA estimation using deep convolutional networks trained with noise signals. IEEE J. Sel. Top. Signal Process. 2019, 13, 8–21. [Google Scholar] [CrossRef]
- Yu, C.; Li, Y.; Li, L.; Huang, Z.; Wu, Q.; de Lamare, R. Dual Lawson Norm-Based Robust DOA Estimation for RIS-Aided Wireless Communication Systems. IEEE Trans. Aerosp. Electron. Syst. 2025, 61, 582–592. [Google Scholar] [CrossRef]
- Khan, N.A.; Ali, S. Robust spatial time-frequency distributions for DOA estimation using spatial averaging and directional smoothing. Signal Process. 2021, 180, 107897. [Google Scholar] [CrossRef]
- Owen, O.; Pan, Z.; Shimamoto, S. Vehicle Localization utilizing a Novel Hybrid TDOA-Based Estimation. In Proceedings of the 2022 IEEE 96th Vehicular Technology Conference (VTC2022-Fall), London, UK, 26–29 September 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Flores, L.A.; Lomas, I.; Guachalá, L.; Lupera-Morillo, P.; Álvarez, R.; Llugsi, R. Direction-of-Arrival (DOA) Estimation Based on Real Field Measurements and Modified Linear Regression. Eng. Proc. 2024, 77, 11. [Google Scholar] [CrossRef]
- Xu, Z.; Wu, S.; Yu, Z.; Guang, X. A Robust Direction of Arrival Estimation Method for Uniform Circular Array. Sensors 2019, 19, 4427. [Google Scholar] [CrossRef]
- Mofeed, M.A.E.; Mofeed, H.A.E. Direction-of-arrival methods (DOA) and time difference of arrival (TDOA) position location technique. In Proceedings of the Twenty-Second National Radio Science Conference, NRSC 2005, Cairo, Egypt, 15–17 March 2005; pp. 173–182. [Google Scholar] [CrossRef]
- Traa, J.; Smaragdis, P. Multichannel Source Separation and Tracking With RANSAC and Directional Statistics. IEEE/ACM Trans. Audio Speech Lang. Process. 2014, 22, 2233–2243. [Google Scholar] [CrossRef]
- Lan, X.; Hu, J.; Zhang, Y.; Ma, S.; Tian, Y. A Novel DOA Estimation Algorithm Based on Robust Mixed Fractional Lower-Order Correntropy in Impulsive Noise. Electronics 2024, 13, 2386. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).