Prediction of Degradation of Concrete Surface Layer Using Neural Networks Applied to Ultrasound Propagation Signals
Abstract
1. Introduction
2. Methods and Materials
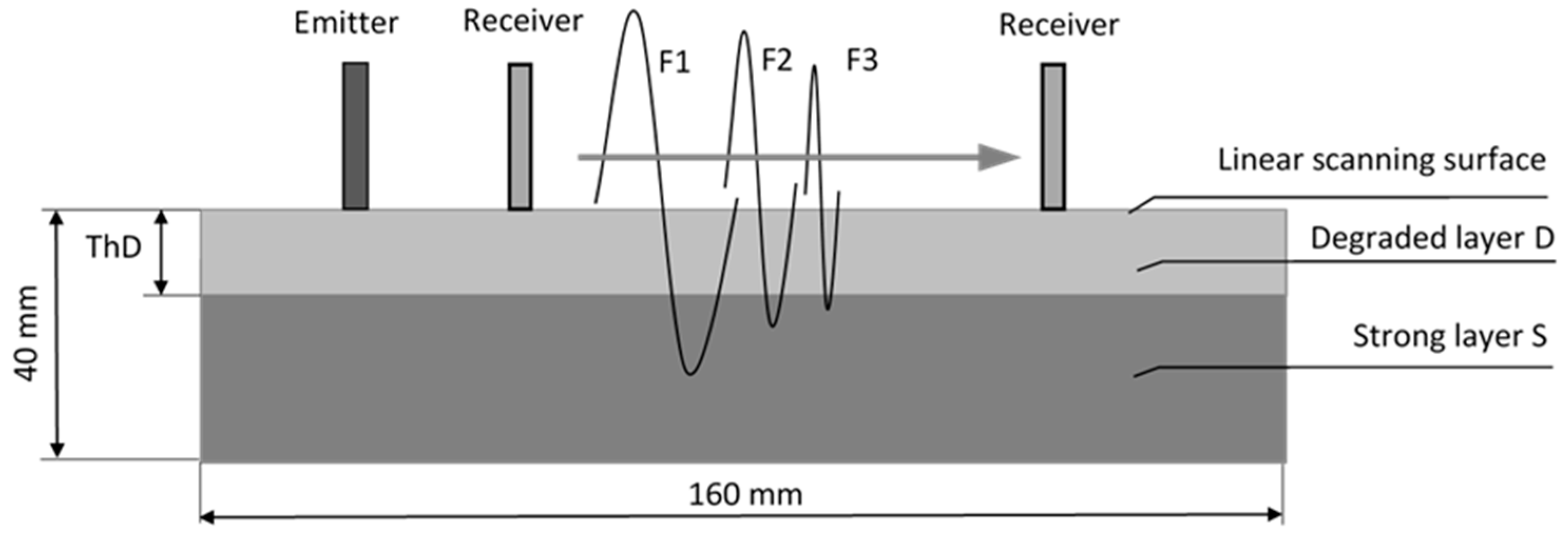
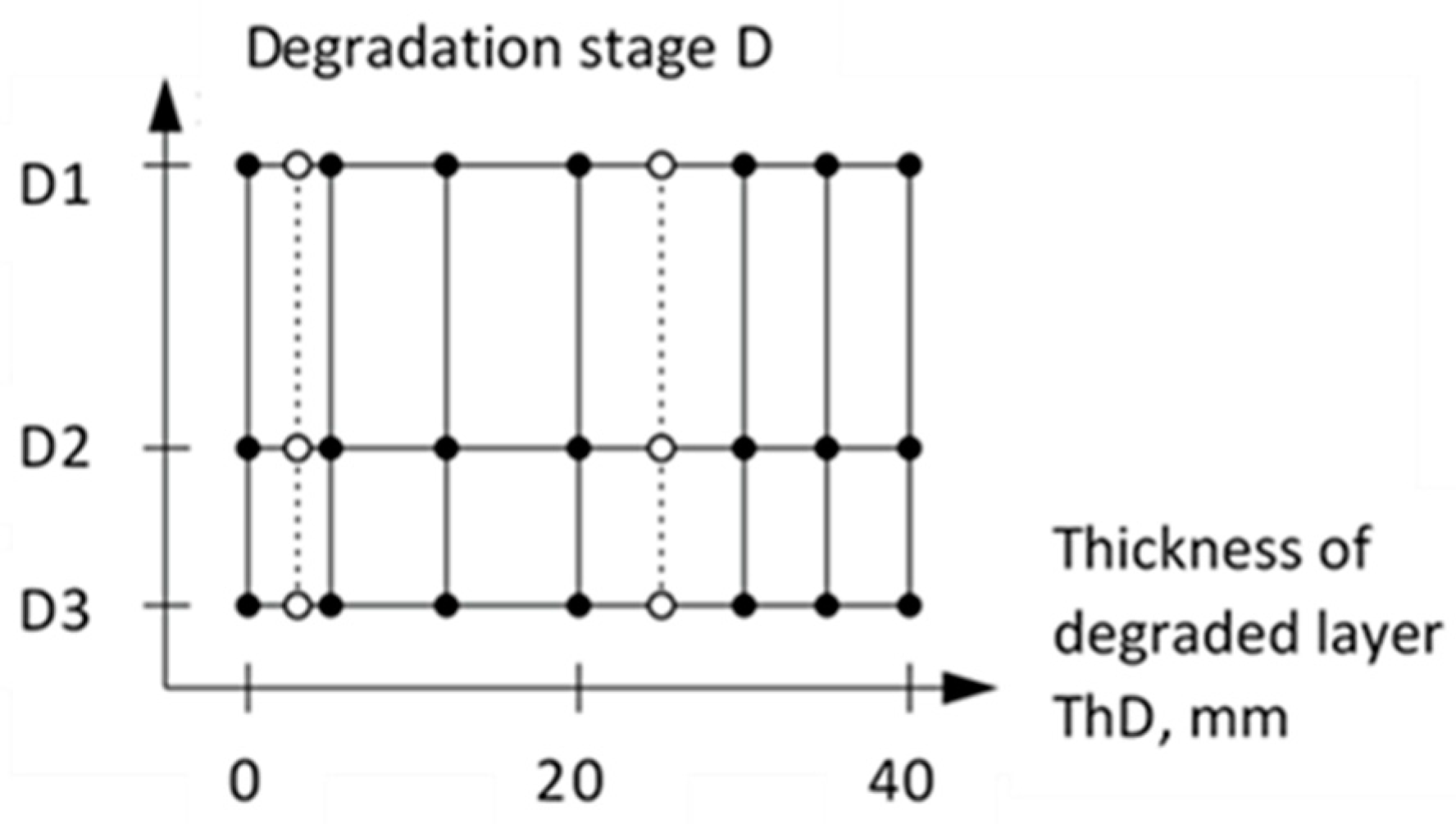
2.1. Concrete Specimens Modeling Degradation of Surface Layer
2.2. Ultrasonic Data Acquisition
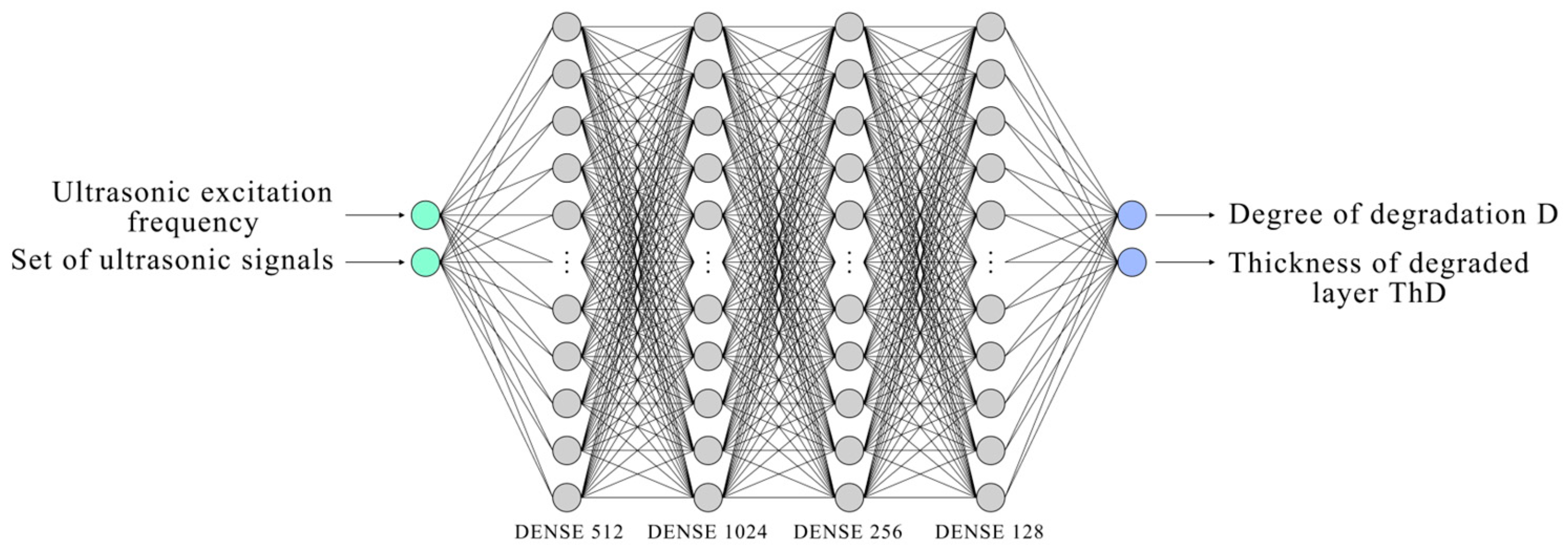
2.3. Building Neural Networks Based on Signals Obtained During Ultrasonic Measurements on the Surfaces of Concrete Specimens
3. Results
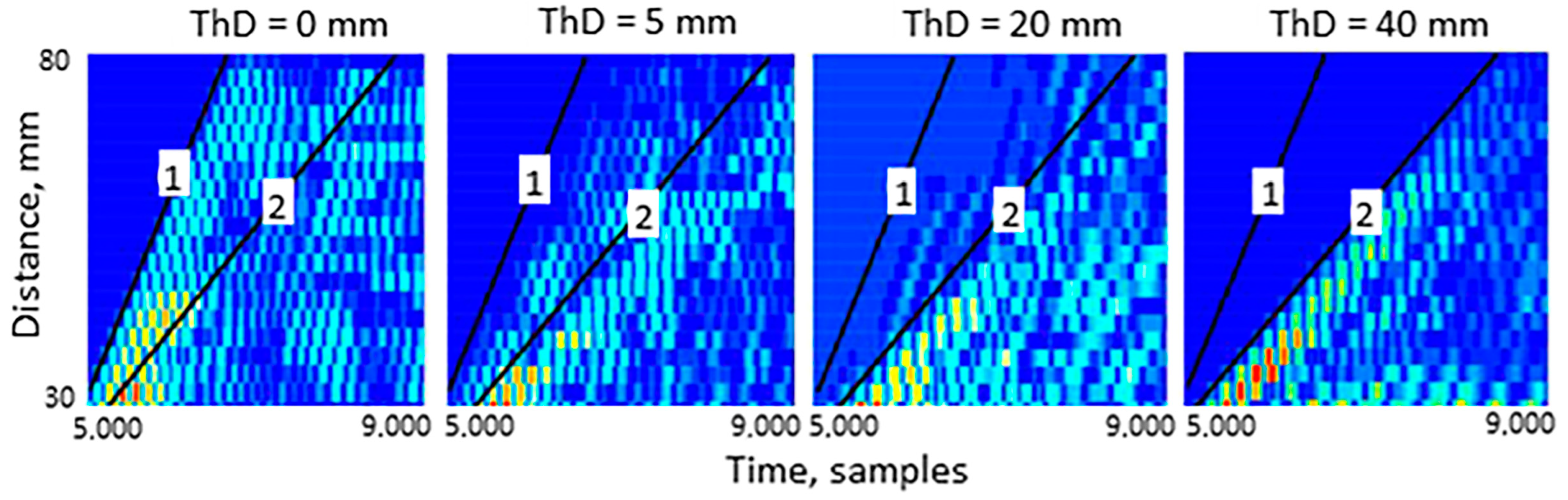
3.1. Spatiotemporal Waveform Profiles
3.2. Application of NN
3.2.1. Classification Results for Ultrasonic Signals
3.2.2. Classification Results for Ultrasonic Signals in Frequency Domain After FFT
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Breugel, K. Societal burden and engineering challenges of ageing infrastructure. Procedia Eng. 2017, 171, 53–63. [Google Scholar] [CrossRef]
- Hobbs, D.W. Concrete deterioration: Causes, diagnosis, and minimising risk. Int. Mater. Rev. 2001, 46, 117–144. [Google Scholar] [CrossRef]
- Rosenqvist, M.; Pham, L.-W.; Terzic, A.; Fridh, K.; Hassanzadeh, M. Effects of interactions between leaching, frost action and abrasion on the surface deterioration of concrete. Constr. Build. Mater. 2017, 149, 849–860. [Google Scholar] [CrossRef]
- Bahafid, S.; Hendriks, M.; Jacobsen, S.; Geiker, M. Revisiting concrete frost salt scaling: On the role of the frozen salt solution micro-structure. Cem. Concr. Res. 2022, 157, 106803. [Google Scholar] [CrossRef]
- ElKhatib, L.W.; Khatib, J.; Assaad, J.J.; Elkordi, A.; Ghanem, H. Refractory Concrete Properties—A Review. Infrastructures 2024, 9, 137. [Google Scholar] [CrossRef]
- Malaiškienė, J.; Antonovič, V.; Boris, R.; Kudžma, A.; Stonys, R. Analysis of the Structure and Durability of Refractory Castables Impregnated with Sodium Silicate Glass. Ceramics 2023, 6, 2320–2332. [Google Scholar] [CrossRef]
- Schabowicz, K. Non-destructive testing of materials in civil engineering. Materials 2019, 12, 3237. [Google Scholar] [CrossRef]
- Khan, A.A. Guidebook on Non-Destructive Testing of Concrete Structures; Training Courses Series; IAEC (International Atomic Energy Agency): Vienna, Austria, 2002; Volume 17. [Google Scholar]
- Kundu, T. (Ed.) Ultrasonic Non-Destructive Evaluation Engineering Biological Material Characterization; CRC Press: Boca Raton, FL, USA, 2003; 848p. [Google Scholar]
- Komlos, K.; Popovics, S.; Niirnbergeroh, T.; Babd, B.; Popovics, J.S. Ultrasonic pulse velocity test of concrete properties as specified in various standards. Cem. Concr. Compos. 1996, 18, 357–364. [Google Scholar] [CrossRef]
- Lencis, U.; Udris, A.; Kara De Maeijer, P.; Korjakins, A. Methodology for determining the correct ultrasonic pulse velocity in concrete. Buildings 2024, 14, 720. [Google Scholar] [CrossRef]
- Irrigaray, M.A.P.; Pinto, R.; Padaratz, I.J. A new approach to estimate compressive strength of concrete by the UPV method. Rev. IBRACON De Estrut. E Mater. 2016, 9, 395–402. [Google Scholar] [CrossRef]
- Chakraborty, J.; Wang, X.; Stolinski, M. Analysis of sensitivity of distance between embedded ultrasonic sensors and signal processing on damage detectability in concrete structures. Acoustics 2022, 4, 89–110. [Google Scholar] [CrossRef]
- Victorov, I.A. Rayleigh and Lamb Waves. Physical Theory and Applications; Plenum Press: New York, NY, USA, 1967. [Google Scholar]
- Li, M.; Anderson, N.; Sneed, L.; Maerz, N. Application of ultrasonic surface wave techniques for concrete bridge deck condition assessment. J. Appl. Geophys. 2016, 126, 148–157. [Google Scholar] [CrossRef]
- Cho, Y.S. Non-destructive testing of high strength concrete using spectral analysis of surface waves. NDTE Int. 2003, 36, 229–235. [Google Scholar] [CrossRef]
- RILEM NDT 4, Recommendation for In Situ Concrete Strength Determination by Combined Non-Destructive Methods, Compendium of RILEM Technical Recommendations; E&FN Spon: London, UK, 1993.
- Tatarinov, A.; Sisojevs, A.; Chaplinska, A.; Shahmenko, G.; Kurtenoks, V. An approach for assessment of concrete deterioration by surface waves. Procedia Struct. Integr. 2022, 37, 453–461. [Google Scholar] [CrossRef]
- Li, M.; Salucci, M. Applications of Deep Learning in Electromagnetics: Teaching Maxwell’s Equations to Machines; IET Digital Library: Stevenage, UK, 2022; 480p. [Google Scholar] [CrossRef]
- Bowler, A.L.; Pound, M.P.; Watson, N.J. A review of ultrasonic sensing and machine learning methods to monitor industrial processes. Ultrasonics 2022, 124, 106776. [Google Scholar] [CrossRef]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press Massachusetts Institute of Technology: Cambridge, MA, USA, 2016; ISBN 9780262035613. [Google Scholar]
- Chan, K.Y.; Abu-Salih, B.; Qaddoura, R.; Al-Zoubi, A.M.; Palade, V.; Pham, D.S.; Del Ser, J.; Muhammad, K. Deep neural networks in the cloud: Review, applications, challenges and research directions. Neurocomputing 2023, 545, 126327. [Google Scholar] [CrossRef]
- Hind, T.; Mas, J.-F. Multilayer Perceptron (MLP); In Geomatic Approaches for Modeling Land Change Scenarios; Springer: Cham, Switzerland, 2018. [Google Scholar] [CrossRef]
- Khotanzad, A.; Chung, C. Application of multi-layer perceptron neural networks to vision problems. Neural Comput. Applic. 1988, 7, 249–259. [Google Scholar] [CrossRef]
- Haykin, S. Neural Networks: A Comprehensive Foundation, 2nd ed.; Prentice Hall: Englewood Cliffs, NJ, USA, 1998; 842p, ISBN 978-0-13-273350-2. [Google Scholar]
- Abdi, H.; Williams, L.J. Principal component analysis. Wiley Interdiscip. Rev. Comput. Stat. 2010, 2, 433–459. [Google Scholar] [CrossRef]
- Salas-Gonzalez, D.; Górriz, J.M.; Ramírez, J.; Illán, I.A.; López, M.; Segovia, F.; Chaves, R.; Padilla, P.; Puntonet, C.G.; Alzheimer’s Disease Neuroimage Initiative. Feature selection using factor analysis for Alzheimer’s diagnosis using 18F-FDG PET images. Med. Phys. 2010, 37, 6084–6095. [Google Scholar] [CrossRef]
- Zhang, K.; Lv, G.; Guo, S.; Chen, D.; Liu, Y.; Feng, W. Evaluation of subsurface defects in metallic structures using laser ultrasonic technique and genetic algorithm-back propagation neural network. NDT E Int. 2020, 116, 102339. [Google Scholar] [CrossRef]
- Liu, J.; Xu, G.; Ren, L.; Qian, Z.; Ren, L. Defect intelligent identification in resistance spot welding ultrasonic detection based on wavelet packet and neural network. Int. J. Adv. Manuf. Technol. 2017, 90, 2581–2588. [Google Scholar] [CrossRef]
- Wang, Y. Wavelet transform based feature extraction for ultrasonic flaw signal classification. J. Comput. 2014, 9, 725–732. [Google Scholar] [CrossRef]
- Mousavi, M.; Taskhiri, M.S.; Holloway, D.; Olivier, J.; Turner, P. Feature extraction of woodhole defects using empirical mode decomposition of ultrasonic signals. NDT E Int. 2020, 114, 102282. [Google Scholar] [CrossRef]
- Waszczyszyn, Z.; Ziemianski, L. Neural networks in mechanics of structures and materials—New results and prospects of applications. Comput. Struct. 2001, 79, 2261–2276. [Google Scholar] [CrossRef]
- Liu, S.W.; Huang, J.H.; Sung, J.C.; Lee, C.C. Detection of cracks using neural networks and computational mechanics. Comput. Methods Appl. Mech. Eng. 2002, 191, 2831–2845. [Google Scholar] [CrossRef]
- Khandetsky, V.; Antonyuk, I. Signal processing in defect detection using back-propagation neural networks. NDTE Int. 2002, 35, 483–488. [Google Scholar] [CrossRef]
- Xu, Y.; Liu, G.; Wu, Z.; Huang, X. Adaptive multilayer perceptron networks for detection of cracks in anisotropic laminated plates. Int. J. Solids Struct. 2001, 38, 5625–5645. [Google Scholar] [CrossRef]
- Fang, X.; Luo, H.; Tang, J. Structural damage detection using neural network with learning rate improvement. Comput. Struct. 2005, 83, 2150–2161. [Google Scholar] [CrossRef]
- Hernández-Gómez, L.H.; Durodola, J.; Fellows, N.; Urriolagoitia-Calderón, G. Locating defects using dynamic strain analysis and artificial neural networks. Appl. Mech. Mater. 2005, 3–4, 325–330. [Google Scholar] [CrossRef]
- Shi, S.; Jin, S.; Zhang, D.; Liao, J.; Fu, D.; Lin, L. Improving Ultrasonic Testing by Using Machine Learning Framework Based on Model Interpretation Strategy. Chin. J. Mech. Eng. 2023, 36, 127. [Google Scholar] [CrossRef]
- Lv, G.; Guo, S.; Chen, D.; Feng, H.; Zhang, K.; Liu, Y.; Feng, W. Laser ultrasonics and machine learning for automatic defect detection in metallic components. NDT E Int. 2023, 133, 102752. [Google Scholar] [CrossRef]
- Ferreira, G.R.B.; Ribeiro, M.G.d.C.; Kubrusly, A.C.; Ayala, H.V.H. Improved feature extraction of guided wave signals for defect detection in welded thermoplastic composite joints. Measurement 2022, 198, 111372. [Google Scholar] [CrossRef]
- Solov’ev, A.N.; Cherpakov, A.V.; Vasil’ev, P.V.; Parinov, I.A.; Kirillova, E.V. Neural network technology for identifying defect sizes in half-plane based on time and positional scanning. Adv. Eng. Res. 2020, 20, 205–215. [Google Scholar] [CrossRef]
- Shrestha, A.; Mahmood, A. Review of deep learning algorithms and architectures. IEEE Access 2019, 7, 53040–53065. [Google Scholar] [CrossRef]
- Hu, T.; Zhao, J.; Zheng, R.; Wang, P.; Li, X.; Zhang, Q. Ultrasonic based concrete defects identification via wavelet packet transform and GA-BP neural network. PeerJ Comput. Sci. 2021, 7, e635. [Google Scholar] [CrossRef]
- Shin, H.K.; Ahn, Y.H.; Lee, S.H.; Kim, H.Y. Automatic concrete damage recognition using multi-level attention convolutional neural network. Materials 2020, 13, 5549. [Google Scholar] [CrossRef]
- Nyathi, M.A.; Bai, J.; Wilson, I.D. Deep Learning for Concrete Crack Detection and Measurement. Metrology 2024, 4, 66–81. [Google Scholar] [CrossRef]
- Rodrigues, L.F.M.; Cruz, F.C.; Oliveira, M.A.; Filho, E.F.S.; Albuquerque, M.S.C.; da Silva, I.C.; Farias, C.T.T. Identification of carburization level in industrial HP pipes using ultrasonic evaluation and machine learning. Ultrasonics 2018, 94, 145–151. [Google Scholar] [CrossRef]
- Almasaeid, H. Ultrasonic pulse velocity and artificial neural network prediction of high-temperature damaged concrete splitting strength. Discov. Appl. Sci. 2024, 6, 4. [Google Scholar] [CrossRef]
- Bonagura, M.; Nobile, L. Artificial Neural Network (ANN) Approach for Predicting Concrete Compressive Strength by SonReb. Struct. Durab. Health Monit. 2021, 15, 125–137. [Google Scholar] [CrossRef]
- Park, J.Y.; Yoon, Y.G.; Oh, T.K. Prediction of Concrete Strength with P-, S-, R-Wave Velocities by Support Vector Machine (SVM) and Artificial Neural Network (ANN). Appl. Sci. 2019, 9, 4053. [Google Scholar] [CrossRef]
- Wang, J.; Schmitz, M.; Jacobs, L.J.; Qu, J. Deep learning-assisted locating and sizing of a coating delamination using ultrasonic guided waves. Ultrasonics 2024, 141, 107351. [Google Scholar] [CrossRef] [PubMed]
- Trtnik, G.; Kavcic, F.; Turk, G. Prediction of concrete strength using ultrasonic pulse velocity and artificial neural networks. Ultrasonics 2009, 49, 53–60. [Google Scholar] [CrossRef] [PubMed]
- Terven, J.; Cordova-Esparza, D.-M.; Ramirez-Pedraza, A.; Chávez Urbiola, E. Loss Functions and Metrics in Deep Learning. A Review. arXiv 2024. [Google Scholar] [CrossRef]
- Stone, J.V. The Fourier Transform: A Tutorial Introduction; Sebtel Press, University of Shefield: Sheffield, UK, 2021; 91p. [Google Scholar]
- Li, Y.; Feng, Z.; Hao, L.; Huang, L.; Xin, C.; Wang, Y.; Bilotti, E.; Essa, K.; Zhang, H.; Li, Z.; et al. A Review on Functionally Graded Materials and Structures via Additive Manufacturing: From Multi-Scale Design to Versatile Functional Properties. Adv. Mater. Technol. 2020, 5, 1900981. [Google Scholar] [CrossRef]
- Lu, L.; Chekroun, M.; Abraham, O.; Maupin, V.; Villain, G. Mechanical properties estimation of functionally graded materials using surface waves recorded with a laser interferometer. NDT E Int. 2011, 44, 169–177. [Google Scholar] [CrossRef]
- Vatulyan, A.O.; Bogachev, I.V. The Projection Method for Identification of the Characteristics of Inhomogeneous Solids. Dokl. Phys. 2018, 63, 82–85. [Google Scholar] [CrossRef]







| Parameter | Value |
|---|---|
| Applied ultrasonic frequencies | 50, 100, 200 kHz |
| Excitation waveform | 2-period sine tone-burst |
| Output voltage | 100 V p-t-p |
| ADC of received ultrasonic signals | 10-bit, 30 MHz |
| Length and step of scanning | 100 mm, 5 mm |
| Number of ultrasonic signals in a profile set | 21 |
| Ultrasonic Frequency, kHz | Velocity, m/s | |||
|---|---|---|---|---|
| S | D1 | D2 | D3 | |
| 50 | 2287 | 1916 | 1676 | 1266 |
| 100 | 2300 | 1978 | 1784 | 1278 |
| 200 | 2353 | 2020 | 1780 | 1318 |
| Ultrasonic Frequency, kHz | Projected Values | Predicted Values with Different Networks | ||||||
|---|---|---|---|---|---|---|---|---|
| “NN” | “NN3000” | “NN10000” | ||||||
| D, Degree | ThD, mm | D, Degree | ThD, mm | D, Degree | ThD, mm | D, Degree | ThD, mm | |
| 50 | D1 | 3.0 | D3 ** | 3.67 | D1 | 2.31 | D1 | 3.69 |
| 50 | D2 | 3.0 | D2 | 4.08 | D2 | 3.83 | D2 | 3.09 |
| 50 | D3 | 3.0 | D1 ** | 3.99 | D3 | 2.91 | D3 | 2.44 |
| 100 | D1 | 3.0 | D1 | 3.34 | D1 | 2.36 | D1 | 3.50 |
| 100 | D2 | 3.0 | D2 | 3.44 | D2 | 2.60 | D2 | 3.56 |
| 100 | D3 | 3.0 | D3 | 2.53 | D3 | 3.91 | D3 | 3.06 |
| 200 | D1 | 3.0 | D1 | 2.84 | D1 | 3.40 | D1 | 2.80 |
| 200 | D2 | 3.0 | D2 | 3.94 | D2 | 3.45 | D2 | 2.84 |
| 200 | D3 | 3.0 | D3 | 2.94 | D3 | 3.40 | D3 | 3.60 |
| 50 | D1 | 25.0 | D1 | 23.64 | D1 | 25.98 | D1 | 25.65 |
| 50 | D2 | 25.0 | D2 | 25.32 | D2 | 24.99 | D2 | 24.63 |
| 50 | D3 | 25.0 | D3 | 27.87 | D3 | 25.73 | D3 | 25.76 |
| 100 | D1 | 25.0 | D1 | 26.44 | D1 | 24.60 | D1 | 24.84 |
| 100 | D2 | 25.0 | D2 | 27.00 | D2 | 25.04 | D2 | 24.27 |
| 100 | D3 | 25.0 | D3 | 25.67 | D3 | 25.34 | D3 | 24.50 |
| 200 | D1 | 25.0 | D1 | 27.26 | D1 | 25.85 | D1 | 25.19 |
| 200 | D2 | 25.0 | D2 | 27.09 | D2 | 25.66 | D2 | 25.42 |
| 200 | D3 | 25.0 | D3 | 24.70 | D3 | 24.53 | D3 | 24.29 |
| Ultrasonic Frequency, kHz | Projected Values | Predicted Values with Different Networks | ||||||
|---|---|---|---|---|---|---|---|---|
| “NNFT” | “NNFT3000” | “NNFT10000” | ||||||
| D, Degree | ThD, mm | D, Degree | ThD, mm | D, Degree | ThD, mm | D, Degree | ThD, mm | |
| 50 | D1 | 3.0 | D2 * | 0.99 | D3 ** | 3.92 | D1 | 4.99 |
| 50 | D2 | 3.0 | D2 | 3.67 | D2 | 2.83 | D2 | 4.09 |
| 50 | D3 | 3.0 | D1 ** | 5.93 | D3 | 4.55 | D3 | 1.37 |
| 100 | D1 | 3.0 | D1 | 1.23 | D3 ** | 3.36 | D1 | 1.80 |
| 100 | D2 | 3.0 | D3 * | 0.024 | D3 * | 4.34 | D2 | 1.87 |
| 100 | D3 | 3.0 | D3 | 1.86 | D3 | 4.92 | D3 | 4.09 |
| 200 | D1 | 3.0 | D1 | 3.95 | D3 ** | 6.65 | D1 | 2.19 |
| 200 | D2 | 3.0 | D2 | 5.09 | D2 | 3.97 | D2 | 2.29 |
| 200 | D3 | 3.0 | D2 * | 5.98 | D3 | 4.87 | D2* | 4.37 |
| 50 | D1 | 25.0 | D1 | 22.32 | D1 | 28.73 | D1 | 23.66 |
| 50 | D2 | 25.0 | D3 * | 22.89 | D2 | 27.47 | D3* | 25.00 |
| 50 | D3 | 25.0 | D3 | 26.10 | D3 | 28.35 | D3 | 26.21 |
| 100 | D1 | 25.0 | D1 | 24.91 | D1 | 26.88 | D1 | 23.98 |
| 100 | D2 | 25.0 | D2 | 25.66 | D2 | 23.31 | D2 | 24.51 |
| 100 | D3 | 25.0 | D1 ** | 22.69 | D3 | 28.12 | D1** | 24.55 |
| 200 | D1 | 25.0 | D1 | 26.75 | D1 | 28.20 | D1 | 23.92 |
| 200 | D2 | 25.0 | D2 | 23.42 | D2 | 28.55 | D2 | 24.47 |
| 200 | D3 | 25.0 | D3 | 26.58 | D3 | 25.34 | D3 | 24.29 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kirillova, E.; Tatarinov, A.; Kovalenko, S.; Shahmenko, G. Prediction of Degradation of Concrete Surface Layer Using Neural Networks Applied to Ultrasound Propagation Signals. Acoustics 2025, 7, 19. https://doi.org/10.3390/acoustics7020019
Kirillova E, Tatarinov A, Kovalenko S, Shahmenko G. Prediction of Degradation of Concrete Surface Layer Using Neural Networks Applied to Ultrasound Propagation Signals. Acoustics. 2025; 7(2):19. https://doi.org/10.3390/acoustics7020019
Chicago/Turabian StyleKirillova, Evgenia, Alexey Tatarinov, Savva Kovalenko, and Genadijs Shahmenko. 2025. "Prediction of Degradation of Concrete Surface Layer Using Neural Networks Applied to Ultrasound Propagation Signals" Acoustics 7, no. 2: 19. https://doi.org/10.3390/acoustics7020019
APA StyleKirillova, E., Tatarinov, A., Kovalenko, S., & Shahmenko, G. (2025). Prediction of Degradation of Concrete Surface Layer Using Neural Networks Applied to Ultrasound Propagation Signals. Acoustics, 7(2), 19. https://doi.org/10.3390/acoustics7020019







