1. Introduction
The Baroque style in Europe was born from the religious confrontation between Protestants and Catholics, prompting changes in mentality that were unequivocally reflected in cultural aspects, and in turn, in the definition of buildings, especially churches. This new style, which emerged in Europe, spread to South America as part of the inevitable transfer of knowledge that had been taking place between both continents since the arrival of Europeans in the Americas.
At the Council of Trent (1545–1563), convened in response to the Protestant Reformation, decisions were made regarding aspects other than Catholic doctrine and rites. As Navarro and Sendra [
1] highlighted, while in Protestant churches, everything revolves around the word, the aspect of visibility must also be considered in Catholic churches as the word is accompanied by ritual gesture. In any case, both Catholic and Protestant churches show a greater concern for the intelligibility of the word, and during the Baroque period, this concern spread to other areas such as theatre, where elements such as the proscenium arch [
2] were introduced.
In the final sessions of the Council, questions were raised concerning the architectural characteristics of the churches, as detailed by the Jesuit Carlos Borromeo in his book
Fabricae et Supellectilis Ecclesiasticae [
3]. In the case of floor plans, the cross shape, preferably Latin and single-nave, is proposed as a symbol of Christianity and favoured over the central floor plan, which was considered more appropriate by Renaissance architects.
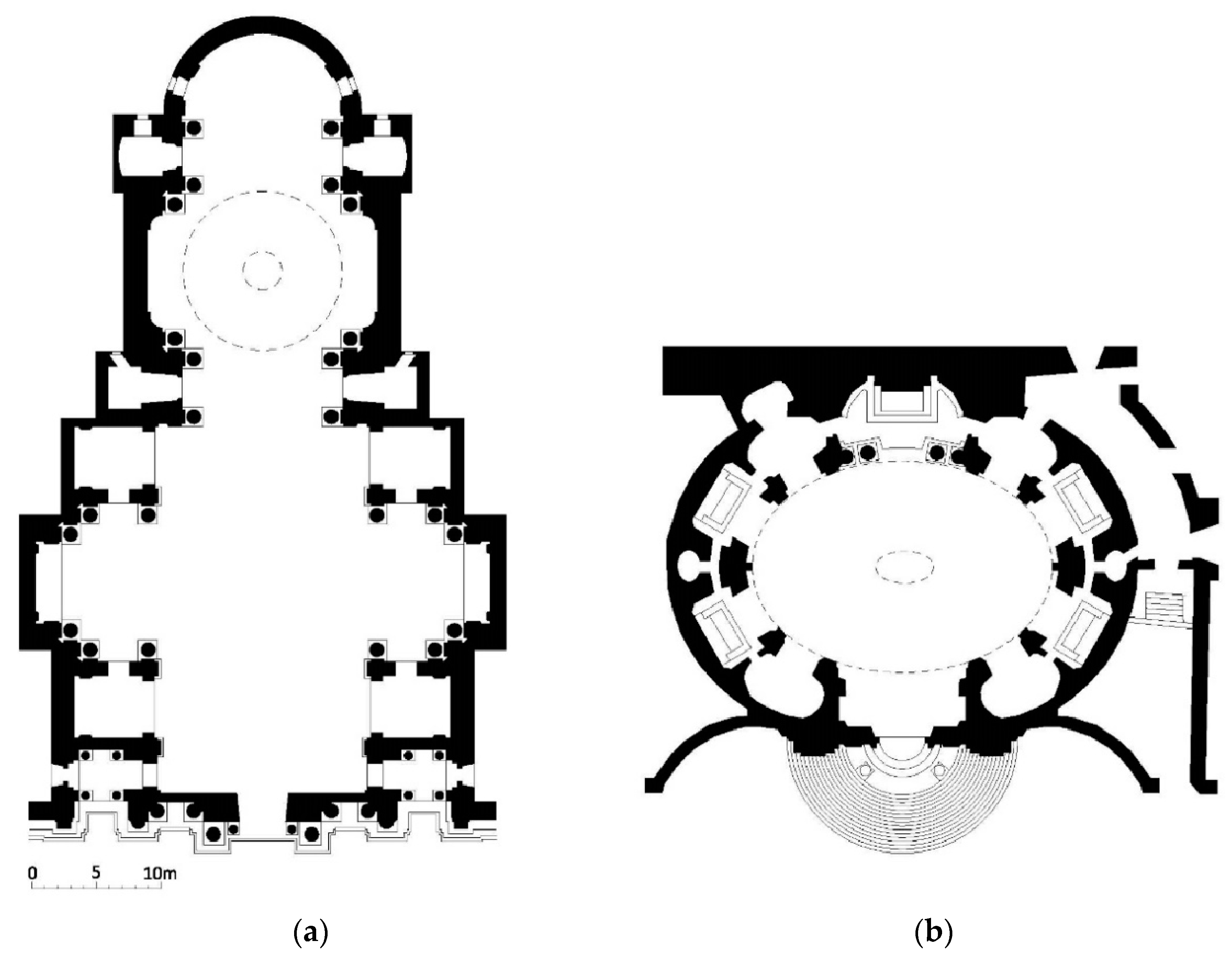
The starting point of Baroque churches can be traced back to the church of Il Gesú in Rome. Churches with a central longitudinal plan or elongated central plan are based on this model, while the dome appears as the centralising element in larger churches. The smaller churches and chapels are resolved on many occasions with a central plan organised on a longitudinal axis [
4], developed from three types: circular, Greek cross and oval. According to Sendra and Navarro [
1], when examining typologies, we can take the church of Santa Maria in Campitelli, by the architect Carlo Rainaldi, as an example as it clearly follows the longitudinal plan scheme, while the oval plan of San Andrea al Quirinale by Bernini, also in Rome, corresponds to the central plan model (
Figure 1).
This church by Bernini is a clear example of the substitution of rectilinear forms for curved forms in a concave and convex succession aiming to create a greater overall dynamic effect. Bernini achieves a non-centripetal space in an oval-shaped central plan by lengthening the transversal axis of the oval and placing pilasters at the ends instead of chapels. For Wittkober, R. [
5], this model paved the way for the solution of central floor plans suited to liturgical needs, something that had not been the case until then.
The influence of Baroque architecture, which had originated in Rome, reached Central Europe, where it can be clearly seen in examples such as Karlskirche in Vienna (Austria, 1715–1737), by the architect J.B. Fischer von Erlach, or the pilgrimage church of Wieskirche in Wies-bei-Steingaden, (Germany, 1745–1757), designed by Zimmermann. The Baroque style, which spread through Europe following its creation in Italy, adapts to the materials and constructive capacities of individual regions, at times displaying unique features. This was the case in Andalusia (Spain) with the development of the Andalusian Baroque, where local artists blended the Mudejar and Baroque traditions, combining them with a clear Italian influence. This fusion of styles also spread to Latin America, where it was widely developed.
In terms of acoustics, especially high-pitched sounds, as indicated by Navarro and Sendra [
1], the conditions in Baroque churches improved with respect to the earlier Renaissance churches, mainly due to ornamentation. The mouldings, pilasters, entablatures, cornices, capitals, wooden altarpieces and other decorative elements contribute to the better diffusion of high-frequency sounds, while the larger side chapels result in a greater diffusion of low-pitched sounds. Thus, they show that the extensive ornamentation used in churches during the 17th and 18th centuries, especially in large religious celebrations, results in modified characteristics for the acoustic absorption of the walls, accommodating musical and choral performances.
In the last 50 years, different research groups have carried out numerous studies aimed at ascertaining the acoustic conditions of places of worship of different characteristics and periods. Many of these were collected in the study carried out by Girón [
6] et al., which offers a comprehensive review of acoustics in churches over time. In this work, we will focus exclusively on the comprehensive review of the acoustics of the Catholic religious spaces of the Baroque period between the second half of the 16th century and the first half of the 18th century.
In the field of acoustics concerning Catholic Baroque church spaces, it is worth highlighting the studies by Lottermoser [
7], who analysed the reverberation times by frequency in five Baroque churches belonging to abbeys in Swabia and Alsace (Germany), noting that the acoustic properties are especially favourable in these enclosures (
Figure 2).
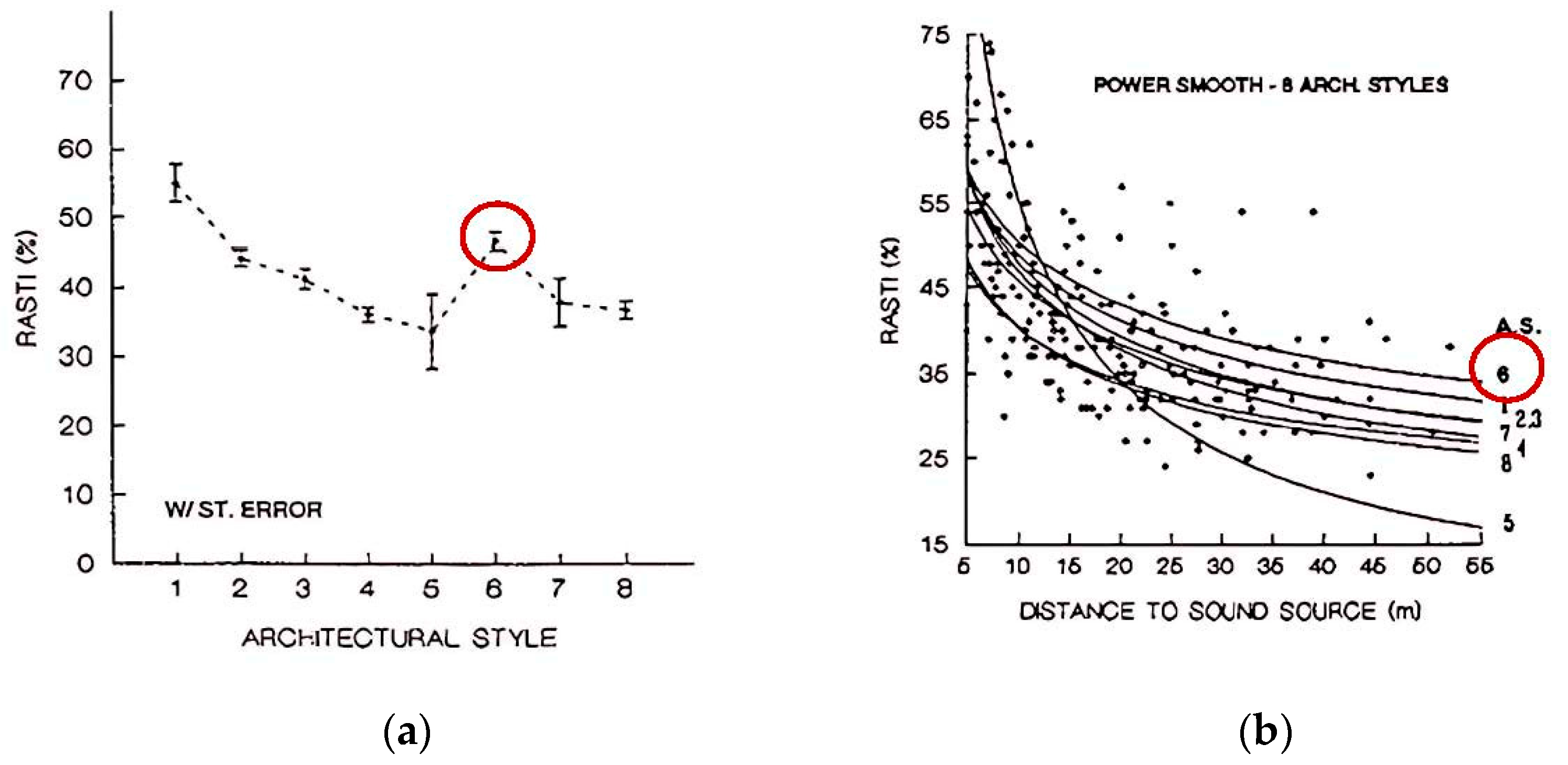
In Portugal, Carvalho and Desarnaulds [
8,
9] analysed a wide sample of Portuguese Catholic churches of different styles, including at least eight Baroque churches from the 17th and 18th centuries. In his studies, monaural and binaural parameters were analysed, observing improved speech intelligibility in churches from the Baroque period. The studies focusing on the analysis of the average RASTI values stand out, as these decreased from the Visigoth period to the Renaissance, later increased in the Baroque, and decreased again until the present (
Figure 3).
A large group of researchers in Italy has analysed the acoustics of church buildings. In addition, the studies carried out by Shankland [
10] on patriarchal basilicas show that the large number of diffusing surfaces found in Baroque decoration contribute to increased absorption, while also increasing the potential presence of coupled spaces in the side naves of churches. Cirillo-Martellotta [
11] carried out an interesting analysis of liturgy, architecture and acoustics, studying a group of thirty-one churches, six of which are in the Baroque style. The construction process, architectural characteristics, interior materials and main dimensions of the individual characteristics are presented to ultimately contribute a single-number value of the main acoustic parameters related to the subjective characteristics of human hearing. Among the main conclusions, it is worth highlighting the volume of the enclosures for the architectural style, which, with an average volume of 14,000 m
3 for the sample of Baroque churches, is smaller than in previous architectural styles. When comparing the reverberation time against the architectural style, a decrease can be observed in relation to its predecessors, as reflected by Carvalho in the Portuguese churches.
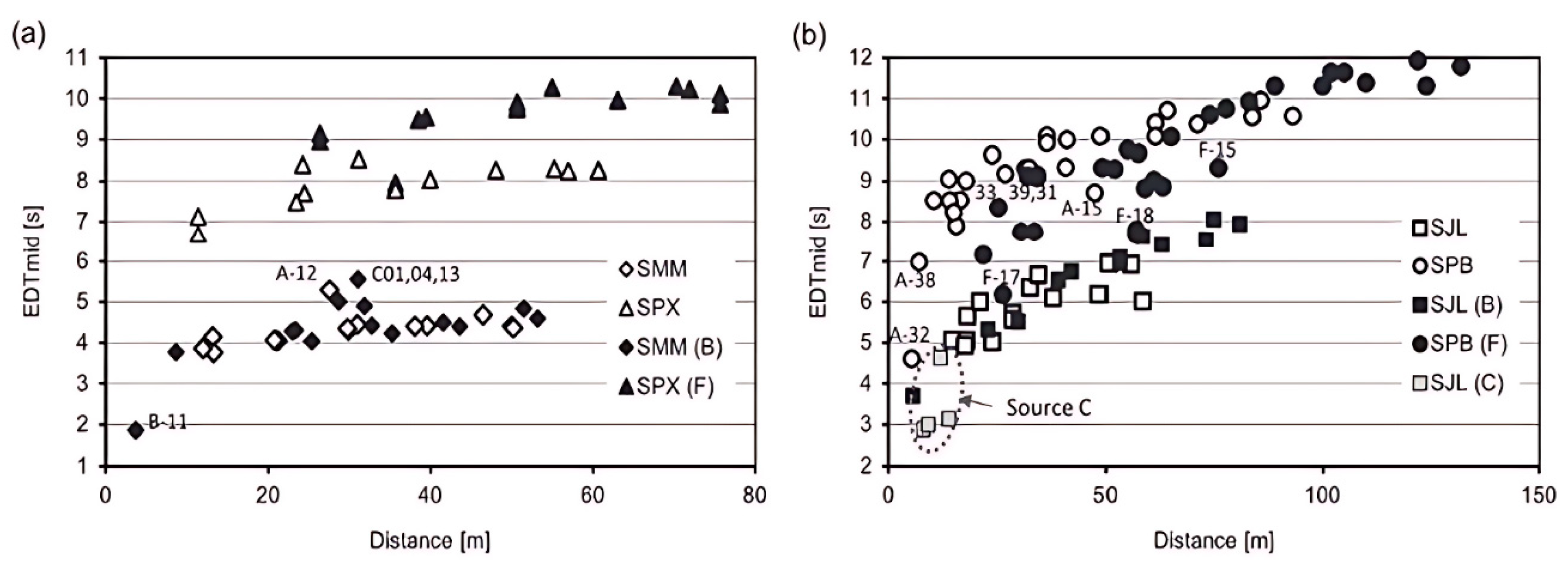
Furthermore, when Martellotta [
12] returns to study the basilica spaces of Rome using a Bayesian analysis through the algorithm proposed by Xiang et al. [
13], he investigates the existence of double slope behaviour as a consequence of coupled spaces, extremely common in this type of large enclosure, along with the presence of domes, side naves and numerous chapels. In order to explain the anomalies that were observed in the distribution of the energy parameters in each church in the analysis carried out, the basilicas were considered a system of acoustically coupled volumes, while secondary spaces such as corridors and chapels played a different role depending on the amount of sound absorption in the main hall. It is concluded that the presence of coupled spaces does not always imply a drop in reverberation time. This study evidenced the trend in the early reverberation time (EDT) as a function of the source–receiver distance, with lower values at distances close to the source due to the presence of direct sound and very energetic early reflections and a gradual increase the further removed from the source as a consequence of low or no energetic early reflections (
Figure 4).
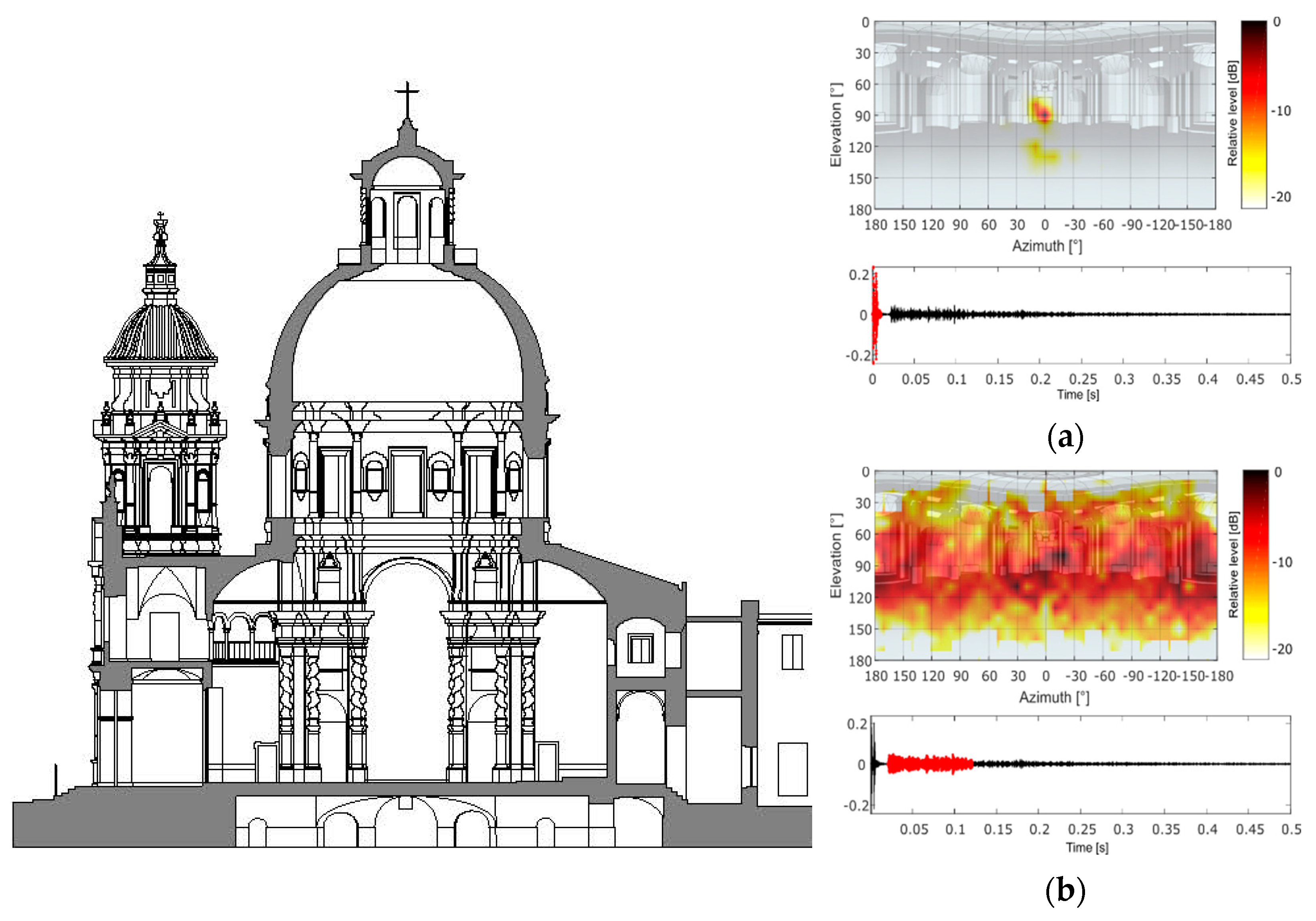
This behaviour, typical of coupled volumes, is also found in spaces with a single volume, such as central floor plans, as observed in the study by Alberdi et al. [
14] on the Baroque church of San Luis de los Franceses (Seville, Spain), in which the shape of the concave dome can give rise to unexpected acoustic phenomena, such as focalizations that can increase the sound pressure level or cause colorations in the sound or echoes.
The studies carried out by Álvarez-Morales and Martellotta [
15], analysing the effect of the occupation and the position of the sound source of several Christian churches through acoustic simulations including the Baroque church of Santi Luca, conclude that the position of the pulpit, a common element from the 15th century onwards, produces better results due to the decrease in source–receiver distances.
The studies by Magrini and Ricciardi [
16,
17] focus on a group of churches in the Italian city of Genoa, built between the 11th and 16th centuries. Three of these churches can be considered to have a totally Baroque interior finish. The values of reverberation time, clarity and definition versus frequency are presented, and it can be observed that the churches of S.S. Annunziata and S.M. delle Vigne, more similar in terms of typology, display similar tendencies. In addition, Ricciardi presents studies carried out on a group of churches with a central floor plan, including three Baroque churches with a Greek cross plan. Among the Italian researchers we highlight the contributions made by Caniato et al. [
18] on the study of Baroque churches with a central floor plan. This study analysed the church of San Lorenzo in Turin, with a profusely decorated interior, which resulted in a high diffusion of sound.
This octagonal church is made up of two connected spaces: the main room, subdivided into two spaces, and the chapel of the Crucifix. The authors analyse reverberation times, clarity and definition for three source positions, one of them under the dome, observing anomalous behaviours at various points, which seem to suggest the possibility of non-linear energy decay curves and/or coupled spaces (
Figure 5).
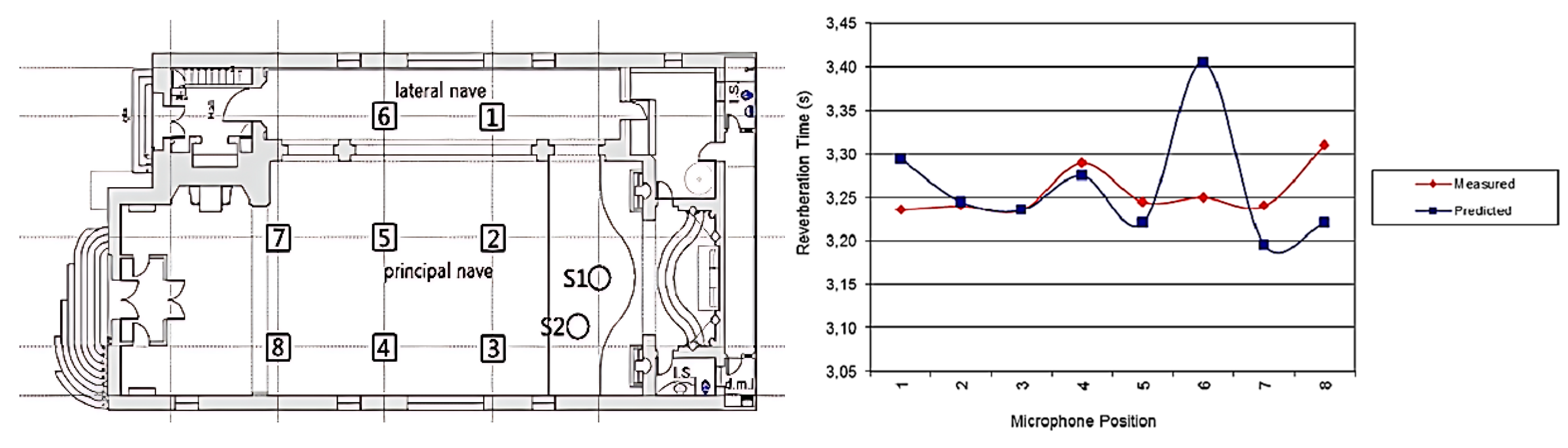
In Spain, we highlight the work carried out by Segura et al. [
19] on the Basilica of Sant Jaume, where the results obtained are compared using different commercial programmes for the measurement of impulse responses and two acoustic simulation programmes. This comparison of the results obtained uses the subjective values of perception, just noticeable difference (JND), as a reference for comparison. Garcia et al. [
20] and Planells et al. [
21] carry out acoustic research on its current state and the initial stages of the basilica of Santa María de Elche. To do so, they simulate the representation of the “Misteri d’Élx”, which has been carried out continuously since the 15th century, showing the importance of ephemeral assemblies for festivities, prevalent in the Baroque period. Finally, auralisations of this choral representation are generated.
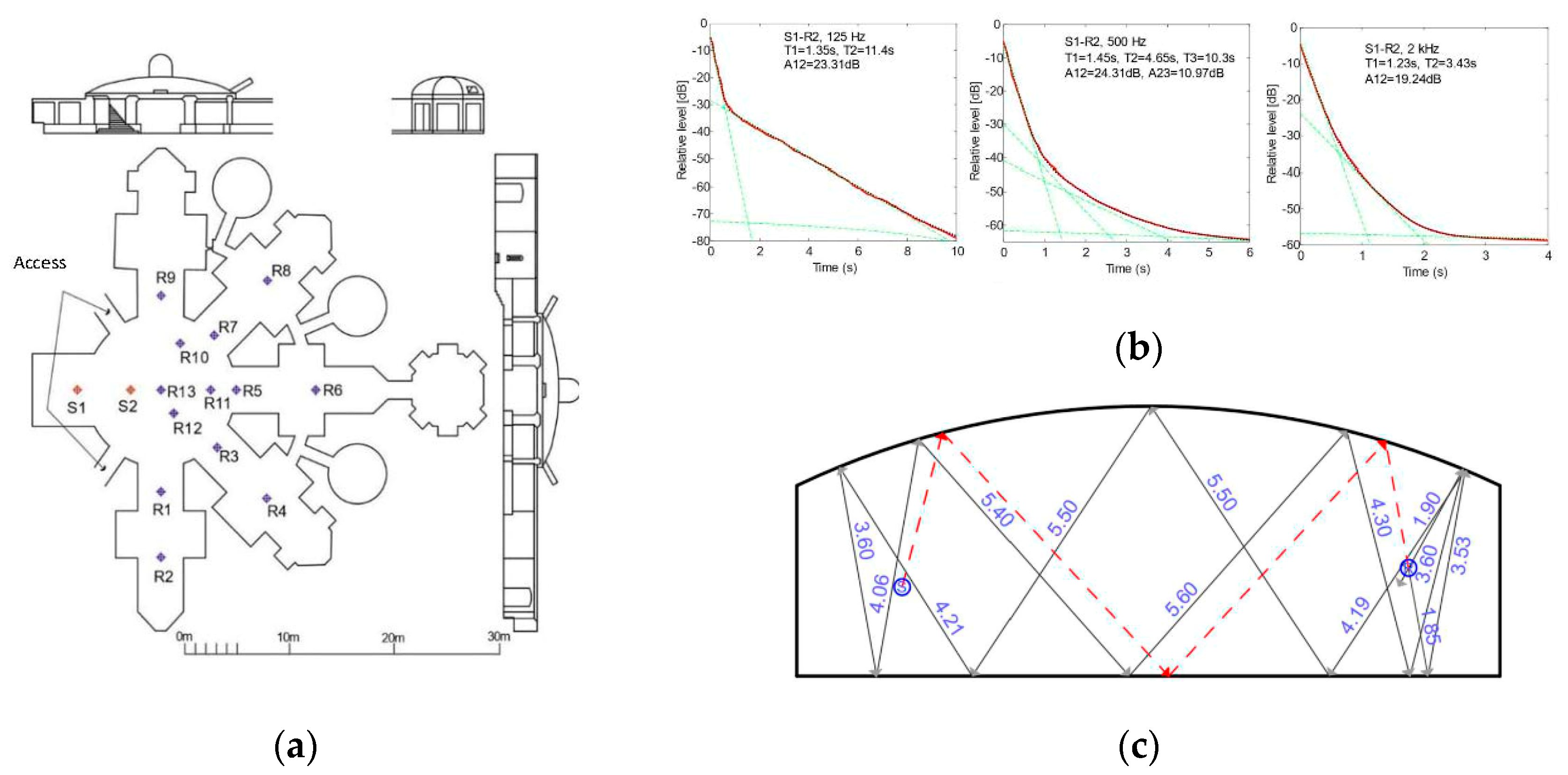
Within the research project carried out on acoustics in Spanish cathedrals, the Baroque-style cathedral of Cádiz is analysed by Álvarez et al. [
22]. According to this study, when the source is located in the back choir, the intelligibility can be defined as fair, which suggests that this associated space is suitable for the celebration of certain activities requiring a good understanding of the spoken message. Moreover, it is confirmed that the use of the pulpit slightly improves both music and speech in the audience area and has no influence on the subjective sound level or spatial impression. As for central spaces, the cathedral, which has a crypt consisting of a circular rotunda covered with a low dome, is connected to radial galleries linked to the main space through multiple small openings, resulting in almost unique acoustic characteristics in this space. The acoustic study carried out by Martellotta et al. [
23] on this space using a Bayesian analysis showed a late fall appearing in the crypt at a rate different to that observed in the cathedral. Therefore, the acoustic coupling of different volumes was ruled out. Directional intensity maps obtained showed that the late fall originated from the rotunda where a repetitive pattern of reflections appeared between the ground and the dome, causing flutter echoes and a longer reverberation time (
Figure 6).
Finally, the studies carried out by Alberdi et al. focus on Andalusian Baroque-style churches in the city of Seville. These analyse central spaces such as the church of San Luis de los Franceses [
14], where the presence of the dome can be associated with an uneven distribution of direct sound energy caused by acoustic coupling between different sub-volumes (
Figure 7).
In addition to the analysis of different church typologies, both with a Latin cross and a single-nave plan [
24], the study is complemented with an archaeoacoustic analysis of these churches and their different spatial configurations, as well as the positions of sources and receivers, from the time of construction up to the present day [
25]. In addition, for the church of Santa María Magdalena, several positions of simultaneous sources are considered based on polychoral musical compositions typical of the 18th century. An analysis of the most favourable source combinations shows how the use of different source combinations improves the subjective sensation of sound, tending to homogenise the ranges in all parameters, except for EDT [
26].
It is worth noting the research by Niemas [
27], Engel [
28,
29] and Kosala [
30] in Poland on a wide sample of churches, some of them Baroque, contributing to the calculation of an objective global index for the word and music.
In the case of studies carried out in Baroque churches in Latin America, the work by Queiroz et al. [
31] in Brazil on the Baroque church of Nossa Senhora do Rosário is especially noteworthy for the acoustic measurements and simulations carried out. According to the results obtained, simulation, applying the engineering precision level combined with the Lambert sound diffusion method to all materials, provides a better prediction than in situ measurements (
Figure 8).
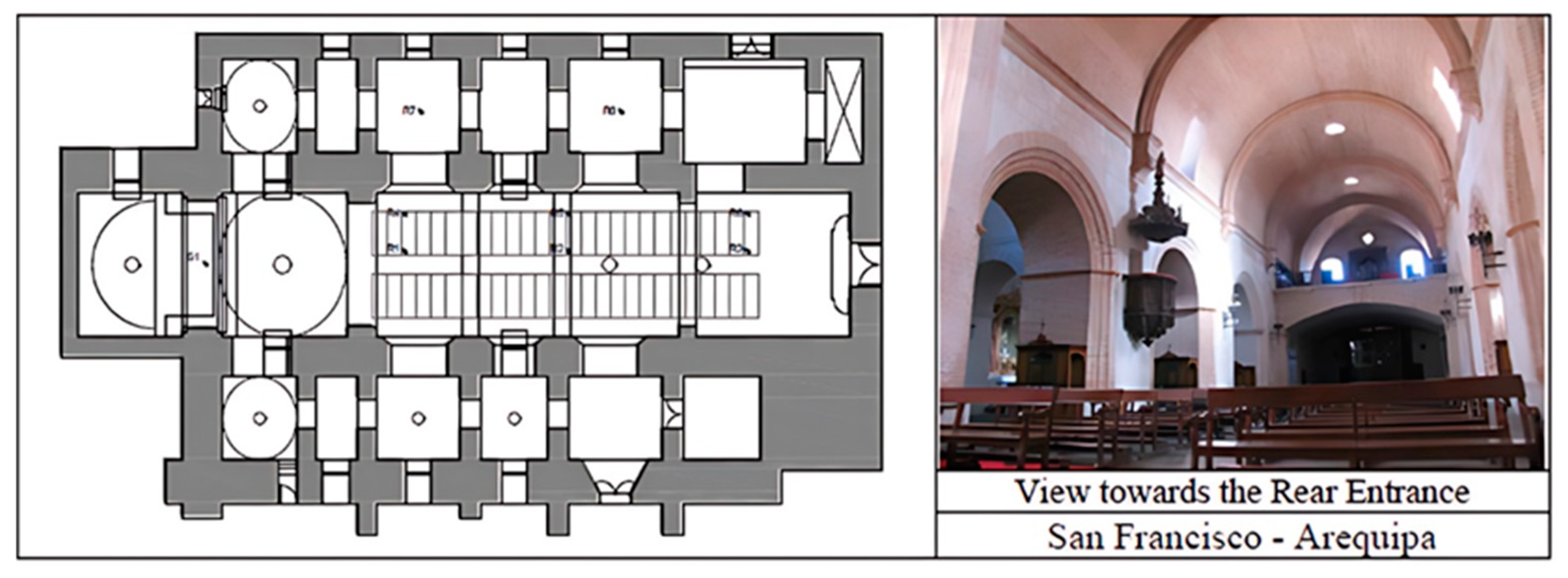
In Peru, the doctoral thesis by Jimenez Dianderas [
32] studies a large sample of 52 churches, 28 of which are Baroque. Some of the aspects investigated include the relationships of the geometrical and acoustic parameters and were analysed by architectural style. It is observed how the architectural changes affect the means of the objective acoustic parameters, which improved from the Renaissance to the Baroque. Based on these results, the three styles of the Renaissance, Baroque and Neoclassical [
33] are compared in search of correlations between acoustic and architectural parameters. The correlations established are not significant, even when dealing with churches in the same style. Furthermore, together with Carvalho [
34], Jimenez Dianderas analysed the acoustic behaviour of 10 Portuguese and 10 Peruvian churches, dating from a period when both countries were ruled by the same king (1580–1640). Most of the churches selected are in the Baroque style and therefore follow the same architectural patterns. Based on the statistical analysis of the dispersion and regression values (r
2) between the acoustic parameters of reverberation time and musical clarity and the geometrical parameters of the churches (maximum height and volume), it was ascertained that in all cases r
2 values were lower and non-significant in the churches of Peru than in Portugal. The investigation concludes that this could be due mainly to the different construction procedures and materials typically used in churches in Peru (
Figure 9).
Finally, the work of Abadía Succi [
35], studying Jesuit churches in Argentina, four of which are Baroque, should also be noted. In this study, data about their acoustic characteristics are provided and audience surveys are carried out on acoustic and psychoacoustic parameters, with a very good correlation observed between reverberation times and all subjective parameters, as well as with the average responses obtained in the surveys.
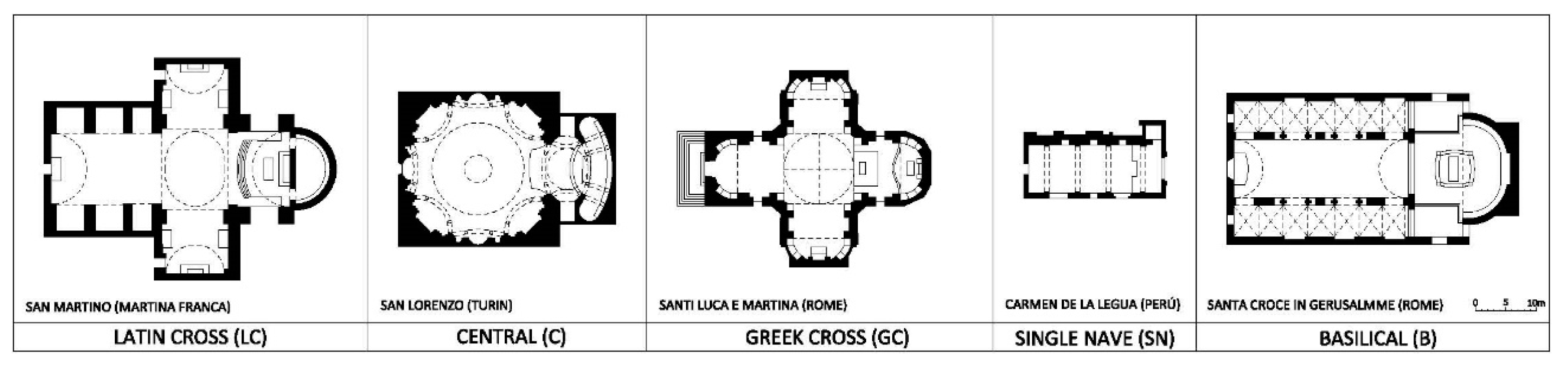
The aim of this work is to provide an overview of the acoustics of baroque Catholic churches worldwide, based on results contributed by researchers in prestigious journals and conferences. A total of 66 Catholic churches with five different typologies in eight countries are analysed. From these data, the possible relationships between acoustic parameters and geometrical characteristics, and the dependencies between acoustic parameters, will be analysed. The analysis of the relationships between the different acoustic and geometric parameters could make it possible to evaluate acoustic parameters not measured in situ in Catholic churches of the Baroque period in a predictive way as a function of other measured acoustic or geometric parameters.
5. Conclusions
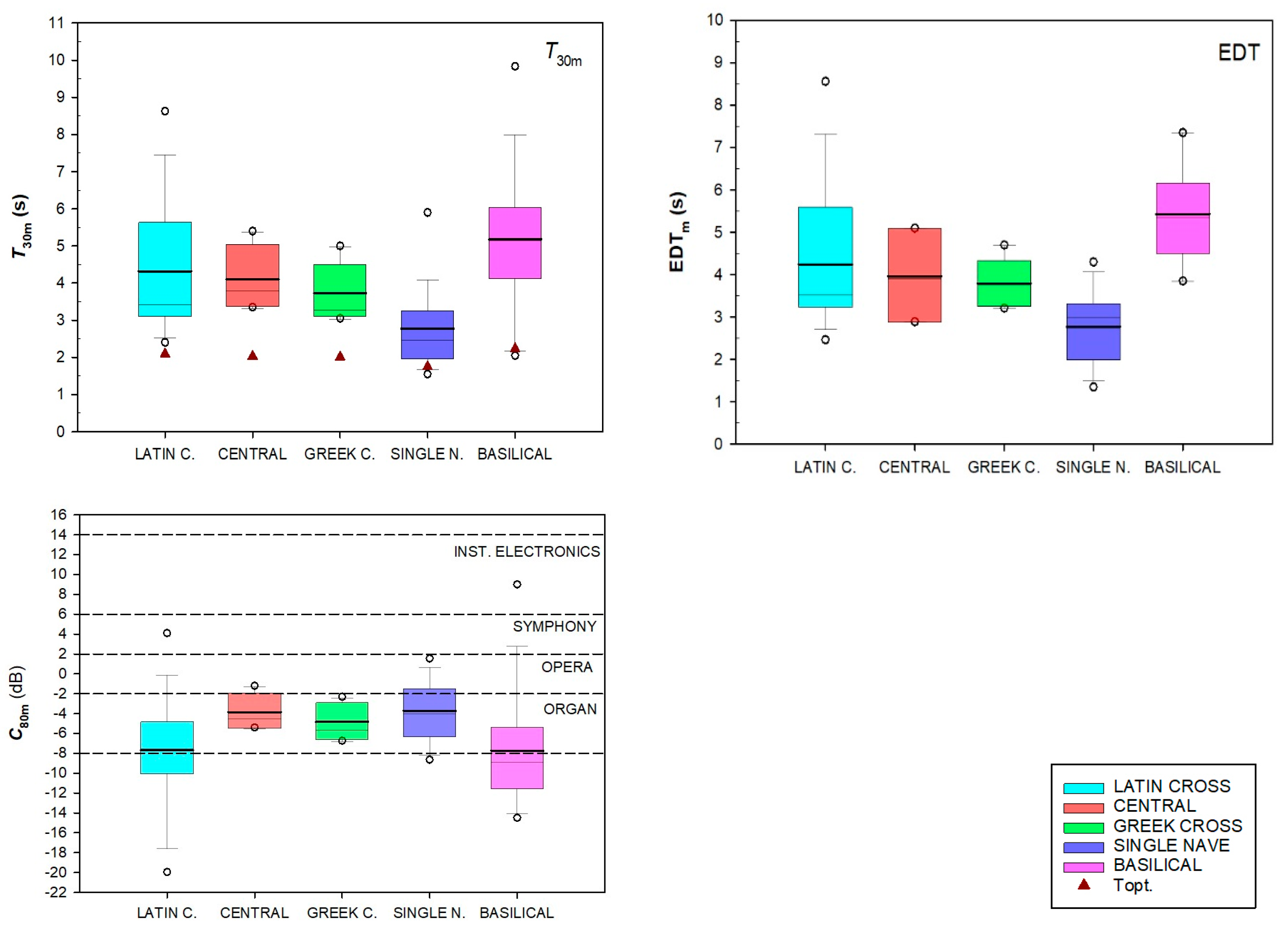
Baroque churches, both in Europe and Latin America, reflected the Catholic Church’s response to Protestant doctrine by emphasising contrasts of light, alternating concave and convex forms, and rich decoration. This research has analysed the acoustics of these spaces, taking a sample of 66 Catholic churches across eight countries with five types of plans (Latin cross, central, Greek cross, single-nave and basilica). These have been analysed by different research groups, comparing the results of the sample as a whole. For the analysis of the sample, we have considered the single-number acoustic parameters for which the sample is larger. The reverberation was analysed using the T30m parameter, and the initial reverberation (EDTm) and the clarity of the sound was analysed using musical clarity (C80m), definition (D50m) and central time (Tsm).
When analysing the sample according to typology, it can be seen that the floor plans with three naves, such as the basilica churches, have higher reverberation times (T30m) with an average value of 5.17 s, while the single-nave churches are at the opposite end of the scale with an average volume more than seven times lower and an average T30m of 2.81 s. The proposal made during the Council of Trent, based on the Latin cross plan model developed from the Il Gesú model in Rome, or central plans, resolved as central or Greek cross plans, have similar average reverberation time values (4.39 Latin cross; 4.10 s central; and 3.79 s Greek cross), even though the average volume of the Latin cross churches (20,670 m3) is practically double the average volume of the central churches (10,983 m3) or Greek cross churches (11,308 m3). For the Latin cross plans, corresponding to a more diverse sample, a higher variability of results is also observed. However, the use of central floor plans (central and Greek cross) in smaller churches during the Baroque period improves musical clarity compared to the Latin cross typology, with average values for C80m of −3.85 and −4.83 dB, respectively, compared to −7.69 dB for Latin cross churches. The central configurations (central and Greek cross), with volumes three times higher than the single-nave floors, have similar musical clarity, with an average value of C80m for single-nave churches of −3.70 dB. Comparing the sample means for musical clarity in the two highest volume typologies (Latin cross (−7.79 dB) and basilica (−7.73 dB)), the results are similar. In general, the central plan and Greek cross configurations are those with the most suitable average C80m values when related to the average volume of the sample of each typology.
No significant dependence (R2 ≥ 0.5 exceeding the significant p level) was found between the values of the acoustic parameters and one of the geometrical variables for the whole sample due to the different typologies studied. The same can be said when the study was extended to two geometrical variables. When the linear and non-linear regressions studied were obtained between a pair of acoustic parameters or one acoustic parameter with another two of those studied, correlations with R2 ≥ 0.61 are obtained for all the acoustic parameters with the exception of C80m.
Due to the clear typological differences, the analysis was carried out on an individual basis, excluding the central plan and Greek cross churches as the sample size was too small, while the Basilica was analysed for acoustic parameter dependencies. Only correlations with R2 ≥ 0.65 exceeding the significant p level are presented.
For the Latin cross typology and acoustic or geometrical variables, only 2D correlations with reverberation parameters (T30 and EDT) are found. In the case of more homogeneous samples, churches with volumes of between 10.000 and 20.000 cubic metres, 2D correlations are found with acoustic variables for all the acoustic parameters with the exception of C80m (R2 ≥ 0.75).
For the basilica typology, only one correlation between one acoustic parameter and two geometrical variables is obtained for T30.
For the single-nave typology, only significant dependencies between acoustic parameters are found. These are especially significant between pairs of acoustic parameters when the sample is analysed by volumetric intervals.
In Latin cross and basilica churches, the 2D typological analysis between acoustic parameters shows significant results, when the sample is analysed in volumetric intervals, compared to the full sample.
The 3D typological analysis between acoustic parameters does not yield significant results compared to the full sample.