A Study on Adaptive Implicit–Explicit and Explicit–Explicit Time Integration Procedures for Wave Propagation Analyses
Abstract
1. Introduction
2. Methods
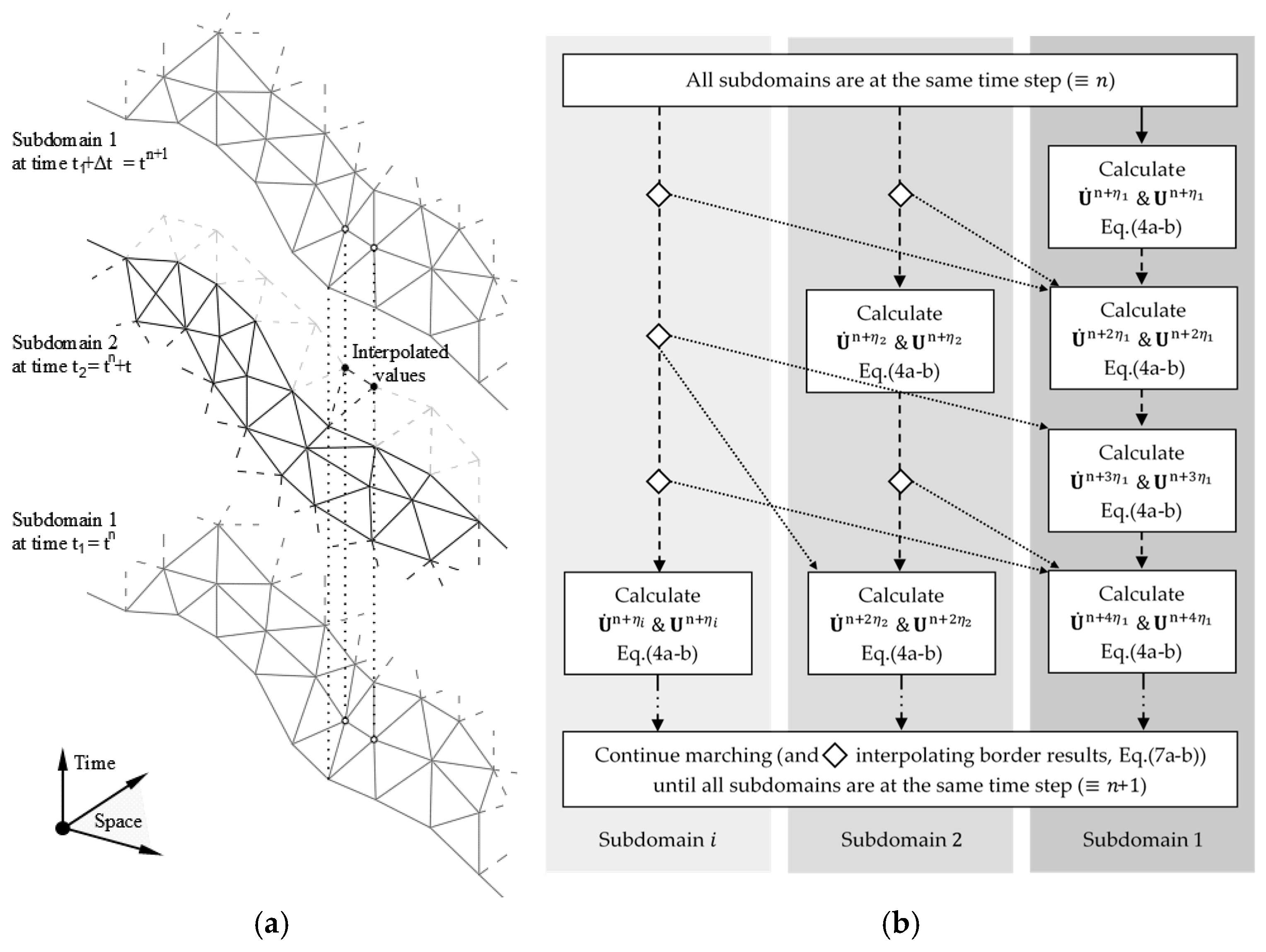
2.1. Implicit–Explicit Approach
2.2. Explicit–Explicit Approach
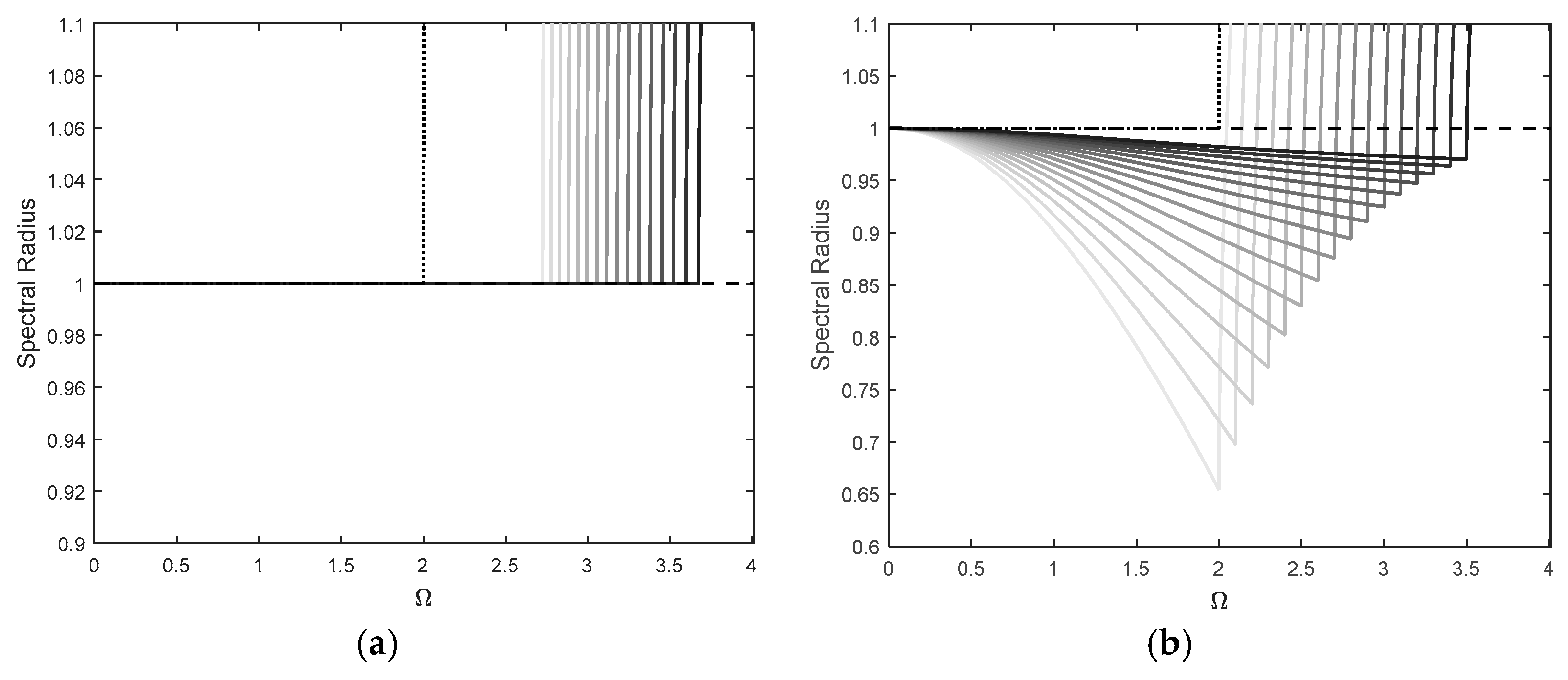
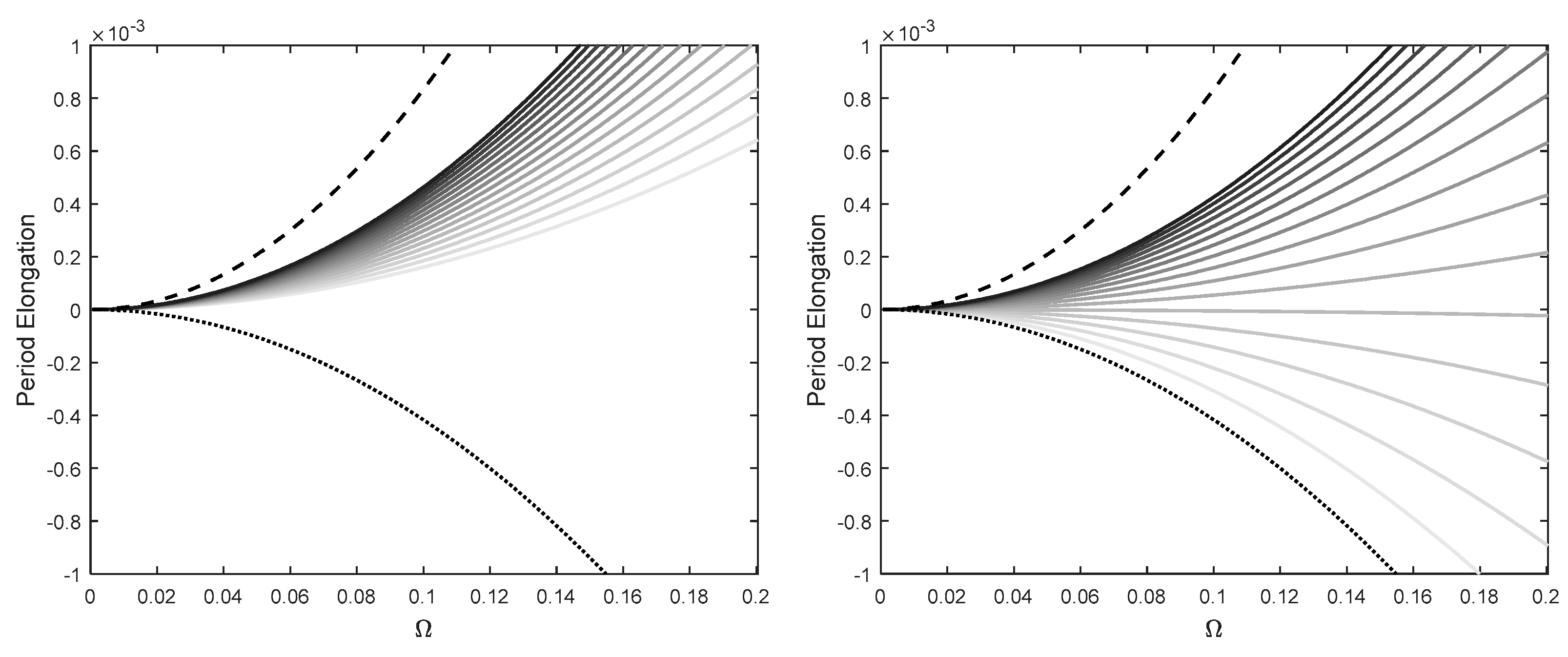
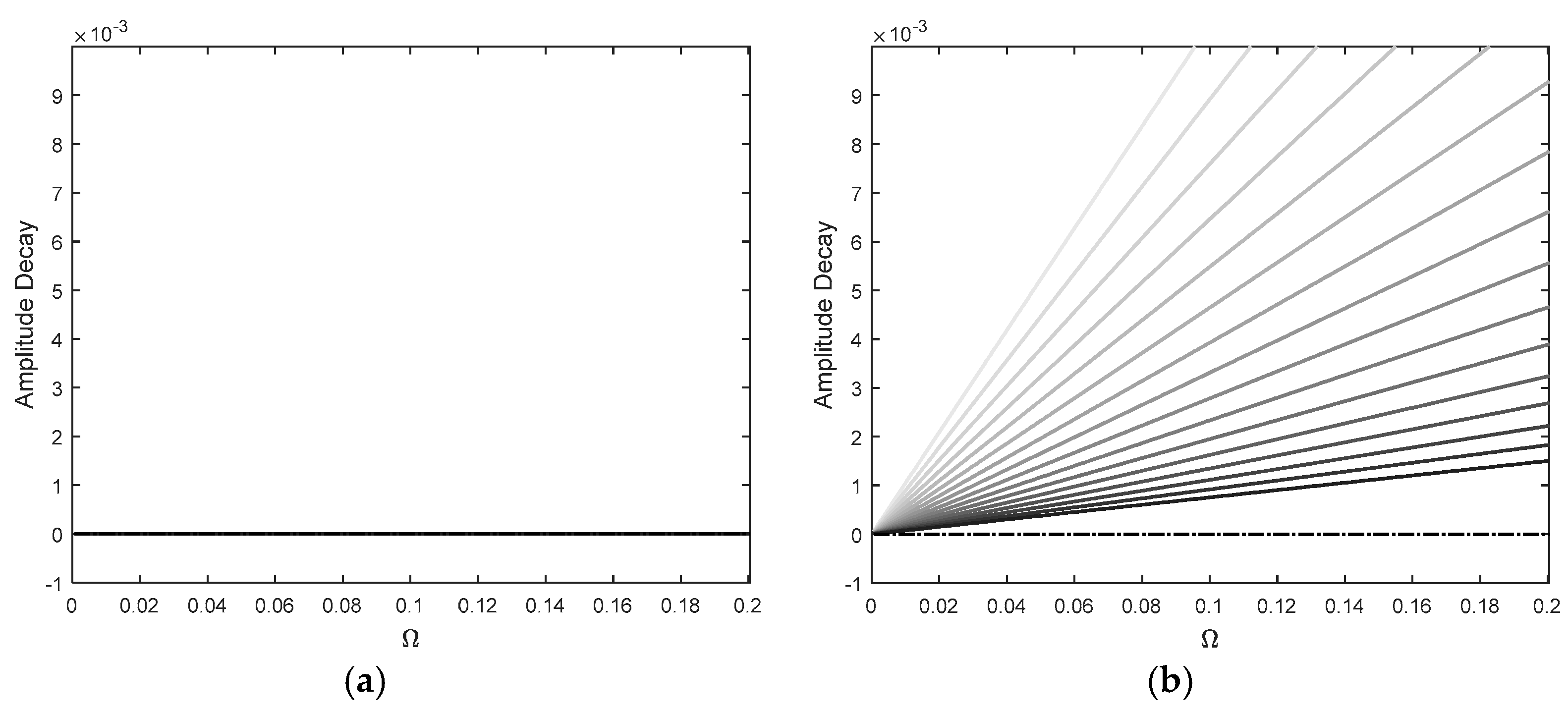
2.3. Properties of the Methods
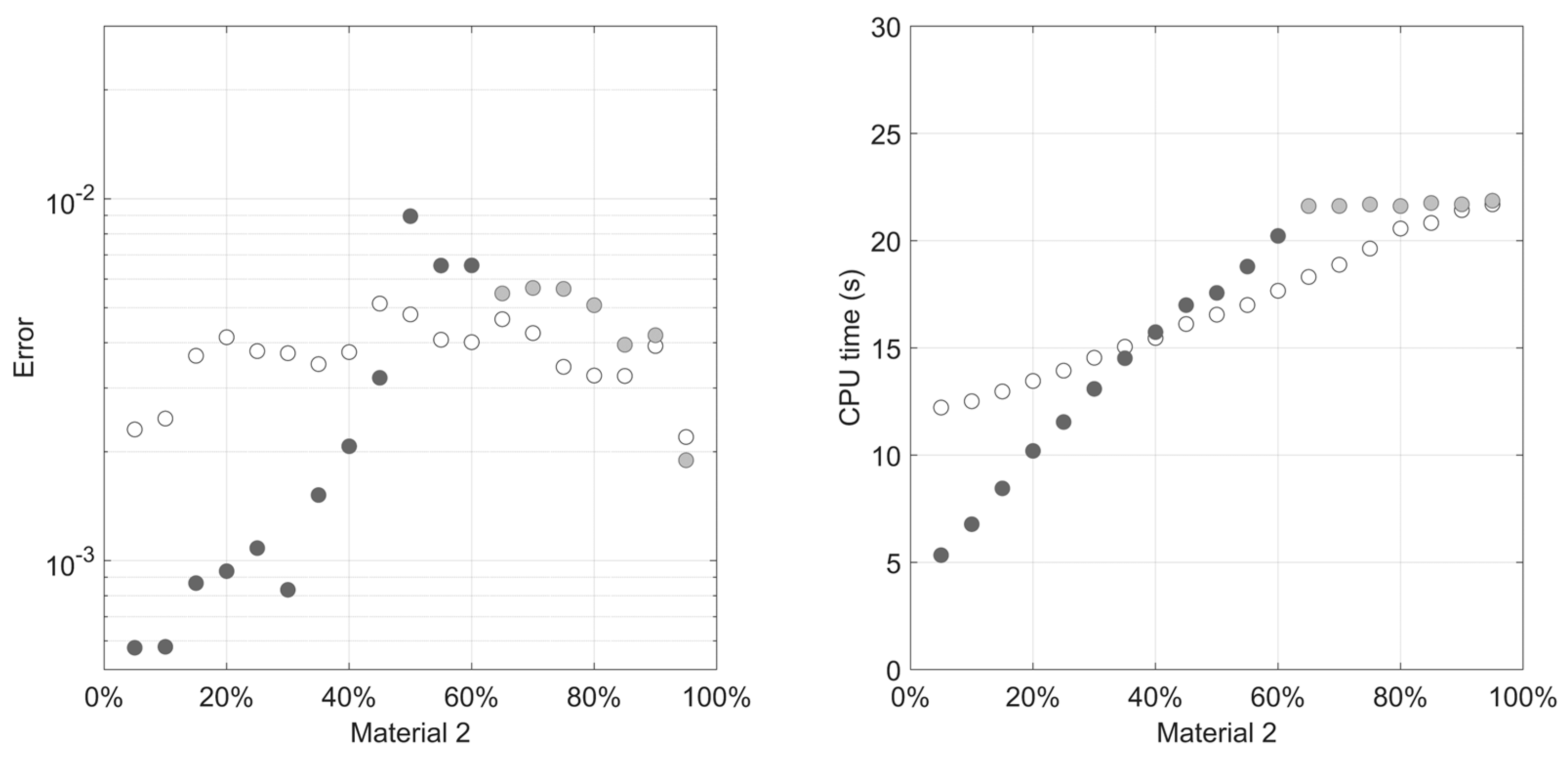
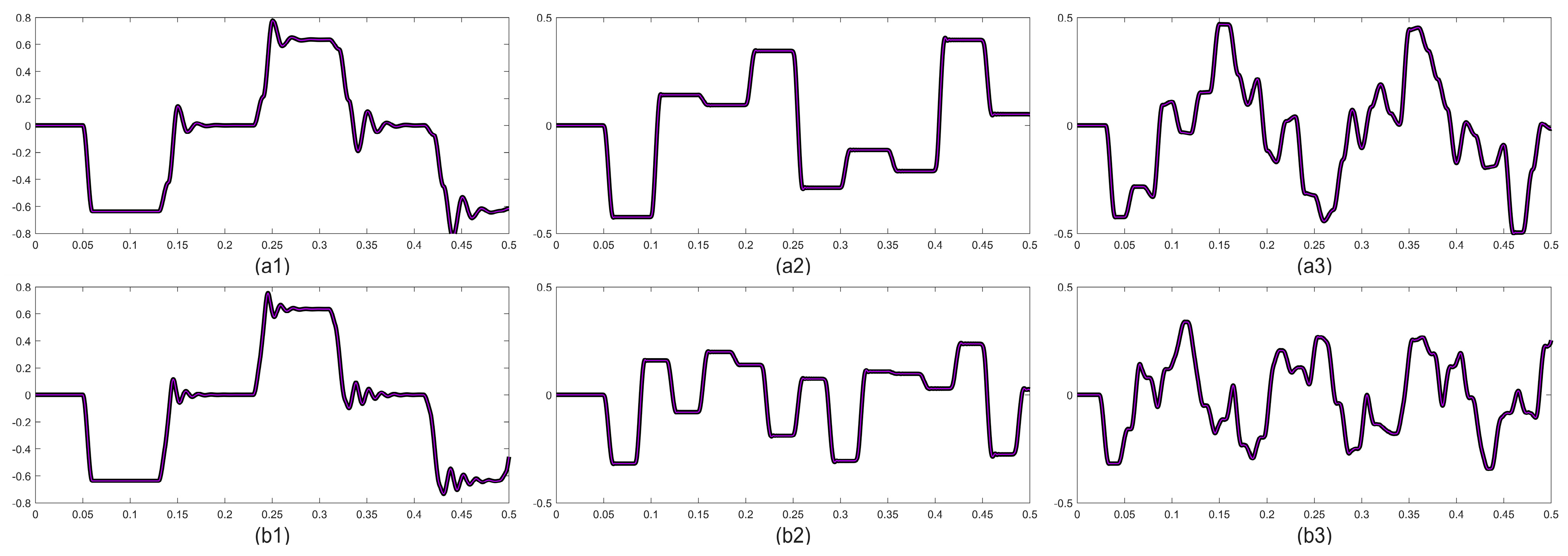
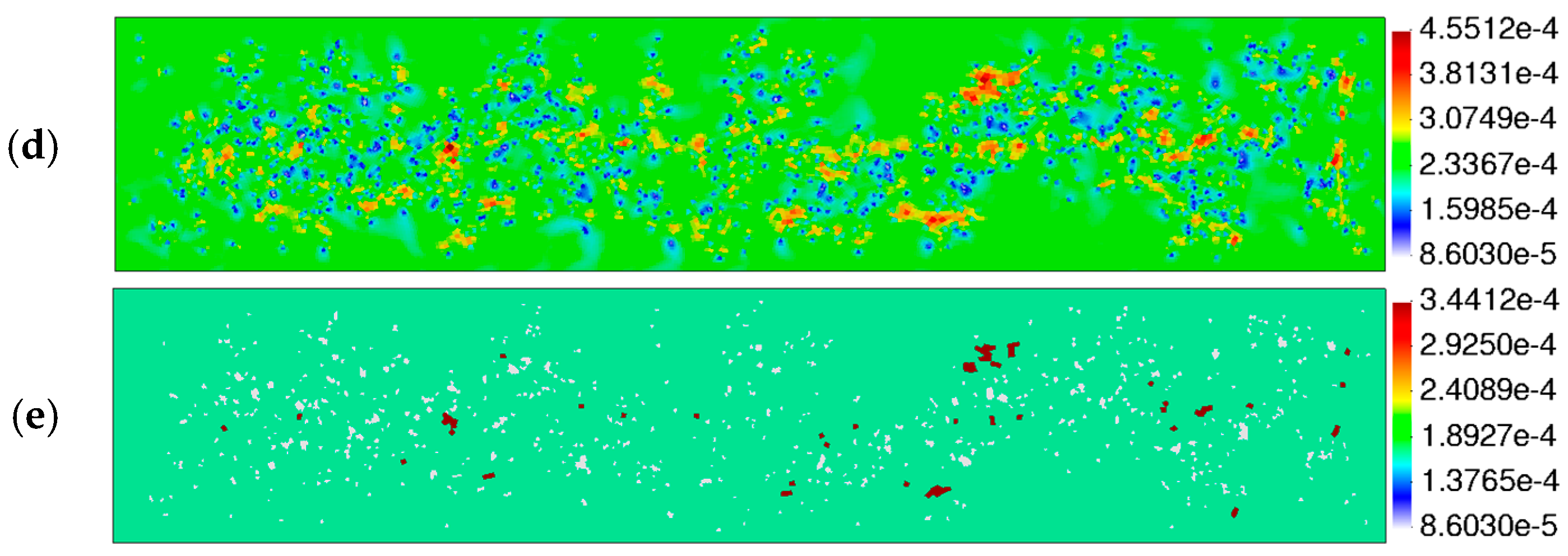
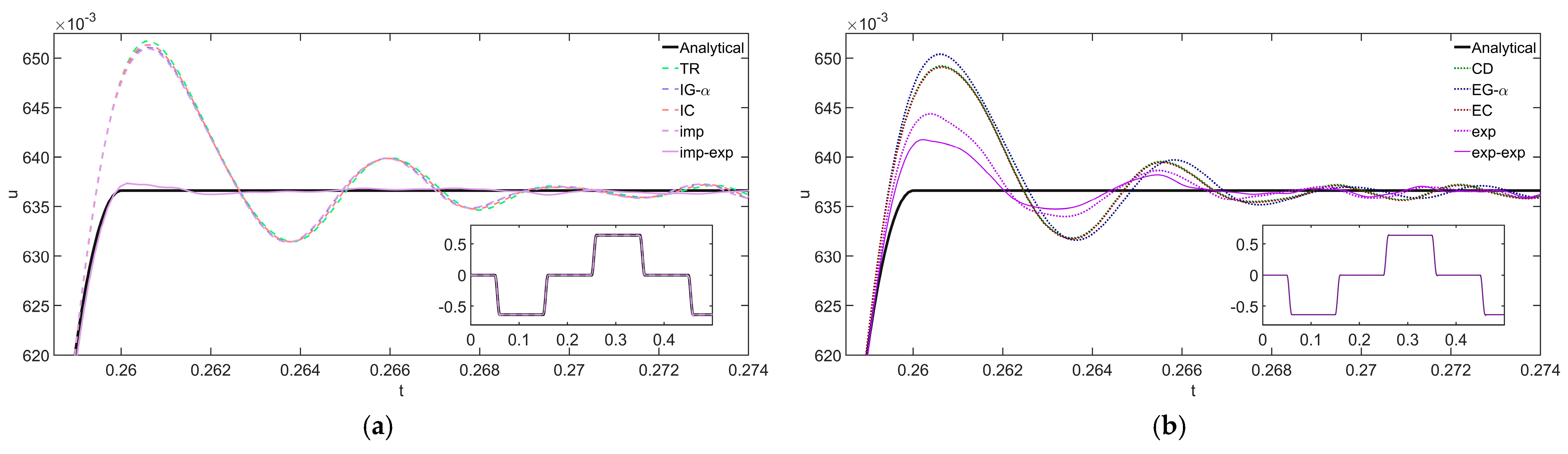
3. Results and Discussions
3.1. Theoretical Models
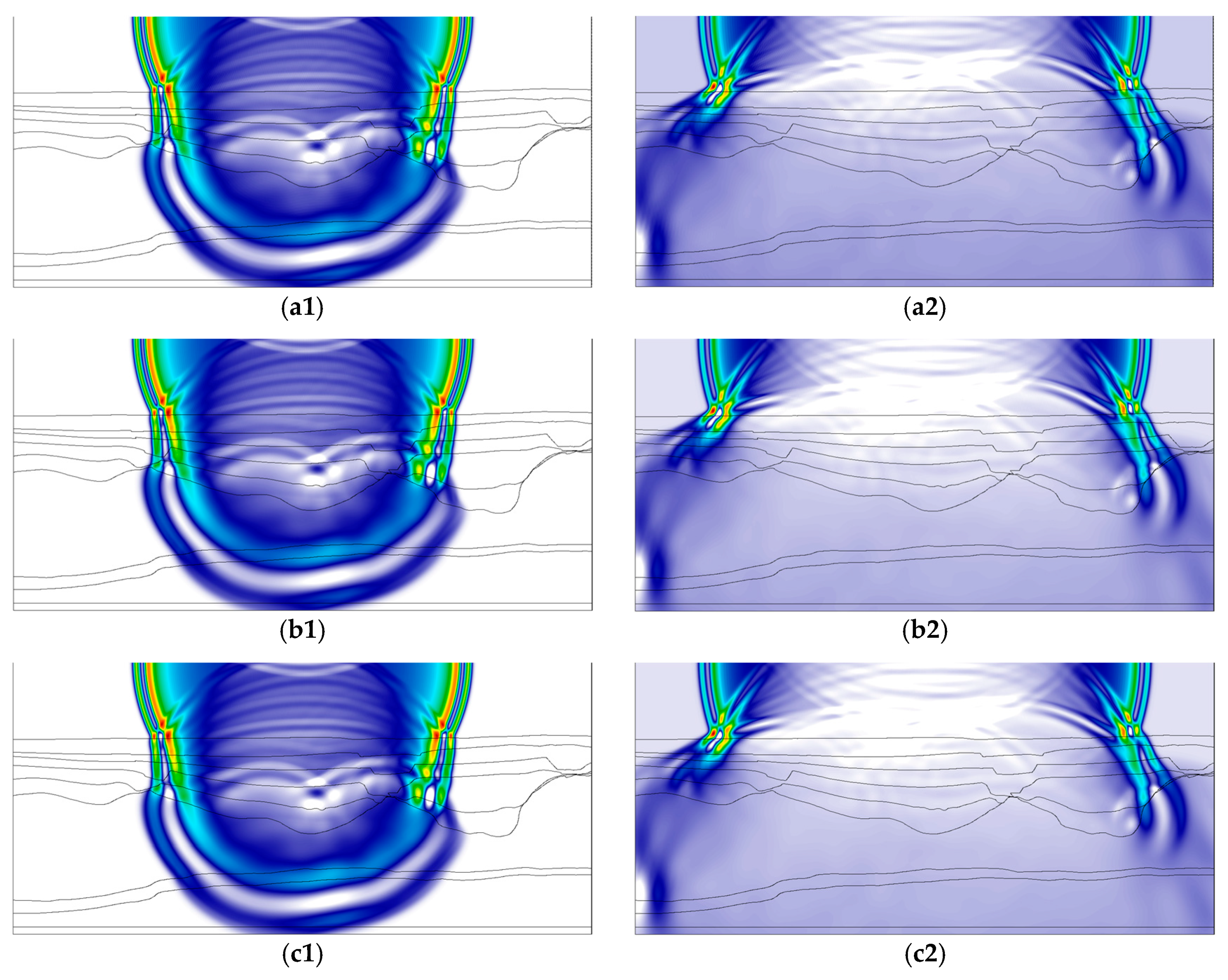
3.2. Applied Models
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Belytschko, T.; Mullen, R. Stability of explicit-implicit mesh partitions in time integration. Int. J. Numer. Methods Eng. 1978, 12, 1575–1586. [Google Scholar] [CrossRef]
- Hughes, T.J.; Pister, K.S.; Taylor, R.L. Implicit-explicit finite elements in nonlinear transient analysis. Comput. Methods Appl. Mech. Eng. 1979, 17, 159–182. [Google Scholar] [CrossRef]
- Soleimani, B.; Knoth, O.; Weiner, R. IMEX peer methods for fast-wave–slow-wave problems. Appl. Numer. Math. 2017, 118, 221–237. [Google Scholar] [CrossRef]
- Miranda, I.; Ferencz, R.M.; Hughes, T.J. An improved implicit-explicit time integration method for structural dynamics. Earthq. Eng. Struct. Dyn. 1989, 18, 643–653. [Google Scholar] [CrossRef]
- Soares, D., Jr. A model/solution-adaptive explicit-implicit time-marching technique for wave propagation analysis. Int. J. Numer. Methods Eng. 2019, 119, 590–617. [Google Scholar] [CrossRef]
- Soares, D., Jr. An enhanced explicit–implicit time-marching formulation based on fully-adaptive time-integration parameters. Comput. Methods Appl. Mech. Eng. 2023, 403, 115711. [Google Scholar] [CrossRef]
- Dujardin, G.; Lafitte, P. Asymptotic behaviour of splitting schemes involving time-subcycling techniques. IMA J. Numer. Anal. 2016, 36, 1804–1841. [Google Scholar] [CrossRef]
- Belytschko, T.; Smolinski, P.; Liu, W.K. Stability of multi-time step partitioned integrators for first-order finite element systems. Comput. Methods Appl. Mech. Eng. 1985, 49, 281–297. [Google Scholar] [CrossRef]
- Pinto, L.R.; Soares, D., Jr.; Mansur, W.J. Elastodynamic wave propagation modelling in geological structures considering fully-adaptive explicit time-marching procedures. Soil Dyn. Earthq. Eng. 2021, 150, 106962. [Google Scholar] [CrossRef]
- Soares, D., Jr.; Pinto, L.R.; Mansur, W.J. A truly-explicit time-marching formulation for elastodynamic analyses considering locally-adaptive time-integration parameters and time-step values. Int. J. Solids Struct. 2023, 271, 112260. [Google Scholar] [CrossRef]
- Tamma, K.K.; Zhou, X.; Sha, D. The time dimension: A theory towards the evolution, classification, characterization and design of computational algorithms for transient/dynamic applications. Arch. Comput. Methods Eng. 2000, 7, 67–290. [Google Scholar] [CrossRef]
- Butcher, J.C. A history of Runge-Kutta methods. Appl. Numer. Math. 1996, 20, 247–260. [Google Scholar] [CrossRef]
- Hulbert, G.M.; Chung, J. Explicit time integration algorithms for structural dynamics with optimal numerical dissipation. Comput. Methods Appl. Mech. Eng. 1996, 137, 175–188. [Google Scholar]
- Noh, G.; Bathe, K.J. An explicit time integration scheme for the analysis of wave propagations. Comput. Struct. 2013, 129, 178–193. [Google Scholar] [CrossRef]
- Kim, W. An accurate two-stage explicit time integration scheme for structural dynamics and various dynamic problems. Int. J. Numer. Methods Eng. 2019, 120, 1–28. [Google Scholar] [CrossRef]
- Soares, D., Jr. An improved adaptive formulation for explicit analyses of wave propagation models considering locally-defined self-adjustable time-integration parameters. Comput. Methods Appl. Mech. Eng. 2022, 399, 115324. [Google Scholar] [CrossRef]
- Newmark, N.M. A method of computation for structural dynamics. J. Eng. Mech. Div. 1959, 85, 67–94. [Google Scholar]
- Chung, J.; Hulbert, G. A time integration algorithm for structural dynamics with improved numerical dissipation: The generalized-α method. ASME. J. Appl. Mech. 1993, 60, 371–375. [Google Scholar] [CrossRef]
- Bathe, K.J.; Baig, M.M.I. On a composite implicit time integration procedure for nonlinear dynamics. Comput. Struct. 2005, 83, 2513–2524. [Google Scholar]
- Soares, D., Jr. A material/element-defined time integration procedure for dynamic analysis. Eng. Comput. 2023, 40, 1575–1601. [Google Scholar]
- Gravouil, A.; Combescure, A. Multi-time-step explicit–implicit method for non-linear structural dynamics. Int. J. Numer. Methods Eng. 2001, 50, 199–225. [Google Scholar] [CrossRef]
- Noels, L.; Stainier, L.; Ponthot, J.P. Combined implicit/explicit time-integration algorithms for the numerical simulation of sheet metal forming. J. Comput. Appl. Math. 2004, 168, 331–339. [Google Scholar] [CrossRef]
- Curiel Sosa, J.L.; de Souza Neto, E.; Owen, D.R.J. A combined implicit–explicit algorithm in time for non-linear finite element analysis. Commun. Numer. Methods Eng. 2006, 22, 63–75. [Google Scholar] [CrossRef]
- Ongaro, G.; Shojaei, A.; Mossaiby, F.; Hermann, A.; Cyron, C.J.; Trovalusci, P. Multi-adaptive spatial discretization of bond-based peridynamics. Int. J. Fract. 2023, 244, 1–24. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95-International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar]
- Mansur, W.J. A Time-Stepping Technique to Solve Wave propagation Problems Using the Boundary Element Method. Ph.D. Thesis, University of Southampton, Southampton, UK, 1983. [Google Scholar]
- Batra, R.C.; Porfiri, M.; Spinello, D. Free and forced vibrations of a segmented bar by a meshless local Petrov–Galerkin (MLPG) formulation. Comput. Mech. 2008, 41, 473–491. [Google Scholar] [CrossRef]
- Freitas, D.F.; Siqueira, R.; Cetale, M.; González, M.; Soares, D.M. 3D Velocity Model Building of Búzios oil field—Improvements and updates. In Proceedings of the IX Simpósio Brasileiro de Geofísica, Curitiba, PR, Brazil, 4–6 October 2022. [Google Scholar]
- Fehler, M. SEAM update: SEAM phase I-RPSEA update: Status of simulations. Lead. Edge 2012, 31, 1424–1426. [Google Scholar] [CrossRef]
- Billette, F.J.; Brandsberg-Dahl, S. The 2004 BP velocity benchmark. In Proceedings of the 67th EAGE Conference & Exhibition, Madrid, Spain, 13–16 June 2005; p. cp-1. [Google Scholar]
- Basu, U. Perfectly Matched Layers for Acoustic and Transient Waves. Dam Safety Research Program U.S. Department of the Interior Bureau of Reclamation: Washington, DC, USA, 2008. [Google Scholar]
- Hughes, T.J. The Finite Element Method: Linear Static and Dynamic Finite Element Analysis; Dover Publications Inc.: New York, NY, USA, 2000. [Google Scholar]
- Van Pamel, A.; Sha, G.; Rokhlin, S.I.; Lowe, M.J.S. Finite-element modelling of elastic wave propagation and scattering within heterogeneous media. Proc. R. Soc. A Math. Phys. Eng. Sci. 2017, 473, 20160738. [Google Scholar] [CrossRef]
- Imperiale, A.; Chatillon, S.; Darmon, M.; Leymarie, N.; Demaldent, E. UT simulation using a fully automated 3D hybrid model: Application to planar backwall breaking defects inspection. AIP Conf. Proc. 2018, 1949, 050004. [Google Scholar]



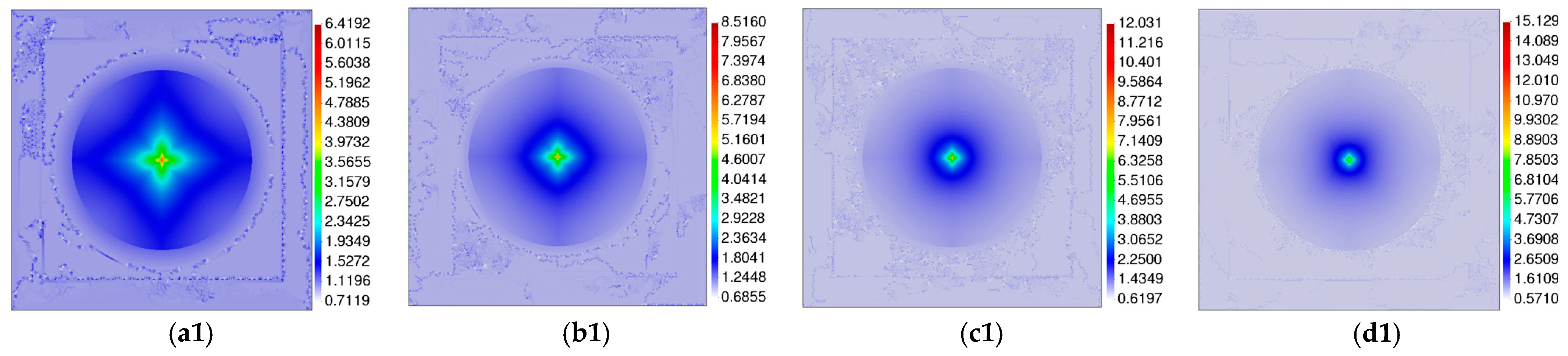
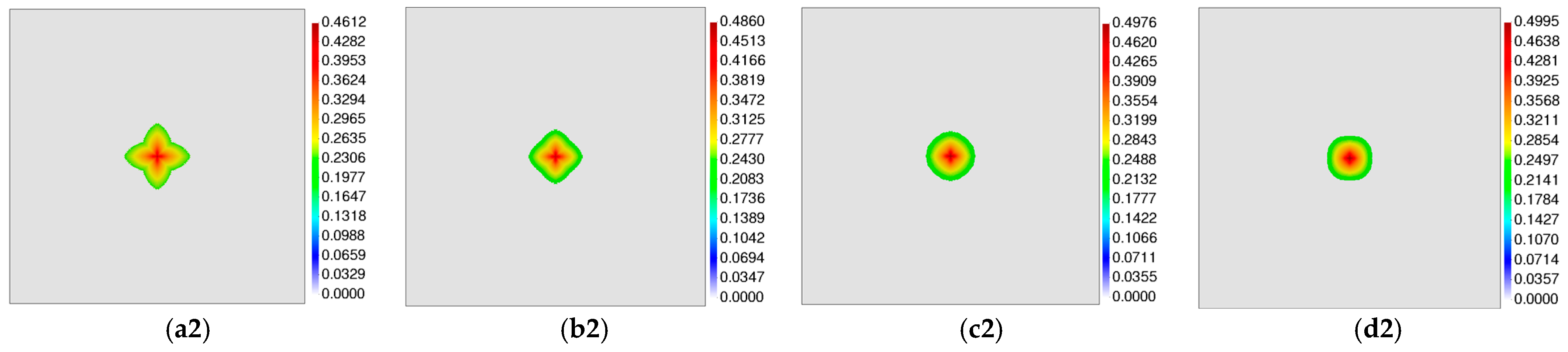
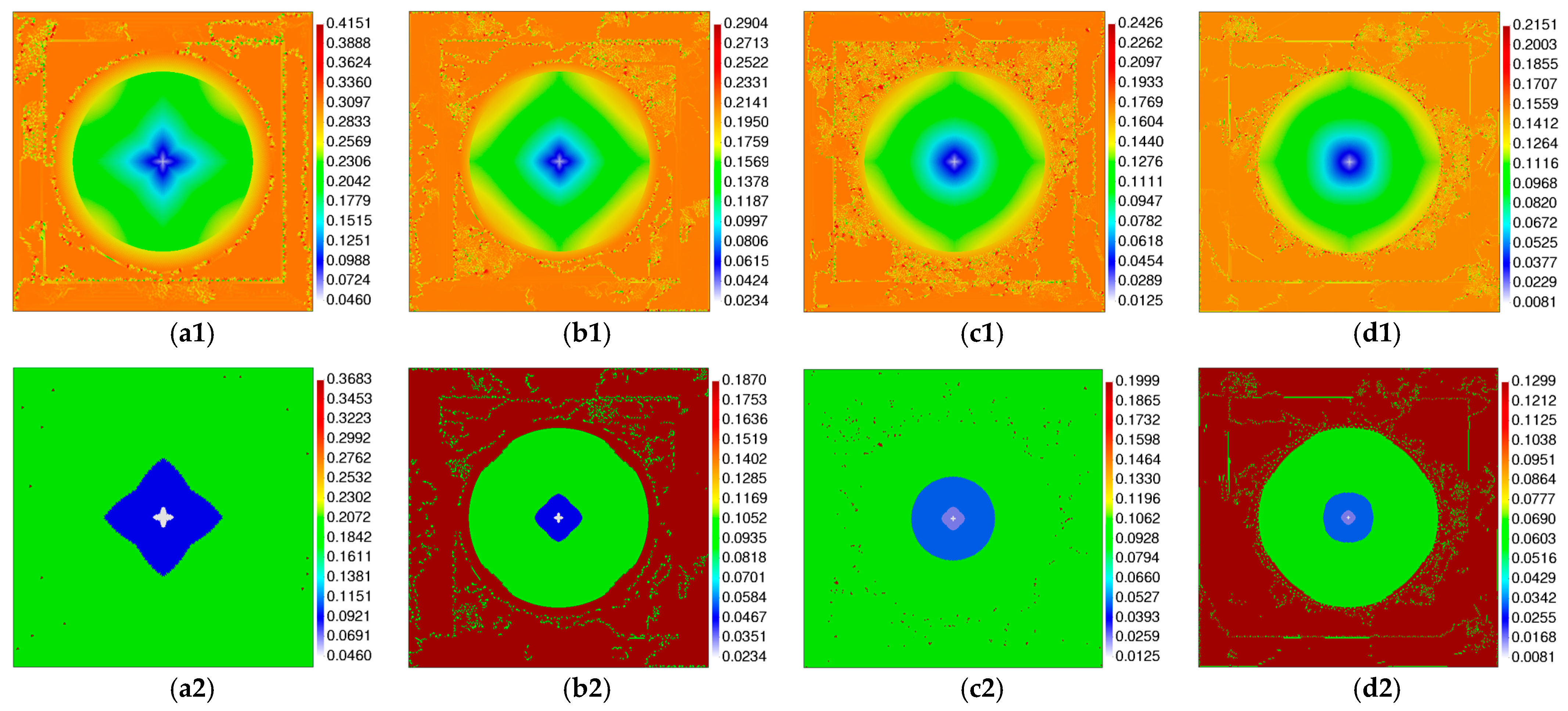
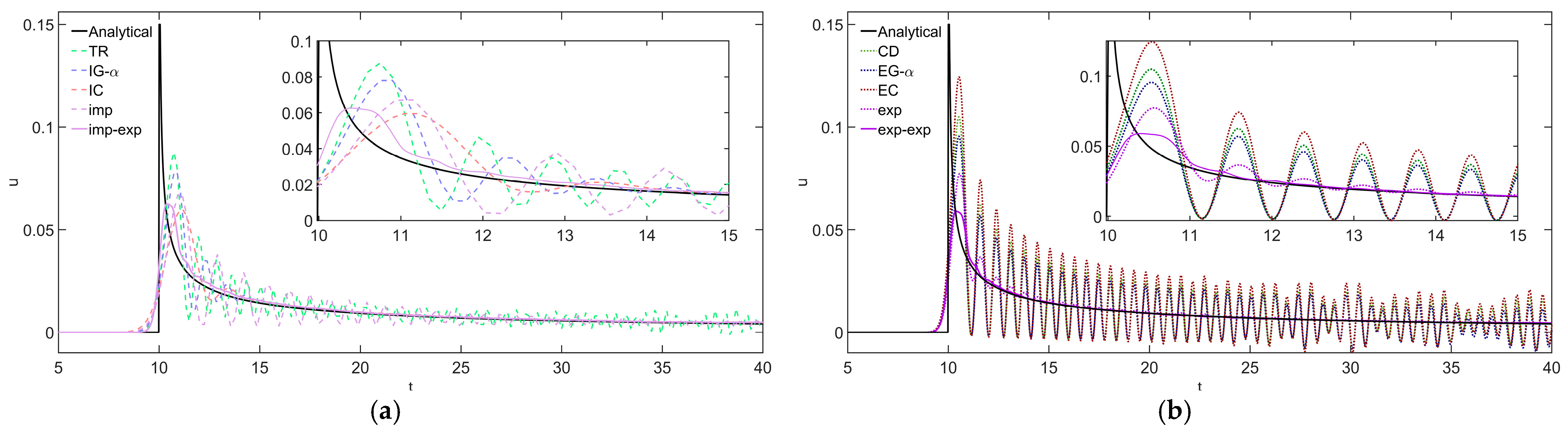












| Discretization | Method | Δt (10−2 s) | Error (10−1) | CPU Time (s) |
|---|---|---|---|---|
| 1 | TR | 14.9256 (3.60) | 7.78 (2.08) | 19.6 (2.27) |
| IG-α | 14.9256 (3.60) | 7.15 (1.91) | 19.8 (2.29) | |
| IC | 14.9256 (3.60) | 7.31 (1.96) | 20.6 (2.38) | |
| imp | 14.9256 (3.60) | 7.51 (2.01) | 19.5 (2.25) | |
| CD | 4.60382 (1.11) | 7.98 (2.13) | 14.5 (1.67) | |
| EG-α | 4.14927 (1.00) | 7.85 (2.10) | 15.9 (1.85) | |
| EC | 8.62073 (2.08) | 7.91 (2.12) | 16.1 (1.86) | |
| exp | 4.60382 (1.11) | 5.24 (1.40) | 14.0 (1.61) | |
| imp–exp | 14.9256 (3.60) | 4.20 (1.12) | 9.45 (1.09) | |
| exp–exp | 36.8306 (8.88) | 3.73 (1.00) | 8.67 (1.00) | |
| 2 | TR | 10.0516 (4.77) | 7.22 (2.76) | 32.7 (3.02) |
| IG-α | 10.0516 (4.77) | 6.68 (2.25) | 32.6 (3.01) | |
| IC | 10.0516 (4.77) | 6.81 (2.29) | 34.2 (3.17) | |
| imp | 10.0516 (4.77) | 7.01 (2.36) | 32.8 (3.03) | |
| CD | 2.33704 (1.11) | 7.62 (2.57) | 22.9 (2.12) | |
| EG-α | 2.10629 (1.00) | 7.39 (2.49) | 24.2 (2.42) | |
| EC | 4.37614 (2.08) | 7.51 (2.53) | 28.9 (2.67) | |
| exp | 2.33704 (1.11) | 5.09 (1.71) | 22.7 (2.09) | |
| imp–exp | 10.0516 (4.77) | 3.46 (1.17) | 11.2 (1.04) | |
| exp–exp | 18.6963 (8.88) | 2.97 (1.00) | 10.8 (1.00) | |
| 3 | TR | 7.59321 (6.74) | 6.53 (3.08) | 101.4 (4.71) |
| IG-α | 7.59321 (6.74) | 6.02 (2.84) | 101.9 (4.74) | |
| IC | 7.59321 (6.74) | 6.12 (2.88) | 118.9 (5.53) | |
| imp | 7.59321 (6.74) | 6.32 (2.98) | 103.6 (4.81) | |
| CD | 1.24956 (1.11) | 7.03 (3.32) | 50.0 (2.33) | |
| EG-α | 1.12619 (1.00) | 6.73 (3.17) | 57.4 (2.67) | |
| EC | 2.33983 (2.08) | 6.92 (3.27) | 64.8 (3.01) | |
| exp | 1.24956 (1.11) | 4.57 (2.15) | 50.2 (2.34) | |
| imp–exp | 7.59321 (6.74) | 2.60 (1.23) | 21.5 (1.00) | |
| exp–exp | 19.9930 (17.8) | 2.12 (1.00) | 26.4 (1.23) | |
| 4 | TR | 6.20276 (8.48) | 6.17 (3.55) | 159.9 (3.85) |
| IG-α | 6.20276 (8.48) | 5.60 (3.22) | 160.2 (3.86) | |
| IC | 6.20276 (8.48) | 5.71 (3.29) | 174.1 (4.19) | |
| imp | 6.20276 (8.48) | 5.93 (3.41) | 160.2 (3.14) | |
| CD | 0.81175 (1.11) | 6.66 (3.84) | 88.8 (2.14) | |
| EG-α | 0.73160 (1.00) | 6.38 (3.67) | 114.9 (2.77) | |
| EC | 1.52001 (2.08) | 6.59 (3.79) | 126.7 (3.05) | |
| exp | 0.81174 (1.11) | 4.18 (3.40) | 89.0 (2.15) | |
| imp–exp | 6.20276 (8.48) | 2.19 (1.26) | 41.5 (1.00) | |
| exp–exp | 12.9880 (17.8) | 1.74 (1.00) | 49.5 (1.19) |
| Method | CPU Time (s) | |||
|---|---|---|---|---|
| 4 | TR | 0.62499 (1.11) | 7.96 (9.68) | 121.4 (8.70) |
| IG-α | 0.62499 (1.11) | 7.56 (9.19) | 120.1 (8.61) | |
| IC | 0.62499 (1.11) | 8.36 (10.1) | 230.4 (16.5) | |
| imp | 0.62499 (1.11) | 5.77 (7.01) | 120.6 (8.64) | |
| CD | 0.62499 (1.11) | 5.84 (7.10) | 16.6 (1.19) | |
| EG-α | 0.56317 (1.00) | 6.20 (7.53) | 18.3 (1.31) | |
| EC | 1.17046 (2.08) | 6.24 (7.58) | 22.4 (1.60) | |
| exp | 0.62499 (1.11) | 5.75 (6.98) | 16.6 (1.19) | |
| imp–exp | 0.62499 (1.11) | 5.75 (6.98) | 16.6 (1.19) | |
| exp–exp | 2.49998 (4.44) | 0.82 (1.00) | 13.9 (1.00) | |
| 6 | TR | 2.49998 (6.66) | 18.87 (3.94) | 30.43 (1.84) |
| IG-α | 2.49998 (6.66) | 22.23 (4.64) | 31.52 (1.91) | |
| IC | 2.49998 (6.66) | 18.99 (3.96) | 56.68 (3.43) | |
| imp | 2.49998 (6.66) | 18.50 (3.86) | 30.35 (1.83) | |
| CD | 0.41666 (1.11) | 8.49 (1.77) | 20.65 (1.25) | |
| EG-α | 0.37545 (1.00) | 8.70 (1.82) | 25.29 (1.53) | |
| EC | 0.78030 (2.08) | 8.78 (1.83) | 28.25 (1.71) | |
| exp | 0.41666 (1.11) | 8.41 (1.76) | 20.78 (1.26) | |
| imp–exp | 2.49998 (6.66) | 8.93 (1.86) | 16.56 (1.00) | |
| exp–exp | 1.66664 (4.44) | 4.79 (1.00) | 16.54 (1.00) |
| Method | CPU Time (s) | ||
|---|---|---|---|
| TR | 1.42924 (1.84) | 8.65 (1.67) | 28.8 (4.97) |
| IG-α | 1.42924 (1.84) | 8.34 (1.61) | 29.9 (5.15) |
| IC | 1.42924 (1.84) | 8.49 (1.63) | 53.1 (9.15) |
| imp | 1.42924 (1.84) | 8.29 (1.60) | 28.6 (4.92) |
| CD | 0.86030 (1.11) | 7.42 (1.43) | 8.2 (1.41) |
| EG-α | 0.77536 (1.00) | 8.01 (1.54) | 9.4 (1.61) |
| EC | 1.61092 (2.08) | 7.43 (1.43) | 11.0 (1.89) |
| exp | 0.86090 (1.11) | 6.41 (1.23) | 8.3 (1.42) |
| imp–exp | 1.42924 (1.84) | 5.18 (1.00) | 6.4 (1.11) |
| exp–exp | 3.44120 (4.44) | 6.19 (1.19) | 5.8 (1.00) |
| Model | Method | CPU Time (s) | |
|---|---|---|---|
| 1 | CD | 0.64051 (1.11) | 5233.7 (1.68) |
| EG-α | 0.57727 (1.00) | 5462.8 (1.75) | |
| EC | 1.19936 (2.08) | 5683.6 (1.83) | |
| exp | 0.64051 (1.11) | 5261.2 (1.69) | |
| imp–exp | 0.86751 (1.50) | 4282.5 (1.38) | |
| exp–exp | 2.56204 (4.44) | 3112.9 (1.00) | |
| 2 | CD | 0.24255 (1.11) | 8661.5 (1.99) |
| EG-α | 0.21861 (1.00) | 8991.6 (2.06) | |
| EC | 0.45419 (2.08) | 9511.1 (2.18) | |
| exp | 0.24255 (1.11) | 8654.5 (1.98) | |
| imp–exp | 0.34235 (1.57) | 5436.3 (1.25) | |
| exp–exp | 1.94044 (8.88) | 4362.2 (1.00) | |
| 3 | CD | 0.32415 (1.11) | 11322.8 (2.15) |
| EG-α | 0.29215 (1.00) | 12283.3 (2.34) | |
| EC | 0.60698 (2.08) | 14773.1 (2.81) | |
| exp | 0.32415 (1.11) | 11737.7 (2.23) | |
| imp–exp | 0.42489 (1.45) | 5259.40 (1.00) | |
| exp–exp | 10.3729 (35.5) | 5883.30 (1.11) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Soares, D., Jr.; Sales, I.d.S.; Pinto, L.R.; Mansur, W.J. A Study on Adaptive Implicit–Explicit and Explicit–Explicit Time Integration Procedures for Wave Propagation Analyses. Acoustics 2024, 6, 651-680. https://doi.org/10.3390/acoustics6030036
Soares D Jr., Sales IdS, Pinto LR, Mansur WJ. A Study on Adaptive Implicit–Explicit and Explicit–Explicit Time Integration Procedures for Wave Propagation Analyses. Acoustics. 2024; 6(3):651-680. https://doi.org/10.3390/acoustics6030036
Chicago/Turabian StyleSoares, Delfim, Jr., Isabelle de Souza Sales, Lucas Ruffo Pinto, and Webe João Mansur. 2024. "A Study on Adaptive Implicit–Explicit and Explicit–Explicit Time Integration Procedures for Wave Propagation Analyses" Acoustics 6, no. 3: 651-680. https://doi.org/10.3390/acoustics6030036
APA StyleSoares, D., Jr., Sales, I. d. S., Pinto, L. R., & Mansur, W. J. (2024). A Study on Adaptive Implicit–Explicit and Explicit–Explicit Time Integration Procedures for Wave Propagation Analyses. Acoustics, 6(3), 651-680. https://doi.org/10.3390/acoustics6030036







