Acoustic Properties of Surfaces Covered by Multipole Resonators

Abstract

Different types of resonators are used to create acoustic metamaterials and metasurfaces. Recent studies focused on the use of multiple resonators of the dipole, quadrupole, octupole, and even hexadecapole types. This paper considers the theory of an acoustic metasurface, which is a flat surface with a periodic arrangement of multipole resonators. The sound field reflected by the metasurface is determined. If the distance between the resonators is less than half the wavelength of the incident plane wave, the far field can be described by a reflection coefficient that depends on the angle of incidence. This allows us to characterize the acoustic properties of the metasurface by a homogenized boundary condition, which is a high-order tangential impedance boundary condition. The tangential impedance depending on the multipole order of the resonators is introduced. In addition, we analyze the sound absorption properties of these metasurfaces, which are a critical factor in determining their performance. The paper presents a theoretical model for the subwavelength case that accounts for the multipole orders of resonators and their impact on sound absorption. The maximum absorption coefficient for a diffuse sound field, as well as the optimal value for the homogenized impedance, are calculated for arbitrary multipole orders. The examples of the multipole resonators, which can be made from a set of Helmholtz resonators or membrane resonators, are discussed as well.

1. Introduction

Resonators are often used as meta-atoms to create acoustic metamaterials, which are complex structures with specific properties. At scales significantly exceeding the sound wavelength, the acoustic metamaterial behaves like a continuous media described by macroscopic effective parameters [1]. In some cases, the effective parameters have features which cannot be met in natural materials. For example, acoustic metamaterials with negative effective density or negative bulk modulus are known as well as double-negative media having both parameters simultaneously negative [2]. The elastic media with monopole resonators has a negative bulk modulus in a certain frequency range [3]. A well-known example is a liquid with gas bubbles, which are considered as isotropic scatterers [4]. The negative effective density can be achieved by dipole resonators [3] included in the natural media. The light dipoles in liquid provide a very wide frequency range of the negative density [5]. One of the simplest double-negative acoustic materials is a dispersive composite in the form of an elastic porous medium with empty spherical cavities [6]. A similar idea has been recently proposed in [7] investigating crack-like inhomogeneities or voids in a multilayer structure.

Researchers apply different types of resonators in order to construct metamaterials and metasurfaces. The most popular type is monopole resonators like Helmholtz resonators, quarter- and half-wave resonators, folded tubes, and membranes [8,9]. The resonators should be much smaller than the controlled wavelength to apply the homogenization technique [1] for the derivation of the effective bulk parameters of the metamaterials or an equivalent boundary condition for the metasurfaces. An array of identical monopole resonators on a rigid backing can be described by an ordinary impedance boundary condition [10]. If the resonators’ parameters vary periodically in the array, the gradient phase metasurface is formed [11]. Such surfaces can redirect the incident sound wave in a different way with respect to the traditional law of reflection.

The resonators with a higher order of multiplicity are increasingly being used as meta-atoms. The resonator of the next order after the monopole one belongs to the dipole type. The simplest physical model of the dipole resonator is a rigid sphere on a spring [12]. Also, the dipole resonator can be implemented by a membrane in a ring oscillating at the first eigenmode [12] or a membrane embedded in a rigid baffle oscillating at the second eigenmode [13]. Alternatively, the dipole-type metasurface can be formed by a set of short beams clamped on one side [14]. Two coupled Helmholtz resonators have a mode for which they oscillate with opposite phases [15]; hence, two monopole resonators can form the dipole one. The meta-atom with monopole and dipole moments proposed in [16] provides more benefits for sound field control. Note that a combination of the monopole and dipole resonators named monopole–dipole resonators was suggested earlier for noise reduction in tubes [17,18]. A regular array formed by the monopole–dipole resonators can totally absorb an incident sound wave in free space [19] or in a waveguide [20]. It is important to note that a surface covered by the dipole resonators can not be described by the ordinary acoustic impedance. The special boundary condition in the form of a tangential impedance is needed for the equivalent surface with uniform properties [21].

Two coupled dipole resonators give a quadrupole resonator, which is used for a higher-order topological insulator [22]. A 2D lattice made of quadrupole resonators is realized and experimentally studied in [23]. An elastic sphere has many eigenmodes [24], and the third one provides the quadrupole scattering of sound waves. So, the elastic sphere as well as an elastic cylinder can be assumed as the quadrupole resonator in a certain frequency range. Another quadrupole resonator for water is composed of a hard cylinder with an elliptical rubber coating [25]. The coupling of two quadrupole resonators allows the building of an octupole resonator [26], while the coupling of two octupole resonators results in a hexadecapole resonator [27]. By repeating this process, we can create resonators of any order of multiplicity. Recent reviews [28,29,30] have shown growing interest in the development of metamaterials using higher-order topological resonators. Following this trend, this paper is dedicated to studying the homogenized acoustic properties of the metasurfaces formed by multipole resonators.

In this study, we investigate the acoustic properties of a rigid surface covered by multipole resonators. In Section 2, the physical model of the multipole resonator and its characteristics are described. Also, in Section 2 the sound reflection properties of the surface with a periodic array of the resonators are considered and the homogenized boundary condition for the metasurface is introduced. The sound absorption properties of the metasurfaces are analyzed in Section 3. In Section 4, possible ways to create multipole resonators are discussed.

2. Materials and Methods

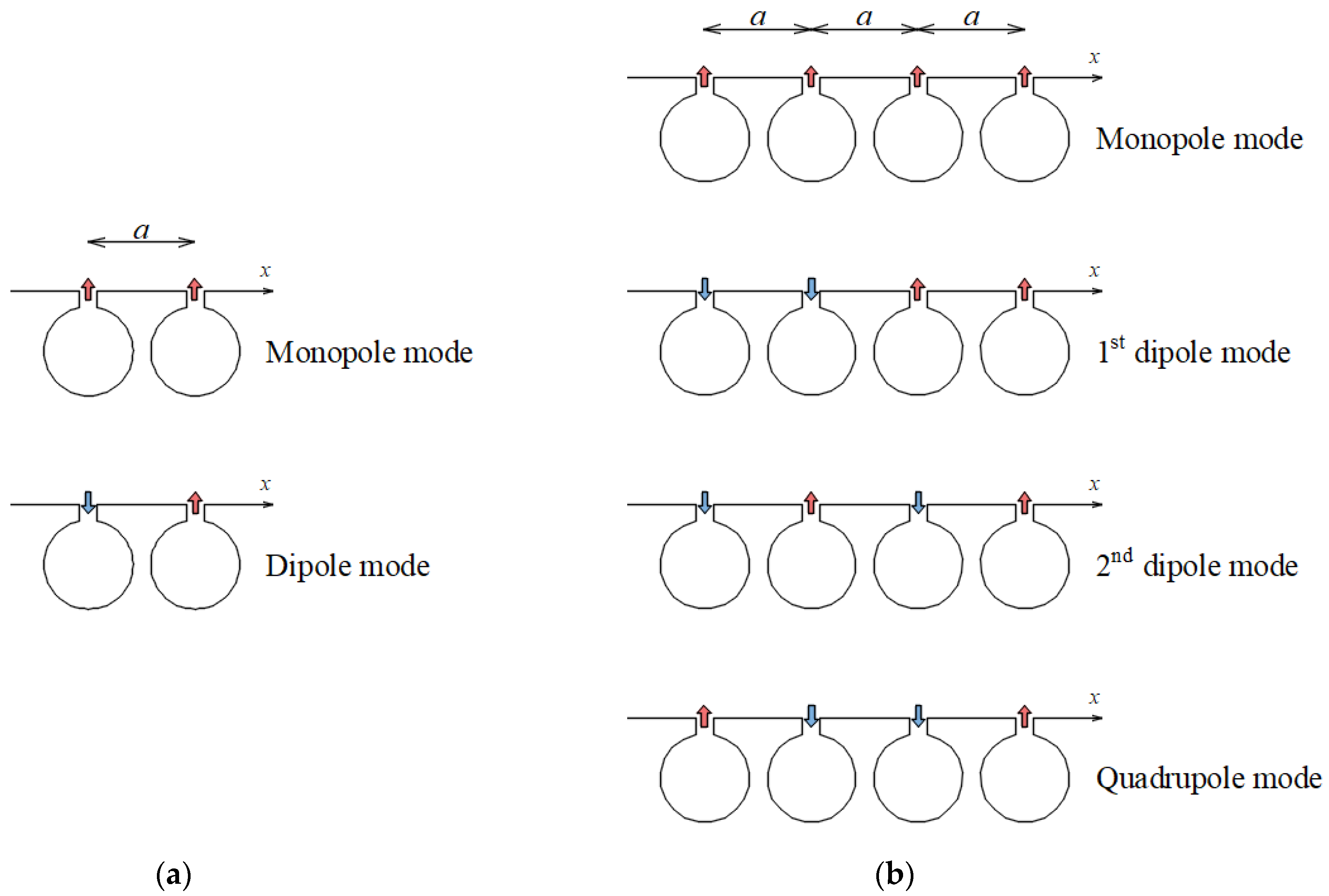
2.1. Linear Multipole

A multipole sound source can be described as a set of monopole sources. If the monopoles are located on a straight line, the multipole source is linear [31]. In the same way, a multipole sound scatterer can be presented as a system of monopoles whose volume velocities are not independent, but they are adjusted to yield a specific scattered sound field. Let us combine the monopoles to create a sound scatterer with the multipole order $N$ and moment $Q_N$. The idea is to use a set of $2^N$ monopoles with the volume velocities $+q$ and $-q$ and distances $a$ between each other. The signs of the volume velocities are selected to ensure that the lower order moments are zero, i.e., $Q_M=0$ if $M<N$. The physical models and their parameters are given in Figure 1.

2.1.1. Monopole

The simplest scatterer contains only one monopole with the volume velocity $q$. The sound pressure field $P$ consists of two components: the first one is the incident field $p$ and the second one is the field produced by the monopole $p_0$. Due to the superposition principle, we can write $P=p+p_0$. The impedance of the monopole scatterer is

$$Z_0=-\frac{P}{q}.$$

(1)

The motion of the monopole scatterer is excited by sound pressure. In a general way, the equation of motion is given by

$$m\ddot{w}+\gamma \dot{w}+\kappa w=-\sigma P,$$

(2)

where $m$ on the mass of the monopole, $\kappa$ is its stiffness, $\gamma$ is the friction coefficient, $w$ is the displacement of the moving part, and $\sigma$ is the surface area of the moving part. The volume velocity is related to the displacement by $q=\sigma \dot{w}$. From (1) and (2), we can find the monopole impedance

$$Z_0=\frac{1}{{\sigma }^2}\left(\gamma -i\omega m\left(1-\frac{{\omega }_0^2}{{\omega }^2}\right)\right),$$

(3)

where ${\omega }_0^2=\kappa /m$ is the resonance frequency.

Note that the impedance $Z_0$ is defined only by the intrinsic properties of the scatterer and does not depend on radiation conditions. They are usually described by the radiation impedance, which is a ratio of the own field to the volume velocity [32]

$$R_0=\frac{p_0}{q}.$$

(4)

The volume velocity of the monopole scatterer in response to the incident field $p$ is found from (1) and (4)

$$q=-\frac{p}{Z_0+R_0}.$$

(5)

At resonance, the volume velocity is maximal. The resonance condition follows from (5)

$$\mathrm{Im}\left(Z_0+R_0\right)=0.$$

(6)

Condition (6) is well known: at resonance frequency, the imaginary part of the resonator impedance compensates for the imaginary part of the radiation impedance [32]. Commonly, the frequency ${\omega }_0$ differs from the resonance frequency ${\mathsf{\Omega }}_0$ determined from condition (6) due to the influence of the surrounding medium and reflecting boundaries in the vicinity of the resonator. The value of ${\mathsf{\Omega }}_0$ depends both on the mechanical parameters of the resonator and the sound radiation conditions.

Equations (1)–(6) are enough to describe the motion of the monopole resonator and its interaction with the external sound field.

2.1.2. Dipole

Now we apply the same formalism for the sound scatterers of higher order of multiplicity, which is indicated by $N$. The dipole scatterer has the order $N=1$ and is assumed as a pair of monopoles with opposite volume velocities positioned with spacing $a$ as shown in Figure 1. Both the monopoles are on the axis $x$; the monopoles with the volume velocities $+q$ and $-q$ are located at the points $x=a/2$ and $x=-a/2$, respectively.

The sound field generated by the two monopoles is $p_1$ and the total field is $P=p+p_1$. Using (2) and (3), we obtain two equations of motion

$$-q{Z}_0=-{P|}_{x=-\frac{a}{2}},$$

(7)

$$q{Z}_0=-{P|}_{x=\frac{a}{2}}.$$

(8)

Subtracting (8) from (7), we can find

$$2Z_{0}q={P|}_{x=-\frac{a}{2}}-{P|}_{x=\frac{a}{2}}.$$

(9)

The dipole moment is $Q_1=aq$. Decomposing $P$ near $x=0$ into a Taylor series like $P\left(x\right)=P\left(0\right)+x{\left(\partial P/\partial x\right)}_{x=0}+\cdots$, we define the impedance of the dipole scatterer

$$Z_1=-\frac{{\left(\partial P/\partial x\right)}_{x=0}}{Q_1}.$$

(10)

Formally, the monopole and dipole impedances are connected by the ratio $Z_1=2Z_0/a^2$. But the impedance $Z_1$ is determined by the properties of the dipole resonator and can be expressed in another way. For example, the impedance for the membrane dipole resonator is proposed in [12]. At the same time, Equation (10) establishes the universal relationship between the force acting on the dipole by the sound field given by $\partial P/\partial x$, the moment $Q_1$ characterizing the motion of the resonator, and the impedance $Z_1$ defining the mechanical properties of the resonator.

2.1.3. Quadrupole

If $N=2$ we deal with a quadrupole resonator, which can be presented as an array of four monopoles (Figure 2) positioned at a distance $a$ from each other. The monopoles with the volume velocities $+q$ and $-q$ are located at $x=-3a/2,x=3a/2$ and $x=-a/2$, $x=a/2$, respectively. The equations of motion for four monopoles are

$$q{Z}_0=-{P|}_{x=-\frac{3a}{2}}, -q{Z}_0=-{P|}_{x=-\frac{a}{2}}, -q{Z}_0=-{P|}_{x=\frac{a}{2}}, q{Z}_0=-{P|}_{x=\frac{3a}{2}}.$$

(11)

The size of the quadrupole is $3a$; therefore, we can introduce the quadrupole moment $Q_2={\left(3a\right)}^{2}q$. From (11), we obtain the impedance of the quadrupole scatterer

$$Z_2=-\frac{{\left({\partial }^{2}P/\partial x^2\right)}_{x=0}}{Q_2}.$$

(12)

The impedance of the monopoles and the quadrupole are related by $Z_2=2Z_0/3a^4$.

2.1.4. Multipole

A linear multipole of an arbitrary order can be built in the same way. Figure 1 shows the octupole ($N=3$) consisting of eight monopoles. The multipole of order $N$ is formed by $2^N$ monopoles. Its size is $l_N=\left(2^N-1\right)a$. The multipole moment is defined as $Q_N={\left(l_N\right)}^{N}q$, and for the monopole we have $N=0$ and $Q_0=q$. The impedance of the multipole scatterer is

$$Z_N=-\frac{{\left({\partial }^{N}P/\partial x^N\right)}_{x=0}}{Q_N}.$$

(13)

where $P=p+p_N$ is the total sound field, and $p_N$ is the field radiated by the scatterer. Its radiation impedance is defined in an ordinary way

$$R_N=\frac{p_N}{Q_N}.$$

(14)

The moment of the scatterer in response to the incident field $p$ is

$$Q_N=-\frac{{\left({\partial }^{N}p/\partial x^N\right)}_{x=0}}{Z_N+R_N}.$$

(15)

The condition of the resonance is

$$\mathrm{Im}\left(Z_N+R_N\right)=0.$$

(16)

We assume that Equation (16) is satisfied at a certain frequency ${\mathsf{\Omega }}_N$. So, the multipole scatterer can be considered as a resonator and below we will focus on this specific case. However, Equations (13)–(15) remain valid for any scatterer, not just those that are resonant, and can be used to describe multipole scatterers regardless of how they are formed. The main goal is to determine the impedance $Z_N$, which is strongly influenced by the structure of the scatterer. If the scatterer consists of a linear array of monopoles, with an impedance $Z_0$, as is shown in Figure 1, then the impedance of the entire system is $Z_N=C_N{Z}_0/a^{2N}$, where $C_N$ is a coefficient that depends only on the order $N$ of the array.

It is important to note that the impedances of the multipole scatterers introduced by (13) have different dimensions depending on the order $N$.

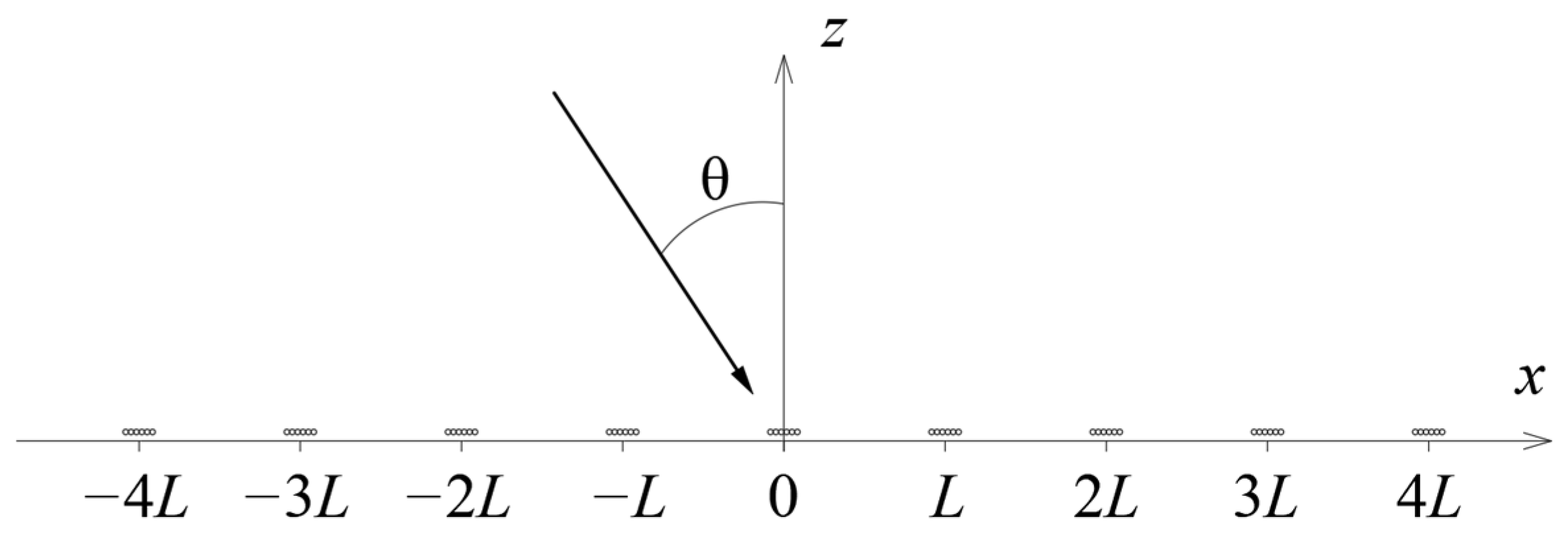
2.2. Array of Multipoles

In this section, we consider the acoustic properties of surfaces covered by a periodic array of multipole scatterers. These surfaces are named metasurfaces due to their unusual equivalent boundary condition. First of all, we find the sound field reflected by the metasurface. Next, we introduce a homogenized boundary condition and use it to describe the far-field behavior of the reflected sound.

2.2.1. Reflection Coefficient

The studied metasurface is shown in Figure 2. The scatterers with the order of multiplicity $N$ are spaced periodically with a distance L near the rigid surface. The special period L is assumed to be much larger than the length of the multipole scatterer $l_N\ll L$. We consider the two-dimensional problem, so the surface coincides with the plane $z=0$ and the scatterers are at points $x_n=nL$, where n is the number of resonators in the array. Assuming a time-harmonic disturbance in the form of $e^{-i\omega t}$, where t is time and $\omega$ is an angular frequency, the sound pressure in the half-space $z\ge 0$ can be given as follows:

$$P=A{e}^{i{\xi }_{0}x-i{\kappa }_{0}z}+A{e}^{i{\xi }_{0}x+i{\kappa }_{0}z}+p_N,$$

(17)

where $p_N$ is the sound field radiated by the array, $A$ is the amplitude of the incident plane wave, and ${\xi }_0$ and ${\kappa }_0$ are the components of the wave vector. The second term in the right part of (17) is the plane wave reflected by the rigid surface. Also, we can use an incidence angle $\theta$, which is related to the wave vector components by the equations ${\xi }_0=k\sin \theta$ and ${\kappa }_0=k\cos \theta$, where $k=\omega /c$, $c$ is the speed of sound.

The sound field of the periodic array formed by the monopole scatterers is found in [13] by the means of the Floquet theorem for periodic systems and the Fourier method. The sound pressure field is

$$p_0=Q_0\frac{\omega \rho }{L}{\displaystyle \sum }_n\frac{e^{i{\xi }_{n}x+i{\kappa }_{n}z}}{{\kappa }_n},$$

(18)

where ${\xi }_n={\xi }_0+2\pi n/L$, ${\kappa }_n=\sqrt{k^2-{\xi }_n^2}$, $\rho$ is the density of the medium, and $Q_0$ is the monopole moment of the scatterer placed at the point $x=0$.

The sound field produced by the array consisting of the $N$-pole scatterers can be found by differentiating (18) with respect to the coordinate $x$ [33]. For arbitrary multipoles, we have

$$p_N=Q_N\frac{{\left(-1\right)}^N}{N!}\frac{{\partial }^N{p}_0}{\partial x^N}=Q_N\frac{\omega \rho }{L}\frac{{\left(-i\right)}^N}{N!}{\displaystyle \sum }_n{\xi }_n^N\frac{e^{i{\xi }_{n}x+i{\kappa }_{n}z}}{{\kappa }_n},$$

(19)

where $Q_N$ is the multipole moment of the scatterer placed at the point $x=0$.

Substituting (19) into (17) and then (17) into (13), we obtain the multipole moment

$$Q_N=-2A\frac{i^N{\xi }_0^N}{Z_N+R_N},$$

(20)

where the radiation impedance of the multipole is introduced as follows:

$$R_N=\frac{\omega \rho }{LN!}{\displaystyle \sum }_n\frac{{\xi }_n^{2N}}{{\kappa }_n}.$$

(21)

From (19) and (20), we find the sound field radiated by the array

$$p_N=-2A\frac{\omega \rho }{L\left(Z_N+R_N\right)N!}{\xi }_0^N{\displaystyle \sum }_n{\xi }_n^N\frac{e^{i{\xi }_{n}x+i{\kappa }_{n}z}}{{\kappa }_n}.$$

(22)

The field (22) is valid for the arbitrary period $L$. Furthermore, we limit this study to the period $L<\lambda /2$, where $\lambda =2\pi /k$ is the sound wavelength. All terms in the sum (22) with $n\ne 0$ are proportional to $e^{-\mathrm{Im}{\kappa }_{n}z}$; therefore, in the far field, where field $kz\gg 1$, they tend to be zero. So, the array radiates only one plane wave $e^{i{\xi }_{0}x+i{\kappa }_{0}z}$. In this case, the radiation impedance can be written as

$$R_N={R^{\prime }}_N+i{R^{″}}_N=\frac{\omega \rho }{LN!}\frac{{\xi }_0^{2N}}{{\kappa }_0}-i\frac{\omega \rho }{LN!}{\displaystyle \sum }_{n\ne 0}\frac{{\xi }_n^{2N}}{{\alpha }_n},$$

(23)

where ${\alpha }_n=\sqrt{{\xi }_n^2-k^2}$.

The field (17) is determined only by the term $n=0$ and is equal to $P=A{e}^{i{\xi }_{0}x-i{\kappa }_{0}z}+AV{e}^{i{\xi }_{0}x+i{\kappa }_{0}z}$, where $V$ is the reflection coefficient of the metasurface. Using (22) and (23), we find the reflection coefficient

$$V=\frac{Z_N+i{R^{″}}_N-{R^{\prime }}_N}{Z_N+i{R^{″}}_N+{R^{\prime }}_N}.$$

(24)

By the means of the incidence angle $\theta$, Equation (24) is transformed into

$$V=\frac{{\tilde{Z}}_N\cos \theta -{\sin }^{2N}\theta }{{\tilde{Z}}_N\cos \theta +{\sin }^{2N}\theta },$$

(25)

where ${\tilde{Z}}_N$ is a dimensionless value given by

$${\tilde{Z}}_N=\frac{LN!}{\omega \rho }\left(Z_N+i{R^{″}}_N\right).$$

(26)

In the far field, the sound wave reflected by the metasurface is simply a specularly reflected plane wave. The reflection coefficient can be calculated using (24) or (25). However, for a more accurate analysis of the near field, the exact Equation (22) should be used.

2.2.2. Equivalent Boundary Condition

Equations (17) and (22) yield the sound field in a half-space $z>0$; however, at distances $kz\gg 1$, it is enough to know only the reflection coefficient (24) in order to calculate the sound field. This means that it is possible to apply a uniform boundary condition for the surface $z=0$, which provides the same far field. In this sense, the boundary condition is equivalent to the considered metasurface. The homogenization swaps the difficult structure for a simple model convenient to characterize the interaction of the sound fields and metasurfaces. If the periodic array shown in Figure 1 consists of the monopole scatterers, the usual impedance is the equivalent boundary condition [10]. It has a form at $z=0$

$$Z_0^{\prime }=\frac{P}{v_z},$$

(27)

where $v_z$ is the normal velocity of the metasurface.

In the case of the dipole scatterers [13] the equivalent boundary condition is

$$Z_1^{\prime }=-\frac{{\partial }^{2}P/\partial x^2}{v_z}.$$

(28)

Taking into account (27) and (28), it is possible to assume that the array of the scatterers of the order $N$ has the following equivalent boundary condition at $z=0$

$$Z_N^{\prime }=\frac{{\left(-1\right)}^N}{v_z}\frac{{\partial }^{2N}P}{\partial x^{2N}}.$$

(29)

Applying boundary condition (29) for the plane $z=0$ and using the relation $i\omega \rho v_z=\partial P/\partial z$, we can find the reflection coefficient of a plane wave with the incidence angle $\theta$.

$$V=\frac{Z_N^{\prime }\cos \theta -\rho c{k}^{2N}{\sin }^{2N}\theta }{Z_N^{\prime }\cos \theta +\rho c{k}^{2N}{\sin }^{2N}\theta }.$$

(30)

Comparing (26) and (30), we can state that the reflection coefficient (25) of the rigid surface covered by the multipole scatterers and the reflection coefficient (30) with the uniform impedance (29) are the same. The relation of the impedances in (25) and (30) is as follows:

$$Z_N^{\prime }=\rho c{k}^{2N}{\tilde{Z}}_N.$$

(31)

Now the physical meanings of the values in (31) are clear. ${\tilde{Z}}_N$ is the dimensionless impedance characterizing at a certain frequency $\omega$ the metasurface formed by the array of the scatterers. $Z_N^{\prime }$ is the homogenized boundary condition which does not depend directly on frequency. The impedance $Z_N^{\prime }$ is local and can be used for metasurfaces without taking into account their structure. For $N=0$, the impedance $Z_0^{\prime }$ is the ordinary surface impedance, which is a ratio of the sound pressure to the normal velocity. For $N\ge 1$, the motion of the surface is excited by a tangential force; therefore, condition (29) can be called the tangential impedance [13,20].

Boundary conditions similar to (29) are widely known in electromagnetism [34,35], and they belong to high-order impedance boundary conditions or HOIBC. At the same time, in acoustics, the HOIBC are not often met. A model for homogenizing rigid structured surfaces, which allows for the derivation of higher-order equivalent boundary conditions, can be found in [36].

3. Results

In this section, we analyze the acoustic properties of the metasurfaces with boundary condition (29) and assume the scatterers as resonators. We are interested in the case when condition (16) is fulfilled. In other words, we consider the behavior of the metasurface at the resonance frequency of the scatterers. According to (16), the impedances ${\tilde{Z}}_N$ and $Z_N^{\prime }$ are real at this frequency as well as the reflection coefficient.

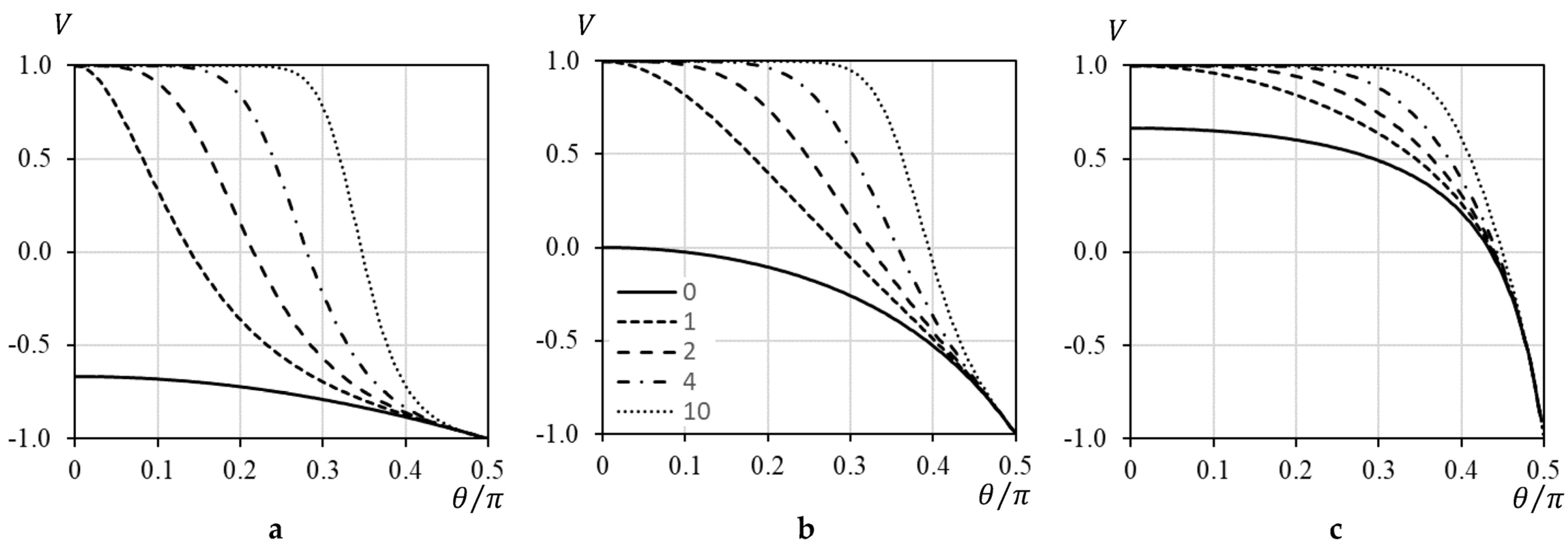
3.1. Reflection Coefficient

The reflection coefficient from the metasurface with boundary condition (29) is given by (25) and (30). Figure 3 shows the dependence of the reflection coefficient $V$ on the incidence angle $\theta$ for different values of the dimensionless impedance ${\tilde{Z}}_N$. The reflection coefficient is calculated for five orders of multiplicity.

For $N\ge 1$ at normal incidence ($\theta =0$), the reflection coefficient is one. It means that the normally incident plane wave does not excite the motion of the scatterers and the metasurface is equivalent to a rigid plane. With an increase in the angle of incidence, the reflection coefficient changes from 1 to $-1$. For all values of ${\tilde{Z}}_N$, there is the incidence angle ${\theta }^{\prime }$ at which $V=0$; hence, the incident wave is totally absorbed by the metasurface. The angle ${\theta }^{\prime }$ increases with the order $N$, and the range of the incidence angles at which absorption is effective ($\left|V\right|\ll 1$) decreases.

The surface with monopole scatterers ($N=0$) absorbs the normally incident wave at any value of ${\tilde{Z}}_0$, but total absorption at a certain angle is possible only if ${\tilde{Z}}_0\ge 1$. This is the main difference between the normal and tangential impedances.

Under the grazing incidence, when $\theta \to \pi /2$, from (30) the reflection coefficient is $V\approx -1+2{\tilde{Z}}_N\delta$, where $\delta =\pi /2-\theta$ and $\delta \to 0$. All metasurfaces behave like a soft boundary because the reflection coefficient $V\to -1$. As one can see in Figure 3, the function $V\left(\theta \right)$ at $\theta \approx \pi /2$ is the same for any order of the multiplicity $N$ and impedance ${\tilde{Z}}_N$.

3.2. Diffuse Field Absorption

Let us consider sound absorption by metasurfaces. The absorption coefficient of the plane wave is $\alpha =1-{\left|V\right|}^2$ and can be found using (30). The considered metasurface can completely absorb the incident wave at a certain angle. In the case of a diffuse sound field, the absorption coefficient should be averaged over the angle. So, the diffuse absorption coefficient is

$${\alpha }_d=\frac{2}{\pi }{{\displaystyle \int }}_0^{\frac{\pi }{2}}\alpha d\theta .$$

(32)

Figure 4 presents the calculation of the diffuse absorption coefficient ${\alpha }_d$ for the real values of the impedance ${\tilde{Z}}_N$ and different orders $N$. If the impedance is close to zero, the absorption coefficient is about zero as well. All curves have a maximal; therefore, the impedance of the metasurfaces can be optimized to provide maximal absorption. After the maximum, the absorption coefficient slowly decreases with the increase in ${\tilde{Z}}_N$. The maximums of the curves in Figure 4 are not sharp peaks, so, the efficiency of sound absorption has values close to the maximal one in a wide range of ${\tilde{Z}}_N$.

The fundamental difference of the metasurfaces formed by the scatterers of different order $N$ is that the sound absorption decreases with the increase in the order $N$. For example, the absorption coefficient is only about 0.2 for $N=10$. Also, the weak absorption properties for higher orders are demonstrated in Figure 3, where we can notice that the reflection coefficient is $V\approx 1$ for the orders $N\ge 4$ and the incidence angles $\theta <\pi /4$.

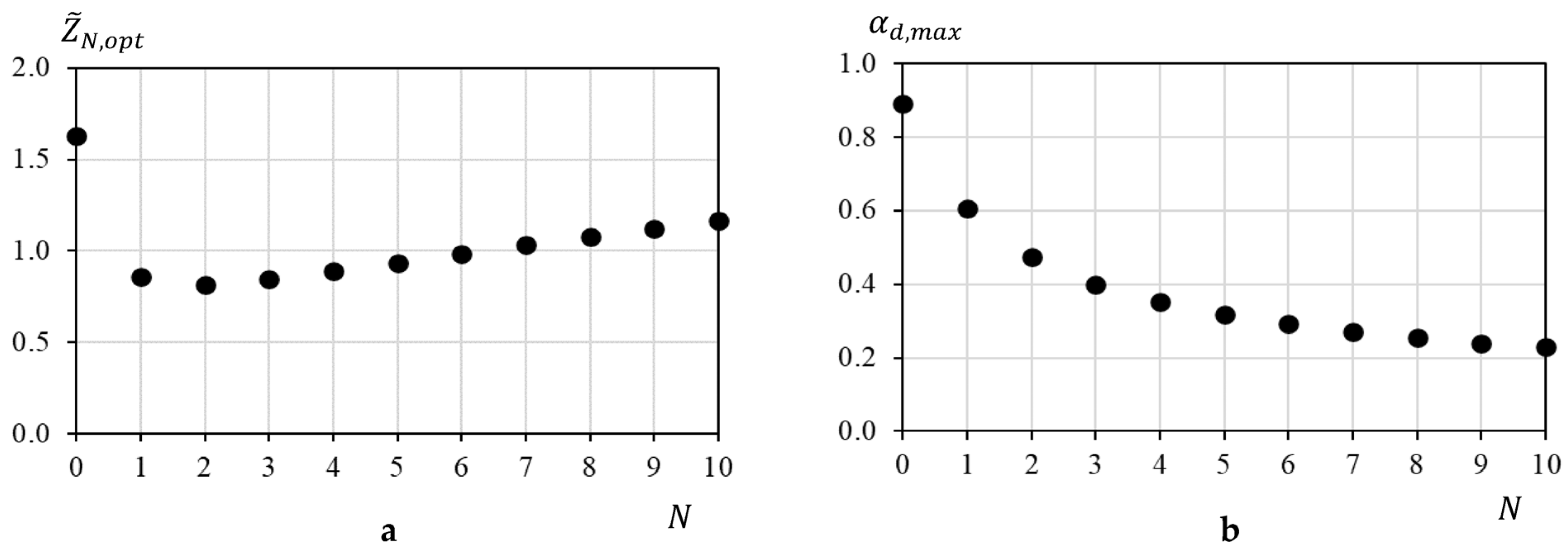
3.3. Optimal Impedance

Figure 4 shows that sound absorption can be maximized. The optimal impedance is found in the equation $d{\alpha }_d/d{\tilde{Z}}_N=0$, which gives the optimal values ${\tilde{Z}}_{N,opt}$ for the metasurface formed by the $N$-pole resonators. They are shown in Figure 5a. For the monopole resonators, the optimal impedance is ${\tilde{Z}}_{0,opt}=1.63$, whereas for $N\ge 1$ it has the values ${\tilde{Z}}_{N,opt}\approx 1$. This simple approximation can be used for a rough estimation of absorption provided by the metasurface.

The maximal absorption coefficient is ${\alpha }_{d,max}={\alpha }_d\left({\tilde{Z}}_{N,opt}\right)$, which is shown in Figure 5b. The found values of ${\alpha }_{d,max}$ decrease with the order $N$. For $N\ge 2$, the absorption coefficient is less than 0.5. We can state that the sound-absorbing properties of the metasurfaces decrease with the order of multiplicity.

4. Discussion

The proposed theory describes the arrays of multipole scatterers in a general view without taking into account the structure of the scatterers. To apply this theory, we need to introduce the multipole moment $Q_N$ of the scatterer. Acoustic metasurfaces [8,11] are usually regular systems of resonators of various kinds. Due to the interaction between the resonators, the systems have a lot of eigenmodes, some of which cause multipole sound scattering. To illustrate this point, we consider two examples of commonly used types of resonators and demonstrate how high-order eigenmodes can occur.

4.1. Helmholtz Resonators

The acoustic metasurface can be created using built-in Helmholtz resonators [10]. A single Helmholtz resonator has only one mode, but if two resonators are placed close to each other, they have two modes [14]. Figure 6a shows two resonators built into the rigid surface at a distance $a$ that is small relative to the wavelength, i.e., $ka\ll 1$. At the first mode, they oscillate in phase and the far field appears like the field generated by a single resonator with double volume velocity. Therefore, this mode is called “monopole mode” in Figure 6a. In the second mode, the resonators oscillate out of phase and the pair of them behaves like a dipole in the far field. In this case, they can be described as a multipole with $N=1$, as shown in Figure 1. The impedance of the Helmholtz resonator can be calculated using Equation (3), where $\sigma$ is the cross-sectional area of the neck.

Now we consider four Helmholtz resonators as shown in Figure 6b. A system with four degrees of freedom has four modes. In the first one, all the resonators are in phase, and they behave like a single monopole. There are two dipole modes at which two resonators oscillate in phase, while the other two oscillate out of phase. The fourth mode is of particular interest. The resonators act as a quadrupole scatterer with respect to the incident wave. The physical model with $N=2$ can be applied directly for the quadrupole mode with the moment $Q_2$, as depicted in Figure 1.

Considering a larger number of Helmholtz resonators, we can find more complex eigenmodes. A set of $2^N$ equidistant resonators has a mode corresponding to $N$-pole radiation. Therefore, it can be assumed as an $N$-pole scatterer, and the physical model in Figure 1 as well as the multipole moment $Q_N$ can be applied. The $N$-pole oscillations of $2^N$ resonators can be described by the equations given in Section 2.1.4.

4.2. Membrane Resonators

Stretched membranes are successfully used for producing acoustic metasurfaces [37] depending on frequency. A membrane embedded in a rigid baffle is both a monopole and dipole scatterer [13]. The monopole mode shown is in Figure 7a for the membrane clamped at the points $x=\pm a$. At the frequency of the first eigenmode, the velocity of the membrane is

$$u_1=u\cos \frac{\pi x}{2a},$$

(33)

where $u$ is the oscillation amplitude. From (33), we can find the monopole moment

$$Q_0=\underset{-a}{\overset{a}{{\displaystyle \int }}}{u}_{1}dx=\frac{4a}{\pi }u.$$

(34)

The second eigenmode of the same membrane is shown in Figure 7b and given by

$$u_2=u\sin \frac{\pi x}{a}.$$

(35)

The dipole moment found from (35) is

$$Q_1=\underset{-a}{\overset{a}{{\displaystyle \int }}}{u}_{2}xdx=\frac{2a^2}{\pi }u.$$

(36)

The higher eigenmodes $u_n$ of the membrane produce only monopole (if $n$ is odd) or dipole (if $n$ is even) scattering. To obtain quadrupole scattering, we need the coupled membranes oscillating in the second eigenmodes as shown in Figure 7c. Both membranes are clamped at the point $x=0$. We can also consider one membrane of a length $4a$ with a fixed center. The coupled membranes have two modes in which they move in phase and out of phase. The latter provides quadrupole scattering.

We can note that the quadrupole mode is similar to the physical model of the quadrupole scatterer shown in Figure 1. The velocity of the coupled membranes is $u_2$ for $-2a<x<0$ and $-u_2$ for $0<x<2a$. Their quadrupole moment is

$$Q_2=\underset{-2a}{\overset{0}{{\displaystyle \int }}}{u}_2{x}^{2}dx-\underset{0}{\overset{2a}{{\displaystyle \int }}}{u}_2{x}^{2}dx=\frac{8a^3}{\pi }u.$$

(37)

The $N$-pole scatterer can be created using the $2^{N-1}$ membranes shown in Figure 7b. Examples with the Helmholtz resonators and membrane resonators demonstrate possible ways to construct a resonant multipole scatterer that can be used as a meta-atom for an acoustic metasurface.

5. Conclusions

The acoustic properties of a rigid surface covered with a periodic arrangement of linear multipole scatterers are analyzed for a subwavelength spatial period. First of all, the sound field reflected by the surface with the scatterers is found analytically. If the distance between the scatterers is less than half of a wavelength, the scattered field is just the plane wave whose direction coincides with that of the plane wave reflected from the rigid surface. This means that in the far field, a reflection coefficient can be used to calculate the sound field, and an equivalent boundary condition can be imposed on the surface. The found dependence of the reflection coefficient on the incidence angle can not be obtained using an ordinary impedance if the order of the multipole scattering is one or greater. In this case, a special boundary condition is required to match the exact solution, which is a tangential impedance (29) that depends on the multipole order. Due to the unusual boundary condition, the surfaces with the resonators are referred to as metasurfaces.

The equivalent boundary condition for a metasurface formed by the $N$-pole scatterers is the ratio of a derivative of the sound pressure of the order $2N$ along the metasurface to its normal velocity. This type of boundary condition is known as a high-order impedance boundary condition. The tangential impedance (29), given in a simple form, can be used to describe surfaces with complex microstructures for the study of acoustic metasurfaces.

Resonant scatterers are of particular interest. If a multipole scatterer is a resonator, there is a frequency at which a sum of the imaginary parts of its impedance and the radiation impedance is zero, and the equivalent impedance is real. This situation is analyzed and the optimal impedance as well as the maximum absorption coefficient for a diffuse sound field are found. With an increase in the multipole order of the resonators, the absorption efficiency decreases. It means that the metasurfaces composed of the high-order multipole resonators are not effective absorbers.

The proposed high-order multipole metasurfaces exhibit interesting acoustic properties that can be applied to and studied in various problems. Examples may include the attenuation of sound waves propagating in ducts or enclosed spaces, as well as the control of sound fields scattered by various obstacles.