Reducing Data Requirements for Simple and Effective Noise Mapping: A Case Study of Noise Mapping Using Computational Methods and GIS for the Raebareli City Intersection
Abstract
:1. Introduction
Objectives of the Research
- (a)
- Determining the noise prediction value using large data sets.
- (b)
- Determining the noise prediction value with a small number of data points and comparing the results to those from many data points to determine the deviation.
- (c)
- Determining the noise prediction value using the same source point average value and comparing the results with many noise prediction methods to find the deviation.
- (d)
- Determining the noise prediction value using Google Navigation data methods and comparing the results with large data noise prediction methods to find the deviation.
- (e)
- Determining the accurate noise prediction value using the ANN (artificial neural network) method and comparing the results with all other methods to find the deviation. ANN results are also compared to the observed value to check the accuracy of the method.
- (f)
- Determining the noise prediction value using an automated method based on the machine learning approach and freely available Google data.
- (g)
- Determining the noise exposure value for the study area for a 12-h exposure to noise for the people living in this vicinity.
2. Materials and Methods
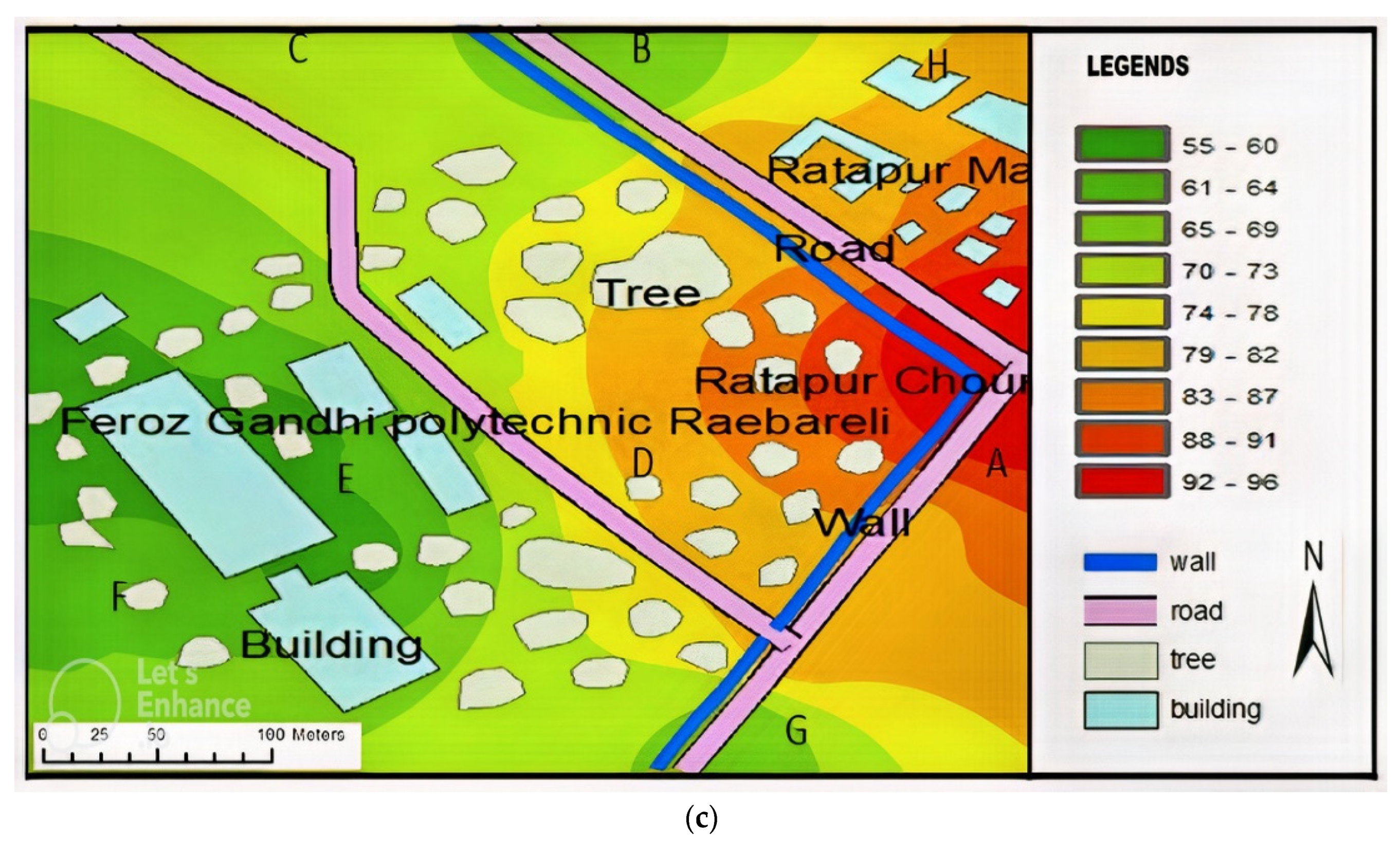
2.1. Study Area
2.2. Data Collection and Processing
2.2.1. High-Grade Sound Pressure Level Meter
2.2.2. Total Station and GPS
2.2.3. Mapping Software
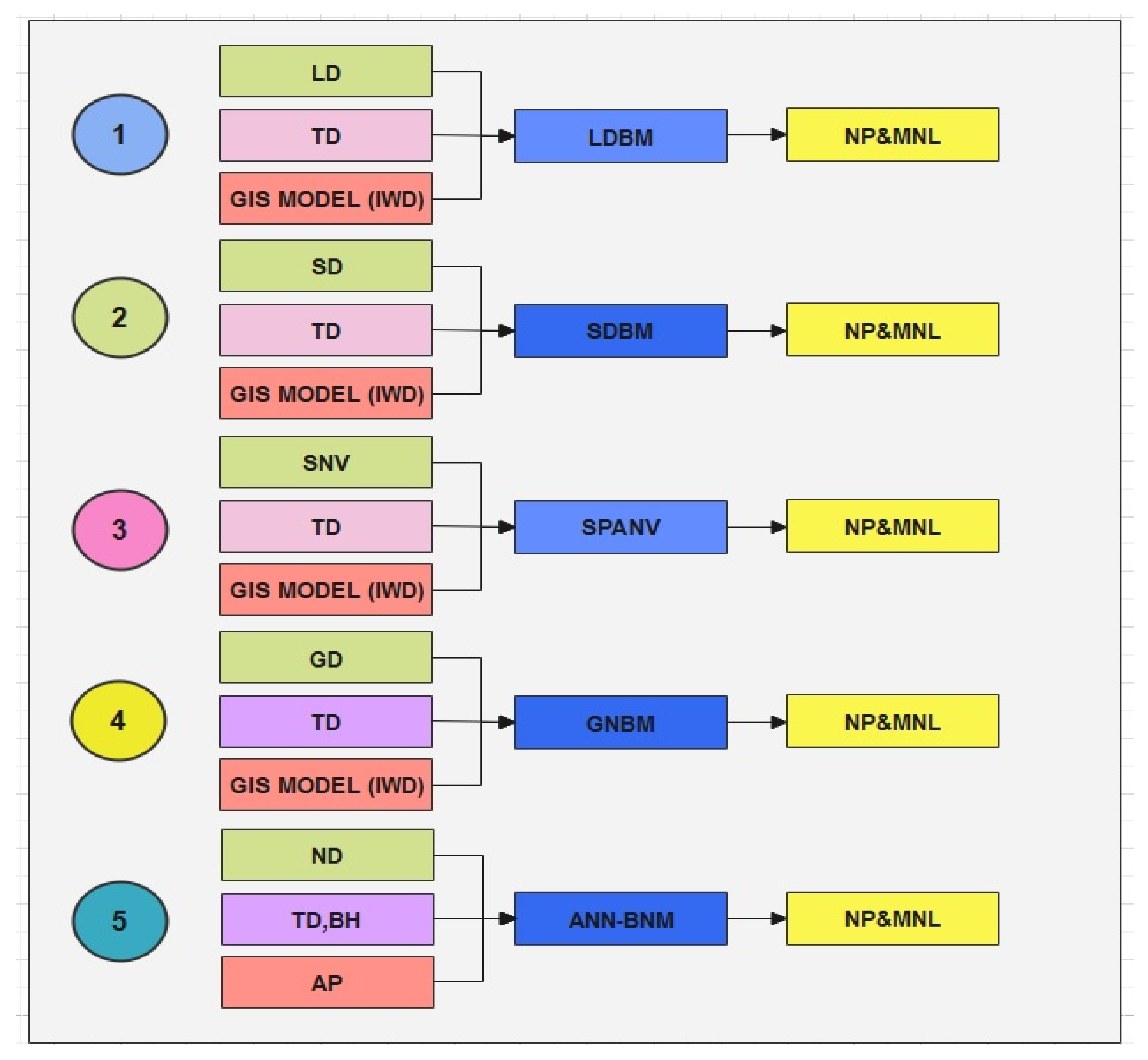
3. Methodology
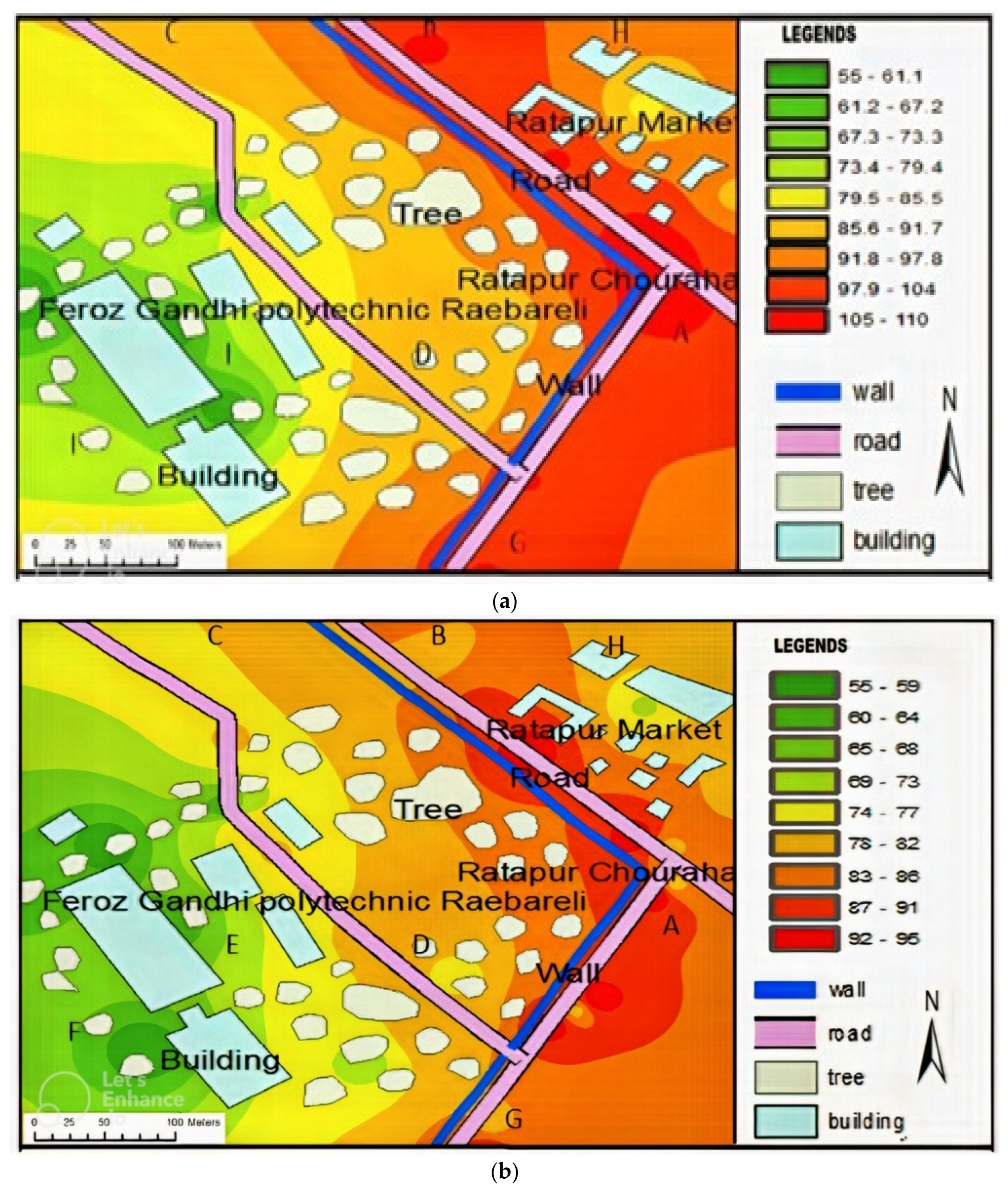
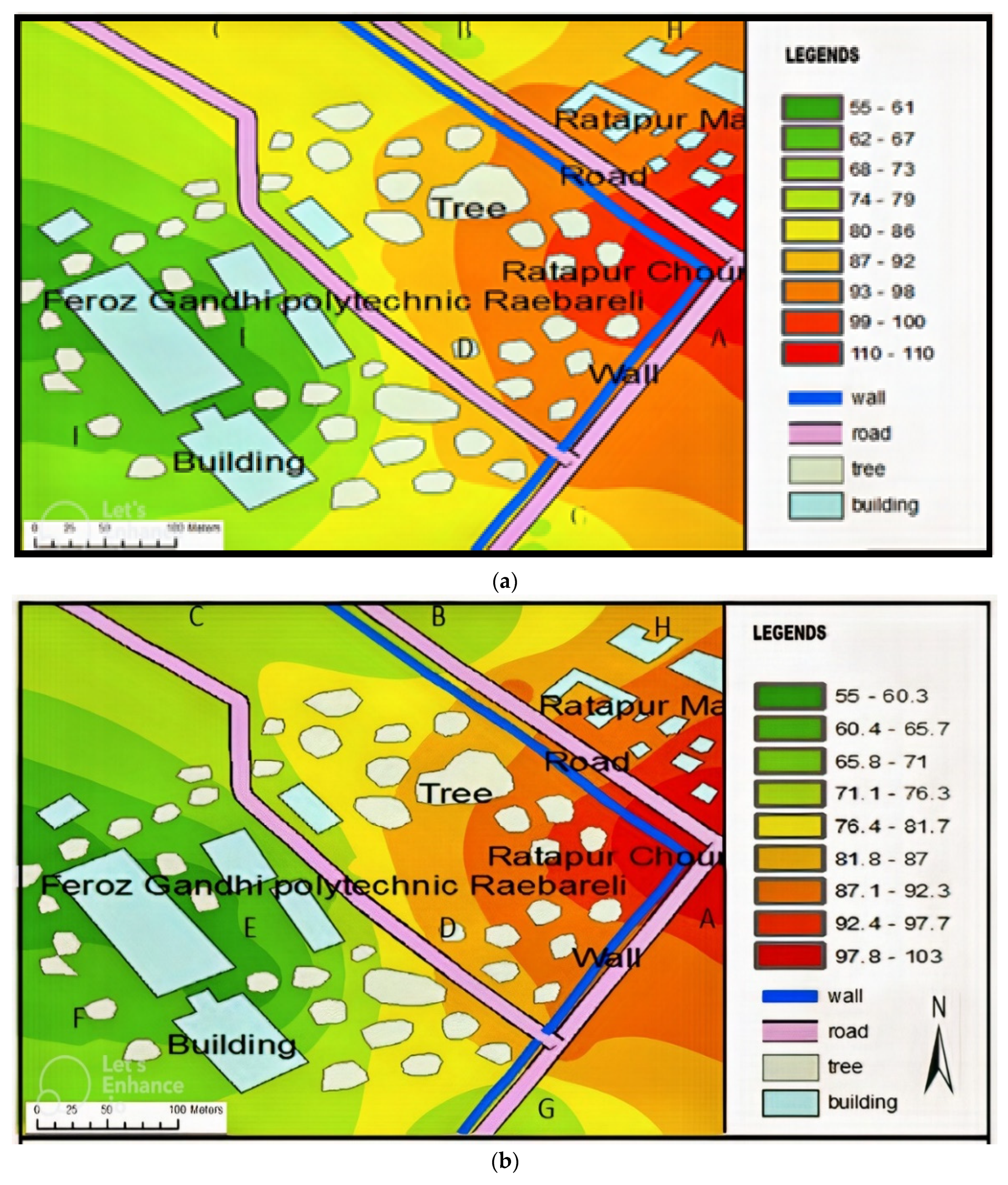
3.1. Large Data-Based Noise Prediction Method (LDBM)
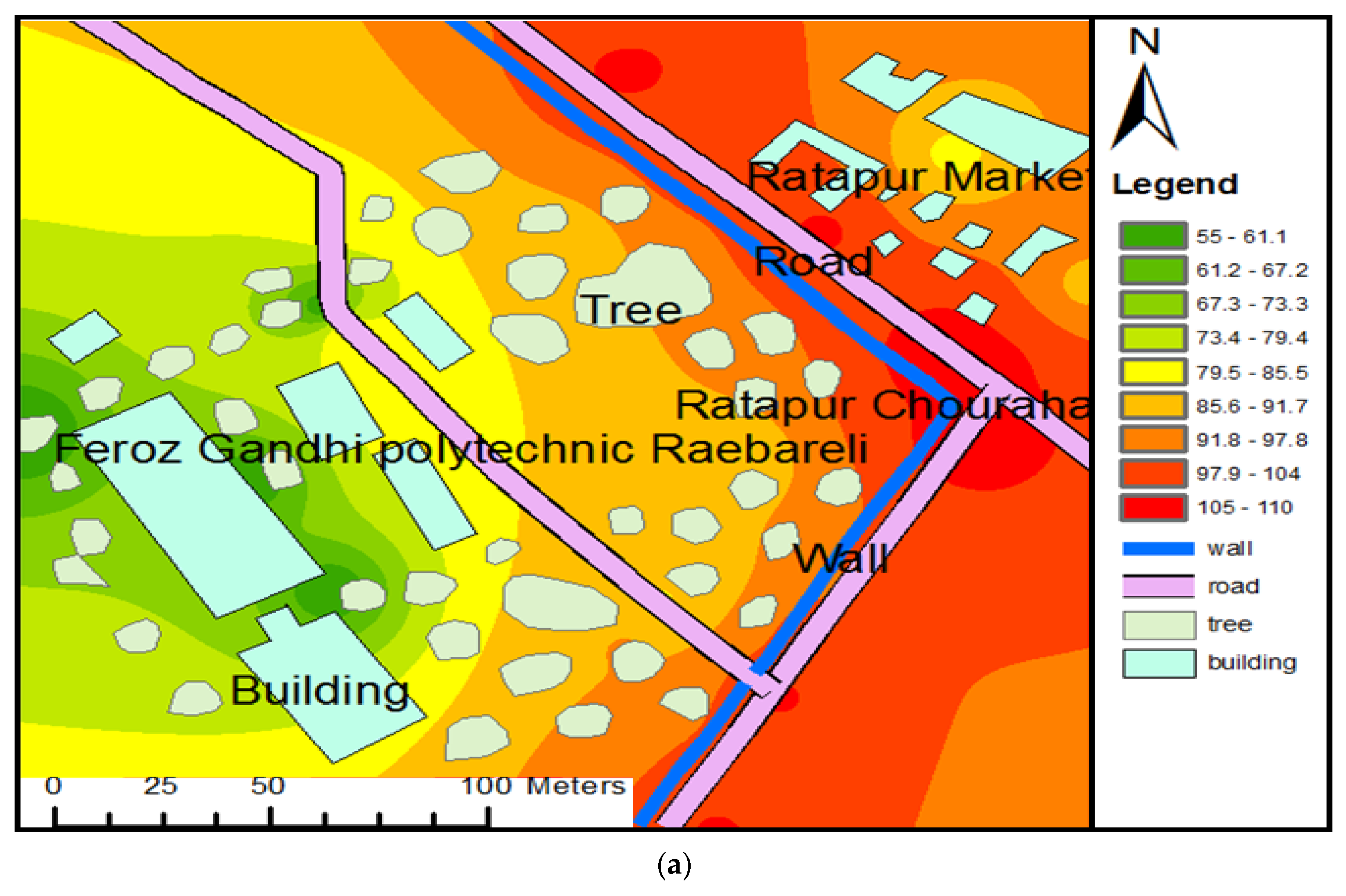
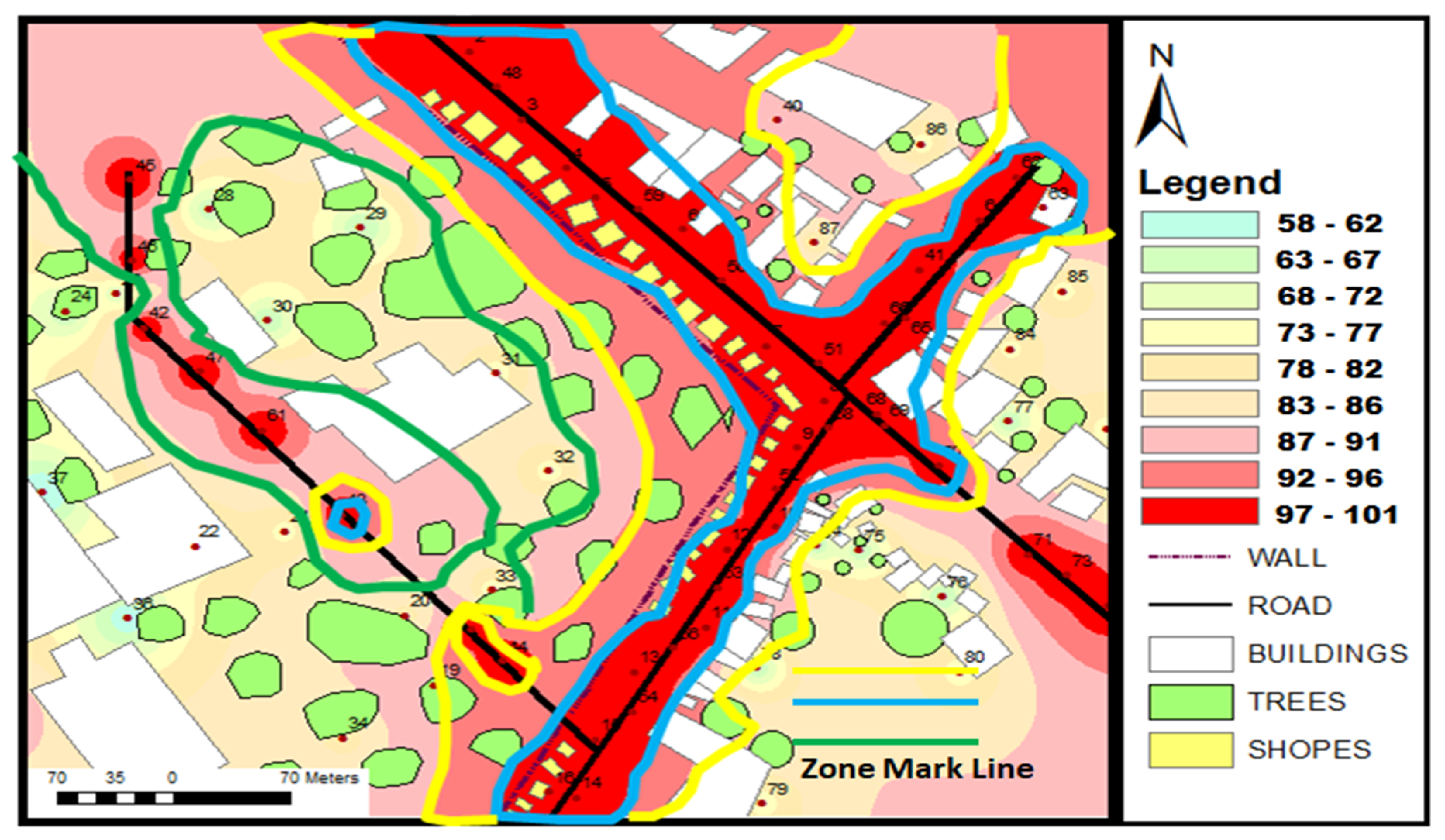
- In this study, a noise map was developed using GIS for selected noisy areas around Ratapur Chauraha in Raebareli. Noise data were collected from 60 points, consisting of 40 points along roads and 20 points away from roads, considered as a large dataset (LD). Predictions were also made for three different time intervals based on traffic load: high, medium, and low traffic load [31]. Researchers deemed these data points sufficient for reasonably accurate predictions. Equivalent noise levels were determined for each point and integrated spatially in GIS using IDW interpolation to determine noise levels at various locations. All the data were collected over a period of 6 months, and noise levels were monitored daily in a cyclic manner from Monday to Saturday. Each day, data were collected at 10 different points, varying in traffic loads. Locations were marked with a permanent marker to ensure accurate identification and data collection of noise levels.
- A total of 40 data points were within the road corridor 1.5 m away from the noise source point on the road.
- Out of 40 points, 25 points were taken at Lucknow–Allahabad highway and 15 points were taken as Ratapur–Raebareli city road.
- All points were at equal distance maintaining a gap of 12 m from each other.
- The total road length for the Lucknow–Allahabad highway was 301 m whereas at Ratapur–Raebareli city road, it was 179 m.
- Noise data were collected at three different levels: high traffic and noise levels (H), moderate traffic and noise levels (M), and low traffic and noise levels (L).
3.2. Small Data-Based Noise Prediction Method (SDBM)
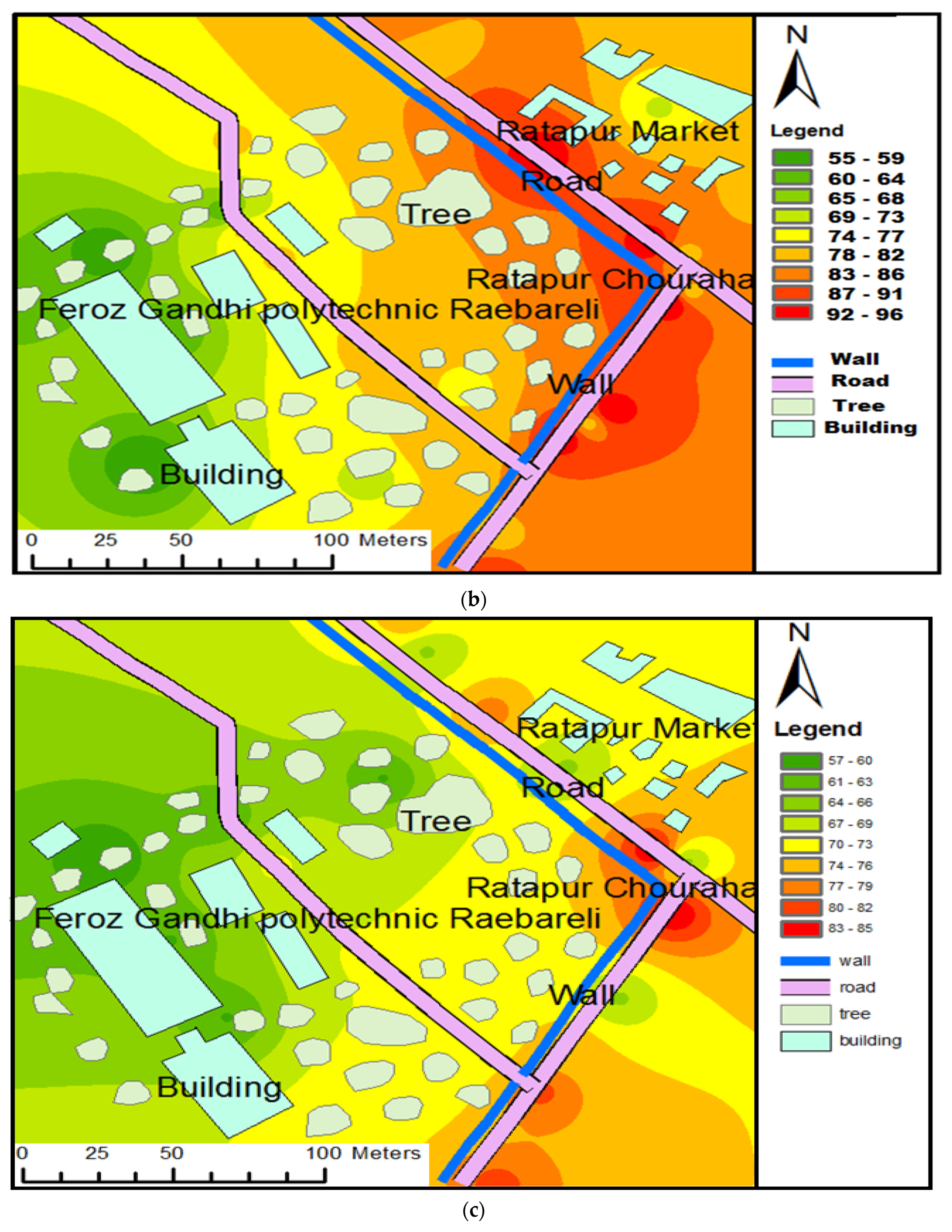
- In this method, the number of noise monitoring points was reduced from 60 locations to 30 locations, considered as small data (SD). The methodology was implemented to evenly distribute data points around Ratapur Chauraha in Raebareli City. The reduced noise data points were input into GIS to generate an equivalent noise level map using interpolation. The study aimed to demonstrate the impact of using a smaller dataset for noise prediction (NP) compared to a larger dataset employed in another scheme for the same region. Maintaining uniform spacing between data points is a time-consuming task, involving extensive physical and mental calculations [32]. Predictions were also made for three different time intervals at each location, followed by GIS-based mapping. The authors utilized the GIS model IDW (inverse distance weighting) interpolation to predict noise values and create noise level maps (MNL). Out of 30 points, 20 points were taken as road points (noise source points) while 10 points were away points (noise receiving points).
- Out of these 20 points, 12 points were taken at Allahabad–Lucknow highway and 8 points were taken at Ratapur city road.
- All points were at an equal distance of 24 m from each other.
- The same method is also applied as a large data prediction method for data collection.
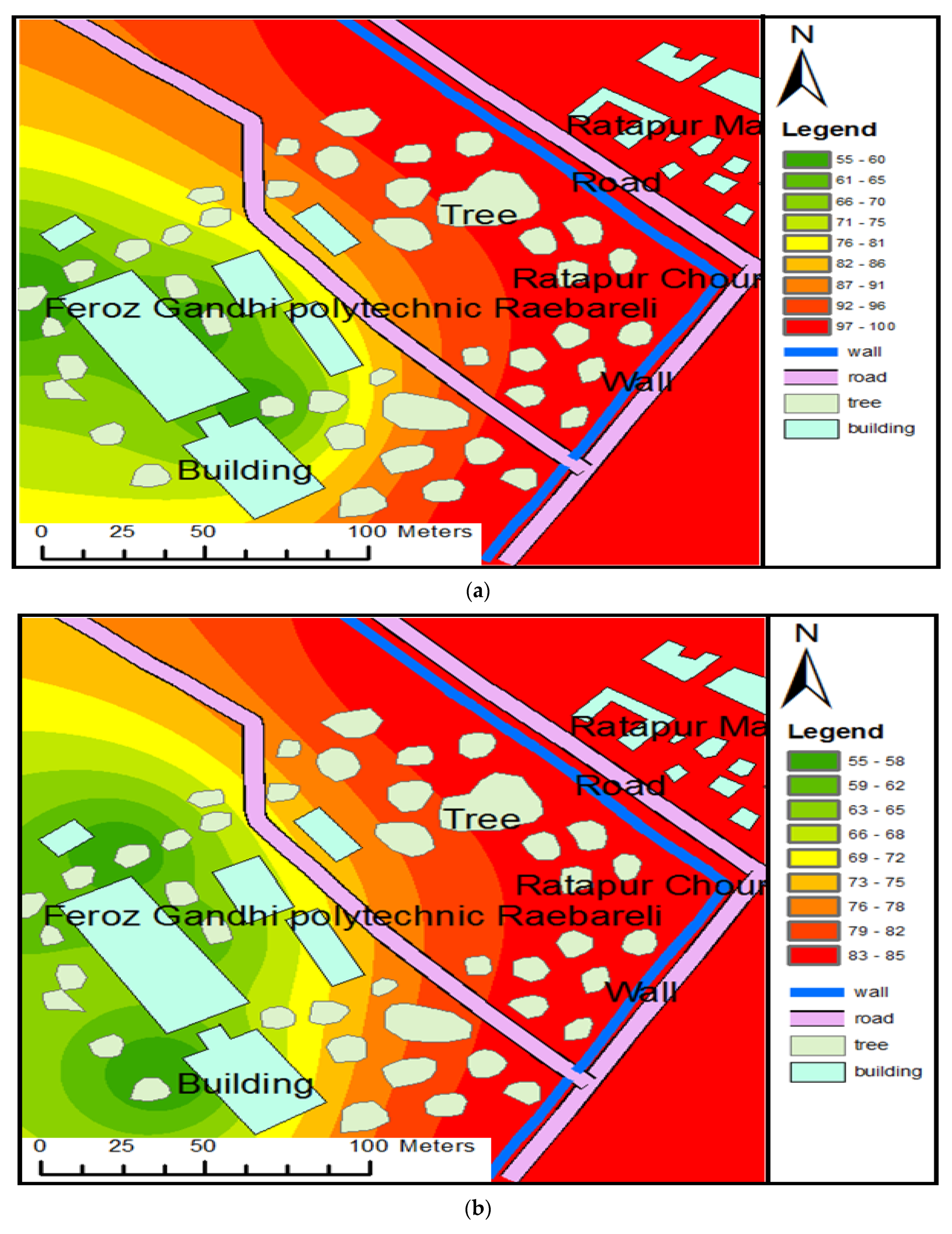
3.3. Source Point Averaging (Using One Source Noise Level Data) Based Method of Noise Prediction (SPANV)
- All points were distributed at equal distances of 24-m spatial intervals.
- A total of 12 points were taken on Lucknow–Allahabad Highway and 8 points were taken at Raebareli city road.
3.4. Google Navigation Data Method for Noise Prediction (GNBM)
- Google Navigation color codes provide different dB values for noise based on the calibrated value in Table 2. For red, it gives 96–110 dB, orange, 81–95 dB, and green or blue, 65–79 dB, at the summation of different time intervals with a varying range of 7 dB from its average value. For the traffic noise prediction of the entire study area, the authors considered a low range of dB for (1–3 p.m.) where traffic load is minimal, an average dB value for medium traffic load (9–11 a.m.), and a high dB value for maximum traffic load (4–6 p.m.).
- Out of 23 points, 20 points were road or source points, and 3 points were away, or noise receiver points (background noise) used for GIS mapping.
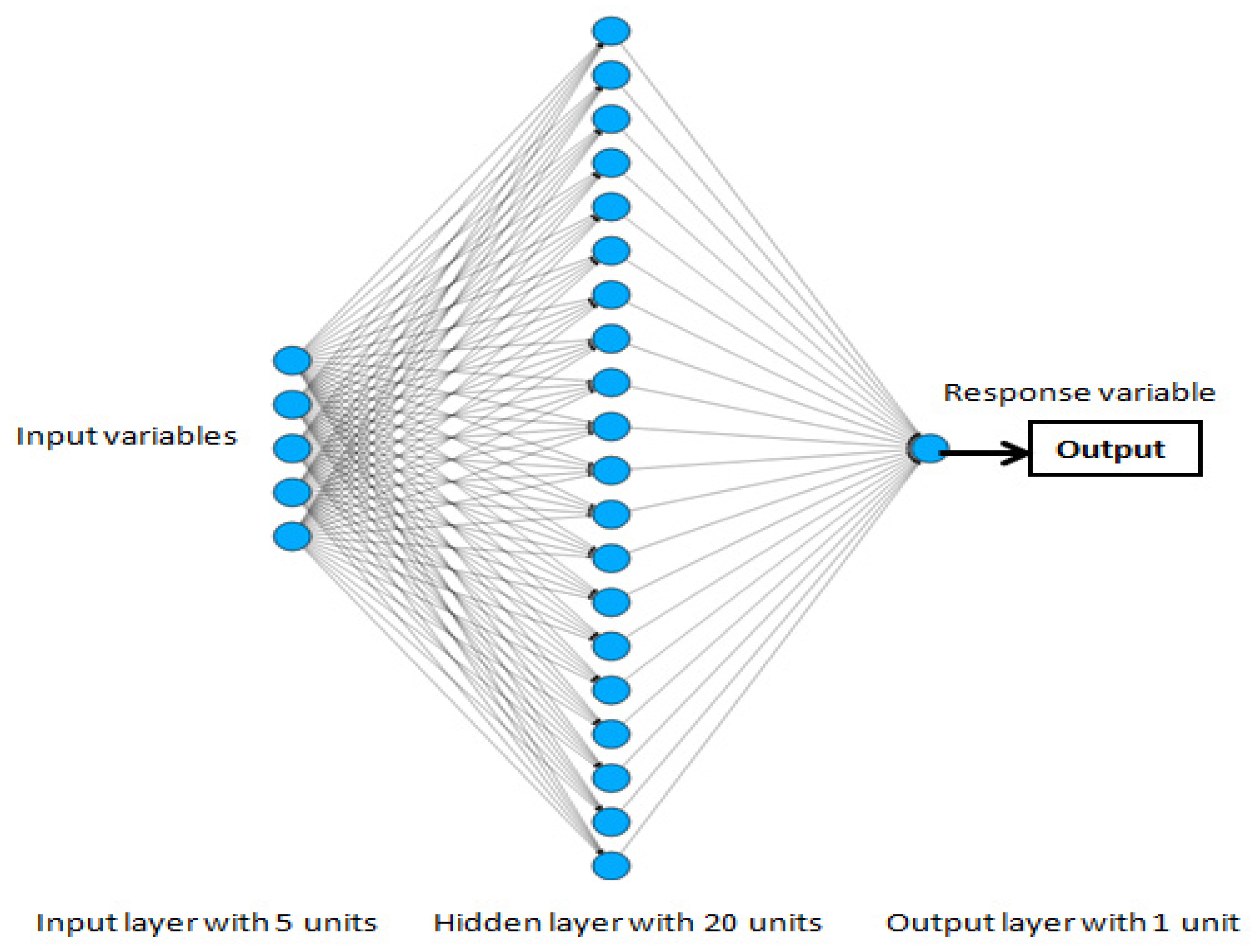
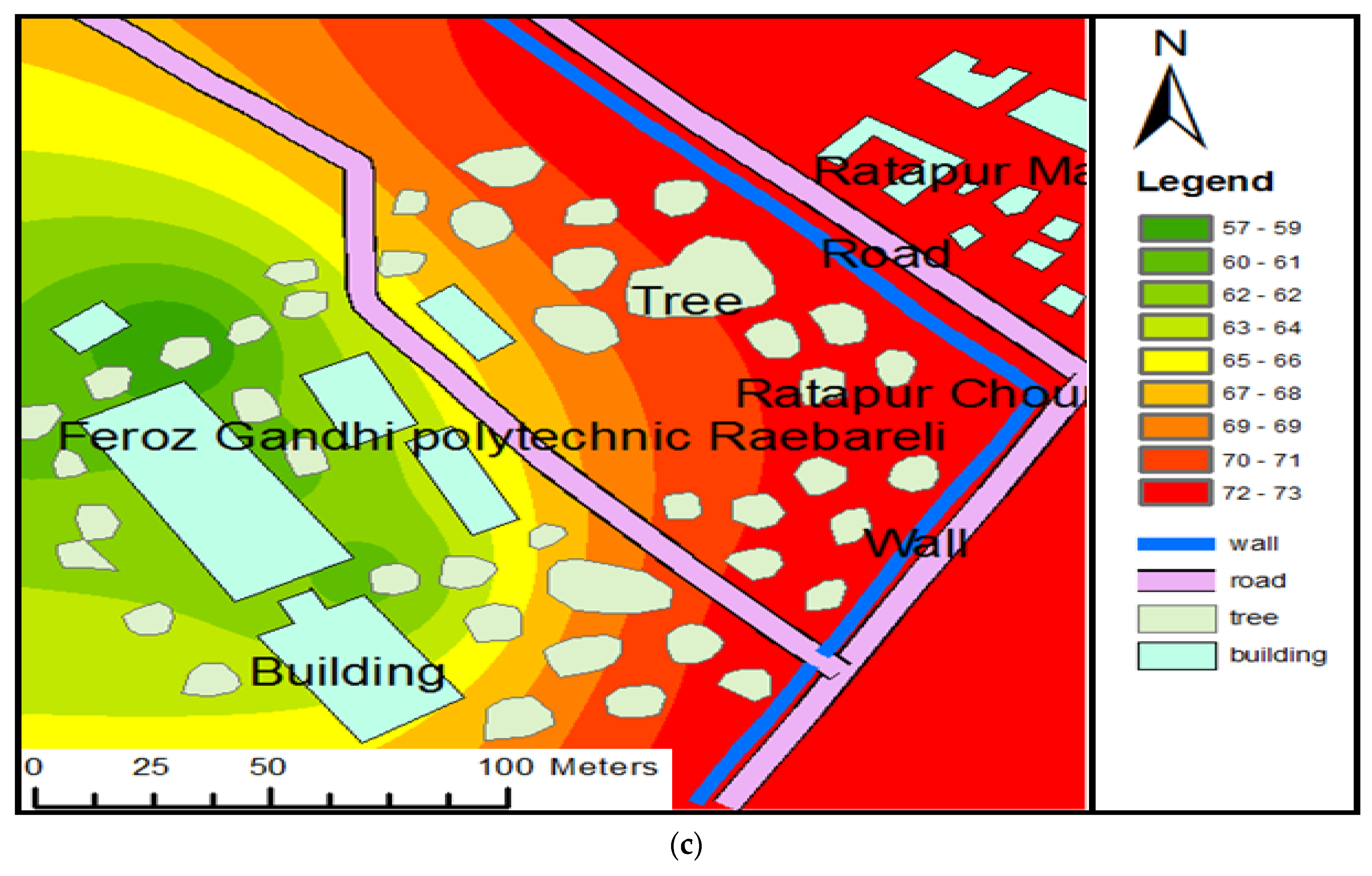
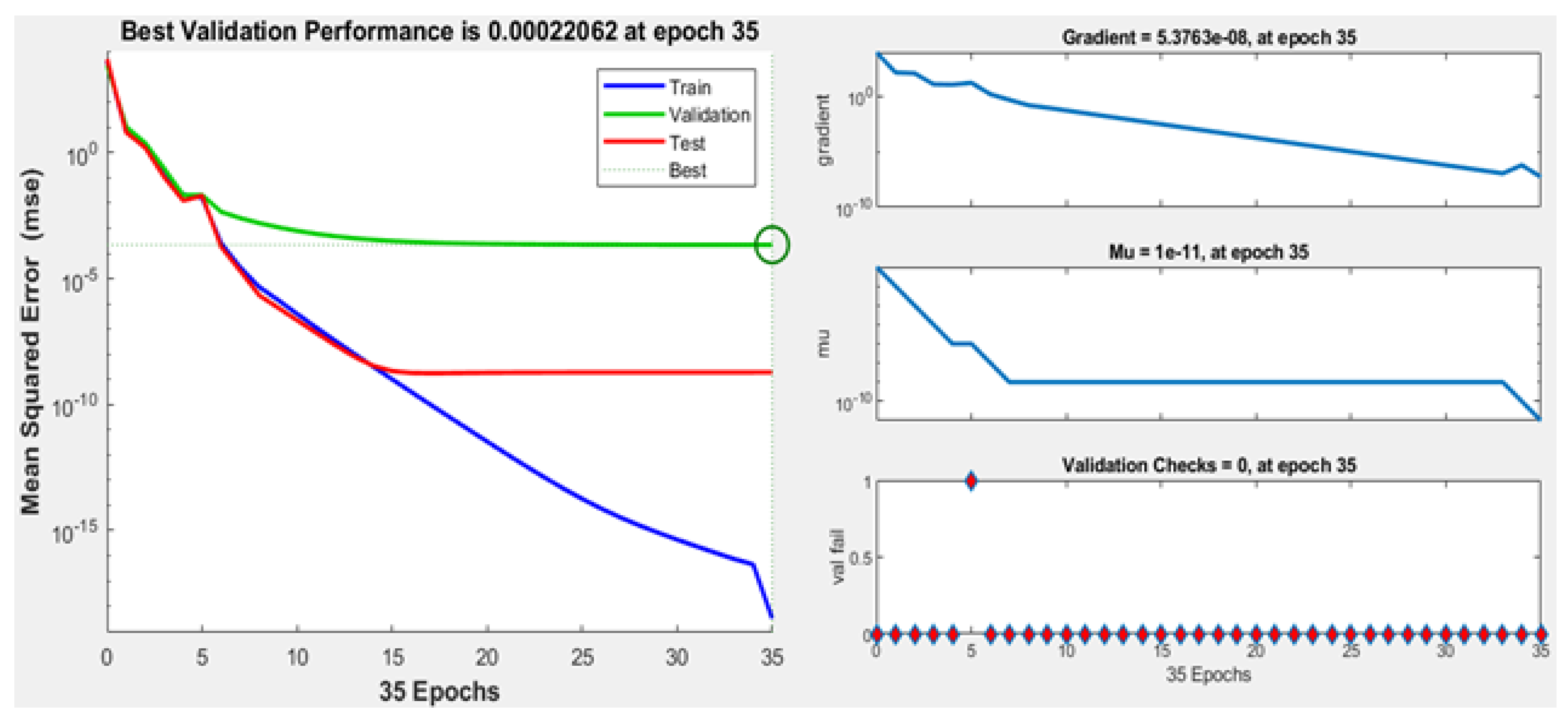
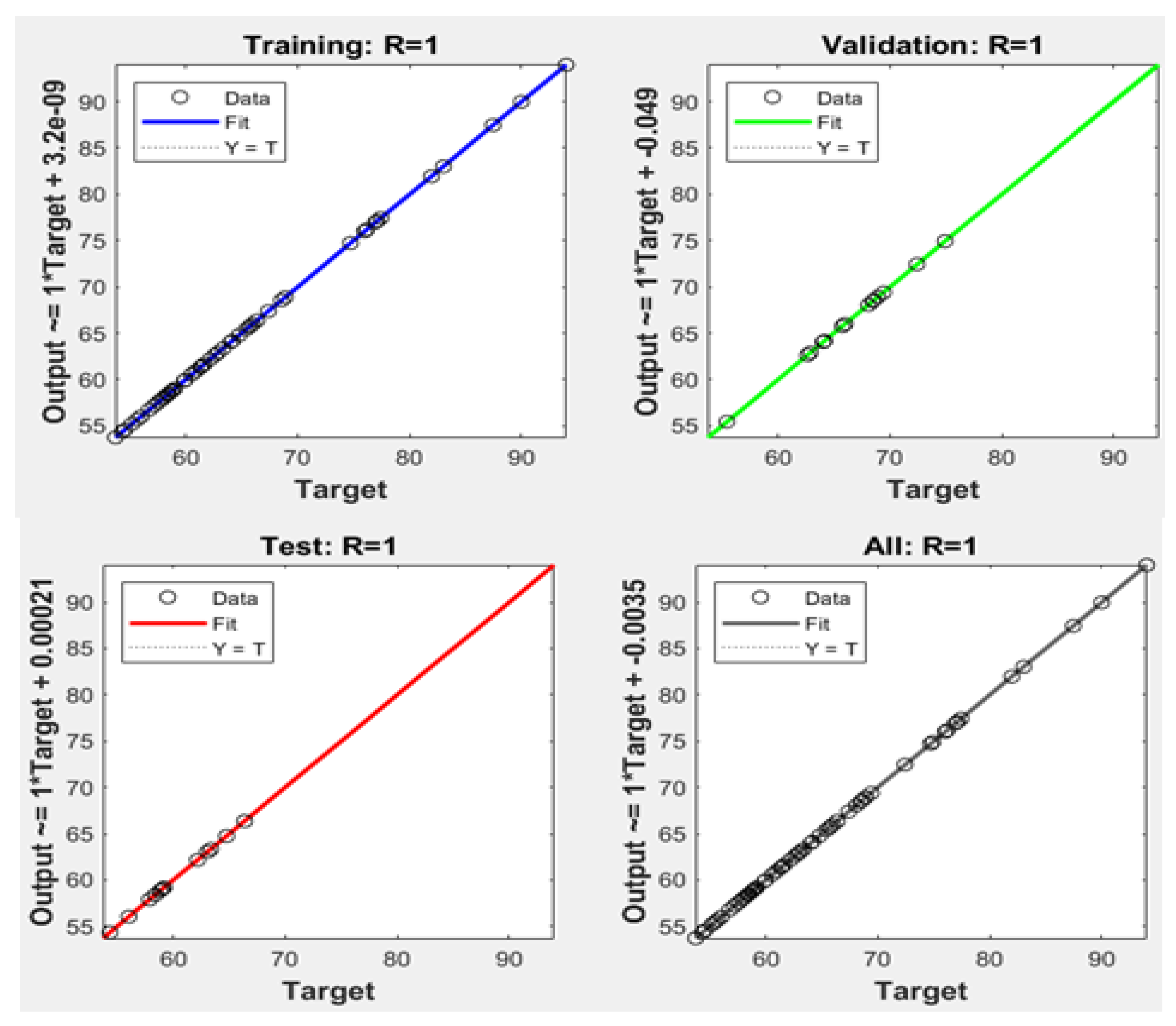
3.5. Accurate Modelling for ANN-Based Prediction with Fine Data (ANN-BNM)
3.6. Automated Noise dB Calculation Method for Noise Prediction
3.7. Noise Exposure Mapping
- —is the equivalent sound exposure level in 8 h?
- —sum of the values in the enclosed expression for all noise incidents from i = 1 to i = n.
- —is a distance incident leading to noise level impacted worker/dweller.
- —is the duration in hours of i.
- —is the sound level of in dB.
- n = the total number of noise events for the people living in the area during the evaluation period.
4. Results and Discussion
4.1. Large Data-Based Noise Prediction Method (LDBM)
4.2. Small Data-Based Noise Prediction Method (SDBM)
4.3. Source Point Averaging (Using One Noise Level for All Source Points)-Based Method Noise Prediction (SPANV)
4.4. Google Navigation Data Based Prediction Method (GNBM)
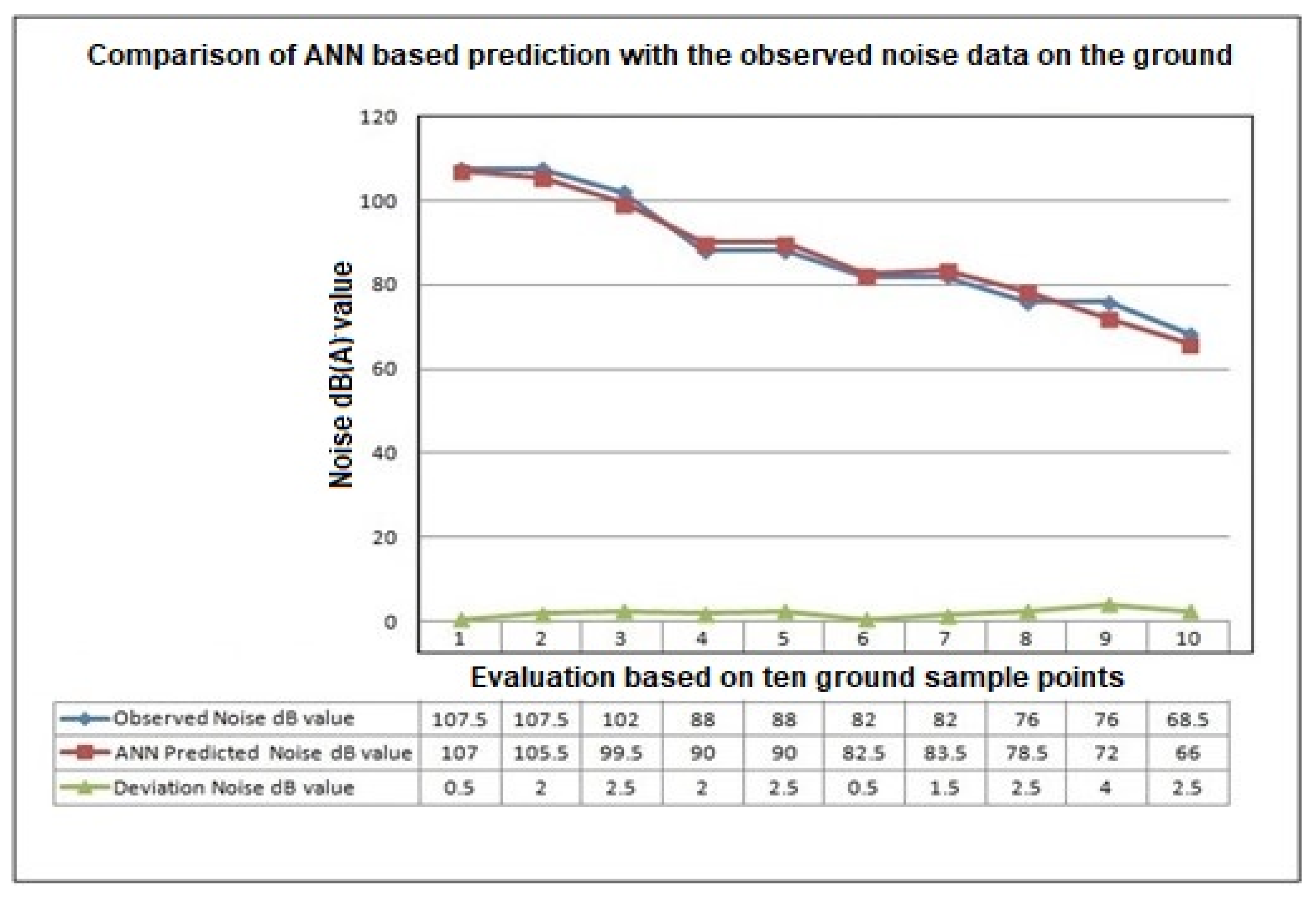
4.5. Accurate ANN Modelling-Based Noise Prediction
4.6. Automated Noise dB(A) Calculation Method for Noise Prediction without the Recording of Noise Levels of the Sources
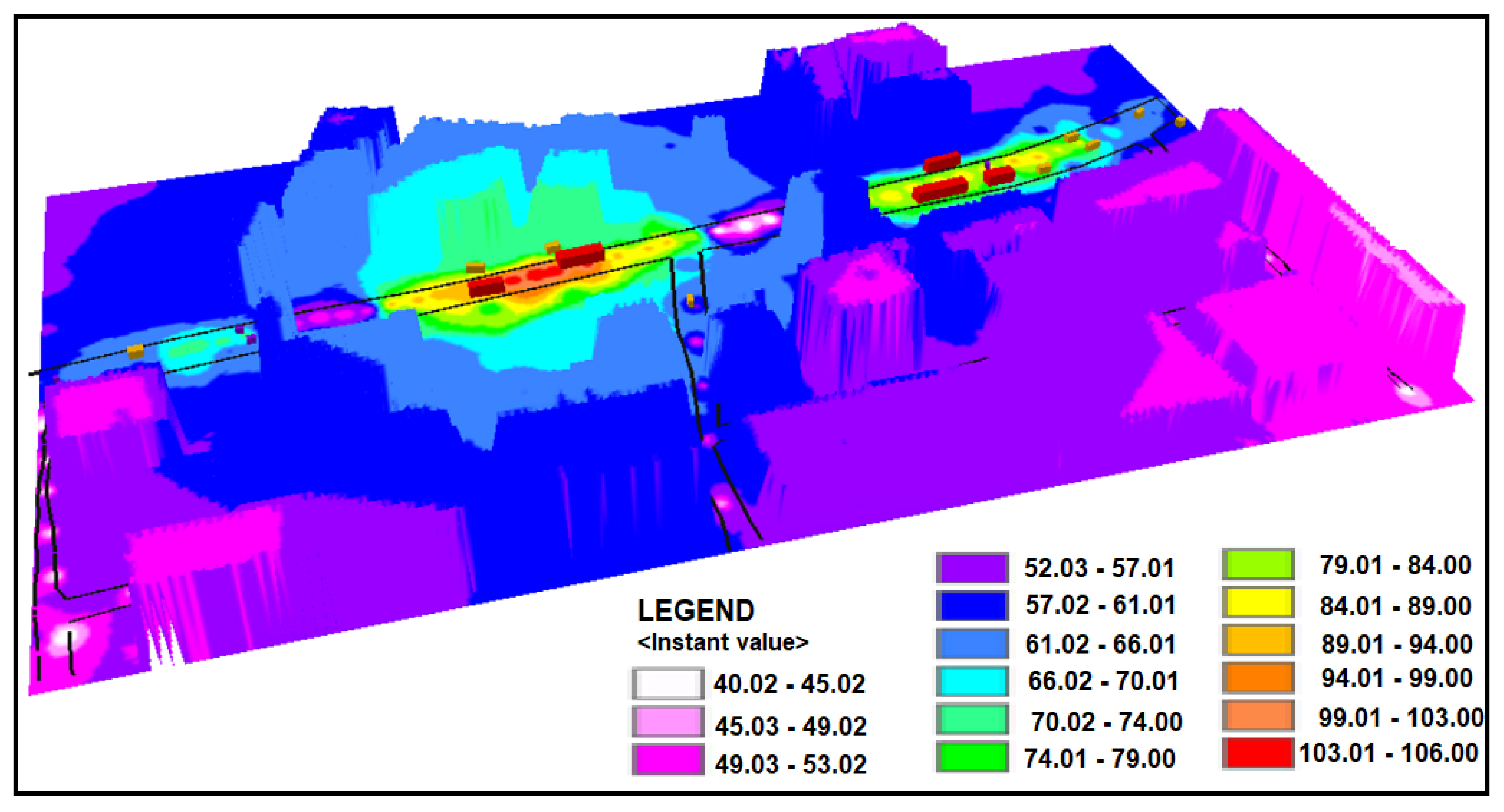
4.7. Noise Exposure Mapping
4.8. Comparison of Various Methods
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Sample No | X | Y | H (4–6 p.m.) 10 min Duration | M (9–11 a.m.) 10 min Duration | L (1–3 p.m.) 10 min Duration |
|---|---|---|---|---|---|
| 1 | 81.24109 | 26.24493 | 100 | 85 | 75 |
| 2 | 81.24123 | 26.24474 | 105 | 90 | 80 |
| 3 | 81.24133 | 26.24458 | 103 | 88 | 77 |
| 4 | 81.24142 | 26.24447 | 105 | 90 | 80 |
| 5 | 81.24148 | 26.2444 | 110 | 95 | 85 |
| 6 | 81.24165 | 26.24433 | 110 | 95 | 85 |
| 7 | 81.24182 | 26.24405 | 110 | 95 | 85 |
| 8 | 81.24193 | 26.24393 | 110 | 95 | 85 |
| 9 | 81.24188 | 26.24382 | 110 | 95 | 85 |
| 10 | 81.24183 | 26.24363 | 110 | 95 | 85 |
| 11 | 81.2417 | 26.2434 | 110 | 95 | 85 |
| 12 | 81.24174 | 26.24358 | 110 | 95 | 85 |
| 13 | 81.24156 | 26.2433 | 100 | 95 | 75 |
| 14 | 81.24144 | 26.243 | 102 | 87 | 77 |
| 15 | 81.24148 | 26.24314 | 105 | 90 | 80 |
| 16 | 81.24139 | 26.24302 | 108 | 92 | 82 |
| 17 | 81.24135 | 26.24279 | 105 | 90 | 80 |
| 18 | 81.2413 | 26.24272 | 95 | 85 | 75 |
| 19 | 81.24116 | 26.24327 | 92 | 80 | 70 |
| 20 | 81.2411 | 26.24343 | 87 | 75 | 75 |
| 21 | 81.24086 | 26.24362 | 87 | 75 | 70 |
| 22 | 81.24069 | 26.24359 | 84 | 72 | 63 |
| 23 | 81.24053 | 26.24418 | 58 | 61 | 61 |
| 24 | 81.24043 | 26.24414 | 58 | 55 | 55 |
| 25 | 81.24018 | 26.24402 | 55 | 55 | 57 |
| 26 | 81.24008 | 26.24394 | 58 | 55 | 58 |
| 27 | 81.23991 | 26.24384 | 55 | 60 | 60 |
| 28 | 81.24072 | 26.24437 | 75 | 65 | 60 |
| 29 | 81.24102 | 26.24433 | 88 | 70 | 60 |
| 30 | 81.24083 | 26.24411 | 72 | 65 | 60 |
| 31 | 81.24128 | 26.24399 | 85 | 75 | 65 |
| 32 | 81.24139 | 26.24376 | 86 | 75 | 70 |
| 33 | 81.24127 | 26.24349 | 86 | 75 | 70 |
| 34 | 81.24098 | 26.24314 | 90 | 70 | 71 |
| 35 | 81.24086 | 26.24294 | 88 | 70 | 72 |
| 36 | 81.24055 | 26.24342 | 57 | 55 | 60 |
| 37 | 81.24038 | 26.24371 | 57 | 60 | 60 |
| 38 | 81.2403 | 26.2432 | 55 | 55 | 55 |
| 39 | 81.24163 | 26.24484 | 87 | 75 | 70 |
| 40 | 81.24184 | 26.24458 | 84 | 72 | 70 |
| 41 | 81.24212 | 26.24423 | 90 | 80 | 75 |
| 42 | 81.24059 | 26.2441 | 85 | 78 | 70 |
| 43 | 81.24098 | 26.24366 | 85 | 78 | 70 |
| 44 | 81.24129 | 26.24332 | 85 | 78 | 70 |
| 45 | 81.24056 | 26.24444 | 85 | 78 | 70 |
| 46 | 81.24056 | 26.24425 | 85 | 78 | 70 |
| 47 | 81.24069 | 26.244 | 85 | 78 | 70 |
| 48 | 81.24128 | 26.24466 | 105 | 80 | 66 |
| 49 | 81.24115 | 26.24481 | 105 | 80 | 66 |
| 50 | 81.24173 | 26.24421 | 105 | 80 | 66 |
| 51 | 81.24192 | 26.24401 | 105 | 80 | 66 |
| 52 | 81.24183 | 26.24372 | 100 | 80 | 66 |
| 53 | 81.24172 | 26.24349 | 100 | 80 | 66 |
| 54 | 81.24155 | 26.2432 | 100 | 80 | 66 |
| 55 | 81.24137 | 26.2429 | 100 | 80 | 66 |
| 56 | 81.24163 | 26.24335 | 100 | 80 | 66 |
| 57 | 81.24123 | 26.2434 | 85 | 78 | 70 |
| 58 | 81.24194 | 26.24386 | 105 | 80 | 66 |
| 59 | 81.24156 | 26.24437 | 105 | 80 | 66 |
| 60 | 81.24118 | 26.2448 | 105 | 80 | 66 |
| S.No. | Sample No | 1st Week | 2nd Week | 3rd Week | 4th Week | 5th Week | 6th Week |
|---|---|---|---|---|---|---|---|
| 1 | 1–10 | Monday | Tuesday | Wednesday | Thursday | Friday | Saturday |
| 2 | 11–20 | Tuesday | Wednesday | Thursday | Friday | Saturday | Monday |
| 3 | 21–30 | Wednesday | Thursday | Friday | Saturday | Monday | Tuesday |
| 4 | 31–40 | Thursday | Friday | Saturday | Monday | Tuesday | Wednesday |
| 5 | 41–50 | Friday | Saturday | Monday | Tuesday | Wednesday | Thursday |
| 6 | 51–60 | Saturday | Monday | Tuesday | Wednesday | Thursday | Friday |
| Zone | Full Data (60) | Half Data (30) | Difference | Same Source (1) | Difference | Average Difference | Google Navigation | Difference | Average Difference |
|---|---|---|---|---|---|---|---|---|---|
| A. High Traffic Noise (4–6 p.m.) | |||||||||
| A | 105–110 | 105–110 | 0 | 97–100 | 8–10 | 9 | 110–110 | 0–5 | 2.5 |
| B | 97.9–104 | 97.9–104 | 0 | 97–100 | 8–10 | 9 | 74–79 | 23.9–25 | 24.45 |
| C | 85.6–91.7 | 85.6–91.7 | 0 | 92–96 | 6.4–4.3 | 5.3 | 80–86 | 5.6–5.7 | 5.6 |
| D | 85.6–91.7 | 85.6–91.7 | 0 | 92–96 | 6.4–4.3 | 5.3 | 87–92 | 2.6–0.3 | 1.4 |
| E | 67.3–73.3 | 67.3–73.3 | 0 | 61–65 | 6.3–8.3 | 7.3 | 62–67 | 5.3–6.3 | 5.8 |
| F | 73.4–79.4 | 73.4–79.4 | 0 | 71–75 | 2.4–4.4 | 3.4 | 62–67 | 11.3–12.4 | 11.8 |
| G | 97.9–104 | 97.9–104 | 0 | 97–100 | 0.9–4 | 2.5 | 80–86 | 17.9–18 | 18 |
| H | 91.8–97.8 | 91.8–97.8 | 0 | 97–100 | 6.8–2.2 | 4.5 | 93–98 | 1.2–0.2 | 0.7 |
| B. Medium traffic noise (9–11 a.m.) | |||||||||
| A | 87–91 | 87–91 | 0 | 83–85 | 4–6 | 5 | 97.8–103 | 10.8–12 | 11.4 |
| B | 78–82 | 78–82 | 0 | 83–85 | 3–5 | 4 | 71.1–76.3 | 6.9–5.7 | 6.3 |
| C | 74–77 | 74–77 | 0 | 79–82 | 5–5 | 5 | 71.1–76.3 | 2.9–0.7 | 1.8 |
| D | 78–82 | 78–82 | 0 | 79–82 | 0–1 | 0.5 | 81.8–87 | 3.8–5 | 4.4 |
| E | 69–73 | 69–73 | 0 | 63–65 | 6–8 | 7 | 60.4–65.7 | 8.6–7.3 | 15.9 |
| F | 60–64 | 60–64 | 0 | 59–62 | 1–2 | 1.5 | 60.4–67.7 | 0.4–3.7 | 2 |
| G | 83–86 | 83–86 | 0 | 79–82 | 4–4 | 4 | 71.1–76.3 | 11.9–9.7 | 10.8 |
| H | 78–82 | 78–82 | 0 | 79–82 | 0–1 | 0.5 | 81.8–87 | 3.8–5 | 4.4 |
| C. Low traffic noise (1–3 p.m.) | |||||||||
| A | 77–79 | 77–79 | 0 | 72–73 | 5–6 | 5.5 | 92–96 | 15–17 | 16 |
| B | 67–69 | 67–69 | 0 | 72–73 | 4–5 | 4.5 | 65–69 | 0–2 | 1 |
| C | 67–69 | 67–69 | 0 | 69–69 | 0–2 | 1 | 70–73 | 3–4 | 3.5 |
| D | 70–73 | 70–73 | 0 | 70–71 | 0–2 | 1 | 79–82 | 9–9 | 9 |
| E | 64–66 | 64–66 | 0 | 62–62 | 2–4 | 3 | 55–60 | 6–9 | 7.5 |
| F | 64–66 | 64–66 | 0 | 63–64 | 1–2 | 1.5 | 61–64 | 2–3 | 2.5 |
| G | 77–79 | 77–79 | 0 | 70–71 | 7–8 | 7.5 | 65–69 | 10–12 | 11 |
| H | 70–73 | 70–73 | 0 | 70–71 | 0–2 | 1 | 79–82 | 9–9 | 9 |
| Hours of Exposure per Week | One-Hour Exposure Level (LAeq) dB | ||||
|---|---|---|---|---|---|
| 80 | 85 | 90 | 95 | 100 | |
| 40 (8 h per day, 5 days per week) | 74 | 79 | 84 | 89 | 94 |
| 168 (24 h per day, 7 days per week) | 80 | 85 | 90 | 95 | 100 |
References
- Oyedepo, S.O. Development of Noise Map for Ilorin Metropolis, Nigeria. Int. J. Environ. Stud. 2013, 70, 503–514. [Google Scholar] [CrossRef]
- Dubey, R.; Bharadwaj, S.; Zafar, M.I.; Mahajan, V.; Srivastava, A.; Biswas, S. GIS Mapping of Short-Term Noisy Event of Diwali Night in Lucknow City. ISPRS Int. J. Geo-Inf. 2021, 11, 25. [Google Scholar] [CrossRef]
- Nega, T.; Smith, C.; Bethune, J.; Fu, W.H. An Analysis of Landscape Penetration by Road Infrastructure and Traffic Noise. Comput. Environ. Urban Syst 2012, 36, 245–256. [Google Scholar] [CrossRef]
- Li, B.; Tao, S.; Dawson, R.W.; Cao, J.; Lam, K. A GIS Based Road Traffic Noise Prediction Model. Appl. Acoust. 2002, 63, 679–691. [Google Scholar] [CrossRef]
- Bharadwaj, S.; Dubey, R.; Zafar, M.I.; Tiwary, S.K.; Faridi, R.A.; Biswas, S. A Novel Method to Determine the Optimal Location for a Cellular Tower by Using LiDAR Data. Appl. Syst. Innov. 2022, 5, 30. [Google Scholar] [CrossRef]
- Bharadwaj, S.; Dubey, R. Raster Data Based Automated Noise Data Integration for Noise Raster Data Based Automated Noise Data Integration for Noise. ISPRS Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2021, XLIII-B4-2, 159–166. [Google Scholar] [CrossRef]
- Dubey, R.; Bharadwaj, S.; Bhushan, V.S.; Biswas, S. Collaborative Noise Mapping Using Smart Phone. Int. Arch. Photogramm. Remote Sens. Spatial Inf. Sci. 2020, 43, 253–260. [Google Scholar] [CrossRef]
- Cai, M.; Yao, Y.; Wang, H. A Traffic-Noise-Map Update Method Based on Monitoring Data. J. Acoust. Soc. Am. 2017, 141, 2604. [Google Scholar] [CrossRef]
- Sonaviya, D.R.; Tandel, B.N. A Review on GIS-Based Approach for Road Traffic Noise Mapping. Indian J. Sci. Technol. 2019, 12, 1–6. [Google Scholar] [CrossRef]
- Colvile, R.N.; Woodfield, N.K.; Carruthers, D.J.; Fisher, B.E.A.; Rickard, A.; Neville, S.; Hughes, A. Uncertainty in Dispersion Modelling and Urban Air Quality Mapping. Environ. Sci. Policy 2002, 5, 207–220. [Google Scholar] [CrossRef]
- KANG, J. From DBA to Soundscape Indices: Managing Our Sound Environment. Front. Eng. Manag. 2017, 4, 184. [Google Scholar] [CrossRef]
- Miedema, H.M.E.; Oudshoorn, C.G.M. Annoyance from Transportation Noise: Relationships with Exposure Metrics DNL and DENL and Their Confidence Intervals. Environ. Health Perspect. 2001, 109, 409. [Google Scholar] [CrossRef]
- Muzet, A. Environmental Noise, Sleep and Health. Sleep Med. Rev. 2007, 11, 135–142. [Google Scholar] [CrossRef]
- D’Alessandro, F.; Asdrubali, F.; Schiavoni, S. The Noise Abatement Plan of an Italian Road Network: A Comparison Between Standard and Innovative Methodologies. Open Transp. J. 2014, 8, 26–38. [Google Scholar] [CrossRef]
- WHO. World Health Statistics; WHO: Geneva, Switzerland, 2009; pp. 5–6.
- Basner, M.; Babisch, W.; Davis, A.; Brink, M.; Clark, C.; Janssen, S.; Stansfeld, S. Auditory and Non-Auditory Effects of Noise on Health. Lancet 2014, 383, 1325. [Google Scholar] [CrossRef]
- Alam, M.S.; Corcoran, L.; King, E.A.; McNabola, A.; Pilla, F. Modelling of Intra-Urban Variability of Prevailing Ambient Noise at Different Temporal Resolution. Noise Mapp. 2017, 4, 20–44. [Google Scholar] [CrossRef]
- Xie, D.; Liu, Y.; Chen, J. Mapping Urban Environmental Noise: A Land Use Regression Method. Environ. Sci. Technol. 2011, 45, 7358–7364. [Google Scholar] [CrossRef]
- Villarrubia, G.; De Paz, J.F.; Chamoso, P.; De La Prieta, F. Artificial Neural Networks Used in Optimization Problems. Neurocomputing 2017, 272, 10–16. [Google Scholar] [CrossRef]
- Alani, R.A.; Ogunmoyela, O.M.; Okolie, C.J.; Daramola, O.E. Geospatial Analysis of Environmental Noise Levels in a Residential Area in Lagos, Nigeria. Noise Mapp. 2020, 7, 223–238. [Google Scholar] [CrossRef]
- Verma, D.; Jana, A.; Ramamritham, K. Classification and Mapping of Sound Sources in Local Urban Streets through AudioSet Data and Bayesian Optimized Neural Networks. Noise Mapp. 2019, 6, 52–71. [Google Scholar] [CrossRef]
- Oyedepo, S.O.; Adeyemi, G.A.; Olawole, O.C.; Ohijeagbon, O.I.; Fagbemi, O.K.; Solomon, R.; Ongbali, S.O.; Babalola, O.P.; Dirisu, J.O.; Efemwenkiekie, U.K.; et al. A GIS—Based Method for Assessment and Mapping of Noise Pollution in Ota Metropolis, Nigeria. MethodsX 2019, 6, 447–457. [Google Scholar] [CrossRef]
- Onuu, M. Environmental Noise Pollution in Nigerian Universities: A Case Study of the University of Calabar, Calabar, Nigeria. J. Niger. Environ. Soc. 2004, 2, 100–109. [Google Scholar]
- Okokon, E.O.; Yli-Tuomi, T.; Turunen, A.W.; Tiittanen, P.; Juutilainen, J.; Lanki, T. Traffic Noise, Noise Annoyance and Psychotropic Medication Use. Environ. Int. 2018, 119, 287–294. [Google Scholar] [CrossRef]
- Paiva, K.M.; Cardoso, M.R.A.; Zannin, P.H.T. Exposure to Road Traffic Noise: Annoyance, Perception and Associated Factors among Brazil’s Adult Population. Sci. Total Environ. 2019, 650, 978–986. [Google Scholar] [CrossRef]
- Blanes, N.; Houthuijs, D.; Swart, W.; Sainz de la Maza, M.; Ramos, M.; Castell, N.; Van Kempen, E. Noise in Europe 2017: Updated Assessment ETC/ACM Technical Paper 2016/13. Eur. Top. Cent. Air Pollut. Clim. Change Mitig. 2017, 13, 200–203. [Google Scholar]
- Fritschi, L.; Brown, L.; Kim, R. Burden of Disease from Environmental Noise—Quantification of Healthy Life Years Lost in Europe; WHO European Centre for Environment and Health: Bonn, Germany, 2011; 106p. [Google Scholar]
- WHO. Burden of Disease from Burden of Disease From; WHO: Geneva, Switzerland, 2011; 126p.
- Biswas, S.; Lohani, B. Development of High Resolution 3D Sound Propagation Model Using LIDAR Data and Air Photo. Int. Arch. Photogramm. 2008, XXVII, 1735–1740. [Google Scholar]
- Zambon, G.; Roman, H.E.; Smiraglia, M.; Benocci, R. Monitoring and Prediction of Traffic Noise in Large Urban Areas. Appl. Sci. 2018, 8, 251. [Google Scholar] [CrossRef]
- Lokhande, S.K.; Dhawale, S.A.; Pathak, S.S.; Gautam, R.; Jain, M.C.; Bodhe, G.L. Appraisal of Noise Level Dissemination Surrounding Mining and Industrial Areas of Keonjhar, Odisha: A Comprehensive Approach Using Noise Mapping. Arch. Acoust. 2017, 42, 423–432. [Google Scholar] [CrossRef]
- Enmarker, I. The Effects of Meaningful Irrelevant Speech and Road Traffic Noise on Teachers’ Attention, Episodic and Semantic Memory. Scand. J. Psychol. 2004, 45, 393–405. [Google Scholar] [CrossRef]
- Matlab Code for Artificial Neural Networks. Available online: https://libraryfile.university/download/4667282 (accessed on 2 March 2023).
- Kůrková, V. Kolmogorov’s Theorem and Multilayer Neural Networks. Neural Netw. 1992, 5, 501–506. [Google Scholar] [CrossRef]
- Sun, X.; Liu, L.; Li, C.; Yin, J.; Zhao, J.; Si, W. Classification for Remote Sensing Data with Improved CNN-SVM Method. IEEE Access 2019, 7, 164507–164516. [Google Scholar] [CrossRef]
- Li, W.; Wang, Z.; Wang, Y.; Wu, J.; Wang, J.; Jia, Y.; Gui, G. Classification of High-Spatial-Resolution Remote Sensing Scenes Method Using Transfer Learning and Deep Convolutional Neural Network. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 1986–1995. [Google Scholar] [CrossRef]
- Environmental Noise Guidelines for the European Region. Available online: https://apps.who.int/iris/handle/10665/279952 (accessed on 2 March 2023).
- Occupational Health and Safety Act, RSO 1990, c O.1. Available online: https://qweri.lexum.com/w/onlegis/rso-1990-c-o1-en#!fragment//BQCwhgziBcwMYgK4DsDWszIQewE4BUBTADwBdoByCgSgBpltTCIBFRQ3AT0otokLC4EbDtyp8BQkAGU8pAELcASgFEAMioBqAQQByAYRW1SYAEbRS2ONWpA (accessed on 2 March 2023).
- Ragettli, M.S.; Goudreau, S.; Plante, C.; Fournier, M.; Hatzopoulou, M.; Perron, S.; Smargiassi, A. Statistical Modeling of the Spatial Variability of Environmental Noise Levels in Montreal, Canada, Using Noise Measurements and Land Use Characteristics. J. Expo. Sci. Environ. Epidemiol. 2016, 26, 597–605. [Google Scholar] [CrossRef]
- Singh, M.; Dong, M.; Wu, W.; Nejat, R.; Tran, D.K.; Pradhan, N.; Raghavan, D.; Douglas, J.F.; Wooley, K.L.; Karim, A. Enhanced Dielectric Strength and Capacitive Energy Density of Cyclic Polystyrene Films. ACS Polym. Au. 2022, 2, 324–332. [Google Scholar] [CrossRef]
- Singh, M.; Agrawal, A.; Wu, W.; Masud, A.; Armijo, E.; Gonzalez, D.; Zhou, S.; Terlier, T.; Zhu, C.; Strzalka, J.; et al. Soft-Shear-Aligned Vertically Oriented Lamellar Block Copolymers for Template-Free Sub-10 Nm Patterning and Hybrid Nanostructures. ACS Appl. Mater. Interfaces 2022, 14, 12824–12835. [Google Scholar] [CrossRef]
- Shreyash, N.; Sonker, M.; Bajpai, S.; Tiwary, S.K. Review of the Mechanism of Nanocarriers and Technological Developments in the Field of Nanoparticles for Applications in Cancer Theragnostics. ACS Appl. Bio. Mater. 2021, 4, 2307–2334. [Google Scholar] [CrossRef]




| Name of Instruments and Software | Model/Version | Purpose |
|---|---|---|
| High-grade sound pressure level meter | CESVA SC-310 | Measuring and capturing noise data |
| Total station and GPS | Trimble M3 and Trimble Juno | Collection of coordinates for the selected location |
| Mapping software | ArcGIS 10.2 and Simulation Model | Mapping and prediction |
| MATLAB—MathWorks | 2009–2022 | Modeling and prediction |
| Color | Range Value dB(A) | Average (Medium Traffic Load dB(A)) | High Traffic Load (+7), dB(A) | Low Traffic Load (−7), dB(A) |
|---|---|---|---|---|
| Red | 96–110 | 103 | 110 | 96 |
| Orange | 81–95 | 88 | 95 | 81 |
| Green/Blue | 65–79 | 72 | 79 | 65 |
| S.No. | X | Y | High (4–6 p.m.) dB(A) | Medium (9–11 a.m.) dB(A) | Low (1–3 p.m.) dB(A) |
|---|---|---|---|---|---|
| 1 | 81.24109 | 26.24493 | 79 | 72 | 65 |
| 2 | 81.24133 | 26.24458 | 95 | 88 | 81 |
| 3 | 81.24182 | 26.24405 | 110 | 103 | 96 |
| 4 | 81.24188 | 26.24382 | 110 | 103 | 96 |
| 5 | 81.24156 | 26.2433 | 95 | 88 | 81 |
| 6 | 81.24148 | 26.24314 | 95 | 88 | 81 |
| 7 | 81.24135 | 26.24279 | 79 | 72 | 65 |
| 8 | 81.24116 | 26.24327 | 79 | 72 | 65 |
| 9 | 81.24102 | 26.24433 | 79 | 72 | 65 |
| 10 | 81.24139 | 26.24376 | 79 | 72 | 65 |
| 11 | 81.24127 | 26.24349 | 95 | 88 | 81 |
| 12 | 81.24212 | 26.24423 | 110 | 103 | 96 |
| 13 | 81.24115 | 26.24481 | 79 | 72 | 65 |
| 14 | 81.24192 | 26.24401 | 110 | 103 | 96 |
| 15 | 81.24172 | 26.24349 | 95 | 88 | 81 |
| 16 | 81.24137 | 26.2429 | 79 | 72 | 65 |
| 17 | 81.24194 | 26.24386 | 110 | 103 | 96 |
| 18 | 81.24156 | 26.24437 | 95 | 88 | 81 |
| 19 | 81.24118 | 26.2448 | 79 | 72 | 65 |
| 20 | 81.24163 | 26.24335 | 79 | 72 | 65 |
| 21 | 81.23991 | 26.24384 | 55 | 55 | 55 |
| 22 | 81.24055 | 26.24342 | 57 | 57 | 57 |
| 23 | 81.24038 | 26.24371 | 57 | 57 | 57 |
| Algorithm | |
| Data Division | Random |
| Training | Levenberg-Marquardt |
| Performance | Mean Squared Error |
| Calculation | MEX |
| Progress | |
| Epoch | 35 iterations |
| Time | 0:00:0 |
| Performance | |
| Gradient | |
| Mu | |
| Validation Check | 0 |
| S. No | No. of Vehicles (Large) | No. of Vehicles (Medium) | No. of Vehicles (Small) | Total No. of Vehicles | Noise db(A) Value |
|---|---|---|---|---|---|
| 1 | 3 | 1 | 2 | 6 | 100 |
| 2 | 3 | 3 | 2 | 8 | 105 |
| 3 | 2 | 2 | 2 | 6 | 98 |
| 4 | 4 | 2 | 2 | 8 | 106 |
| 5 | 2 | 2 | 2 | 6 | 96 |
| 6 | 2 | 2 | 2 | 6 | 95 |
| 7 | 2 | 2 | 1 | 5 | 95 |
| 8 | 1 | 2 | 2 | 5 | 85 |
| 9 | 1 | 2 | 1 | 4 | 81 |
| 10 | 1 | 2 | 3 | 5 | 81 |
| 11 | 1 | 2 | 3 | 5 | 79 |
| 12 | 1 | 1 | 3 | 5 | 75 |
| 13 | 1 | 1 | 2 | 4 | 70 |
| 14 | 0 | 2 | 2 | 4 | 68 |
| 15 | 0 | 2 | 2 | 4 | 65 |
| Time | dB Value Frequency (31.5 Hz) | dB Value Frequency (2 KHz) | dB Value Frequency (16 KHz) |
|---|---|---|---|
| 20 min | 74.5 | 67.1 | 53.5 |
| 25 min | 81.2 | 73.4 | 59.2 |
| 15 min | 62.3 | 55.1 | 45 |
| Traffic Noise Value dB(A) | Noise Exposure Value for 12 h dB(A) |
|---|---|
| 105 | 106.8 |
| 96 | 97.8 |
| 91 | 92.8 |
| 86 | 87.8 |
| 82 | 83.8 |
| 77 | 78.8 |
| 72 | 73.8 |
| 67 | 68.8 |
| 62 | 63.8 |
| S.No. | Observed | Predicted Large Data | Dev. | Avg. Dev. | Predicted Small Data | Dev. | Avg. Dev. | Predicted Source Average Data | Dev. | Avg. Dev. | Google Navigation Data | Dev. | Avg. Dev. | ANN Prediction | Dev. | Avg. Dev. |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 105–110 | 105–110 | 0 | 0 | 97–104 | 6–8 | 7 | 96–101 | 9 | 9 | 101–110 | 0–5 | 2.5 | 105–109 | 0–1 | 0.5 |
| 2 | 105–110 | 97–100 | 8–10 | 9 | 95–100 | 10 | 10 | 96–101 | 9 | 9 | 87–92 | 18 | 18 | 103–108 | 2–2 | 2 |
| 3 | 100–104 | 97–100 | 3–4 | 3.5 | 85–91 | 13–15 | 14 | 92–96 | 8 | 8 | 87–92 | 12–13 | 12.5 | 97–102 | 2–3 | 2.5 |
| 4 | 85–91 | 91–97 | 6 | 6 | 95–99 | 8–10 | 9 | 96–101 | 10–11 | 10.5 | 81–87 | 4 | 4 | 89–91 | 0–4 | 2 |
| 5 | 85–91 | 92–96 | 5–7 | 6 | 94–98 | 7–9 | 8 | 90–95 | 4–5 | 4.5 | 81–87 | 4 | 4 | 88–92 | 2–3 | 2.5 |
| 6 | 79–85 | 87–91 | 6–8 | 7 | 90–95 | 10–11 | 10.5 | 70–76 | 9–11 | 10 | 76–81 | 3–4 | 3.5 | 82–83 | 2–3 | 2.5 |
| 7 | 79–85 | 82–86 | 1–3 | 2 | 85–88 | 3–6 | 4.5 | 66–71 | 13–14 | 13.5 | 71–76 | 8–9 | 8.5 | 82–85 | 0–3 | 1.5 |
| 8 | 73–79 | 76–81 | 2–3 | 2.5 | 79–84 | 5–6 | 5.5 | 60–64 | 13–14 | 13.5 | 65–71 | 8 | 8 | 76–81 | 2–3 | 2.5 |
| 9 | 73–79 | 66–70 | 7–9 | 8 | 64–68 | 9–11 | 10 | 55–59 | 18–20 | 19 | 60–65 | 13–14 | 13.5 | 69–75 | 4 | 4 |
| 10 | 65–72 | 61–67 | 4–5 | 4.5 | 55–61 | 10–11 | 10.5 | 55–60 | 10–12 | 11 | 55–60 | 10–12 | 11 | 62–70 | 2–3 | 2.5 |
| Sample Observation No. | Avg Dev. Large Data ±dB(A) | Avg Dev. Small Data ±dB(A) | Avg Dev. Source Avg. ±dB(A) | Avg Dev. Google Navigation Data ±dB(A) | Avg. ANN Prediction ±dB(A) |
|---|---|---|---|---|---|
| 1 | 0 | 7 | 9 | 2.5 | 0.5 |
| 2 | 9 | 10 | 9 | 18 | 2 |
| 3 | 3.5 | 14 | 8 | 12.5 | 2.5 |
| 4 | 6 | 9 | 10.5 | 4 | 2 |
| 5 | 6 | 8 | 4.5 | 4 | 2.5 |
| 6 | 7 | 10.5 | 10 | 3.5 | 2.5 |
| 7 | 2 | 4.5 | 13.5 | 8.5 | 1.5 |
| 8 | 2.5 | 5.5 | 13.5 | 8 | 2.5 |
| 9 | 8 | 10 | 19 | 13.5 | 4 |
| 10 | 4.5 | 10.5 | 11 | 11 | 2.5 |
| Mean | 4.85 | 8.9 | 10.8 | 8.55 | 2.3 |
| Standard Deviation | 2.86 | 2.76 | 3.89 | 5.15 | 0.78 |
| ANOVA: Single Factor | ||||||
|---|---|---|---|---|---|---|
| SUMMARY | ||||||
| Groups | Count | Sum | Average | Variance | ||
| Column 1 | 10 | 48.5 | 4.85 | 8.17 | ||
| Column 2 | 10 | 89 | 8.9 | 7.65 | ||
| Column 3 | 10 | 108 | 10.8 | 15.17 | ||
| Column 4 | 10 | 85.5 | 8.55 | 26.58 | ||
| Column 5 | 10 | 23 | 2.3 | 0.62 | ||
| ANOVA | ||||||
| Source of Variation | SS | df | MS | F | p-value | F crit |
| Between Groups | 471.33 | 4 | 117.83 | 10.12 | 2.59 | |
| Within Groups | 523.85 | 45 | 11.64 | |||
| Total | 995.18 | 49 |
| ANOVA: Single Factor | ||||||
|---|---|---|---|---|---|---|
| SUMMARY | ||||||
| Groups | Count | Sum | Average | Variance | ||
| Column 1 | 10 | 89 | 8.9 | 7.65 | ||
| Column 2 | 10 | 108 | 10.8 | 15.17 | ||
| Column 3 | 10 | 85.5 | 8.55 | 26.58 | ||
| ANOVA | ||||||
| Source of Variation | SS | df | MS | F | p-value | F crit |
| Between Groups | 29.32 | 2 | 14.66 | 0.89 | 0.42 | 3.35 |
| Within Groups | 444.73 | 27 | 16.47 | |||
| Total | 474.04 | 29 | ||||
| ANOVA: Single Factor | ||||||
|---|---|---|---|---|---|---|
| SUMMARY | ||||||
| Groups | Count | Sum | Average | Variance | ||
| Column 1 | 10 | 89.00 | 8.9 | 7.66 | ||
| Column 2 | 10 | 85.50 | 8.55 | 26.58 | ||
| ANOVA | ||||||
| Source of Variation | SS | df | MS | F | p-value | F crit |
| Between Groups | 0.61 | 1 | 0.61 | 0.036 | 0.85 | 4.41 |
| Within Groups | 308.12 | 18 | 17.11 | |||
| Total | 308.73 | 19 | ||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zafar, M.I.; Bharadwaj, S.; Dubey, R.; Tiwary, S.K.; Biswas, S. Reducing Data Requirements for Simple and Effective Noise Mapping: A Case Study of Noise Mapping Using Computational Methods and GIS for the Raebareli City Intersection. Acoustics 2023, 5, 1066-1098. https://doi.org/10.3390/acoustics5040061
Zafar MI, Bharadwaj S, Dubey R, Tiwary SK, Biswas S. Reducing Data Requirements for Simple and Effective Noise Mapping: A Case Study of Noise Mapping Using Computational Methods and GIS for the Raebareli City Intersection. Acoustics. 2023; 5(4):1066-1098. https://doi.org/10.3390/acoustics5040061
Chicago/Turabian StyleZafar, Md Iltaf, Shruti Bharadwaj, Rakesh Dubey, Saurabh Kr Tiwary, and Susham Biswas. 2023. "Reducing Data Requirements for Simple and Effective Noise Mapping: A Case Study of Noise Mapping Using Computational Methods and GIS for the Raebareli City Intersection" Acoustics 5, no. 4: 1066-1098. https://doi.org/10.3390/acoustics5040061
APA StyleZafar, M. I., Bharadwaj, S., Dubey, R., Tiwary, S. K., & Biswas, S. (2023). Reducing Data Requirements for Simple and Effective Noise Mapping: A Case Study of Noise Mapping Using Computational Methods and GIS for the Raebareli City Intersection. Acoustics, 5(4), 1066-1098. https://doi.org/10.3390/acoustics5040061






