1. Introduction
Signal processing devices based on surface acoustic waves (SAW), like frequency filters, delay lines and others, have, nowadays, far-reaching applications in various fields, especially in the growing market of mobile communication. The working principle of almost all these devices makes use of the piezoelectric effect with interdigital electrode structures and relies on linear behavior. New standards like 5G further raise the linearity requirements. This has led to an urgent need for gaining an in-depth understanding of the influence of nonlinearity on the propagation of SAWs and for means to reduce this influence.
Major undesired nonlinear effects that occur in SAW devices and need to be counteracted are harmonic generation and intermodulations, which can deteriorate signal quality in mobile communication. Of similar importance is the power dependence of the resonance frequencies. All these effects will be addressed in this review.
So far, modelling of nonlinear effects in SAW devices has mostly been carried out phenomenologically by extending coupling of modes (COM) and P-matrix theory [
1,
2,
3,
4] or by nonlinear extensions of an equivalent circuit model (especially the Mason model) [
5]. The latter were successfully applied to bulk acoustic wave (BAW) devices [
6,
7] (and references therein). Parameters containing information on nonlinearity were obtained by fitting to experimental data. Calculations, relating nonlinear effects like third-order intermodulational distortions (IMD3) directly to linear and nonlinear material constants of the elastic media involved, use the finite element method (FEM) [
8,
9,
10,
11,
12,
13,
14,
15]. In contrast to the phenomenological models mentioned above, finite element calculations do not rely on restrictive model assumptions. They yield reliable results without the need for fit parameters, if the relevant material constants are known to a sufficient extent and accuracy. In addition, they provide full-wave fields, which can be very useful for the designer of SAW devices and allow for detailed insights into the nonlinear behavior of a device.
To the authors’ knowledge, detailed investigations of nonlinear propagation effects in connection with SAWs began in the mid-sixties of the previous century (for a review see [
16]). The field was boosted by the development of the elastic convolver, an analog, nonlinear, signal-processing device based on SAWs, which, however, did not reach the market (see the reviews [
17,
18]). Here, electro-acoustic nonlinearity was a desired effect. Nonlinearity in the context of SAWs has gained renewed attention in connection with further miniaturization, leading to higher power densities, and tightened linearity requirements for signal processing devices, as well as in the field of non-destructive evaluation [
19].
The major “classical” sources of nonlinearity are the third- and higher-order terms in an expansion of the materials’ potential energy per unit volume in powers of displacement gradients and electrical field components. The theory of nonlinear electro-elasticity was presented in detail in classical texts [
20,
21,
22,
23]. Theoretical studies of effects of this classical nonlinearity on the propagation of surface acoustic waves were first carried out with the help of coupled amplitude equations, derived by Reutov [
24], or evolution equations in the form of integral equations ([
25] and references therein). They focused on homogeneous media and layered structures, including piezoelectric materials, with planar surfaces and interfaces. They allowed for simulations and, hence, for quantitative predictions of nonlinear propagation effects directly on the basis of material constants. The investigations included intermodulations at an early stage [
26,
27].
The complexity of the displacement field and the spatial distribution of electrostatic potential in SAW-based devices with their arrangements of electrodes on the surface or buried in a dielectric film calls for the use of numerical techniques, such as FEM for quantitative predictions of nonlinear effects. The goal of this review paper is to outline, in detail, a two-dimensional FEM-based approach, treating the nonlinearity within perturbation theory. To demonstrate its applicability to quantitative analysis of electrical currents and mechanical displacements generated by the electro-elastic nonlinearities of the constituent materials of a SAW device, a few numerical results are shown, which refer to a temperature-compensated SAW system (TC-SAW system) consisting of copper electrodes on a LiNbO3 128°YX substrate and a silicon oxide film. The presentation focuses on methods and algorithms rather than on numerical results. The complexity of the simulation methods and their theoretical basis in nonlinear electro-elasticity induced us to confine this review to methodological aspects concerning theory rather than including experimental results or giving a detailed overview of the field’s historical development.
The paper is structured in the following way:
In
Section 2, the part of nonlinear elasticity theory underlying the FEM model is briefly summarized, and the notation used in the following sections is introduced. In particular, we introduce a four-component generalized displacement field, its fourth component being the electrostatic potential. In this context, the material constants used as input data in the numerical calculations for the considered TC-SAW system are mentioned and their sources provided.
Section 3 presents the FEM model itself for an infinite periodic arrangement of electrodes and for a finite number of electrodes.
In
Section 4, two different methods of calculating the current in the electrodes due to third-order intermodulations are introduced. One of them allows the calculation of the nonlinear current generated by third-order intermodulations without first determining the displacement field and electrostatic potential associated with the third-order intermodulations.
In
Section 5, we show how the influence of nonlinearity on the resonance curve and phase response of a SAW resonator can be efficiently determined by combining FEM with perturbation theory.
In
Section 6, reflections of bulk waves from the bottom of the substrate are considered, which are part of the (generalized) displacement field of the second harmonic of a SAW excited in an interdigital transducer.
Section 7 is concerned with FEM calculations for systems with a finite number of equidistantly arranged electrodes. A recursive algorithm is introduced that enables calculations of nonlinear quantities (mechanical and electrical displacement fields associated with intermodulations and higher harmonics) for a large number of electrodes with considerably reduced numerical effort as compared to the standard approach. The paper ends with a short conclusion.
2. Nonlinear Electro-Elasticity
2.1. General Theory
The theory of nonlinear electro-elasticity underlying our FEM calculations was developed in detail in the nineteen-sixties to eighties (see, e.g., [
20,
21,
22,
23,
25]). Here, only a brief summary is provided. Further references to earlier work may be found in [
16,
23].
As degrees of freedom, we consider the three Cartesian components of the displacement field,
u1,
u2,
u3, referring to the spatial frame [
20] and the electrical potential. The latter will be treated as the fourth component,
u4, of a four-component generalized displacement field. This concept was introduced for linear piezoelectricity in [
28] and was applied to nonlinearity in [
25,
29,
30,
31,
32]. The components of the generalized displacement field are labelled by lower-case Latin indices. They depend on time
t and on the Cartesian coordinates
X1,
X2,
X3, referring to the material frame [
20] and being the Cartesian components of the position vector
X. We invoke a summation convention that implies summation over repeated lower-case Latin indices from 1 to 4 and summation over repeated upper-case Latin indices from 1 to 3. These indices are always subscripts. (We note that there is no implicit summation over any other kind of index.).
The equations of motion and, partly, the boundary conditions for the four-component generalized displacement field can be derived from a Lagrangian,
via Hamilton’s principle (see for example [
20,
23,
33]). In (1),
denotes the volume element in material coordinates, and the integral extends over the entire space filled with elastic material. The kinetic energy per unit volume of undeformed elastic medium is
Consequently, is the mass density at position X of the undeformed medium. Furthermore, is a generalized Kronecker symbol defined as if m = n and , and otherwise.
For the systems we are considering here, which consist of elastic and partially piezo-electric media, it is assumed that the potential energy per unit volume of the undeformed medium,
, may be expanded in powers of gradients of the generalized displacement field components
,
The expansion coefficients on the right-hand side of (3) may be regarded as components of generalized tensors C, S(2), S(3), which may depend on position X. In order to avoid confusion, we note that the superscripts (2) and (3) in the above equation refer to second-order (i.e., lowest-order) and third-order nonlinearity, respectively, and do not correspond to the order in the expansion of in powers of generalized displacement gradient components. For simplicity, we only treat cases where the system is in static equilibrium, where no external static stress or electric field is applied to the system. In such cases, the expansion coefficients in the first term on the right-hand side of (3) have the following meaning:
For the indices m, n ranging from 1 to 3, are second-order elastic constants (SOECs). are the linear piezoelectric constants, and , apart from the minus-sign, are the static dielectric constants of the corresponding medium.
In the second term on the right-hand side of (3), are linear combinations of second-order and third-order elastic constants (TOECs), if the indices m, n, p range between 1 and 3. The coefficients with n, p ranging between 1 and 3 are linear combinations of electro-elastic and piezoelectric constants; with p = 1,2,3, are related to the electrostriction constants, and to the static second-order electrical permittivities.
In the third term on the right-hand side of (3),
are linear combinations of second-order, third-order and fourth-order elastic constants (FOECs), if the lower-case indices
m,
n, p, q range between 1 and 3 [
34]. If at least one of the indices
m,
n, p, q is equal to 4, the corresponding coefficient is related to the electrical potential. All fourth-order material constants entering the generalized eighth-rank tensor
S(3) are specified in [
23]. (For further details, see [
16,
20,
23,
25,
34].) Explicit expressions for the elements of the tensors
S(2),
S(3) in terms of the material constants are provided in the
Appendix A.
We note that the index pairs, consisting of a lower-case and an upper-case index, may be permuted at the quantities and .
2.2. Input Data for the TC-SAW System
In order to obtain reliable results in FEM simulations, all material constants entering the generalized tensors C, S(2) and S(3) must be known for the materials that constitute the device to be modelled. For the example system of a TC-SAW interdigital transducer considered here, these are 128° rotated Y-cut LiNbO3 as substrate material (Euler angles: λ = 0.0°, μ = 37.85°, θ = 0.0°), copper electrodes and a temperature-compensating silicon oxide film, which covers the electrodes and the substrate surface. For simplicity, the surface of the SiO2 film is taken to be planar in our model. A complete set of material constants occurring in C, S(2) and S(3) is hardly available for any material. The situation for the three materials in our example system will now be discussed.
2.2.1. Material Constants for LiNbO3
The second-order elastic constants, piezoelectric constants and dielectric constants entering the generalized tensor
C were taken from [
35]. For the third-order material constants (TOECs, electro-elastic constants, electrostriction constants and second-order electrical permittivities) a complete set of measured data is available [
36] and was used in the generalized tensor
S(2), along with the linear material constants of [
35]. Since no fourth-order material constants for LiNbO
3 are known to us, we have equated the generalized tensor
S(3) to zero in most of our calculations of IMD3. To demonstrate the role of the material constants of second and third order in the tensor
S(3), we compare, in
Section 4, the results for IMD3 and the third harmonic obtained when equating
S(3) to zero, with those obtained with
S(3) containing certain second-order and third-order, but no fourth-order material constants.
As a caveat, we would like to mention here that substantial compensations of material constants of different orders can occur in the tensors
S(2) and
S(3). In order to account for the unknown FOECs in a rough approximate way, an isotropic approximation was introduced in [
15], and the four fourth-order Lamé constants were treated as fit parameters. For the mass density of LiNbO
3, we chose the value of 4628 kg/m
3.
2.2.2. Material Constants for SiO2
The two second-order elastic constants and mass density of the isotropic SiO
2 film are provided in [
37] (second row in Table II). Our sources for the three TOECs are [
38,
39] and for the four FOECs [
40]. For the static relative dielectric constant, the value 3.75 was chosen. All third-order and fourth-order material constants related to the electrostatic potential either vanish or have been neglected. We note that the material constants of the SiO
2 film may be sensitive to its fabrication process. Yost and Breazeale [
39] point out that residual stress has a considerable influence on the TOECs of SiO
2.
2.2.3. Material Constants for Copper Electrodes
As mentioned above, subtle compensations between elastic constants of different order may occur in the generalized tensors
S(2) and
S(3). Therefore, a consistent data set of material constants is desirable, which is obtained from the same source. In the case of crystalline copper, such a data set is available from
ab-initio calculations based on density functional theory [
41]. Good agreement for second-order and third-order elastic moduli was found between the
ab-initio results and measured data. All FOECs are provided in [
41], too. These constants have been isotropized by averaging using the Voigt assumption [
42,
43]. The mass density value chosen for our calculations was 8920 kg/m
3.
3. FEM Modeling of Nonlinear SAW Systems
3.1. General Considerations
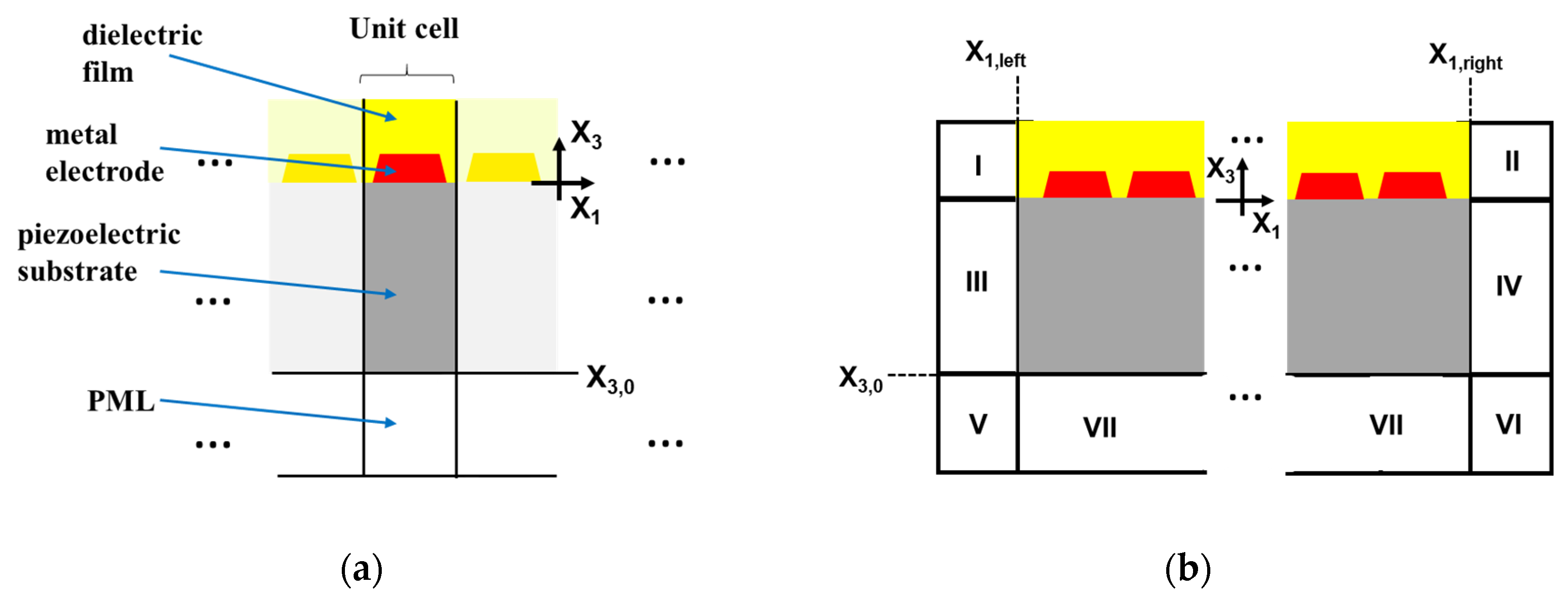
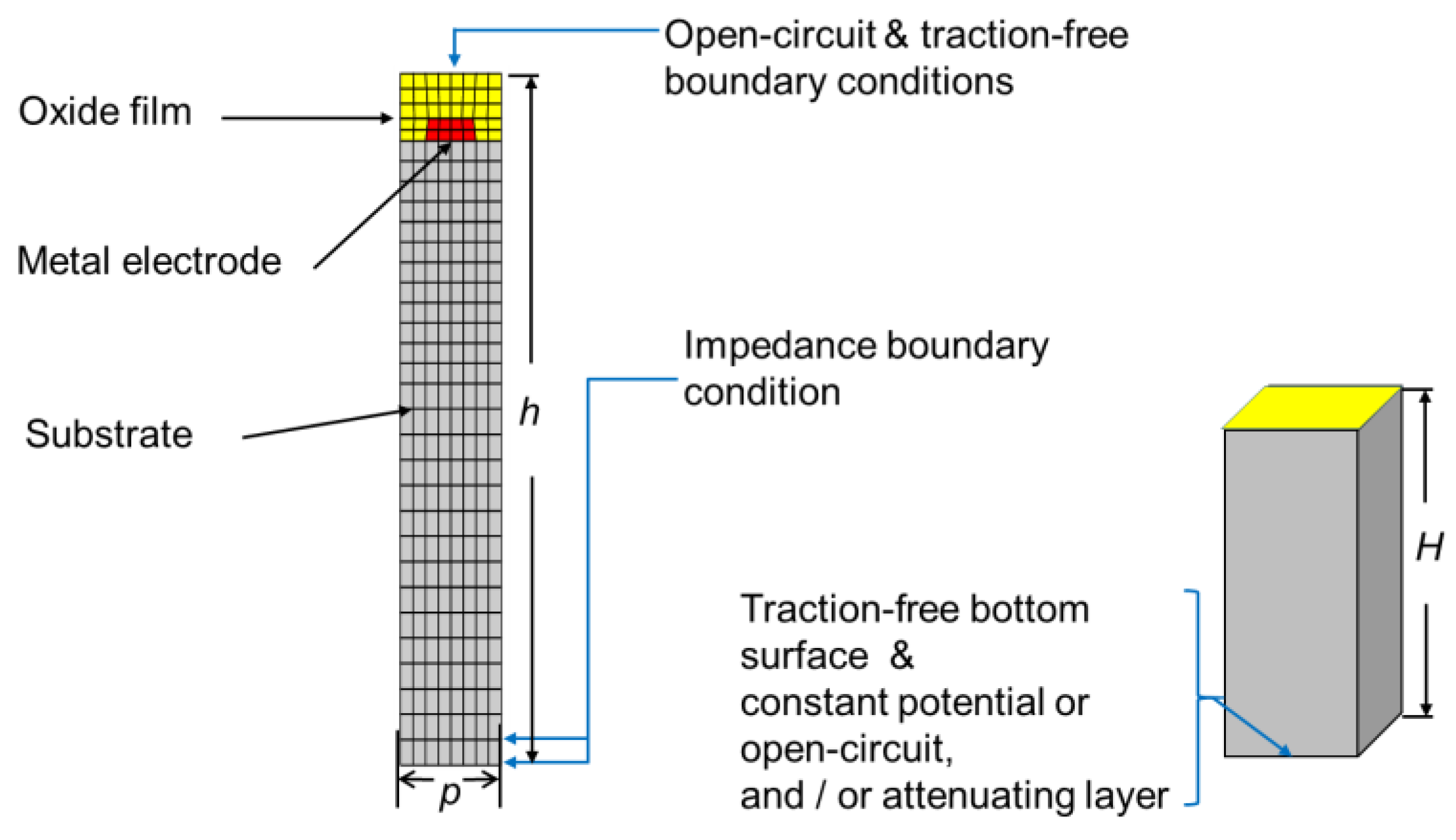
Our FEM modeling of SAW systems was confined to two dimensions, assuming an infinite aperture of the electrodes and no dependence of the displacement field and electric potential on
X2 in the coordinate system introduced in
Figure 1. However, all three Cartesian components of the displacement field are taken into account. On the planar surface of a piezoelectric substrate, metal electrodes are placed, which are embedded in a dielectric film covering the substrate surface and have a trapezoidal cross-section. An extension to substrates consisting of several layers stratified parallel to the (
X1,
X2)-plane is straight-forward.
Two types of systems are distinguished: Infinite periodic (I) and finite (II) arrangements of electrodes on the substrate surface (
Figure 1). The surface of the dielectric film is traction-free, and the normal component of the material electric displacement vector vanishes at this surface (open-circuit boundary condition).
When reflections must be avoided, a perfectly matched layer (PML) is placed underneath the substrate part of the simulated system (
Figure 1) and—in case (II)—at the right and left sides of the finite system, too. When reflections from the bottom of the substrate are to be investigated, an impedance boundary condition has been applied that mimics certain prescribed boundary conditions (e.g., zero traction and zero normal component of the material electric displacement field, or a prescribed value of the electric potential) at the bottom surface of a wafer with realistic thickness. These boundary conditions will be described in more detail below. In addition, periodic boundary conditions along the
X1-direction are imposed in case (I).
Following the iso-parametric concept, the four-components of the generalized displacement field,
, are represented in each element as a linear combination of test functions
with
corresponding to rectangular 8-node elements [
44]. Here,
are non-dimensional internal variables. When inserting this representation into the Lagrangian (1) with (2) and (3), Hamilton’s principle yields nonlinear coupled equations for the four degrees of freedom
with
which are the three Cartesian components of the node displacement vector and the electrical potential at the corresponding node position in the un-deformed medium,
The superscript labels the nodes of the total mesh. In (4), M is the global mass matrix and K(2) is the linear global stiffness matrix. K(3), K(4), … are higher-order global stiffness matrices, where K(3) depends linearly on S(2), and likewise, K(4) depends linearly on S(3). The drive term on the right-hand side of (4) results from the time-dependent electrical potential prescribed at the electrodes. It is non-zero only if refers to a node of an element in an electrode.
A dimensionless quantity characterizing the size of the nonlinearity in the systems considered here is the dynamic strain associated with a SAW. Since this quantity is much smaller than one, the application of perturbation theory is justified. When expanding the node variables in powers of a dimensionless expansion parameter
ε,
a hierarchy of systems of linear inhomogeneous ordinary differential equations is obtained from (4).
Among the nonlinear phenomena relevant for SAW devices, we shall focus at first on third-order intermodulations (IMD3). The electrical potential of the electrodes is fixed and chosen as a superposition of two input tones
,
where
are complex potential values and
c.c. stands for the conjugate complex. The potential alternates between neighboring electrodes. Equation (6) implies for the time-dependence of the right-hand side of (4):
where
are non-zero only for nodes belonging to elements in the electrodes. For the time dependence of the node variables at first order up to third order of
ε we may assume a superposition of time-harmonic functions.
At first order of
ε, we may decompose
with time-independent node variables
The symbols
F1 and
F2 denote the first and second fundamental (input tone), respectively. The time-independent node variables satisfy the linear inhomogeneous equations
where
n =1, 2 labels the two input tones. In order to account for the constant pre-defined electrical potential on the electrodes, we define two additional matrices
and
as follows:
The matrix differs from in the following components: For nodes belonging to an electrode, the components are zero for j = 1, …, 4 and all nodes except for the diagonal elements which are equal to 1.
At second order of
ε, it is sufficient to account for the frequencies
(second harmonic of first input tone, 2H) and
(low-frequency component, LF) for the computation of the IMD3 generalized displacement field. Decomposing
where
stands for the remaining terms which oscillate with frequencies
and
. The corresponding systems of linear algebraic equations are:
modified such that
and
vanish at nodes of elements in the electrodes.
At third order of
ε, we only consider third-order intermodulations with frequency
. Therefore, we write
where
contains all other frequency components of the complete solution at third order of
ε.
The system of linear algebraic equations to be solved in order to obtain the generalized displacement field of IMD3 is the following:
The first two terms on the right-hand side of (15) represent an effective third-order nonlinearity as a result of cascading the second-order nonlinearity, having a quadratic dependence on the generalized tensor S(2), whereas the third term on the right-hand side depends linearly on S(3).
It is straightforward to apply this scheme to other nonlinear processes such as higher harmonic generation and nonlinear mixing of three input tones.
As an alternative to the presented derivation of the above equations, one may apply the expansion in powers of
ε directly to the generalized displacement field,
insert this expansion into the Lagrangian (1), and apply the variational principle to each individual order of
ε. For the investigation of IMD3 with the two input tones
, the functions
have the form
where
are irrelevant for the determination of the IMD3 generalized displacement field with frequency
at third order of
ε.
For systems of type (I) (infinite periodic arrangement of electrodes), the generalized displacement field, associated with the various frequency components, can be set up as Bloch functions, where is a p-periodic function This allows to confine the calculations to a unit cell with extension along the x1-direction equal to the mechanical period p (pitch) of the system. In this case, the node variables are the values of the corresponding periodic function at the position of node in the undeformed state of the system. The Bloch–Floquet exponent k may be chosen to be equal to plus an integer multiple of for the fields of the fundamentals (F1, F2) and of the third-order intermodulation (IM3). For the fields associated with the second harmonic (2H) and the low-frequency contribution (LF), k has to be chosen as zero plus an integer multiple of . The stiffness matrices K(n), n = 2, 3, 4… will then depend on the Bloch–Floquet exponents. Viscous damping can be introduced in a straightforward way, leading to the additional term on the right-hand side of (10). The matrix G depends on the viscosity tensor η of each material in the same way as the linear stiffness matrix K(2) on the tensor of second-order elastic moduli.
3.2. Nonlinear Perfectly Matched Layers
Unless effects of reflections from the bottom of a substrate of finite thickness are the topic of investigation, a semi-infinite substrate is assumed, and bulk-wave reflections are suppressed by placing a perfectly matched layer (PML) below the part of the substrate that is included in the simulation domain (
Figure 1a,b). When simulating finite arrays of electrodes, additional PMLs are applied as shown in
Figure 1b.
Our implementation of linear PMLs largely follows [
45]. Complex functions
hL =
pL +
i qL,
L = 1, 3, are defined in each PML with real (imaginary) parts
pL (
qL). The argument of the real functions
pL,
qL is the Cartesian coordinate
XL. In our implementation we have chosen
p1(
X1) =
p3(
X3) = 1 in all PMLs and
q1(
X1) = 0,
q3(
X3) = σ
3 (
X3 −
X3,0)
2 for the PML in
Figure 1a and for the PML domain VII in
Figure 1b,
q1(
X1) = σ
1 (
X1−
X1,left)
2,
q3(
X3) = 0 for the PML domains I, III,
q1(
X1) =−σ
1 (
X1 −
X1,right)
2,
q3(
X3) = 0 for the PML domains II, IV,
q1(
X1) = σ
1 (
X1 −
X1,left)
2,
q3(
X3) = σ
3 (
X3 −
X3,0)
2 for the PML domain V,
q1(
X1) =−σ
1 (
X1 −
X1,right)
2,
q3(
X3) = σ
3 (
X3 −
X3,0)
2 for the PML domain VI in
Figure 1b with two real parameters σ
1, σ
3. Their values must be determined in tests such that reflections are minimized over a sufficiently wide frequency range. For each PML domain, a 3 × 3 matrix
H is defined via
and the quantity
.
In linear PMLs, the mass density
and the components of the generalized fourth-rank tensor
containing the second-order elastic, the piezoelectric and dielectric constants, are defined as
where
and
C are the corresponding quantities in the neighboring (piezo-)elastic medium.
In order to avoid reflections at the interface between the PML and the neighboring medium in the presence of nonlinearity (nonlinear PML), generalized tensors
are introduced and defined as
where
S(n) is the corresponding generalized tensor in the neighboring medium.
In calculations of the IMD2, IMD3, second or third harmonics in an infinitely periodic arrangement of electrodes (
Figure 1a) according to the perturbation scheme outlined above, this extension of the PML to nonlinearity is not necessary as long as the generalized displacement fields of the fundamentals are localized at the surface. However, it is needed if at least one of the fundamental waves corresponds to a leaky surface mode or the input frequency of a fundamental is much larger than the resonance frequency. In this case, a linear PML is insufficient, and the Extension (23) does in fact eliminate reflections in the limit of infinitely small element sizes.
5. Nonlinear Amplitude and Phase Response of a SAW Resonator
An important, normally undesired effect occurring in oscillators with effective third-order nonlinearity is the bending of the resonance curve, often termed the Duffing effect, which can lead to bistability. It may be demonstrated with the help of the Duffing equation [
46]
where
is the resonance frequency in the linear limit without damping,
is a damping constant,
is the pre-factor of the third-order nonlinearity, and
and
, respectively, are the frequency and strength of the drive.
Using asymptotic perturbation theory (see for example [
47]), it is straightforward to derive a first-order differential equation that describes the behavior of the Duffing oscillator for drive frequencies in the neighborhood of the linear resonance frequency. For this purpose, an expansion parameter
ε and a “stretched” time coordinate
are introduced. Also, quantities
,
and
are defined via
,
,
, and are assumed to be of order
O(1) in the expansion parameter
ε. Expanding
u in powers of
ε,
the following evolution equation is obtained for the complex amplitude
:
with the coefficient
in the nonlinear term. (For more details of this approach see Chapter 6 in [
16] and references therein).
The evolution equation (41) also holds for the complex amplitude
of the generalized displacement field
in a SAW resonator in the neighborhood of the resonance frequency
. To show this, we write this field as an asymptotic expansion (16) and introduce, as before, the “stretched” time coordinate
. On the
l-th electrode we impose the electric potential
with drive frequency
close to the resonance frequency
,
.
The quantities and are of order O(1) in the expansion parameter . For the viscosity tensor, we apply the scaling with the tensor being of order O(1).
The first-order term,
is a solution of the linear boundary value problem following from the Lagrangian (1) obeying the condition that the electric potential on the electrodes vanishes. It is easily determined by FEM by solving a generalized eigenvalue problem, where
is the eigenvalue and
is the corresponding eigenvector, normalized in a suitable way. A convenient normalization adopted in the following is
.
In the same way as in
Section 4, the double integrals in (44) and in the following have to be carried out over the area
A filled with material in the finite system (
Figure 1b) or in a unit cell of the infinite periodic system (
Figure 1a). To ensure the convergence of the integrals occurring in this derivation, we require that the field
is fully surface-localized. In the case of a finite system of electrodes, we assume, in addition, that the geometry of the system is such that
decays exponentially into the positive and negative
X1-direction or is spatially confined to a stripe with finite extension along the
X1-axis. In the case of an infinite periodic arrangement of electrodes (
Figure 1a), area integrals of the kind (44) need to be extended over a unit cell only, as mentioned above.
The second-order field consists of two parts, the second harmonic (2
H) and a static contribution (
S),
Both contributions can be determined by applying FEM and solving an inhomogeneous system of linear equations.
The third-order field
, contains a contribution of the form
. The equation of motion and Poisson’s equation, obeyed by this contribution, has the following form:
where
Following [
48], (46) is projected on the field
; i.e., both sides of (46) are multiplied by
, summed over
m and integrated over
. In the same way as in the derivation of (38) in the previous section, two integrations by parts are subsequently carried out and the boundary conditions satisfied by the fields
and
are made use of. Especially, one has to account for the jump of the component of the material electric displacement field
D(F) normal to the electrode boundaries, where
and the imposed electric potential (42). In the integrations by parts, all boundary terms vanish except for the line integrals
l = 1,…,
NE, over the boundaries
of the
NE electrodes. Here,
is the charge per unit length of aperture on the
l-th electrode, associated with the field
.
This procedure yields the evolution Equation (41) for the amplitude
with the following expressions for the coefficients
,
and
N in terms of the fields
, which are evaluated with our FEM code. The strength of the drive term is provided by
with (49) and (48), and the damping constant by
The coefficient
N in front of the nonlinear term in (41) may be decomposed into three parts,
which all have the form of overlap integrals. The first term results from the second harmonic,
The second term is related to the static part of the second-order field,
The third term is the direct contribution of third-order nonlinearity,
While
and
are real, the contribution
of the second harmonic is ordinarily complex due to radiation of the second harmonic into the bulk. We shall denote the real part of the total effective nonlinearity parameter
N by
N′ and its imaginary part by
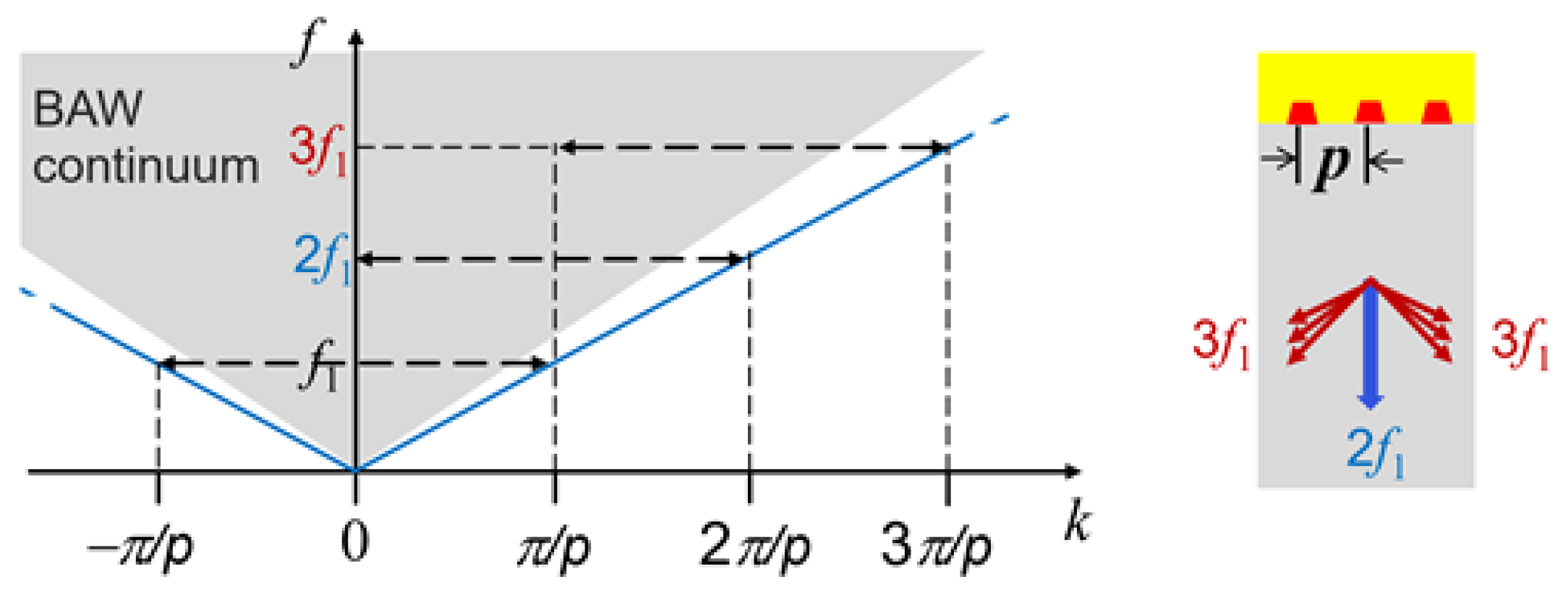
N″. In an infinite periodic system, bulk waves are radiated at the second harmonic frequency into the substrate with wave-vector vertical to the surface. The reason for their generation is explained in
Figure 5. In an infinite periodic structure, the Bloch–Floquet exponent of the generalized displacement field, associated with the second harmonic of a Brillouin zone boundary excitation, is equal to zero in the reduced zone scheme. Consequently, it consists of bulk waves with wave-vectors vertical to the surface (blue arrow in the right subfigure of
Figure 5). In the case of the third harmonic, the magnitude of the Bloch–Floquet exponent in the reduced zone scheme is equal to
. Therefore, the generalized displacement field associated with the third harmonic contains bulk waves with wave-vectors inclined to the surface normal (red arrows in the right subfigure of
Figure 5). The inclination angles of these wave-vectors may be obtained from the sections of the (
X1,
X3)-plane and the corresponding sheets of the slowness surface of bulk waves in the substrate material.
Bulk-wave radiation at the second and third harmonic frequencies in a SAW resonator was verified experimentally in [
49]. For an infinite periodic system, it may be shown in a way similar to the derivation of Equation (6.71) in [
16] that the imaginary part of
is related to the power flow of the second harmonic away from the electrodes and that it must be positive. Unless the bottom of the substrate reflects the bulk waves at the second harmonic frequency back to the electrodes and their damping is negligible, the imaginary part of
is larger than zero. In
Table 1, the real part of the effective nonlinearity coefficient
N and the relative sizes of the second harmonic contribution (both real and imaginary parts), of the static and of the direct contributions are provided for a TC-SAW system. The normalization
was chosen. The data show that there is a significant dependence of the nonlinearity coefficient on the metallization ratio. The direct contribution via the generalized tensor
S(3) plays a dominant role.
We note that the above considerations also apply to BAW resonators. For solidly mounted resonators with the piezoelectric layer between upper and lower electrode placed on a Bragg reflector, the coefficient N can acquire an imaginary part if the second harmonic of the linear resonance does not fall into a stop band of the Bragg reflector.
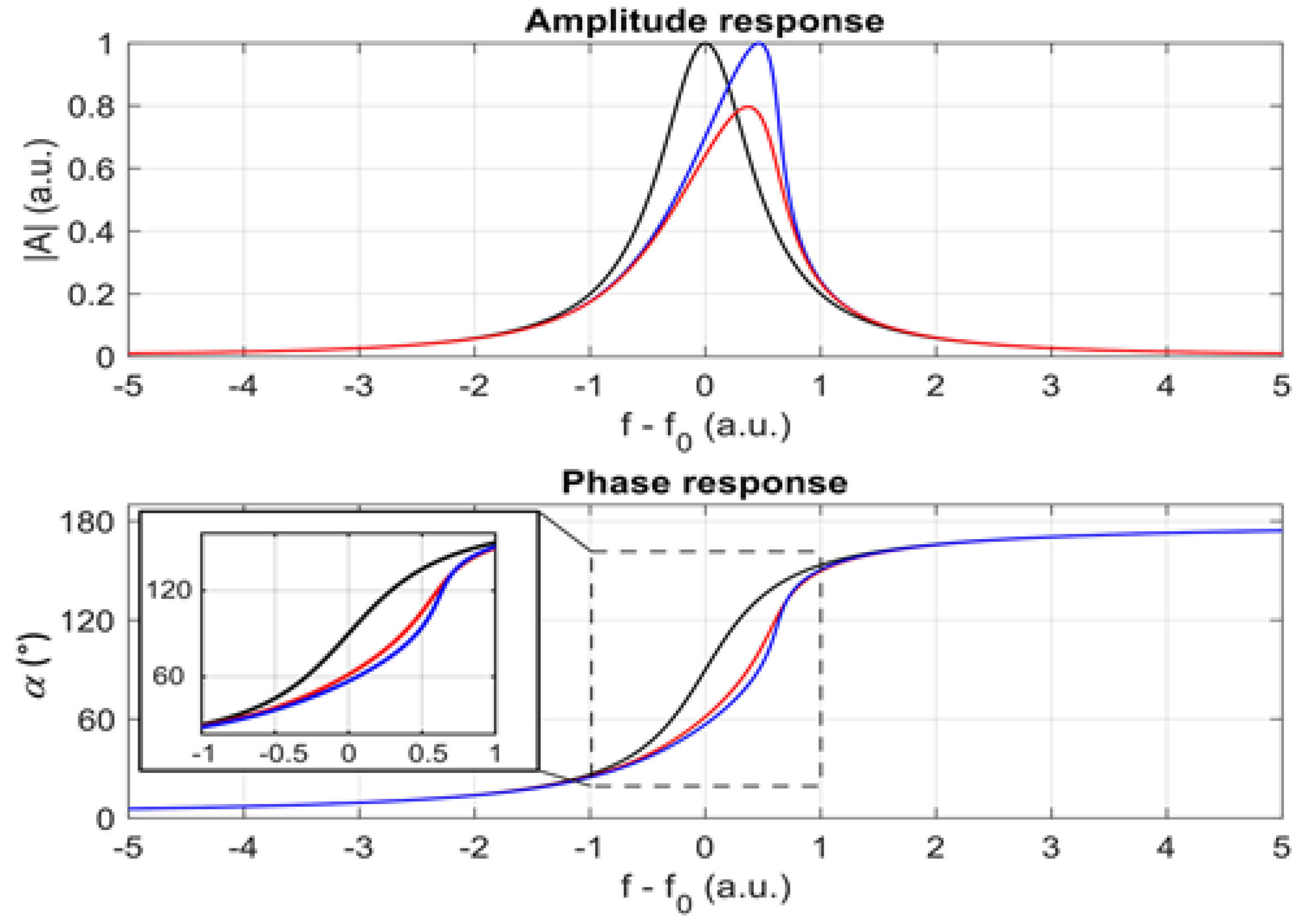
For frequencies in the neighborhood of the resonance frequency, the shape of the resonance curve and the phase response follows from (41). Inserting the stationary Ansatz
in (41) yields a cubic equation in
, which may be brought into the form
From (57), one readily deduces that the sign of the real part
of the complex coefficient
N decides on whether the resonance curve is inclined to negative (
) or positive (
) frequencies. The amplitude |
A0| reaches its maximum when the argument of the square root in (57) vanishes. Consequently, the presence of a positive imaginary part
of
N reduces this maximum in comparison to the linear case. The effect of the real and imaginary parts of
N on the amplitude and phase response of a resonator is shown schematically in
Figure 6.
The phase response of the resonator is affected by both real and imaginary parts of the coefficient
N, too. Choosing
F to be real and writing
, we obtain for the phase angle
:
6. Reflection of Bulk Waves from the Bottom of the Substrate
As mentioned in the previous subsection, even an infinite periodic arrangement of electrodes generates bulk waves as part of second and third harmonics of fundamentals that are surface waves. If the bottom surface of the substrate is sufficiently smooth, these bulk waves undergo specular reflection, travel back to the upper surface and influence the current in the electrodes. This has been verified experimentally by Solal et al. [
48]. In order to simulate this phenomenon, it is desirable to restrict computations to an area in the (
X1,
X3)-plane that is not larger in depth than the area used in FEM simulations of linear SAWs (
h in
Figure 7). However, in practice, the distance between the two surfaces of the sample (
H in
Figure 7) is much larger,
H >>
h. In order to bypass this problem, one can take advantage of the fact that below a certain depth, the generalized displacement field at the second-harmonic or third-harmonic frequency of a fundamental surface wave is approximately that of pure bulk waves, and apply an impedance boundary condition at the bottom of a simulation area of thickness
h. This is demonstrated in the following for bulk wave radiation of the second harmonic frequency in a system with an infinite periodic arrangement of electrodes.
In this system, the generalized displacement field associated with the second harmonic,
, is a
p-periodic function of
X1 and may therefore be written as a Fourier series,
In the substrate, the functions
are of the form
with generalized four-component polarization vectors
, normalized in a suitable way, wave-vector components
and coefficients
. For
the number
of partial waves in the sum on the right-hand side of (60) is eight, while in the case
it is equal to six. The polarization vectors and wave-vector components follow from the Christoffel equation for the substrate, extended to account for piezoelectricity. The coefficients
are unknown.
Depending on the value of
, the functions
are localized at the surface, i.e., they decay exponentially into the substrate, or they contain plain wave components that radiate energy into the bulk of the substrate and from the bottom of the substrate back to the top surface. For frequencies
smaller or close to the resonance frequency, it is only the Fourier component
n = 0 in (60) that contains bulk wave contributions. At the bottom of the substrate (
X3 = −
H), boundary conditions must be specified. As an example, we require that the bottom surface is traction-free and the electric potential is zero. This yields the four equations
.
At
, the generalized four-component displacement field of the second harmonic and its first derivative with respect to
is continuous, which yields the eight equations
for
. The depth
h was chosen to be sufficiently large, such that the
X1-dependence of
may be neglected. Solving (61)–(63) for eight variables
and inserting this solution in (64) yields an effective boundary condition at
X3 = −
h of the form
with a frequency-dependent matrix
M, which follows from the solution of a system of eight linear equations.
This procedure can be extended to Fourier components
in a straightforward way.
Figure 8 shows the three components of the displacement field associated with the second harmonic at a fixed depth. They were computed with the boundary condition (65). For two different thicknesses of the substrate, typical Fabry–Perot type resonances are visible. For a rough estimate of the periodicity of the resonance peaks in the case of the displacement component
U3, one may argue as follows. The distance between neighboring frequencies of plate vibrations with displacements predominantly vertical to the surfaces is approximately
vL/(2
L), where
L is the thickness of the plate and
vL is the phase velocity of quasi-longitudinal bulk waves with wave vector vertical to the surfaces of the plate. In the plots of the displacement field associated with the second harmonic as a function of the fundamental frequency
f1, we therefore expect a distance Δ
f1 vL/(4
H) between neighboring resonance peaks of the same kind for the displacement component
U3. With the velocity of quasi-longitudinal waves in the substrate (LiNbO
3-rot128YX) with wave-vector in the
X3-direction
vL = 7091 m/s, we expect Δ
f1 ≈ 30 MHz for
H = 59.24 µm and Δ
f1 ≈ 8.5 MHz for
H = 209.24 µm. This corresponds well with the data in
Figure 8. The reflected quasi-transverse waves, polarized predominantly in the
X2-direction, and purely transverse waves, polarized in the
X1-direction, together with the quasi-longitudinal waves give rise to complex interference patterns, since all three components are coupled in the spatial domain close to the surface.
The Fabry–Perot resonances in the generalized displacement field of the second harmonic influences the IMD3 current as shown in
Figure 9.
At frequencies f1 much larger than the resonance frequency, where terms of the Fourier series (59) with are not localized at the surface, the corresponding bulk waves propagate away from the surface at an angle different from 90°. After being reflected at the bottom of the substrate, they will travel back and reach the top surface outside the area covered by electrodes in the case of a finite device. Nevertheless, they may influence the IMD3 current in this device.
7. Recursive Procedure for Finite, Truncated Periodic Systems
In this section, a method is presented for an efficient calculation of the nonlinearly generated fields and currents for a system consisting of a periodically arranged, but finite number of electrodes (
Figure 1b). In the case of third-order intermodulations, this concerns the fields
and the IMD3 current. The basic task is to numerically solve the inhomogeneous systems of linear Equations (9), (12), (13) and (15) with the structure of the matrix
and the inhomogeneities (right-hand sides of the linear equations) resulting from the geometry of the system.
Recently, Koskela and Plessky [
50,
51] introduced a method for the FEM calculation of linear fields and admittances in such systems, which leads to an enormous reduction of computing time as compared to the standard FEM approach. This method is based on the elimination of the internal degrees of freedom in a unit cell via the Schur complement and the principle of cascading, well-known in P-matrix theory [
52]. For the computations of nonlinear fields within the perturbation scheme used here, cascading is not directly applicable. This is because the inhomogeneities differ between different cells unlike the linear case, where the inhomogeneities result from the electrodes’ electric potential and, consequently, there are only two different cell inhomogeneities.
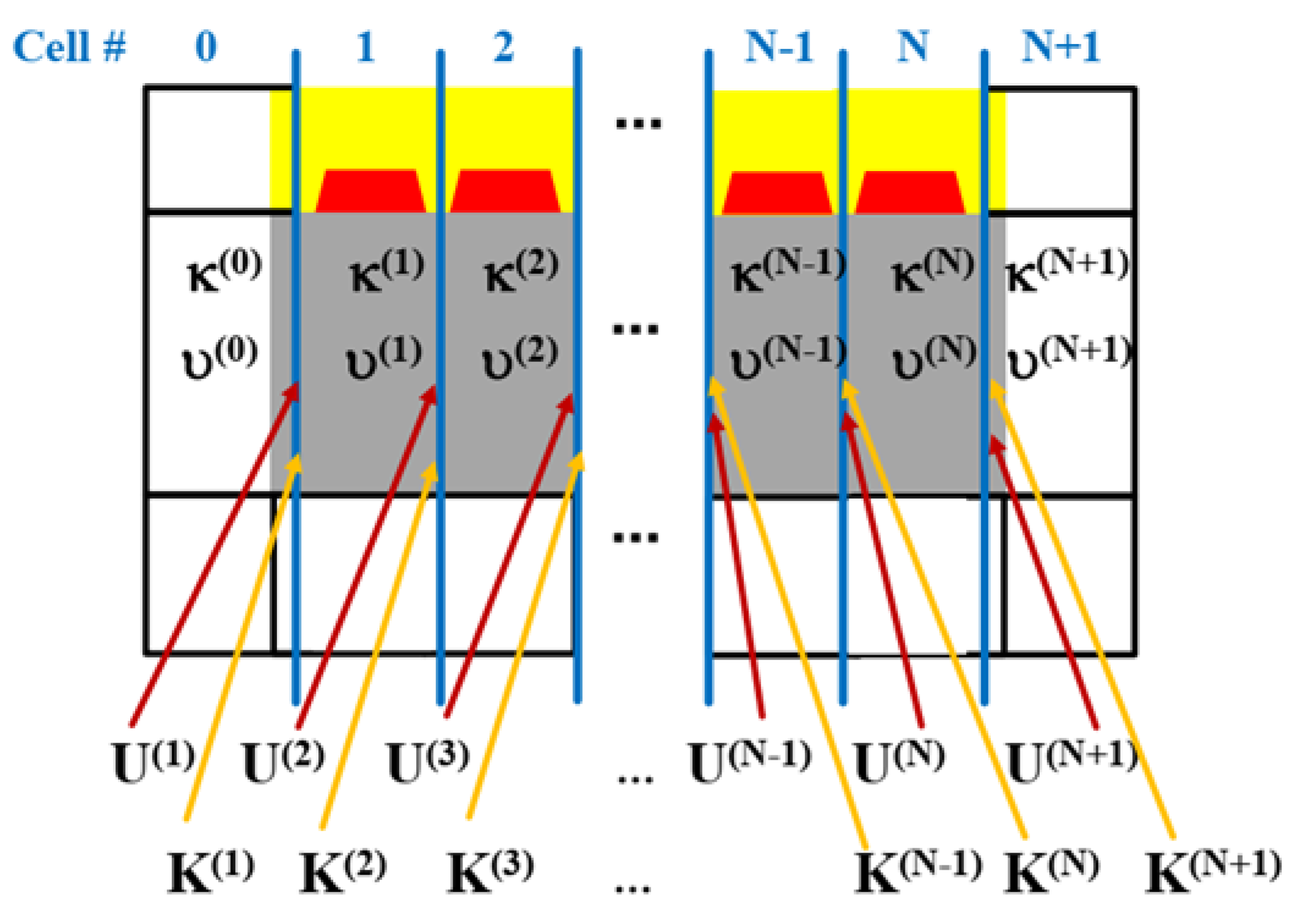
Here, we present a simple scheme which makes use of recursion relations and which is described in the following. It is applied to the system shown in
Figure 10, which is divided in
N + 2 cells,
N of them being identical. The mesh is chosen such that no boundary between neighboring cells divides a finite element into two parts. In addition, we impose the following requirements on the arrangement of the mesh. The finite elements on the left side of a boundary between two neighboring cells (blue vertical line in
Figure 10), having common nodes with this boundary, form a vertical layer. We require that these vertical layers are identical in the cells with numbers 0 to
N. Likewise, the vertical layers of finite elements on the right of a boundary having common nodes with this boundary are identical in the cells with numbers 1 to
N + 1. These additional requirements to the mesh are not essential, but simplify the calculations. The sub-meshes in the cells 1 to
N are identical.
7.1. Derivation of the Recursion Relation
The systems of linear Equations (9), (12), (13) and (15) are of the general form
We now introduce a cell index n and group the degrees of freedom on nodes in the interior of the n-th cell in a column vector . The degrees of freedom on nodes , which are situated on the boundary between the n-th and (n−1)-th cell, are grouped in a column vector . In the same way, with the quantities on the right-hand side of (66) with node number referring to the interior of the n-th cell, a column vector is formed. The quantities with node number referring to the boundary between the n-th and (n−1)-th cell form the column vector .
The interior degrees of freedom may be eliminated by using the following relation:
for
n = 1,…,
N. For
n = 0, the second term on the right-hand side and for
n =
N + 1 the third term on the right-hand side of (67) is absent.
are submatrices of the coefficient matrix on the left-hand side of (66) with the left node index
of its matrix elements
referring to all nodes in the interior of the
n-th cell. The matrix elements of
connect two nodes in the interior of cell
n (these two nodes may be identical). The right node indices of the matrix elements of
(
) refer to nodes on the left (right) boundary of cell
n.
The system of Equation (67) is solved for
and the result is inserted in
for
n = 1,…,
N + 1, where
are submatrices of the coefficient matrix in (66). The right node indices of
and
refer to nodes in the interior of cell
n. The left node indices of the matrix elements of
(
) refer to nodes on the left (right) boundary of cell
n, whereas the matrix elements of
connect two (possibly identical) nodes on the left boundary of cell
n.
We note that with the conditions we have imposed on the mesh, the matrices are independent of the cell number n for the cells 1 to N. In addition, . Therefore, we shall drop the cell number in the notation of these matrices and keep this number only in .
Having eliminated
,
n = 0,…,
N + 1, the following recursion relation results for the vectors
,
for
n = 2,…,
N. Furthermore
The matrices
are related to the quantities introduced before via
The column vectors
, are defined as:
and
From (69)–(71), the degrees of freedom on the cell boundaries, , are determined in the following way.
First, we compute matrices
, and vectors
, recursively via
starting the recursions with
and defining
With the help of these matrices and vectors, which have been stored, the vectors
are subsequently computed by making use of the following downwards recursion:
for
, and starting with
7.2. Results for IMD2 Displacements
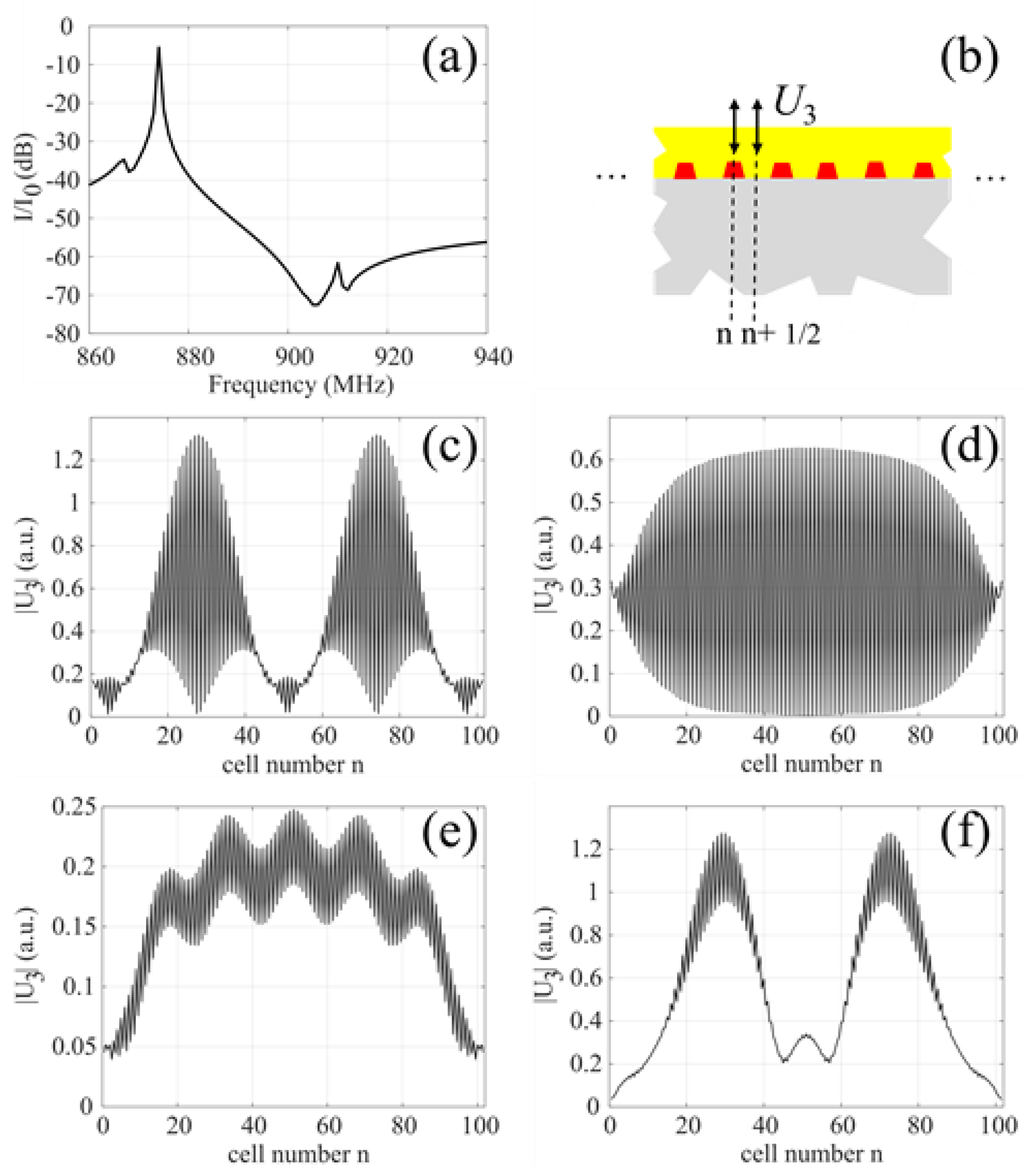
The recursion scheme outlined in the previous subsection has been implemented for the computation of displacements and electrical currents, generated by second-order nonlinearity, in TC-SAW systems consisting of finite numbers of electrodes. In
Figure 11, results are shown for the displacements at the surface of the SiO
2 film at positions above the centers of the electrodes and halfway between the surface points above the centers of neighboring electrodes (
Figure 11b). The pitch, metallization ratio, electrode height and film thickness were the same as those in the infinite periodic system that
Figure 2,
Figure 3 and
Figure 4 refer to. The linear admittance of this system is shown in
Figure 11a. The displacement patterns for two input frequencies as linear response to a periodic electric potential of
1 V (peak value) are shown in
Figure 11c,d. The input frequency
f1 (=860 MHz) is about 14 MHz below, and
f2 (=890 MHz) about 16 MHz above the resonance frequency.
Figure 11e shows the displacement pattern for the second harmonic (H2) of the input tone
f2. It varies more strongly along the length of the device than the displacement associated with its fundamental (
Figure 11d). The displacement pattern of the second order intermodulation (IMD2) at frequency
f1 +
f2, is shown in
Figure 11f. Similar to the pattern associated with the input tone
f1 (
Figure 11c), the displacements in the center of the device are small as compared to those near the 30th and 70th cells.
8. Conclusions
In summary, a perturbation-theoretical approach, based on nonlinear electro-elasticity theory and the finite element method, has been presented, which allows for calculations of quantities in SAW devices generated by second-order and third-order nonlinearity. These include displacements and electric fields as well as electrical currents associated with intermodulations of second and third order, second and third harmonic generation and the dependence of the resonance curve and phase response of a SAW resonator on input voltage. The FEM approach works with two-dimensional elements, but fully accounts for all three Cartesian components of the mechanical and electric displacement field. Infinite periodic as well as finite systems with spatial periodicities can be treated. The application of perturbation theory is justified by the smallness of typical strains occurring in SAW devices. It leads to a hierarchy of linear boundary value problems. By this approach, complex systems become accessible to numerical simulations of nonlinear effects, which would be hard to deal with by numerical schemes solving directly nonlinear partial differential equations.
A major goal of our approach was to enable computations of third-order intermodulations on a laptop computer. This opens the possibility for the designer of SAW devices to minimize undesired nonlinear effects with the help of simulations, which can be carried out with reasonable numerical effort and which are directly based on material properties. For this purpose, algorithms were developed that increase the efficiency of certain parts of the computations. These include an alternative way of calculating IMD2 and IMD3 currents in the electrodes via overlap integrals, which avoid the computation of the IMD2/IMD3 field. In addition, an impedance boundary condition is presented to account for reflections of bulk waves from the bottom of a thick substrate and, in particular, a recursive algorithm for finite periodic systems which is related to the cascading method introduced by Koskela and Plessky for FEM computations of linear quantities in SAW devices [
50,
51].
The recursive scheme, introduced here in the context of electro-elastic nonlinearity, may also be applied to simulations of thermal effects in SAW devices to reduce computational effort; for example, the effect of intrinsic heating on the resonance frequency, giving rise to additional nonlinearity (e.g., [
53] for the case of BAW resonators). The variation of the temperature field between different unit cells of the interdigital transducers or reflectors precludes cascading, but still allows for application of the recursive algorithm.
Prerequisite of quantitative simulations of nonlinear effects is the availability of reliable nonlinear material constants up to fourth order for all materials that fill those parts of the SAW device where comparatively large strains or electric fields occur. In the case of thin films, the required material constants may differ from those of the corresponding bulk material and may depend on details of the fabrication process.