Limitations of Curl and Directional Filters in Elastography
Abstract
1. Introduction
2. Theory
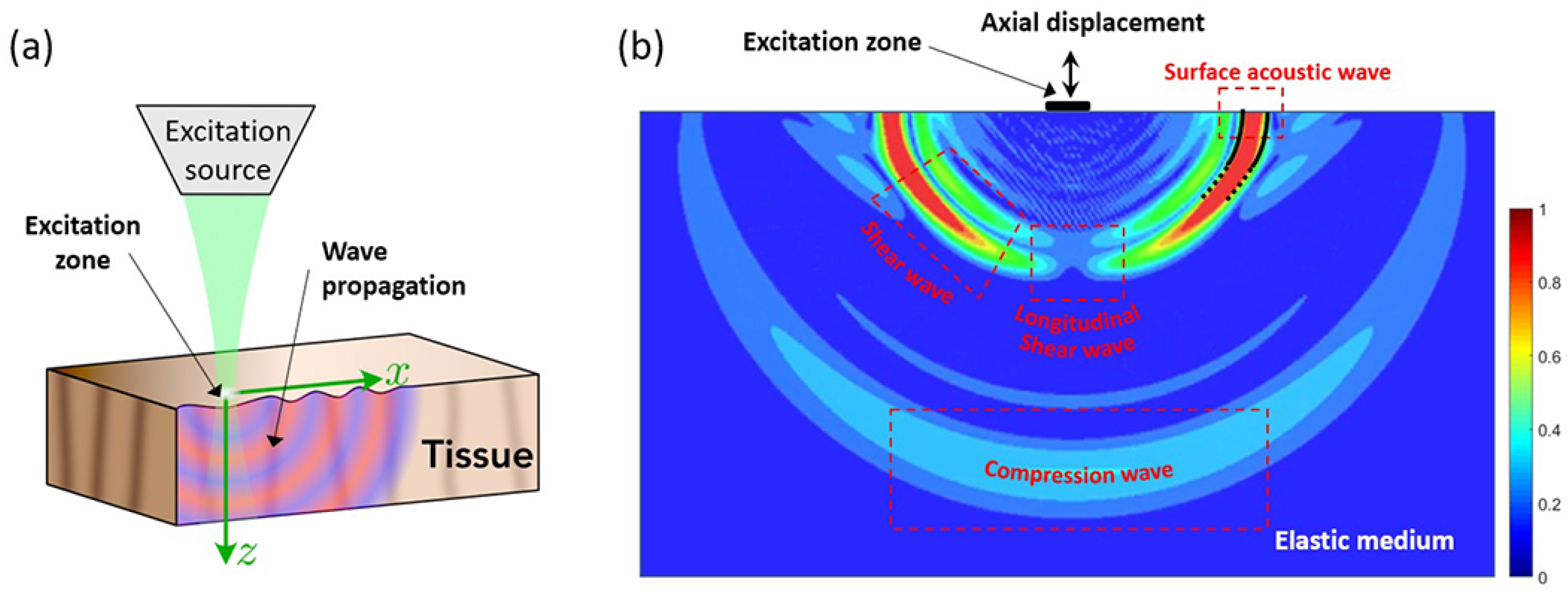
3. Limitations within a Semi-Infinite Medium
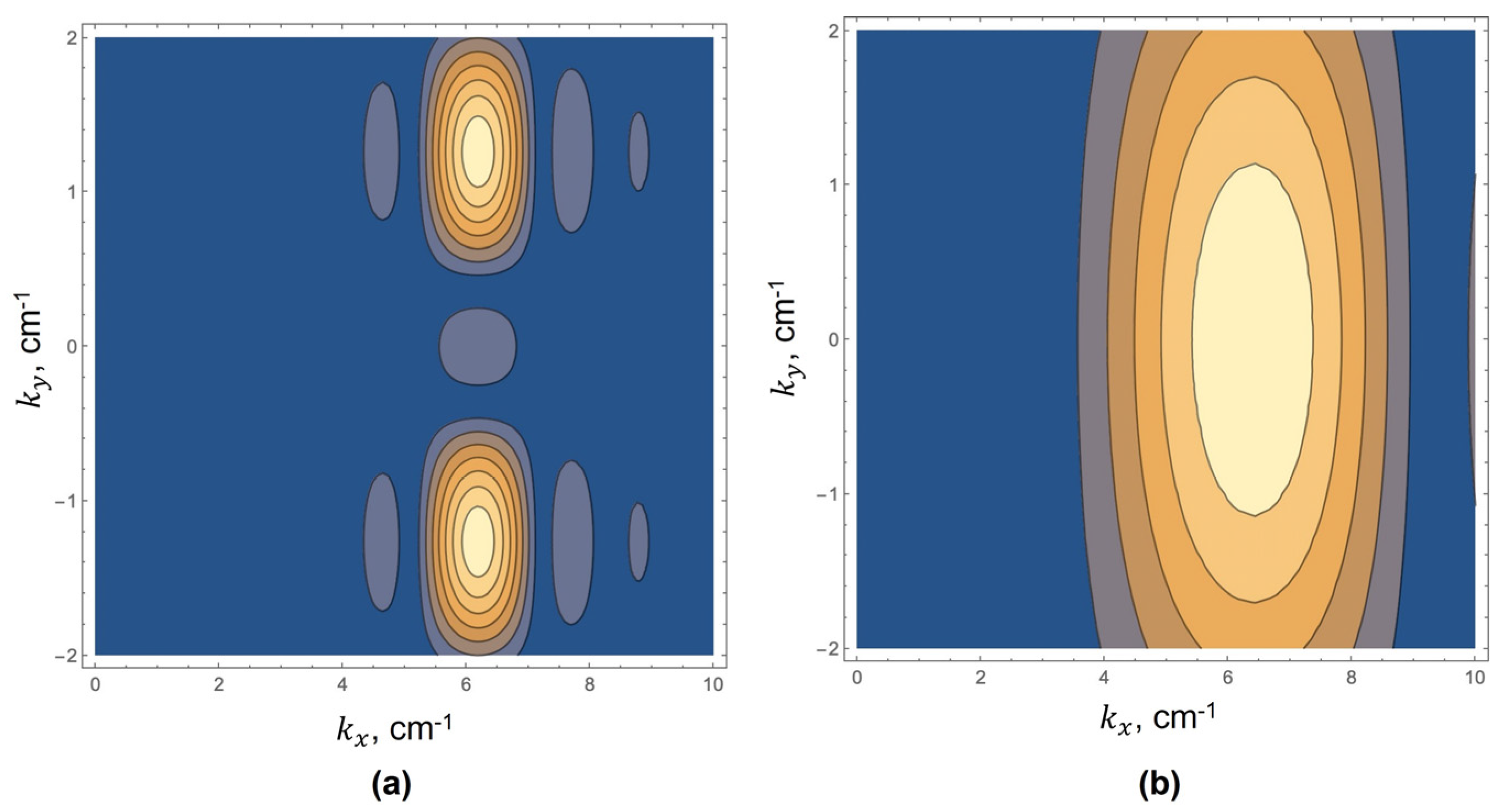
3.1. The 2D Imaging Plane in Arbitrary Location
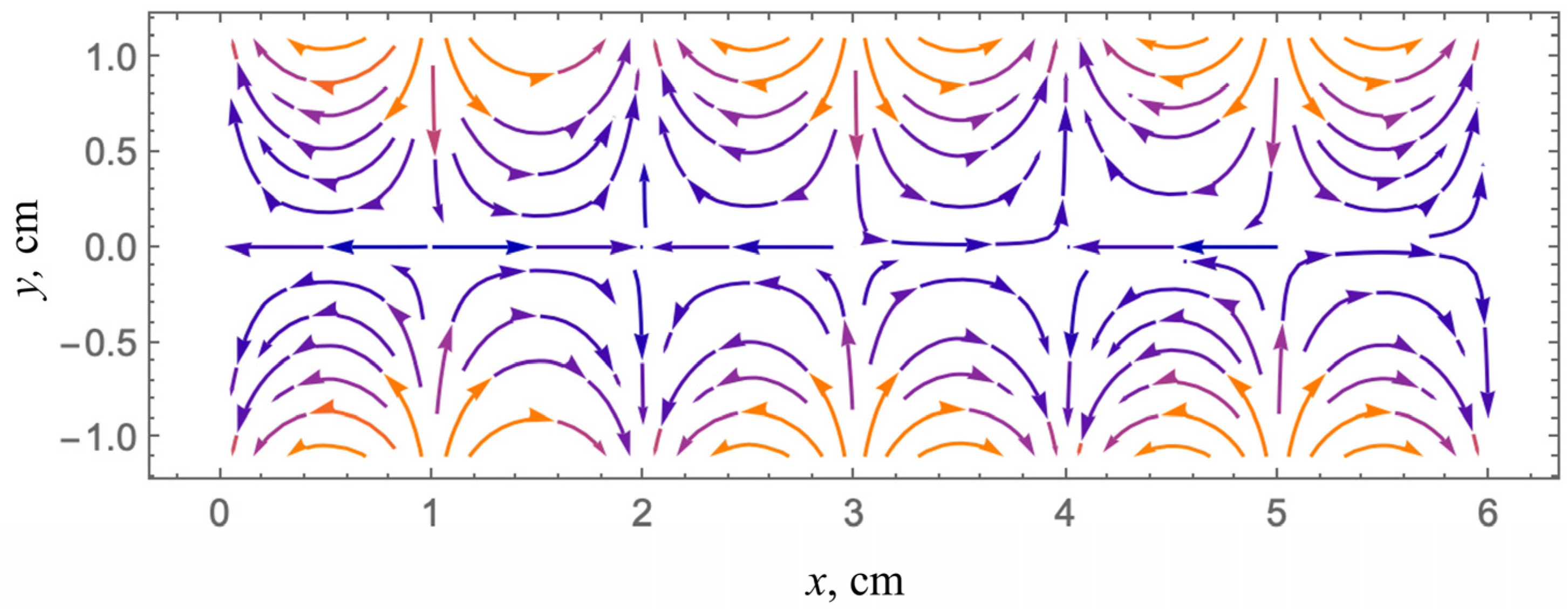
3.2. The 2D Imaging Plane with Several Shear Wave Sources
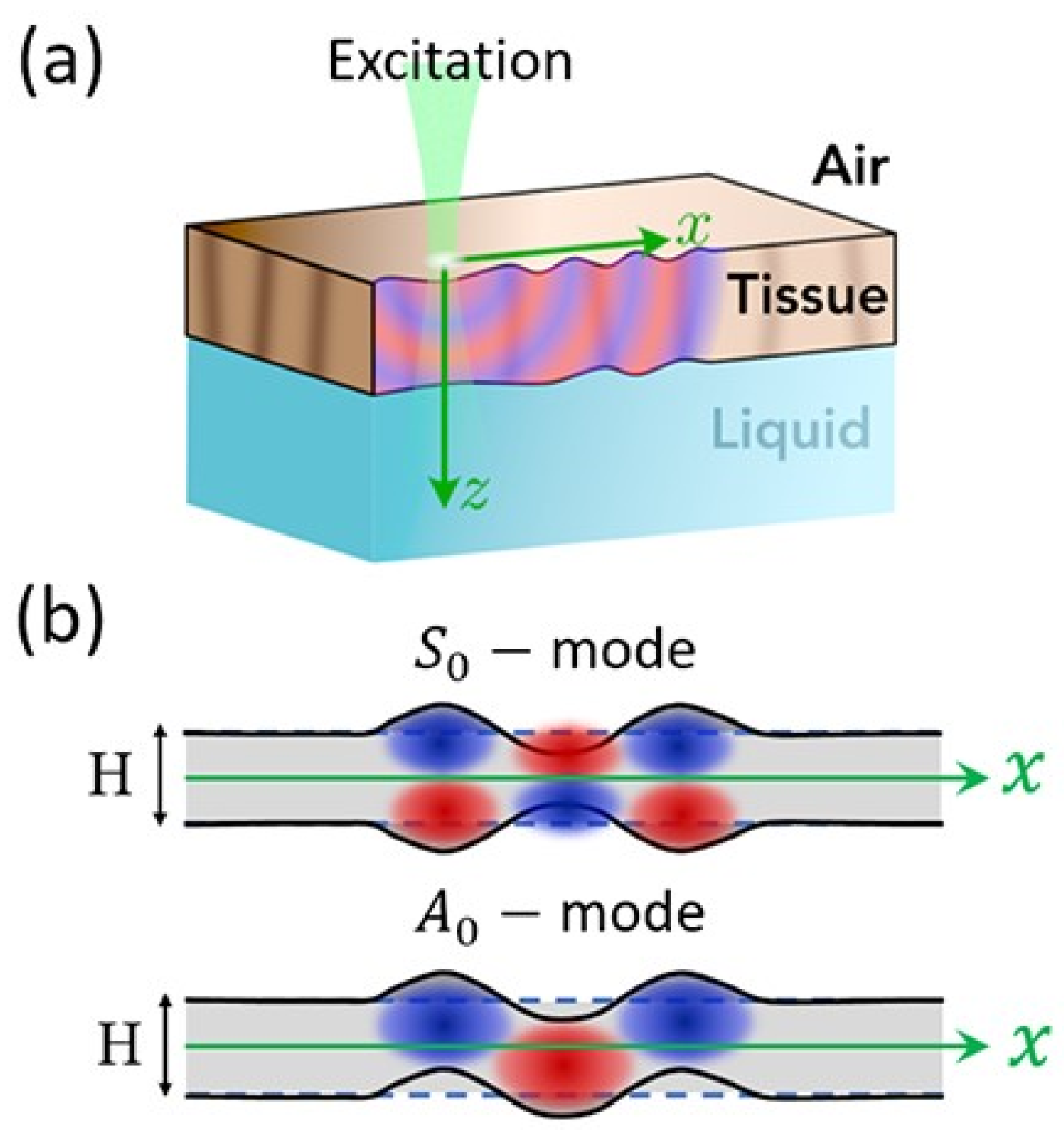
4. Limitations within Guided Wave Structures
5. Discussion
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Graff, K.F. Wave Motion in Elastic Solids; Clarendon Press: Oxford, UK, 1975; 649p. [Google Scholar]
- Baghani, A.; Salcudean, S.; Rohling, R. Theoretical limitations of the elastic wave equation inversion for tissue elastography. J. Acoust. Soc. Am. 2009, 126, 1541–1551. [Google Scholar] [CrossRef] [PubMed]
- Sinkus, R.; Tanter, M.; Xydeas, T.; Catheline, S.; Bercoff, J.; Fink, M. Viscoelastic shear properties of in vivo breast lesions measured by MR elastography. Magn. Reson. Imaging 2005, 23, 159–165. [Google Scholar] [CrossRef] [PubMed]
- Kwon, O.I.; Park, C.; Nam, H.S.; Woo, E.J.; Seo, J.K.; Glaser, K.J.; Manduca, A.; Ehman, R.L. Shear Modulus Decomposition Algorithm in Magnetic Resonance Elastography. IEEE Trans. Med. Imaging 2009, 28, 1526–1533. [Google Scholar] [CrossRef]
- Honarvar, M.; Sahebjavaher, R.; Sinkus, R.; Rohling, R.; Salcudean, S.E. Curl-Based Finite Element Reconstruction of the Shear Modulus Without Assuming Local Homogeneity: Time Harmonic Case. IEEE Trans. Med. Imaging 2013, 32, 2189–2199. [Google Scholar] [CrossRef] [PubMed]
- Hirsch, S.; Guo, J.; Reiter, R.; Schott, E.; Büning, C.; Somasundaram, R.; Braun, J.; Sack, I.; Kroencke, T.J. Towards compression-sensitive magnetic resonance elastography of the liver: Sensitivity of harmonic volumetric strain to portal hypertension. J. Magn. Reson. Imaging 2013, 39, 298–306. [Google Scholar] [CrossRef] [PubMed]
- Manduca, A.; Bayly, P.V.; Ehman, R.L.; Kolipaka, A.; Royston, T.J.; Sack, I.; Sinkus, R.; Van Beers, B.E. MR elastography: Principles, guidelines, and terminology. Magn. Reson. Med. 2021, 85, 2377–2390. [Google Scholar] [CrossRef]
- Baghani, A.; Zahiri Azar, R.; Salcudean, S.; Rohling, R. A curl-based approach to ultrasound elastography. In Proceedings of the ASME 2010 International Mechanical Engineering Congress and Exposition, Vancouver, BC, Canada, 12–18 November 2010; pp. 865–867. [Google Scholar] [CrossRef]
- Hashemi, H.S.; Salcudean, S.E.; Rohling, R.N. Ultrafast ultrasound imaging for 3D shear wave absolute vibro-elastography. arXiv 2022, arXiv:2203.13949. [Google Scholar]
- Manduca, A.; Lake, D.; Kruse, S.; Ehman, R. Spatio-temporal directional filtering for improved inversion of MR elastography images. Med. Image Anal. 2003, 7, 465–473. [Google Scholar] [CrossRef]
- Kruse, S.A.; Rose, G.H.; Glaser, K.J.; Manduca, A.; Felmlee, J.P.; Jack, C.R.; Ehman, R.L. Magnetic resonance elastography of the brain. Neuroimage 2008, 39, 231–237. [Google Scholar] [CrossRef]
- Deffieux, T.; Gennisson, J.-L.; Bercoff, J.; Tanter, M. On the effects of reflected waves in transient shear wave elastography. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 2011, 58, 2032–2035. [Google Scholar] [CrossRef]
- Song, P.; Zhao, H.; Manduca, A.; Urban, M.W.; Greenleaf, J.F.; Chen, S. Comb-Push Ultrasound Shear Elastography (CUSE): A Novel Method for Two-Dimensional Shear Elasticity Imaging of Soft Tissues. IEEE Trans. Med. Imaging 2012, 31, 1821–1832. [Google Scholar] [CrossRef] [PubMed]
- Zhao, H.; Song, P.; Meixner, D.D.; Kinnick, R.R.; Callstrom, M.R.; Sanchez, W.; Urban, M.W.; Manduca, A.; Greenleaf, J.F.; Chen, S. External Vibration Multi-Directional Ultrasound Shearwave Elastography (EVMUSE): Application in Liver Fibrosis Staging. IEEE Trans. Med. Imaging 2014, 33, 2140–2148. [Google Scholar] [CrossRef] [PubMed]
- Song, S.; Le, N.M.; Huang, Z.; Shen, T.; Wang, R.K. Quantitative shear-wave optical coherence elastography with a programmable phased array ultrasound as the wave source. Opt. Lett. 2015, 40, 5007–5010. [Google Scholar] [CrossRef] [PubMed]
- Tzschätzsch, H.; Ipek-Ugay, S.; Trong, M.N.; Guo, J.; Eggers, J.; Gentz, E.; Fischer, T.; Schultz, M.; Braun, J.; Sack, I. Multifrequency Time-Harmonic Elastography for the Measurement of Liver Viscoelasticity in Large Tissue Windows. Ultrasound Med. Biol. 2015, 41, 724–733. [Google Scholar] [CrossRef] [PubMed]
- Khodayi-Mehr, R.; Urban, M.W.; Zavlanos, M.M.; Aquino, W. Plane wave elastography: A frequency-domain ultrasound shear wave elastography approach. Phys. Med. Biol. 2021, 66, 125017. [Google Scholar] [CrossRef]
- Bochev, P.B.; Garasi, C.J.; Hu, J.J.; Robinson, A.C.; Tuminaro, R.S. An Improved Algebraic Multigrid Method for Solving Maxwell’s Equations. SIAM J. Sci. Comput. 2003, 25, 623–642. [Google Scholar] [CrossRef]
- Hochbruck, M.; Pažur, T. Implicit Runge--Kutta Methods and Discontinuous Galerkin Discretizations for Linear Maxwell’s Equations. SIAM J. Numer. Anal. 2015, 53, 485–507. [Google Scholar] [CrossRef]
- Daugman, J.G. Uncertainty relation for resolution in space, spatial frequency, and orientation optimized by two-dimensional visual cortical filters. J. Opt. Soc. Am. A 1985, 2, 1160–1169. [Google Scholar] [CrossRef]
- Bracewell, R.N. Two-Dimensional Imaging; Prentice Hall: Englewood Cliffs, NJ, USA, 1995; Volume xiv, 689p. [Google Scholar]
- Miller, G.F.; Pursey, H. The field and radiation impedance of mechanical radiators on the free surface of a semi-infinite isotropic solid. Proc. R. Soc. London. Ser. A Math. Phys. Sci. 1954, 223, 521–541. [Google Scholar] [CrossRef]
- Zvietcovich, F.; Larin, K.V. Wave-based optical coherence elastography: The 10-year perspective. Prog. Biomed. Eng. 2022, 4, 012007. [Google Scholar] [CrossRef]
- Tzschätzsch, H.; Ipek-Ugay, S.; Guo, J.; Streitberger, K.-J.; Gentz, E.; Fischer, T.; Klaua, R.; Schultz, M.; Braun, J.; Sack, I. In vivo time-harmonic multifrequency elastography of the human liver. Phys. Med. Biol. 2014, 59, 1641–1654. [Google Scholar] [CrossRef] [PubMed]
- Sarvazyan, A.P.; Rudenko, O.V.; Swanson, S.D.; Fowlkes, J.; Emelianov, S.Y. Shear wave elasticity imaging: A new ultrasonic technology of medical diagnostics. Ultrasound Med. Biol. 1998, 24, 1419–1435. [Google Scholar] [CrossRef]
- Sandrin, L.; Fourquet, B.; Hasquenoph, J.-M.; Yon, S.; Fournier, C.; Mal, F.; Christidis, C.; Ziol, M.; Poulet, B.; Kazemi, F.; et al. Transient elastography: A new noninvasive method for assessment of hepatic fibrosis. Ultrasound Med. Biol. 2003, 29, 1705–1713. [Google Scholar] [CrossRef] [PubMed]
- Wu, Z.; Taylor, L.S.; Rubens, D.J.; Parker, K.J. Shear wave focusing for three-dimensional sonoelastography. J. Acoust. Soc. Am. 2002, 111, 439–446. [Google Scholar] [CrossRef] [PubMed]
- Partin, A.; Hah, Z.; Barry, C.T.; Rubens, D.J.; Parker, K.J. Elasticity Estimates from Images of Crawling Waves Generated by Miniature Surface Sources. Ultrasound Med. Biol. 2014, 40, 685–694. [Google Scholar] [CrossRef]
- Ueber die Fortpflanzungsgeschwindigkeiten kleiner Schwingungen in einem unbegrenzten isotropen Kreiscylinder. Walter Gruyter 1876, 1876, 324–336. [CrossRef]
- Rayleigh, L. On the Free Vibrations of an Infinite Plate of Homogeneous Isotropic Elastic Matter. Proc. Lond. Math. Soc. 1888, s1-20, 225–237. [Google Scholar] [CrossRef]
- Love, A.E.H. A Treatise on the Mathematical Theory of Elasticity, 2nd ed.; University Press: Cambridge, UK, 1906; Volume xviii, 551p. [Google Scholar]
- Lamb, H. On the Flexure of an Elastic Plate. Proc. Lond. Math. Soc. 1889, s1-21, 70–91. [Google Scholar] [CrossRef]
- Lamb, H. On waves in an elastic plate. Proc. R. Soc. London. Ser. A Contain. Pap. Math. Phys. Character 1917, 93, 114–128. [Google Scholar] [CrossRef]
- Mercado, K.P.; Langdon, J.; Helguera, M.; McAleavey, S.A.; Hocking, D.C.; Dalecki, D. Scholte wave generation during single tracking location shear wave elasticity imaging of engineered tissues. J. Acoust. Soc. Am. 2015, 138, EL138–EL144. [Google Scholar] [CrossRef]
- Kirby, M.A.; Pelivanov, I.; Song, S.; Ambrozinski, Ł.; Yoon, S.J.; Gao, L.; Li, D.; Shen, T.T.; Wang, R.; O’donnell, M. Optical coherence elastography in ophthalmology. J. Biomed. Opt. 2017, 22, 121720. [Google Scholar] [CrossRef] [PubMed]
- Couade, M.; Pernot, M.; Prada, C.; Messas, E.; Emmerich, J.; Bruneval, P.; Criton, A.; Fink, M.; Tanter, M. Quantitative Assessment of Arterial Wall Biomechanical Properties Using Shear Wave Imaging. Ultrasound Med. Biol. 2010, 36, 1662–1676. [Google Scholar] [CrossRef]
- di Novi, R.A. Theory of Lamb waves. In Proceedings of the Symposium on Physics and Nondestructive Testing, Argonne National Laboratory, Metallurgy Division, Lemont, IL, USA, 4–5 October 1960; p. 72. [Google Scholar]
- Pelivanov, I.; Gao, L.; Pitre, J.; Kirby, M.A.; Song, S.; Li, D.; Shen, T.T.; Wang, R.K.; O’Donnell, M. Does group velocity always reflect elastic modulus in shear wave elastography? J. Biomed. Opt. 2019, 24, 076003. [Google Scholar] [CrossRef]
- Pagneux, V.; Maurel, A. Determination of Lamb mode eigenvalues. J. Acoust. Soc. Am. 2001, 110, 1307–1314. [Google Scholar] [CrossRef]
- Manmohan, S.; Aglyamov, S.R.; Li, J.; Singh, M.; Wang, S.; Vantipalli, S.; Wu, C.; Liu, C.H.; Twa, M.; Larin, K.V. Quantitative assessment of corneal viscoelasticity using optical coherence elastography and a modified Rayleigh–Lamb equation. J. Biomed. Opt. 2015, 20, 020501. [Google Scholar] [CrossRef]
- Sun, M.G.; Son, T.; Crutison, J.; Guaiquil, V.; Lin, S.; Nammari, L.; Klatt, D.; Yao, X.; Rosenblatt, M.I.; Royston, T.J. Optical coherence elastography for assessing the influence of intraocular pressure on elastic wave dispersion in the cornea. J. Mech. Behav. Biomed. Mater. 2022, 128, 105100. [Google Scholar] [CrossRef]
- Manduca, A.; Oliphant, T.; Dresner, M.; Mahowald, J.; Kruse, S.; Amromin, E.; Felmlee, J.; Greenleaf, J.; Ehman, R. Magnetic resonance elastography: Non-invasive mapping of tissue elasticity. Med. Image Anal. 2001, 5, 237–254. [Google Scholar] [CrossRef]
- Doyley, M.M. Model-based elastography: A survey of approaches to the inverse elasticity problem. Phys. Med. Biol. 2012, 57, R35–R73. [Google Scholar] [CrossRef] [PubMed]
- de Felice, G.; Marra, F.; Rufolo, G. Regularized solutions for the discrete forms of the div–curl problem in CFD. Comput. Vis. Sci. 2002, 4, 175–182. [Google Scholar] [CrossRef]
- Dong, H.; Egbert, G.D. Divergence-free solutions to electromagnetic forward and adjoint problems: A regularization approach. Geophys. J. Int. 2018, 216, 906–918. [Google Scholar] [CrossRef]
- Aleman-Castaneda, L.A.; Zvietcovich, F.; Parker, K.J. Reverberant Elastography for the Elastic Characterization of Anisotropic Tissues. IEEE J. Sel. Top. Quantum Electron. 2021, 27, 1–12. [Google Scholar] [CrossRef]
- Ge, G.R.; Song, W.; Nedergaard, M.; Rolland, J.P.; Parker, K.J. Theory of sleep/wake cycles affecting brain elastography. Phys. Med. Biol. 2022, 67, 225013. [Google Scholar] [CrossRef] [PubMed]
- Kabir, I.E.; Caban-Rivera, D.A.; Ormachea, J.; Parker, K.J.; Johnson, C.L.; Doyley, M.M. Reverberant magnetic resonance elastographic imaging using a single mechanical driver. Phys. Med. Biol. 2023, 68, 055015. [Google Scholar] [CrossRef] [PubMed]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Parker, K.J. Limitations of Curl and Directional Filters in Elastography. Acoustics 2023, 5, 575-585. https://doi.org/10.3390/acoustics5020035
Parker KJ. Limitations of Curl and Directional Filters in Elastography. Acoustics. 2023; 5(2):575-585. https://doi.org/10.3390/acoustics5020035
Chicago/Turabian StyleParker, Kevin J. 2023. "Limitations of Curl and Directional Filters in Elastography" Acoustics 5, no. 2: 575-585. https://doi.org/10.3390/acoustics5020035
APA StyleParker, K. J. (2023). Limitations of Curl and Directional Filters in Elastography. Acoustics, 5(2), 575-585. https://doi.org/10.3390/acoustics5020035





