Effects of Varying Levels of Background Noise on Room Acoustic Parameters, Measured with ESS and MLS Methods
Abstract
1. Introduction
2. Methods
2.1. Acoustic Parameters
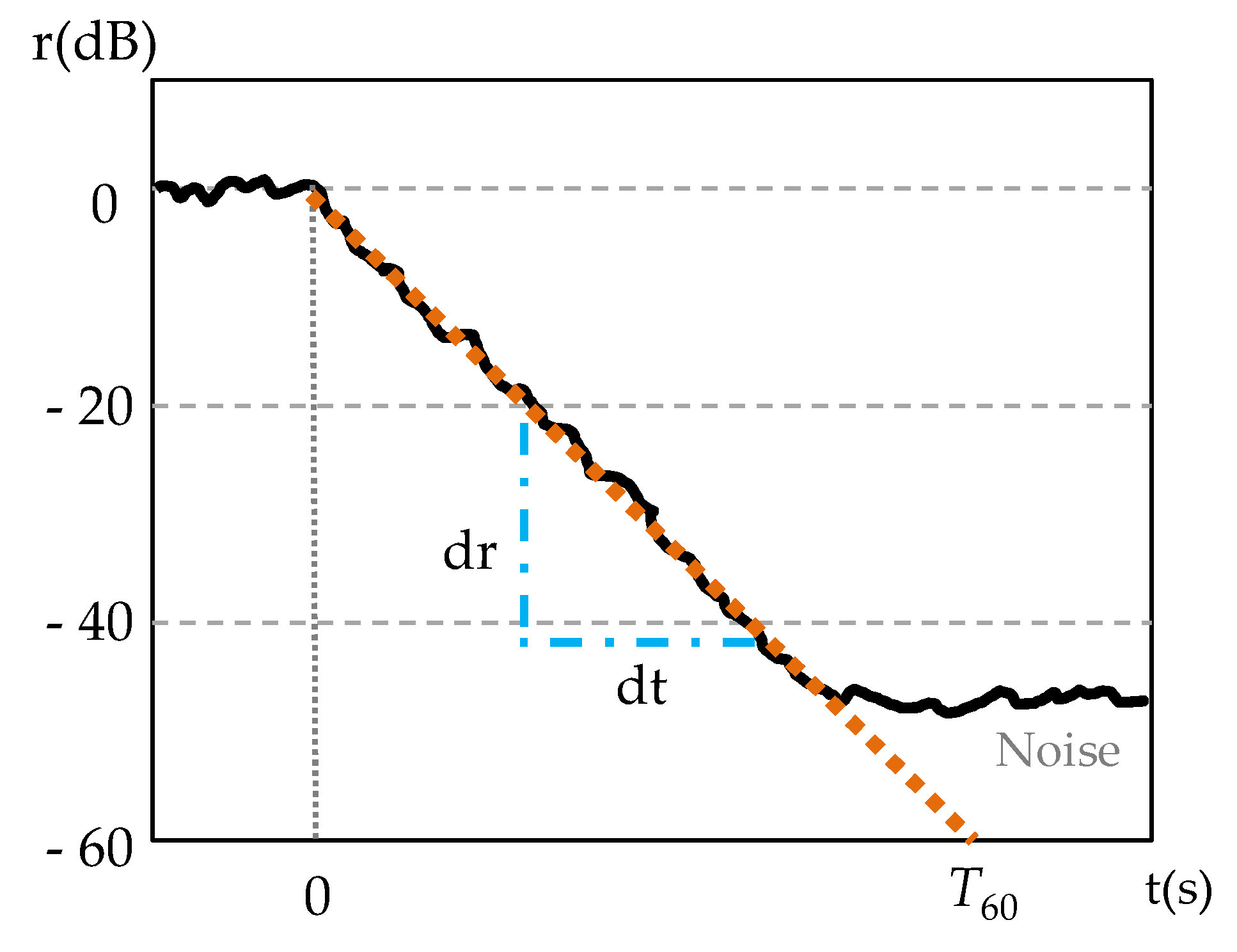
2.1.1. Reverberation Time (T)
2.1.2. Early Decay Time (EDT)
2.1.3. Clarity (C80)
2.1.4. Definition (D50)
2.2. Measurements
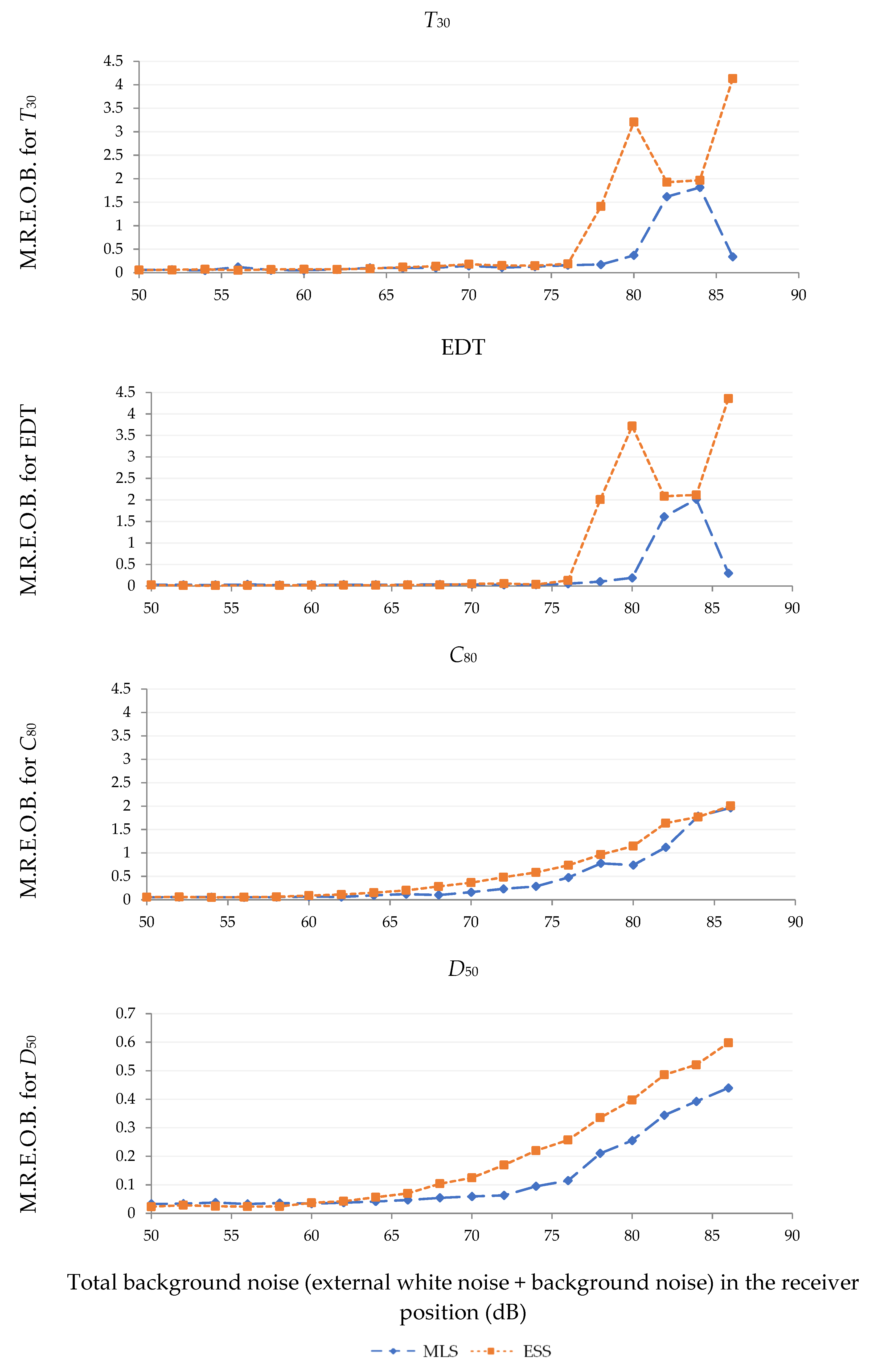
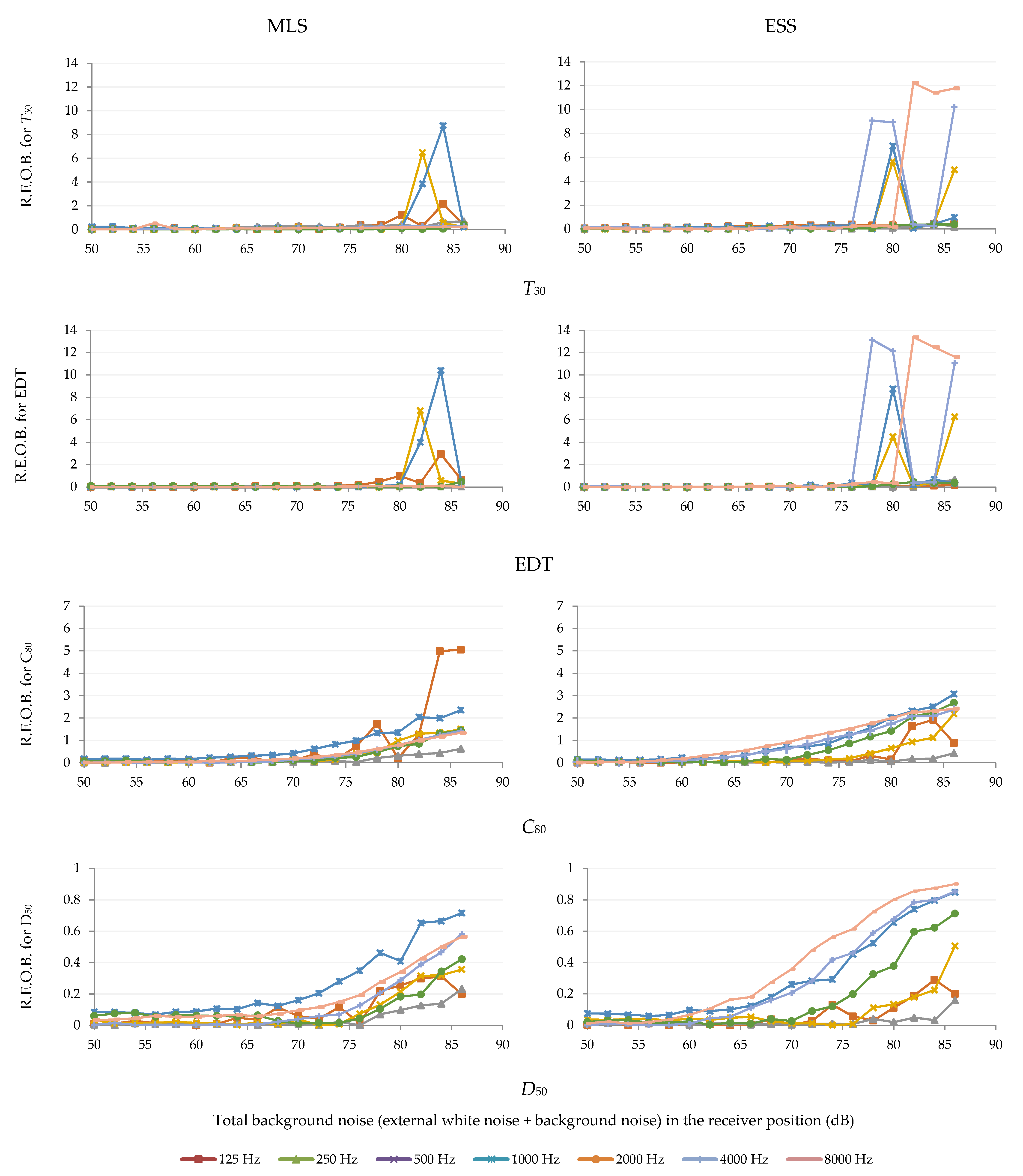
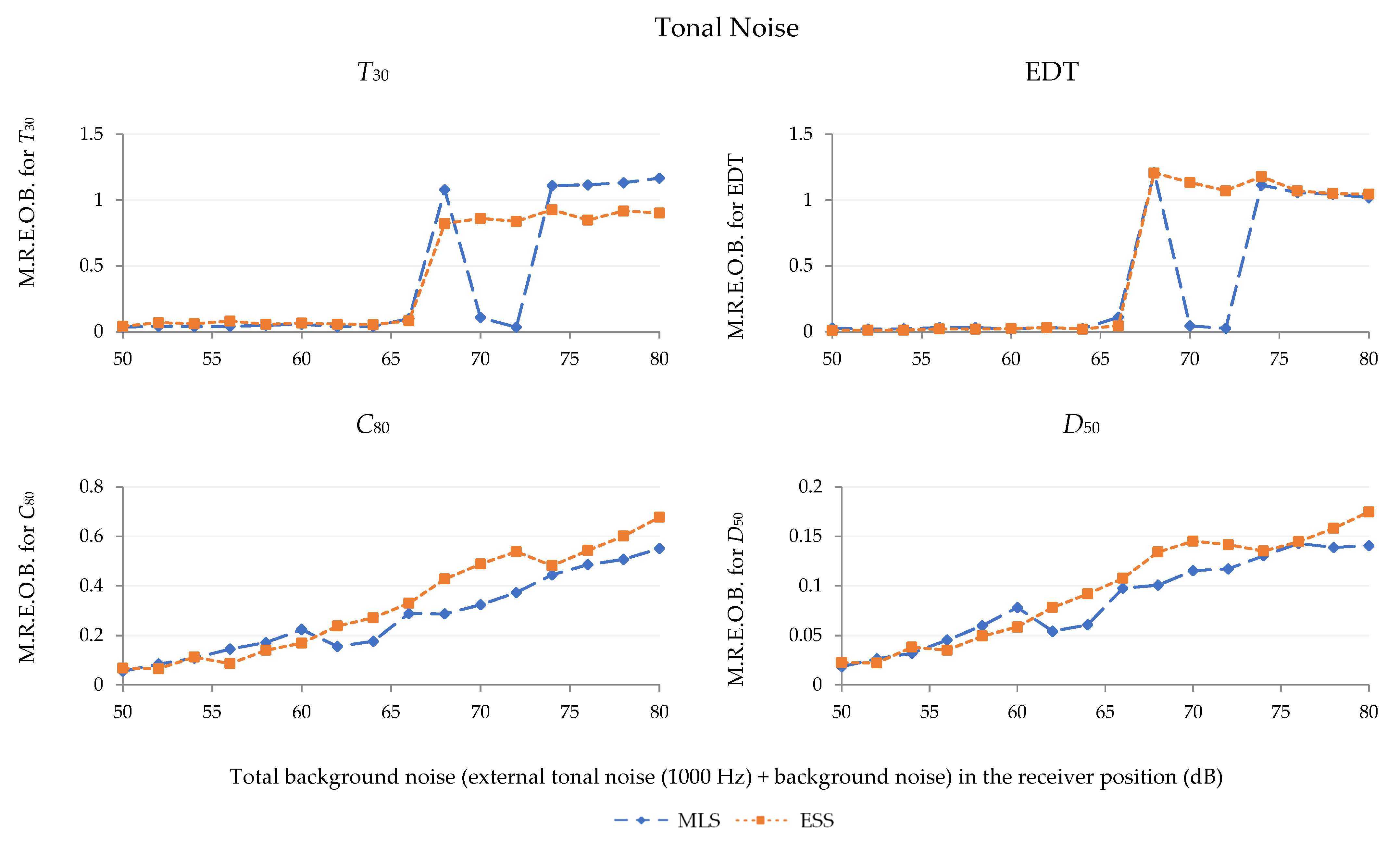
3. Results
4. Discussion
Limitations
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Vorländer, M. Computer simulations in room acoustics: Concepts and uncertainties. J. Acoust. Soc. Am. 2013, 133, 1203–1213. [Google Scholar] [CrossRef] [PubMed]
- Papadakis, N.M.; Stavroulakis, G.E. Time domain finite element method for the calculation of impulse response of enclosed spaces. Room acoustics application. AIP Conf. Proc. 2015, 1703, 100002. [Google Scholar] [CrossRef]
- Hornikx, M. Ten questions concerning computational urban acoustics. Build. Environ. 2016, 106, 409–421. [Google Scholar] [CrossRef]
- Papadakis, N.M.; Stavroulakis, G.E. Finite Element Method for the Estimation of Insertion Loss of Noise Barriers: Comparison with Various Formulae (2D). Urban Sci. 2020, 4, 77. [Google Scholar] [CrossRef]
- ISO 3382-1: 2009; Measurement of Room Acoustic Parameters–Part 1: Performance Spaces. ISO: Geneva, Switzerland, 2009.
- ISO 3382-2: 2008; Measurement of Room Acoustic Parameters–Part 2: Reverberation Time in Ordinary Rooms. ISO: Geneva, Switzerland, 2009.
- ISO 3382-3: 2012; Measurement of Room Acoustic Parameters–Part 3: Open Plan Offices Rooms. ISO: Geneva, Switzerland, 2009.
- ISO 354: 2003; Acoustics–Measurement of Sound Absorption in a Reverberation Room. ISO: Geneva, Switzerland, 2003.
- Yu, G.-Z.; Xie, B.-S.; Rao, D. Directivity of spherical polyhedron sound source used in near-field HRTF measurements. Chin. Phys. Lett. 2010, 27, 124302. [Google Scholar] [CrossRef]
- Kleiner, M. Acoustics and Audio Technology; J. Ross Publishing, Inc.: Fort Lauderdale, FL, USA, 2011. [Google Scholar]
- Papadakis, N.M.; Stavroulakis, G.E. Review of Acoustic Sources Alternatives to a Dodecahedron Speaker. Appl. Sci. 2019, 9, 3705. [Google Scholar] [CrossRef]
- Schroeder, M.R. Integrated-impulse method measuring sound decay without using impulses. J. Acoust. Soc. Am. 1979, 66, 497–500. [Google Scholar] [CrossRef]
- Stan, G.-B.; Embrechts, J.-J.; Archambeau, D. Comparison of different impulse response measurement techniques. J. Audio Eng. Soc. 2002, 50, 249–262. [Google Scholar]
- Dunn, C.; Hawksford, M.J. Distortion immunity of MLS-derived impulse response measurements. J. Audio Eng. Soc. 1993, 41, 314–335. [Google Scholar]
- Bleakley, C.; Scaife, R. New formulas for predicting the accuracy of acoustical measurements made in noisy environments using the averaged m-sequence correlation technique. J. Acoust. Soc. Am. 1995, 97, 1329–1332. [Google Scholar] [CrossRef]
- Rife, D.D. MLSSA Reference Manual; DRA Laboratories, 4587 Cherrybark Court: Sarasota, FL, USA, 1996. [Google Scholar]
- Vorländer, M.; Kob, M. Practical aspects of MLS measurements in building acoustics. Appl. Acoust. 1997, 52, 239–258. [Google Scholar] [CrossRef]
- Vanderkooy, J. Aspects of MLS measuring systems. J. Audio Eng. Soc. 1994, 42, 219–231. [Google Scholar]
- Ream, N. Nonlinear identification using inverse-repeat sequences. In Proceedings of the Institution of Electrical Engineers; IET Digital Library, 1970; pp. 213–218. [Google Scholar] [CrossRef]
- Farcas, A.C.; Topa, M.D. On the Choice of the Method for Obtaining the Room Impulse Response. Acta Tech. Napoc. 2013, 54, 34. [Google Scholar]
- Aoshima, N. Computer-generated pulse signal applied for sound measurement. J. Acoust. Soc. Am. 1981, 69, 1484–1488. [Google Scholar] [CrossRef]
- Farina, A. Simultaneous measurement of impulse response and distortion with a swept-sine technique. In Proceedings of the Audio Engineering Society Convention 108, Audio Engineering Society, the 108th Convention, Paris, France, 19–22 February 2000. [Google Scholar]
- Müller, S.; Massarani, P. Transfer-function measurement with sweeps. J. Audio Eng. Soc. 2001, 49, 443–471. [Google Scholar]
- ISO 18233-2006; Acoustics–Application of New Measurement Methods in Building and Room Acoustics. ISO: Geneva, Switzerland, 2006.
- Guidorzi, P.; Barbaresi, L.; D’Orazio, D.; Garai, M. Impulse responses measured with MLS or Swept-Sine signals applied to architectural acoustics: An in-depth analysis of the two methods and some case studies of measurements inside theaters. Energy Procedia 2015, 78, 1611–1616. [Google Scholar] [CrossRef]
- Torras-Rosell, A.; Jacobsen, F. Measuring long impulse responses with pseudorandom sequences and sweep signals. In Proceedings of the 39th International Congress Noise Control Eng. (INTER-NOISE 2010), Lisbon, Portugal, 13–16 June 2010. [Google Scholar]
- Mateljan, I.; Ugrinović, K. The comparison of room impulse response measuring systems. In Proceedings of the First Congress of Alps Adria Acoustics Association, Čudina, Mirko, Portorož, Slovenija, 1–2 September 2003. [Google Scholar]
- Holters, M.; Corbach, T.; Zölzer, U. Impulse response measurement techniques and their applicability in the real world. In Proceedings of the 12th International Conference on Digital Audio Effects (DAFx-09), Como, Italy, 1–4 September 2009; pp. 108–112. [Google Scholar]
- Jordan, V.L. Acoustical criteria for auditoriums and their relation to model techniques. J. Acoust. Soc. Am. 1970, 47, 408–412. [Google Scholar] [CrossRef]
- Rossing, T.D. Springer Handbook of Acoustics; Springer: New York, NY, USA, 2007. [Google Scholar]
- Thiele, R. Richtungsverteilung und zeitfolge der schallrückwürfe in räumen. Acta Acust. United Acust. 1953, 3, 291–302. [Google Scholar]
- Papadakis, N.M.; Stavroulakis, G.E. Low Cost Omnidirectional Sound Source Utilizing a Common Directional Loudspeaker for Impulse Response Measurements. Appl. Sci. 2018, 8, 1703. [Google Scholar] [CrossRef]
- Papadakis, N.M.; Stavroulakis, G.E. Handclap for Acoustic Measurements: Optimal Application and Limitations. Acoustics 2020, 2, 224–245. [Google Scholar] [CrossRef]
- de Vos, R.; Papadakis, N.M.; Stavroulakis, G.E. Improved Source Characteristics of a Handclap for Acoustic Measurements: Utilization of a Leather Glove. Acoustics 2020, 2, 803–811. [Google Scholar] [CrossRef]
- Martellotta, F. Optimizing stepwise rotation of dodecahedron sound source to improve the accuracy of room acoustic measures. J. Acoust. Soc. Am. 2013, 134, 2037–2048. [Google Scholar] [CrossRef] [PubMed]
- Guidorzi, P.; Garai, M. A Low-Cost System for Quick Measurements on Noise Barriers in Situ. IEEE Trans. Instrum. Meas. 2022, 71, 1–14. [Google Scholar] [CrossRef]
- Prawda, K.; Schlecht, S.J.; Välimäki, V. Robust selection of clean swept-sine measurements in non-stationary noise. J. Acoust. Soc. Am. 2022, 151, 2117–2126. [Google Scholar] [CrossRef]
- Guski, M.; Vorländer, M. Comparison of noise compensation methods for room acoustic impulse response evaluations. Acta Acust. United Acust. 2014, 100, 320–327. [Google Scholar] [CrossRef]
- Cabrera, D.; Xun, J.; Guski, M. Calculating reverberation time from impulse responses: A comparison of software implementations. Acoust. Aust. 2016, 44, 369–378. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Papadakis, N.M.; Antoniadou, S.; Stavroulakis, G.E. Effects of Varying Levels of Background Noise on Room Acoustic Parameters, Measured with ESS and MLS Methods. Acoustics 2023, 5, 563-574. https://doi.org/10.3390/acoustics5020034
Papadakis NM, Antoniadou S, Stavroulakis GE. Effects of Varying Levels of Background Noise on Room Acoustic Parameters, Measured with ESS and MLS Methods. Acoustics. 2023; 5(2):563-574. https://doi.org/10.3390/acoustics5020034
Chicago/Turabian StylePapadakis, Nikolaos M., Smaro Antoniadou, and Georgios E. Stavroulakis. 2023. "Effects of Varying Levels of Background Noise on Room Acoustic Parameters, Measured with ESS and MLS Methods" Acoustics 5, no. 2: 563-574. https://doi.org/10.3390/acoustics5020034
APA StylePapadakis, N. M., Antoniadou, S., & Stavroulakis, G. E. (2023). Effects of Varying Levels of Background Noise on Room Acoustic Parameters, Measured with ESS and MLS Methods. Acoustics, 5(2), 563-574. https://doi.org/10.3390/acoustics5020034








