Sound Scattering by Gothic Piers and Columns of the Cathédrale Notre-Dame de Paris
Abstract
1. Introduction
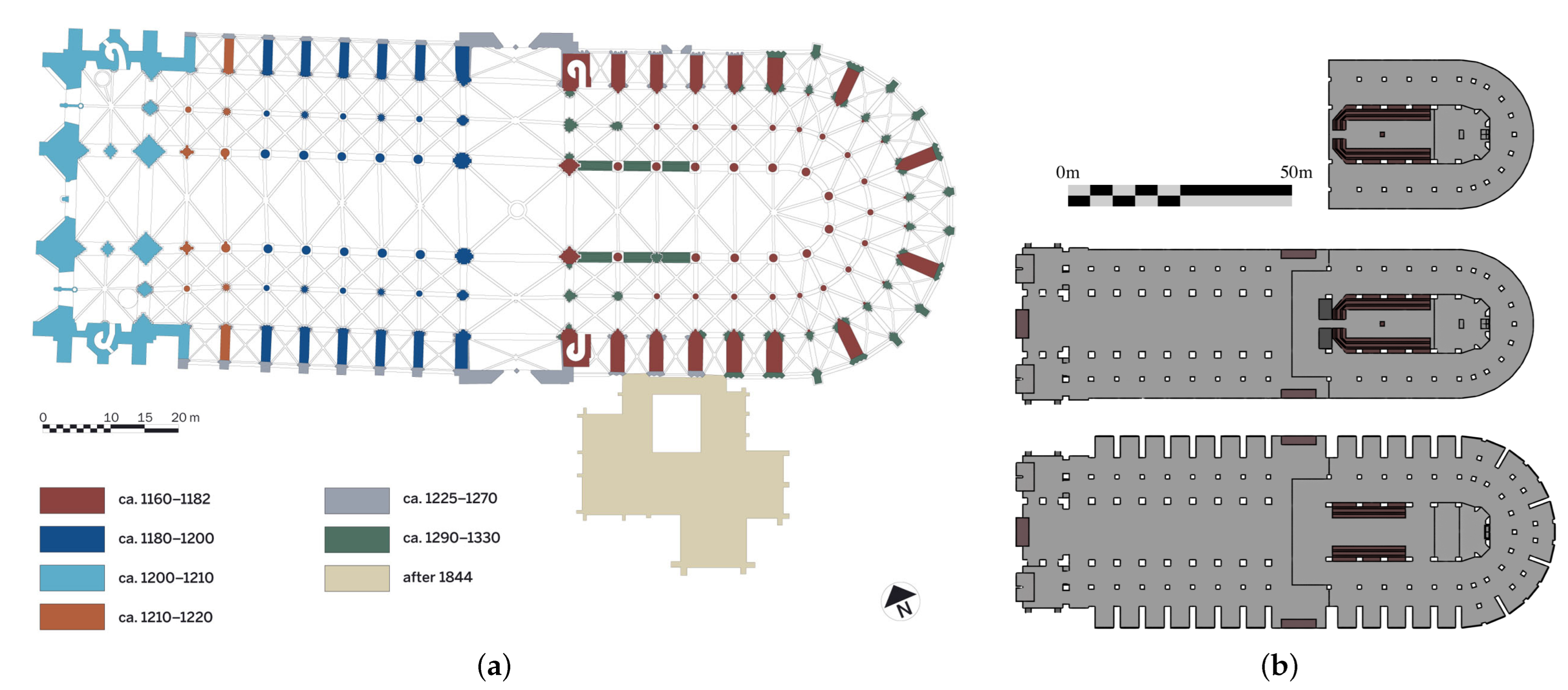
1.1. Introduction to the History of the Construction of Notre-Dame de Paris
1.2. General Acoustics of Notre-Dame de Paris
2. Materials and Methods
2.1. Columns and Piers of Interest
2.1.1. Compound Piers
2.1.2. Piers with Detached colonnettes en délit
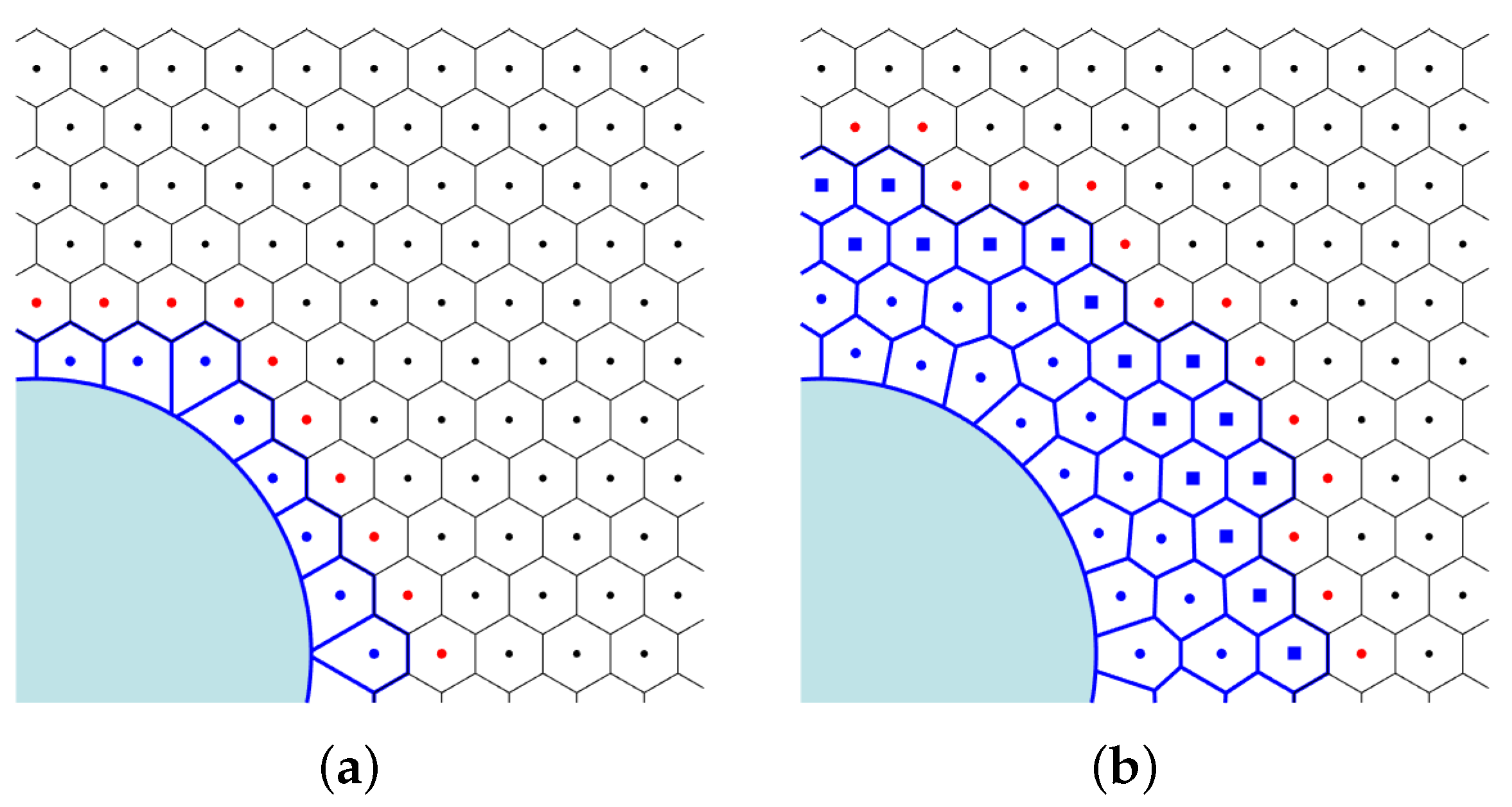
2.2. Numerical Methods
Setup
2.3. Experimental Methods
3. Results
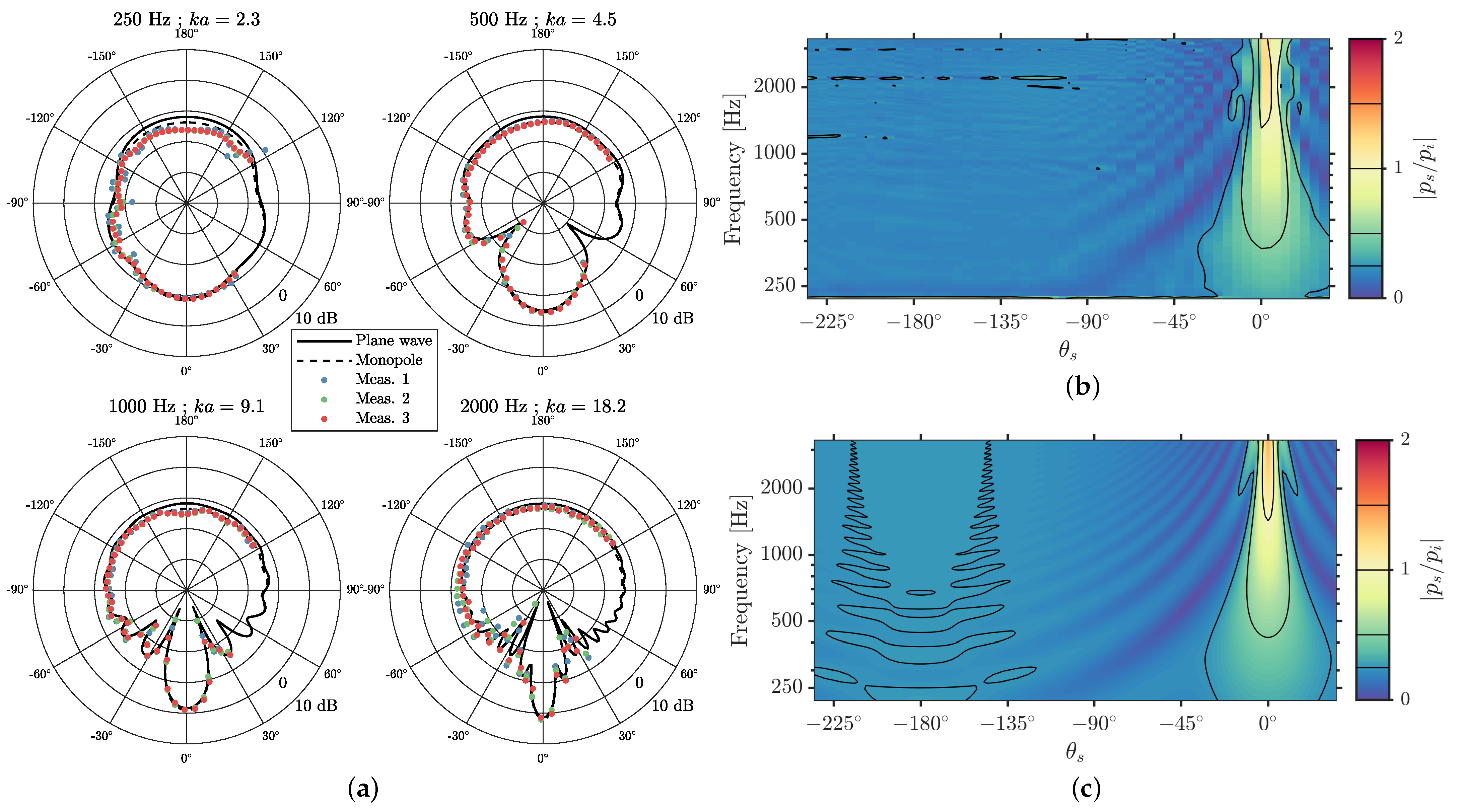
3.1. Validation of the Experimental Methods with a Rigid Circular Cylinder
3.2. Measurements Compared to Simulations
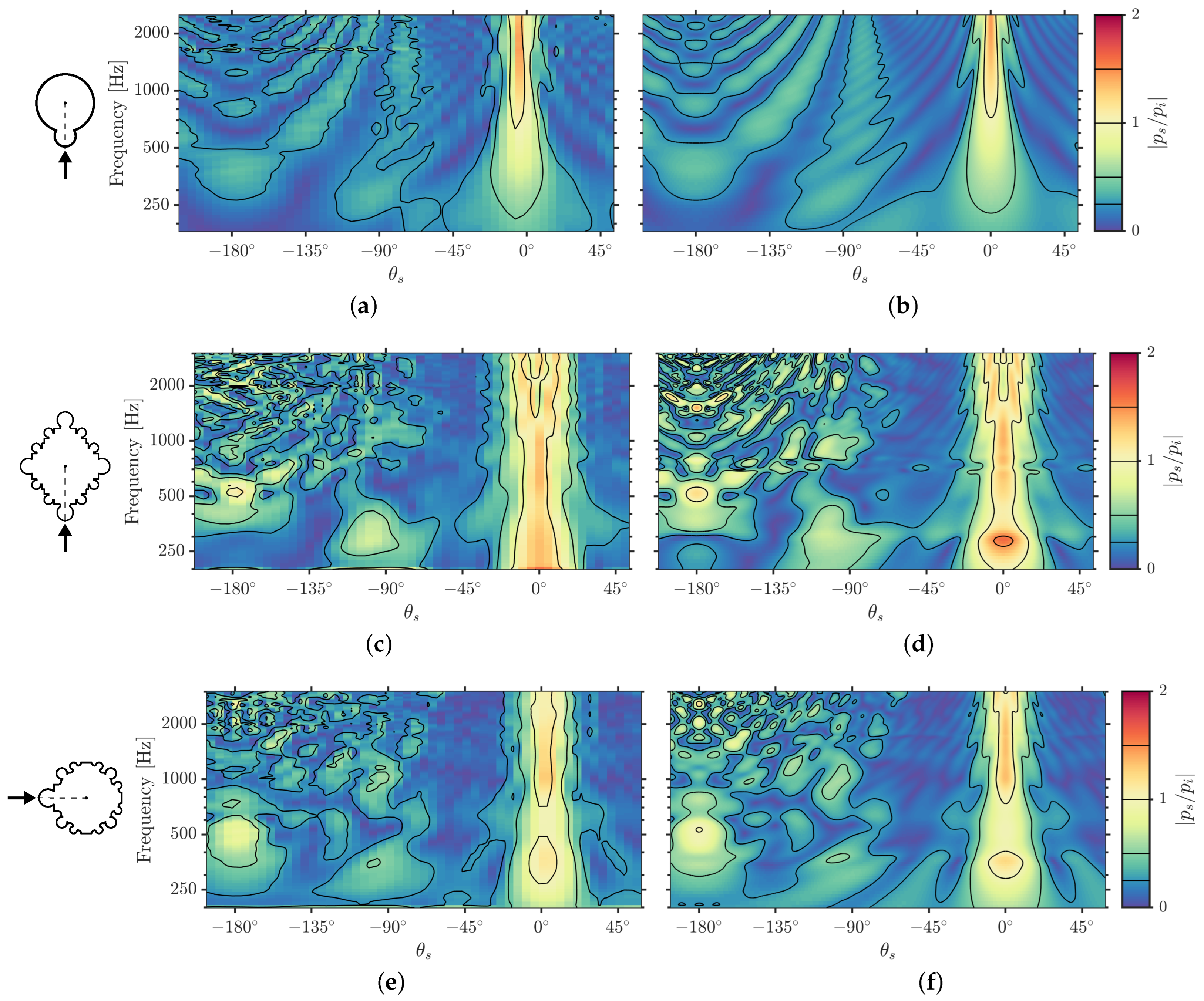
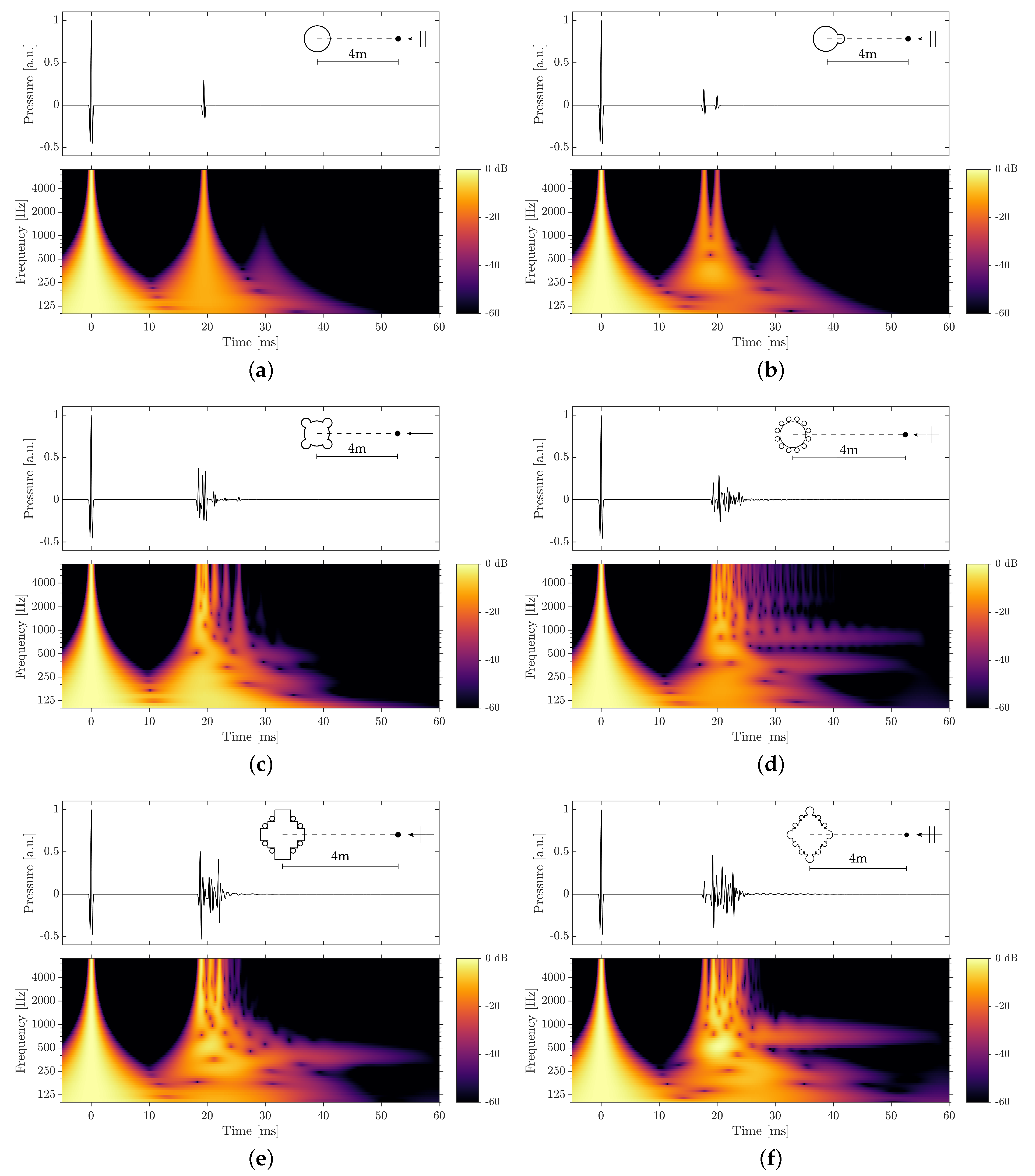
3.3. Simulation Results
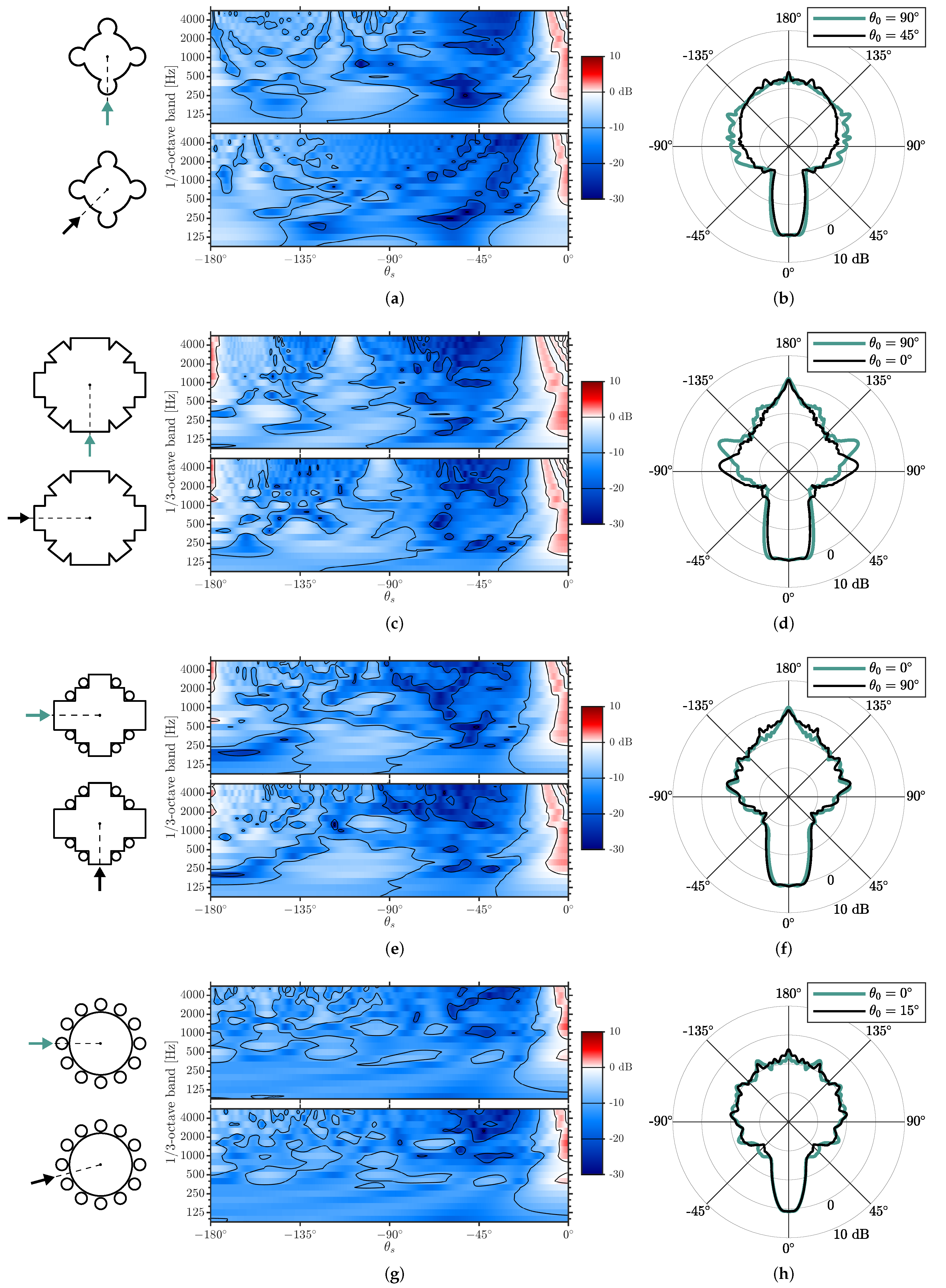
3.3.1. Time-Frequency Analysis
3.3.2. Reflected-to-Direct Level Differences
4. Discussion
4.1. Gothic Piers as Volumetric Diffusers
4.2. Audibility of Scattering by Cylindrical Obstacles
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| FD | Finite difference |
| FV | Finite volume |
| RDLD | Reflected-to-Direct Level Difference |
| SNR | Signal-to-noise ratio |
Appendix A. Measurements vs. Simulations: Additional Examples
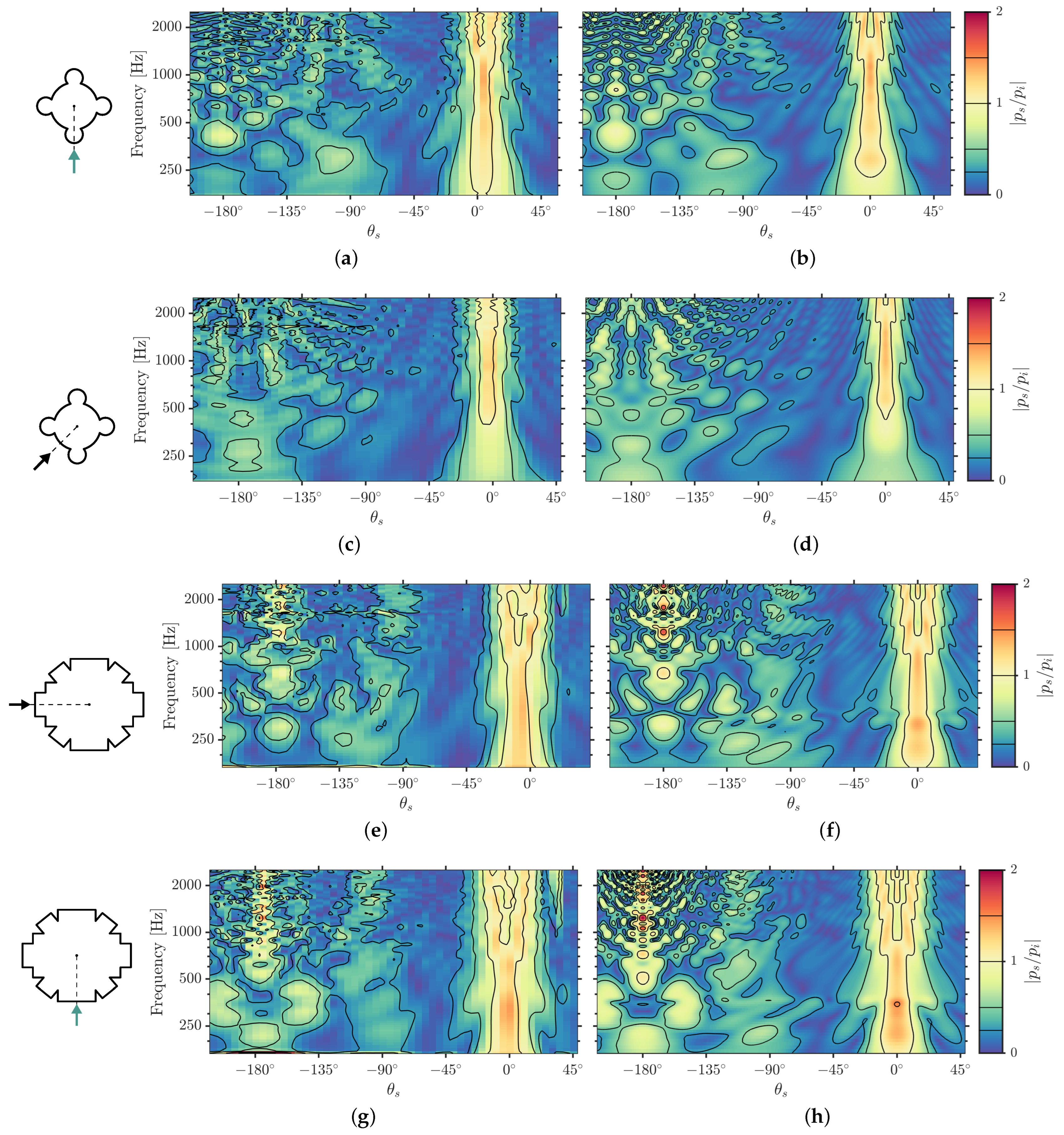
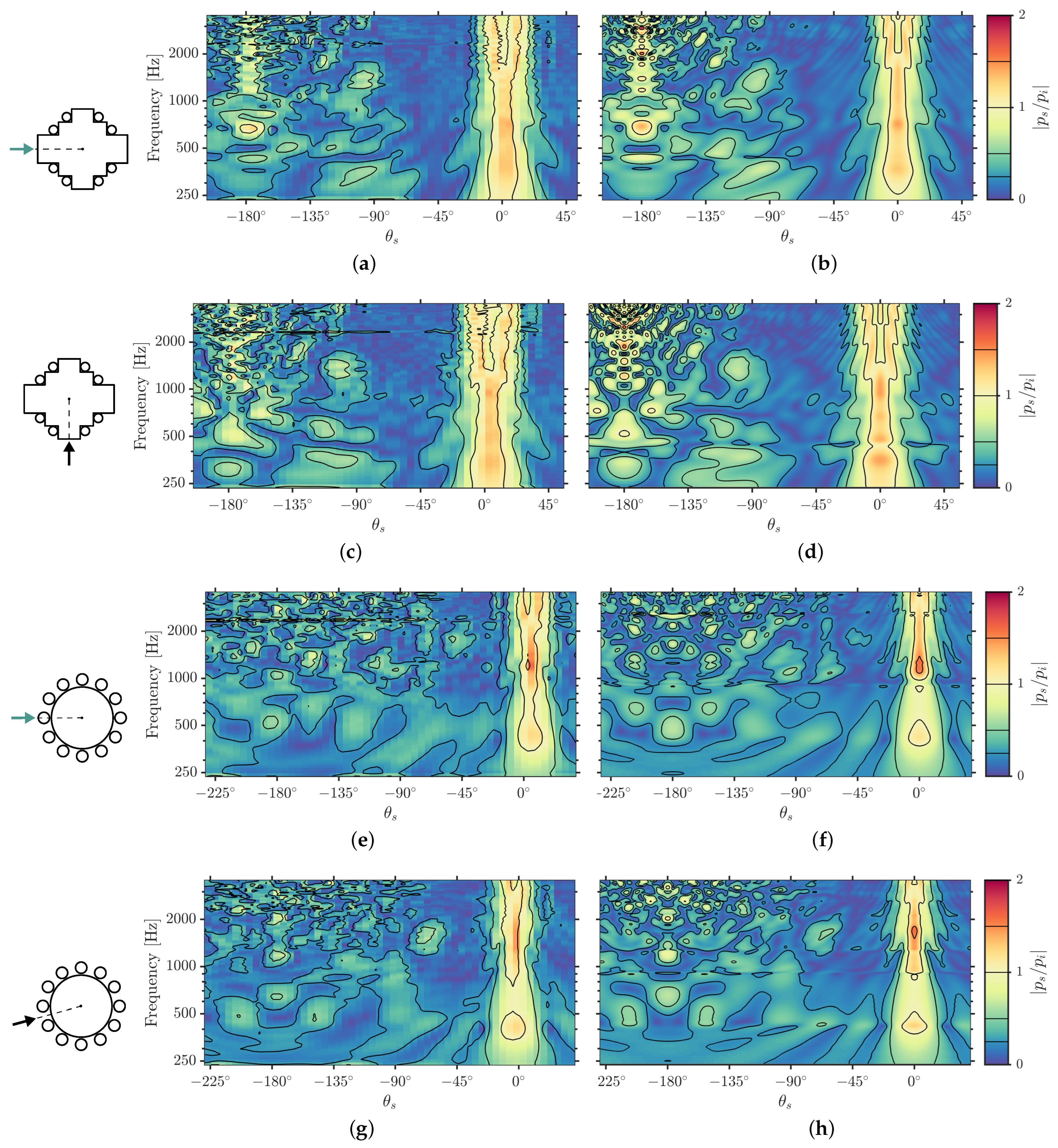
References
- Cox, T.; D’Antonio, P. Acoustic Absorbers and Diffusers: Theory, Design and Application; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar] [CrossRef]
- Rindel, J.H. Design of new ceiling reflectors for improved ensemble in a concert hall. Appl. Acoust. 1991, 34, 7–17. [Google Scholar] [CrossRef]
- Bradley, D.T.; Müller-Trapet, M.; Adelgren, J.; Vorländer, M. Comparison of Hanging Panels and Boundary Diffusers in a Reverberation Chamber. Build. Acoust. 2014, 21, 145–152. [Google Scholar] [CrossRef]
- Rindel, J.H. Attenuation of Sound Reflections due to Diffraction. In Proceedings of the Nordic Acoustical Meeting, Aalborg, Denmark, 20–22 August 1986. [Google Scholar]
- Szeląg, A.; Kamisiński, T.; Lewińska, M.; Rubacha, J.; Pilch, A. The Characteristic of Sound Reflections from Curved Reflective Panels. Arch. Acoust. 2014, 39, 549–558. [Google Scholar] [CrossRef][Green Version]
- Rathsam, J.; Wang, L.M. Planar Reflector Panels with Convex Edges. Acta Acust. United Acust. 2010, 96, 905–913. [Google Scholar] [CrossRef]
- Medwin, H.; Clay, C.S. Fundamentals of Acoustical Oceanography; Applications of Modern Acoustics, Academic Press: San Diego, CA, USA, 1998. [Google Scholar] [CrossRef]
- Standard ISO 17497-1:2004; Acoustics—Sound-Scattering Properties of Surfaces—Part 1: Measurement of the Random-Incidence Scattering Coefficient in a Reverberation Room. International Organization for Standardization: Geneva, Switzerland, 2004.
- Standard ISO 17497-2:2012; Acoustics—Sound-Scattering Properties of Surfaces—Part 2: Measurement of the Directional Diffusion Coefficient in a Free Field. International Organization for Standardization: Geneva, Switzerland, 2012.
- Ryu, J.K.; Jeon, J.Y. Subjective and objective evaluations of a scattered sound field in a scale model opera house. J. Acoust. Soc. Am. 2008, 124, 1538–1549. [Google Scholar] [CrossRef]
- Jeon, J.Y.; Jo, H.I.; Seo, R.; Kwak, K.H. Objective and subjective assessment of sound diffuseness in musical venues via computer simulations and a scale model. Build. Environ. 2020, 173, 106740. [Google Scholar] [CrossRef]
- Kim, Y.H.; Kim, J.H.; Jeon, J.Y. Scale Model Investigations of Diffuser Application Strategies for Acoustical Design of Performance Venues. Acta Acust. United Acust. 2011, 97, 791–799. [Google Scholar] [CrossRef]
- Shtrepi, L.; Astolfi, A.; Pelzer, S.; Vitale, R.; Rychtáriková, M. Objective and perceptual assessment of the scattered sound field in a simulated concert hall. J. Acoust. Soc. Am. 2015, 138, 1485–1497. [Google Scholar] [CrossRef]
- Shtrepi, L.; Astolfi, A.; Puglisi, G.E.; Masoero, M.C. Effects of the Distance from a Diffusive Surface on the Objective and Perceptual Evaluation of the Sound Field in a Small Simulated Variable-Acoustics Hall. Appl. Sci. 2017, 7, 224. [Google Scholar] [CrossRef]
- Suzumura, Y.; Sakurai, M.; Ando, Y.; Yamamoto, I.; Iizuka, T.; Oowaki, M. An evaluation of the effects of scattered reflections in a sound field. J. Sound Vib. 2000, 232, 303–308. [Google Scholar] [CrossRef]
- Strutt, H.J.X. On the light from the sky, its polarization and colour. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1871, 41, 107–120. [Google Scholar] [CrossRef]
- Morse, P.; Ingard, K. Theoretical Acoustics; International Series in Pure and Applied Physics; Princeton University Press: Princeton, NJ, USA, 1986. [Google Scholar]
- Bowman, J.; Senior, T.; Uslenghi, P.; Asvestas, J. Electromagnetic and Acoustic Scattering by Simple Shapes; Taylor & Francis: Abingdon, UK, 1988. [Google Scholar]
- Hughes, R.J.; Angus, J.A.S.; Cox, T.J.; Umnova, O.; Gehring, G.A.; Pogson, M.; Whittaker, D.M. Volumetric diffusers: Pseudorandom cylinder arrays on a periodic lattice. J. Acoust. Soc. Am. 2010, 128, 2847–2856. [Google Scholar] [CrossRef]
- Yashiro, K.; Ohkawa, S. Boundary element method for electromagnetic scattering from cylinders. IEEE Trans. Antennas Propag. 1985, 33, 383–389. [Google Scholar] [CrossRef]
- Liu, Y. On the BEM for acoustic wave problems. Eng. Anal. Bound. Elem. 2019, 107, 53–62. [Google Scholar] [CrossRef]
- Ihlenburg, F. (Ed.) Finite Element Analysis of Acoustic Scattering; Springer: Berlin/Heidelberg, Germany, 1998. [Google Scholar] [CrossRef]
- Taflove, A.; Hagness, S. Computational Electrodynamics: The Finite-Difference Time-Domain Method; Artech House Antennas and Propagation Library, Artech House: Norwood, MA, USA, 2005. [Google Scholar]
- Redondo, J.; Picó, R.; Roig, B.; Avis, M.R. Time Domain Simulation of Sound Diffusers Using Finite-Difference Schemes. Acta Acust. United Acust. 2007, 93, 611–622. [Google Scholar]
- Hoare, S.; Murphy, D. Prediction of scattering effects by sonic crystal noise barriers in 2d and 3d finite difference simulations. In Proceedings of the Acoustics 2012, Nantes, France, 23–27 April 2012; Société Française d’Acoustique, Paris, France, 2012. [Google Scholar]
- Redondo, J.; Picó, R.; Sánchez-Morcillo, V.J.; Woszczyk, W. Sound diffusers based on sonic crystals. J. Acoust. Soc. Am. 2013, 134, 4412–4417. [Google Scholar] [CrossRef]
- Tornberg, A.K.; Engquist, B. Consistent boundary conditions for the Yee scheme. J. Comput. Phys. 2008, 227, 6922–6943. [Google Scholar] [CrossRef]
- Bilbao, S.; Hamilton, B.; Botts, J.; Savioja, L. Finite Volume Time Domain Room Acoustics Simulation under General Impedance Boundary Conditions. IEEE/ACM Trans. Audio Speech Lang. Process. 2016, 24, 161–173. [Google Scholar] [CrossRef]
- Hamilton, B.; Bilbao, S. Hexagonal vs. rectilinear grids for explicit finite difference schemes for the two-dimensional wave equation. J. Acoust. Soc. Am. 2013, 133, 3532. [Google Scholar] [CrossRef]
- Olive, S.E.; Toole, F.E. The Detection of Reflections in Typical Rooms. J. Audio Eng. Soc. 1988, 37, 539–553. [Google Scholar]
- Buchholz, J.M. A quantitative analysis of spectral mechanisms involved in auditory detection of coloration by a single wall reflection. Hear. Res. 2011, 277, 192–203. [Google Scholar] [CrossRef] [PubMed]
- Burgtorf, W.; Oehlschlägel, H.K. Untersuchungen über die richtungsabhängige Wahrnehmbarkeit verzögerter Schallsignale. Acta Acust. United Acust. 1964, 14, 254–266. [Google Scholar]
- Seraphim, H. Über die Wahrnehmbarkeit mehrerer Rückwürfe von Sprachschall. Acta Acust. United Acust. 1961, 11, 80–91. [Google Scholar]
- Brunner, S.; Maempel, H.J.; Weinzierl, S. On the Audibility of Comb Filter Distortions. In Proceedings of the 122nd AES Convention, Vienna, Austria, 5–8 May 2007; Audio Engineering Society: New York, NY, USA, 2007. [Google Scholar]
- Begault, D.R.; McClain, B.U.; Anderson, M.R. Early Reflection Thresholds for Anechoic and Reverberant Stimuli within a 3-D Sound Display. In Proceedings of the 18th International Congress on Acoustics (ICA04), Kyoto, Japan, 4–9 April 2004. [Google Scholar]
- Zhong, X.; Guo, W.; Wang, J. Audible Threshold of Early Reflections with Different Orientations and Delays. Sound Vib. 2018, 52, 18–22. [Google Scholar] [CrossRef]
- Walther, A.; Robinson, P.W.; Santala, O. Effect of spectral overlap on the echo suppression threshold for single reflection conditions. J. Acoust. Soc. Am. 2013, 134, EL158–EL164. [Google Scholar] [CrossRef]
- Pelegrín-García, D.; Rychtáriková, M. Audibility Thresholds of a Sound Reflection in a Classical Human Echolocation Experiment. Acta Acust. United Acust. 2016, 102, 530–539. [Google Scholar] [CrossRef]
- Pelegrín-García, D.; Rychtáriková, M.; Glorieux, C. Single Simulated Reflection Audibility Thresholds for Oral Sounds in Untrained Sighted People. Acta Acust. United Acust. 2017, 103, 492–505. [Google Scholar] [CrossRef]
- Robinson, P.W.; Walther, A.; Faller, C.; Braasch, J. Echo thresholds for reflections from acoustically diffusive architectural surfaces. J. Acoust. Soc. Am. 2013, 134, 2755–2764. [Google Scholar] [CrossRef]
- Wendt, F.; Höldrich, R. Precedence effect for specular and diffuse reflections. Acta Acust. 2021, 5, 1. [Google Scholar] [CrossRef]
- Kleiner, M.; Svensson, P.; Dalenbäck, B.I. Auralization of qrd and other diffusing surfaces using scale modelling. In Proceedings of the 93rd AES Convention, San Francisco, CA, USA, 1–4 October 1992; Audio Engineering Society: New York, NY, USA. [Google Scholar]
- Meyer, J.; Savioja, L.; Lokki, T. A case study on the perceptual differences in finite-difference time-domain-simulated diffuser designs. In Proceedings of the 146th AES Convention, Dublin, Ireland, 20–23 March 2019; Audio Engineering Society: New York, NY, USA. [Google Scholar]
- Kritly, L.; Sluyts, Y.; Pelegrín-García, D.; Glorieux, C.; Rychtáriková, M. Discrimination of 2D wall textures by passive echolocation for different reflected-to-direct level difference configurations. PLoS ONE 2021, 16, e0251397. [Google Scholar] [CrossRef]
- Aubert, M.; Vitry, P. La Cathédrale Notre-Dame de Paris: Notice Historique et Archéologique; Notices Historiques et Archéologiques sur les Grands Monuments; D.-A. Longuet: Paris, France, 1919. [Google Scholar]
- Bruzelius, C. The Construction of Notre-Dame in Paris. Art Bull. 1987, 69, 540–569. [Google Scholar] [CrossRef]
- Sandron, D.; Tallon, A.; Cook, L. Notre Dame Cathedral: Nine Centuries of History; Penn State University Press: University Park, PA, USA, 2020. [Google Scholar] [CrossRef]
- Celtibère, M.; Lemercier, M.; Hibon, A.; Ribaud, A.; Normand, A.; Bisson, B. Monographie de Notre-Dame de Paris et de la Nouvelle Sacristie de MM. Lassus et Viollet-Le-Duc; A. Morel: Paris, France, 1853. [Google Scholar]
- Mullins, S.S.; Canfield-Dafilou, E.K.; Katz, B.F.G. The development of the early acoustics of the chancel in Notre-Dame de Paris: 1160–1230. In Proceedings of the 2nd Symposium: The Acoustics of Ancient Theatres, Verona, Italy, 6–8 July 2022. [Google Scholar]
- Lassus, J.B.A.; Viollet-le-Duc, E.E. Projet de Restauration de Notre-Dame de Paris par MM. Lassus et Viollet-Leduc: Rapport…Annexé au Projet de Restauration, Remis le 31 Janvier 1843; Imprimerie de Mme de Lacombe: Paris, France, 1843. [Google Scholar]
- Travaux de Notre-Dame de Paris—Journal des Travaux 1844–1865. Available online: https://mediatheque-patrimoine.culture.gouv.fr/travaux-de-notre-dame-de-paris-1844-1865 (accessed on 1 June 2022).
- Postma, B.N.; Katz, B.F.G. Acoustics of Notre-Dame Cathedral de Paris. In Proceedings of the 22nd International Congress on Acoustics (ICA), Buenos Aires, Argentina, 5–9 September 2016; pp. 5–9. [Google Scholar]
- Katz, B.F.G.; Weber, A. An acoustic survey of the Cathédrale Notre-Dame de Paris before and after the fire of 2019. Acoustics 2020, 2, 791–802. [Google Scholar] [CrossRef]
- Hoey, L.R. Pier Form and Vertical Wall Articulation in English Romanesque Architecture. J. Soc. Archit. Hist. 1989, 48, 258–283. [Google Scholar] [CrossRef]
- Thurlby, M. Aspects of the architectural history of Kirkwall Cathedral. Proc. Soc. Antiqu. Scotl. 1998, 127, 855–888. [Google Scholar]
- CNRS/MC. Chantier Scientifique Notre-Dame de Paris. Available online: https://www.notre-dame.science/ (accessed on 1 June 2022).
- Klein, B. Naissance et formation de l’architecture gothique en France et dans les pays limitrophes. In L’art Gothique, Architecture-Sculpture-Peinture; Toman, R., Ed.; Könemann: Köln, Germany, 1999; Chapter 3; pp. 28–114. [Google Scholar]
- Murray, S. Notre-Dame of Paris and the Anticipation of Gothic. Art Bull. 1998, 80, 229–253. [Google Scholar] [CrossRef]
- Davis, M.T. Splendor and Peril: The Cathedral of Paris, 1290–1350. Art Bull. 1998, 80, 34–66. [Google Scholar] [CrossRef]
- Viollet-le-Duc, E.E. Dictionnaire Raisonné de l’Architecture Française du XIe au XVIe Siècle; B. Bance: Paris, France, 1859. [Google Scholar]
- Fernie, E. La fonction liturgique des piliers cantonnés dans la nef de la cathédrale de Laon. Bull. Monum. 1987, 145, 257–266. [Google Scholar] [CrossRef]
- Olson, V. Colonnette Production and the Advent of the Gothic Aesthetic. Gesta 2004, 43, 17–29. [Google Scholar] [CrossRef]
- Bony, J. French Influences on the Origins of English Gothic Architecture. J. Warbg. Court. Inst. 1949, 12, 1–15. [Google Scholar] [CrossRef]
- Hoey, L. Piers versus Vault Shafts in Early English Gothic Architecture. J. Soc. Archit. Hist. 1987, 46, 241–264. [Google Scholar] [CrossRef]
- Fabero, J.; Bautista, A.; Casasús, L. An explicit finite differences scheme over hexagonal tessellation. Appl. Math. Lett. 2001, 14, 593–598. [Google Scholar] [CrossRef]
- Yamashita, O.; Tsuchiya, T.; Iwaya, Y.; Otani, M.; Inoguchi, Y. Reflective boundary condition with arbitrary boundary shape for compact-explicit finite-difference time-domain method. Jpn. J. Appl. Phys. 2015, 54, 07HC02. [Google Scholar] [CrossRef]
- Tolan, J.G.; Schneider, J.B. Locally conformal method for acoustic finite-difference time-domain modeling of rigid surfaces. J. Acoust. Soc. Am. 2003, 114, 2575–2581. [Google Scholar] [CrossRef] [PubMed]
- Bilbao, S.; Hamilton, B. Passive volumetric time domain simulation for room acoustics applications. J. Acoust. Soc. Am. 2019, 145, 2613–2624. [Google Scholar] [CrossRef] [PubMed]
- Vázquez, P.; Menéndez, B.; Denecker, M.F.C.; Thomachot-Schneider, C. Comparison between petrophysical properties, durability and use of two limestones of the Paris region. In Sustainable Use of Traditional Geomaterials in Construction Practice; Geological Society of London: London, UK, 2016. [Google Scholar] [CrossRef]
- Botteldooren, D. Acoustical finite-difference time-domain simulation in a quasi-Cartesian grid. J. Acoust. Soc. Am. 1994, 95, 2313–2319. [Google Scholar] [CrossRef]
- Hamilton, B. Finite Volume Perspectives on Finite Difference Schemes and Boundary Formulations for Wave Simulation. In Proceedings of the 17th International Conference on Digital Audio Effects (DAFx-14), Erlangen, Germany, 1–5 September 2014. [Google Scholar]
- Du, Q.; Faber, V.; Gunzburger, M. Centroidal Voronoi Tessellations: Applications and Algorithms. SIAM Rev. 1999, 41, 637–676. [Google Scholar] [CrossRef]
- Geuzaine, C.; Remacle, J.F. Gmsh: A 3-D finite element mesh generator with built-in pre- and post-processing facilities. Int. J. Numer. Methods Eng. 2009, 79, 1309–1331. [Google Scholar] [CrossRef]
- Rasmussen, K. Calculation Methods for the Physical Properties of Air Used in the Calibration of Microphones; Report PL-11b; Department of Acoustical Technology, Technical University of Denmark: Kongens Lyngby, Denmark, 1997. [Google Scholar]
- Sheaffer, J.; van Walstijn, M.; Fazenda, B. Physical and numerical constraints in source modeling for finite difference simulation of room acoustics. J. Acoust. Soc. Am. 2014, 135, 251–261. [Google Scholar] [CrossRef] [PubMed]
- Müller, S.; Massarani, P. Transfer-Function Measurement with Sweeps. J. Audio Eng. Soc. 2001, 49, 443–471. [Google Scholar]
- Robinson, P.; Xiang, N. On the subtraction method for in-situ reflection and diffusion coefficient measurements. J. Acoust. Soc. Am. 2010, 127, EL99–EL104. [Google Scholar] [CrossRef]
- Zhang, L.; Wu, X. On cross correlation based-discrete time delay estimation. In Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP’05), Philadelphia, PA, USA, 23 March 2005; Volume 4, pp. iv/981–iv/984. [Google Scholar] [CrossRef]
- Krynkin, A.; Umnova, O.; Vicente Sánchez-Pérez, J.; Yung Boon Chong, A.; Taherzadeh, S.; Attenborough, K. Acoustic insertion loss due to two dimensional periodic arrays of circular cylinders parallel to a nearby surface. J. Acoust. Soc. Am. 2011, 130, 3736–3745. [Google Scholar] [CrossRef]
- Markowskei, A.J.; Smith, P.D. Measuring the effect of rounding the corners of scattering structures. Radio Sci. 2017, 52, 693–708. [Google Scholar] [CrossRef]
- Lilly, J.; Olhede, S. Higher-Order Properties of Analytic Wavelets. IEEE Trans. Signal Process. 2009, 57, 146–160. [Google Scholar] [CrossRef]
- Robinson, P.W.; Xiang, N.; Braasch, J. Understanding the perceptual effects of diffuser application in rooms. Proc. Meet. Acoust. 2011, 12, 015002. [Google Scholar] [CrossRef]
- Berry, D.L.; Taherzadeh, S.; Attenborough, K. Acoustic surface wave generation over rigid cylinder arrays on a rigid plane. J. Acoust. Soc. Am. 2019, 146, 2137–2144. [Google Scholar] [CrossRef]
- Farhat, M.; Chen, P.Y.; Bağcı, H. Localized acoustic surface modes. Appl. Phys. A 2016, 122, 1–8. [Google Scholar] [CrossRef]
- Weber, A.; Katz, B.F.G. An investigation of sound scattering by ancient and Gothic piers and columns. Acta Acust. 2022, submitted.
- Zitron, N.R.; Davis, J. A note on scattering of cylindrical waves by a circular cylinder. Can. J. Phys. 1966, 44, 2941–2944. [Google Scholar] [CrossRef]

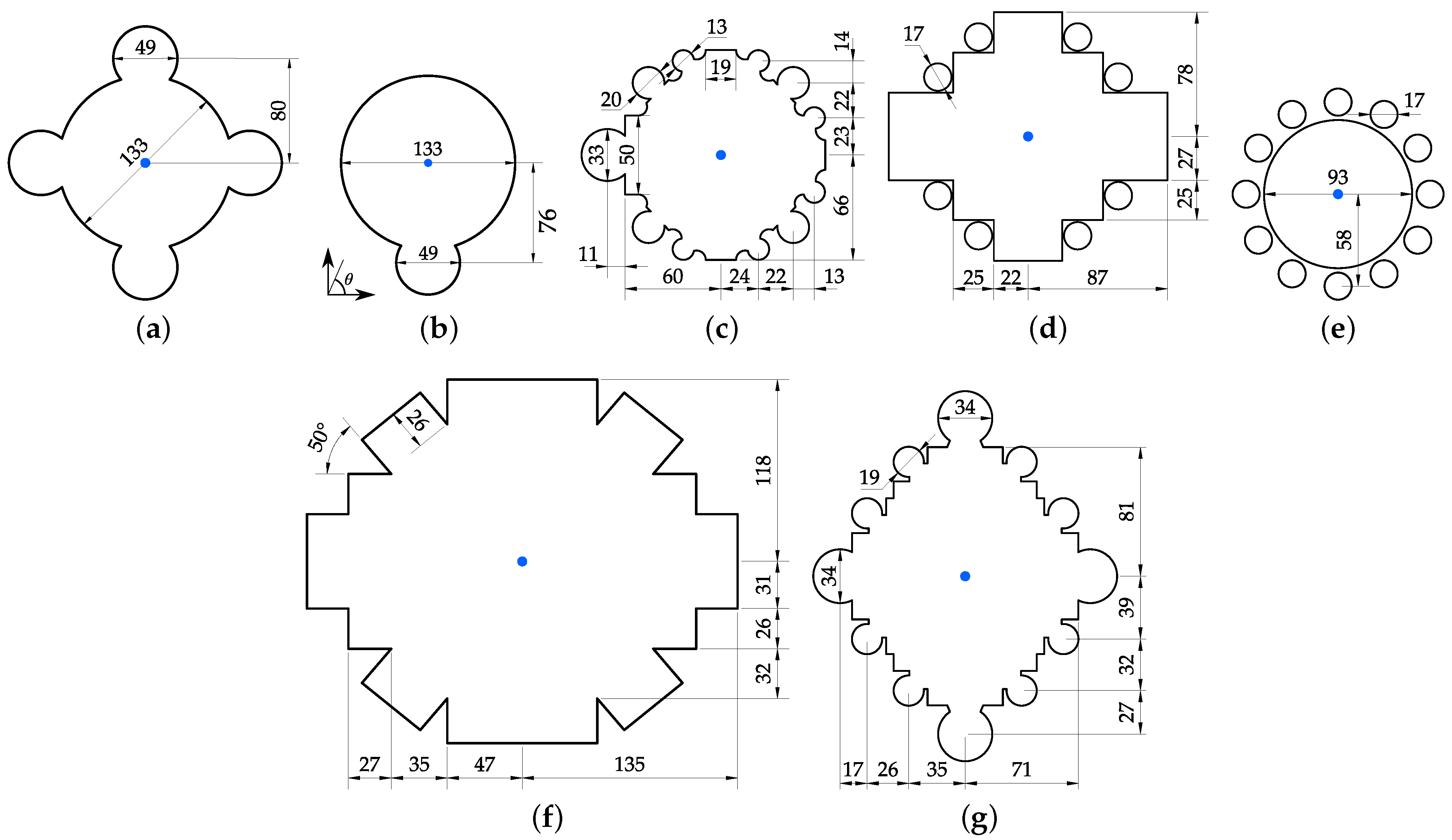

| Label (Fig.) | Scale Factor | Incidence Angle | Distance from Center 1 | c [m s−1] | ||
|---|---|---|---|---|---|---|
| Source [cm] | Receiver [cm] | |||||
| N1 (Figure 3b) | 1:12 | 90° | 31 | 307 | 346.2 | 0.755 |
| N2 (Figure 3a) | 1:12 | 90° | 32 | 307 | 345.7 | 0.751 |
| 45° | 32 | 307 | 345.8 | 0.731 | ||
| C1 (Figure 3f) | 1:12 | 0° | 32 | 306 | 345.7 | 0.753 |
| 90° | 32 | 306 | 346.2 | 0.742 | ||
| T (Figure 3g) | 1:10 | 90° | 31 | 319 | 346.1 | 0.744 |
| Ch (Figure 3c) | 1:10 | 0° | 31 | 319 | 346.5 | 0.743 |
| C2 (Figure 3d) | 1:8.5 | 90° | 33 | 307 | 346.1 | 0.753 |
| 0° | 33 | 307 | 345.9 | 0.739 | ||
| N3 (Figure 3e) | 1:8.5 | 0° | 33 | 338 | 346.6 | 0.745 |
| 15° | 37 | 317 | 346.6 | 0.762 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Weber, A.; Katz, B.F.G. Sound Scattering by Gothic Piers and Columns of the Cathédrale Notre-Dame de Paris. Acoustics 2022, 4, 679-703. https://doi.org/10.3390/acoustics4030041
Weber A, Katz BFG. Sound Scattering by Gothic Piers and Columns of the Cathédrale Notre-Dame de Paris. Acoustics. 2022; 4(3):679-703. https://doi.org/10.3390/acoustics4030041
Chicago/Turabian StyleWeber, Antoine, and Brian F. G. Katz. 2022. "Sound Scattering by Gothic Piers and Columns of the Cathédrale Notre-Dame de Paris" Acoustics 4, no. 3: 679-703. https://doi.org/10.3390/acoustics4030041
APA StyleWeber, A., & Katz, B. F. G. (2022). Sound Scattering by Gothic Piers and Columns of the Cathédrale Notre-Dame de Paris. Acoustics, 4(3), 679-703. https://doi.org/10.3390/acoustics4030041







