A Review of Finite Element Studies in String Musical Instruments
Abstract
1. Introduction
2. Modal Analysis
3. Numerical Methods
4. FEM Studies on Soundboards of String Musical Instruments
4.1. Bowed Stringed Musical Instruments
4.2. Plucked Musical Instruments
4.3. Hammered Musical Instruments
5. FEM Studies of Assembled String Musical Instrument Box
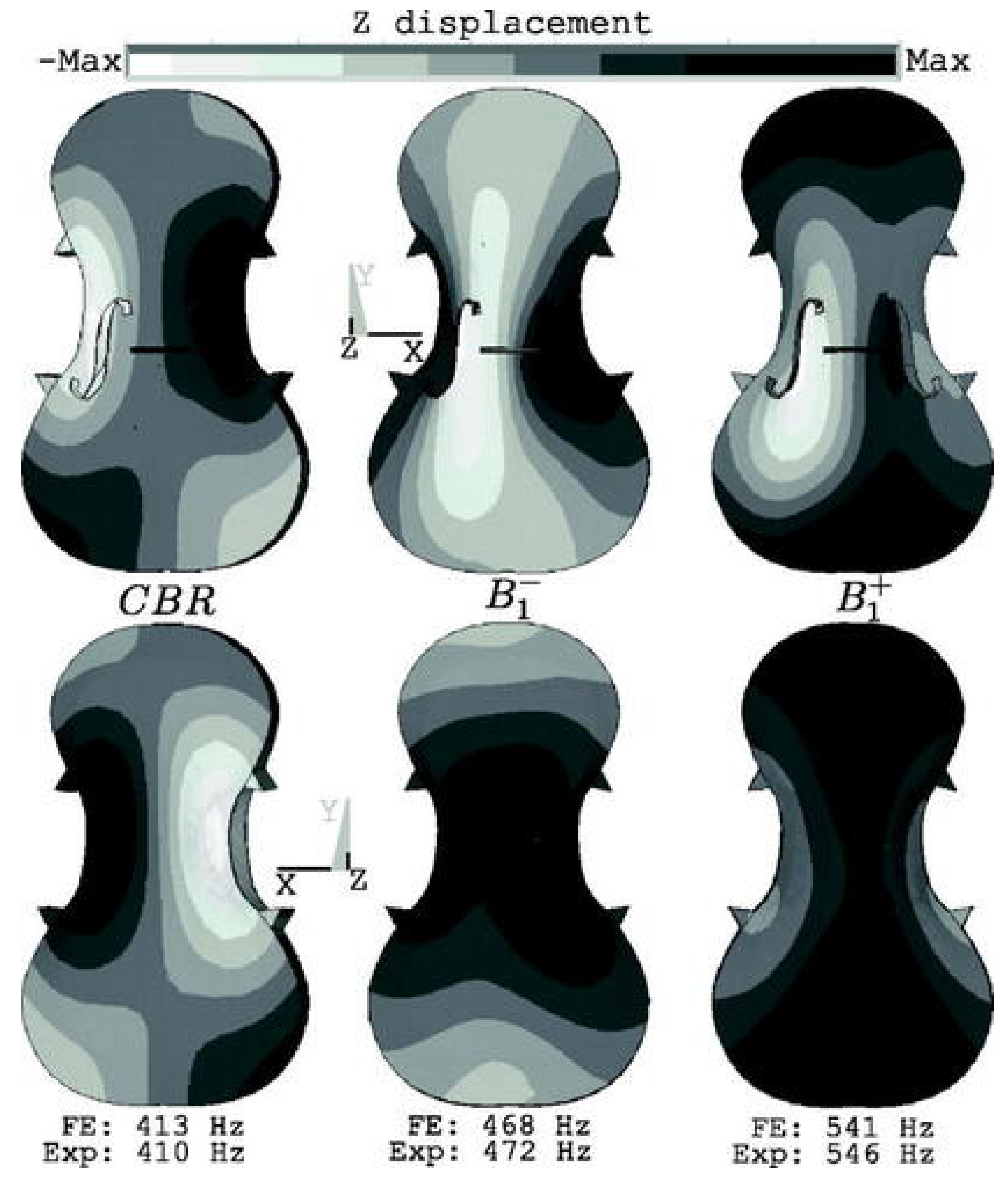
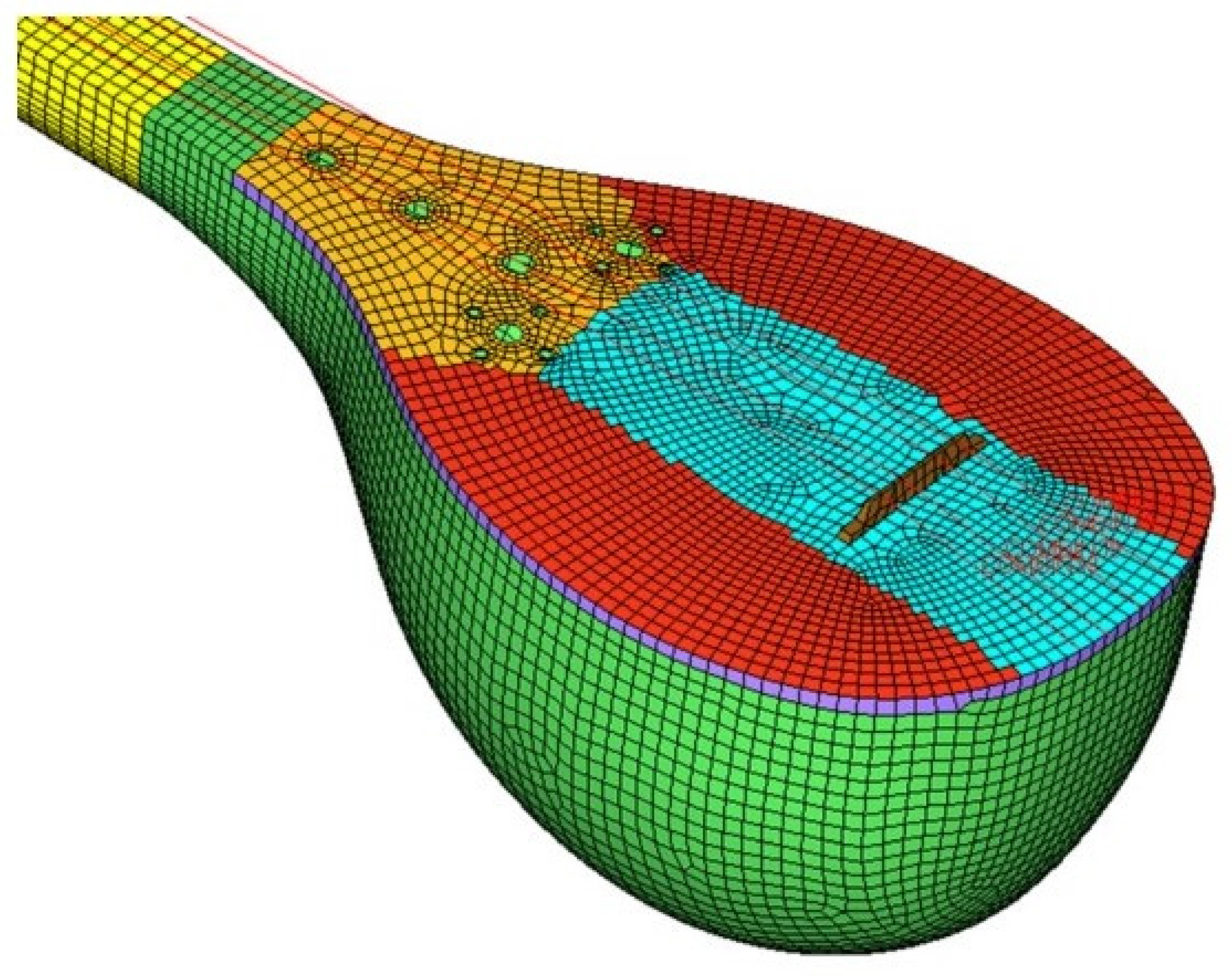
5.1. Bowed Musical Instruments
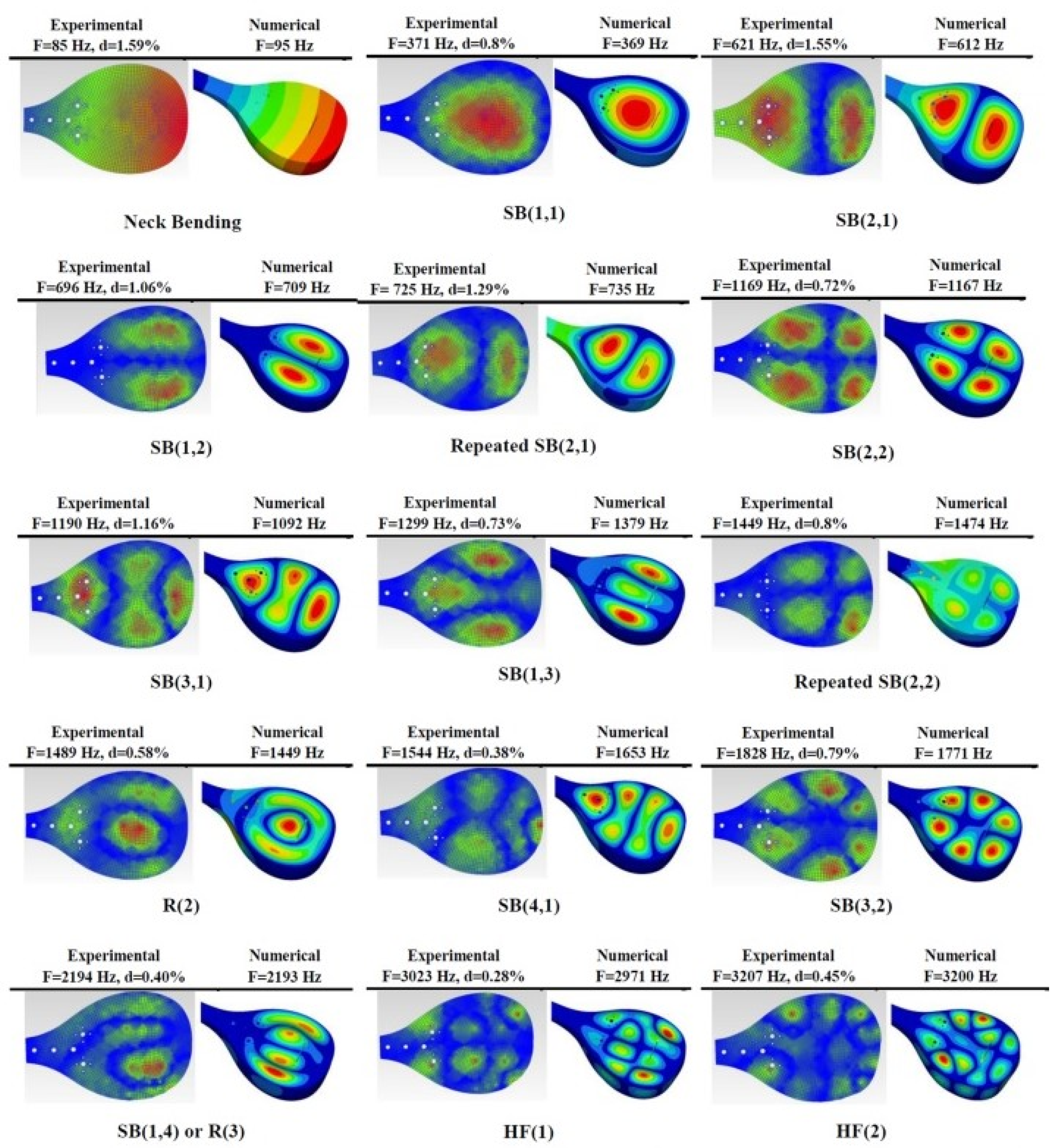
5.2. Plucked Musical Instruments
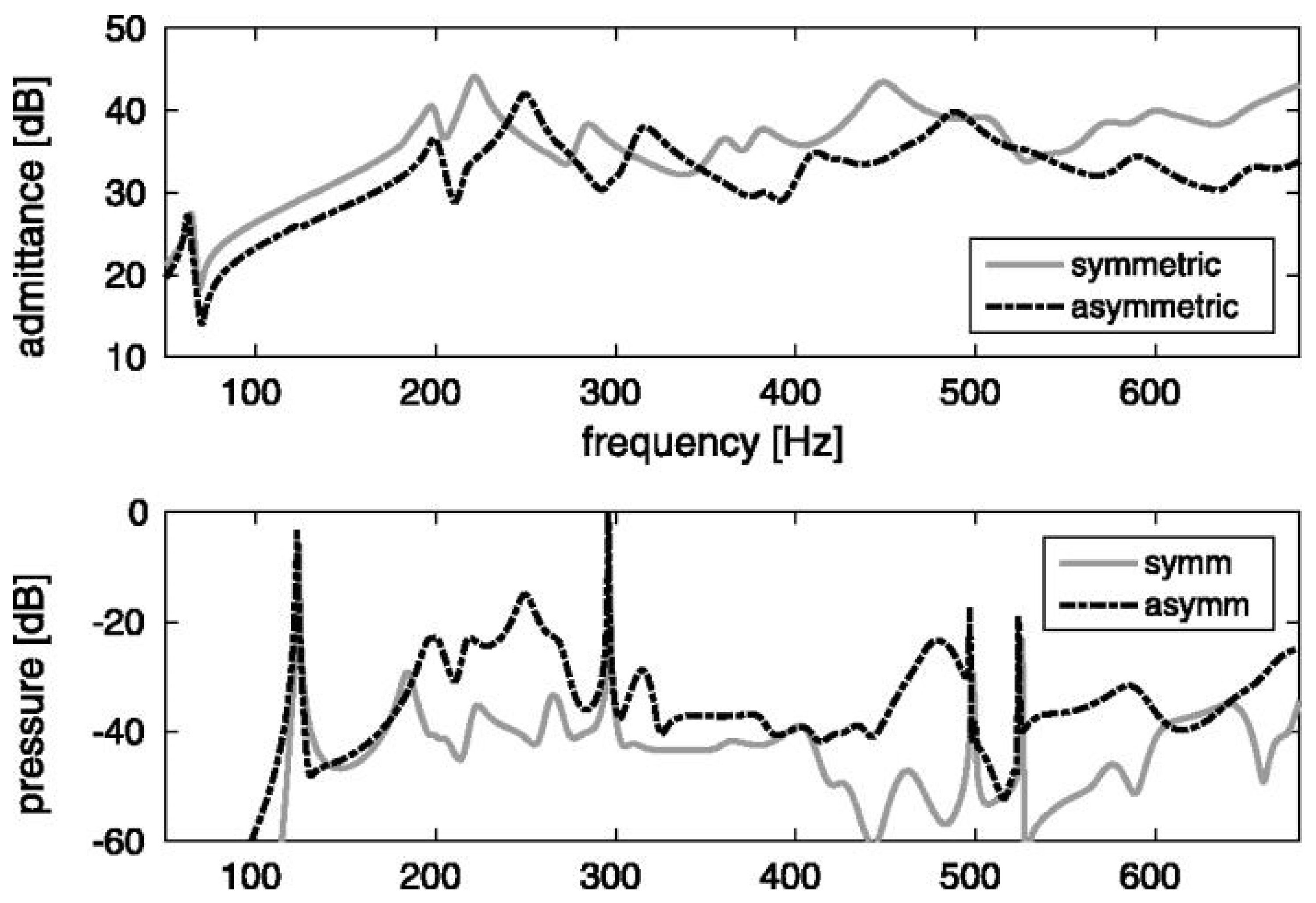
6. FEM Fluid–Structure Interaction Studies of Assembled String Musical Instruments
7. FEM Studies of String Musical Instrument Resonance Box Interaction with the Surrounding Air
8. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Sachs, C. The History of Musical Instruments; W. W. Norton & Company: New York, NY, USA, 1940. [Google Scholar]
- Fletcher, N.; Rossing, T. The Physics of Musical Instruments; Springer: New York, NY, USA, 1998. [Google Scholar]
- Benade, A.H. Fundamentals of Musical Acoustics; Oxford University Press: New York, NY, USA, 2012. [Google Scholar]
- Bucur, V. Handbook of Materials for String Musical Instruments; Springer: Cham, Switzerland, 2016. [Google Scholar]
- Giordano, N. Some observations on the Physics of stringed instruments. In Springer Handbook of Systematic Musicology; Springer: Berlin/Heidelberg, Germany, 2018; pp. 105–119. [Google Scholar]
- Bader, R.; Hansen, U. Modeling of Musical Instruments. In Handbook of Signal Processing in Acoustics; Springer: New York, NY, USA, 2008; pp. 419–446. [Google Scholar]
- Bader, R. Characterizing Classical Guitars Using Top Plate Radiation Patterns Measured by a Microphone Array. Acta Acust. United Acust. 2011, 97, 830–839. [Google Scholar] [CrossRef]
- McIntyre, M.E.; Woodhouse, J. The acoustics of stringed musical instruments. Inter. Sci. Rev. 1978, 3, 157–173. [Google Scholar] [CrossRef]
- Rossing, T.D. Modal analysis. In Springer Handbook of Acoustics; Springer: New York, NY, USA, 2007; pp. 1127–1138. [Google Scholar]
- Jones, R.; Wykes, C. Holographic and Speckle Interferometry; Cambridge University Press: Cambridge, UK, 1989. [Google Scholar]
- Castellini, P.; Revel, G.M.; Tomasini, E.P. Laser Doppler vibrometry: Development of advanced solutions answering to technology’s needs. Mech. Syst. Signal. Process. 2006, 20, 1265–1285. [Google Scholar] [CrossRef]
- Wang, C.P. Laser Doppler velocimetry. J. Quant. Spectrosc. Radiat. Transfer. 1988, 40, 309–319. [Google Scholar] [CrossRef]
- Bakarezos, E.; Orphanos, Y.; Kaselouris, E.; Dimitriou, V.; Tatarakis, M.; Papadogiannis, N.A. Laser-based interferometric techniques for the study of musical instruments. In Computational Phonogram Archiving; Springer: Cham, Switzerland, 2019; pp. 251–268. [Google Scholar]
- Bakarezos, E.; Vathis, V.; Brezas, S.; Orphanos, Y.; Papadogiannis, N.A. Acoustics of the Chelys—An ancient Greek tortoise-shell lyre. Appl. Acoust. 2012, 73, 478–483. [Google Scholar] [CrossRef]
- Herrero-Durá, I.; Picó, R.; Sánchez-Morcillo, V.J.; Garcia-Raffi, L.M. Modelling of continuous elastic systems by using the Finite Element Method. Model. Sci. Educ. Learn. 2017, 10, 193–202. [Google Scholar] [CrossRef][Green Version]
- Klímová, H.; Tippner, J. Modal analysis of soundboard of the upright piano by Finite Element Method (FEM). Wood Res. 2014, 59, 123–136. [Google Scholar]
- Zienkiewicz, O.C.; Taylor, R.L. The Finite Element Method; McGraw Hill Book Company: London, UK, 1967. [Google Scholar]
- Hughes, J.R. The Finite Element Method: Linear Static and Dynamic Finite Element Analysis; Dover Publications: Mineola, NY, USA, 1987. [Google Scholar]
- Kaselouris, E.; Nikolos, I.K.; Orphanos, Y.; Bakarezos, M.; Papadogiannis, N.A.; Tatarakis, M.; Dimitriou, V. Elastoplastic study of nanosecond-pulsed laser interaction with metallic films using 3D multiphysics fem modeling. Int. J. Damage Mech. 2016, 25, 42–55. [Google Scholar] [CrossRef]
- Kaselouris, E.; Nikolos, I.K.; Orphanos, Y.; Bakarezos, E.; Papadogiannis, N.A.; Tatarakis, M.; Dimitriou, V. A review of simulation methods of laser matter interactions focused on nanosecond laser pulsed systems. J. Multiscale Model. 2013, 5, 1330001. [Google Scholar] [CrossRef]
- Bilbao, S. Conclusion and perspectives. In Numerical Sound Synthesis: Finite Difference Schemes and Simulation in Musical Acoustics; John Wiley & Sons: Hoboken, NJ, USA, 2009; pp. 386–388. [Google Scholar]
- Välimäki, V.; Pakarinen, J.; Erkut, C.; Karjalainen, M. Discrete-time modelling of musical instruments. Rep. Prog. Phys. 2006, 69, 1–78. [Google Scholar] [CrossRef]
- Chauhan, C.; Singru, P.; Vathsan, R. The effect of the extended bridge on the Timbre of the Sarasvati Veena: A numerical and experimental study. J. Meas. Eng. 2021, 9, 23–35. [Google Scholar] [CrossRef]
- Bader, R. Physical model of a complete classical guitar body. In Proceedings of the Stockholm Music Acoustics Conference, Stockholm, Sweden, 6–9 August 2003; Volume 1, pp. 21–124. [Google Scholar]
- Bader, R. Computational Mechanics of the Classical Guitar; Springer: Berlin/Heidelberg, Germany, 2005. [Google Scholar]
- Moosrainer, M.; Fleischer, H. Application of BEM and FEM to musical instruments. In Boundary Elements in Acoustics; Advances and Applications; WIT Press: Southampton, UK, 2000. [Google Scholar]
- Richardson, B. Numerical modeling of stringed musical instruments. In SMAC 93; Friberg, A., Ed.; Royal Swedish Academy of Music: Stockholm, Sweden, 1993; pp. 457–462. [Google Scholar]
- Kaselouris, E.; Alexandraki, C.; Orphanos, Y.; Bakarezos, M.; Tatarakis, M.; Papadogiannis, N.A.; Dimitriou, V. Acoustic analysis of impact sound on vibrating circular membranes. In Proceedings of the INTER-NOISE 2021—2021 International Congress and Exposition of Noise Control Engineering, Washington, DC, USA, 1–4 August 2021; Institute of Noise Control Engineering: Reston, VA, USA, 2021; Volume 63, pp. 3378–3385. [Google Scholar]
- Schleske, M. Empirical Tools in Contemporary Violin Making: Part I. Analysis of Design, Materials, Varnish, and Normal Modes. Catgut Acoust. Soc. J. 2002, 4, 50–64. [Google Scholar]
- Hutchins, C.M. A history of violin research. J. Acoust. Soc. Am. 1983, 73, 1421–1440. [Google Scholar] [CrossRef]
- Woodhouse, J. The acoustics of the violin: A review. Rep. Prog. Phys. 2014, 77, 115901. [Google Scholar] [CrossRef]
- Hutchins, C.M.; Benade, V. (Eds.) Research Papers in Violin Acoustics, 1975–1993; Acoustical Society of America: Washington, DC, USA, 1996; Volumes 1 & 2. [Google Scholar]
- Knott, G.A.; Shin, Y.S.; Chargin, M.A. Modal analysis of the violin. Finite Elem. Anal. Des. 1989, 5, 269–279. [Google Scholar] [CrossRef]
- Bretos, J.; Santamaria, C.; Moral, J.A. Vibrational patterns and frequency responses of the free plates and box of a violin obtained by finite element analysis. J. Acoust. Soc. Am. 1999, 105, 1942–1950. [Google Scholar] [CrossRef]
- Rodgers, O.; Anderson, P. Finite element analysis of violin corpus. Catgut Acoust. Soc. J. 2001, 4, 13–26. [Google Scholar]
- Gough, C.E. A violin shell model: Vibrational modes and acoustics. J. Acoust. Soc. Am. 2015, 137, 1210–1225. [Google Scholar] [CrossRef]
- Marshall, K.D. Modal analysis of a violin. J. Acoust. Soc. Am. 1985, 77, 695–709. [Google Scholar] [CrossRef]
- Jansson, E.; Molin, N.-E.; Saldner, H.O. On eigen modes of the violin—Electronic holography and admittance measurements. J. Acoust. Soc. Am. 1994, 95, 1100–1105. [Google Scholar] [CrossRef]
- Rossing, T.D.; Molin, N.-E.; Runnemalm, A. Modal analysis of violin bodies viewed as three-dimensional structures. J. Acoust. Soc. Am. 2003, 114, 2438. [Google Scholar] [CrossRef]
- Bissinger, G. Structural acoustics of good and bad violins. J. Acoust. Soc. Am. 2008, 124, 1764–1773. [Google Scholar] [CrossRef] [PubMed]
- Hutchins, C.M. The acoustics of violin plates. Sci. Am. 1981, 245, 170–186. [Google Scholar] [CrossRef]
- Rubin, C.; Farrat, D.F. Finite element modelling of violin plate vibrational characteristics. J. Catgut Acoust. Soc. 1987, 47, 8–11. [Google Scholar]
- Rodgers, O. The effect of elements of wood stiffness on violin plate vibration. J. Catgut Acoust. Soc. 1988, 1, 2–8. [Google Scholar]
- Schumacher, R.T. Compliances of wood for violin top plates. J. Acoust. Soc. Am. 1988, 84, 1223–1235. [Google Scholar] [CrossRef]
- Yu, Y.; Jang, I.G.; Kim, I.K.; Kwak, B.M. Nodal line optimization and its application to violin top plate design. J. Sound Vib. 2010, 329, 4785–4796. [Google Scholar] [CrossRef]
- Stanciu, M.D.; Coşereanu, C.; Dinulică, F.; Bucur, V.T. Effect of wood species on vibration modes of violins plates. Eur. J. Wood Wood Prod. 2020, 78, 785–799. [Google Scholar] [CrossRef]
- Lu, Y. Comparison of Finite Element Method and Modal Analysis of Violin Top Plate. Master’s Thesis, McGill University, Montréal, QC, Canada, 2013. [Google Scholar]
- Molin, N.E.; Lindgren, L.-E.; Jansson, E.V. Parameters of violin plates and their influence on the plate modes. J. Acoust. Soc. Am. 1988, 83, 281–291. [Google Scholar] [CrossRef]
- Richardson, B.E.; Roberts, G.W.; Walker, G.P. Numerical modelling of two violin plates. J. Catgut Acoust. Soc. 1987, 47, 12–16. [Google Scholar]
- Gough, C. Violin plate modes. J. Acoust. Soc. Am. 2015, 137, 139–153. [Google Scholar] [CrossRef]
- Curtin, J. Tap tones and weights of old Italian violin tops. J. Violin Soc. Am. 2005, 20, 161–174. [Google Scholar]
- Gonzalez, S.; Salvi, D.; Baeza, D.; Antonacci, F.; Sarti, A. A data-driven approach to violin making. Sci. Rep. 2021, 11, 9455. [Google Scholar] [CrossRef] [PubMed]
- Gonzalez, S.; Salvi, D.; Antonacci, F.; Sarti, A. Eigenfrequency optimisation of free violin plates. J. Acoust. Soc. Am. 2021, 149, 1400–1410. [Google Scholar] [CrossRef] [PubMed]
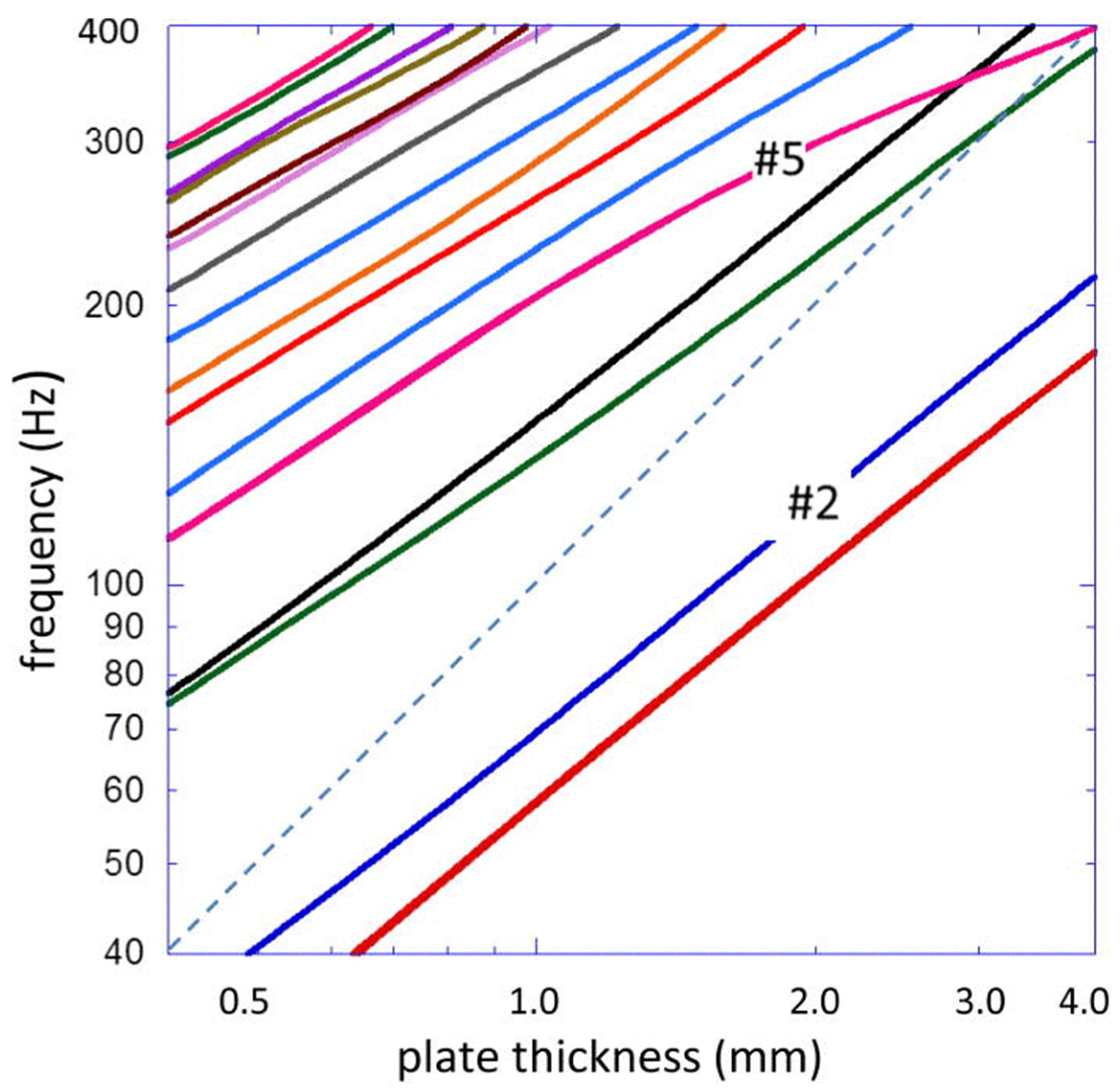
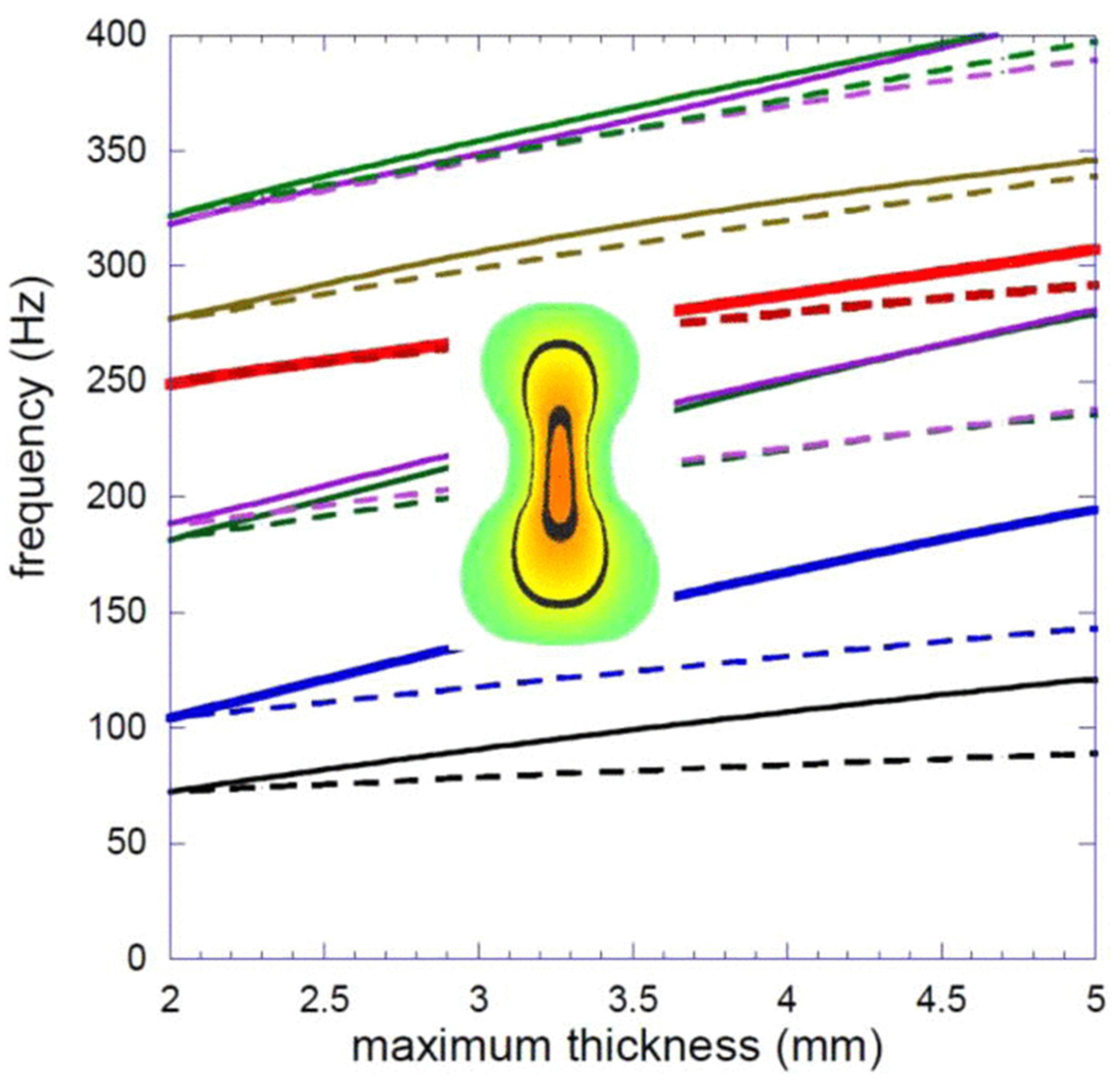
- Kaselouris, E.; Orphanos, Y.; Bakarezos, M.; Tatarakis, M.; Papadogiannis, N.A.; Dimitriou, V. Influence of the plate thickness and material properties on the violin top plate modes. In Proceedings of the INTER-NOISE 2021—2021 International Congress and Exposition of Noise Control Engineering, Washington, DC, USA, 1–4 August 2021; Institute of Noise Control Engineering: Reston, VA, USA, 2021; Volume 263, pp. 3369–3377. [Google Scholar]
- Wilczyński, T.J.; Filipek, R.; Wilczyński, P. Investigation of influence of pre-stresses on Viola da Gamba sound using FEM. In Proceedings of the 7th Forum Acusticum, FA 2014, Krakow, Poland, 7–12 September 2014. [Google Scholar]
- Bakarezos, M.; Gymnopoulos, S.; Brezas, S.; Orphanos, Y.; Maravelakis, E.; Papadopoulos, C.I.; Tatarakis, M.; Antoniadis, A.; Papadogiannis, N.A. Vibration analysis of the top plates of traditional greek string musical instruments. In Proceedings of the 13th International Congress on Sound and Vibration 2006, ICSV 2006, Vienna, Austria, 2–6 July 2006; Volume 6, pp. 4939–4946. [Google Scholar]
- Elejabarrieta, M.J.; Ezcurra, A.; Santamaría, C. Evolution of the vibrational behavior of a guitar soundboard along successive construction phases by means of the modal analysis technique. J. Acoust. Soc. Am. 2000, 108, 369–378. [Google Scholar] [CrossRef] [PubMed]
- Skrodzka, E.; Lapa, A.; Linde, B.B.J.; Rosenfeld, E. Modal parameters of two incomplete and complete guitars differing in the bracing pattern of the soundboard. J. Acoust. Soc. Am. 2011, 130, 2186–2194. [Google Scholar] [CrossRef]
- Torres, J.A.; Boullosa, R.R. Influence of the bridge on the vibrations of the top plate of a classical guitar. Appl. Acoust. 2009, 70, 1371–1377. [Google Scholar] [CrossRef]
- Ezcurra, A. Influence of the material constants on the low frequency modes of a free guitar plate. J. Sound Vib. 1996, 194, 640–644. [Google Scholar] [CrossRef]
- Torres, J.A.; De Icaza, M.; Boullosa, R.R. Variations in Mechanical Properties of Wood Plates Due Fluctuations on Relative Humidity of Air Mater. Res. Soc. Symp. Proc. 2012, 1, 139–144. [Google Scholar]
- Shepherd, M.R.; Hambric, S.A.; Wess, D.B. The effects of wood variability on the free vibration of an acoustic guitar top plate. J. Acoust. Soc. Am. 2014, 136, EL357. [Google Scholar] [CrossRef]
- Salvi, D.; Gonzalez, S.; Antonacci, F.; Sarti, A. Modal analysis of free archtop guitar top plates. J. Acoust. Soc. Am. 2021, 150, 1505–1513. [Google Scholar] [CrossRef] [PubMed]
- Viala, R.; Pérez, M.A.; Placet, V.; Manjón, A.; Foltête, E.; Cogan, S. Towards model-based approaches for musical instruments making: Validation of the model of a Spanish guitar soundboard and characterization features proposal. Appl. Acoust. 2021, 172, 107591. [Google Scholar] [CrossRef]
- Kindel, J.; Wang, I.-C. Modal analysis and finite element analysis of a piano soundboard. In Proceedings of the 5th International Modal Analysis Conference (IMAC), London, UK, 6–9 April 1987; pp. 1545–1549. [Google Scholar]
- Berthaut, J.; Ichchou, M.N.; Jézéquel, L. Piano soundboard: Structural behavior, numerical and experimental study in the modal range. Appl. Acoust. 2003, 64, 1113–1136. [Google Scholar] [CrossRef]
- Moore, T.R.; Zietlow, S.A. Interferometric studies of a piano soundboard. J. Acoust. Soc. Am. 2006, 119, 1783–1793. [Google Scholar] [CrossRef] [PubMed]
- Mamou-Mani, A.; Frelat, J.; Besnainou, C. Numerical simulation of a piano soundboard under downbearing. J. Acoust. Soc. Am. 2008, 123, 2401–2406. [Google Scholar] [CrossRef] [PubMed]
- Ege, K.; Boutillon, X.; Rébillat, M. Vibroacoustics of the piano soundboard: (Non)linearity and modal properties in the low- and mid-frequency ranges. J. Sound Vib. 2013, 332, 1288–1305. [Google Scholar] [CrossRef]
- Corradi, R.; Miccoli, S.; Squicciarini, G.; Fazioli, P. Modal analysis of a grand piano soundboard at successive manufacturing stages. Appl. Acoust. 2017, 125, 113–127. [Google Scholar] [CrossRef][Green Version]
- Zhang, C.-Z.; Ye, B.-Y.; Hu, X.-Z.; Zhao, X.-Z.; Cao, Y.-F. Finite element simulation application for vibration characteristic of violin. Key Eng. Mater. 2014, 620, 662–667. [Google Scholar] [CrossRef]
- Torres, J.A.; Soto, C.A.; Torres-Torres, D. Exploring design variations of the Titian Stradivari violin using a finite element model. J. Acoust. Soc. Am. 2020, 148, 1496–1506. [Google Scholar] [CrossRef]
- Zygmuntowicz, S. The Strad 3D project: Scientists, musicians, and violinmakers study three classic violins. J. Acoust. Soc. Am. 2010, 127, 1791. [Google Scholar] [CrossRef]
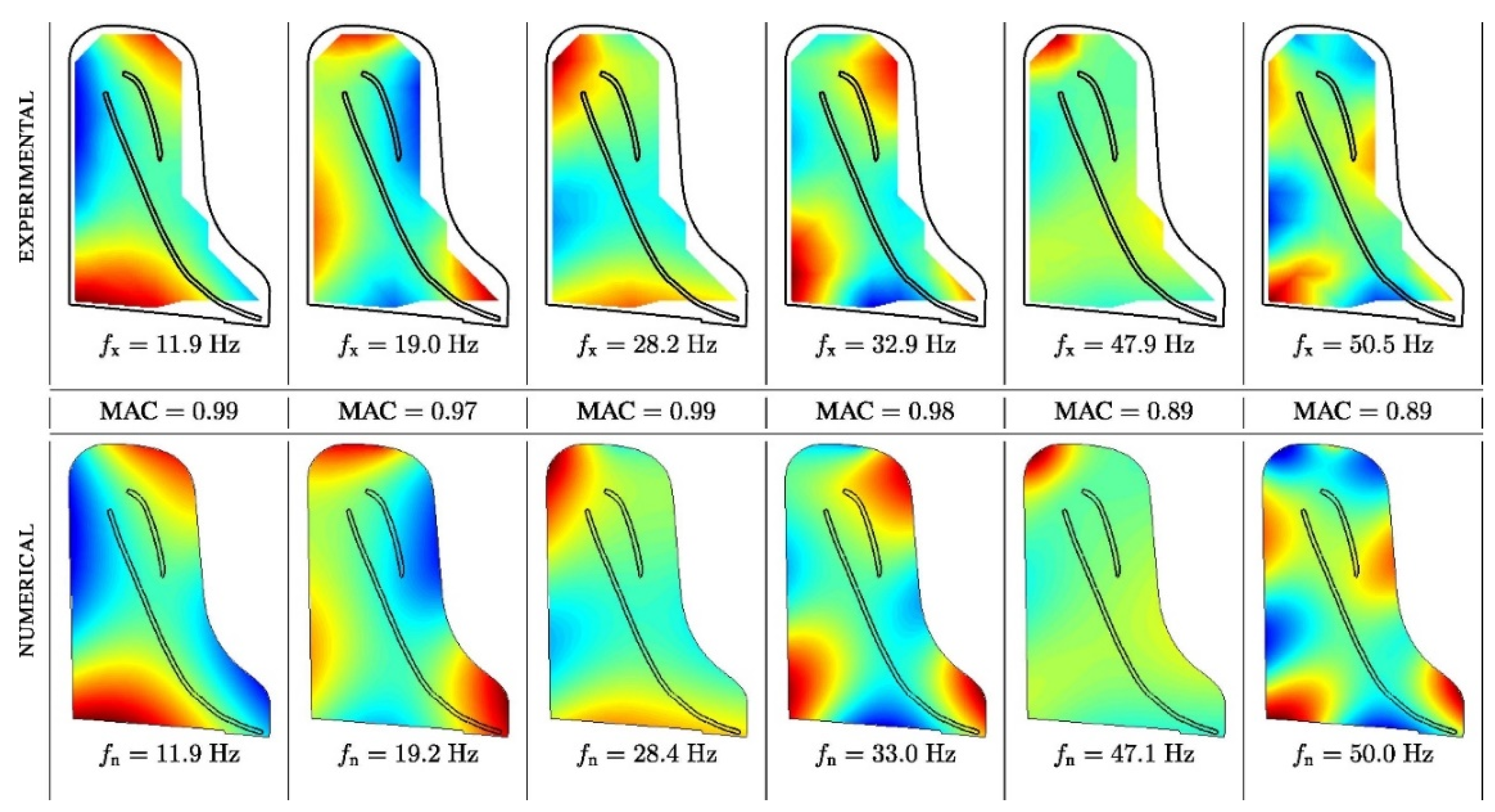
- Viala, R.; Placet, V.; Le Conte, S.; Vaiedelich, S.; Cogan, S. Model-Based decision support methods applied to the conservation of musical instruments: Application to an antique cello. In Model Validation and Uncertainty Quantification; Conference Proceedings of the Society for Experimental Mechanics Series; Springer: Cham, Switzerland, 2020; pp. 223–227. [Google Scholar]
- Pedrammehr, S.; Aghdam, N.J.; Pakzad, S.; Ettefagh, M.M.; Sadeghi, M.H. A study on vibration of Setar: Stringed Persian musical instrument. J. Vibroeng. 2018, 20, 2680–2689. [Google Scholar] [CrossRef]
- Mansour, H. Modal Analysis of the Setar: A Numerical-Experimental Comparison. J. Vib. Acoust. Trans. ASME 2015, 137, 61006. [Google Scholar] [CrossRef]
- Patil, K.; Baqersad, J.; Ludwigsen, D.; Dong, Y. Extracting vibration characteristics of a guitar using finite element, modal analysis, and digital image correlation techniques. Proc. Meet. Acoust. 2016, 29, 065003. [Google Scholar]
- Fleischer, H. Vibration of an electric bass guitar. Acta Acust. United Acust. 2005, 91, 247–260. [Google Scholar]
- Elejabarrieta, M.J.; Santamaría, C.; Ezcurra, A. Air cavity modes in the resonance box of the guitar: The effect of the sound hole. J. Sound Vib. 2002, 252, 584–590. [Google Scholar] [CrossRef]
- Jansson, E.V. Acoustical properties of complex cavities prediction and measurements of resonance properties of violin-shaped and guitar-shaped cavities. Acustica 1977, 37, 211–221. [Google Scholar]
- Rossing, T.D.; Popp, J.; Polstein, D. Acoustical response of guitars. In SMAC 83; Royal Swedish Academy of Music: Stockholm, Sweden, 1985; pp. 311–332. [Google Scholar]
- Runnelmalm, A.; Molin, N.E. Air cavity modes in sound boxes recorded by TV holography. J. Acoust. Soc. Am. 1999, 105, 1125. [Google Scholar] [CrossRef]
- Elejabarrieta, M.J.; Ezcurra, A.; Santamaria, C. Coupled modes of the resonance box of the guitar. J. Acoust. Soc. Am. 2002, 111, 2283–2292. [Google Scholar] [CrossRef]
- Ezcurra, A.; Elejabarrieta, M.J.; Santamaría, C. Fluid-structure coupling in the guitar box: Numerical and experimental comparative study. Appl. Acoust. 2005, 66, 411–425. [Google Scholar] [CrossRef]
- Paiva, G.O.; Dos Santos, J.M.C. Modeling fluid-structure interaction in a Brazilian guitar resonance box. In Proceedings of the 22nd International Congress of Mechanical Engineering (COBEM 2013), Ribeirão Preto, SP, Brazil, 3–7 November 2013. [Google Scholar]
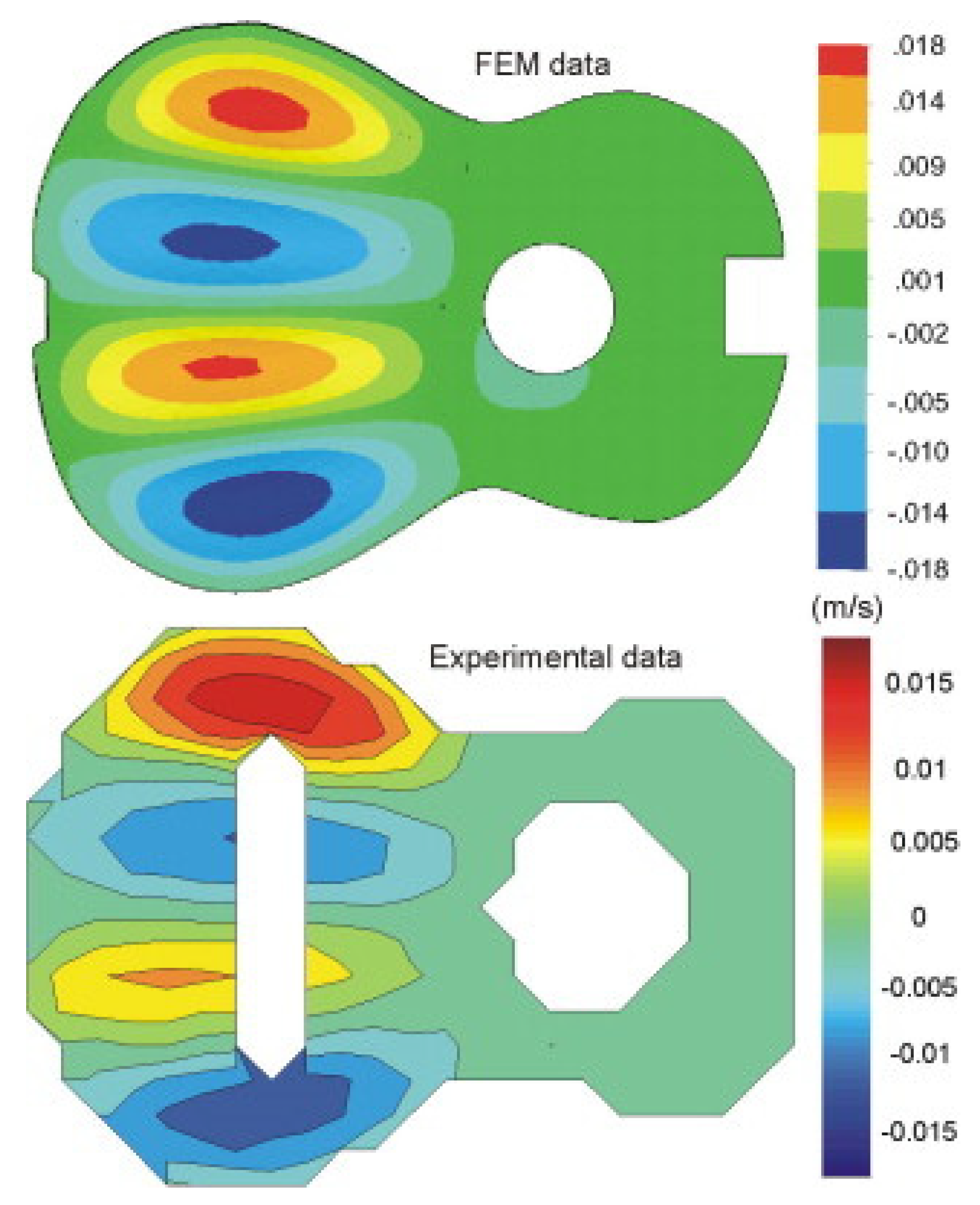
- Vieira, M.; Infante, V.; Serrão, P.; Ribeiro, A.M.R. Experimental-numerical correlation of the dynamic behavior of the Portuguese guitar. Appl. Acoust. 2018, 131, 51–60. [Google Scholar] [CrossRef]
- Chauhan, C.; Singru, P.M.; Vathsan, R. Vibro-acoustic modeling, numerical and experimental study of the resonator and its contribution to the timbre of Sarasvati veena, a South Indian stringed instrument. J. Acoust. Soc. Am. 2021, 149, 540–555. [Google Scholar] [CrossRef] [PubMed]
- Brooke, M.; Richardson, B.E. Numerical modeling of guitar radiation fields using boundary elements. J. Acoust. Soc. Am. 1991, 89, 1878. [Google Scholar] [CrossRef]
- Pyrkosz, M.A.; Van Karsen, C. Coupled vibro-acoustic model of the Titian stradivari violin. In Topics in Modal Analysis I; Conference Proceedings of the Society for Experimental Mechanics Series; Springer: Berlin/Heidelberg, Germany, 2014; Volume 7, pp. 317–332. [Google Scholar]
- Yokoyama, M. Coupled numerical simulations of the structure and acoustics of a violin body. J. Acoust. Soc. Am. 2021, 150, 2058–2064. [Google Scholar] [CrossRef] [PubMed]
- Chatziioannou, V. Reconstruction of an early viola da gamba informed by physical modeling. J. Acoust. Soc. Am. 2019, 145, 3435–3442. [Google Scholar] [CrossRef] [PubMed]
- Mansour, H.; Kasaiezadeh, A.; Arzanpour, S.; Behzad, M. Finite element modeling of setar, a stringed musical instrument. In Proceedings of the ASME 2009 International Mechanical Engineering Congress and Exposition, Sound, Vibration and Design, Lake Buena Vista, FL, USA, 13–19 November 2009; Volume 15, pp. 591–597. [Google Scholar]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kaselouris, E.; Bakarezos, M.; Tatarakis, M.; Papadogiannis, N.A.; Dimitriou, V. A Review of Finite Element Studies in String Musical Instruments. Acoustics 2022, 4, 183-202. https://doi.org/10.3390/acoustics4010012
Kaselouris E, Bakarezos M, Tatarakis M, Papadogiannis NA, Dimitriou V. A Review of Finite Element Studies in String Musical Instruments. Acoustics. 2022; 4(1):183-202. https://doi.org/10.3390/acoustics4010012
Chicago/Turabian StyleKaselouris, Evaggelos, Makis Bakarezos, Michael Tatarakis, Nektarios A. Papadogiannis, and Vasilis Dimitriou. 2022. "A Review of Finite Element Studies in String Musical Instruments" Acoustics 4, no. 1: 183-202. https://doi.org/10.3390/acoustics4010012
APA StyleKaselouris, E., Bakarezos, M., Tatarakis, M., Papadogiannis, N. A., & Dimitriou, V. (2022). A Review of Finite Element Studies in String Musical Instruments. Acoustics, 4(1), 183-202. https://doi.org/10.3390/acoustics4010012






