Abstract
Prior to Sabine’s work on the Fogg Art Museum and Boston Symphony Hall, several numerical guidelines had been developed and applied to the design of rooms with specific acoustic demands such as theatres, concert halls, and opera houses. Previous papers have discussed guidelines based on the following principles: voice directivity, which was employed in the design of at least 11 rooms; “echo theory”, which quantifies the perception threshold between direct sound and first order reflections in order to prevent echoes from occurring, aiding in the design of at least 7 rooms and leading to the first known use of an acoustic scale model; and notions of reverberation, which influenced the design of at least 14 rooms. This paper discusses three additional pre-Sabine numerical guidelines that were used in room acoustic design: (1) audience rake, (2) stage acoustics and proscenium design, and (3) length, width, and height ratios. The origin of these theories, as well as examples of rooms in which they were applied, are discussed and compared to current practices in room acoustic design.
1. Introduction
With the proposal of the reverberation time formula in 1898, Wallace Clement Sabine was the first to describe an objective and quantifiable relationship that could be used in architectural acoustics design [1]. This discovery laid the foundation for architectural room acoustics as a science. However, many concert halls with outstanding acoustic reputations, such as the Wiener Musikvereinssaal (1870) and the Amsterdam Concertgebouw (1888), were constructed prior to Sabine’s work [2], making acoustical design practices from the pre-Sabine era a point of interest for the analysis of historical room acoustics.
Several design concepts have been observed in pre-Sabine times. [3] identified two pre-Sabine design approaches—undulatory and geometrical acoustics [3,4]. The first can be traced back to the writings of Vitruvius [5] (p. 132), who stated that sound propagates in a circular shape, like the waves caused by a stone cast in still water (called “undulatory” acoustics by [4]). Based on this concept, referencing ancient Greek authors, Vitruvius discussed four acoustic behaviours of reflecting sites (from [6]):
- Acoustically dissonant (“kat-echountes”). This would be associated with prevalent diffusion or scattering.
- Reverberant (“peri-echountes”).
- Echoic (“anti-echountes”). This would be associated with noticeable, unwanted echoes.
- Acoustically consonant (“syn-echountes”). This would be associated with a supportive acoustic, beneficial reflections, being desirable for theatres.
Based on these quality indicators, Vitruvius argued that the voices of actors should be unobstructed, in order to create favorable room-acoustic conditions (according to [3] termed circulation of sound or unobstruction of propagation). Therefore, a theater should be constructed so that a line drawn from the first to the last seats should connect the tops of all seats. In addition, he recommended that a cornice be constructed halfway up the perimeter walls in order to prevent the sound from dispersing upwards.
Based on undulatory acoustics, a metric guideline was developed, building on the directivity and propagation distance of the human voice—this was utilized in several halls also during the 18th and 19th centuries [7]. Acoustic experimentation was used to determine how far sound was perceivable towards the front, sides, and rear of a speaking person. The results were used in the acoustical design of at least five lecture halls, four theaters, one opera hall, and one concert hall constructed in Germany, England, and the USA.
The 17th century saw the emergence of geometrical acoustics, based on the assumption that the trajectory of sound was analogous to light rays reflected from a surface [3]. Architects employed this concept to “guide” the sound by adjusting the space’s geometry. At the end of the 18th century numerical guidelines were developed based on geometrical acoustics [8,9]. This so-called “echo theory” was based on a quantification of the perception threshold between direct and reflected sounds. If a first order reflection exceeded a certain threshold, an echo would be perceived, which was considered detrimental for the acoustics. In at least seven rooms with specific acoustical demands, architects based the shape of the auditorium and/or placement of reflective or absorbent materials on this echo theory. Ref [10] studied the archeoacoustic history of the Palais du Trocadero (1878–1937), one of these seven rooms [10]. The room acoustic design concept and the 1909 renovation were carried out in order to improve the acoustics and were based on “echo theory”. In this study, numerical computer simulations were carried out to investigate several of the design options and renovations by the architects of the time. Geometrical studies based on “echo theory” during the design process had a slight positive influence on the room-acoustics; however, they could not prevent the poor acoustic results due to sound concentrations caused by numerous curved surfaces. The 1909 renovation was only partially successful in solving the acoustic problems.
In general, one can state that historic voice directivity guidelines concerned the direct sound and that “echo theory” considered early reflections. These theories ignored the late arriving reflections or reverberation. Even before Sabine’s work, Reference [11] showed that several acousticians already considered the influence of sound absorption of materials and room volume on the acoustics of spaces with room acoustic demands [11]. Reference [12] similarly examine pre-Sabine designs, with a specific focus on small Italian Opera halls, highlighting various notions including the relevance of the scenic arch, separation of the acoustic volumes of the stage and the audience, homogeneity of direct sound, geometric ratios, and the echo-flutter phenomena.
The goal of several recent papers [7,8,9,10,11,12] has been to highlight the evolution of room acoustic design and application of different approaches prior to Sabine. This paper reviews the origin, influence on design, and physical viability of three further pre-Sabine design guidelines. In Section 2, early views on the audience rake are discussed. In Section 3, historic theories on stage acoustics and proscenium opening width are presented. In Section 4, historic views on the ratio between the length, width, and height dimensions of the audience volume are presented. Section 5 compares these guidelines to current practices in room acoustic design as well as describing their physical and psychoacoustic viability according to current understanding.
2. Audience Rake
The audience rake of several lecture halls constructed during the 18th and 19th century was curvilinear. The origins of this might lie in Greek and Roman theaters as many Roman theatres had at least two different angles of audience slopes [13]. Examples are the Roman amphitheatre at Nimes, where the height of the steps increased as they become more remote from the arena [14] and the Epidauros theater whose seating area has two different angles [6]. This section discusses the acoustic ideas during the 18th and 19th century behind this curvilinear audience rake.
2.1. Marcus Vitruvius Pollio (20 BC)
Marcus Vitruvius Pollio (hereafter Vitruvius) included ideas about the audience rake in his book Architectura [5]. He argued that the audience should be constructed so that a line drawn from the first to the last step should touch the front angle of the tops of all the seats. According to Vitruvius, in this case the voice meets the receiver without impediment.
2.2. Johann Rhode (1800)
In Theorie der Verbreitung des Schalles für Baukünstler Rhode (1762–1827) reacted to Vitrivius’ statements on the audience rake [15]. He argued that the stepped arrangement of seats, especially where the building in which it is adopted is curved in plan, is eminently advantageous as it reduces the chance of echoes arising. He observed [15] (translation of extract p. 37):
Here it is proper to inquire whether in a theater of curvilinear rake in which the seats are arranged as steps, one above another, any echo of the sound can at all become perceptible. I deny the possibility of it. The sound in such a building never encounters at the same instant of time a resisting mass from which a reflection, sufficient to be perceptible to the hearing, could be possible. It strikes the first range of seats before the second, and the echo from the first is lost before that from the second has arisen, and so on up to the top. The ancients, inasmuch as all their theatres had this arrangement, cannot have depended at all upon the reflex echo of sound.
2.3. John Scott Russell (1839)
In 1839, John Russel (1808–1882) aimed to discover in what manner the audience area of a building for public speaking should be shaped, so that each audience member sees and hears without interruption from other audience members (see Figure 1) [16]. According to Russell, the seats must be arranged not as a straight line, but on a concave curve to be set out as follows:
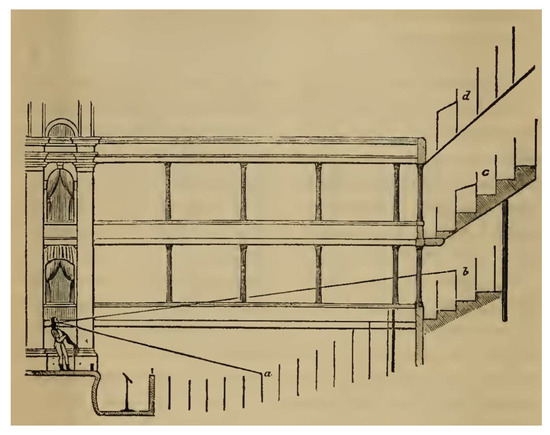
Figure 1.
Illustration of calculation of optimum audience rake after Russell [16]. Positions a, b, c, and d represent the vertical elevations of individuals in different parts of the room.
- The position and height of the speaking person and of the auditor occupying the first seat are determined.
- A line is drawn from the speaking person’s mouth touching the point where the top of the first auditor’s head comes.
- At the proper distance the situation of the seat for the second auditor is to be marked and on the line indicating the back of it a height of 1 foot 6 inches ( ) or less is to be set off upwards from the point where the ray from the speaker’s mouth touched; this is to mark the position of the top of the head of the second auditor.
- By repeating this process, adding 18 inches ( ) at each seat, a series of points are found all ranged in a curve (which Russell called the isacoustic, or equally-hearing curve).
- Each seat will be placed about 2 ft 9 inches ( ) below the mark indicating the top of the head of its occupant, and the floor on which each stands should be about 1 foot 6 inches ( ) lower still.
This curve, when the audience area is significantly below the speaking person on stage, has the property of dipping down slightly at its commencement. In this case Russell stated that a flat floor might be employed without serious disadvantage for part of the curve. The degree of steepness generated will vary with circumstances, for instance whether it is essential for the auditors to look down for taking notes or merely to look up at the speaking person on stage, the more space that can be allowed for each seat from front to back, the greater the inclination that will be required.
2.4. Théodore Lachèz (1848)
This theory was further developed by Théodore Lachèz in Acoustique et optique des salles de réunions publique [17]. He proposed a study of a hall with raised tiered seating along a curve to optimize sightlines. According to Lachèz, this courbe audio-visuelle was dependent on (1) the space between chairs, (2) the elevation of the chairs above the floor, (3) the average height between the visitor’s eye and the chairs’ sitting area, and (4) the average distance between the visitor’s top of the head and eye. Lachèz further studied the implications of this courbe audio-visuelle (see Figure 2), making the following observations:

Figure 2.
Various audience rake studies according to Lachèz [17] and sight-/sound-lines which abide by the courbe audio-visuel. Images courtesy of the Bibliothèque nationale de France.
- The more the object to be seen is elevated, the less inclination the seats for the auditory require; the more the seats for the auditory are elevated, the lower the object to be seen can be placed.
- But the distance from the auditory to the object to be seen exercises a considerable influence upon the inclination of the seats, and the elevation of the point of sight.
2.5. Practical Examples
These theories were widely employed in auditorium design during the 19th century. For instance:
- George Saunders’ Lecture Theatre of the Royal Institution (1802) was designed with a section based on this principle [14]. This lecture hall, with mainly wooden finishes, has established a good reputation for its acoustics [18].
- Two of the rooms in the building for the Collegiate Department of the University of Pennsylvania were designed by Professor A.D. Bache in 1830 following this principle [19].
- After the forming of the Free Church of Scotland in 1843, several new churches adopted Scott Russell’s curve for the seating layout [14].
- One of the classrooms attached to St. Martin’s Hall, designed by Richard Westmacott (1847–1867), used this principle to ensure that the teacher could be distinctly heard and seen by the entire class [14].
- The orchestra and choir seating for the Handel Festival at the Crystal Palace in London (1854) adopted a rake according to this principle [14] (Note, it is quite possible that John Scott Russell was involved in the design of this event as he was secretary to the building committee for its original erection in 1851 and closely involved in its re-erection at Sydenham Hill in 1854. However, direct evidence for this theorem was not uncovered during the course of this study). The acoustics of this concert hall has received mixed reactions [20].
- The houses of Parliament in Vienna (1883) designed by Baron von Hansen (The architect of the Vienna Musikverein) [21].
- The Chicago Auditorium (1889), designed by architects Louis Sullivan and Dankmar Adler [22]. The Auditorium Theatre is known for its good acoustics.
- New Welsh presbyterian chapel, Ruthin, North Wales (1889) [23].
3. Stage Acoustics and Proscenium Opening Width
During the 18th and 19th centuries, a number of books on architectural acoustics described the design of various contemporary theaters, operas, and concert halls [24,25,26]. An important design consideration was the stage acoustics and proscenium opening width. This section presents pre-Sabine thoughts on this topic.
3.1. Carl Friedrich Langhans (1810)
In order to come to an ideal width for the stage opening, architect Carl Friedrich Langhans (1781–1869) studied famous opera halls and recently built theaters (see Table 1) [26]. He concluded that even the most renowned architects had not dared to design a proscenium opening exceeding 47 feet in width ( ). According to Langhans, the main reason for this limit was the limited contemporary lighting possibilities. Based on the design of other theaters, Langhans laid out three ground rules for good visual and acoustical conditions in theaters:

Table 1.
Stage openings of several operas and theaters according to Langhans.
- Places without a sufficient view of the stage should be avoided.
- Places on the sides of the stage should not be as far away as those directly facing the stage, in order to decrease the number of audience members who have a view of the stage and the scenery from the side.
- The stage opening width should not be too large, otherwise, due to the orientation of the actor to the audience at the sides, the intelligibility and transmission of the speech from an actor on the extreme side of the stage would be disadvantageous.
3.2. Ernst Florenz Friedrich Chladni (1826)
Ernst Chladni (1756–1826) wrote about room acoustics in 1826 in an article in the Allgemeine Musikalische Zeitung [27]. Concerning the stage width of concert halls, he mentioned that the space an orchestra takes should not be larger than necessary. This is because too large a distance between the musicians furthest away from each other leads to late arriving sound at the other end of the orchestra, complicating the communication, so that ensemble playing is deteriorated. As an example, he cited a concert in the original Gewandhaus (1781–1886) in Leipzig [27] (translation of extract pp. 567–568):
Not long after the inauguration of the Leipzig concert hall, the conductor Hiller in a rehearsal positioned both choirs during C.P.E. Bach’s two-choir Heilig Cantata away from one other, the one on the stage and the other in the loges opposite, to see its acoustical effect. He stood in the middle of the hall. He was unable to establish ensemble singing between both choirs, as one choir heard the singing of the other too late. He came to the conclusion that both choirs need to be positioned on the stage.
3.3. Johann Wetter (1829)
In 1829, Johann Wetter wrote Untersuchungen über die wichtigsten Gegenstände der Theaterbaukunst [28]. In this book, Wetter describes how the proscenium opening width depends on the building’s size and purpose. Existing theaters presented a proscenium opening width from 25 to 48 Rheinland feet (7.8 to 15.1 ), typically randomly chosen according to Wetter. In theaters for conversation pieces, the stage opening width needs to be seen in opposite ratio to length; the deeper the stage is, the further away the actors and spectators are and consequently the need for sound reinforcement by reflections from the scenery on stage. In addition, narrower walls to the sides of the proscenium are closer to the sound center and are therefore more capable of reflecting the sound into the audience area. On the other hand, the wider the proscenium opening width and the more widely spaced the walls in the auditorium, the less capable they are of keeping the sound together and reflecting it into the audience area. For instance, if the auditorium back wall is 70 to 80 ft (22.0 to 25.1 ) from the stage, it is not advisable to design a stage opening wider than 42 ft ( ) and even better to limit it to 35 ft ( ). When the distance between actor and furthest spectator is less than 70 ft ( ), then the stage opening can be up to 60 ft ( ) wide. When a room is solely meant for opera, the stage opening width could be even further increased as according to Wetter the sound of music spreads much further than speech.
3.4. Practical Examples
In the following rooms, inaugurated during the 19th century, the stage opening width was reduced on acoustic grounds:
- The Iffland Theater, Berlin (1802–1817): The architect, Carl Gotthard Langhans, stated that the size of a theater depends primarily on the stage opening width [29]. He looked at other theaters in Europe and found that in Paris, in London, and in all of Italy, none of the stage opening widths were over 40 to 43 ft ( to ), except for St. Carlos in Naples which according to Langhans Sr. was 48 ft ( ). He ignored this theater as it was merely an opera house. Based on the limitation of the stage opening width and historical voice directivity experiments [7], Langhans chose the theater’s elliptical shape. He stated that since the stage opening determines the diameter of the circular line, one must still try to gain as much space as possible, it follows quite naturally that this results in an ellipse, which also followed the contemporary rules of room acoustics. Despite the design’s intentions, the acoustics turned out to be poor, with disturbing perceivable focusing effects [26].
- Academy of Music, Philadelphia (1857): The architects Napoleon LeBrun and Gustavus Runge designed the opera house with a stage opening of 48 ft () [30]. They employed the rationale that direct sound and first order reflections should reach the auditor as loudly as possible and that disturbing reflections should be prevented. In order to reinforce the first order reflections, they employed “resonating” materials for the stage area. In order to determine which reflections were disturbing they employed “echo theory”. Finally, the architects considered a greater stage opening width detrimental for the acoustics, as it complicates ensemble playing of the actors and the sound “would lose itself in the stage” instead of reaching the audience area. Various conductors have given mixed reviews on the quality of the orchestral sound in the hall [2].
- Victoria Theater, Berlin (1859–1891): The architectural output of Langhans Jr. includes several rooms with specific acoustical demands such as the Stadttheater in Liegnitz (now Legnica, 1839), the Opera in Breslau (now Wroclaw, 1841), Herzogliches Hoftheater in Dessau-Roßlau (1856–1922), the Victoria Theater in Berlin (1859–1891), and the Stadttheater in Leipzig (1867–1945). During the course of this study no documents were uncovered that describe the acoustic concepts behind the Liegnitz, Breslau and Dessau rooms. However, Langhans did describe the acoustic concept of the Victoria Theater in the Zeitschrift für Bauwesen of 1860 [31]. The Victoria Theater was an original architectural experiment which combined a summer and winter theater (i.e., an auditorium with two stages of which one was in the open). Langhans reduced the stage opening from 50 to 38 ft (15.2 to 11.6 ).
4. Length-Width-Height Ratio
Famously, numerous well-known shoe-box concert halls have length, width, and height dimensions that are simple multiples. Additionally, the up-scaling of acoustically satisfying rooms’ dimensions was common practice in pre-Sabine concert hall design. The traces of length-width-height ratio is based on an ancient idea of musical analogy, developed, for example, in the Renaissance architectural theory of Leon Battista Alberti [32]. This section discusses possible justifications for architects in the 18th and 19th century to adopt such approaches.
4.1. William Gardiner (1841)
In 1841, William Gardiner wrote about the ideal proportions for a concert hall [33]. He stated that, in order to prevent sound concentrations, one should avoid curvatures and circular walls. He found the best form for a concert hall was a parallelogram or long square. He recommended the figure of two cubes as a model. He derived his ideas from observation that old cathedrals of this shape were the finest buildings for music.
4.2. Scott Russell (1847)
In a meeting of the Institute of Architects, Scott Russell presented his thoughts on the principles of good room acoustic design [34]. In this presentation he alluded to the spontaneous oscillation of air in a chamber, which was the source of much trouble, but might be turned to useful purpose. He reasoned that a long chamber of air, if caused to oscillate, continued to do so, and would produce a tone depending on the length—as in an organ-pipe. Thus a gallery, 64 ft ( ) long, would produce the note C; and if 32 ft ( ) long, it would be an octave higher. Every chamber had its own voice. A speaker should find out the key-note of the room, and speak in it if possible.
According to Russell, this fact could be employed to improve conditions for hearing by paying attention to the dimensions and proportions. Length, width, and height should be in harmonious proportions, or the sounds produced would sound aggressive: there was a more intimate connection between music and architecture than was generally admitted. Simple multiples for the proportions were desirable; for example, 48 ft ( ) long, 24 ft ( ) wide, and 16 ft ( ) high. With an eye towards modal behaviours, incongruous sounds neutralize each other and produce dead points, or points where the speaker would not be heard. Care was necessary in this respect.
4.3. Jabez Upham (1852)
Similarly, based on phenomena exhibited in the vibration of musical strings and pipes, Jabez Upham (1820–1902) described his experiences in the American Journal of Science:
The proportions as well as the form of a music room, are not a matter of indifference. We have already noticed the tendency of one vibrating body or medium to throw another, in contact or in its immediate vicinity, into a similar state of vibration. In this way the oscillations of the contained air of a room, communicated to its walls, produce therein a sympathetic vibration, which will be more or less perfect according as the structure of these walls, their subdivisions and general relations of length, width, and height, approximate to the acoustic conditions required. From this comes resonance, as we understand, the existence of which, to a considerable extent, in some rooms gives to the voice that peculiar brilliancy and resilient power which every singer must have noticed.
4.4. Thomas Roger Smith (1861)
In his book A Rudimentary Treatise on the Acoustics of Public Buildings, Thomas Smith (1830–1903) stated that he believed in the proper note of a room [14]. He postulated that the production of this note is due to the same laws which regulate the pitch of an organ pipe. Smith gave the example of sound reflections/echoes dying away from a sudden noise created in a room that has dimensions that are a common multiple for the proportion in length, width, and height:
Suppose, now, that the dimensions of the room bear to one another some simple ratio—say that of height 1, width 2, and length 4—it will follow that the repetitions caused by these echoes will strike the ear of any hearer in any part of the room at equally recurring intervals. For instance, in a room 28 ft ( ) high, 56 ft ( ) wide, and 112 ft ( ) long, the echo in each direction would follow paths of which that from floor to ceiling and back would be 56 ft long, and consequently could be traversed 20 times in a second; that from one side to the other and back would be 112 ft long ( ) and traversed 10 times in a second; and that from end to end and back 224 ft ( ), and traversed 5 times in a second. There would be other echoes audible, varying with the relative positions of the hearer, and the point where the sound was made, but the equable recurrence of those just enumerated would be what would excite sonorous agitation in the air.
Smith noted that the 5, 10, or even 20 repetitions in a second are not audible. He reasoned that as with sounding strings or columns of air which divide themselves into equal portions, this would also be the case in a room’s acoustics. Therefore, the “note of the room” would be a harmonic of the aforementioned repetitions per second. If the room did not have a length-width-height ratio that had a common multiple, Smith postulated:
Supposing, however, the dimensions such, that reflections, as they successively strike the ear, come always at irregular and quite incommensurable intervals, that is to say that the pulsation passing and repassing from side to side will very seldom coincide with those passing from end to end, or from floor to ceiling, the result will be that, from the moment that the sound proper to the room and excited in it by the echoes of any other sound, begins to appear, a noise, and not a note, will be audible.
4.5. Practical Examples
In the following rooms, inaugurated during the 19th century, the ratios between length, width, and height were designed to be the multiple of a common number for acoustic reasons:
- Theater of the Royal Institution (1802): The lecture hall’s dimension are in very simple relation to one another, the height, length, and width being in the ratio 2:3:4 respectively, and within a few inches giving dimensions of 30, 45, and 60 feet (, , and ). Smith [14] called this one of the reasons for its room acoustic excellence.
- Boston Music Hall (1852): Based on the previously presented theory, the dimensions of the Boston Music Hall were designed to be 130 ft () long, 78 ft () wide, and 65 ft () high, a ratio of 10:6:5 [35]. Higginson (owner of the Boston Symphony Orchestra) once remarked “[O]ur present hall [Boston Music Hall] gives a piano better than a forte, gives an elegant rather than a forcible return of the instruments—noble but weak—I want both”.
- Reid Concert Hall (1859): This Edinburgh concert hall, by Professor John Donaldson (1789–1865) and Scottish Architect David Cousin, was purposely designed to abide by the principle of harmonic ratios. Its main dimensions are 30 feet, 48 feet, and 90 feet (, , and ), a ratio of 5:8:15 [14].
- Wiener Musikverein (1870): This concert hall has proportions similar to its predecessor, the Redoutensaal [36]. From opening on, the Musikverein’s acoustics have been renowned.
- Neues Gewandhaus (1884–1944): The acoustic concept of the Neues Gewandhaus was based on the original Gewandhaus and the Palais du Trocadero [37]. Architects Martin Gropius and Heino Schmieden copied the dimensions from the existing Gewandhaus and scaled them up by approximately . One can assume that as the original Gewandhaus’ acoustics were well-liked, and the architects attempted to recreate its “sympathetic vibration” in the newly erected concert hall. The acoustics of the Neue Gewandhaus were well received by the German press [38]. The concert hall became an example of excellence in acoustics.
- Amsterdam Concertgebouw (1888): This concert hall has a length of 44 , width of 28 , and a height of 17 , close to a common multiple of 9 [2]. While not directly stated by its architect, one can assume that these dimensions were based on the previously described theory. The acoustics were initially part to mixed reviews, however a stage renovation in 1899 heralded its renowned acoustic reputation [39].
5. Current Practices in Room Acoustic Design
The design strategies developed in the pre-Sabinian era regarding audience rake, stage acoustics, and geometrical ratios for rooms are still of substantial interest and importance in the current room acoustic and architectural design of auditoria. To the detriment of auditoria designed (and built) after the second world war, many of the ideas discussed in the texts referenced in this article were lost in the clamour to modernise architectural design and were only rediscovered in the later 20th century, and/or are continuing to be rediscovered and applied to auditorium design today.
5.1. Audience Rake and Sightlines
The methodologies described by Russell [16] and Lachèz [17] for calculating optimum sight- and sound-lines from a speaker or instrument on stage to all audience locations are still used in contemporary auditorium design. Nowadays, the demands on audience comfort and emergency evacuation have led to greater spacing between rows, larger aisle dimensions, and limitations on the geometry of steps and stairs. Nevertheless, the mathematics of the ideal audience rake for optimum sightlines and sound-lines remains unchanged, it is only the input parameters that have been adjusted. A clear line from the speaker or musician on stage to each audience member – both to provide unimpeded transmission of the direct sound and for a clear view – is still used as the starting point for developing the audience organization, superposition in balconies, and the floor rake. This methodology has been codified in national guidelines and standards, notably in the Chinese standards for auditoria [40] where the geometrical objective is defined by a line between the audience member’s eye and a reference point on stage. At each audience row, a minimum vertical spacing called the c-value (typically around 12 ) is be achieved between these lines to ensure visibility of the target point. The c-value takes into account an average person’s height and head-size as well as the (potential) staggering of seats in the audience rows.
In the earlier part of the 20th century there was a general move away from traditional auditorium (and building) forms, with architects seeking novel layouts and turning to mathematics and (acoustical) science for inspiration. As in cinemas, many auditoria for music, theatre, and opera were designed with mathematically perfect sightlines for all seats, leading to, for instance, fan-shaped auditoria. Experience with such rooms has shown that this approach can not only lead to disappointing acoustic results (fan-shaped rooms have for example been shown to have very low acoustical envelopment [36] (p. 95)), but that the most enjoyable auditoria exhibiting a good sense of community and rapport between audience performers may necessitate some seats with less than optimum sightlines. The horseshoe opera house is a good example of this: as was pointed out in the 19th century texts, the seats in the side balconies cannot see the entire stage, but this disadvantage is weighed against the improved sense of community and connection between the stage and auditorium.
5.2. Stage Acoustics
Langhans’ [26], Chladni’s [27], and Wetter’s [28] texts from the 19th century refer to various acoustical effects related to stage acoustics and the room geometry in the vicinity of the stage: hearing oneself, hearing others, projection of the sound from the stage to the audience, and the amplifying effect of early reflections were variously discussed. The discussions in these texts are prescient and align in many regards with the conclusions from recent research.
At this time there was a clear focus on providing sufficiently strong sound transmission from the sources on stage to the audience, taking into account a number of factors—the directivity of the speaker or instrument (of which measurements had been made [7]); reflected sound paths; as well as ensuring that the sound arriving at the audience was sufficiently loud and intelligible for all source positions and speaker orientations on stage.
In Sabine’s article “Reverberation” [1] the argument for sufficient loudness is the first point that he makes, with his discussion of reverberation being the last point of three. Perhaps due to the attractiveness of a simply measurable and predictable acoustical quantity—as was provided by the Reverberation Time—the focus of auditorium design after Sabine became the provision of an appropriate Reverberation Time and the topics discussed in pre-Sabine references presented here were in many cases not picked up again until over a century later. Many concert halls, theatres, and opera houses were constructed in the meantime with little attention paid to the acoustical conditions on stage and generally for the provision of sufficient and sufficiently homogeneous loudness levels (strength) in the audience area, leading to numerous venues with significant acoustical problems [41,42,43,44]. Since Sabine, achieving an appropriate Reverberation Time for an auditorium has become standard design practice, while many of the positive (and in the authors’ opinion) correct statements and descriptions in these 19th century texts have still not made their way into standard auditorium design practice.
Chladni [27] describes what we now call ensemble or cross-communication in the context of an orchestra stage in a concert hall or rehearsal room. In contemporary concert hall design and in the design of orchestra rehearsal rooms, reflective surfaces are provided to overcome the “musical communication” challenges described by Chladni of distant instruments being heard too late and too weakly. Since the 1980s, reflectors suspended above orchestra stages have become a common sight: these are intended to provide early reflections across the stage as well as in the upstage-downstage direction in order to improve the acoustical communication between distant orchestra sections (while also providing early reflections for improved self-hearing). The soffits and balcony fronts next to the stage may also be acoustically optimized to provide early reflections back to the musicians on stage for improved ensemble and musical communication [43,45,46]. In the 1980s, Gade [41] performed measurements and developed the objective measure Support to describe and measure ensemble conditions within the orchestra.
Wetter’s book includes a thorough summary of the contemporary theory of acoustics in 1829, referring to state-of-the art research by Newton, d’Alembert, Poisson and so forth. While objective and subjective experiments into the effects of early reflections were in their infancy, Wetter nevertheless describes the possible effects of reflected sound—disturbance (echo), confusion, and amplification—in terms very similar to our current understanding. In relation to the stage and the form of the walls and ceiling next to the proscenium in a theatre or opera house, he discusses the optimum width between walls, height of the ceiling, and angle of surfaces to ensure that sound is projected from the stage to the furthest seats, without arriving so late that the reflected sound would be disturbing or confusing. In both Langhans and Wetter, performance practice, the position of actors on stage, and their orientation to the audience are discussed with respect to the directivity of speech—this was investigated previously [7]. The risk of poor speech clarity and intelligibility for seats in side balconies is discussed, related to the directivity of speech and leading to guidelines for the maximum width of the proscenium to ensure that the sound level is sufficient in all seats.
While performance practice has changed since these early writings, the concerns and solutions developed for modern auditoria are similar if not identical, but now thorough measurements and prediction methods using 3D computer models are available to calculate the direction, intensity, and time-of-arrival of direct and reflected sound. Exactly as Wetter describes, in contemporary theatre and opera design, the wall surfaces next to the proscenium are typically kept relatively narrow and splayed to project the sound from the stage to the audience. The audience at the sides is also placed closer to the stage and to the hall centre-line to account for the lower sound level emitted by a speaker in the lateral direction, compared to the frontal direction (4–5 less at 1 and less at 8 ) [47]. Forestage reflectors are also employed in modern opera houses and theatres to generate sufficiently strong and early reflections for the stalls audience [48]. In general, wall and ceiling surfaces are positioned so that the reflection arrives within the critical time window up to 50–80 after the direct sound (depending on source type) so that the reflection enhances the intelligibility and presence of the sound sources [49,50].
5.3. Length-Width-Height Ratios
The theories of “perfect” ratios for room dimensions are no longer applied in modern auditorium design as they were proposed in the 19th century. The ideas that a room should have a desirable “note” and that repeating dimensions somehow “support” the sound transmission or reverberation have been debunked. Sabine [1] himself wrote:
...the most definite and often repeated statements are such as the following, that the dimensions of a room should be in the ratio 2:3:5, or according to some writers, 1:1:2, and others, 2:3:4; it is probable that the basis of these suggestions is the ratios of the harmonic intervals in music, but the connection is untraced and remote.
In large auditoria with dimensions of tens of metres, as was already noted by Smith, the lowest room modes are in any case below the audible frequency range. At the lowest audible frequencies, the modal density in large rooms is generally sufficiently high that a particular “note” is not discernible even in rooms with simple multiples in their dimensional ratios.
Nevertheless, room dimensions and ratios are still extremely important in auditorium design. Instead of considering the relationship between room dimensions and acoustic frequency as in the 19th century, acoustic theory has shifted to considering the temporal and spatial effects of the room dimensions (along with the provision of an appropriate acoustical volume for the source loudness and desired room reverberation). The aim in auditorium design today is to find room dimensions, ratios, and geometries that enhance the transmission, amplification, and projection of the sound from the stage to the audience, and doing so in a non-frequency selective, broadband and balanced manner.
Small rooms for music are a special case—since the lowest room modes can be in the audible frequency range and also in the range of fundamental frequencies for some instruments, simple multiples of room dimensions are generally to be avoided so that the room does not exaggerate a particular note or key. Angled walls and ceilings can be used to reduce the intensity and to increase the bandwidth of room modes. In addition, room ratios [51] have been developed that space the room modes to avoid coincidences and to create rooms that are more homogeneous in their low frequency behaviour.
Room proportions are considered in detail during the acoustical planning of auditoria. A seminal piece of work in this regard is Marshall’s research into the properties of the concert hall cross-section [52]. The sidewall and balcony surfaces in a concert hall are some of the most important for generating early reflections—the width of the hall is therefore important in determining the arrival time of lateral reflections for much of the audience. The height of the ceiling also plays an extremely important role: although the exact ratio of width to height is not critical, the time of arrival of early reflections from the ceiling relative to the sides does have a strong impact on the subjective acoustical quality, and this is also believed to be dependent on source type (speech or music) [46]. In addition, in order to achieve a particular reverberation time and sufficiently large volume, the ceiling height is the main parameter that can be adjusted without creating an excessively wide hall.
A further concept regarding room ratios stems from Arau-Puchades’ work [53] on multidimensional reverberation. Arau-Puchades has developed formulas to predict the overall decay rate of a rectangular room based on the decay in three orthogonal directions, the total decay being the superposition of the three individual decays. More widely spaced surfaces (e.g., floor-to-ceiling or wall-to-wall distance) and lower absorption values on facing surfaces lead to longer mono-dimensional decay rates. The balance (or imbalance) of decay rates in the three dimensions (and/or in different parts of the hall) certainly affects the subjective acoustical quality of a space, with large imbalances leading to non-linear or multi-slope decays. While the audibility of non-linear decays has been investigated [54] and some concert hall designs specifically set out to take advantage of non-linear decays (for example halls with coupled reverberation volumes—Meyerson Hall, Dallas, TX, USA; Birmingham Symphony Hall, UK; KKL Lucerne, Lucerne, Switzerland; The Sage, Gateshead, UK), the application of Arau-Puchades’ formulas in the design of auditoria is not widespread and the understanding of the subjective effect of imbalanced multidimensional decay rates is not thoroughly understood.
6. Discussion
This study presents and discusses three pre-Sabine room acoustical theories used in the design of several rooms in the 19th century. The audience rake theory was mainly employed in lecture halls, historic stage acoustics theories were typically employed in proscenium theaters and opera houses, while theories on the optimum length, width, height ratios were generally applied to concert halls and rooms for music.
In previous papers, pre-Sabine theories on voice directivity [7], “echo theory” [8,9], and reverberation [11] have been examined. Together, these theories considered the entire room impulse response [11]. The direct sound being considered in theories based on historical voice directivity measurements, early reflections by “echo theory”, and the late reverberation was regarded by historic reverberation theories.
The theories presented here can also be analysed with regards to certain parts of the room’s impulse response. When discussing “audience rake”, the 19th century authors presented here all describe both visual and acoustic conditions, it is therefore clear that audience rake theories take direct sound into consideration. As theories on stage acoustics also considered good visual conditions, these theories can also be considered as relating primarily to direct sound. However, as Wetter describes that narrower walls next to the proscenium steer more reflections into the audience area, these theories also considered early reflections. As Upham describes that some rooms give to the voice that “peculiar brilliancy” and “resilient power” the theory on length-width-height ratios considers reverberation. However, this theory can be categorized neither into “undulatory acoustics” nor “geometrical acoustics” as described by [3], but is related to the understanding at the time of the harmonic series and resonances (such as in organ pipes) [3].
It has been shown that the presented historical theory on audience rake during the 19th century was mainly used in rooms for speech. Similar approaches are still used in rooms with both speech and musical use, where a clear line to the sound source is still used as the starting point for developing the audience organization, superposition in balconies, and the floor rake. During the 19th century, various authors referred to acoustical effects related to stage acoustics and the room geometry in the vicinity of the stage including that of hearing oneself, hearing others, projection of the sound from the stage to the audience, and the amplifying effect of early reflections. These notions in general align with the results of current research and similar approaches are still employed in room acoustic design. The historical concept regarding length-width-height ratios are no longer considered relevant. In current room acoustics design, the room dimensions, ratios, and geometries are optimised to enhance the transmission, amplification, and projection of the sound from the stage to the audience while also generating a homogeneous sound field with appropriate degrees of lateral energy and reverberation.
It is of interest to view room acoustic design prior to the work of Sabine as part of an evolution with architects designing halls inspired by the success of previous “good” halls and learning from the failures of “bad” halls. Part of this evolution were the notions, practices, and design guidelines presented here: audience rake, stage acoustics, length-width-height ratios as well as the previously presented historical concepts based on voice directivity, “echo theory”, and reverberation [7,8,9,10,11]. Table 2 presents a non-exhaustive overview of rooms which employed these different theories, or combinations thereof, in their acoustic design and or renovation. The quantity and distribution throughout Europe and North America show that room acoustics was already in these times an important design consideration with much discussion and exchange on the subject.

Table 2.
Rooms in this and previous studies [7,8,9,11] and the historic room acoustical theory employed in their design and or renovation.
7. Conclusions
Five of the six historic theories discussed are still employed in current room acoustic design. From the three theories presented in this study, two are still employed in an almost unchanged form in current room acoustic design—the audience rake is determined as it was in the 19th century and is even codified in standards, while the room acoustic design of surfaces in the stage area of proscenium theatres and opera houses is still an important consideration in room acoustic design. The length-width-height ratio theory has been debunked already before the 20th century. However, in different ways the use of ratios and dimensions are still very significant in room acoustic design. Parameters such as C50, C80, D50, and ITDG have significant similarities to “echo theory”, and voice directivity measurements were used in the 19th century very much as they still are employed to determine the shape and seat positions in auditoria.
It is remarkable that most pre-Sabine discussions on acoustics still have significant value and relevance to current room acoustic design, even if the acoustical and psycho-acoustical sciences behind the ideas were undeveloped or simply false. This is especially notable considering the limited knowledge on room acoustics and measurement equipment available to 19th century architects and scientists. In particular, the importance given to considerations of the strength of sound and sufficient homogeneity of strength throughout the audience, taking into consideration source directivity and performance practice, is notable given the recent attention to such factors [55,56]. However, the emergence and improved feasibility of evaluating strength, with the room acoustic parameter G, provides improved access to acousticians for such concepts [57]. Such considerations have tended to take a back seat since Sabine, leading to acoustical design targets focused on the reverberation time and other decay time or energy-balance based acoustical parameters. This has perhaps been to the detriment of modern room acoustics design and there is still much to learn from scientists and thinkers prior to the 20th century.
Author Contributions
Conceptualization, B.N.J.P.; methodology, B.N.J.P. and B.F.G.K.; software, B.N.J.P. and E.G. and E.K. and B.F.G.K.; validation, B.N.J.P. and E.G. and E.K. and B.F.G.K.; formal analysis, B.N.J.P. and E.G. and E.K. and B.F.G.K.; investigation, B.N.J.P. and E.G. and E.K.; resources, B.N.J.P. and E.G. and E.K. and B.F.G.K.; data curation, B.N.J.P. and E.G. and E.K.; writing–original draft preparation, B.N.J.P. and E.G. and E.K.; writing–review and editing, B.N.J.P. and E.G. and E.K. and B.F.G.K.; visualization, B.N.J.P. and E.G.; supervision, B.F.G.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
References
- Sabine, W. Collected Papers on Acoustics; Harvard University Press: Cambridge, UK, 1922; pp. 1–588. [Google Scholar]
- Beranek, L. How They Sound: Concert and Opera Halls; Acoustical Society of America: Melville, NY, USA, 1996; pp. 1–643. [Google Scholar]
- Barbieri, P. The acoustics of Italian opera houses and auditoriums (ca. 1450–1900). Recercare 1998, 10, 263–328. [Google Scholar]
- Barbieri, P. The state of architectural acoustics in the late renaissance. In Architettura e Musica Nella Venezia del Rinascimento; Howard, D., Moretti, L., Eds.; Bruno Mondadori: Milan, Italy, 2006; pp. 53–78. [Google Scholar]
- Morgan, M. The Ten Books on Architecture. Vitruvius, Translated by Josephus Gwilt; Harvard University Press: Cambridge, UK; Humphrey Milford: London, UK; Oxford University Press: Oxford, UK, 1914; pp. 1–413. [Google Scholar]
- Vassilantonopoulos, S.L.; Mourjopoulos, J. A Study of Ancient Greek and Roman Theater Acoustics. Acta Acust. United Acust. 2003, 89, 123–136. [Google Scholar]
- Postma, B.; Jouan, S.; Katz, B. Pre-Sabine room acoustic design guidelines based on human voice directivity. J. Acoust. Soc. Am. 2018, 143, 2428–2437. [Google Scholar] [CrossRef]
- Postma, B. A History of the Use of Time Intervals After the Direct Sound in Concert Hall Design Before the Reverberation Formula of Sabine Became Generally Accepted. Build. Acoust. 2013, 20, 157–176. [Google Scholar] [CrossRef]
- Postma, B.; Katz, B. A History of the Use of Reflections Arrival Time in Pre-Sabinian Concert Hall Design. In Proceedings of the Forum Acusticum, Krakow, Poland, 7–12 September 2014; pp. 1–6. [Google Scholar]
- Postma, B.; Dubouilh, S.; Katz, B.F.G. An archeoacoustic study of the history of the Palais du Trocadero (1878–1937). J. Acoust. Soc. Am. 2019, 145, 2810–2821. [Google Scholar] [CrossRef] [PubMed]
- Postma, B.; Katz, B.F.G. Pre-Sabine room acoustic assumptions on reverberation and their influence on room acoustic design. J. Acoust. Soc. Am. 2020, 147, 2478–2487. [Google Scholar] [CrossRef] [PubMed]
- D’Orazio, D.; Nannini, S. Towards Italian Opera Houses: A Review of Acoustic Design in Pre-Sabine Scholars. Acoustics 2019, 1, 252–280. [Google Scholar] [CrossRef]
- Cocci, A. Theatre design in ancient times: Science or opportunity? Acta Acust. United Acust. 2013, 99, 14–20. [Google Scholar] [CrossRef]
- Smith, T. A Rudimentary Treatise on the Acoustics of Public Buildings; John Weale: London, UK, 1861; pp. 1–163. [Google Scholar]
- Rhode, J. Theorie der Verbreitung des Schalles Für Baukünstler; English Title: Theory of the Propagation of Sound for Architects; Heinrich Frölich: Berlin, Germany, 1800; pp. 1–82. [Google Scholar]
- Russell, J. Elementary Considerations if some Principles in the Construction of Buildings designed to accommodate Spectators and Auditors. Edinb. New Philos. J. 1839, 27, 131–136. [Google Scholar]
- Lachèz, T. Acoustique et Optique des Salles de Réunion Publiques. Théâtres et Amphithéâtres, Spectacles, Concerts etc.; English Title: Acoustics and Optics of Public Meeting Rooms. Theaters and Amphitheatres, Performances, Concerts, etc.; Lemoine: Paris, France, 1848. [Google Scholar]
- Smith, T. On acoustics. Civ. Eng. Archit. J. 1861, 24, 46–53. [Google Scholar]
- Anonymous. Form of Lecture Rooms. J. Frankl. Inst. 1843, 5, 419. [Google Scholar]
- Smith, T.R. Architecture and Building: The Laws of Sound as Applied to the Arrangments of Buildings; Crosby Lockwood and Son: London, UK, 1895. [Google Scholar]
- Farrow, F. The Godwin Bursary: Report of a visit to Vienna and Budapest. Transactions 1885, 1, 55–64. [Google Scholar]
- Anonymous. Buffalo hot blast system of heating and ventilating, application to theaters. Illus. Gen. Cat. Buffalo Steel Plate Steam Pulley Fans 1892, 1, 84–85. [Google Scholar]
- Anonymous. New welsh presbyterian chapel, Ruthin. Br. Archit. J. Archit. Its Accessory Arts 1889, 32, 193. [Google Scholar]
- Patte, P. Essai sur L’architecture Théatrale; Chez Moutard: Paris, France, 1782; pp. 1–212. [Google Scholar]
- Saunders, G. Treatise on Theaters; I and J Taylor: London, UK, 1790; pp. 1–94. [Google Scholar]
- Langhans, C. Über Theater oder Bemerkungen über Katakustik; In English: About Theaters or Remarks about Catacoustics; Gottfried Hayn: Berlin, Germany, 1810; pp. 1–64. [Google Scholar]
- Chladni, E. Über vortheilhafte Einrichtung eines Locals für gute Wirkung des Schalles. English Title: About the Beneficial Setup of Rooms for the Good Effect of Sound. Allg. Musik. Ztg. 1826, 35, 565–570. [Google Scholar]
- Wetter, J. Untersuchungen über die Wichtigsten Gegenstände der Theaterbaukunst; In English: Studies about the most important theater construction subjects; Joseph Stenz: Mainz, Germany, 1829. [Google Scholar]
- Langhans, K. Vergleichung des Neuen Schauspielhauses zu Berlin mit Verschiedenen Ältern und Neuen Schauspielhuäsern in Rucksicht auf akustische und Optische Grundfäse; In English: Comparison of the New Theater in Berlin with Various Older and Newer Theaters Regarding Acoustics and Optics; Johann Friedrich Unger: Berlin, Germany, 1800; pp. 1–21. [Google Scholar]
- Runge, G. Das neue Opernhaus “Academy of music” in Philidelphia. English Title: The new opera house “Academy of music” in Philidelphia. Z. FÜr Bauwes. 1860, 10, 145–156. [Google Scholar]
- Langhans, C. Das Victoria Theater in Berlin. English Title: The Victoria-Theater in Berlin. Z. Bauwes. 1860, 10, 315–342. [Google Scholar]
- Pintore, A. Musical Symbolism in the Works of Leon Battista Alberti. Nexus Netw. J. 2004, 6, 49–70. [Google Scholar] [CrossRef][Green Version]
- Gardiner, W. The Music of Nature; J.H.Wilkins & R.B. Carter: Boston, MA, USA, 1841. [Google Scholar]
- Russell, J. The interior forms of buildings with reference to the laws of sounds. Builder 1847, 5, 82. [Google Scholar]
- Upham, J. A Consideration of Some of the Phenomena and Laws of Sound, Their Application in the Construction of Buildings, Designed Especially for musical Effects. Am. J. Sci. Art 1853, 65–66, 215–226. [Google Scholar]
- Barron, M. Auditorium Acoustics and Architectural Design; Taylor & Francis: London, UK, 1993; pp. 1–504. [Google Scholar]
- Schmieden, H. Das neue Gewandhaus in Leipzig. In English: The new Gewandhaus in Leipzig; In Zeitschrift Fur Bauwesen; Gewandhaus: Leipzig, Germany, 1886; pp. 1–14. [Google Scholar]
- Skoda, R. Neues Gewandhaus Leipzig. Baugeschichte und Gegenwart Eines Konzertgebäudes; In English: New Leipzig Gewandhaus. Building’s History and Present; Verlag Für Bauwesen: Berlin, Germany, 1985. [Google Scholar]
- van Royen, H. Historie en Kroniek van het Concertgebouw en het Concertgebouworkest 1888–1988. Dl. 1. Voorgeschiedenis 1888–1945; English Title: History and Chronicle of the Concertgebouw and the Concertgebouw Orchestra 1888–1988. part 1. History 1888–1945; Walburg pers: Zutphen, The Netherlands, 1989. [Google Scholar]
- JGJ 57-2016. Code for Design of Theater Building. In Code of China; China Construction Industry Press: Beijjing, China, 2016. [Google Scholar]
- Gade, A. Acoustics of the Orchestra Platform from the Musicians’ Point of View. In Proceedings of Acoustics for Choir and Orchestra, Royal Swedish Academy of Music No. 52; Royal Swedish Academy of Music: Stockholm, Sweden, 1986. [Google Scholar]
- Rindel, J. Design of new ceiling reflectors for improved ensemble in a concert hall. Appl. Acoust. 1991, 34, 7–17. [Google Scholar] [CrossRef]
- Green, E.; Essert, R. On-Stage Hearing: Experience from Orchestra Hall, Minneapolis; Institute of Acoustics: Milton Keynes, UK, 2015; Volume 37. [Google Scholar]
- Taylor, L.; Claringbold, D. Acoustics of the Sydney Opera House concert hall. In Proceedings of the International Congress on Acoustics, Sydney, NSW, Australia, 23–27 August 2010; Volume 20, pp. 1–8. [Google Scholar]
- Jurkiewicz, Y.; Kahle, E.; Katz, B.F. Stavanger Concert Hall, acoustic design and measurement results. In Proceedings of the Auditorium Acoustics, Paris, France, 29–31 October 2015; Volume 37, pp. 300–307. [Google Scholar]
- Miller, G.; Giegold, C.; Pfeiffer, S.; Schuette, D.; Brill, L. Orchestral Preferences for Discrete Overhead and Side Wall On-Stage Reflections. In Proceedings of the International Symposium on Room Acoustics, Amsterdam, The Netherlands, 15–17 September 2019. [Google Scholar]
- Meyer, J. Acoustics and the Performance of Music; Springer: New York, NY, USA, 2009. [Google Scholar]
- Beranek, L.; Hidaka, T.; Masuda, S. Acoustical design of the opera house of the New National Theatre, Tokyo, Japan. J. Acoust. Soc. Am. 2000, 107, 355–367. [Google Scholar] [CrossRef] [PubMed]
- Thiele, R. Richtungsverteilung und Zeitfolge der Schallruckwurfe in Räumen. English title: Directional distribution and sequence of the sound reflections in rooms. Acustica 1953, 3, 291–302. [Google Scholar]
- Reichardt, W.; Abdel Alim, O.; Schmidt, W. Definition und Messgrunde eines objektiven Masses zur Ermittlung der Grenze zwischen brauchbarer und unbrauchbarer Durchsichtigkeit bei Musikarbietung. English title: Definition and Basis of Making an Objective Evaluation to Distinguish Between Useful and Useless Clarity Defining Musical Performances. Acustica 1975, 32, 126–137. [Google Scholar]
- Louden, M.M. Dimension Ratios of Rectangular Rooms with Good Distribution of Eigentones. Acustica 1971, 24, 101–104. [Google Scholar]
- Marshall, A. A Note on the Importance of Room Cross-Section in Concert Halls. J. Sound Vib. 1967, 5, 100–112. [Google Scholar] [CrossRef]
- Arau-Puchades, H. An Improved Reverberation Time Formula. Acustica 1988, 65, 163–180. [Google Scholar]
- Luizard, P.; Katz, B.F.; Guastavino, C. Perceptual thresholds for realistic double-slope decay reverberation in large coupled spaces. J. Acoust. Soc. Am. 2015, 137, 75–84. [Google Scholar] [CrossRef]
- Lokki, T.; Pätynen, J. Architectural Features That Make Music Bloom in Concert Halls. Acoustics 2019, 1, 439–449. [Google Scholar] [CrossRef]
- Lokki, T.; McLeod, L.; Kuusinen, A. Perception of loudness and envelopment for different orchestral dynamics. J. Acoust. Soc. Am. 2020, 148, 2137–2145. [Google Scholar] [CrossRef]
- Katz, B.F.G. In-situ calibration of the sound strength parameter G. J. Acoust. Soc. Am. 2015, 138, EL167–EL173. [Google Scholar] [CrossRef] [PubMed]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).