The results presented in this study explore the effect of resonators spacings on the sound attenuation performance of a two Helmholtz resonator system. The effect of the second resonator and the importance of its location is prevailed by presenting the results of the transmission coefficient and the transmission loss. In addition, a detailed analysis of the acoustic field (pressure and velocity field) both inside the impedance tube and the resonator cavities are presented to elaborate the effect of the spacing between the resonators on the overall performance of the system.
3.1. Acoustic Behaviour of a Two Resonator System
A conventional aircraft acoustic liner consists of multiple resonating cavities. An understanding of optimised distribution may be exploited to maximise the acoustic performance and allow tailoring for targeted frequencies. The addition of multiple resonators in a duct has been known to have a complex effect on the sound field [
23]. To understand the complex nature of resonators interaction within an acoustic liner and its effect on the sound field, a simplified study has been defined using two resonators to characterise the interaction of two resonating cavities separated by a defined distance.
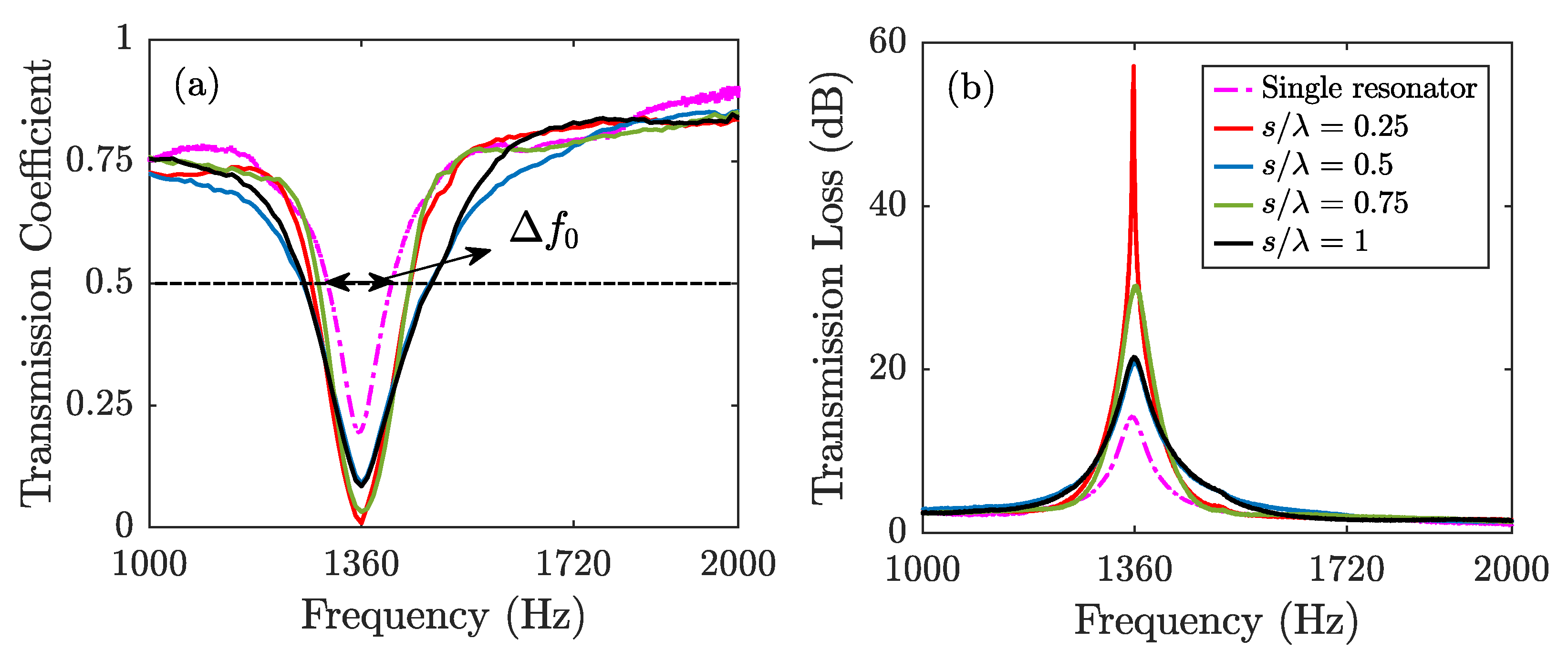
Figure 5 presents the transmission coefficient and transmission loss characteristics of a two resonator system in comparison with a single Helmholtz resonator, with resonator spacings of
.
Figure 5a presents the transmission coefficient, which can be described as the ratio of the transmitted sound power to the incident sound power, and may shed light on the range of frequencies attenuated by an acoustic treatment. The range of frequencies attenuated by the resonators was estimated at a transmission coefficient of 0.5 and was defined as
, as shown in
Figure 5. To further elaborate on the effect of the resonators’ separation distance on the acoustic behaviour, acoustic transmission loss, which is a measure of the magnitude of sound attenuated (in dB), is presented in
Figure 5b. Considering the results for a single resonator, the transmission coefficient exhibits a dip at around
Hz, as expected. In addition, the transmission loss exhibits a peak at around the same frequency. The results presented in
Figure 5 reveal that introducing a second resonator has a considerable effect on both transmission loss and coefficient. The transmission coefficient results in
Figure 5a show that the attenuated frequency range increases for all the separation distances compared to the single resonator results. Moreover, for
,
peaks and is 104% (114 Hz) larger than the single resonator case, whereas the transmission loss for
is 302% (42 dB) higher than a single resonator case. The results indicate that the distance between the resonators may lead to unexpected acoustic behaviours, which need further analyses to prevail the underlying mechanisms.
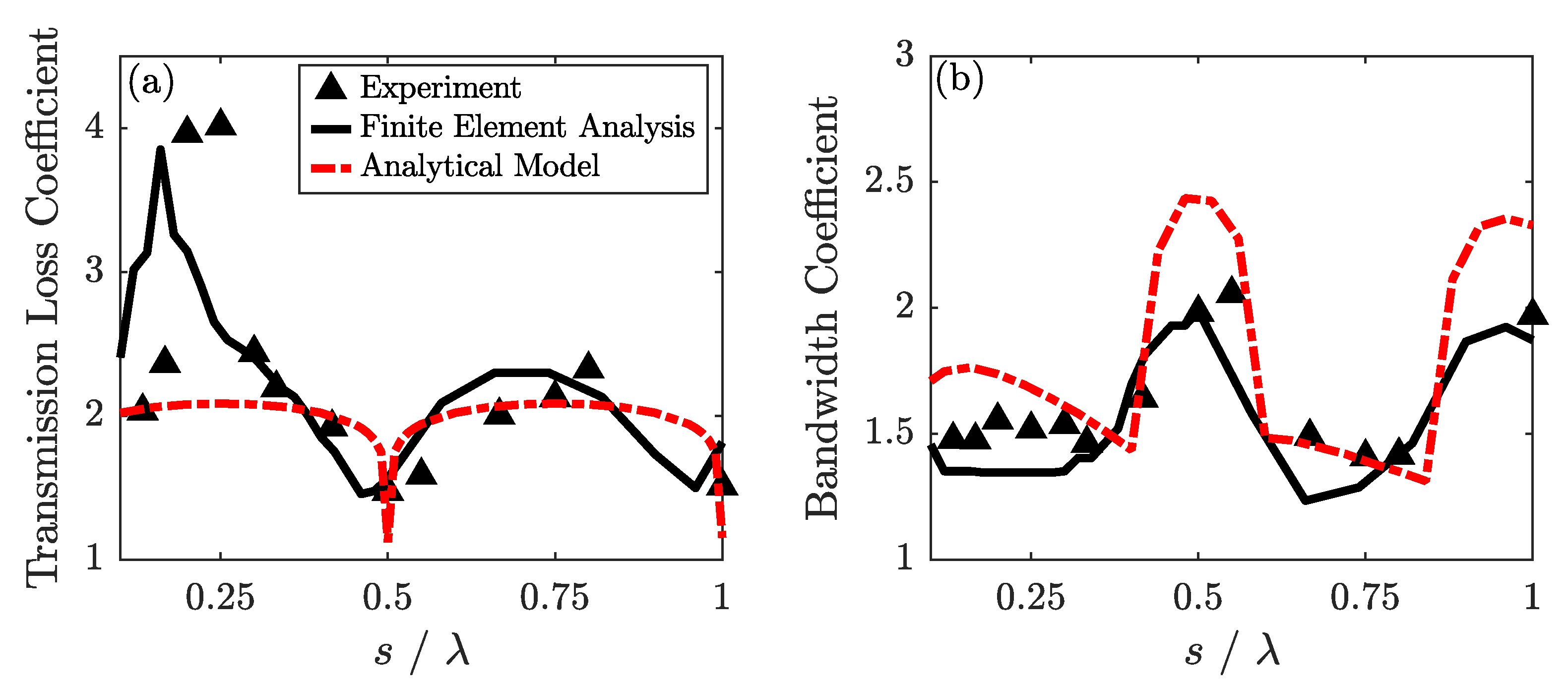
Figure 6 is constructed to gain a better understanding of the effect of the spacing on the sound attenuation performance induced by a two resonator system.
Figure 6a presents the normalised transmission loss as a function of
, over a wide range of separation distance, namely
. The normalised transmission loss is defined as,
where
is the peak transmission loss value for each individual resonator spacing configuration and
is the peak transmission loss value obtained when a single resonator is mounted on the duct. Moreover, the results obtained from both the finite element analysis and the analytical model are also presented along with the experimental results for validation purposes. It is worth noting that the finite element results are consistent with the experimental findings. The results from the analytical model are also consistent with the trends of the experimental and finite element analysis results, apart from cases with a small spacing between the two resonators. The analytical model assumes a plane wave propagation and does not take into account the effect of first resonator on the propagating wave. Moreover, the analytical model does not consider any thermal and viscous losses, which might take place in narrow regions, such as the neck of the resonators. The lack of consistency between the analytical results compared with the experimental and finite element analysis results at resonator spacings
to
may be attributed to the underlying assumptions and simplifications in the model. Considering the experimental results, normalised transmission loss exhibits a sinusoidal like response on changing the spacing between the two resonators. As the spacing between two resonators is increased, a peak transmission loss is obtained at
, which indicates that this particular spacing configuration leads to the highest sound attenuation in magnitude. These results are consistent with those obtained by Coulon et al. [
22] on the optimization of a concentric resonator array. A further increase in spacing leads to a local minimum at a spacing of
. Increasing the spacing beyond
leads to another peak in transmission loss at
, after which a minima is observed at
again.
To characterise the effect of resonator spacing on the bandwidth of the attenuated frequencies, a non-dimensionalised bandwidth coefficient was defined as,
where
is the frequency bandwith obtained at a transmission coefficient of 0.5, and
is the same value for the baseline single resonator case.
Figure 6b shows that the bandwidth coefficient reaches a maximum at
, which indicates that this particular spacing configuration is effective over the broadest range of frequencies. This observation is consistent with the results by Cai et al. [
23]. However, recall that this particular spacing configuration led to the lowest transmission loss peak (see
Figure 6a). Considering these results together, a relation between the resonators spacing, transmission loss, and transmission coefficient may be deduced, suggesting that the two resonator configurations that lead to the lowest transmission loss value, attenuates the broadest range of frequencies, and vice-versa. More interestingly, the results also indicate that there may exist an optimum spacing between the two resonators, at which maximum performance can be achieved.
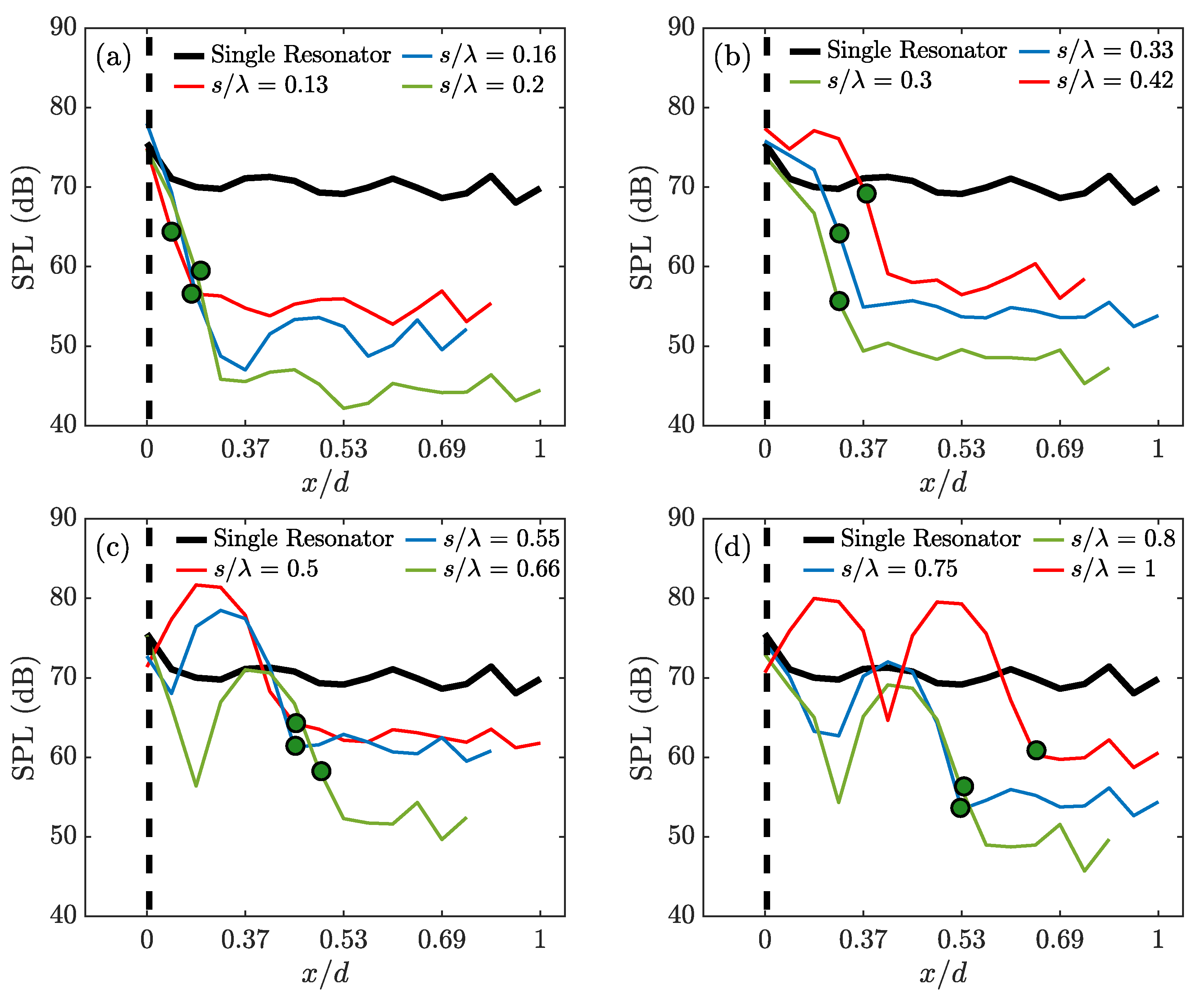
In order to corroborate the sound attenuation patterns observed in
Figure 6, data from microphones G1 to G20 were utilised to study the change in the SPL values at the resonance frequency (
1360 Hz), as the acoustic wave propagates downstream in the impedance tube test section.
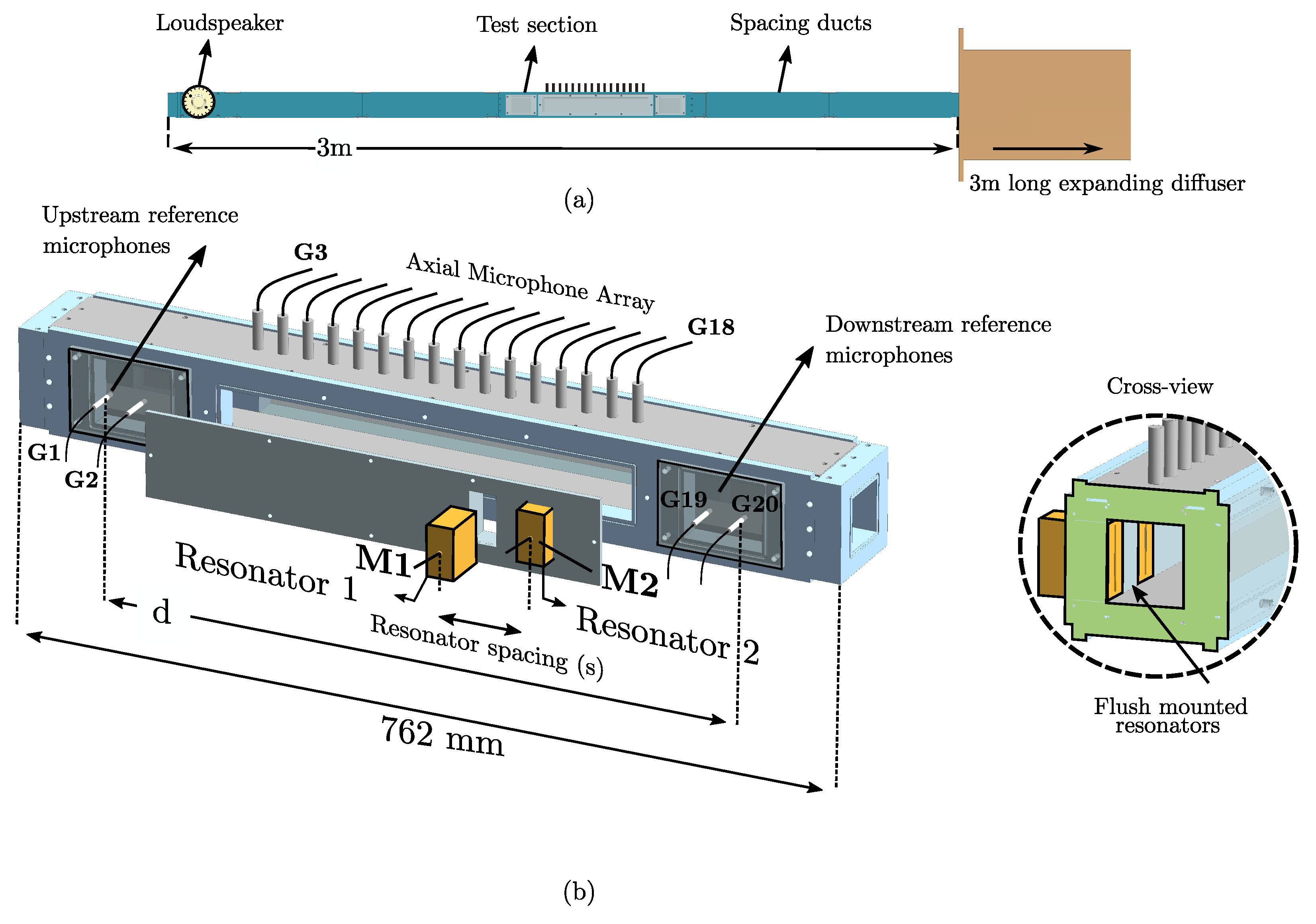
Figure 7 presents the SPL values against the spacing between the microphones G1 to G20, which are distributed along the impedance tube test section (see
Figure 1). The cumulative spacing between the microphones, given by “x”, is non-dimensionalised with the separation distance ‘d’, between microphones, G1 and G20. In order to ease the interpretation, the positions of the first and second resonators are shown with a black dotted line and a green circle, respectively. Considering the results for all spacing configurations (
Figure 7a–d), the SPL trend is seen to be significantly affected by the change in the spacing between the resonators. The overall change in sound pressure level, i.e., the difference between SPL values of the microphones G1 and G20, has an oscillating behaviour, which is consistent with the observations presented in
Figure 6, and not shown here for brevity. The change in sound pressure level gradually increases with distance between the resonators and reaches a maximum at
(
Figure 7a). As shown in
Figure 7b,c, as the spacing is further increased, the change in the SPL reduces gradually to a minimum at
(
Figure 7c). This trend repeats itself for the separation distances of
(
Figure 7d) and
(
Figure 7d), where the SPL change experiences a minimum and maximum, respectively. The cyclic trend seen in the SPL can be attributed to the halfwave resonances in the space between the two resonators. These halfwave resonances can be seen in
Figure 6c,d for
and
. The transmission loss induced by a two-resonator system is also limited by this halfwave resonance behaviour that takes place when the distance between the resonators equals to the integer number of half wavelengths.
To further explore the underlying physical mechanisms of the sound attenuation behaviour observed in
Figure 6 and
Figure 7, the acoustic field in the resonator cavities and the impedance tube was investigated in detail by both experimental and numerical studies. To analyse the time dependant nature of both the pressure and velocity fields inside the resonators, transient FEM simulations were carried out using COMSOL Multiphysics
at the resonance frequency
. Due to distinct behaviours observed at
and
, the following discussions are shaped around these four spacing configurations.
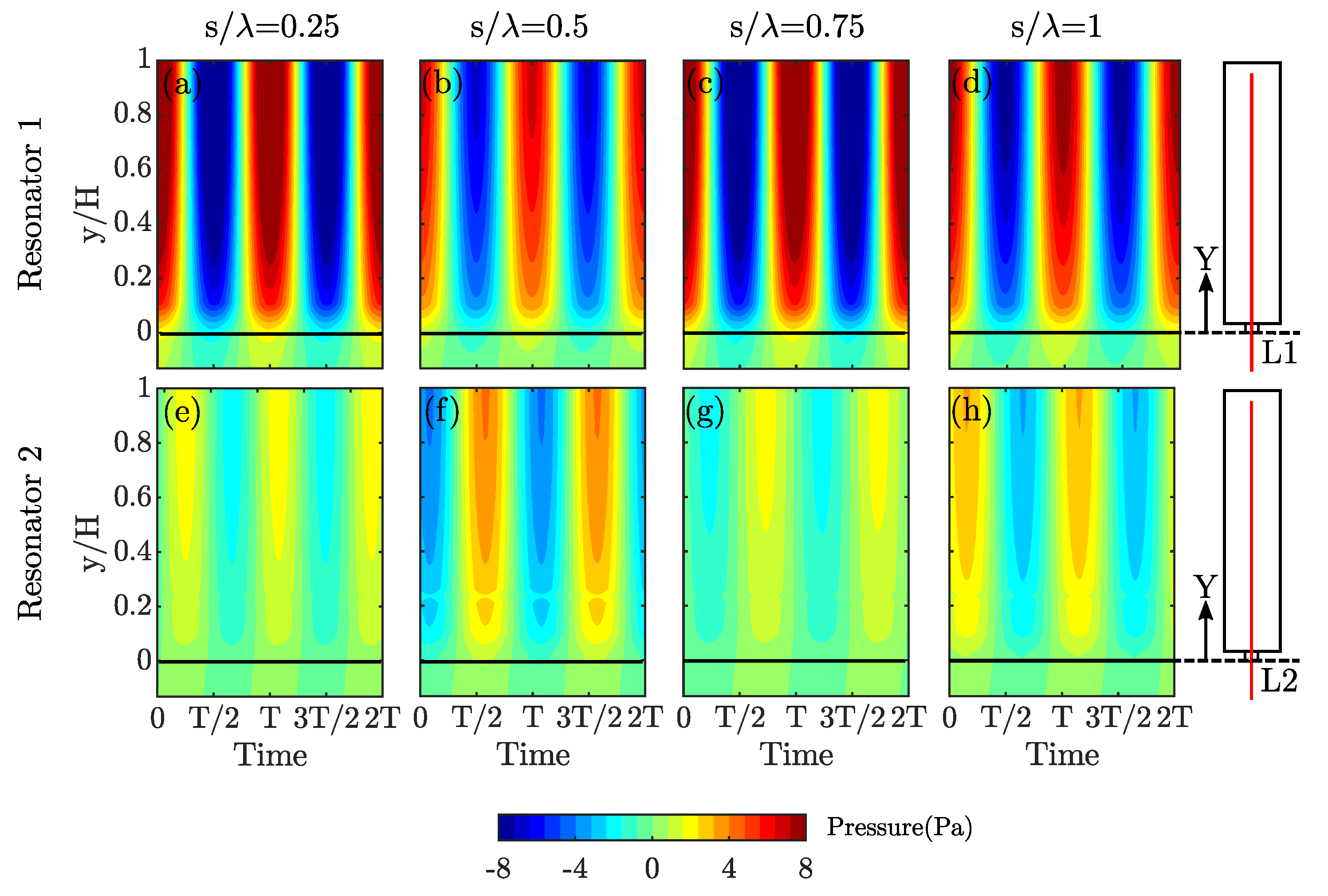
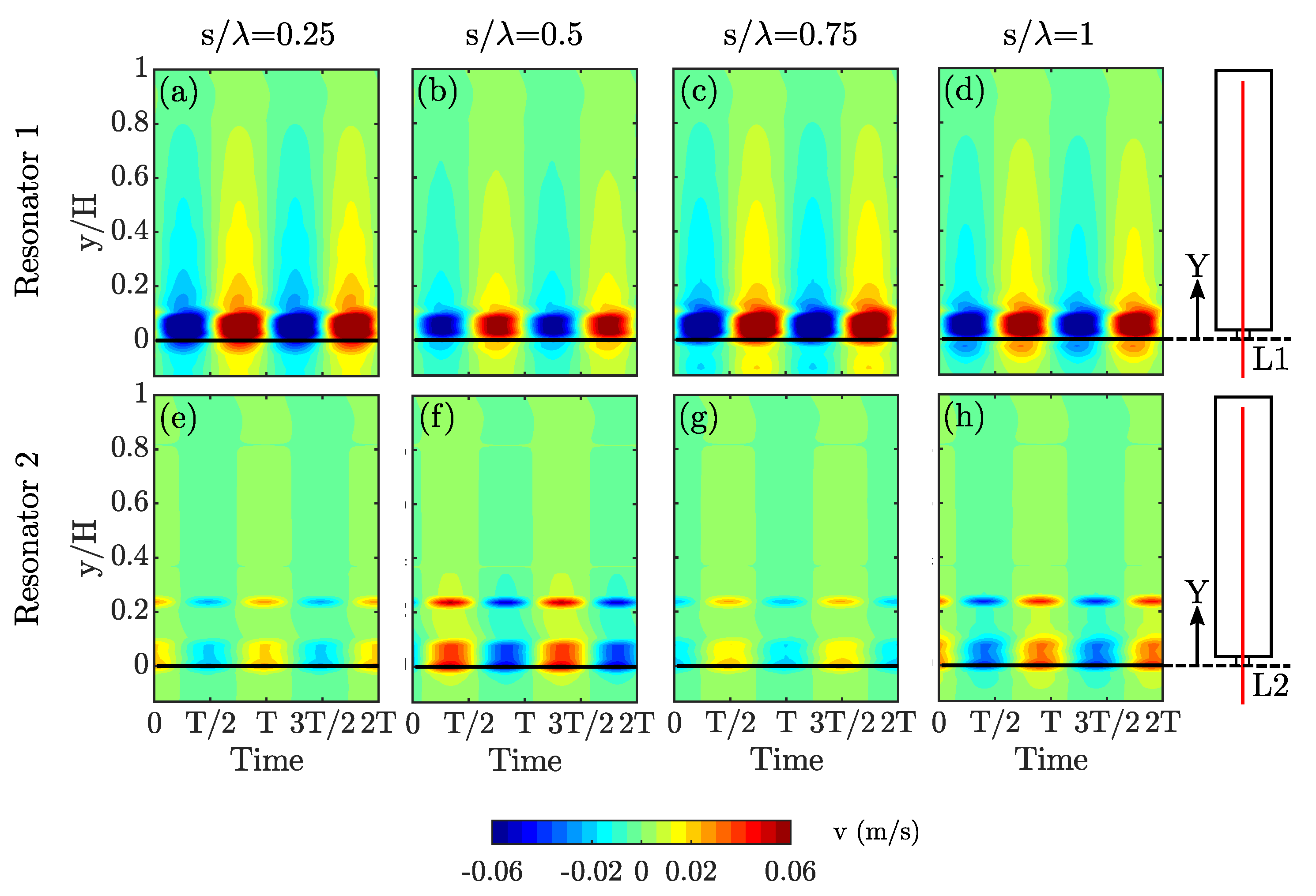
Figure 8 presents the resonator internal pressures, and
Figure 9 illustrates the resonator internal particle velocities. Results were obtained using 50 domain probes distributed along the length of the resonators, and denoted by the lines L1 and L2 in associated figures. The domain probes were spaced 1mm apart.
Figure 8a,e show the contour plots of the acoustic pressure inside the two resonators at the resonance frequency over one period (T), for a separation distance of
. The figure couples,
Figure 8b–d,f–h follow the same structure for
and
, respectively. The results indicate that the distance between the resonators affects the relative phase and the cavity internal pressure of the resonators. Considering the results for
,
Figure 8a,e, it is evident that the pressure magnitudes are significantly lower in Resonator 2 compared to Resonator 1. Moreover, the pressure contours also indicate that both resonators are resonating in phase, as both resonators experience a high and low pressure cycles at a similar time. However, the results at
show a significantly different behaviour compared to the results at
. The pressure results indicate an out-of-phase relation between the two resonators, as both resonators experience high and low pressure cycles with a time delay of around T/2. In addition, the pressure levels in Resonator 2 is lower than that of Resonator 1, similar to the results at
. Nevertheless, a closer look at the pressure levels for these two spacing configurations,
and
, suggests that Resonator 1 experiences an elevated pressure value at
compared to the results of Resonator 1 at
. These values are also higher than the values experienced by a single resonator at the resonance frequency, which is not shown here for brevity. Moreover, the pressure values at
for Resonator 2, are significantly lower compared to the results of Resonator 2 at
. These results indicate that the pressure magnitude difference between the two resonators reaches its maximum at
, while it experiences the minimum difference at at
. A similar pattern in terms of pressure magnitude is repeated for
and
, as of
and
, respectively. However, the phase relation does not follow this cyclic pattern. As shown in
Figure 8c,d,g,h, the two resonators are out-of-phase at
(unlike
) and in-phase at
(unlike
).
Taking all of the foregoing observations together, the following outcomes may be underlined. Even though the resonator configurations at
and
result in the highest transmission loss (see
Figure 5), the phase relation between the resonators for both cases are not following the same trend. However, for both configurations, the pressure values inside Resonator 1 is significantly elevated, and Resonator 2 is significantly lowered compared to the results of a single resonator. For spacing configurations leading to the broadest bandwidth of attenuated frequencies, i.e.,
and
(
Figure 8c,d,g,h), the pressure magnitudes within Resonator 2 is significantly higher than its counterparts at
and
, yet still lower than the values of Resonator 1. These results may suggest that a high transmission loss is induced when the performance of Resonator 1 is enhanced by the presence of another resonator, whereas a wide bandwidth of frequencies is attenuated when both resonators exhibit similar cavity pressure magnitudes.
To further elucidate the results presented in
Figure 8, the associated particle velocity fields were also assessed and presented.
Figure 9 is constructed and presented with the same order as
Figure 9 for velocity magnitude contour plots.
Figure 9a,b show the contour plots of the internal particle velocity over the associated time period (T) at
for Resonators 1 and 2, respectively. As expected, highest particle velocity magnitude is observed at the neck of the resonators, regardless of the spacing configuration. Moreover, the magnitude of the velocity remains almost constant over all the spacing configurations for Resonator 1. Results of Resonator 2, however, exhibit a different behaviour, and show significantly higher velocity values at
(
Figure 9f) and
(
Figure 9h) compared to the results of other spacing values. Interestingly, a second velocity peak is evident inside Resonator 2. Although this second velocity peak is evident for all spacing configurations, it is most prominent for the resonators spacing configurations of
and
. The particle velocity results shown in
Figure 9 indicate that the introduction of a second resonator enforces the downstream resonator to deviate from an ideal performance, which may lead to broader bandwidth of attenuated frequencies for spacing configurations of
and
.
3.2. Resonator Acoustic Field Analysis
To further comprehend the observations made with regards to pressure and particle velocity magnitudes in resonator cavities in
Figure 8 and
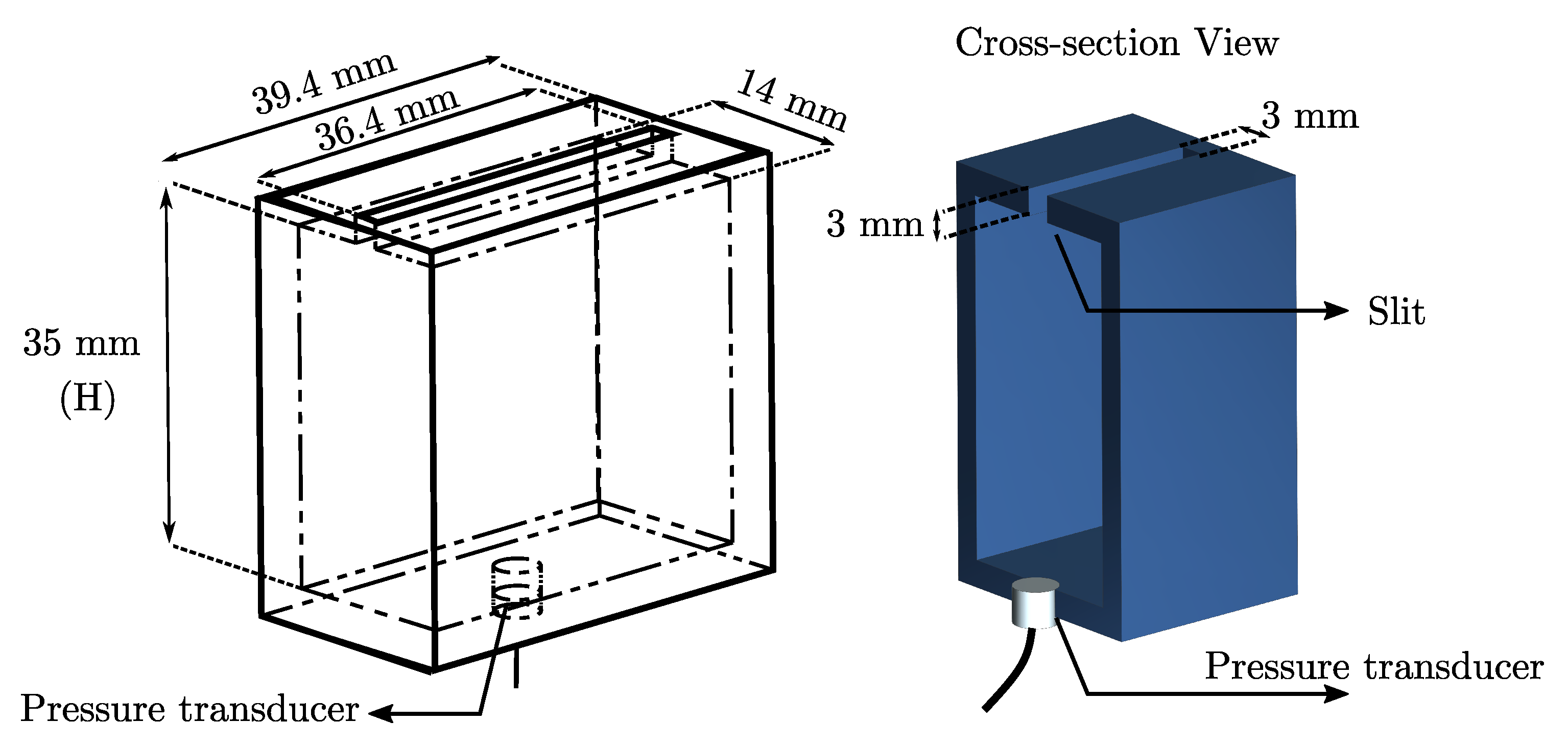
Figure 9, the frequency–energy content of the acoustic pressure field inside the resonators was assessed using the experimental data. The sound pressure levels (SPL) were calculated for the data obtained from the flush-mounted surface microphones M1 and M2 (see
Figure 1 and
Figure 2). Since the speaker was excited with a white noise signal, the effect of the spacing on the performance of the two resonators can be observed over a broad range of frequencies.
Figure 10 presents the comparison of SPL results obtained for data from microphone M1 (Resonator 1) and M2 (Resonator 2) at four different resonator spacing configurations, i.e.,
,
,
and
.
Figure 10a provides a comparison of the SPL spectra calculated for the pressure data obtained from microphones M1 and M2 at a spacing of
over a frequency range of 1000 Hz
2000 Hz. The SPL spectra for the other three spacing configurations,
,
, and
, are presented in
Figure 10b–d, respectively. The SPL values obtained for Resonator 1 (M1) indicate that the energy content is highest at around the design frequency of the resonators, i.e.,
Hz. However, the SPL pattern in Resonator 2 suggests a completely different behaviour. The single peak behavior observed in the first resonator is changed into a double peaked behavior, where the energy content at
and surrounding frequencies are vastly subdued. This anti-resonance-like behavior only affects a narrow frequency range around 1280 Hz
Hz, whereas the rest of the SPL trend is similar to that of M1, with a slight increase in the magnitude for the rest of the domain. These results may be attributed to the high transmission loss characteristics observed for
and
, and broad range of effected frequencies for
and
.
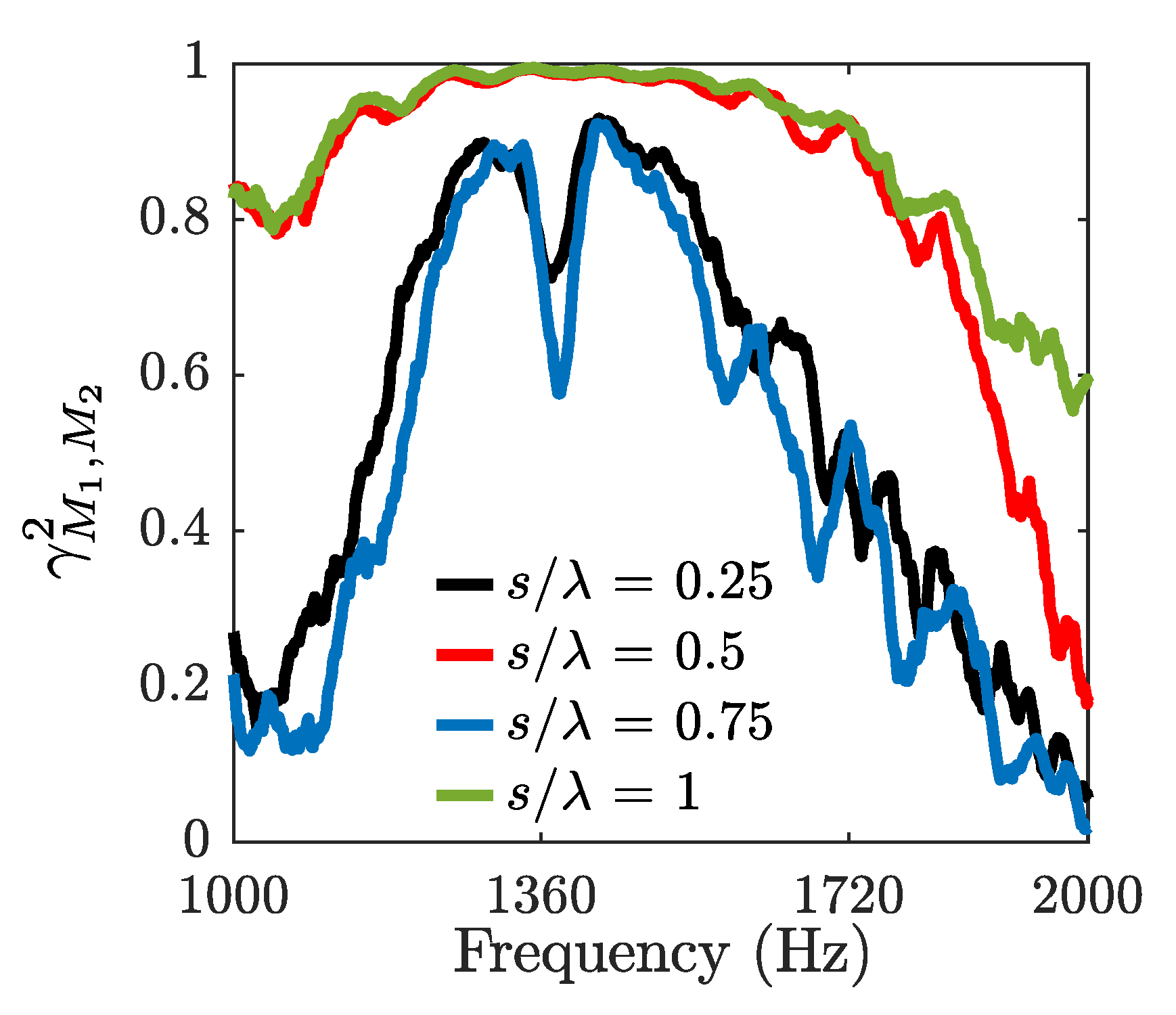
To elucidate the peculiar nature observed for the downstream resonator, the coherence between the signals from microphones M1 and M2 was analysed for four different spacing configurations of
,
,
, and
, and is presented in
Figure 11. The magnitude-squared coherence is defined as,
where
and
are the power spectral densities of the pressure fluctuations obtained from microphones located at a distance, and
is the cross-power spectral density of the pressure fluctuations between microphones. The y-axis of the
Figure 11 represents the magnitude-squared coherence estimate, which illustrates the level of similarity between the signals from microphone M1 to that from microphone M2 at each frequency. The results show that the pressure signals collected by microphones M1 and M2, inside Resonator 1 and 2, respectively, are strongly coherent around the resonance frequency (
Hz) for
and
, which also represent the cases for high transmission loss. However, the coherence trend for the two resonators is considerably different for
and
, where Resonator 1 and 2 are, respectively, only 72% and 57% coherent at their design resonance frequency. This observation further corroborates that in a system of two Helmholtz resonators, the resonance frequency of downstream resonator significantly affected by the distance. Although characterising the acoustic field inside the resonator can offer considerable insight into its sound attenuation mechanism, the resonators’ effect on the acoustic field in the duct has to be investigated to form a complete impression.
3.3. Impedance Tube Acoustic Field Analysis
The previously discussed (in
Section 3.2) effects of introducing a second resonator on the energy-frequency content of each resonator’s pressure field may also be observed in the acoustic pressure field in the impedance tube. These effects may also shed light on the transmission loss and transmission coefficient behaviour observed in
Figure 6. To observe this effect, the coherence between microphones M1, M2, and microphones G3 to G18, flush mounted to the sidewall of the impedance tube, was analysed and presented in
Figure 12. A frequency band between 1000 Hz
Hz is presented to highlight the region of interest around
.
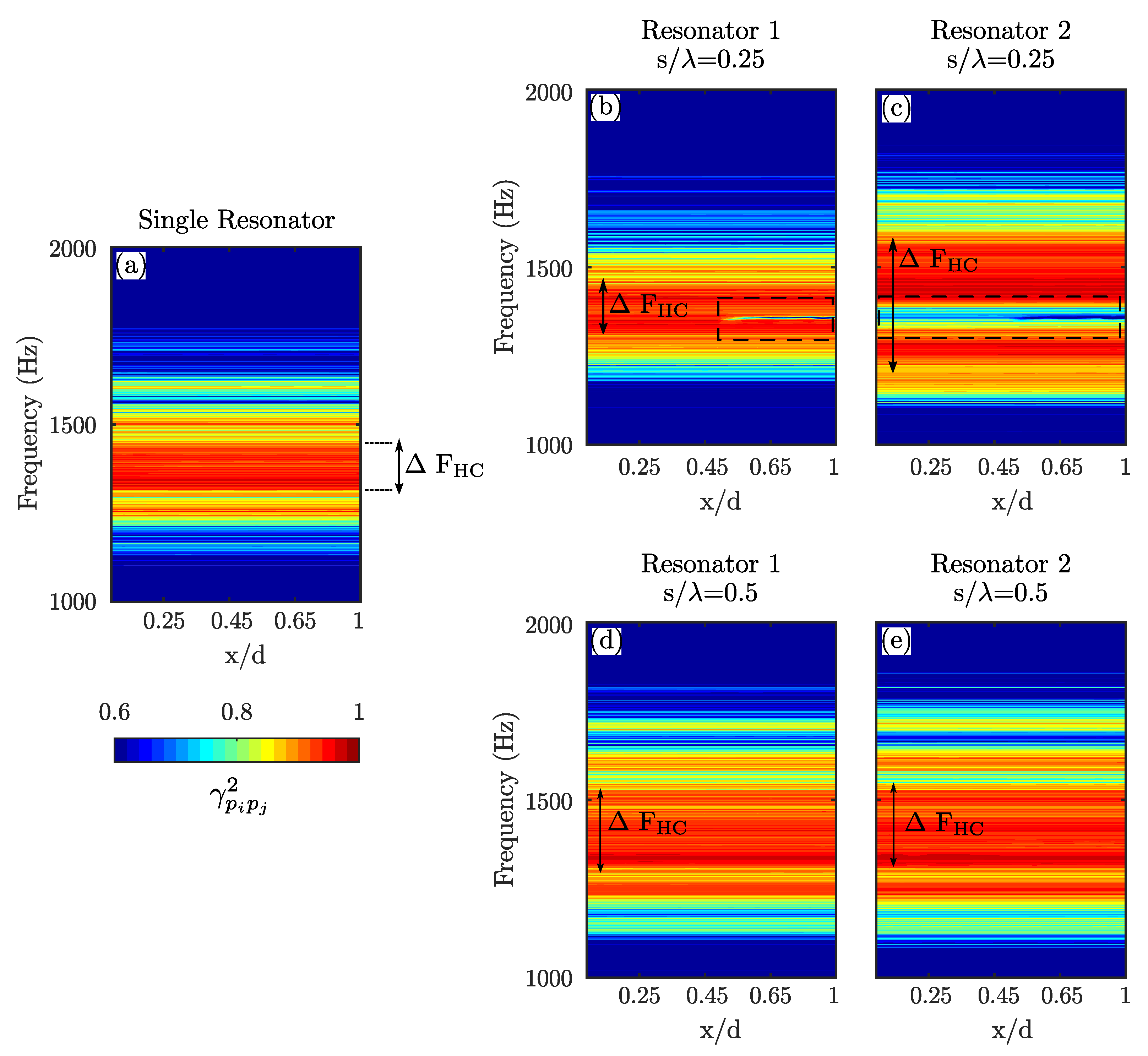
Figure 12a shows the contour plot of magnitude-squared coherence calculated between microphone M1 of a single resonator, i.e., in the absence of the second resonator, and all microphones along the impedance tube, G1 to G20 (see
Figure 1). The location of every microphone (
x) is normalised by the distance between microphones G1 and G20. Similarly,
Figure 12b,c provide the contour plots of magnitude-squared-coherence for the two resonator configuration with a resonator spacing of
. The magnitude-squared-coherence was calculated between M1 and microphones located in the impedance tube, G1 to G20 (
Figure 12b) and between M2 and microphones G1 to G20 (
Figure 12c), respectively.
Figure 12d,e present the magnitude-squared-coherence values with a similar approach for
.
The magnitude-squared-coherence values obtained between the pressure signals from M1 and the microphones in the tube, G1 to G20, are significantly high around frequencies of 1320 Hz
Hz along the whole duct length, as shown in
Figure 1. To ease the interpretation of the results, the bandwidth of the frequencies with significantly high coherence values (
0.9), which envelops the resonance frequency of the resonator, is defined as
.
Figure 12b–e present the contour plots of the magnitude-squared-coherence values for the two-resonator configuration with a spacing of
(
Figure 12b,c), and
(
Figure 12d,e), respectively. A comparison of the
for
against to that of a single resonator shows a similar bandwidth of the high coherence region for Resonator 1 (shown in
Figure 12b). This indicates that for
, the first resonator behaves similarly to a single resonator mounted onto the impedance tube, with a complete loss of coherence at a narrow region around the resonance frequency (
), starting from
and onwards (highlighted with a dashed rectangle). Considering the results for Resonator 2,
increases significantly compared to Resonator 1. However, the increase of
is accompanied by a complete loss of coherence at the resonance frequency for all
locations. Moreover, the magnitude-squared-coherence values indicate that the second resonator affects a broader band of frequencies within the impedance tube duct compared to the first resonator, which reaffirms the previous observations discussed for SPL values in
Figure 10. For results at
(
Figure 12c,d), the coherence values show a significant increase compared to the single resonator case for both resonators. In addition, the results for both resonators exhibit a very similar contour map and a broadened
magnitude. This indicates that both resonators together affect a broad band of frequencies in the duct, unlike the results at
.
The effect of introducing a second resonator and its distance to the upstream resonator can also be studied through the change in the pressure energy content along the impedance tube.
Figure 13 presents the SPL spectra calculated from the signals acquired by microphones G1 to G20 along the impedance tube. For brevity and clarity of the figures, only results at G1, G7, G10, and G20 are presented.
Figure 13a shows the SPL spectra of the farthest upstream (G1) and downstream (G20) microphones and the two microphones directly opposite the resonator openings(G7 and G10), at a separation distance of
. The results show that the SPL values begin to decrease after the second resonator at around the design frequency. Moreover, the SPL decreases gradually until the last microphone. This indicates that for
, the transmission loss introduced by the resonator couple increases as the wave propagates downstream. On the contrary, the results for
show a significantly different behaviour. The results show that the SPL values remain constant after the second resonator and exhibit a lower level of reduction compared to results at
.
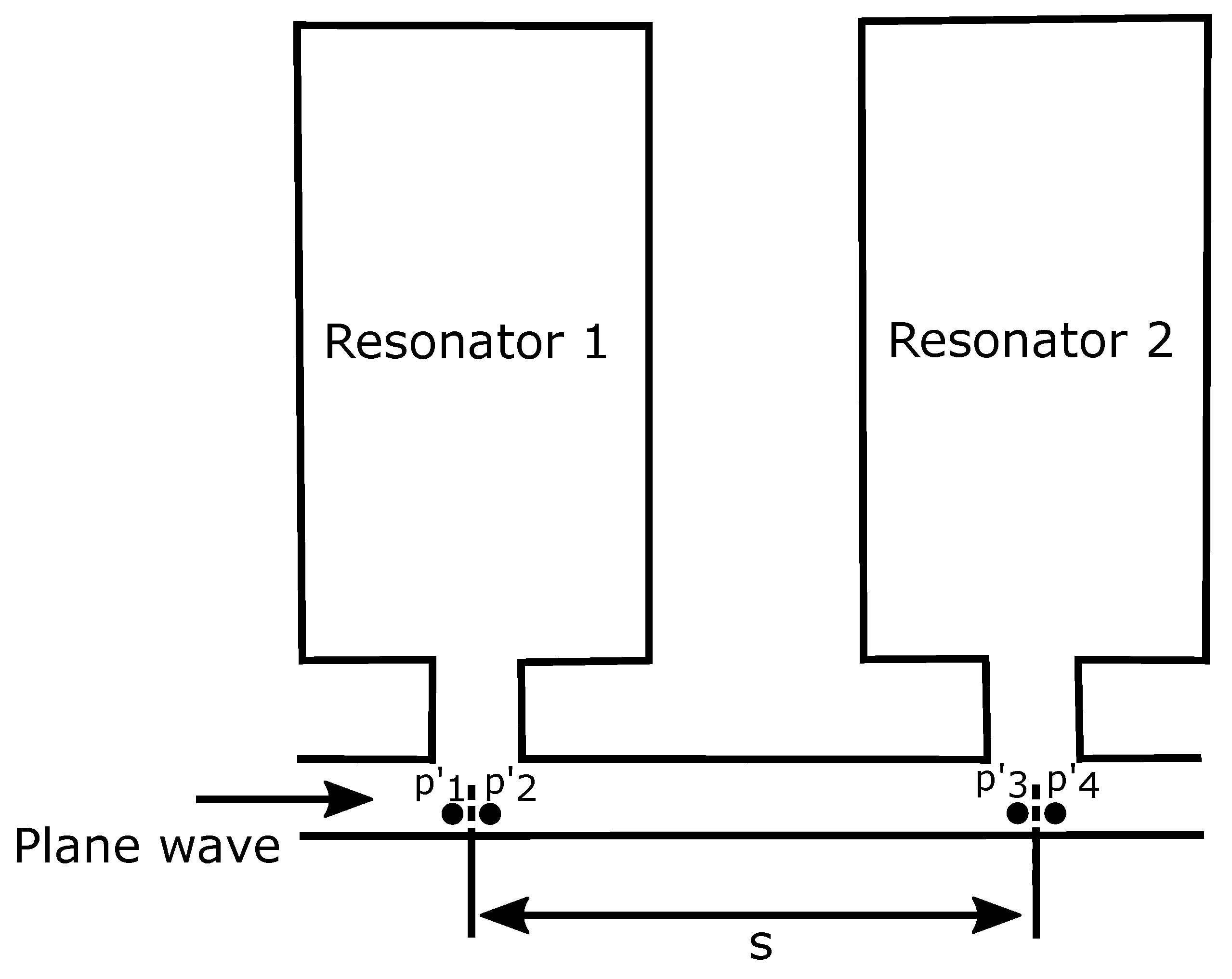
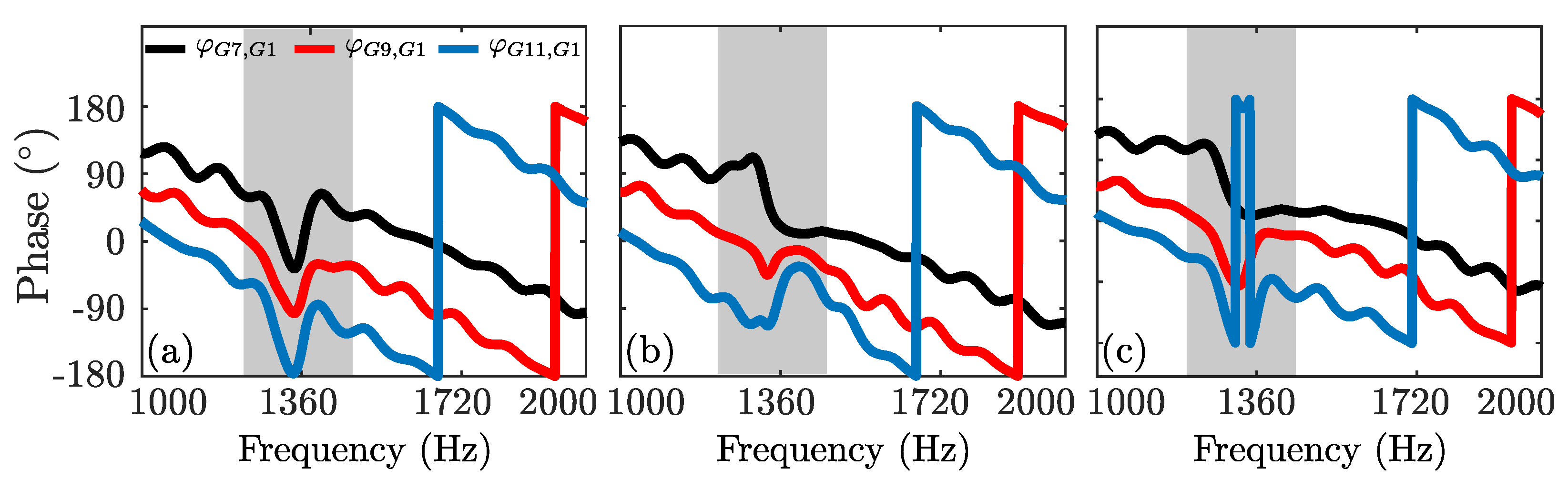
The relative phase information (
) along the impedance tube may also provide insight into the effect of distance on the noise attenuation performance of the two resonator system. The relative phase was calculated based on the cross-spectral calculations between the downstream microphones (G7, G9, and G11) and the upstream microphone, G1.
Figure 14 presents the relative phase information for a single resonator (
Figure 14a) and a two-resonator system with
(
Figure 14b), and
(
Figure 14c). The results are presented for the frequency range, 1000 Hz
Hz. In
Figure 14a, where the results for a single resonator are presented, the relative phase shows a significant change around the resonance frequency. This region is highlighted with a rectangle in the figure to ease the interpretation. The steep decrease in the relative phase indicates a reduction in the speed of propagation around the resonance frequency, which can be observed from the results of all microphones presented [
34]. The introduction of a second resonator at
completely alters the relative phase around the resonance frequency. The observed steep decrease in phase for the single resonator yield to a steep increase at the first resonator location (G7) and downstream location in the tube (G11). Interestingly, the relative phase at the location of the second resonator (G9) has a slight increase compared to other microphones. This narrow band increase in phase for all microphones indicates an increase in the propagation speed. At
, the relative phase exhibits a trend which is similar to that of the single resonator. However, it is worth mentioning that the dip observed at the resonance frequency for a single resonator is less apparent in this case, and is more of a steep decrease at G7 without recovering to its original path. This indicates a change, in this case an increase, in the propagation speed for the frequencies beyond the resonance frequency.
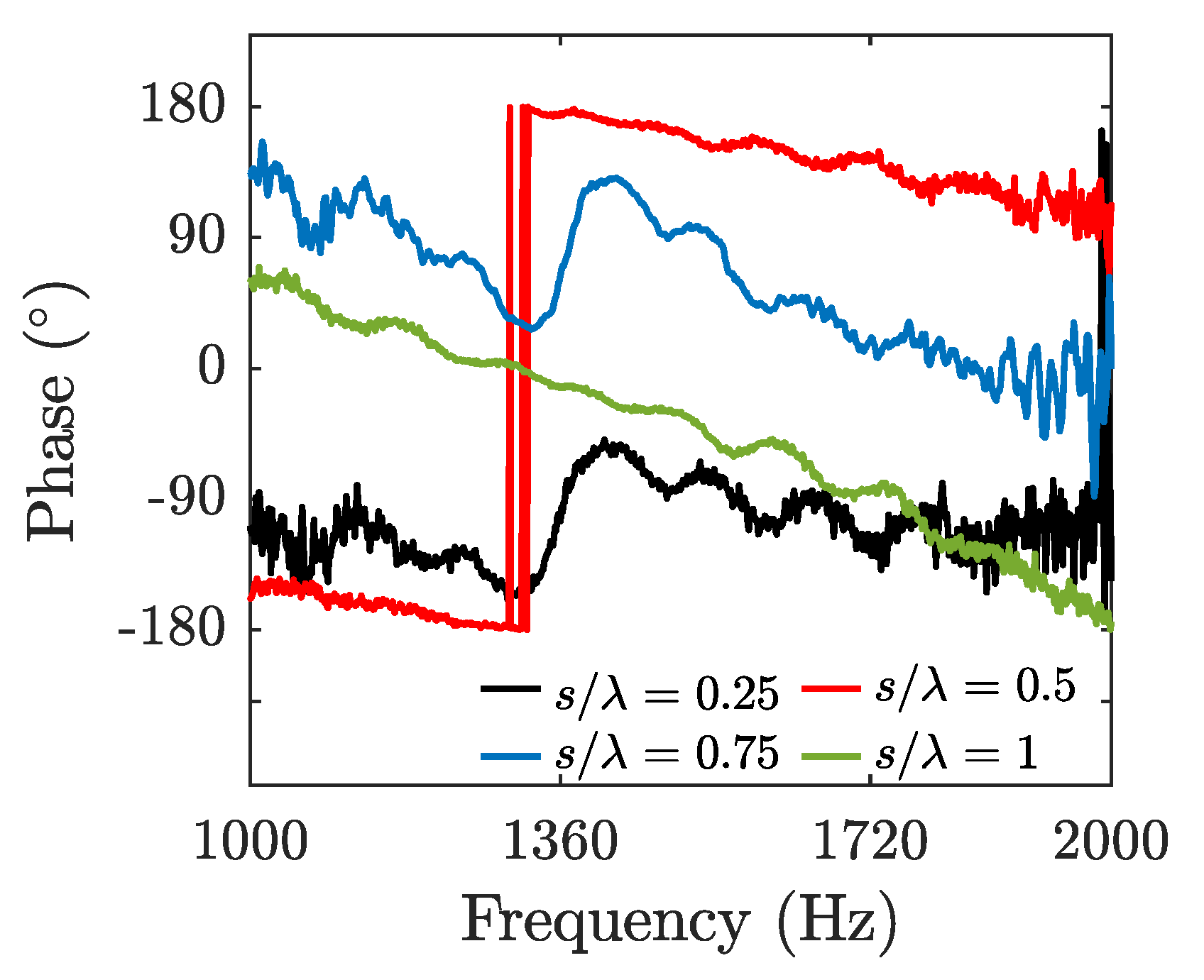
The relative phase between the microphones located in the resonators (M1 and M2) may also shed some light on the effects of resonators spacing on sound attenuation performance of the system.
Figure 15 presents the relative phase of the signals obtained from M2 to M1 (
) at four different spacing configurations,
and
. The results show that at
and
, where the highest transmission loss occur, the relative phase increases at around the resonance frequency and indicates an increase in the propagation speed. On the contrary, at
and
, the relative phase shows a gradual decrease, which implies that the phase relation between the resonators does not alter around the resonance frequency. These observations are consistent with the previous results shown in
Figure 14.