Design, Manufacturing, and Acoustical Analysis of a Helmholtz Resonator-Based Metamaterial Plate

Abstract

Acoustic metamaterials are materials artificially engineered to control sound waves, which is not possible with conventional materials. We have proposed a design of an acoustic metamaterial plate with inbuilt Helmholtz resonators. The plate is made of Polylactic acid (PLA) which is fabricated using an additive manufacturing technique. It consists of Helmholtz resonator-shaped cavities of different sizes. In this paper, we have analyzed the acoustic properties of the Helmholtz resonators-based metamaterial plate experimentally as well as numerically. The experimental results are in good agreement with the numerical results. These types of 3D-printed metamaterial plates can find their application where high sound transmission loss is required to create a quieter ambience. There is an additional advantage of being lightweight because of the Helmholtz resonator-shaped cavities built inside the plate. Thus, these types of metamaterial plates can find their application in the design sector requiring lighter materials with high sound transmission loss.

1. Introduction

In recent years, acoustic metamaterial has gained considerable attention in the field of controlling and manipulating the behavior of sound waves [1]. The evolution of negative effective bulk modulus, effective density, and the refractive index led to various possibilities in the field of acoustics, such as acoustic cloaking, acoustic imaging, and active noise control [2]. Acoustic metamaterials are the combination of artificially designed units that yield desired properties not present in naturally occurring materials [3]. The idea of acoustic metamaterial is derived from electromagnetic materials [4]. The first design of acoustic metamaterial was proposed by Liu et al. in 2000, which successfully manipulated low-frequency sound waves [5]. In his work, a locally resonant structure and deep subwavelength structure were designed using a rubber-coated sphere. Wu et al. proposed a design of the metamaterial which is based on fluid–solid composite inclusions having negative shear modulus and negative mass density [6]. Ciaburro et al. studied the metamaterials made from reused buttons using artificial intelligence techniques [7]. Moreover, various other designs of acoustic metamaterial with different segments of pipes and resonator have been analyzed by the researchers [8,9,10,11,12,13].

Sound transmission efficiency of a material is based on the mass law which intends to increase the mass of the material to achieve higher transmission loss [14]. Although these materials are not suitable in terms of lightness, Nilson et al. and Narayan et al. have discussed sandwiched panels with rubber as damping material [15,16]. Groby et al. studied the acoustic properties of the periodically embedded Helmholtz resonators in a porous medium and discovered increased sound absorption in the foam with the minimal thickness [17]. Other metamaterials’ designs with spherical cavities and disc shaped cavities in the soft medium are studied by Sharma et al. [18,19]. They have purposed an analytical framework to analyze the performance of the array of the closely spaced cavities submerged in water. These metamaterials are very useful to control water-borne sound waves. Transmission loss of the Helmholtz resonators mounted in the multilayer panel is observed by Prydz et al. [20] and various research has also been carried out around the world to study the different geometry of Helmholtz resonators [21,22,23,24,25]. Sugimoto et al. studied the coupling effect of the Bragg reflection and resonance in a tunnel loaded with an array of Helmholtz resonators [26]. Fang et al. performed an analytical and experimental study on the Helmholtz resonators to define the scope of the ultrasonic metamaterial in a superlens below the diffraction limit [27]. Lee et al. experimentally studied the effect of porous media in the neck of the Helmholtz resonator [28].

In this paper, we have presented a small-scale prototype of a metamaterial plate with Helmholtz resonators of different geometries. The metamaterial plate is fabricated using an additive manufacturing technique and the new proposed acoustical metamaterial has a significant amount of transmission loss due to the combined effect of the reflection from the plate and absorption from the resonance frequencies of Helmholtz resonators. Numerical and experimental studies are performed on the metamaterial plate to analyze the required acoustical properties. The organization of the paper is as follows: Section 2 contains the design and the analytical model used for estimating acoustic properties. A four-microphone impedance tube method is explained to carry out experiments. Section 3 describes the fabrication of a metamaterial and the methodology related to conducting experiments and numerical simulations. In Section 4, computed results for transmission coefficients, reflection coefficients, and absorption coefficients are presented for the proposed design of the metamaterial. Based on the latter results, some comments on the evaluated coefficients are offered to justify the reflective behavior of the plate in the frequency range 100 to 450 Hz, and the absorptive behavior of the plate in the frequency range 450 to 2000 Hz. In the end, a conclusion is presented to summarize the findings.

2. Model and Methods

The present study aims to investigate the acoustical properties of the Helmholtz resonators-based metamaterial plate experimentally and numerically. The theoretical aspects have been described in more detail in the following section.

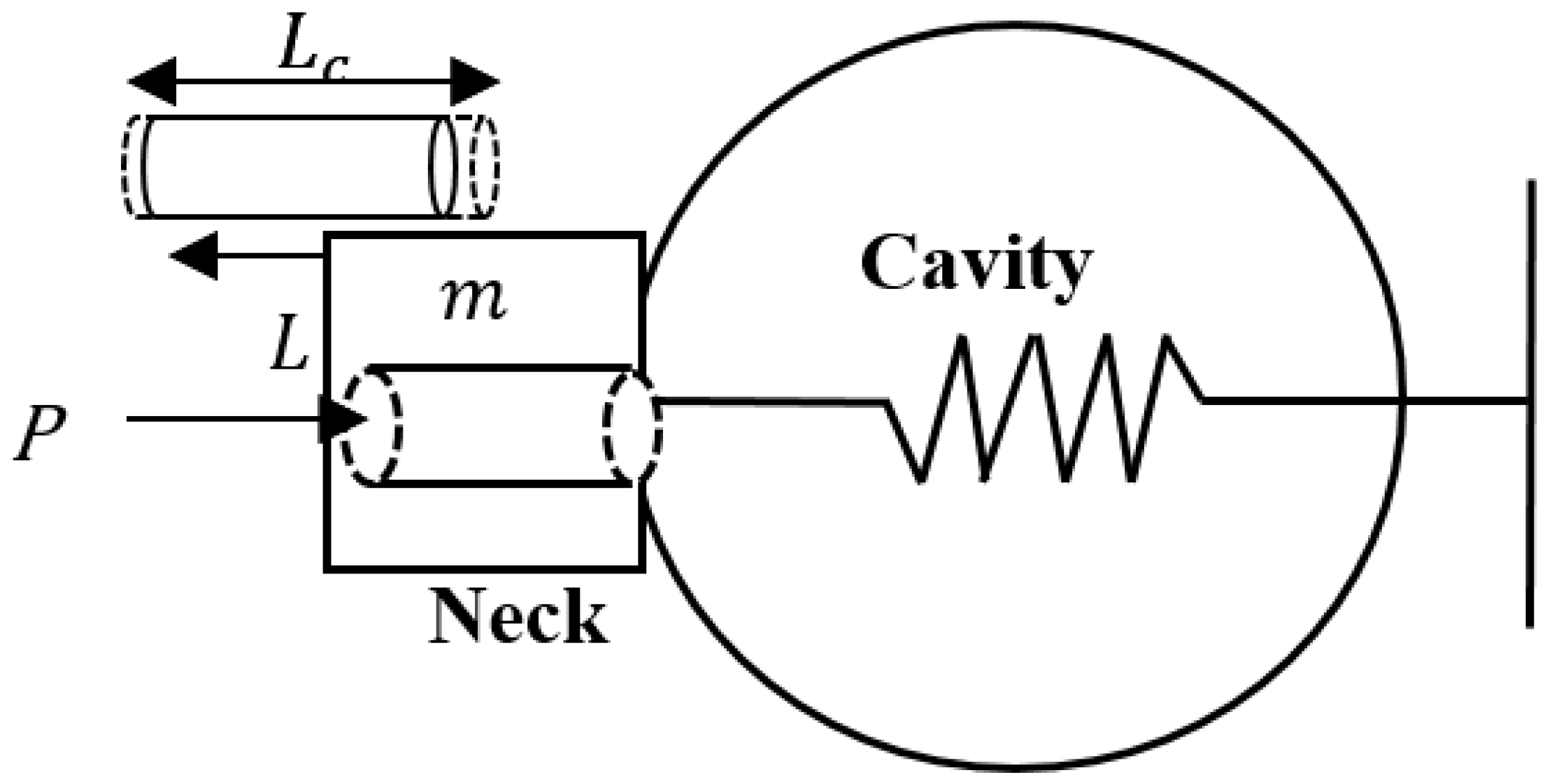
2.1. Helmholtz Resonator

The schematic representation of a Helmholtz resonator is shown in Figure 1. It is a combination of a cylindrical neck and a hollow cavity where the cavity interacts with the outer pressure field via the neck. The Helmholtz resonator is a well-established design to attenuate the sound wave of a particular frequency. The attenuation frequency of the sound wave is decided by the geometry of the Helmholtz resonator. The Helmholtz resonator can be considered as analogous to the spring-mass system in which air in the neck acts as mass $(m)$ and cavity acts as spring of stiffness $\left(K\right)$, as shown in Figure 1 below. The resonance frequency of the Helmholtz resonator is given by [29]:

$${\omega }_0=\frac{C_0}{2\pi }\sqrt{\frac{A}{L_{c}v}}$$

(1)

Here, ${\omega }_0$ represents resonance angular frequency,$C_0$ is the adiabatic speed of sound, A is the cross-sectional area of the neck, $v$ is the volume of the cavity, $L_{c }$ is the effective length of the neck with an end correction factor, and L is the actual length of the neck. P is the acoustic pressure of the incoming sound wave.

The end correction factor is an important parameter to obtain the accurate value of the resonance frequency. Here the effective length is chosen as L_c = L + 0.85d, where d is the diameter of the neck [30].

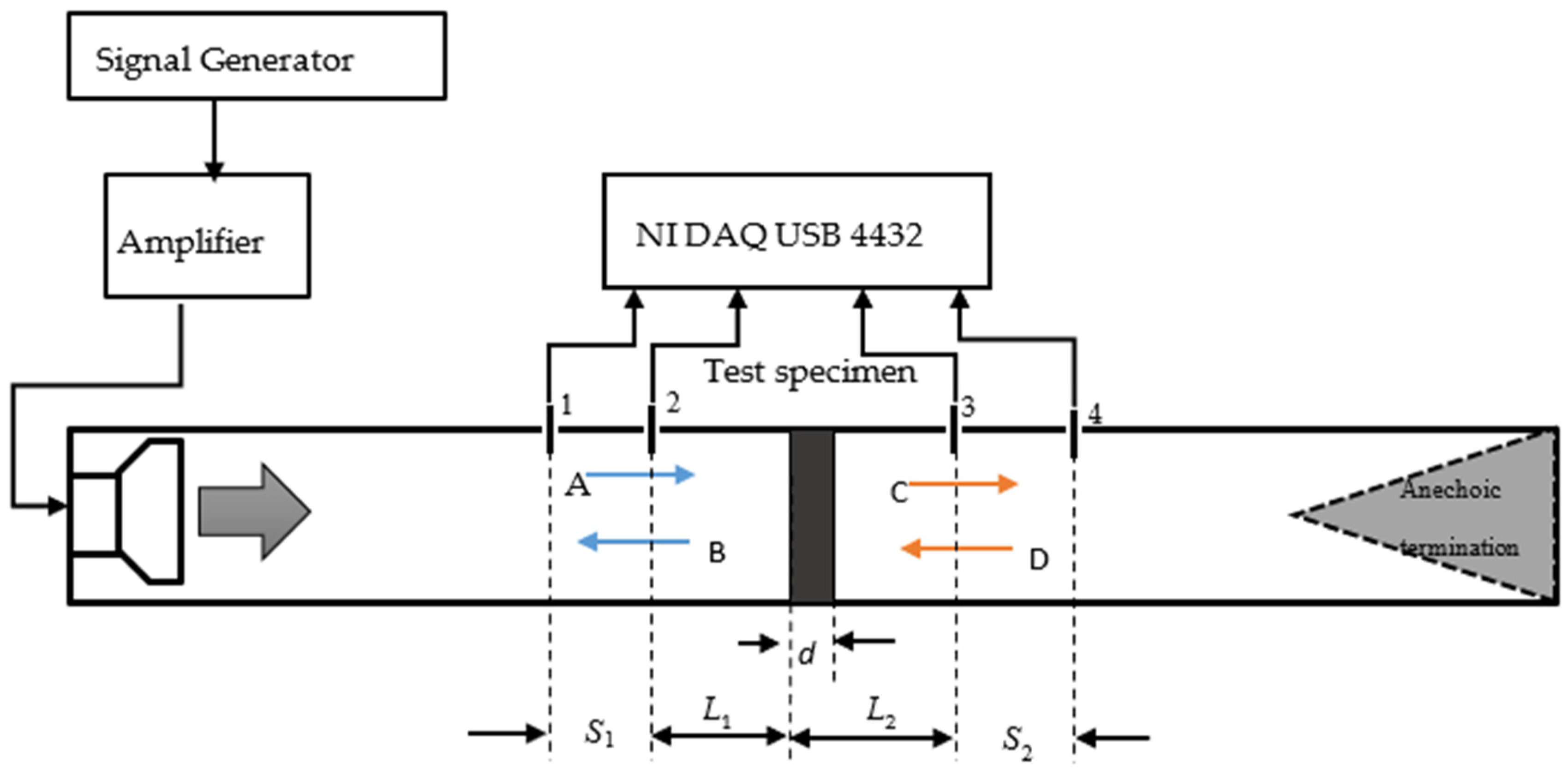
2.2. Four-Microphone Impedance Tube Method

Acoustic properties of the material are measured using a Kundt tube for a long time. The moving probe is used to measure the pressure at different point in the Kundt tube but the high frequencies can be reached only by decreasing the tube diameter and manufacturing of such materials is quite difficult [31]. A four-microphone impedance tube is used to conduct the experiment, in which microphone 1 is chosen as a reference microphone. The acoustical properties of the metamaterial plate are extracted using transfer matrix formulation following the ASTM standard E2611-19 [32]. The four unknown variables upstream pressure ($P_0$) and particle velocity ($U_0$), downstream pressure ($P_b$), and particle velocity ($U_b$) are required to estimate the acoustic properties. The two-load boundary condition method has been used to compute the pressure and particle velocities. The schematic representation of the four-microphone impedance tube has been shown in Figure 2.

The pressure at four microphone locations can be approximated by adding the forward and backward directed plane waves. Here $A$, $B$, $C$, and $D$ represent the complex amplitude of the respective waves. The time-independent pressure amplitude at four microphone positions can be expressed as:

$$\begin{array}{c}{P}_1=A{e}^{-jk{x}_1}+B{e}^{jk{x}_1}\\ P_2=A{e}^{-jk{x}_2}+B{e}^{jk{x}_2}\\ P_3=C{e}^{-jk{x}_3}+D{e}^{jk{x}_3}\\ P_4=C{e}^{-jk{x}_4}+D{e}^{jk{x}_4}\end{array}$$

(2)

Here, $k$ represents the wavenumber, whereas $x_i$ is the location of the $i$th microphone. The above equation yields four equations to estimate the value of $A$ to $D$ in terms of transfer function:

$$\begin{array}{c}A=j\frac{H_{1,ref}{e}^{-jk{L}_1}-H_{2,ref}{e}^{-jk\left(L_1+S_1\right)}}{2\sin k{S}_1}\\ B=j\frac{H_{2,ref}{e}^{+jk\left(L_1+S_1\right)}-H_{1,ref}{e}^{+jk{L}_1}}{2\sin k{S}_1}\\ C=j\frac{H_{3,ref}{e}^{+jk\left(L_2+S_2\right)}-H_{4,ref}{e}^{+jk{L}_2}}{2\sin k{S}_2}\\ D=j\frac{H_{4,ref}{e}^{-jk{L}_2}-H_{3,ref}{e}^{-jk\left(L_2+S_2\right)}}{2\sin k{S}_2}\end{array}$$

(3)

Here, $H_{i,ref}$ refers to the transfer function between the $i$th microphone and the reference microphone. $H$ is computed by taking the ratio of the complex sound pressure at the $i$th microphone to that of the reference microphone. These complex coefficients $A$ to $D$ compute the sound pressures and particle velocities at the front surface ${\left(x=0\right)}_{ }$and a back surface ${\left(x=d\right)}_{ }$ of the metamaterial plate which can be related by a two-by-two transfer matrix assuming different termination as anechoic as ‘$a$’ and rigid as ‘$b$’

Transfer matrix with termination ‘$a$’

$${\left(\begin{array}{c}{P}_a\\ U_a\end{array}\right)}_{x=0}=\left(\begin{array}{cc}{T}_{11}& T_{12}\\ T_{21}& T_{22}\end{array}\right)$$

(4)

Transfer matrix with termination $b$’

$${\left(\begin{array}{c}{P}_b\\ U_b\end{array}\right)}_{x=0}=\left(\begin{array}{cc}{T}_{11}& T_{12}\\ T_{21}& T_{22}\end{array}\right){\left(\begin{array}{c}{P}_b\\ U_b\end{array}\right)}_{x=d}$$

(5)

The pressures and particle velocities at two surfaces of the test sample are expressed as:

$$\begin{array}{c}{P}_0=A+B\\ U_0=\left(A-B\right)/\rho c\\ P_d=C{e}^{-jkd}+D{e}^{+jkd}\\ U_d=\left(C{e}^{-jkd}-D{e}^{+jkd}\right)/\rho c\end{array}$$

(6)

Here $\rho$ and $c$ are the density and speed of sound of the medium, respectively. The transfer matrix in Equations (4) and (5) can also be rewritten as

$${\left(\begin{array}{cc}{P}_a& P_b\\ V_a& V_b\end{array}\right)}_{x=0}=\left(\begin{array}{cc}{T}_{11}& T_{12}\\ T_{21}& T_{22}\end{array}\right){\left(\begin{array}{cc}{P}_a& P_b\\ V_a& V_b\end{array}\right)}_{x=d}$$

(7)

Inverting the above expressions yields the final transfer matrix as

$$TM=\left(\begin{array}{cc}\frac{P_{0a}{U}_{db}-P_{0b}{U}_{da}}{P_{da}{U}_{db}-P_{db}{U}_{da}}& \frac{P_{0b}{U}_{da}-P_{0a}{U}_{db}}{P_{da}{U}_{db}-P_{db}{U}_{da}}\\ \frac{U_{0a}{U}_{db}-U_{0b}{U}_{da}}{P_{da}{U}_{db}-P_{db}{U}_{da}}& \frac{P_{da}{U}_{0b}-P_{db}{U}_{0a}}{P_{da}{U}_{db}-P_{db}{U}_{da}}\end{array}\right)$$

(8)

This can be expressed as

$$TM=\left(\begin{array}{cc}{A}_{11}& A_{12}\\ A_{21}& A_{22}\end{array}\right)$$

2.3. Estimating Acoustic Properties

The acoustic characteristics, such as sound waves reflected back, transmitted, and absorbed by the metamaterial plate, are represented by the reflection, absorption, and transmission coefficient, respectively. Elements of the final transfer matrix in Equation (8) are used to estimates these coefficients, Transmission coefficient (T), reflection coefficient (R), and absorption coefficient ($\alpha$) and transmission loss (TL) in terms of transfer matrix’s elements can be expressed as.

• Transmission Coefficient

  $$T=\frac{2e^{jkd}}{A_{11}+\left(A_{12}/\rho c\right)+A_{21}\rho c+A_{22}}$$

  (9)
• Reflection Coefficient

  $$R=\frac{A_{11}-\rho c{A}_{21}}{A_{11}+\rho c{A}_{21}}$$

  (10)
• Absorption Coefficient

  $$\alpha =1-\left|R^2\right|-\left|T^2\right|$$

  (11)
• Transmission Loss

  $$TL=20{\log }_{10}\left|\frac{1}{T}\right|$$

  (12)

3. Experimental and Numerical Study

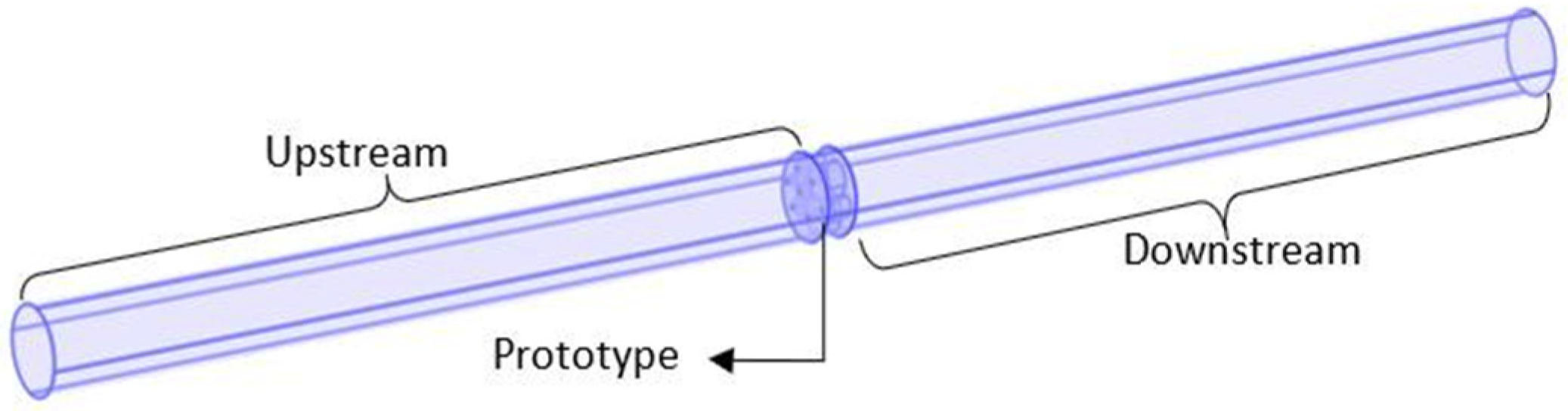
3.1. Fabrication of Metamaterial Plate Using Additive Manufacturing

The metamaterial plate is fabricated using an additive manufacturing technique, i.e., 3D printing, where a CAD model is prepared using Solid Works 2016. Seven Helmholtz resonator cavities with resonant frequencies ranging from 600 to 1900 Hz are designed to investigate the effect of the Helmholtz resonator in metamaterial plates. The metamaterial plate has a diameter of 50 mm and 20 mm thickness. Additive manufacturing is performed on a 3D printer Creality CR-10S pro with polylactic acid (PLA) wire of diameter 1.75 mm and density 1240 kg/m³.

The diameter and the height of the neck have been taken as the same for all Helmholtz resonators as 3 and 5 mm, respectively. The height of the cavity is taken as 13 mm. The radius of the cavity of Helmholtz resonators along with their resonance frequency is shown in

Table 1. Resonance frequency and diameter of different cavities for Helmholtz resonators.

Diameter (mm)	22	20	12	11.6	11	10	8
Resonance (Hz)	682	751	1219	1295	1365	1502	1877

. The CAD model of the metamaterial, the fabrication process, and the final metamaterial plate are showed in Figure 3 below.

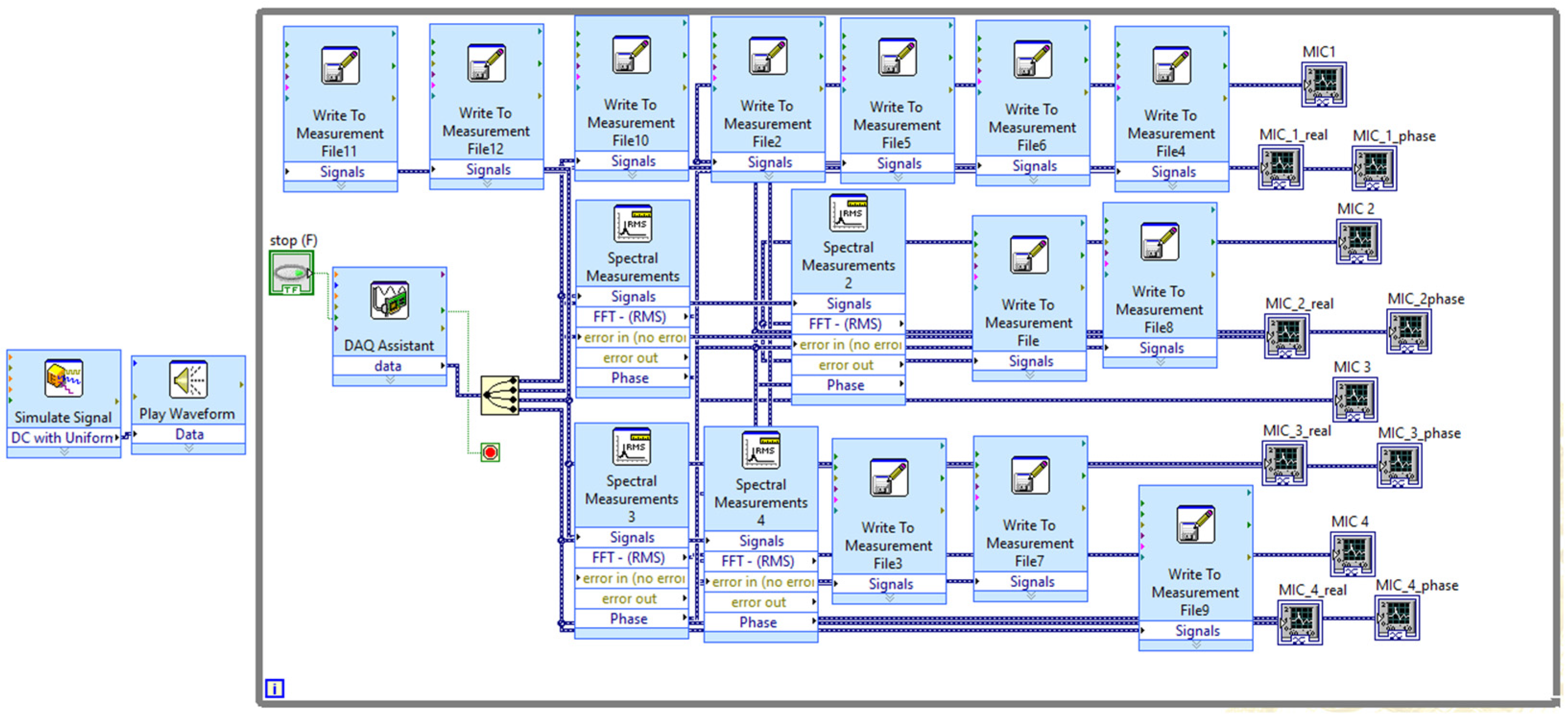
3.2. Experimental Testing of Metamaterial Plate Using a Four-Microphone Impedance Tube

The experimental setup consists of a brass tube with a sound source at one end and a termination at the other. The brass tube has a diameter of 50 mm and a frequency range of 100–2000 Hz. The tube is divided into three sections: upstream, downstream, and sample holder as shown in Figure 4. The distance between the metamaterial plate’s front surface and the second microphone is 20 cm, while the distance between the sample’s rear surface and the third microphone is 18 cm. At one end of the upstream portion, Mark Alpair-10M 6-inch speakers are used to generate sound, and a 30 watt power amplifier with a working range of 20 to 5 kHz is used to amplify the white noise produced by the NI LabVIEW software. Rigid and anechoic termination is provided in the downstream portion by using strong backing of a steel rod and sound-absorbing glass wool, respectively. Data are collected using four pressure field, quarter-inch microphone sensors. Experiments are conducted in an acoustic enclosure to eliminate external disturbances to obtain greater accuracy.

White noise has been used to study the acoustic properties of the metamaterial plate developed using an additive manufacturing technique. To acquire the real-time data of the sound, four microphones are placed in the microphone holder. These microphones are connected to NI DAQ USB 4432. Teflon tape is used between the holder and tube walls to avoid sound leakage through holes. A NI LabVIEW program has been developed to generate the white noise and to take the Fourier transformation of the real-time data. Figure 5 shows the developed LabVIEW program for the experiment. The experiment is performed for 10 s for both rigid and anechoic termination. Eight datasets are extracted of a duration of 1 s each from the middle 8 s of the experiment.

The data for amplitude and phase collected from the experiment is further processed in MATLAB to calculate the transfer function. The transfer function between the sound pressure recorded at the first microphone and the second microphone is estimated as the ratio of the complex pressure recorded at microphone 2 to the complex pressure recorded at microphone 1. Transfer functions for all four microphones are estimated and are plugged in Equation (3) to calculate the $A$, $B$, $C$, and $D$ components of the sound wave. The pressure and velocity of the sound wave are estimated for both anechoic and rigid termination using Equation (6). Transfer matrix is constructed using Equation (8), this matrix is required to calculate the reflection coefficient, absorption coefficient and transmission coefficient.

3.3. Simulation to Estimate Acoustic Properties of Metamaterial Plate

To analyze the metamaterial plate numerically in Finite Element (FE) software COMSOL Multiphysics, a three-dimensional model of the metamaterial plate is designed and placed in the cylindrical cavity as shown in Figure 6. The model is analyzed in the pressure-acoustic frequency domain under acoustic study (COMSOL, 2014). A tetrahedron element is used to discretize the model into a number of elements. To correctly capture the behavior of the system, the model’s convergence is examined by discretizing the domain into 65,000 and 133,000 elements. A plane-wave radiation condition is assumed at the two ends of the cylindrical cavity to model the end as nonreflecting. A sound hard boundary condition is used on the walls of the cylindrical cavity. The material of the metamaterial plate is assigned as PLA with the speed of sound as 2240 m/s. The model is studied using a sine sweep in the same frequency range as per the experiment. The medium inside the cylindrical cavity is chosen as air with the speed of sound as 346.4 m/s and the density as 1.173 Kg/m³ corresponding to a 25 °C ambient temperature. The governing equation for the model analyzed in COMSOL is.

$$\nabla \left(-\frac{\nabla p_{}}{\rho }\right)-\frac{{\omega }_{}^{2}p}{C_0{}^2\rho }=0$$

(13)

Here, p is the acoustic pressure, ρ is the density, and ω is the angular frequency.

$$TL=10lo{g}_{10}\left[\frac{W_{in}}{W_{out}}\right]$$

(14)

where

$$W_{in}={{\displaystyle \int }}_{A_{in}}\frac{p_0^2}{2\rho C_0},W_{out}={{\displaystyle \int }}_{A_{out}}\frac{\left|p^2\right|}{2\rho C_0}$$

Here $W_{in}$ and $W_{out}$ represent the acoustic power at the inlet and the outlet of the cylindrical cavity, respectively. $A_{in}$ and $A_{out}$ are the cross-sectional areas at inlet and outlet of the cylindrical cavity, respectively.

4. Results and Discussion

This work analyzes the acoustic performance of a metamaterial plate made with Helmholtz resonators fabricated using additive manufacturing technology. The performance of the metamaterial plate is analyzed by calculating the transmission coefficient, the reflection coefficient, and the absorption coefficient. During experiments, a four-microphone impedance tube with two load boundary condition is used. Experimental results are compared with numerical results to validate the findings.

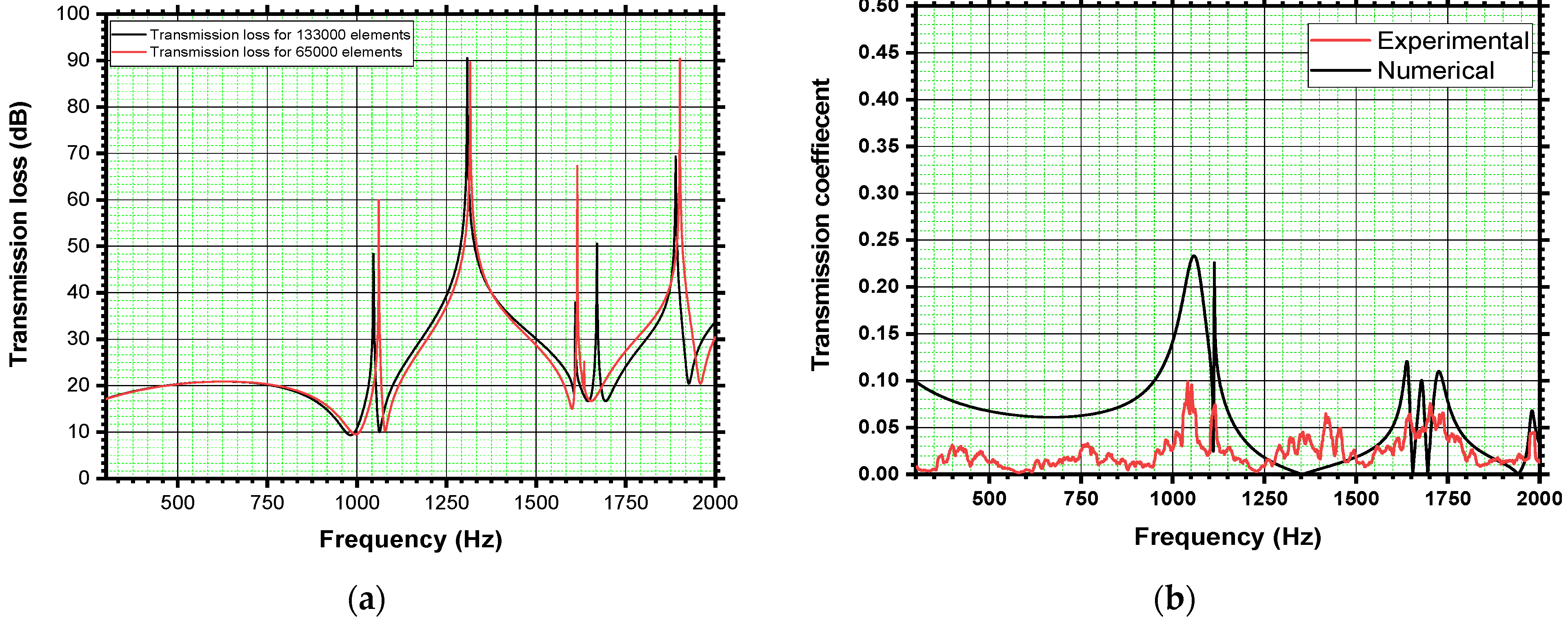
4.1. Transmission Loss

Experimentally, the transmission coefficient is estimated by extracting the pressure and velocity data from four microphones. Equation (9) calculates the transmission coefficient from the transfer matrix and eight sets of data as obtained from MATLAB 2019a. The adjacent averaging technique is used to filter the noise from data and to remove outliers. The transmission coefficient for the numerical model is also calculated. To validate the test case a mesh convergence study is performed, and the total number of elements are doubled. The transmission loss curve is found almost similar in both cases as shown in Figure 7a. The plate’s transmission coefficient is determined using Equation (9). The experimental data are compared with numerical data for validation. The transmission coefficient plot against the frequency is shown in Figure 7b. The plot shows good correlation between the experiment and numerical results particularly from 1000 to 2000 Hz. At the lower frequency range of 100–450 Hz, the plate behaves as a reflecting surface as not much interaction is observed in the Helmholtz resonator, as shown in Figure 8a. As the frequency increases and approaches the resonance frequency of the Helmholtz resonators, the large value of the pressure can be observed in different resonators, as shown in Figure 8b–f. The plot 7b illustrates the plate’s reflecting behavior at lower frequencies while the increase in the curve can be seen when the frequencies approach the Helmholtz resonators’ resonance frequency. Finally, transmission loss data are computed from Equation (12) using the final transfer matrix and plotted in Figure 7a.

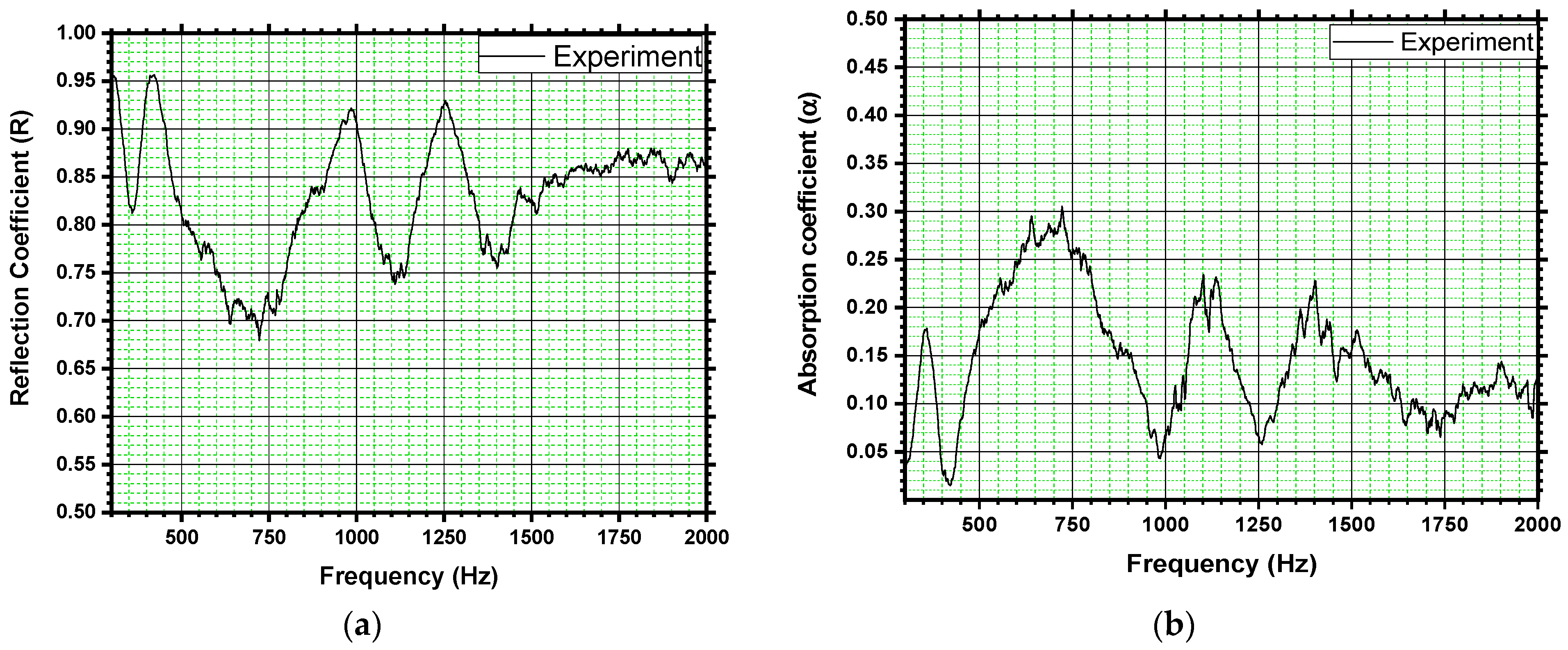
4.2. Reflection Coefficient and Absorption Coefficient

The transfer matrix is used to calculate the reflection coefficient and absorption coefficient. Equations (10) and (11) give the value of the reflection coefficient at various frequencies, and Figure 9a represents the experimental reflection coefficient curve against the frequency. The reflection coefficient curve is plotted from the eight data sets extracted from the experiment. From the reflection coefficient plot, it has been found that at a lower frequency range, i.e., 100–450 Hz, the reflection coefficient is almost 0.9, which means the Helmholtz resonators within the plate do not interact with the incoming sound in this frequency range. This effect can also be observed from the pressure plot in Figure 7a at 125 Hz. Figure 7a depicts that the sound pressure is the same in all Helmholtz resonators and they behave as a reflective wall. Thus, the proposed metamaterials have large attenuation in the frequency range of 100 to 450 Hz. As the frequency approaches the resonance frequency of Helmholtz resonators, a dip in the reflection curve can be observed, which is maximum at around 680 and 750 Hz. Similarly, other dips in the curve can also be observed between 1000—2000 Hz where the resonance frequency of other Helmholtz resonators exists. Figure 7b–f confirms the interaction of the incoming sound with Helmholtz resonators when the incoming sound approaches their resonant frequencies.

The sound absorption tendency of the metamaterial plate can be observed from the absorption coefficient plot as shown in Figure 9b. In the lower frequency range, i.e., 100–450 Hz, the absorption coefficient is almost 0.15 and as sound frequency increases and approaches the resonance frequency of the Helmholtz resonator, the rise in the absorption coefficient can be observed in the experimental absorption coefficient curve. The peak is around 680 and 750 Hz. Other peaks between 1000–2000 Hz can be observed in the absorption plot where the resonance frequencies of other resonators exist. This increase in sound absorption is due to the large movement of air particles within the neck section of Helmholtz resonators.

5. Conclusions

This paper describes the scope of manufacturing metamaterials using additive manufacturing to achieve high transmission loss. The impact of Helmholtz resonators within a metamaterial plate is investigated by creating seven Helmholtz resonator-shaped cavities in a 50 mm diameter and 20 mm thick plate. A 3D-printed metamaterial plate with a Helmholtz resonator is numerically and experimentally examined. The experiments are carried out in the transmission loss tube made up of brass. The transfer matrix method is used to calculate the transmission coefficient. The transmission loss calculated experimentally is in good agreement with the numerical result at higher frequencies, which confirms the validation of our study. The experiments show total transmission loss of around 40 dB for the proposed metamaterial plate at the octave band frequencies. The higher transmission loss is due to the combined effect of reflection of the wall and absorption in the Helmholtz resonator. The sound pressure plot of the numerical simulation results and the reflection coefficient plot of the experimental results indicate the reflective behavior of the plate within the frequency range of 100–450 Hz. As the frequency approaches the resonance frequency of the Helmholtz resonators, the dip in the reflection coefficient plot is observed. Additionally, when the sound wave coincide with the natural frequency of the Helmholtz resonator, peaks can be observed in the absorption coefficient plot. These plates can be used where quieter ambience is important and the noise source has frequencies in a particular band. These types of lightweight metamaterials can be useful for designing the structure in aerospace and aeronautic industries where mass is considered as a deciding factor in designing components.