Contactless Liquid Height and Property Estimation Using Surface Acoustic Waves
Abstract
1. Introduction
2. Methodology
2.1. Operation Principle
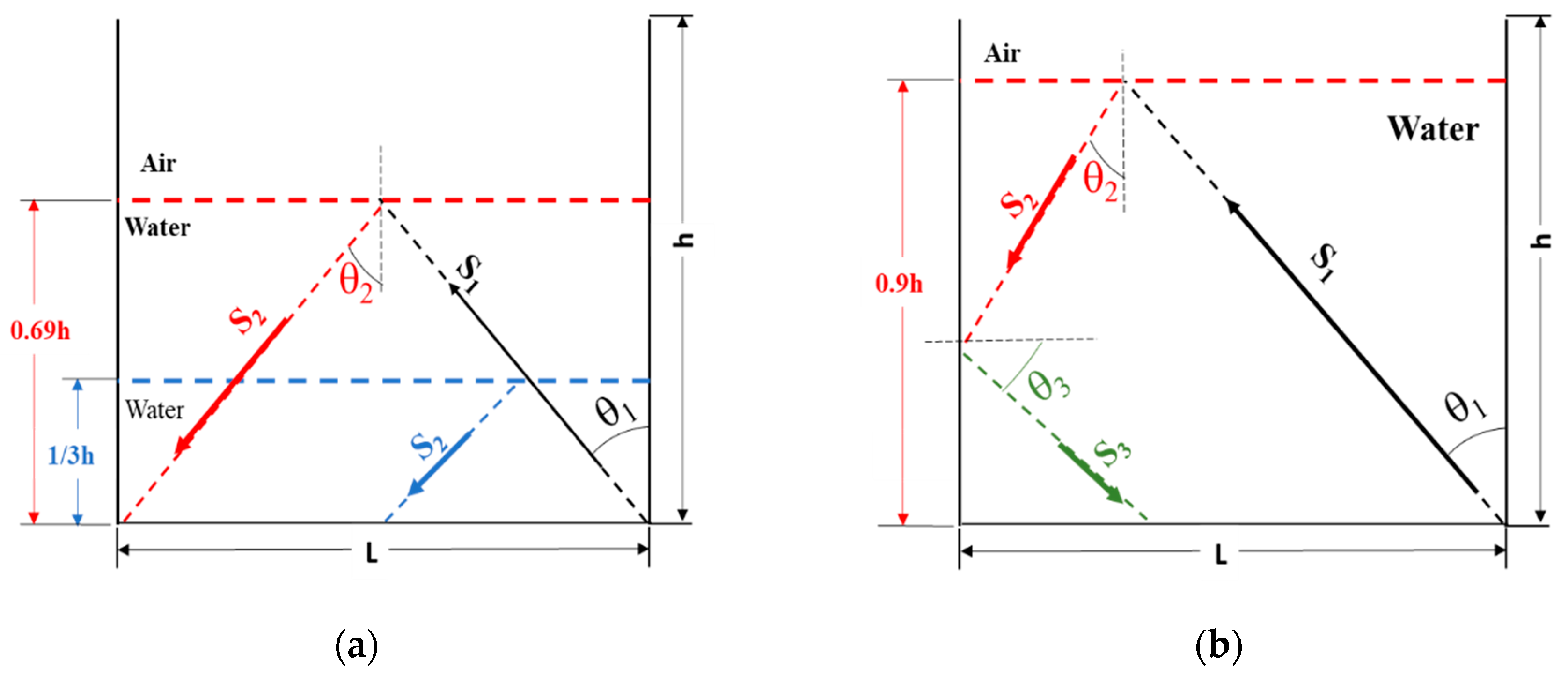
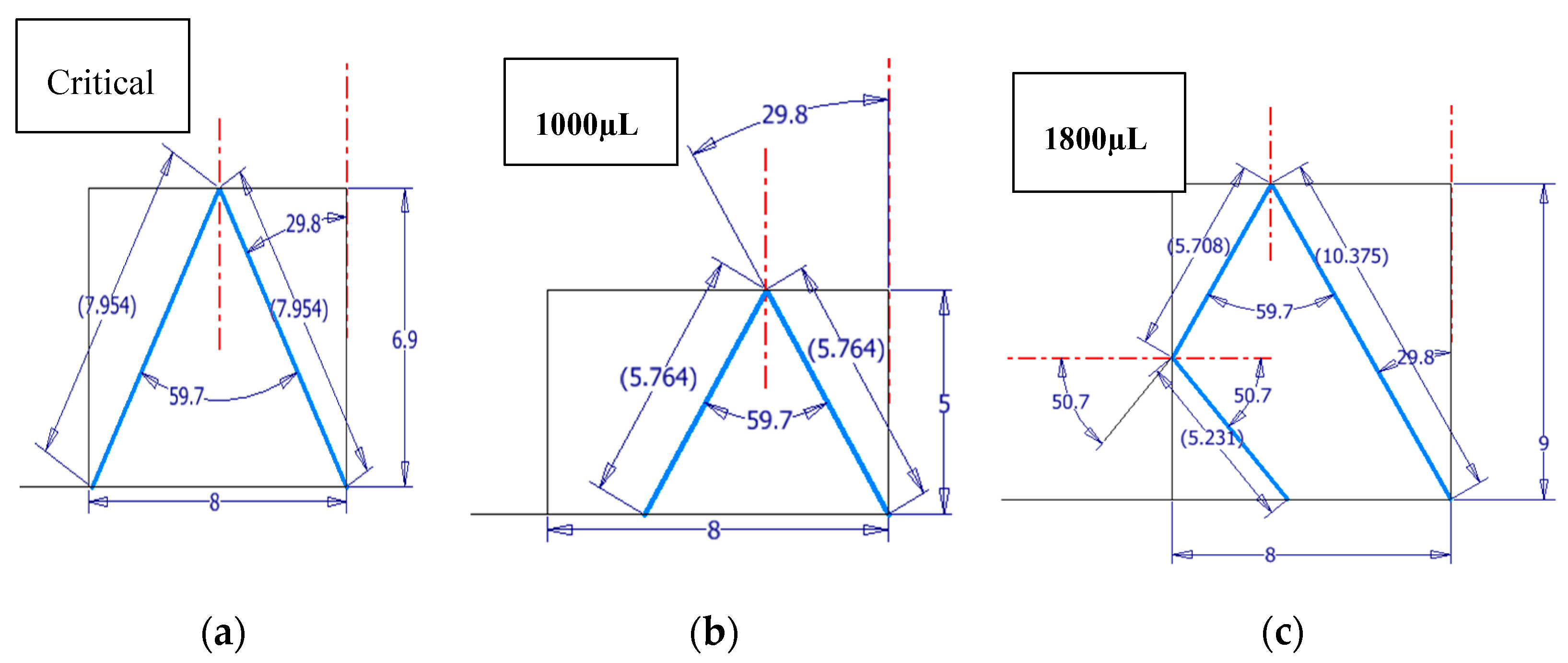
2.2. Liquid Height Estimation
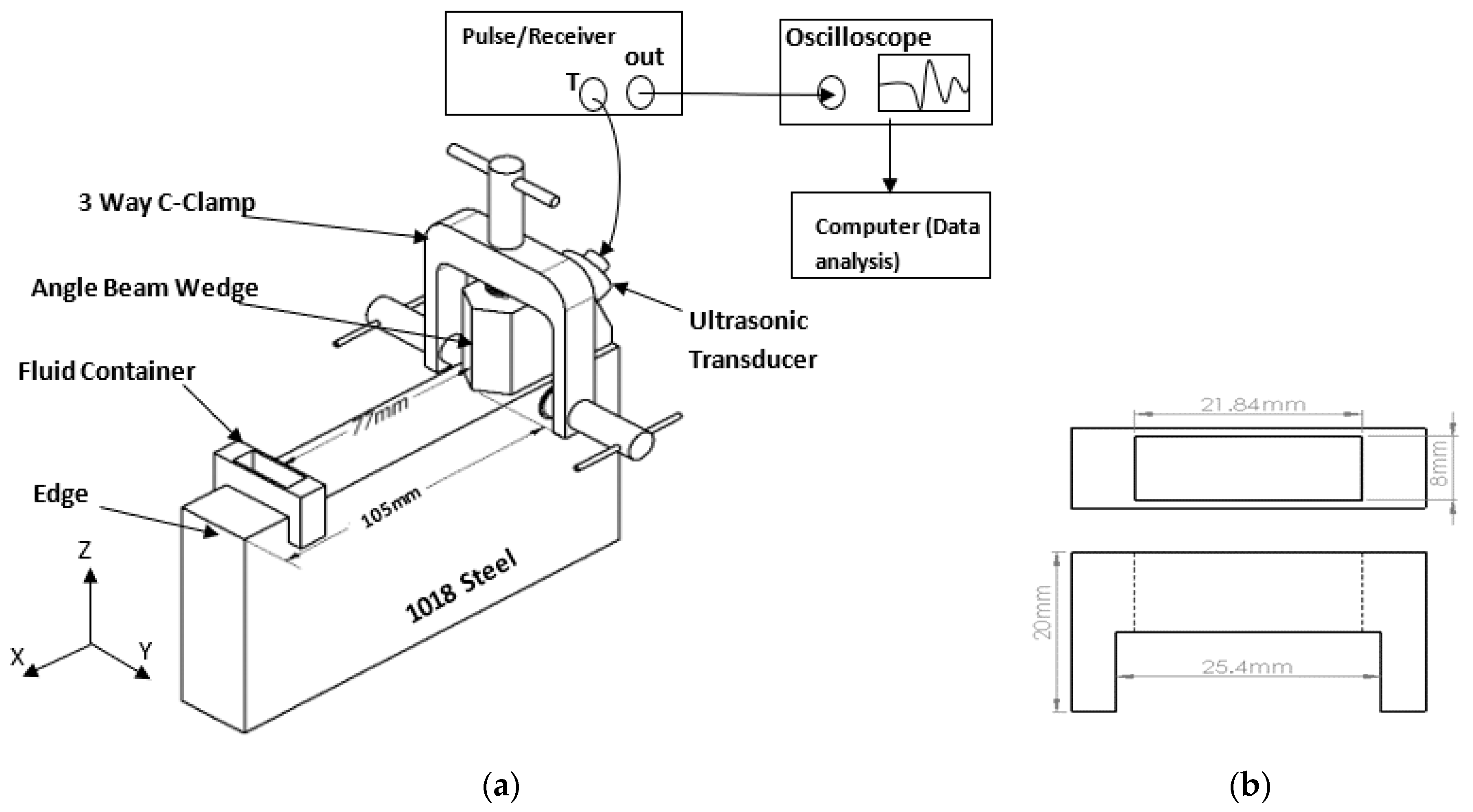
2.3. Experimental Setup
3. Results and Discussion
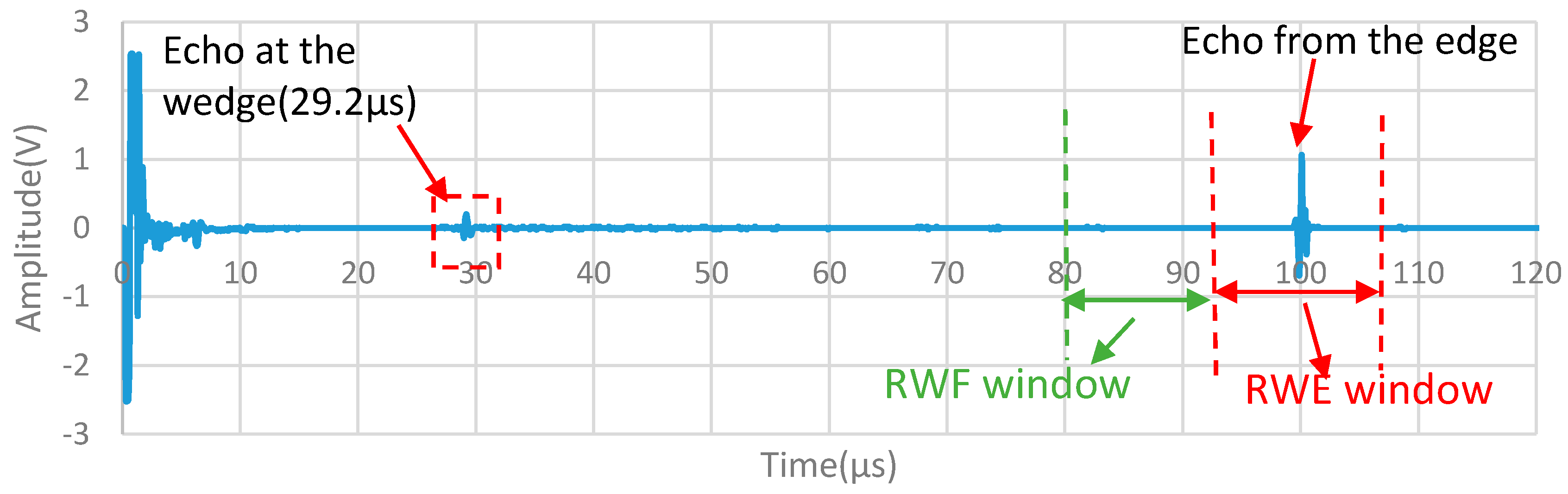
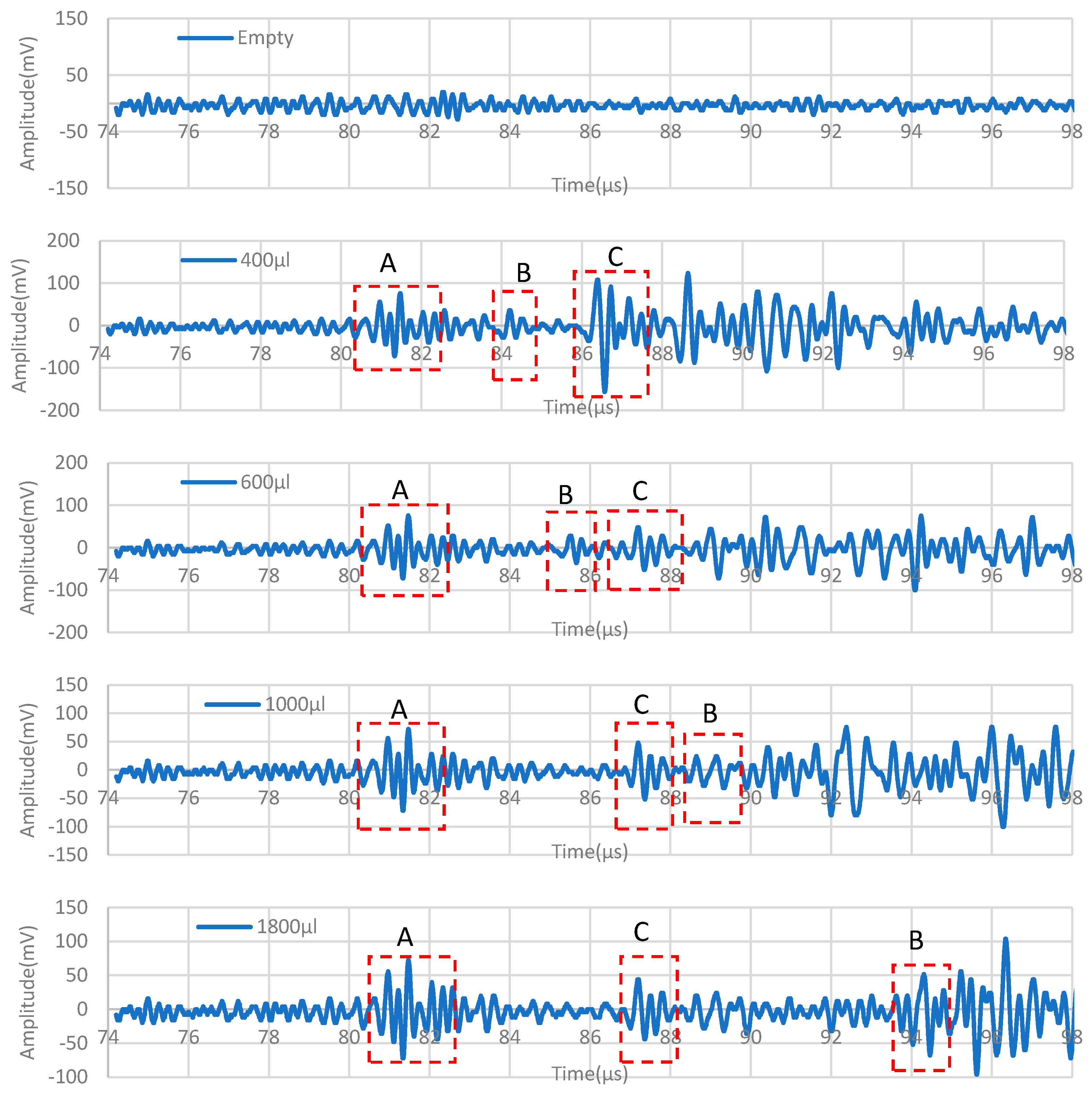
3.1. The Effect of the Presence of Liquid Media on the Propagation Path of the Reflected Wave from a Defect (Edge)
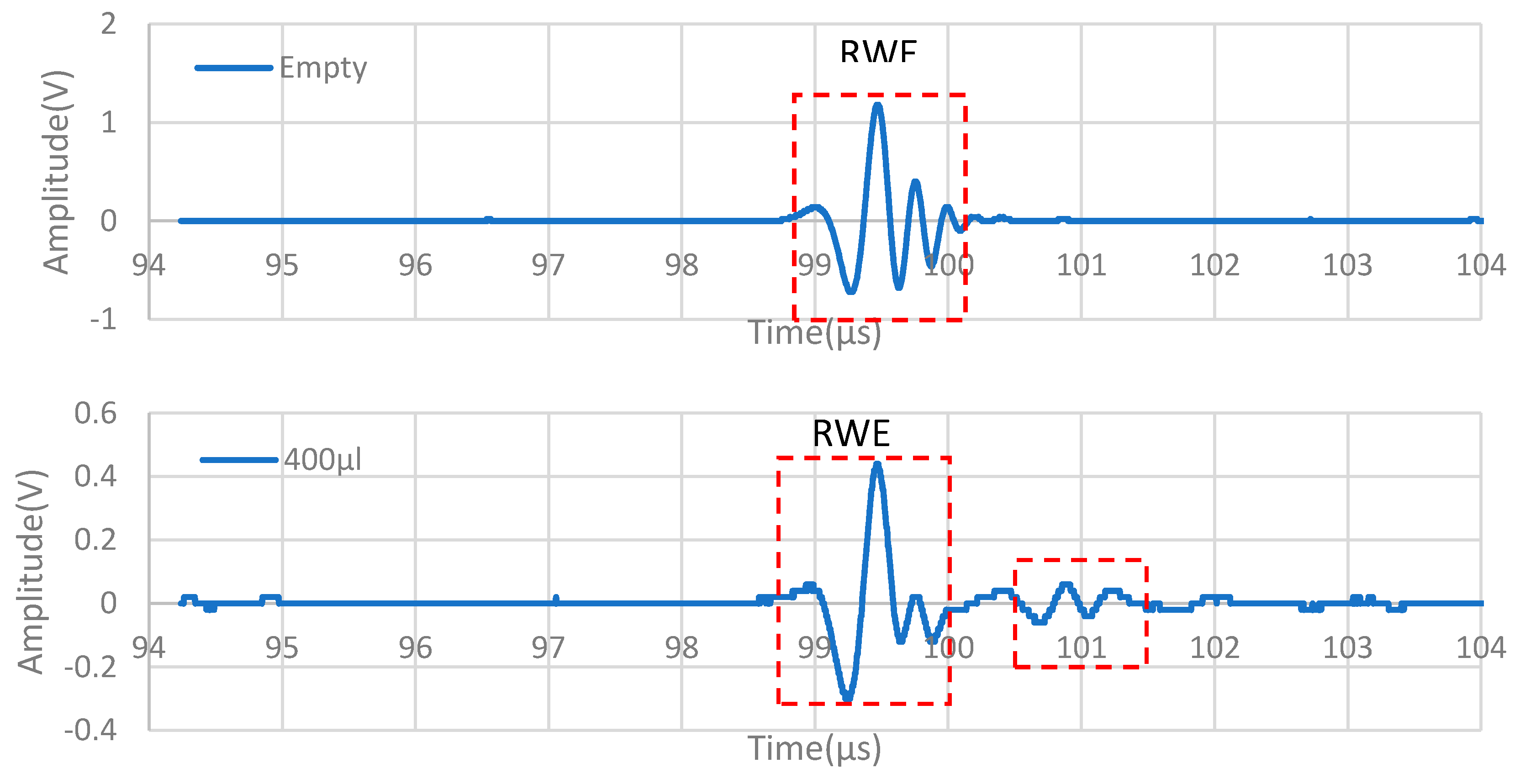
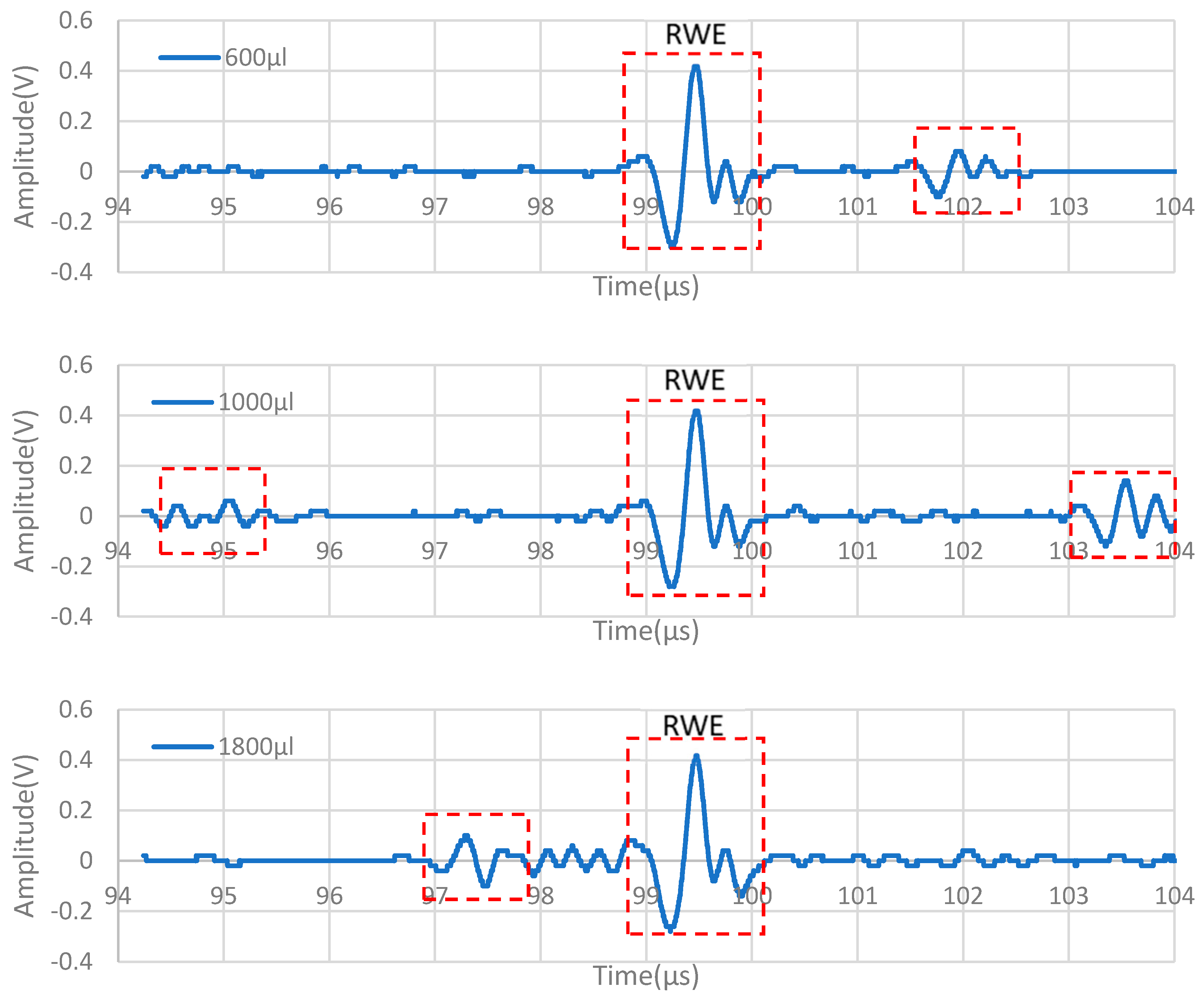
3.2. The Reflected Wave from the Liquid on the Propagation Path
3.3. Estimating Liquid Height
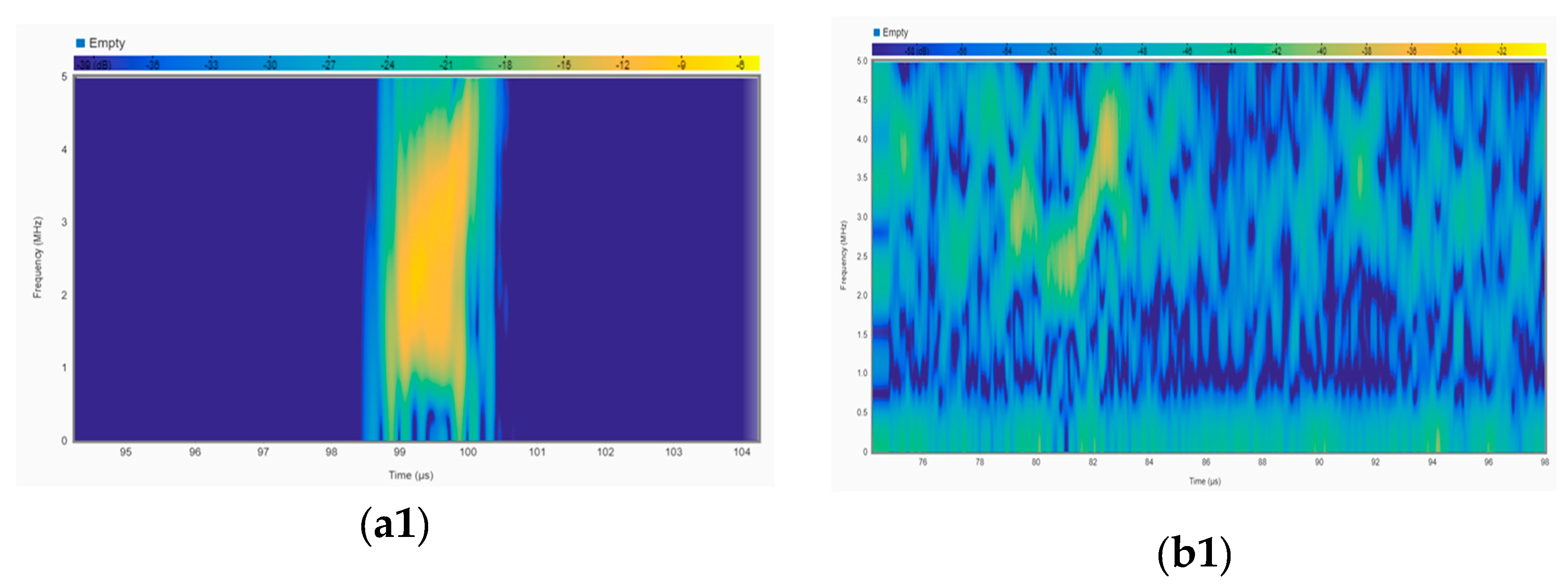
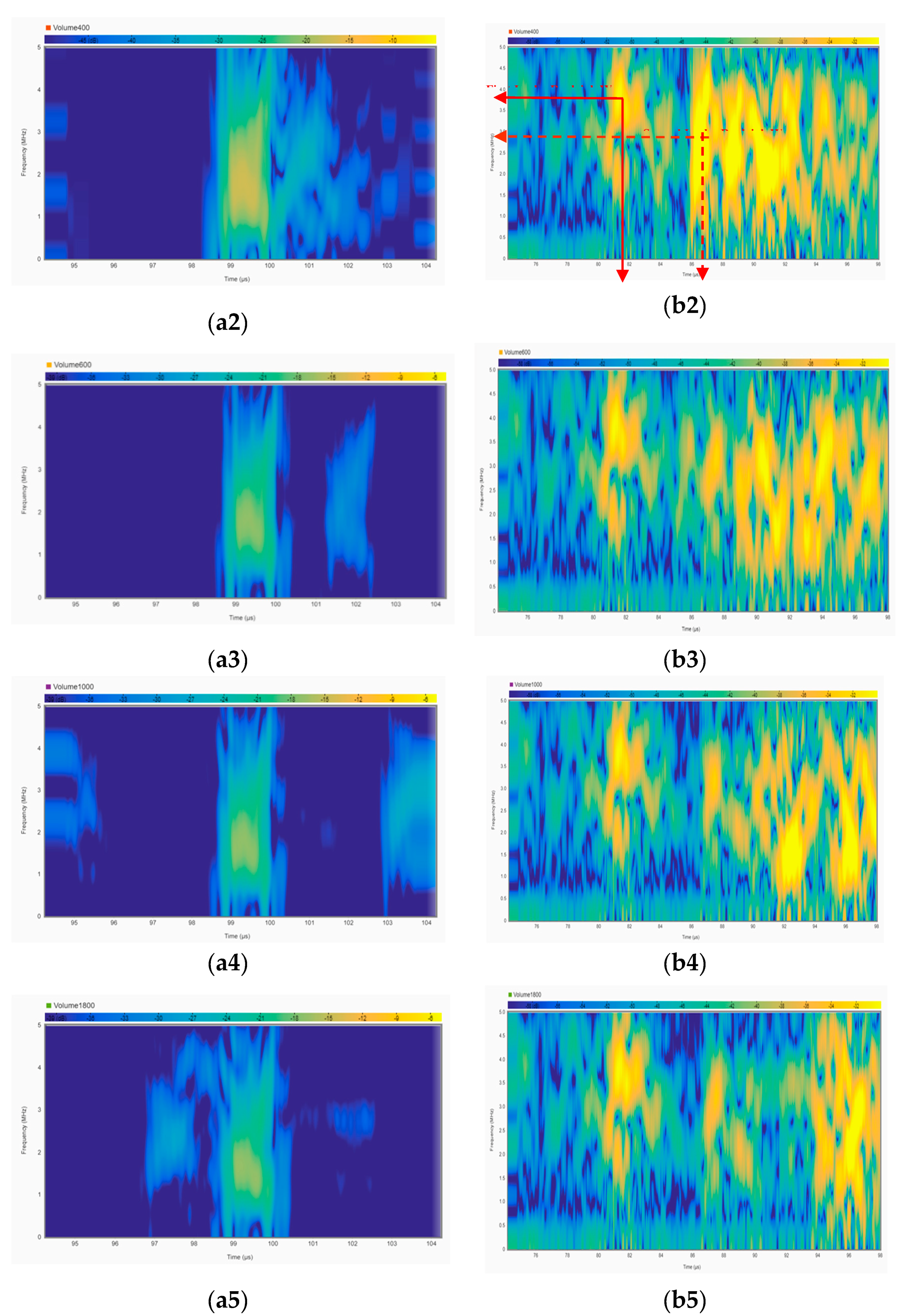
3.4. Short-Time Fourier Transform Analysis for Both the Reflected Wave from the Defect (Edge) and the Liquid
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
Appendix A.1. Finding the Refraction Angle
Appendix A.2. The Derivation Equation for the Second Case when h > 0.86 L
References
- Chamuel, J.R. Laboratory studies on pulsed leaky Rayleigh wave components in a water layer over a solid bottom. In Shear Waves in Marine Sediments; Springer: Berlin/Heidelberg, Germany, 1991; pp. 59–66. [Google Scholar]
- Cheeke, J.D.N. Fundamentals and Applications of Ultrasonic Waves; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar]
- Überall, H. Surface waves in acoustics. Phys. Acoust. 1973, 10, 1–60. [Google Scholar]
- Stoneley, R. Elastic waves at the surface of separation of two solids. In Proceedings of the Royal Society of London. Series A, Containing Papers of a Mathematical and Physical Character; Royal Society: London, UK, 1924; Volume 106, pp. 416–428. [Google Scholar]
- Thompson, D.O.; Chimenti, D.E. Review of Progress in Quantitative Nondestructive Evaluation; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012; Volume 18. [Google Scholar]
- Zhu, J.; Popovics, J.S.; Schubert, F. Leaky Rayleigh and Scholte waves at the fluid–solid interface subjected to transient point loading. J. Acoust. Soc. Am. 2004, 116, 2101–2110. [Google Scholar] [CrossRef]
- Brekhovskikh, L. Waves in Layered Media; Elsevier: Amsterdam, The Netherlands, 2012; Volume 16. [Google Scholar]
- Ewing, M.W. Elastic Waves in Layered Media; McGraw-Hill: New York, NY, USA, 1957. [Google Scholar]
- Padilla, F.; de Billy, M.; Quentin, G. Theoretical and experimental studies of surface waves on solid-fluid interfaces when the value of the fluid sound velocity is located between the shear and the longitudinal ones in the solid. J. Acoust. Soc. Am. 1999, 106, 666–673. [Google Scholar] [CrossRef]
- Gedge, M.; Hill, M. Acoustofluidics 17: Theory and applications of surface acoustic wave devices for particle manipulation. Lab Chip 2012, 12, 2998–3007. [Google Scholar] [CrossRef] [PubMed]
- Ricco, A.; Martin, S. Acoustic wave viscosity sensor. Appl. Phys. Lett. 1987, 50, 1474–1476. [Google Scholar] [CrossRef]
- Yildirim, B.; Senveli, S.U.; Gajasinghe, R.W.; Tigli, O. Surface Acoustic Wave Viscosity Sensor with Integrated Microfluidics on a PCB Platform. IEEE Sens. J. 2018, 18, 2305–2312. [Google Scholar] [CrossRef]
- Franier, B.D.L.; Thompson, M. Early stage detection and screening of ovarian cancer: A research opportunity and significant challenge for biosensor technology. Biosens. Bioelectron. 2019, 135, 71–81. [Google Scholar] [CrossRef] [PubMed]
- Onen, O.; Sisman, A.; Gallant, N.D.; Kruk, P.; Guldiken, R. A urinary Bcl-2 surface acoustic wave biosensor for early ovarian cancer detection. Sensors 2012, 12, 7423–7437. [Google Scholar] [CrossRef]
- Guldiken, R.; Jo, M.C.; Gallant, N.D.; Demirci, U.; Zhe, J. Sheathless size-based acoustic particle separation. Sensors 2012, 12, 905–922. [Google Scholar] [CrossRef]
- Jo, M.C.; Guldiken, R. Active density-based separation using standing surface acoustic waves. Sens. Actuators A Phys. 2012, 187, 22–28. [Google Scholar] [CrossRef]
- Jo, M.C.; Guldiken, R. Particle manipulation by phase-shifting of surface acoustic waves. Sens. Actuators A Phys. 2014, 207, 39–42. [Google Scholar] [CrossRef]
- Jo, M.C.; Guldiken, R. Dual surface acoustic wave-based active mixing in a microfluidic channel. Sens. Actuators A Phys. 2013, 196, 1–7. [Google Scholar] [CrossRef]
- Wang, T.; Ni, Q.; Crane, N.; Guldiken, R. Surface acoustic wave based pumping in a microchannel. Microsyst. Technol. 2017, 23, 1335–1342. [Google Scholar] [CrossRef]
- Wang, T.; Green, R.; Nair, R.R.; Howell, M.; Mohapatra, S.; Guldiken, R.; Mohapatra, S.S. Surface acoustic waves (SAW)-based biosensing for quantification of cell growth in 2D and 3D cultures. Sensors 2015, 15, 32045–32055. [Google Scholar] [CrossRef] [PubMed]
- Alhazmi, H.; Guldiken, R. Quantification of Bolt Tension by Surface Acoustic Waves: An Experimentally Verified Simulation Study. Acoustics 2019, 1, 794–807. [Google Scholar] [CrossRef]
- Martinez, J.; Sisman, A.; Onen, O.; Velasquez, D.; Guldiken, R. A synthetic phased array surface acoustic wave sensor for quantifying bolt tension. Sensors 2012, 12, 12265–12278. [Google Scholar] [CrossRef]
- Wang, T.; Green, R.; Guldiken, R.; Mohapatra, S.; Mohapatra, S. Multiple-layer guided surface acoustic wave (SAW)-based pH sensing in longitudinal FiSS-tumoroid cultures. Biosens. Bioelectron. 2019, 124, 244–252. [Google Scholar] [CrossRef]
- Lynnworth, L.C.; Seger, J.L.; Bradshaw, J.E. Ultrasonic System for Measuring Fluid Impedance or Liquid Level. U.S. Patent 4,320,659, 23 March 1982. [Google Scholar]
- Mohammed, S.L.; Al-Naji, A.; Farjo, M.M.; Chahl, J. Highly Accurate Water Level Measurement System Using a Microcontroller and an Ultrasonic Sensor. In IOP Conference Series: Materials Science and Engineering; IOP Publishing: Bristol, England, 2019; Volume 518, p. 042025. [Google Scholar]
- Zhang, B.; Wei, Y.-J.; Liu, W.-Y.; Zhang, Y.-J.; Yao, Z.; Zhang, L.; Xiong, J.-J. A novel ultrasonic method for liquid level measurement based on the balance of echo energy. Sensors 2017, 17, 706. [Google Scholar] [CrossRef]
- Giurgiutiu, V. Structural Health Monitoring with Piezoelectric Wafer Active Sensors: With Piezoelectric Wafer Active Sensors; Elsevier: Amsterdam, The Netherlands, 2007. [Google Scholar]
- Hevin, G.; Abraham, O.; Pedersen, H.; Campillo, M. Characterization of surface cracks with Rayleigh waves: A numerical model. NDT & E Int. 1998, 31, 289–297. [Google Scholar] [CrossRef]
- Rose, J.L. Ultrasonic Waves in Solid Media; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Ohara, Y.; Oshiumi, T.; Nakajima, H.; Yamanaka, K.; Wu, X.; Uchimoto, T.; Takagi, T.; Tsuji, T.; Mihara, T. Ultrasonic phased array with surface acoustic wave for imaging cracks. AIP Adv. 2017, 7, 065214. [Google Scholar] [CrossRef]
- Parker, N.; Mather, M.; Morgan, S.; Povey, M. Longitudinal acoustic properties of poly (lactic acid) and poly (lactic-co-glycolic acid). Biomed. Mater. 2010, 5, 055004. [Google Scholar] [CrossRef] [PubMed]
- Kehtarnavaz, N.; Kim, N. Digital Signal Processing System-Level Design Using LabVIEW; Elsevier: Amsterdam, The Netherlands, 2011. [Google Scholar]
- Giannakopoulos, T.; Pikrakis, A. Introduction to Audio Analysis: A MATLAB® Approach; Academic Press: Cambridge, MA, USA, 2014. [Google Scholar]

| PRF(Hz) | Energy | Damping (50 Ω) | High Pass Filter (HPF) | Low Pass Filter (LPF) | Amplifier (Gain) |
|---|---|---|---|---|---|
| 100 | 1 | 3 | 1 MHz | 10 MHz | 30 db |
| Deionized Water | 1018 Steel | Air | PLA (25 °C) | |
|---|---|---|---|---|
| Density, ρ (g/cm3) | 1 | 7.870 | 0.001 | 1.24 |
| Speed of Sound (m/s) | 1480 | 2953 (C.R.) | 330–343 | 2200~2300 [31] |
| Empty | 400 µL | 600 µL | 1000 µL | 1800 µL | |
|---|---|---|---|---|---|
| P–P amplitude (V) | 1.90 | 0.74 | 0.72 | 0.70 | 0.70 |
| - | −61.05 | −62.11 | −63.16 | −63.16 |
| Actual Height (mm) | tA (µs) | tB (µs) | tc (µs) | CLW (m/s) | Error in CLW (%) | S1 + S2 (mm) | h (mm) | Error in h (%) | |
|---|---|---|---|---|---|---|---|---|---|
| 400 µL | 2 | 80.96 | 84.19 | 87.18 | 1427.5 | −3.54% | 4.8 | 2.07 | 3.7 |
| 600 µL | 3 | 80.96 | 85.51 | 87.18 | 1520.1 | 2.71% | 6.7 | 2.92 | −2.6 |
| 1000 µL | 5 | 80.96 | 88.64 | 87.21 | 1501 | 1.42% | 11.4 | 4.93 | −1.4 |
| 1800 µL | 9 | 80.96 | 96.36 | 87.22 | 1347.4 | −8.96% | 22.8 | 9.89 | 9.8/2.7 * |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alhazmi, H.; Guldiken, R. Contactless Liquid Height and Property Estimation Using Surface Acoustic Waves. Acoustics 2020, 2, 366-381. https://doi.org/10.3390/acoustics2020021
Alhazmi H, Guldiken R. Contactless Liquid Height and Property Estimation Using Surface Acoustic Waves. Acoustics. 2020; 2(2):366-381. https://doi.org/10.3390/acoustics2020021
Chicago/Turabian StyleAlhazmi, Hani, and Rasim Guldiken. 2020. "Contactless Liquid Height and Property Estimation Using Surface Acoustic Waves" Acoustics 2, no. 2: 366-381. https://doi.org/10.3390/acoustics2020021
APA StyleAlhazmi, H., & Guldiken, R. (2020). Contactless Liquid Height and Property Estimation Using Surface Acoustic Waves. Acoustics, 2(2), 366-381. https://doi.org/10.3390/acoustics2020021







