A High-Frequency Model of a Rectilinear Beam with a T-Shaped Cross Section
Abstract
1. Introduction
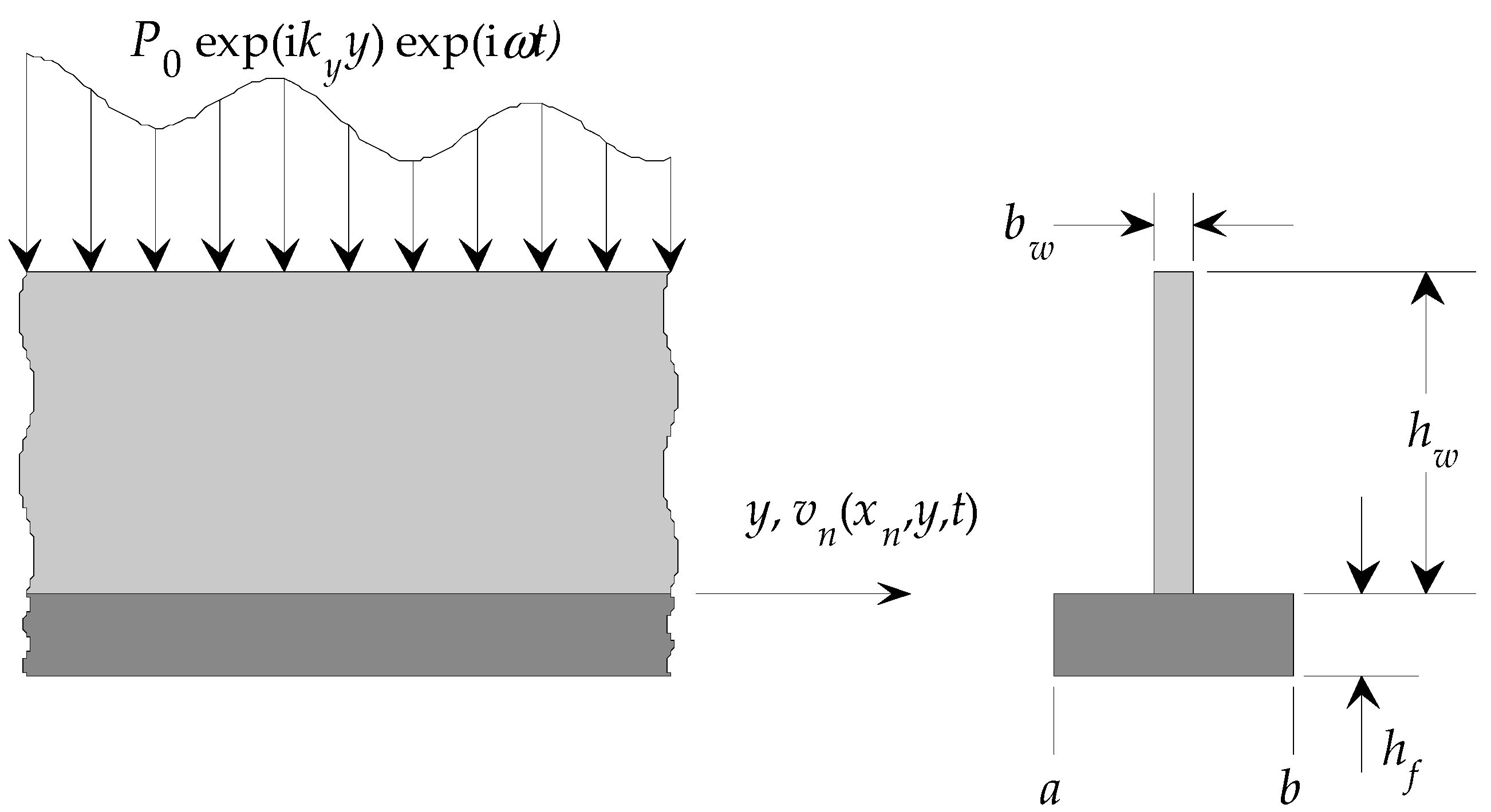
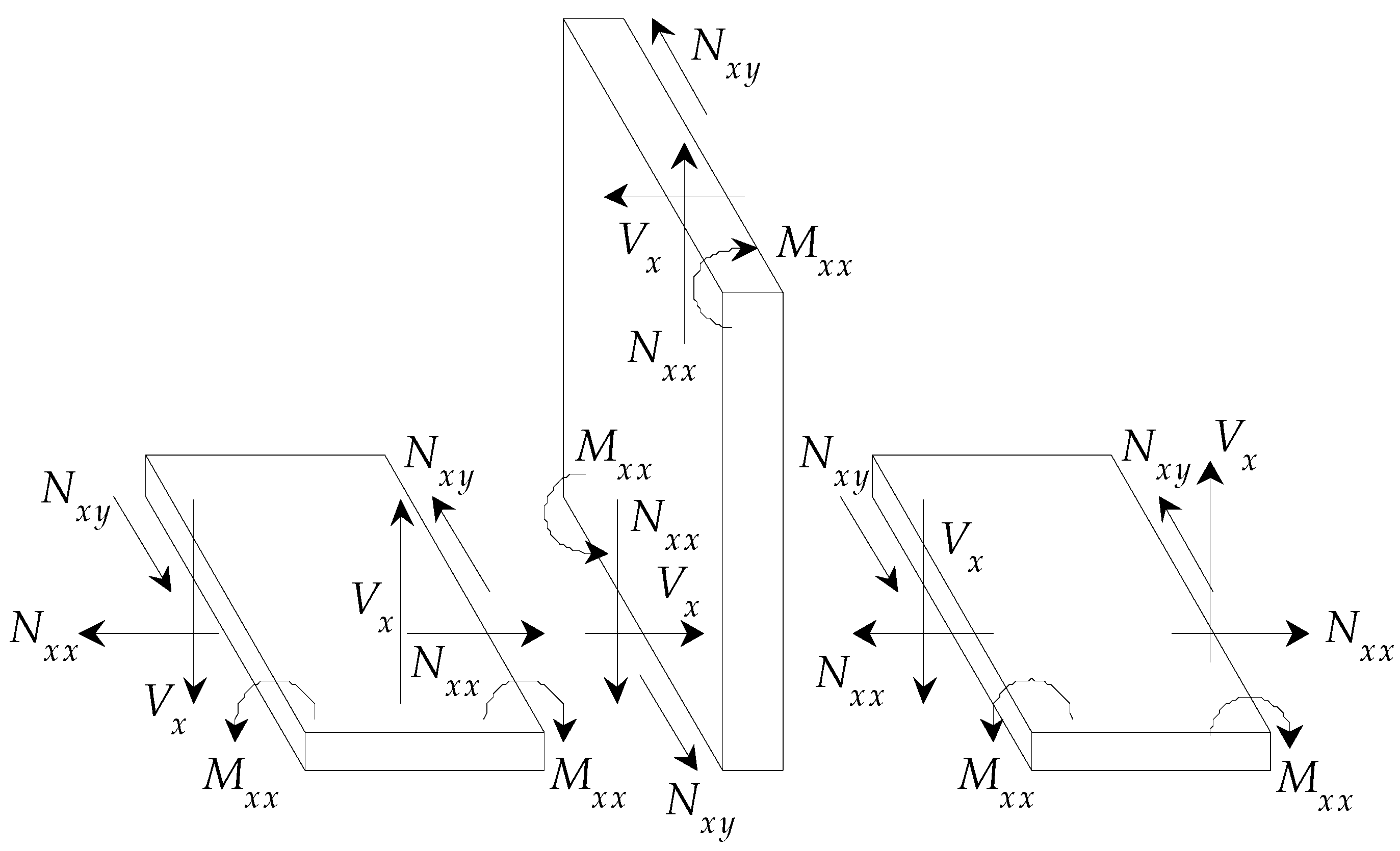
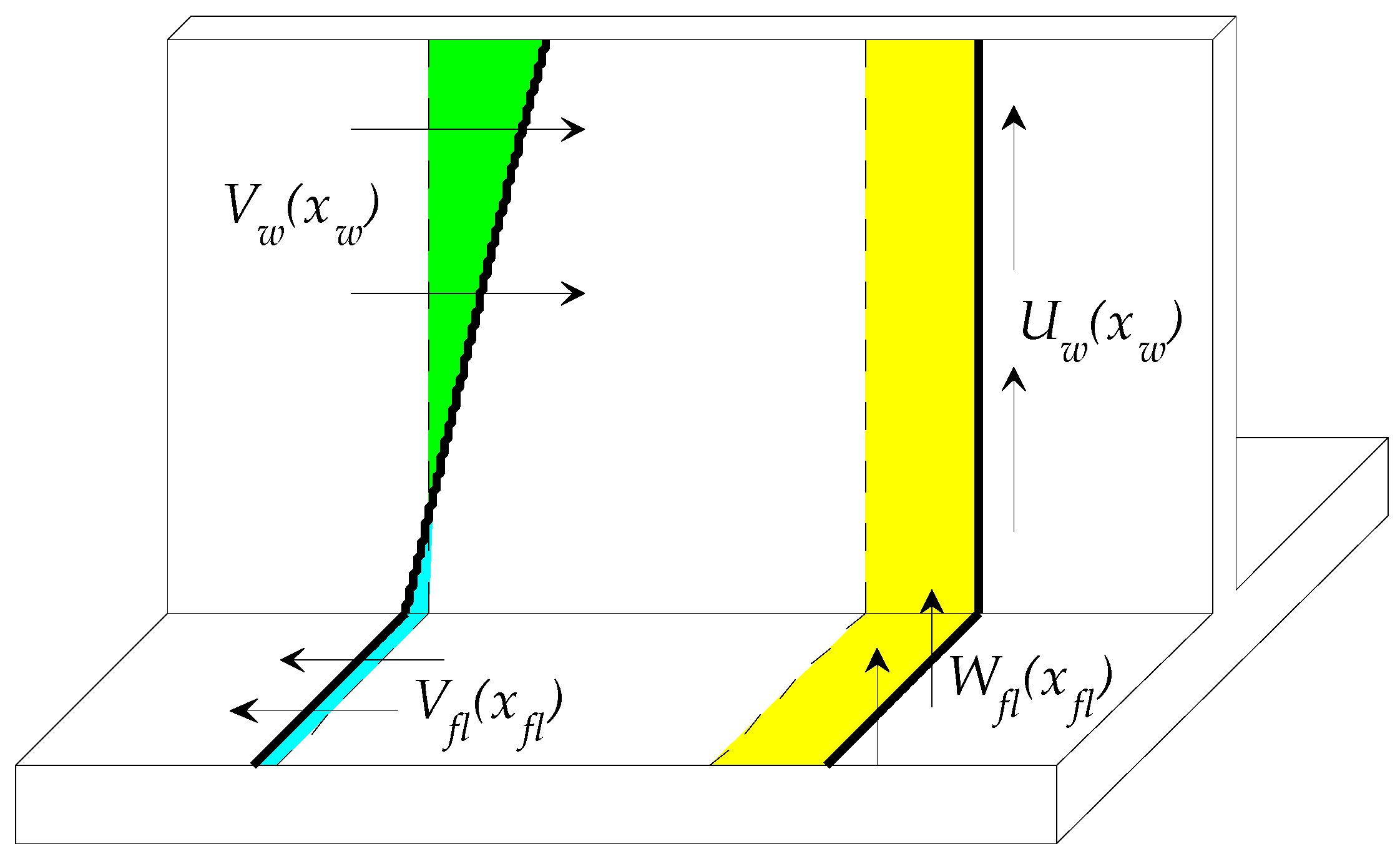
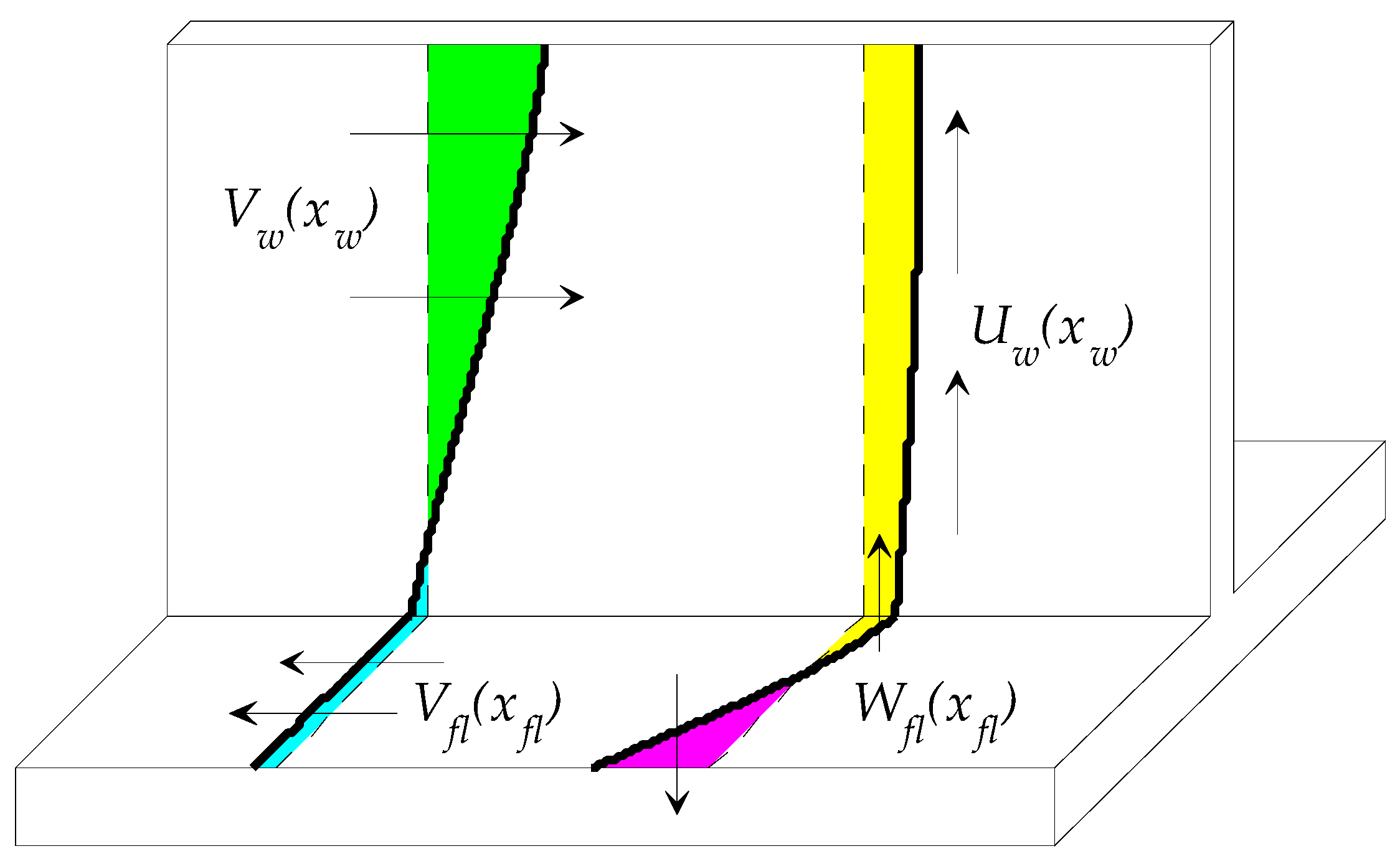
2. Methods
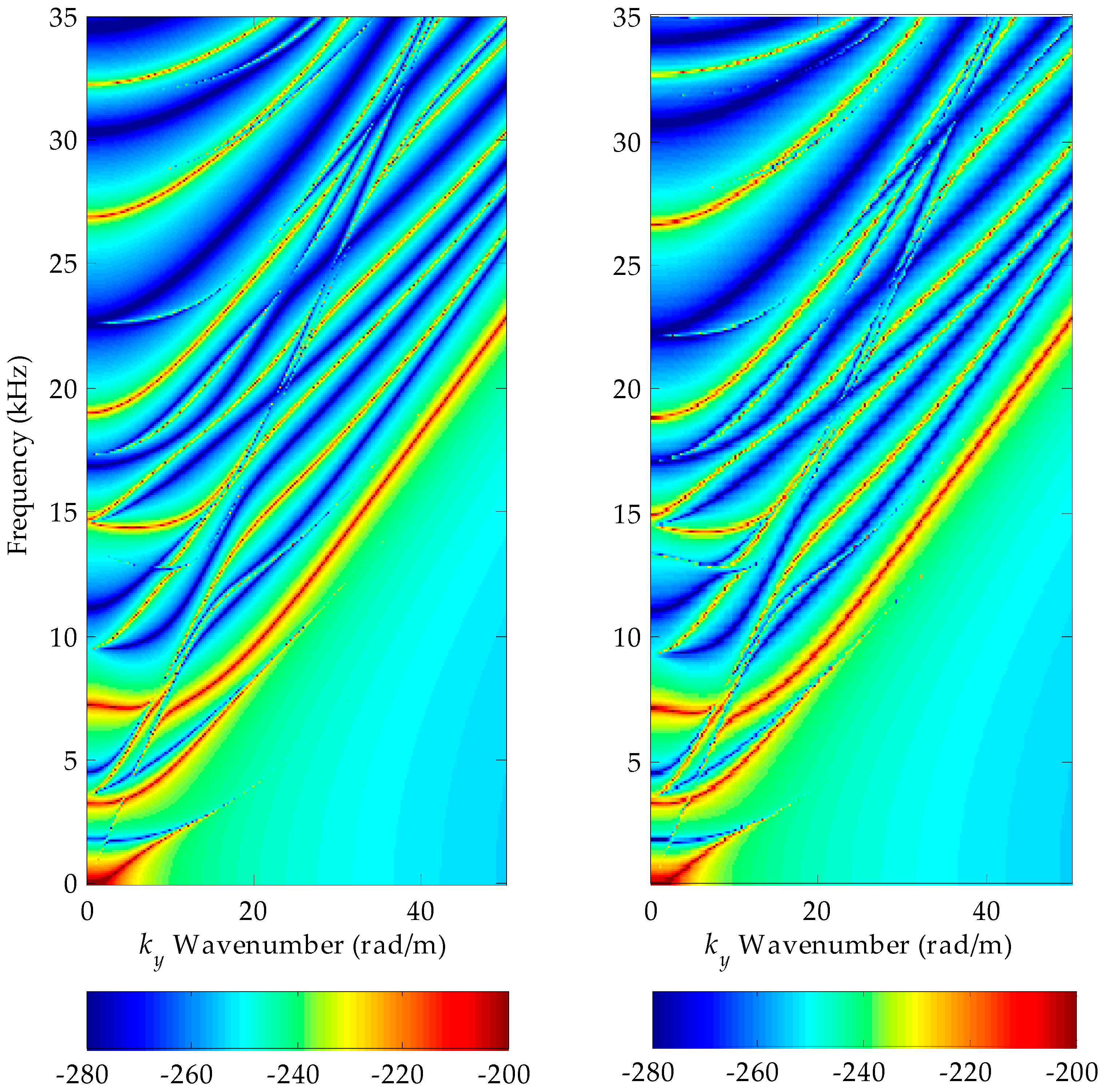
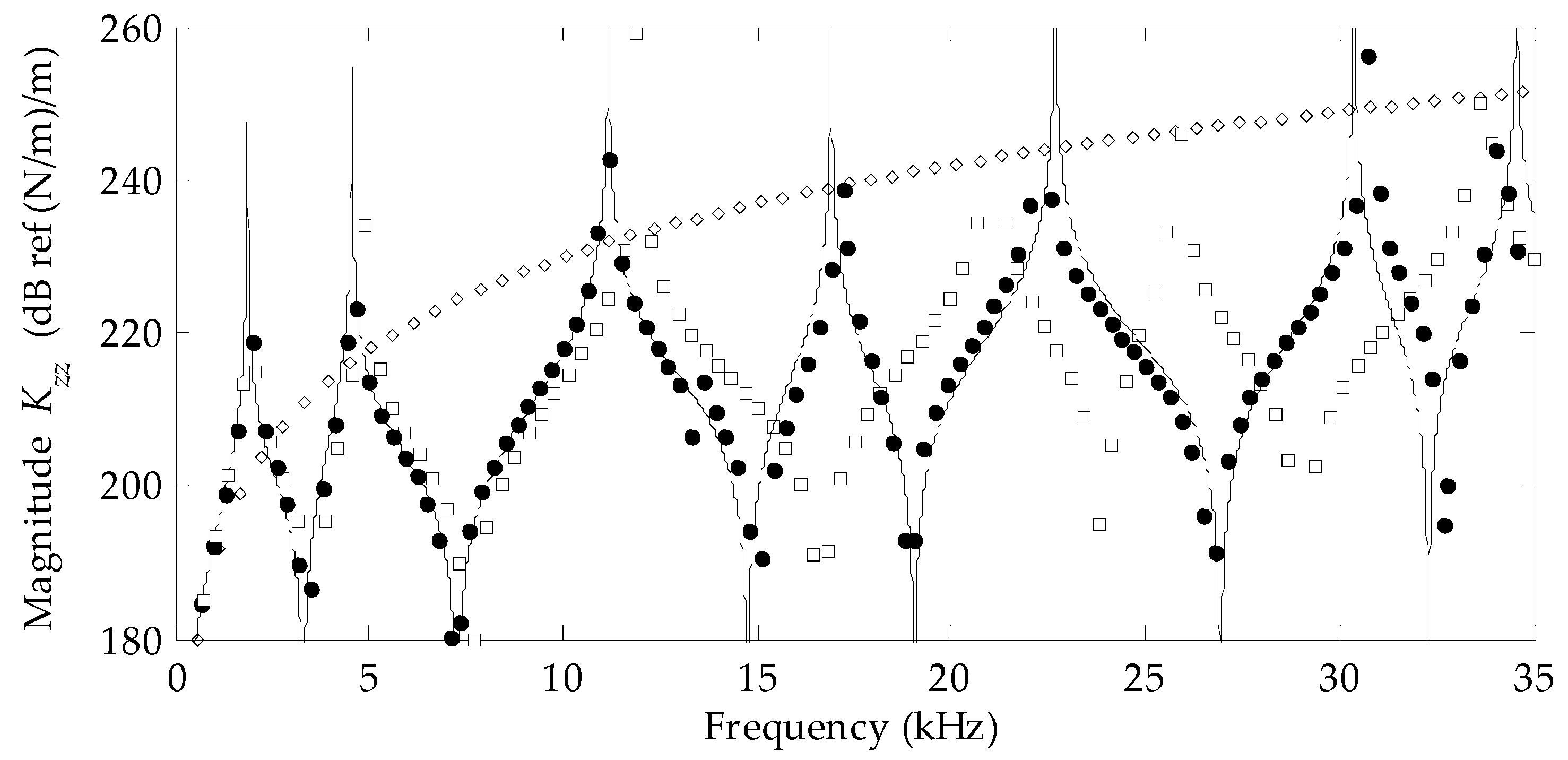
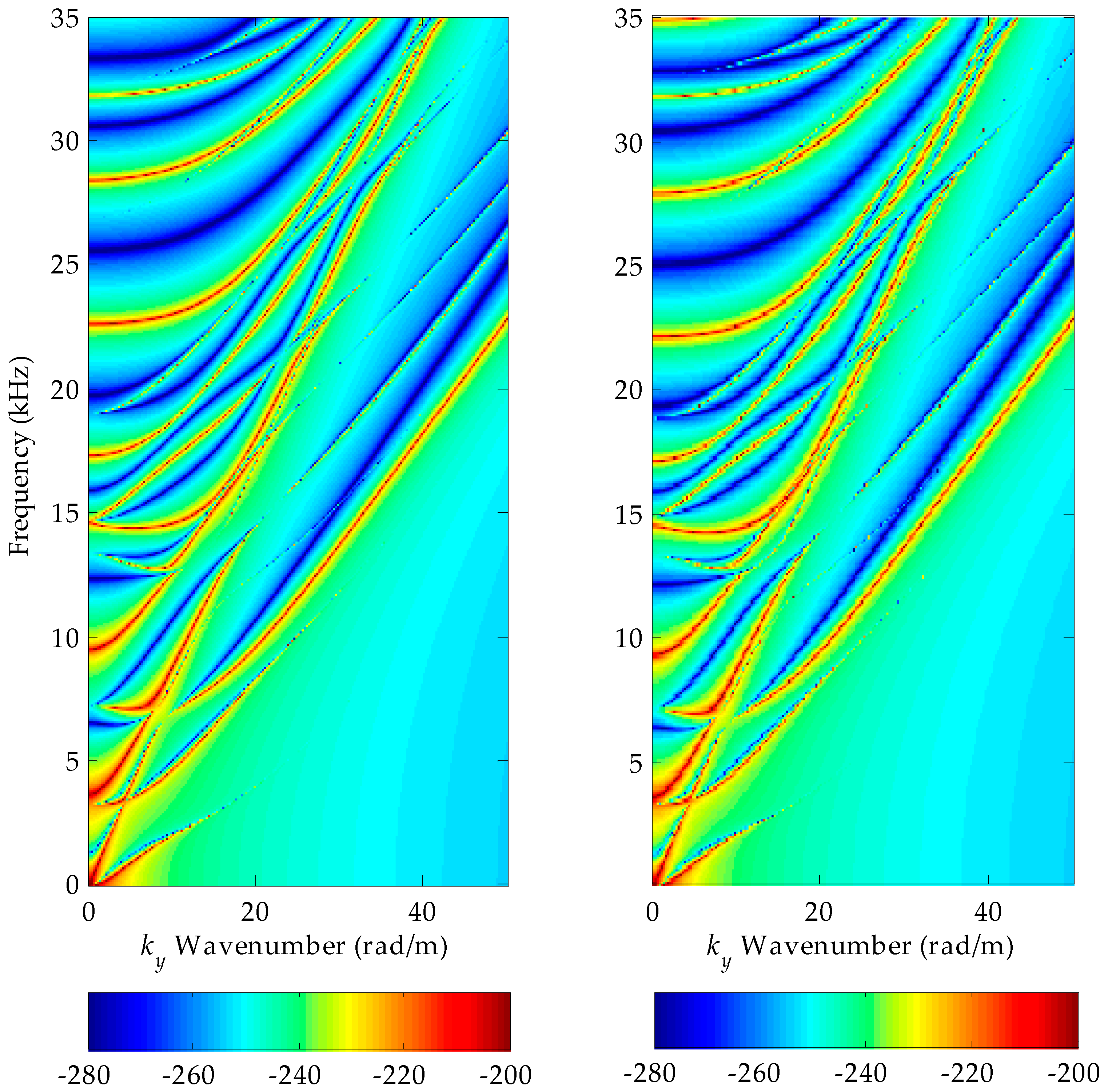
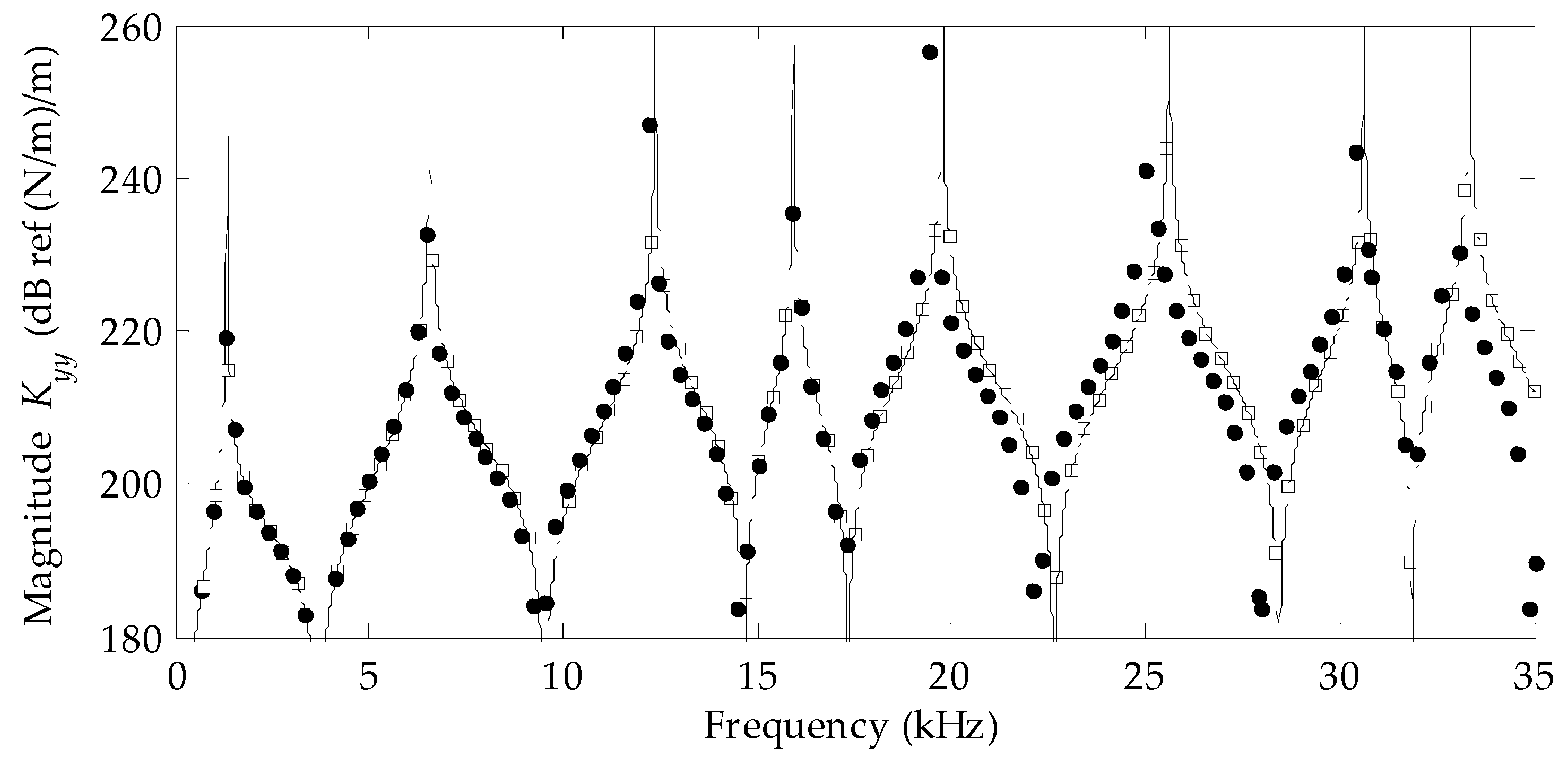
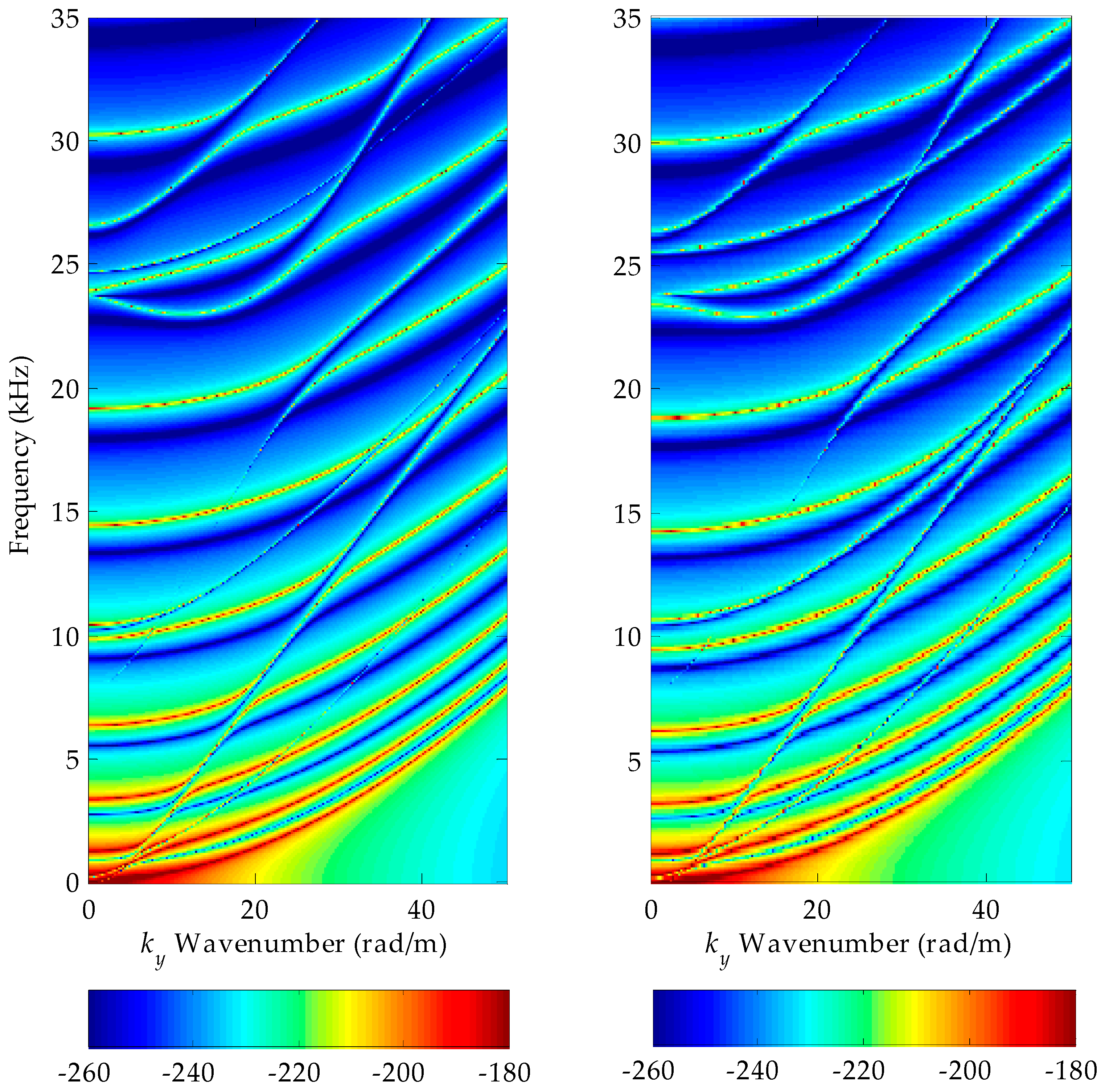
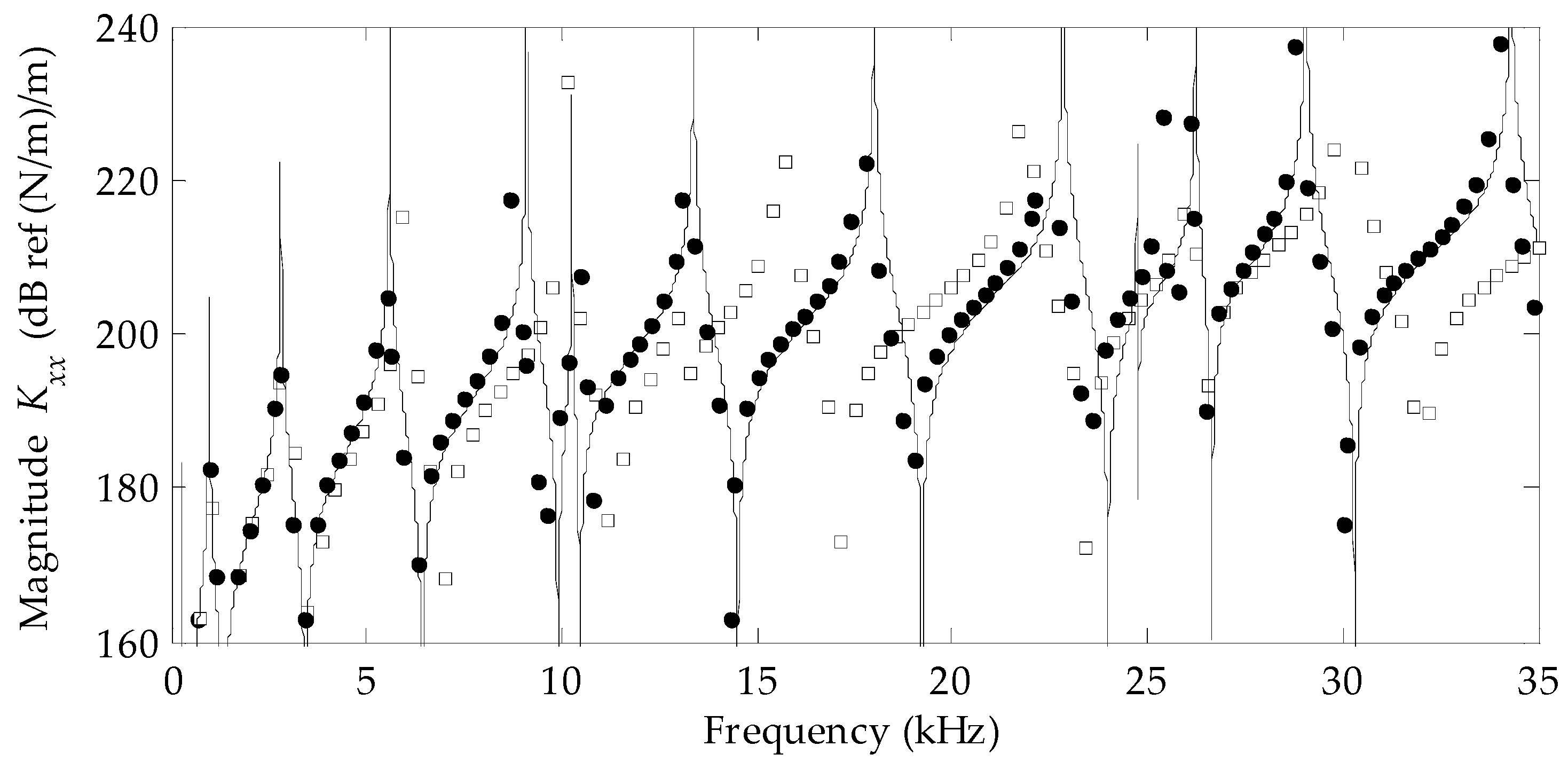
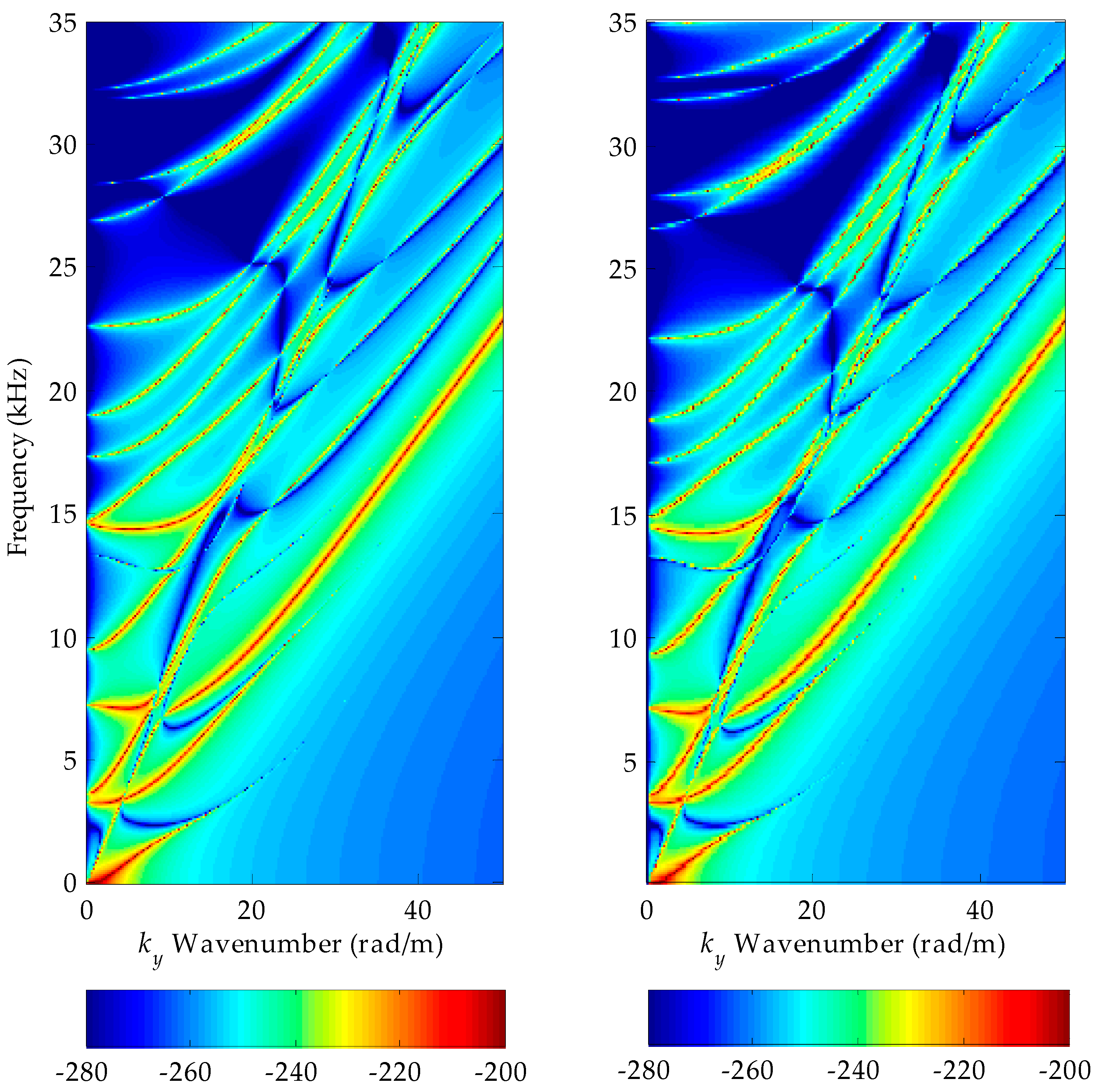
3. Results
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A.
References
- Hull, A.J.; Perez, D.; Cox, D.L. A Hybrid T Beam Model in a Cartesian Coordinate System; NUWC-NPT Technical Memorandum 17-020; Naval Undersea Warfare Center Division: Newport, RI, USA, 15 March 2017. [Google Scholar]
- Hull, A.J.; Perez, D.; Cox, D.L. A comprehensive analytical dynamic model of a T-beam. Int. J. Acoust. Vib. 2019, 24, 139–149. [Google Scholar] [CrossRef]
- Love, A.E.H. On the small free vibrations and deformations of elastic shells. Philos. Trans. R. Soc. Lond. 1888, 179, 491–549. [Google Scholar] [CrossRef]
- Mindlin, R.D. Influence of rotary inertia and shear on flexural motions of isotropic elastic plates. ASME J. Appl. Mech. 1951, 18, 31–38. [Google Scholar]
- Han, S.M.; Benaroya, H.; Wei, T. Dynamics of transversely vibrating beams using four engineering theories. J. Sound Vib. 1999, 225, 935–988. [Google Scholar] [CrossRef]
- Timoshenko, S.P. On the transverse vibrations of bars of uniform cross-section. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1922, 43, 125–131. [Google Scholar] [CrossRef]
- Bickford, W.B. A Consistent Higher Order Beam Theory. In Proceedings of the 11th Southeastern Conference on Theoretical and Applied Mechanics, Huntsville, AL, USA, 8–9 April 1982; pp. 137–150. [Google Scholar]
- Karama, M.; Afaq, K.S.; Mistou, S. Mechanical behavior of laminated composite beam by new multi-layered laminated composite structures model with transverse shear stress continuity. Int. J. Solids Struct. 2003, 40, 1525–1546. [Google Scholar] [CrossRef]
- Reddy, J.N.; Phan, N.D. Stability and vibration of isotropic, orthotropic and laminated plates according to a higher-order shear deformation theory. J. Sound Vib. 1985, 98, 157–170. [Google Scholar] [CrossRef]
- Park, D.-H.; Hong, S.-Y.; Kil, H.-G.; Jeon, J.-J. Power flow models and analysis of in-plane waves in finite coupled thin plates. J. Sound Vib. 2001, 244, 651–668. [Google Scholar] [CrossRef]
- Kessissoglou, N.J. Power transmission in L-shaped plates including flexural and in-plane vibration. J. Acoust. Soc. Am. 2004, 115, 1157–1169. [Google Scholar] [CrossRef]
- Du, J.; Li, W.L.; Liu, Z.; Yang, T.; Jin, G. Free vibration of two elastically coupled rectangular plates with uniform elastic boundary restraints. J. Sound Vib. 2011, 330, 788–804. [Google Scholar] [CrossRef]
- Chen, Y.; Jin, G.; Zhu, M.; Liu, Z.; Du, J.; Li, W.L. Vibration behaviors of a box-type structure built up by plates and energy transmission through the structure. J. Sound Vib. 2012, 331, 849–867. [Google Scholar] [CrossRef]
- Wang, X. Dynamic behavior of finite coupled Mindlin plates with a blocking mass. ASME J. Vib. Acoust. 2016, 138, 061008. [Google Scholar] [CrossRef]
- Abdul-Ahad, R.B.; Aziz, O.Q. Flexural strength of reinforced concrete T-Beams with steel fibers. Cem. Concr. Compos. 1999, 21, 263–268. [Google Scholar] [CrossRef]
- Rahal, K. Combined torsion and bending in reinforced and prestressed concrete beams using simplified method for combined stress-resultants. Aci Struct. J. 2007, 104, 402–411. [Google Scholar] [CrossRef]
- Langley, R.S.; Heron, K. Elastic wave transmission through plate/beam junctions. J. Sound Vib. 1990, 143, 241–253. [Google Scholar] [CrossRef]
- Keir, J.; Kessissoglou, N.J.; Norwood, C.J. An analytical investigation of single actuator and error sensor control in connected plates. J. Sound Vib. 2004, 271, 635–649. [Google Scholar] [CrossRef]
- Mitrou, G.; Ferguson, N.; Renno, J. Wave transmission through two-dimensional structures by the hybrid FE/WFE approach. J. Sound Vib. 2017, 389, 484–501. [Google Scholar] [CrossRef]
- Mace, B.R. Periodically stiffened fluid-loaded plates, I: Response to convected harmonic pressure and free wave propagation. J. Sound Vib. 1980, 73, 473–486. [Google Scholar] [CrossRef]
- Mace, B.R. Periodically stiffened fluid-loaded plates, II: Response to line and point forces. J. Sound Vib. 1980, 73, 487–504. [Google Scholar] [CrossRef]
- Lin, G.G.; Hayek, S.I. Acoustic radiation from point excited rib-reinforced plate. J. Acoust. Soc. Am. 1977, 62, 72–83. [Google Scholar] [CrossRef]
- Hull, A.J.; Welch, J.R. Elastic response of an acoustic coating in a rib-stiffened plate. J. Sound Vib. 2010, 329, 4192–4211. [Google Scholar] [CrossRef]
- Cauchy, A.-L. On the pressure or tension in a solid body. Exp. Math. 1827, 2, 42–56. [Google Scholar]
- Graf, K.F. Wave Motion in Elastic Solids; Dover Publications, Inc.: Mineola, NY, USA, 1975; pp. 311–330. ISBN 0-486-66745-6. [Google Scholar]
- Xing, Y.; Liu, B. Closed form solutions for free vibrations of rectangular Mindlin plates. Acta Mech. Sin. 2009, 25, 689–698. [Google Scholar] [CrossRef]
- Soedel, W. Vibrations of Shells and Plates, Third Edition, Revised and Expanded; Marcel Dekker, Inc.: New York, NY, USA, 2004; pp. 329–333. ISBN 0-8247-5629-0. [Google Scholar]

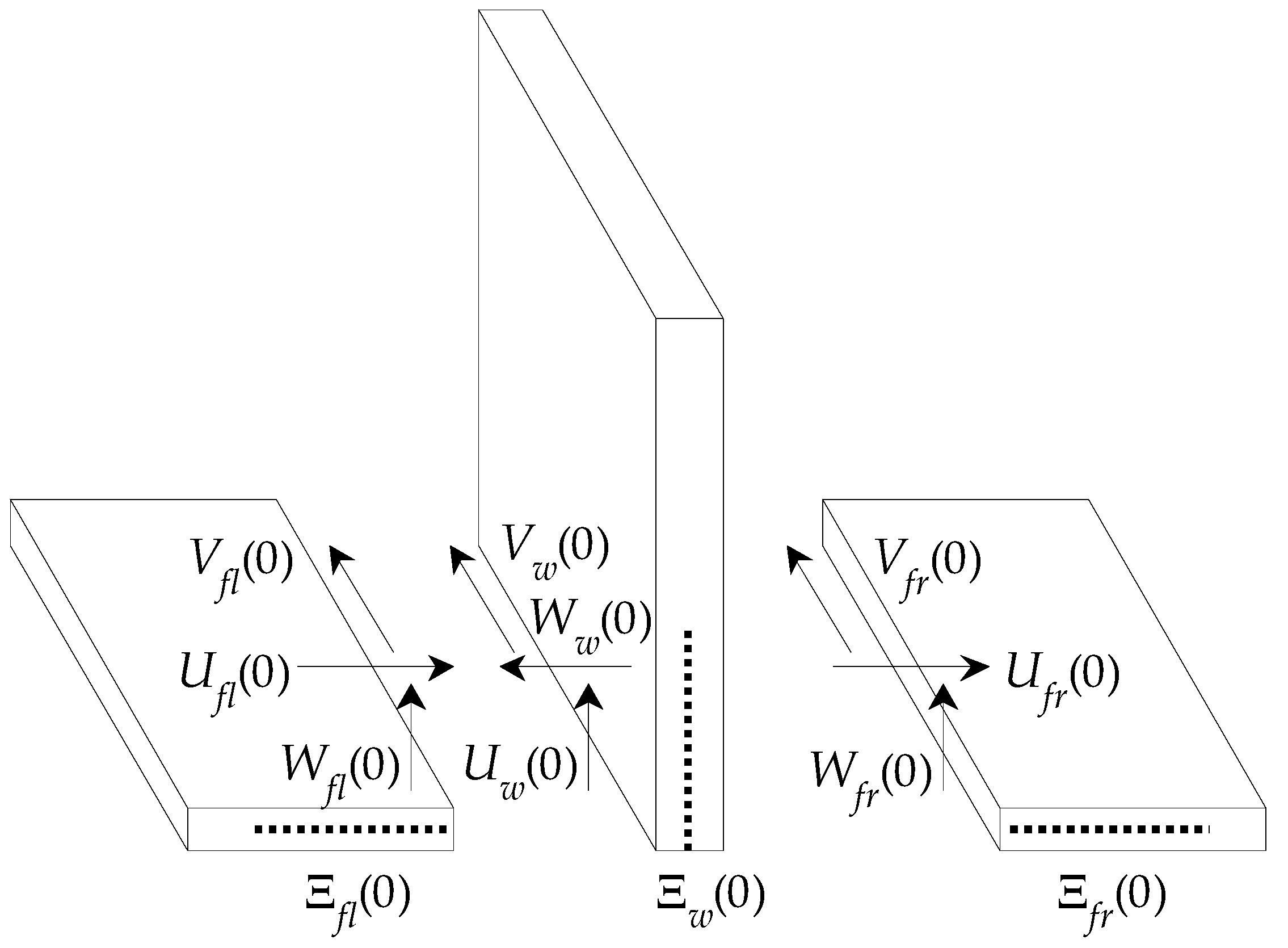

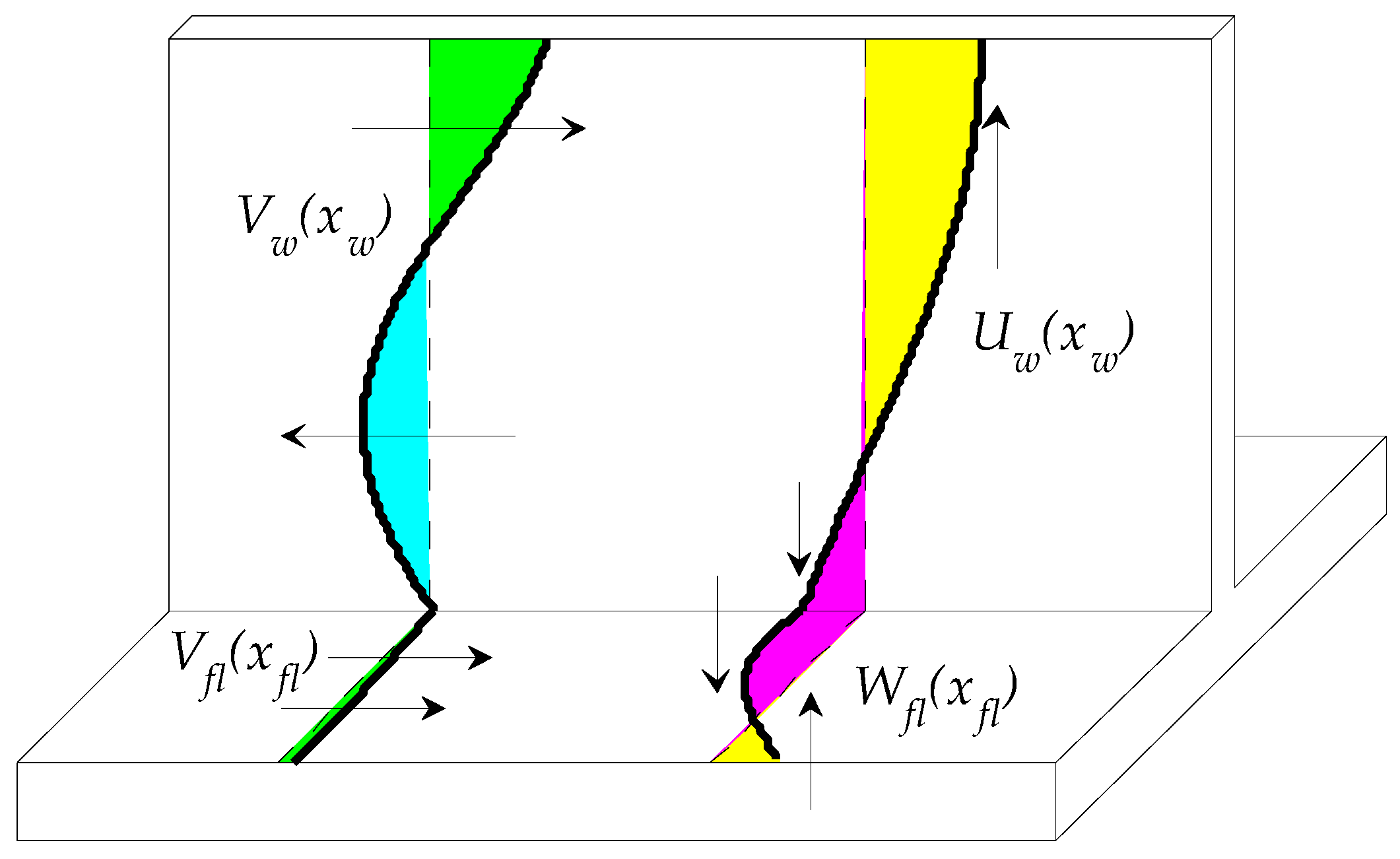
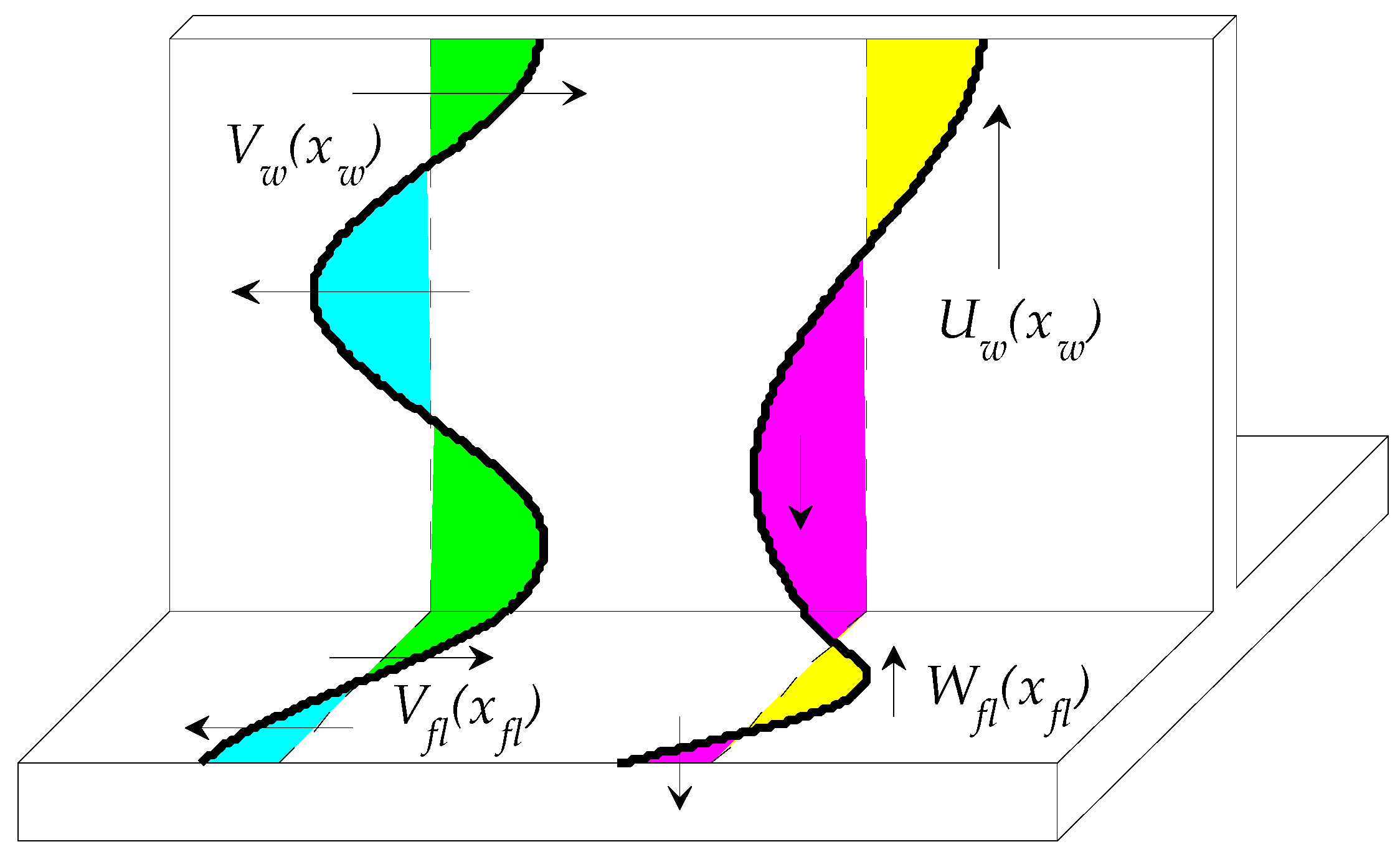
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hull, A.J.; Perez, D.; Cox, D.L. A High-Frequency Model of a Rectilinear Beam with a T-Shaped Cross Section. Acoustics 2019, 1, 726-748. https://doi.org/10.3390/acoustics1030043
Hull AJ, Perez D, Cox DL. A High-Frequency Model of a Rectilinear Beam with a T-Shaped Cross Section. Acoustics. 2019; 1(3):726-748. https://doi.org/10.3390/acoustics1030043
Chicago/Turabian StyleHull, Andrew J., Daniel Perez, and Donald L. Cox. 2019. "A High-Frequency Model of a Rectilinear Beam with a T-Shaped Cross Section" Acoustics 1, no. 3: 726-748. https://doi.org/10.3390/acoustics1030043
APA StyleHull, A. J., Perez, D., & Cox, D. L. (2019). A High-Frequency Model of a Rectilinear Beam with a T-Shaped Cross Section. Acoustics, 1(3), 726-748. https://doi.org/10.3390/acoustics1030043



