Numerical Prediction of Far-Field Combustion Noise from Aeronautical Engines
Abstract
:1. Introduction
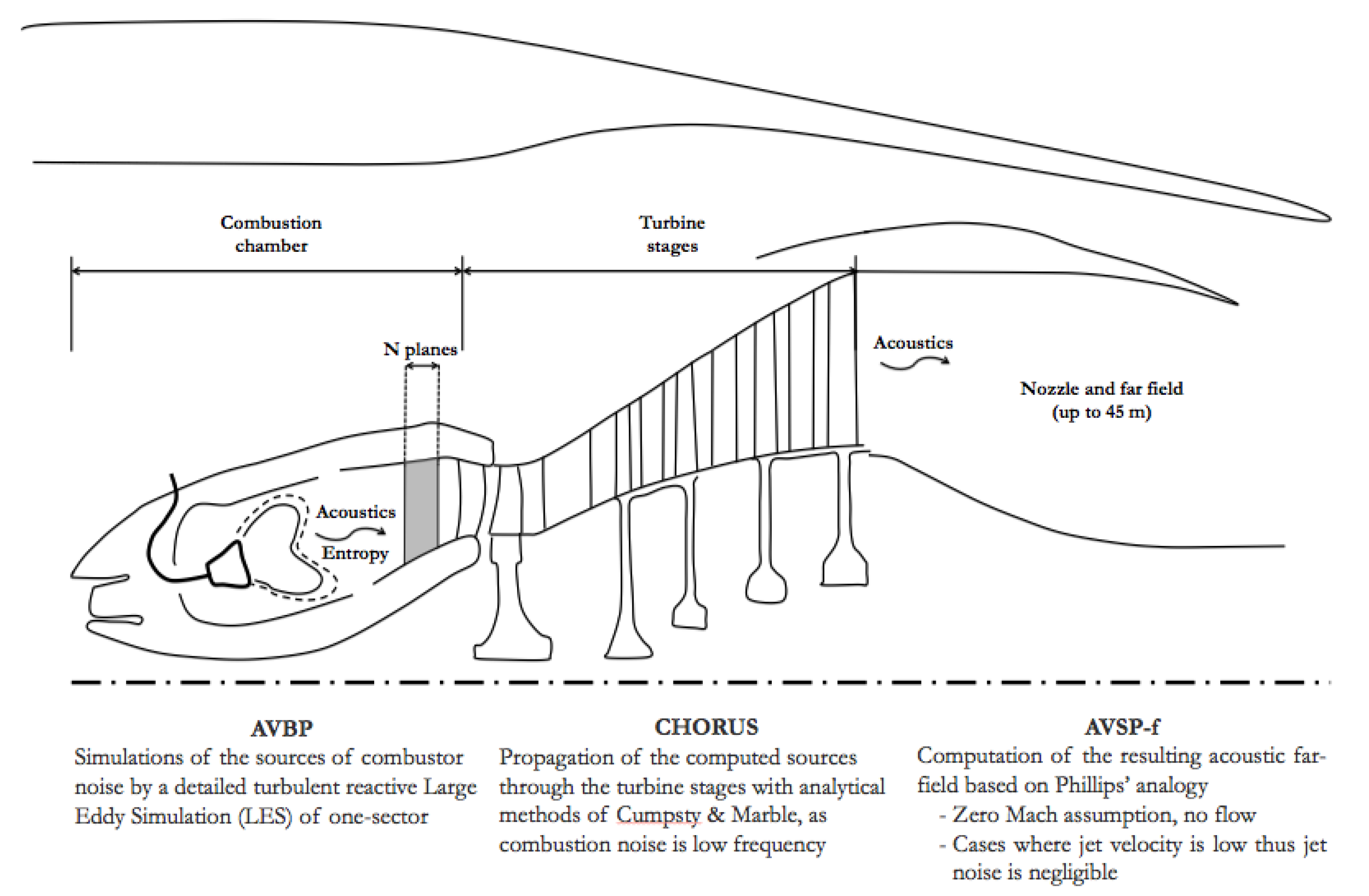
2. Combustion Noise Prediction
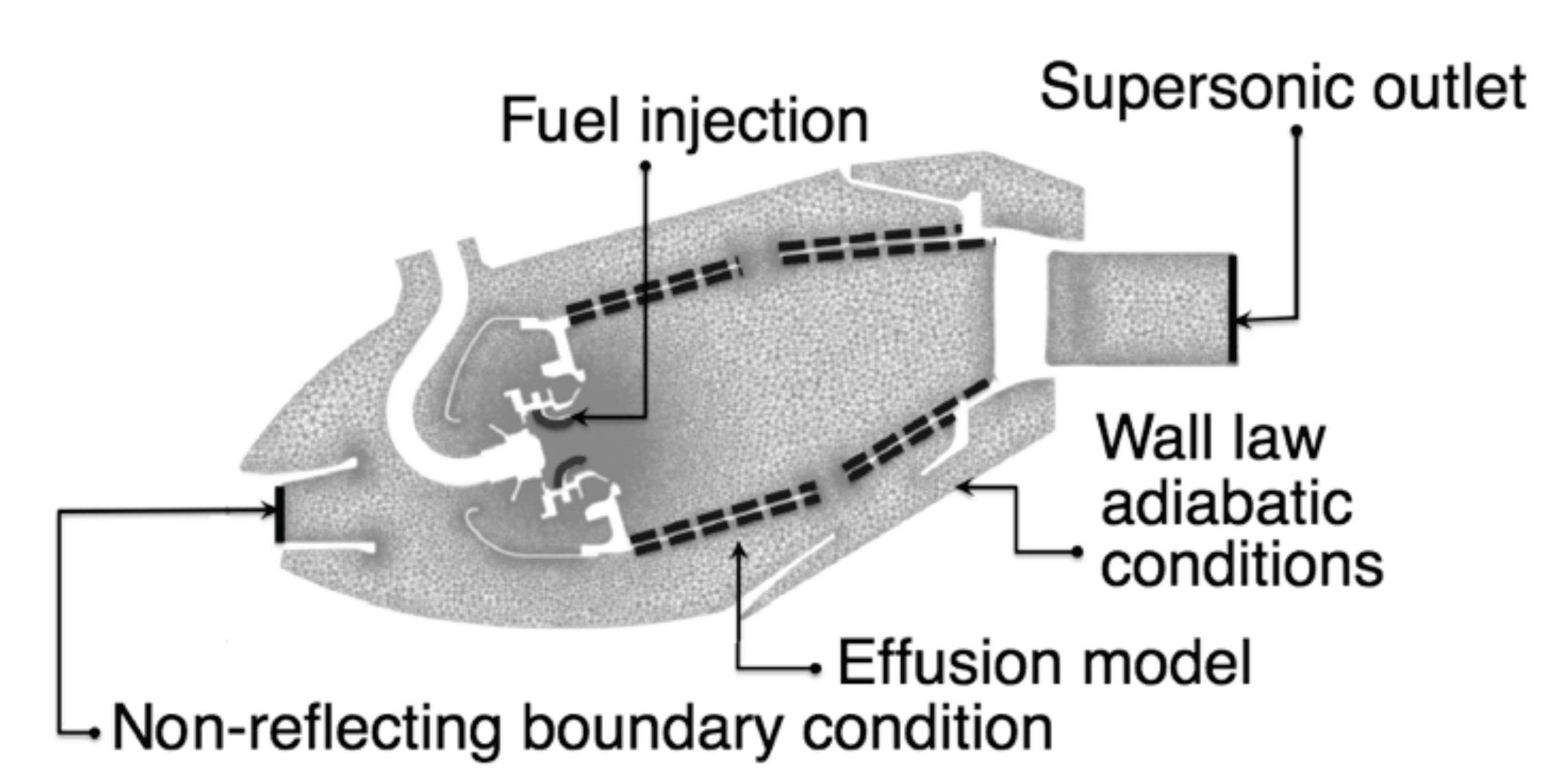
2.1. Large Eddy Simulation of Confined Reactive Flows
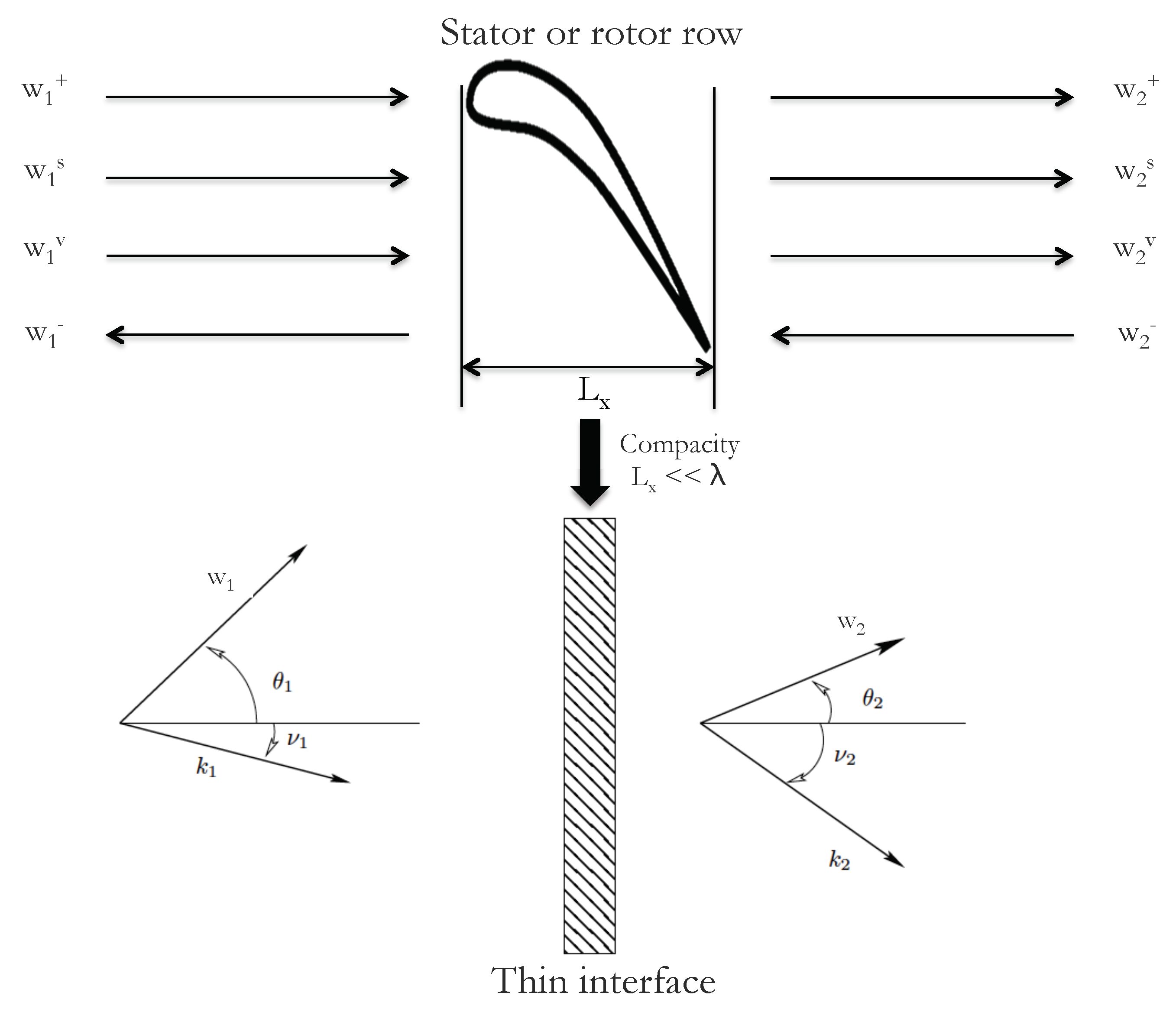
2.2. Direct and Indirect Noise Generation and Propagation through Turbine Blades (CHORUS)
- entropy ()
- velocity magnitude ()
- pressure ()
- flow angle ()
- Instantaneous LES solutions are interpolated over planes (up to a thousand) at the outlet of the combustion chamber, as shown in Figure 1. Primitive variables are radially averaged and decomposed using temporal Fourier transform. Spatial Fourier transforms over the azimuthal direction allow performing an azimuthal modal decomposition (see Livebardon et al. for details [5]).
- Dispersion relations, derived from two-dimensional linearized Euler equations, allow building primitive variables in a waveform (Equations (10) and (11) in [5]).
- The waves are filtered at the exit of the combustion chamber using the set of interpolating planes to extract the propagating components [44], namelywhere is the projection of the wavenumber on the engine axis and are the axial position of the extraction planes. The azimuthal wave numbers are obtained by spatial Fourier transform and the axial wave numbers are derived from the above dispersion relations.
- Using this wave decomposition and an extension of the actuator disk theory [9], CHORUS propagates these waves through turbine stages and computes acoustic power attributed to direct and indirect combustion noise at several locations in a real turbine.
2.3. Far Field Propagation through a Real Nozzle to the Atmosphere
3. Industrial Configurations and Experimental Measurements
3.1. TEENI: A Full-Scale Experimental Test
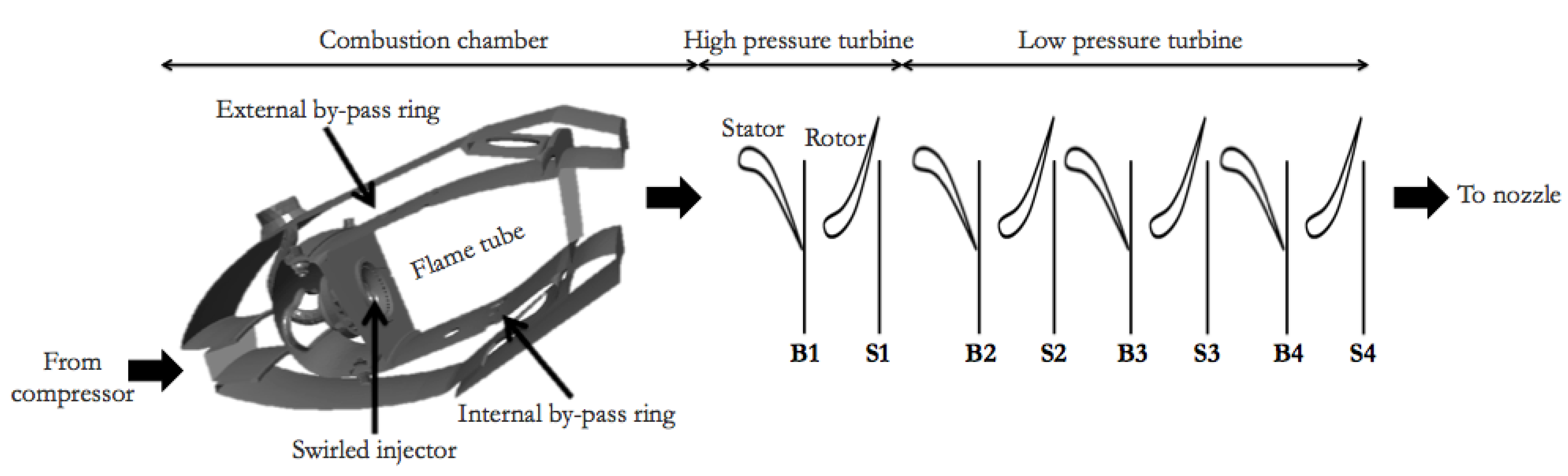
3.2. An Industrial Turbofan Engine
- An injector with two corotative swirlers
- A by-pass duct
- The flame tube
4. CONOCHAIN Results
4.1. TEENI Case
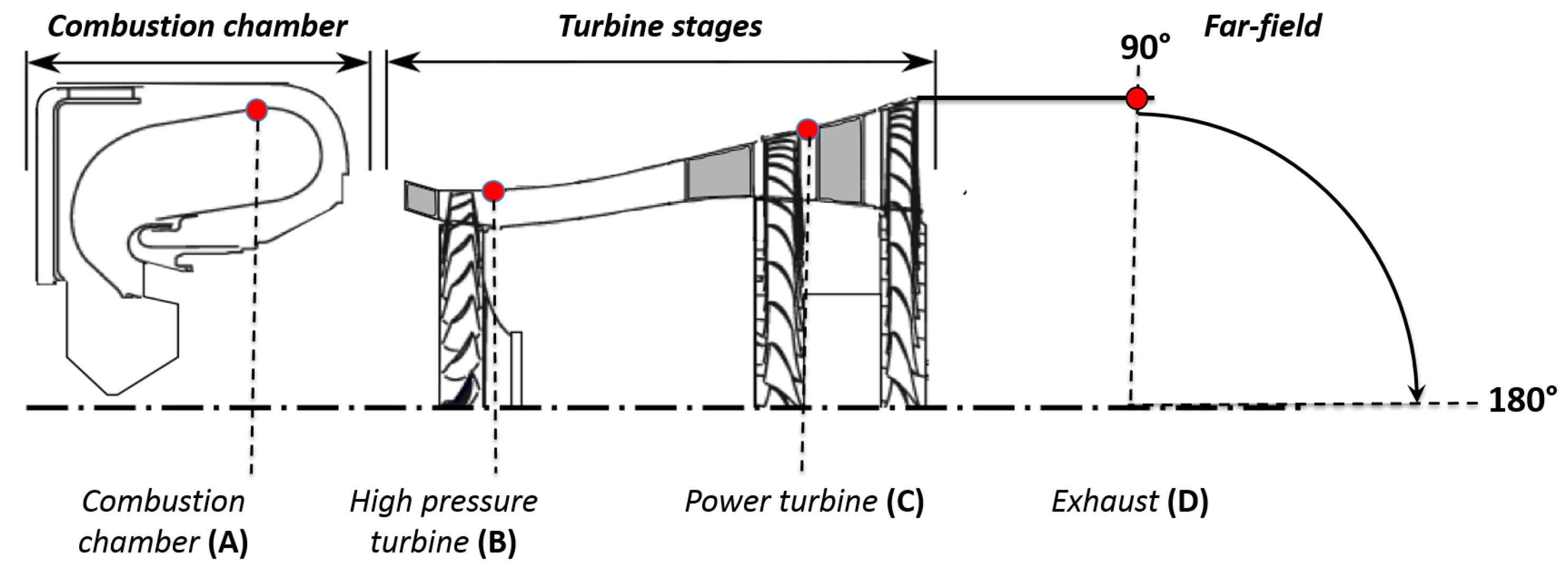
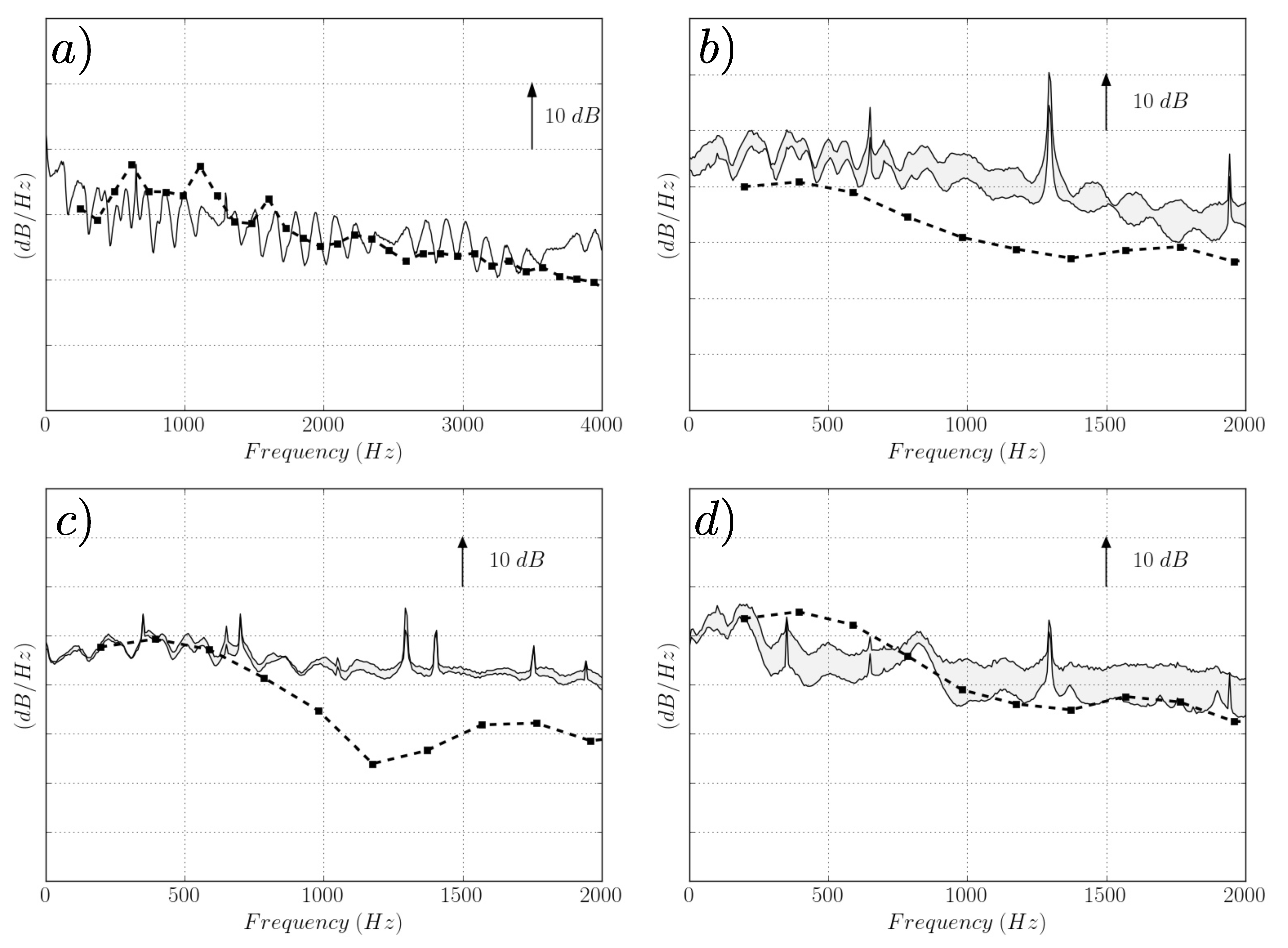
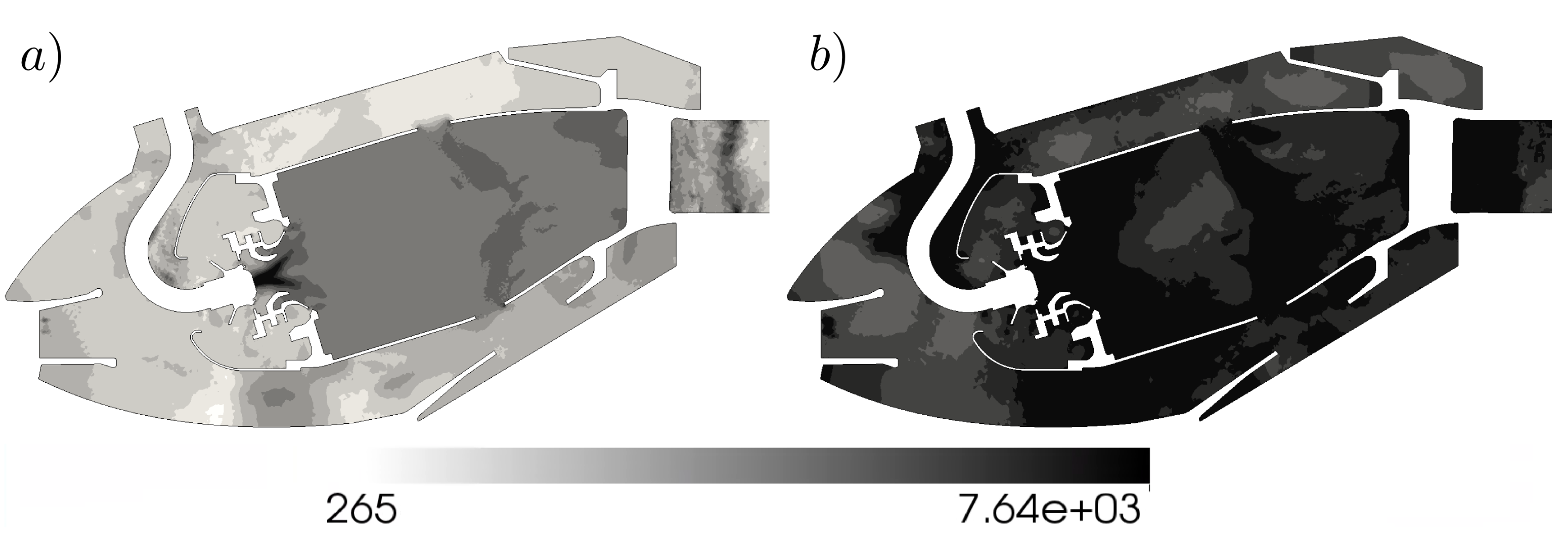
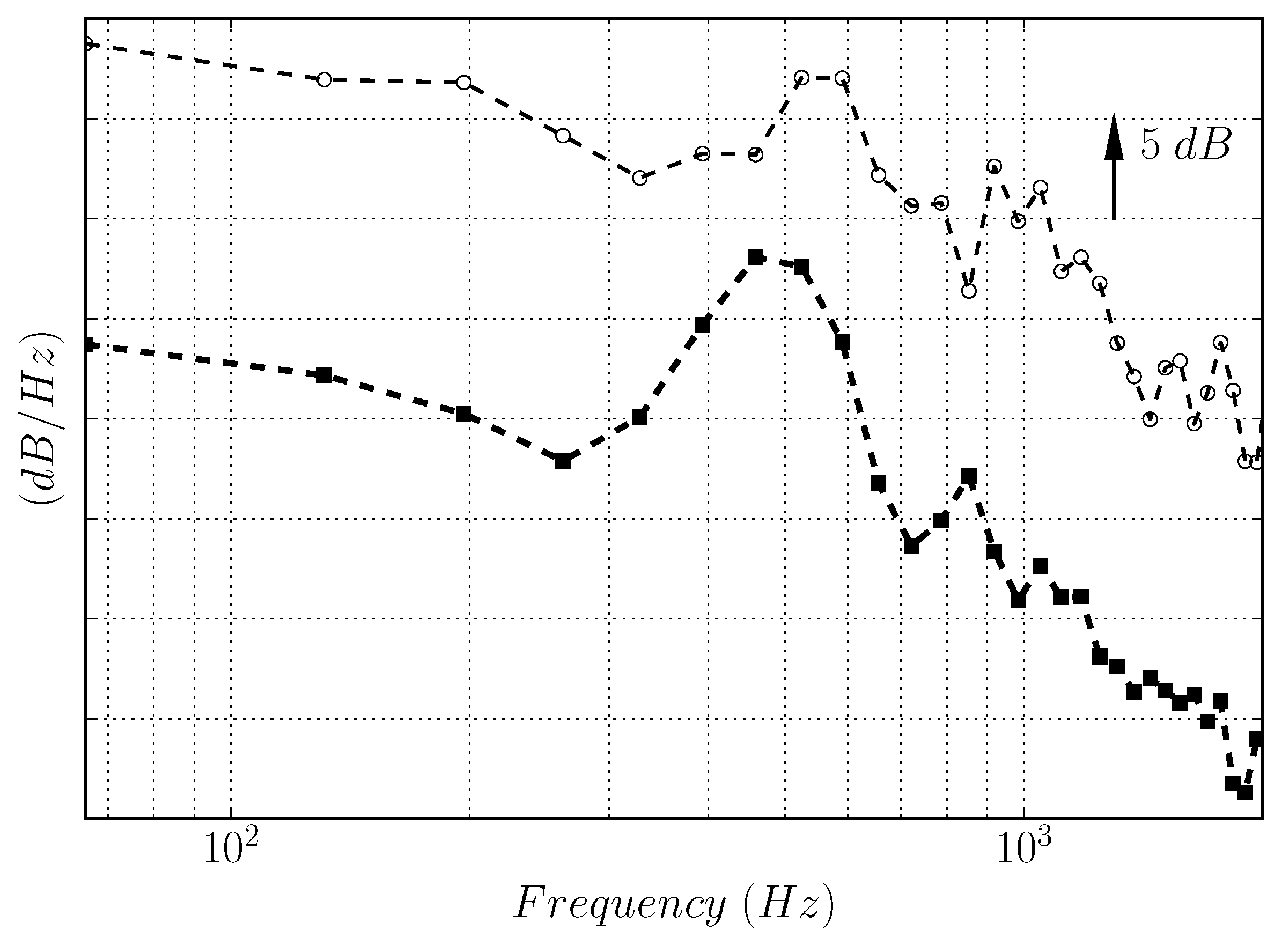
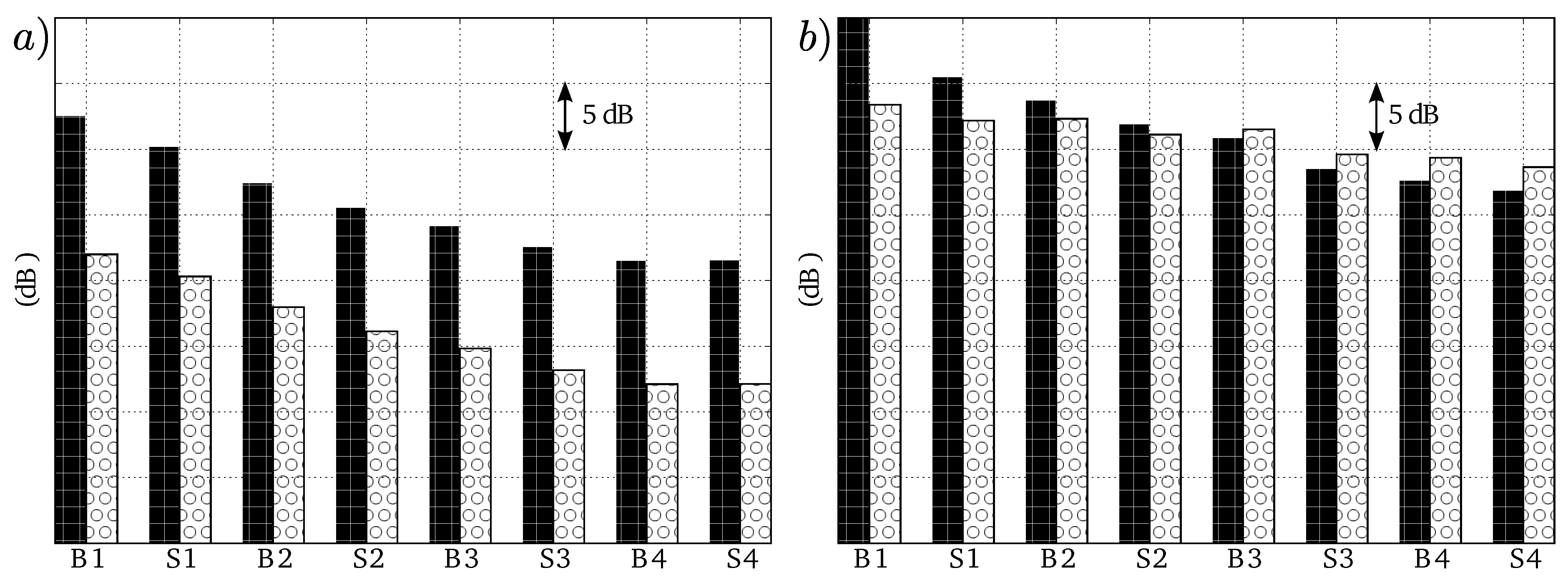
4.1.1. Acoustic Activity from the Chamber to the Engine Exhaust
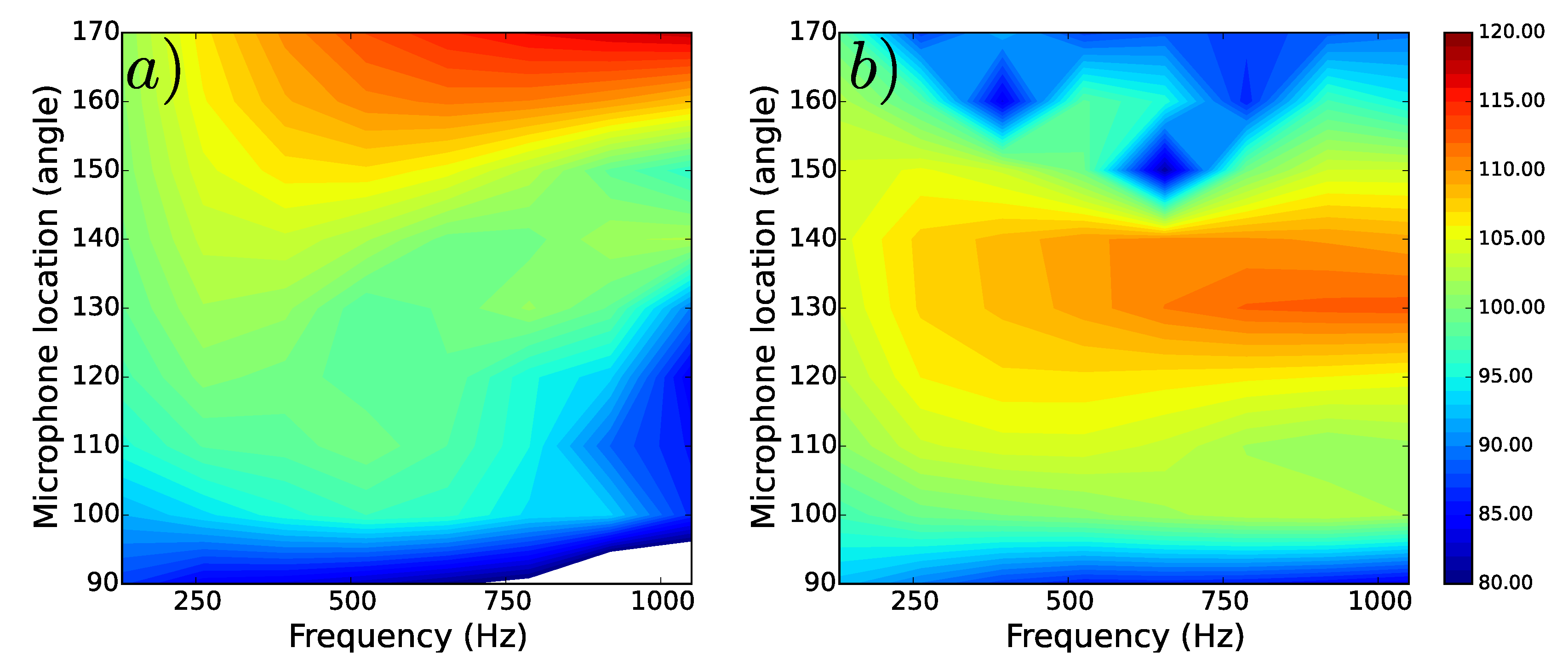
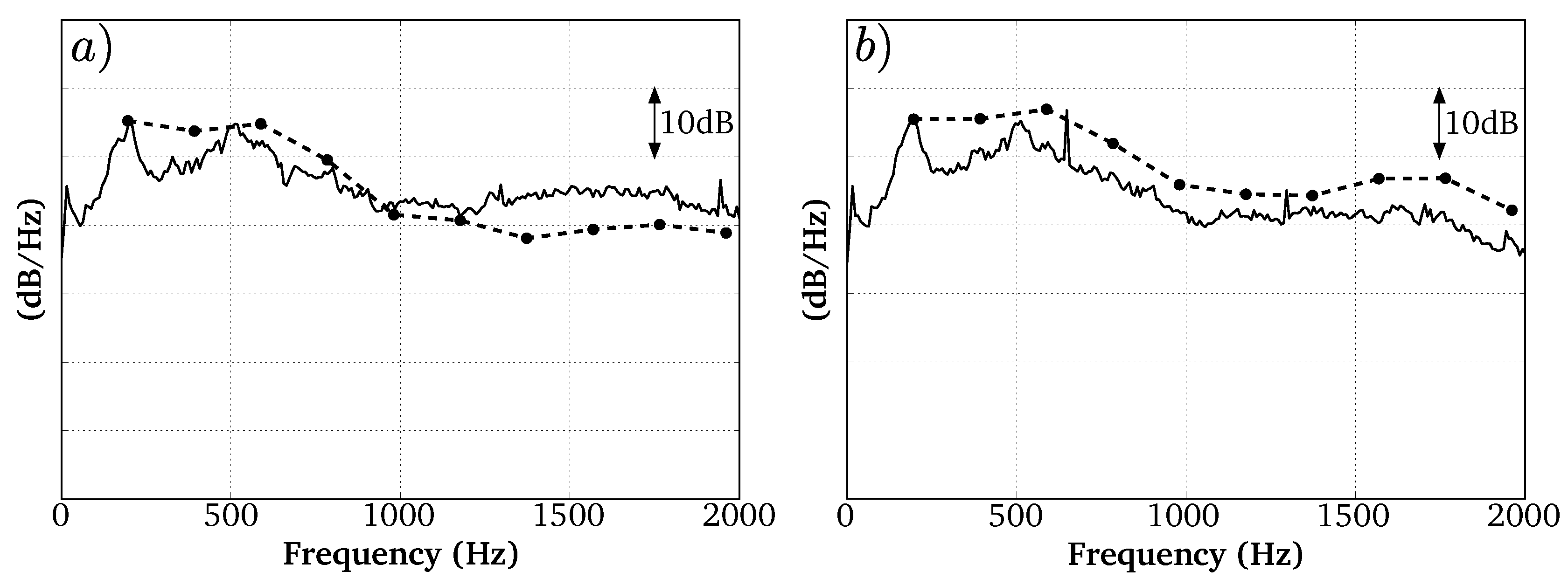
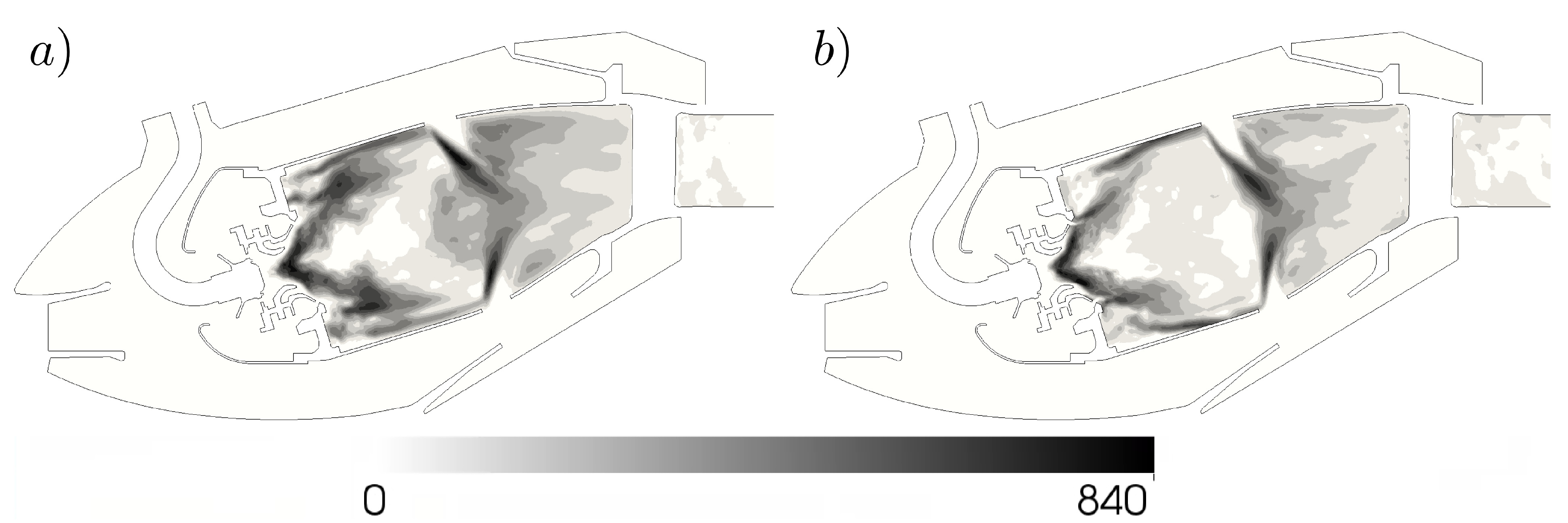
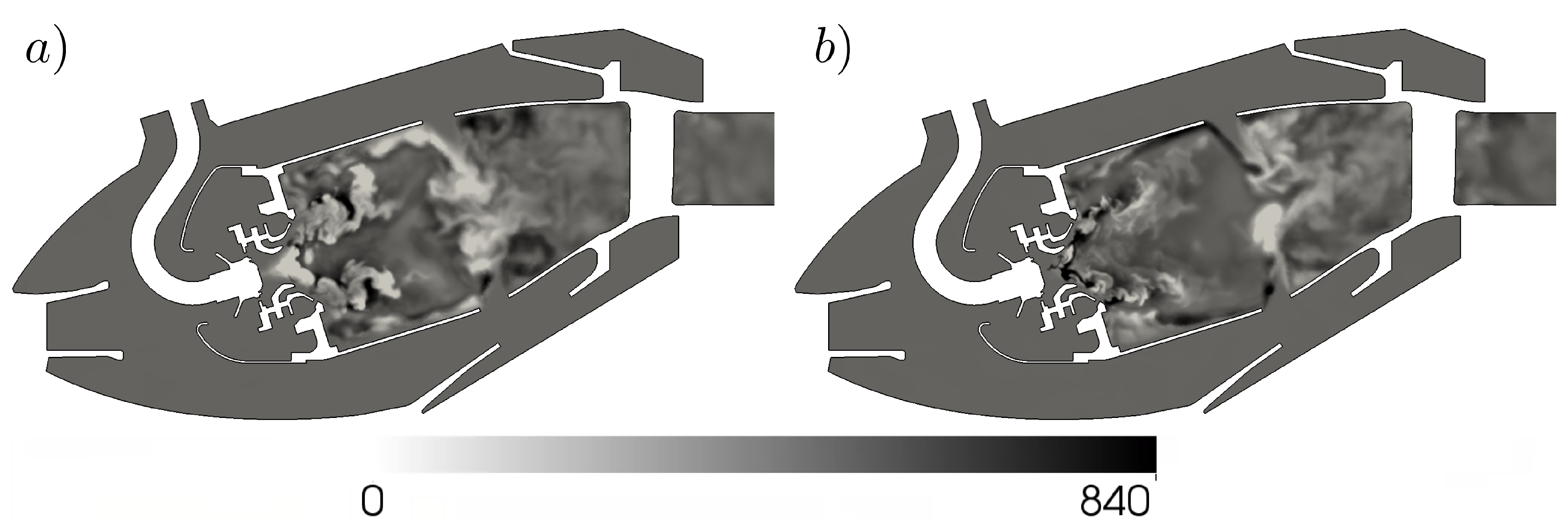
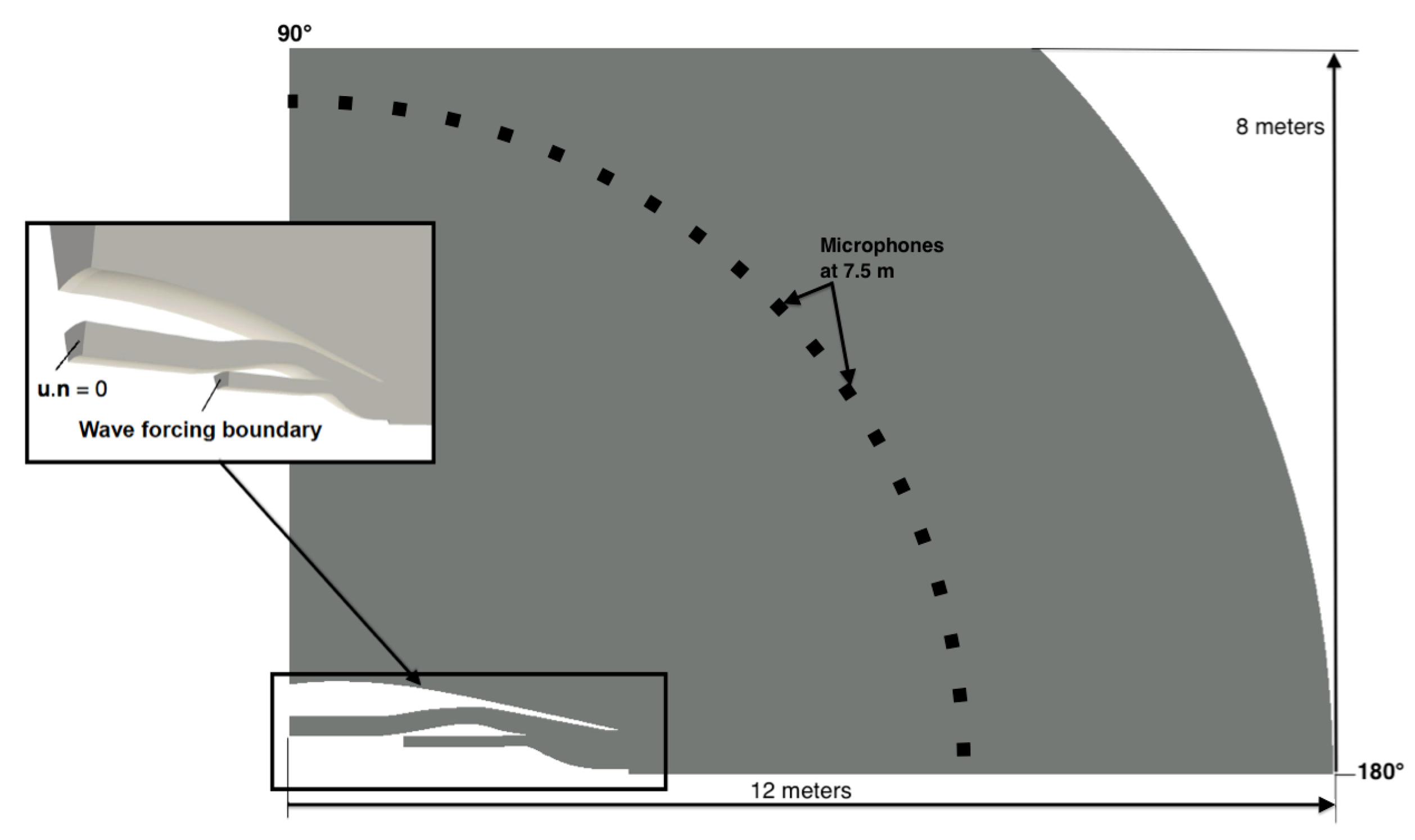
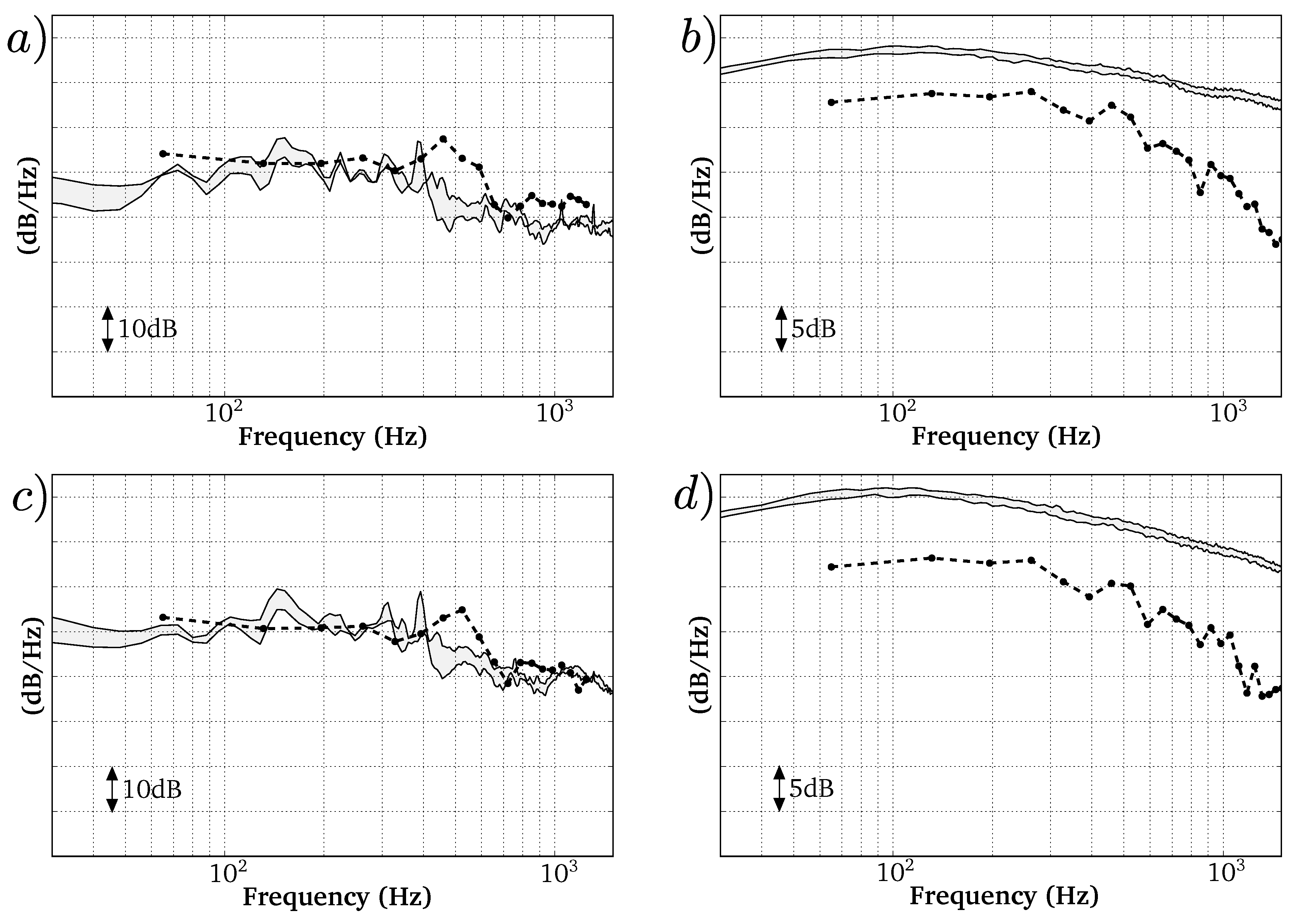
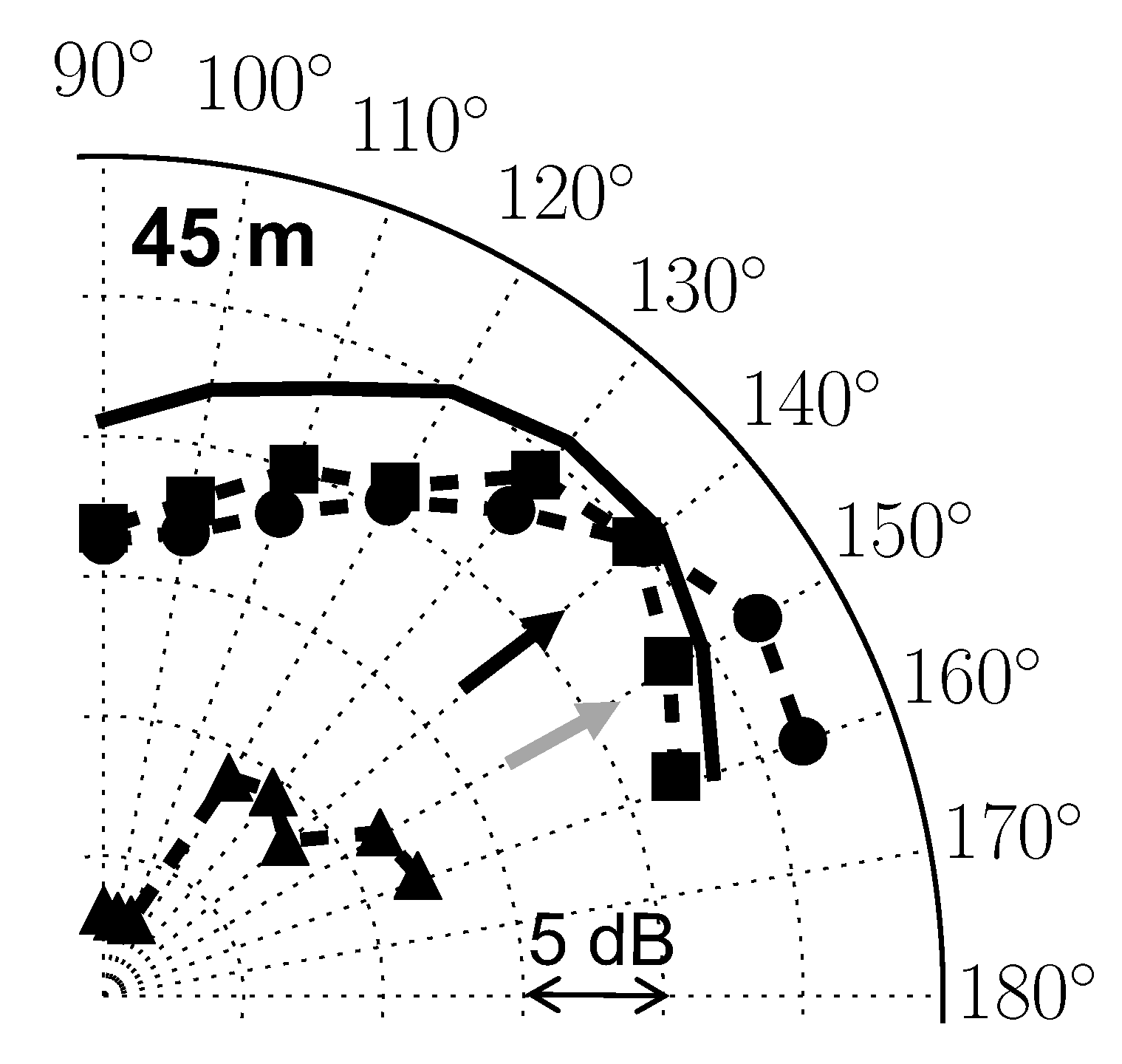
4.1.2. Analysis of the the Far-Field Acoustic Pressure
4.2. Engine B Case
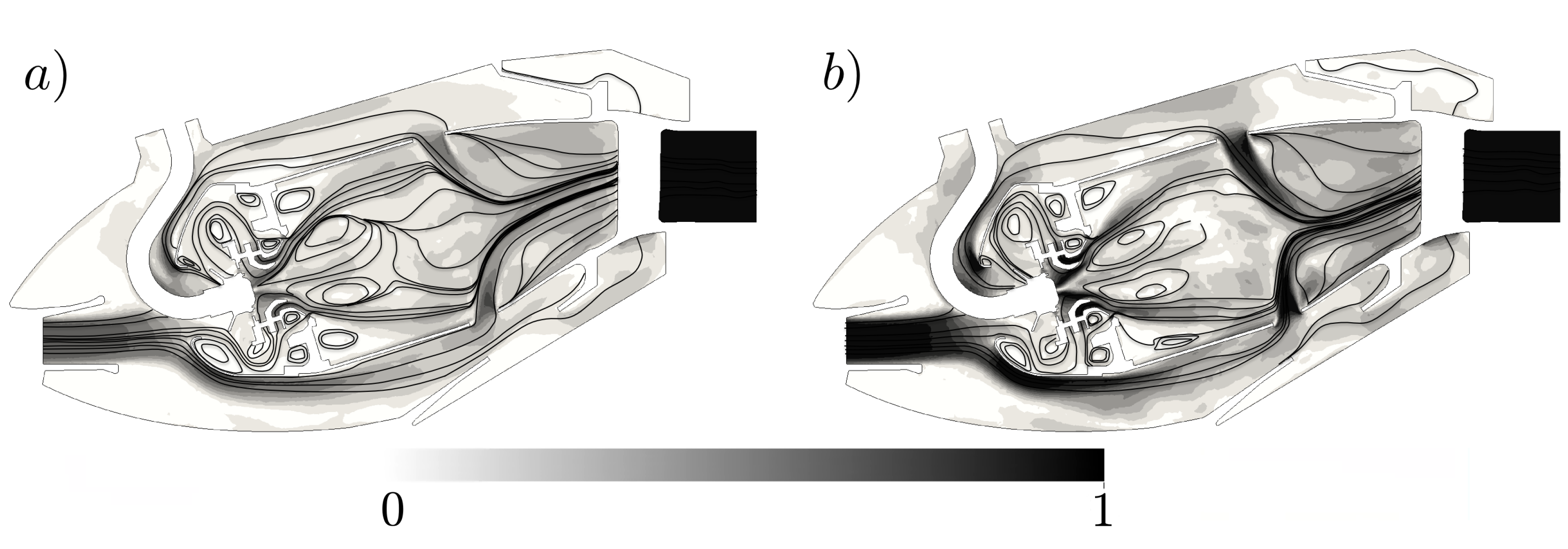
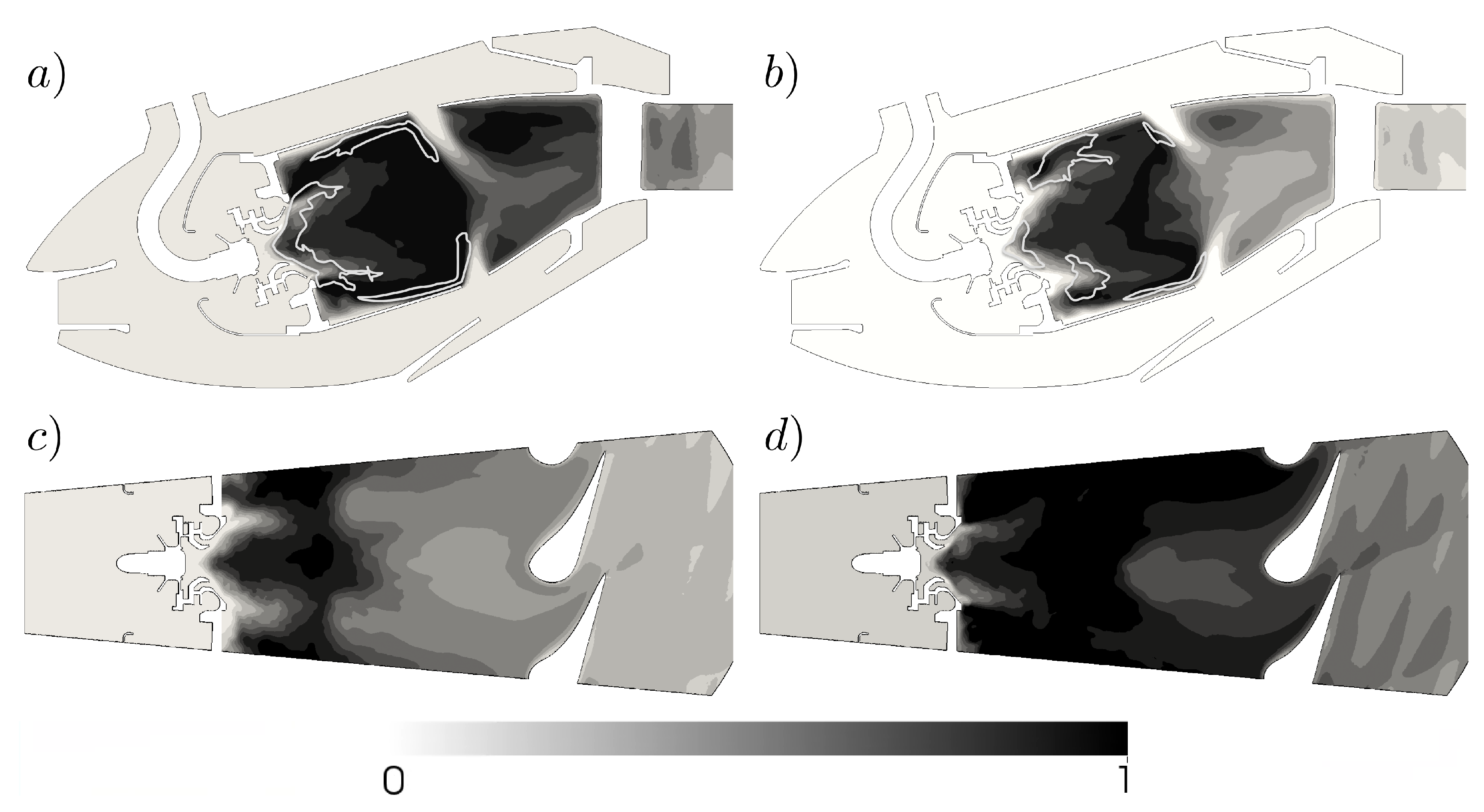
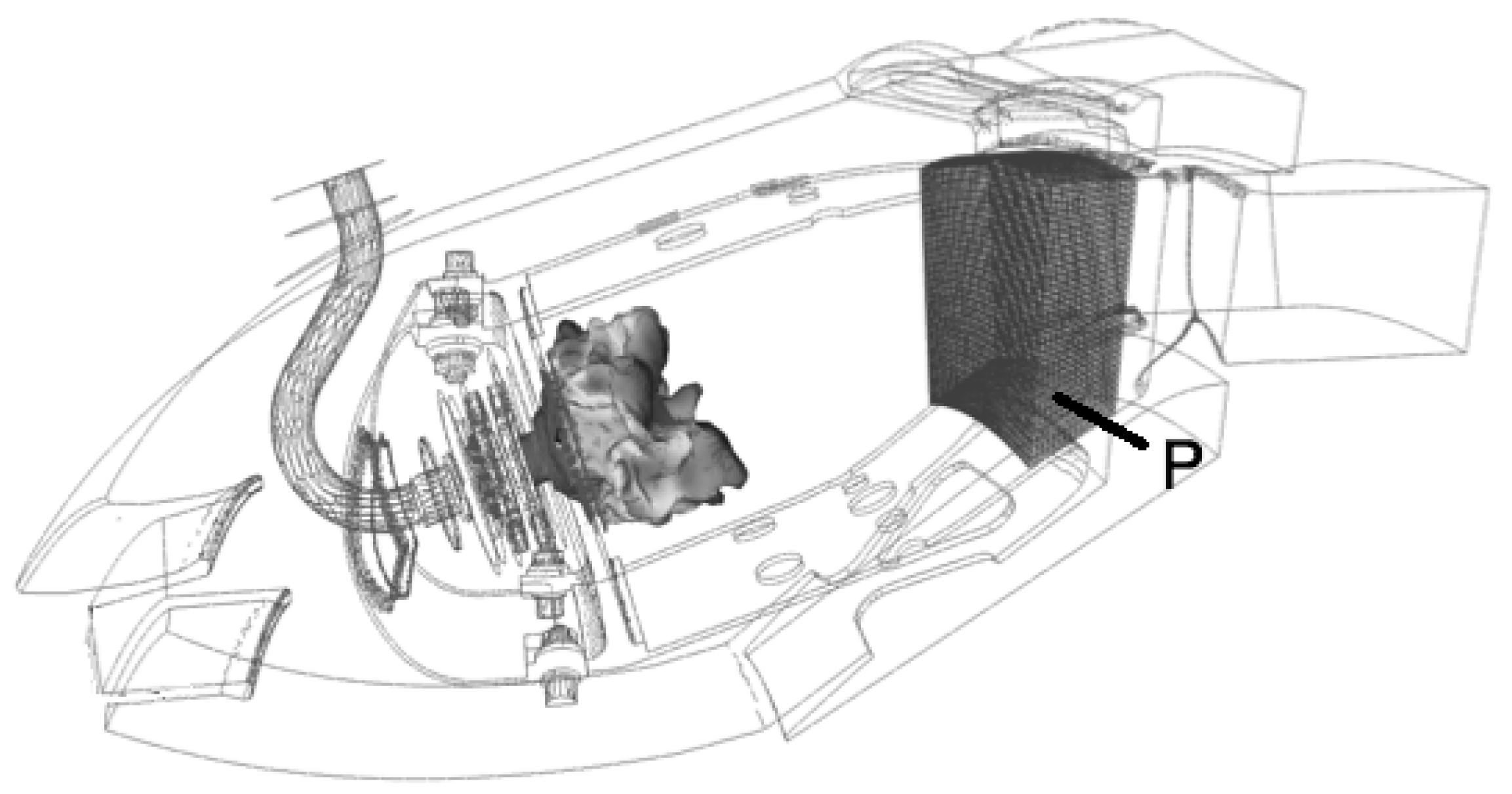
4.2.1. Single-Sector LES of the Combustion Chamber
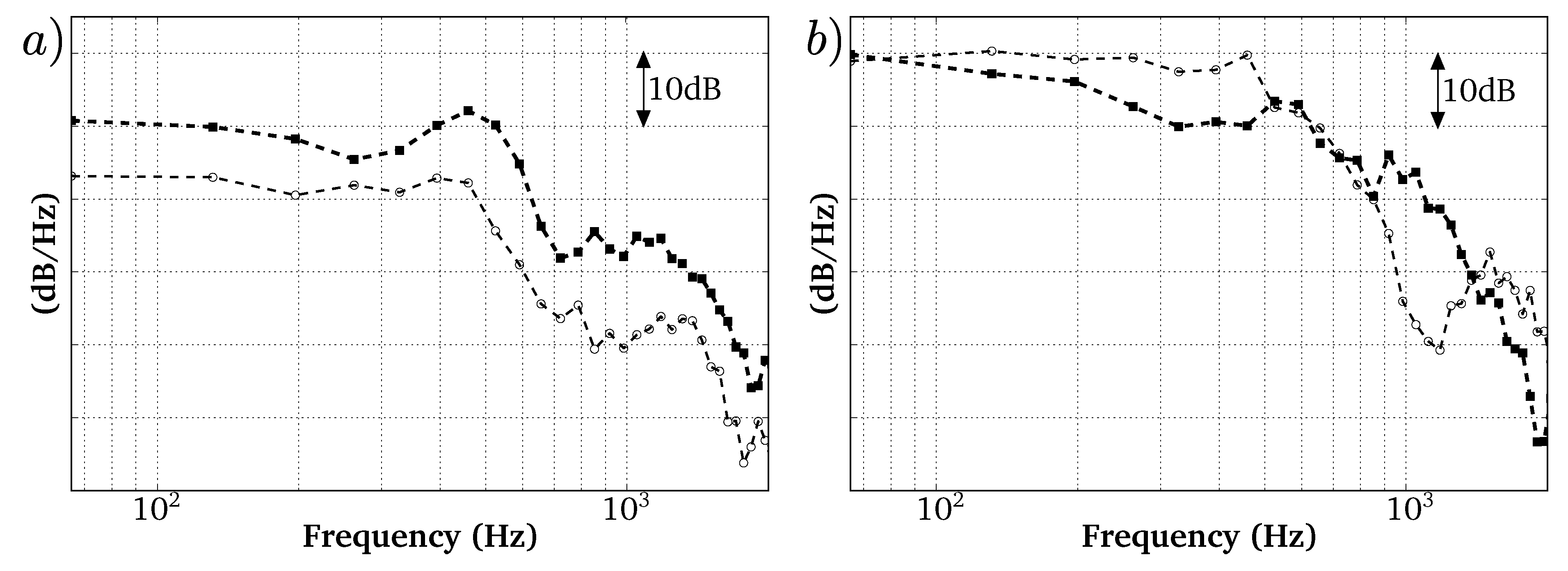
4.2.2. Acoustic Power in the Turbine Stages
4.2.3. Analysis of the Far-Field Acoustic Pressure
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
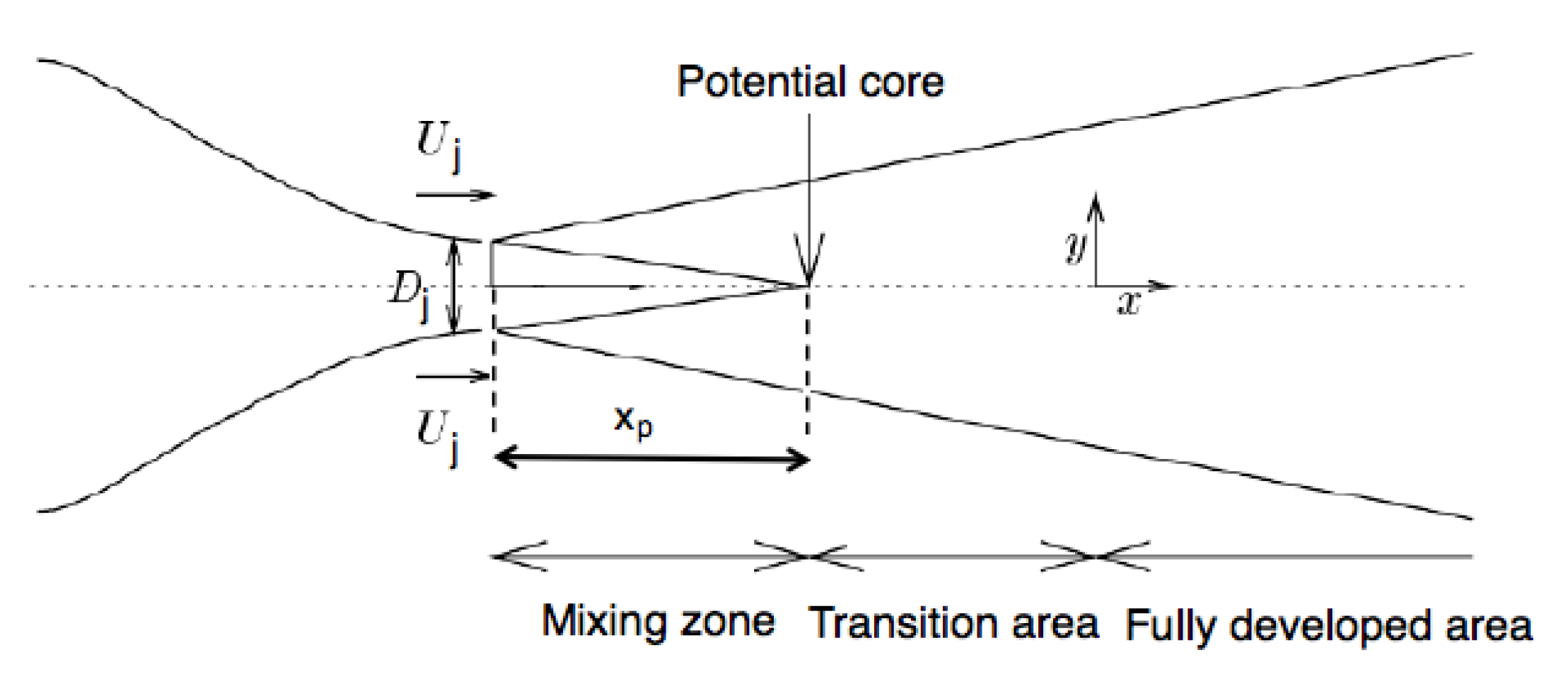
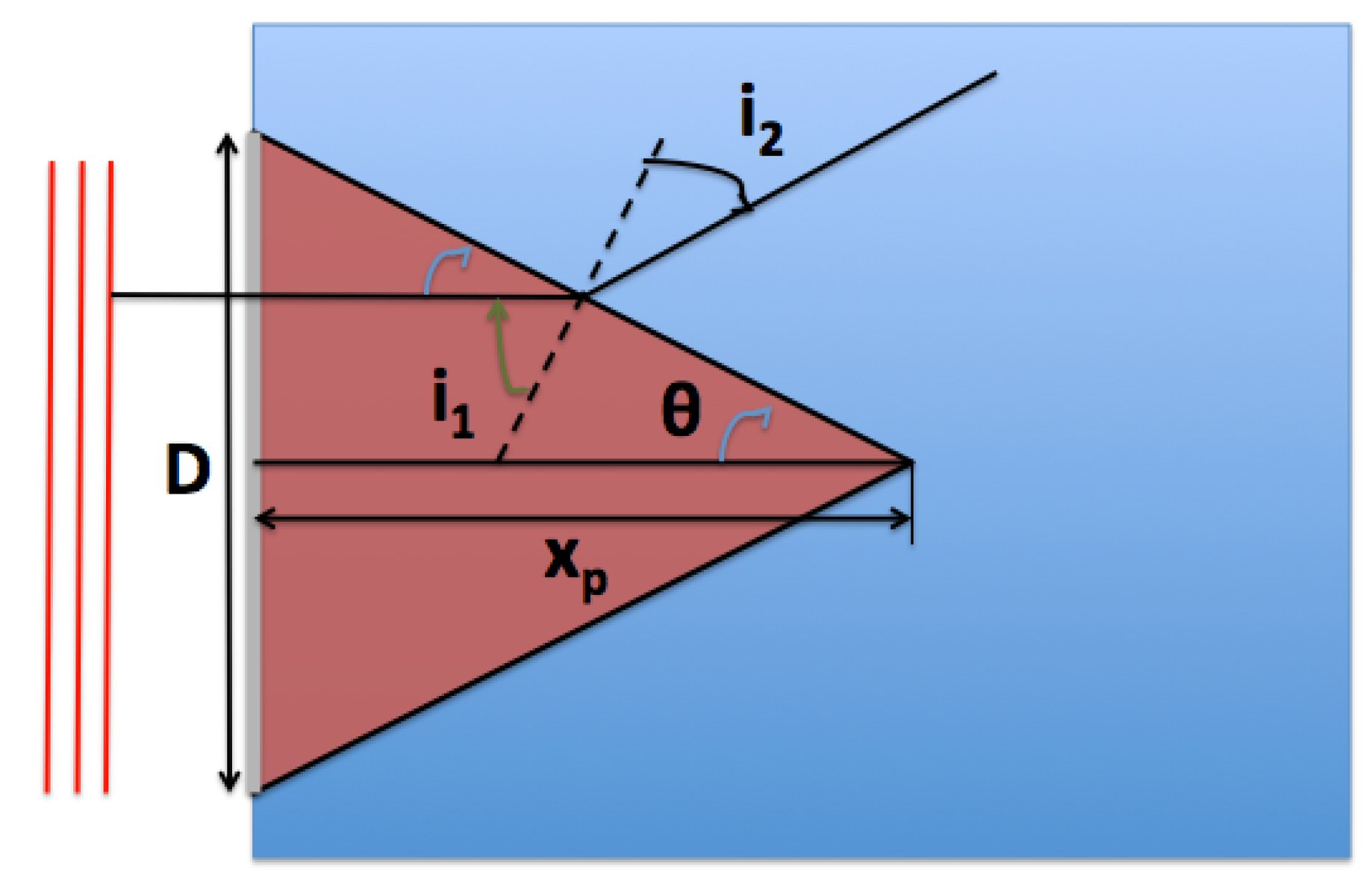
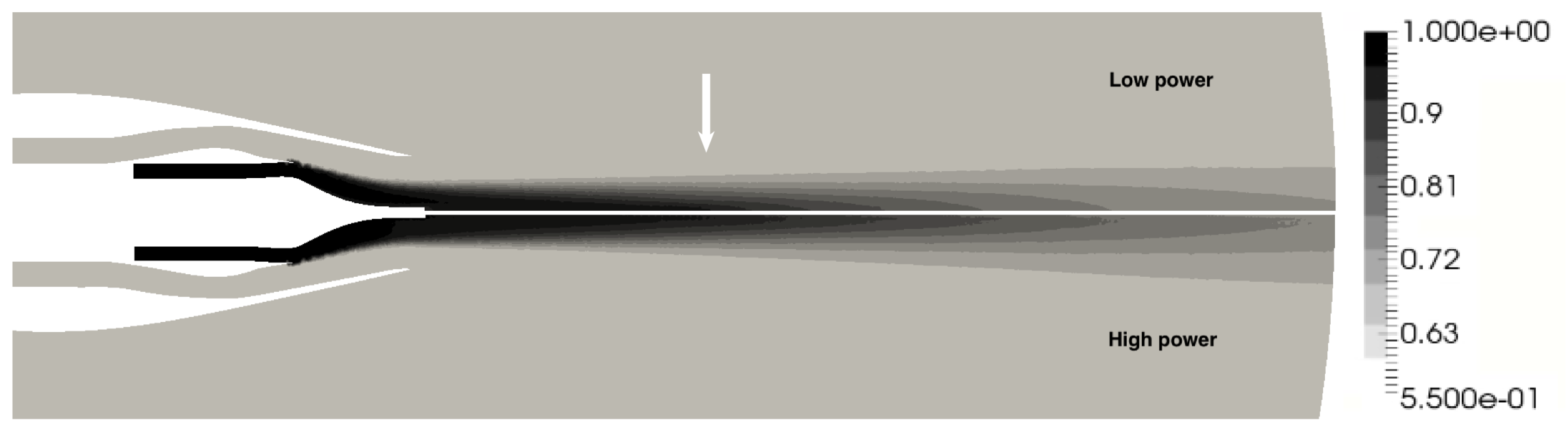
Appendix A. Simple Jet Model
- A developing zone with a potential core surrounded by a shear layer
- A transitional merging zone
- A fully developed turbulent zone
Appendix B. Analytical Model for Combustion Noise Directivity
References
- Duran, I.; Leyko, M.; Moreau, S.; Nicoud, F.; Poinsot, T. Computing combustion noise by combining Large Eddy Simulations with analytical models for the propagation of waves through turbine blades. Comptes Rendus de l’Académie des Sciences—Mécanique 2013, 341, 131–140. [Google Scholar] [CrossRef]
- Liu, Y.; Dowling, A.P.; Swaminathan, N.; Morvant, R.; Macquisten, M.A.; Caracciolo, L.F. Prediction of Combustion Noise for an Aeroengine Combustor. J. Prop. Power 2014, 30, 114–122. [Google Scholar] [CrossRef]
- Dowling, A.P.; Mahmoudi, Y. Combustion noise. Proc. Combust. Inst. 2015, 35, 65–100. [Google Scholar] [CrossRef]
- Morgans, A.S.; Duran, I. Entropy noise: A review of theory, progress and challenges. Int. J. Spray Combust. Dyn. 2016, 8, 285–298. [Google Scholar] [CrossRef]
- Livebardon, T.; Moreau, S.; Gicquel, L.; Poinsot, T.; Bouty, E. Combining LES of combustion chamber and an actuator disk theory to predict combustion noise in a helicopter engine. Combust. Flame 2016, 165, 272–287. [Google Scholar] [CrossRef]
- Ihme, M. Combustion and Engine-Core Noise. Ann. Rev. Fluid Mech. 2017, 49, 277–310. [Google Scholar] [CrossRef]
- Bragg, S. Combustion noise. J. Inst. of Fuel 1963, 36, 12–16. [Google Scholar]
- Marble, F.E.; Candel, S. Acoustic disturbances from gas nonuniformities convected through a nozzle. J. Sound Vib. 1977, 55, 225–243. [Google Scholar] [CrossRef]
- Cumpsty, N.A.; Marble, F.E. The interaction of entropy fluctuations with turbine blade rows; a mechanism of turbojet engine noise. Proc. R. Soc. Lond. A 1977, 357, 323–344. [Google Scholar] [CrossRef]
- Bake, F.; Richter, C.; Muhlbauer, B.; Kings, N.; Rohle, I.; Thiele, F.; Noll, B. The Entropy Wave Generator (EWG): A reference case on entropy noise. J. Sound Vib. 2009, 326, 574–598. [Google Scholar] [CrossRef]
- Leyko, M.; Nicoud, F.; Moreau, S.; Poinsot, T. Numerical and Analytical Investigation of the Indirect Noise in a Nozzle; Center for Turbulence Research, NASA AMES, Stanford University: Stanford, CA, USA, 2008; pp. 343–354. [Google Scholar]
- Leyko, M.; Nicoud, F.; Poinsot, T. Comparison of Direct and Indirect Combustion Noise Mechanisms in a Model Combustor. AIAA J. 2009, 47, 2709–2716. [Google Scholar] [CrossRef]
- Leyko, M.; Moreau, S.; Nicoud, F.; Poinsot, T. Numerical and analytical investigation of the indirect combustion noise in a nozzle. Comptes Rendus Mécanique 2009, 337, 415–425. [Google Scholar] [CrossRef]
- Duran, I.; Moreau, S. Analytical and numerical study of the Entropy Wave Generator experiment on indirect combustion noise. In Proceedings of the 17th AIAA/CEAS Aeroacoustics Conference, Portland, OR, USA, 5–8 June 2011. [Google Scholar]
- Duran, I.; Moreau, S.; Poinsot, T. Analytical and numerical study of combustion noise through a subsonic nozzle. AIAA J. 2013, 51, 42–52. [Google Scholar] [CrossRef]
- Duran, I.; Moreau, S. Solution of the quasi-one-dimensional linearized Euler equations using flow invariants and the Magnus expansion. J. Fluid Mech. 2013, 723, 190–231. [Google Scholar] [CrossRef]
- Giauque, A.; Huet, M.; Clero, F. Analytical Analysis of Indirect Combustion Noise in Subcritical Nozzles. J. Eng. Gas Turbines Power 2012, 134, 111202. [Google Scholar] [CrossRef]
- Huet, M.; Giauque, A. A nonlinear model for indirect combustion noise through a compact nozzle. J. Fluid Mech. 2013, 733, 268–301. [Google Scholar] [CrossRef]
- Lourier, J.; Huber, A.; Noll, B.; Aigner, M. Numerical Analysis of Indirect Combustion Noise Generation Within a Subsonic Nozzle. AIAA J. 2014, 52, 2114–2126. [Google Scholar] [CrossRef]
- Livebardon, T.; Moreau, S.; Poinsot, T.; Bouty, E. Numerical investigation of combustion noise generation in a full annular combustion chamber. In Proceedings of the 21th AIAA/CEAS Aeroacoustics Conference (36rd AIAA Aeroacoustics Conference), Dallas, TX, USA, 22–26 June 2015. [Google Scholar]
- Hultgren, L. A Comparison of Combustor-Noise Models. In Proceedings of the 18th AIAA/CEAS Aeroacoustics Conference (33rd AIAA Aeroacoustics Conference), Colorado Springs, CO, USA, 4–6 June 2012. [Google Scholar]
- Leyko, M.; Duran, I.; Moreau, S.; Nicoud, F.; Poinsot, T. Simulation and Modelling of the waves transmission and generation in a stator blade row in a combustion-noise framework. J. Sound Vib. 2014, 333, 6090–6106. [Google Scholar] [CrossRef]
- Mishra, A.; Bodony, D.J. Evaluation of actuator disk theory for predicting indirect combustion noise. J. Sound Vib. 2013, 332, 821–838. [Google Scholar] [CrossRef]
- Wang, G.; Duchaine, F.; Papadogiannis, D.; Duran, I.; Moreau, S.; Gicquel, L. An overset grid method for large eddy simulation of turbomachinery stages. J. Comput. Phys. 2014, 274, 333–355. [Google Scholar] [CrossRef]
- Bauerheim, M.; Duran, I.; Livebardon, T.; Wang, G.; Moreau, S.; Poinsot, T. Transmission and reflection of acoustic and entropy waves through a stator–rotor stage. J. Sound Vib. 2016, 374, 260–278. [Google Scholar] [CrossRef]
- Wang, G.; Sanjosé, M.; Moreau, S.; Papadogiannis, D.; Duchaine, F.; Gicquel, L. Noise mechanisms in a transonic high-pressure turbine stage. Int. J. Aeroacoust. 2016, 15, 144–161. [Google Scholar] [CrossRef]
- Papadogiannis, D.; Duchaine, F.; Gicquel, L.; Wang, G.; Moreau, S.; Nicoud, F. Assessment of the indirect combustion noise generated in a transonic high-pressure turbine stage. J. Eng. Gas Turb. Power 2016, 138, 041503. [Google Scholar] [CrossRef]
- Zheng, J.; Giauque, A.; Ducruix, S. A 2D-axisymmetric analytical model for the estimation of indirect combustion noise in nozzle flows. In Proceedings of the 21st AIAA/CEAS Aeroacoustics Conference, Dallas, TX, USA, 22–26 June 2015. [Google Scholar]
- Ferand, M.; Livebardon, T.; Moreau, S.; Sensiau, C.; Bouty, E.; Sanjosé, M.; Poinsot, T. Numerical investigation of combustion noise from aeronautical combustor to far-field. In Proceedings of the 22nd AIAA/CEAS Aeroacoustics Conference, Lyon, France, 30 May–1 June 2016. [Google Scholar]
- Ferand, M.; Daviller, G.; Moreau, S.; Sensiau, C.; Poinsot, T. Using LES for combustion noise propagation to the far-field by considering the jet flow of a dual-stream nozzle. In Proceedings of the 24th AIAA/CEAS Aeroacoustics Conference, Atlanta, GA, USA, 25–29 June 2018. [Google Scholar]
- Phillips, O.M. On the generation of sound by supersonic turbulent shear layers. J. Fluid Mech. 1960, 9, 1–28. [Google Scholar] [CrossRef]
- Schønfeld, T.; Rudgyard, M. Steady and Unsteady Flows Simulations Using the Hybrid Flow Solver AVBP. AIAA J. 1999, 37, 1378–1385. [Google Scholar] [CrossRef]
- Poinsot, T.; Veynante, D. Theoretical and Numerical Combustion, 3rd ed.; R.T. Edwards, Inc.: Philadelphia, PA, USA, 2011. [Google Scholar]
- Colin, O.; Rudgyard, M. Development of high-order Taylor-Galerkin schemes for unsteady calculations. J. Comput. Phys. 2000, 162, 338–371. [Google Scholar] [CrossRef]
- Colin, O.; Ducros, F.; Veynante, D.; Poinsot, T. A thickened flame model for large eddy simulations of turbulent premixed combustion. Phys. Fluids 2000, 12, 1843–1863. [Google Scholar] [CrossRef]
- Smagorinsky, J. General circulation experiments with the primitive equations: 1. The basic experiment. Mon. Weather Rev. 1963, 91, 99–164. [Google Scholar] [CrossRef]
- Selle, L.; Lartigue, G.; Poinsot, T.; Koch, R.; Schildmacher, K.U.; Krebs, W.; Prade, B.; Kaufmann, P.; Veynante, D. Compressible Large-Eddy Simulation of turbulent combustion in complex geometry on unstructured meshes. Combust. Flame 2004, 137, 489–505. [Google Scholar] [CrossRef]
- Franzelli, B.; Riber, E.; Sanjosé, M.; Poinsot, T. A two-step chemical scheme for Large-Eddy Simulation of kerosene-air flames. Combust. Flame 2010, 157, 1364–1373. [Google Scholar] [CrossRef]
- Poinsot, T.; Lele, S. Boundary conditions for direct simulations of compressible viscous flows. J. Comput. Phys. 1992, 101, 104–129. [Google Scholar] [CrossRef]
- Selle, L.; Nicoud, F.; Poinsot, T. The actual impedance of non-reflecting boundary conditions: implications for the computation of resonators. AIAA J. 2004, 42, 958–964. [Google Scholar] [CrossRef]
- Leyko, M.; Moreau, S.; Nicoud, F.; Poinsot, T. Waves transmission and generation in turbine stages in a combustion-noise framework. In Proceedings of the 16th AIAA/CEAS Aeroacoustics Conference, Stockholm, Sweden, 7–9 June 2010. [Google Scholar]
- Duran, I.; Moreau, S. Study of the attenuation of waves propagating through fixed and rotating turbine blades. In Proceedings of the 18th AIAA/CEAS Aeroacoustics Conference (33rd AIAA Aeroacoustics Conference), Colorado Springs, CO, USA, 4–6 June 2012. [Google Scholar]
- Duran, I.; Moreau, S. Numerical simulation of acoustic and entropy waves propagating through turbine blades. In Proceedings of the 19th AIAA/CEAS Aeroacoustics Conference (34th AIAA Aeroacoustics Conference), Berlin, Germany, 27–29 May 2013. [Google Scholar]
- Kopitz, J.; Huber, A.; Sattelmayer, T.; Polifke, W. Thermoacoustic Stability Analysis of an Annular Combustion Chamber with Acoustic Low Order Modeling and Validation Against Experiment. In Proceedings of the International Gas Turbine and Aeroengine Congress & Exposition, Reno, NV, USA, 6–9 June 2005. [Google Scholar]
- Duran, I.; Leyko, M.; Moreau, S.; Nicoud, F.; Poinsot, T. Computing combustion noise by combining Large Eddy Simulations with analytical models for the propagation of waves through turbine blades. In Proceedings of the 3rd Colloquium INCA, Toulouse, France, 17–18 November 2011. [Google Scholar]
- Martin, C.; Benoit, L.; Sommerer, Y.; Nicoud, F.; Poinsot, T. LES and acoustic analysis of combustion instability in a staged turbulent swirled combustor. AIAA J. 2006, 44, 741–750. [Google Scholar] [CrossRef]
- Selle, L.; Benoit, L.; Poinsot, T.; Nicoud, F.; Krebs, W. Joint use of Compressible Large-Eddy Simulation and Helmholtz solvers for the analysis of rotating modes in an industrial swirled burner. Combust. Flame 2006, 145, 194–205. [Google Scholar] [CrossRef]
- Silva, C.F.; Nicoud, F.; Schuller, T.; Durox, D.; Candel, S. Combining a Helmholtz solver with the flame describing function to assess combustion instability in a premixed swirled combustor. Combust. Flame 2013, 160, 1743–1754. [Google Scholar] [CrossRef]
- Pardowitz, B.; Tapken, U.; Knobloch, K.; Bake, F.; Bouty, E.; Davis, I.; Bennett, G. Core noise—Identification of broadband noise sources of a turbo-shaft engine. In Proceedings of the 21st AIAA/CEAS Aeroacoustics Conference, Atlanta, GA, USA, 16–20 June 2014. [Google Scholar]
- Zaman, K. Asymptotic spreading rate of initially compressible jets-experiment and analysis. Phys. Fluids 1998, 10, 2652–2660. [Google Scholar] [CrossRef]
- Pope, S.B. Turbulent flows; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Livebardon, T. Modélisation du Bruit de Combustion Dans Les Turbines D’hélicoptères. Ph.D Thesis, INP, Toulouse, France, 2015. [Google Scholar]
- Mendez, S.; Eldredge, J. Acoustic modeling of perforated plates with bias flow for Large-Eddy Simulations. J. Comput. Phys. 2009, 228, 4757–4772. [Google Scholar] [CrossRef]
- Lucca-Negro, O.; O’Doherty, T. Vortex breakdown: A review. Prog. Energy Comb. Sci. 2001, 27, 431–481. [Google Scholar] [CrossRef]
- Fosso Pouangué, A.; Sanjosé, M.; Moreau, S.; Daviller, G.; Deniau, H. Subsonic Jet Noise Simulations Using Both Structured and Unstructured Grids. AIAA J. 2015, 53, 55–69. [Google Scholar] [CrossRef]
- Amiet, R.K. Refraction of sound by a shear layer. J. Sound Vib. 1978, 58, 467–482. [Google Scholar] [CrossRef]

| Low | Full | |
|---|---|---|
| Inlet pressure ratio | 12% | 100% |
| Temperature ratio | 54% | 100% |
| Air mass-flow rate ratio | 13% | 100% |
| Fuel mass-flow rate ratio | 9% | 100% |
| Fuel/Air ratio | 1.2446 | 1.92 |
| Low | Full | ||
|---|---|---|---|
| HPT | Dimensionless rotational speed | 62% | 100% |
| Inlet Pressure ratio | 100% | 100% | |
| Inlet Temperature ratio | 100% | 100% | |
| Outlet Pressure ratio | 59% | 31% | |
| Outlet Temperature ratio | 79% | 70% | |
| LPT | Dimensionless rotational speed | 22% | 100% |
| Inlet Pressure ratio | 53% | 26% | |
| Inlet Temperature ratio | 75% | 68% | |
| Outlet Temperature ratio | 73% | 53% | |
| Number of cells | 33,134,438 |
| Number of nodes | 6,199,870 |
| Smallest volume | m |
| Time step | s |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Férand, M.; Livebardon, T.; Moreau, S.; Sanjosé, M. Numerical Prediction of Far-Field Combustion Noise from Aeronautical Engines. Acoustics 2019, 1, 174-198. https://doi.org/10.3390/acoustics1010012
Férand M, Livebardon T, Moreau S, Sanjosé M. Numerical Prediction of Far-Field Combustion Noise from Aeronautical Engines. Acoustics. 2019; 1(1):174-198. https://doi.org/10.3390/acoustics1010012
Chicago/Turabian StyleFérand, Mélissa, Thomas Livebardon, Stéphane Moreau, and Marlène Sanjosé. 2019. "Numerical Prediction of Far-Field Combustion Noise from Aeronautical Engines" Acoustics 1, no. 1: 174-198. https://doi.org/10.3390/acoustics1010012
APA StyleFérand, M., Livebardon, T., Moreau, S., & Sanjosé, M. (2019). Numerical Prediction of Far-Field Combustion Noise from Aeronautical Engines. Acoustics, 1(1), 174-198. https://doi.org/10.3390/acoustics1010012






