A Basic Complete Numerical Toolbox for Picosecond Ultrasonics

Abstract

A complete numerical complete toolbox is proposed concerning the simulation of photo-induced propagative mechanical wave, and concerning the optical reflectometric measured response of the material, which is initially exposed to a first pump laser beam that photo-induces the acoustic wavefronts. The deformation field and its propagation into a bulk material are simulated. Based on this field expression, the complex transient reflectivity is given for a medium considered as homogeneous. The real part of this quantity permits afterwards to propose a numerical simulation of the transient reflectivity, which corresponds to the optical signal measured during experimental works. The frequency acoustic spectrum is simulated and successfully compared to the measured frequency spectrum. For the first time, numerical complete developments are explicitly proposed and fully-developed under the SciLab${}^{\circledR }$ environment, related to the simulation of laser-induced picosecond acoustic wavefront photogenerated through an opto-acoustic transduction process (ultrasonics and pretersonics).

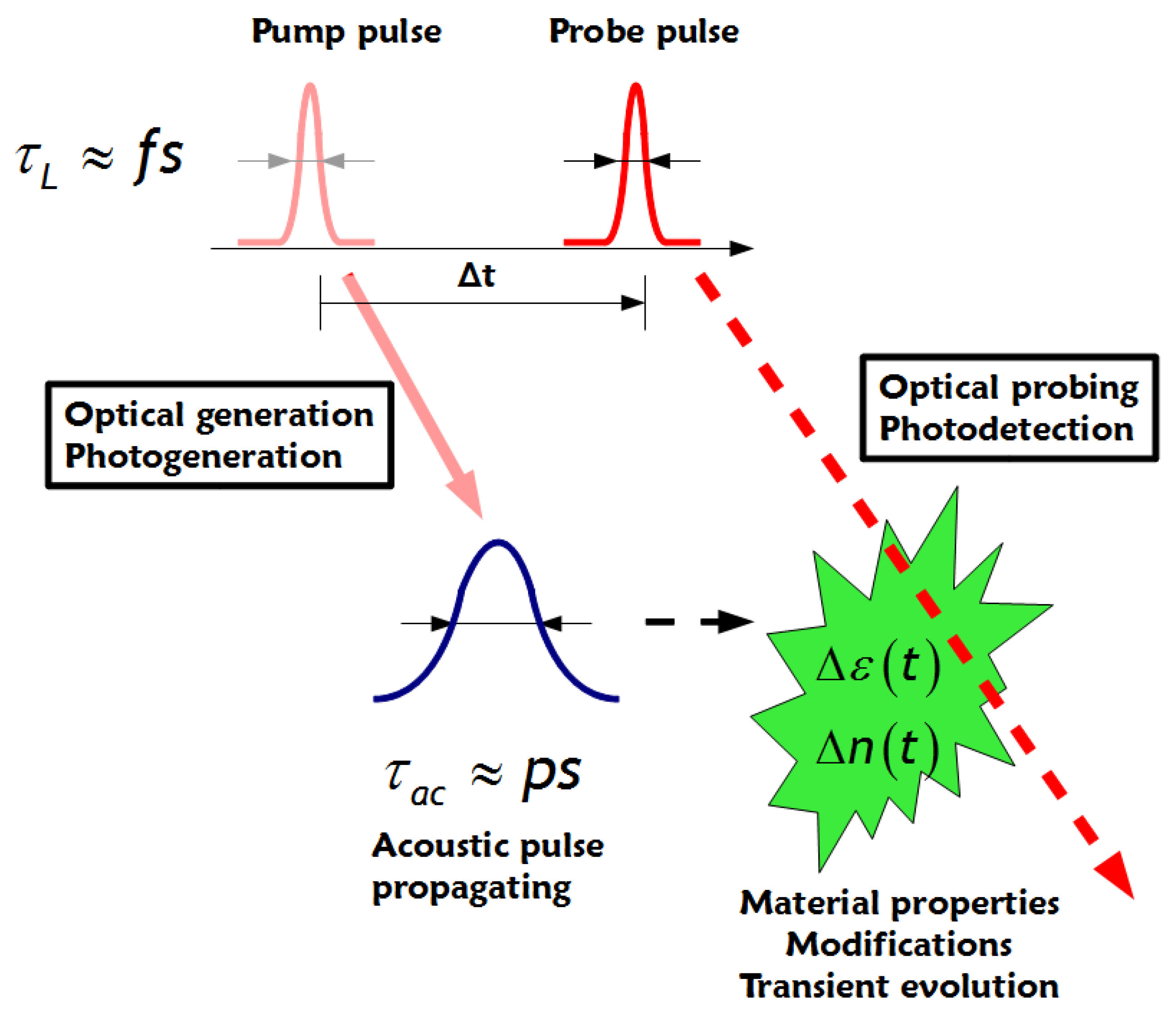
1. Presentation of the General Concept

Ultra-high frequency coherent acoustic phonons can be photogenerated and photodetected using a pump–probe laser scheme [1,2,3]. High frequency acoustic waves into the $GHz$ or into the sub-$THz$ frequency domain can be optically excited and detected by femtoseconde ($fs$) laser pulses [4]. Conventional (piezo-electric) transducers approach or photo-acoustic transduction approach involving a metal layer absorbing a nanoseconde ($ns$) laser pump pulse [5] are unable to reach such ultra-high frequency content [6]. The ultrasonic approach becomes, therefore, the only relevant way to generate and to detect such high frequency ranges. Schematically, a transient mechanical strain pulse is photogenerated into the bulk of the material, after interaction of the first pump laser pulse with the matter, through an opto-acoustic transduction (Figure 1). These photo-induced coherent phonons (propagative elastic disturbance) can be afterwards detected using a second laser light temporally synchronized and delayed-in-time to the first pump pulse [4]. The photodetection is based onto an acousto-optic transduction, revealing the propagation of the acoustic signal. Acoustical waves (laser-induced transient stress) can be, therefore, generated using ultrashort optical pulses [1,7]. The detection process [4,7,8,9,10,11] corresponds to a time domain optical spectroscopy [1,2,4,7,8,12,13,14]. The time-resolved optical pump–probe experimental set-up involved is given in Figure 2.

From these optical reflectivity measurements [8], key quantities can be extracted such as thickness, sound velocity, attenuation coefficient, refractive index, elastic, optical, thermophysical and mechanical properties [4,15] of submicrometric and nanometric size substrates, nano-multilayers, or bulk materials [10] and even liquids [16]. Longitudinal acoustic (LA) propagative acoustic waves can be detected, for instance, in liquid water, monitoring backscattered probe light from the sound wave propagating into the liquid [17], and, therefore, providing information about the medium itself. This opto-acoustic approach has then been found relevant for material characterization [18] and non-destructive evaluation (NDE) of mechanical or elastic properties of thin film [19,20], for mechanical strength determination of industrial materials (such as silicon wafers) [21,22] or non-destructive testing of materials (NDT) such as graphite fibers re-inforced composites for instance [23,24], for detection of residual stress into metal [6,25], for non-invasive photo-acoustic diagnostics of biological tissues [26], for photo-acoustic gas spectroscopy [27,28], for interface defect detection [18,29], for breaking cracks, voids, faults, flaws, or surface and sub-surface defects into semi-conductors [30,31,32], for bubbles or volumic defects [33], considering the modification of the photo-elastic response if local defects are present into the material [5]. This ultrasonic (also called picosecond laser acoustics) proposes then a versatile, precise and contact-free analytic tool for material sciences or industrial process control [4,34].

If extensive research activities and fundamental or engineering aspects have been extensively studied, no particular works proposed developments around numerical simulations and coding of reflectometric signal simulations, wavefronts simulations, and ultrasonics. Simulations of several experimental quantities are, therefore, proposed into the present work, considering the absence of any shockwaves [35], nor ablation or any destructive processes, and considering a linear absorption of the photogeneration laser beam at the interface (modelization out of any special conditions).

A complete numerical study is then presented, for the first time, given under the SciLab${}^{\circledR }$ environment, based on a commonly accepted experimental set-up, described in Figure 2. A complete numerical study is proposed under a basic approach. The optical absorption parameter $\alpha$, the optical depth penetration $\xi$, and the elastic stiffness C will be first numerically introduced, as primary inputs into the codes. Acoustics velocities will be afterwards directly estimated. Brillouin frequencies will be calculated next, estimating the impact of the incidence angle $\theta$ of the laser probe beam and the impact of the medium temperature T. The deformation field and its dynamic evolution can be then evaluated. Based onto these elements and primary parameters, the transient reflectivity is numerically and entirely simulated, and compared to original experimental measured data, obtained using the optical set-up described. All the given simulation codes given provide a complete numerical toolbox for laser ultrasonics works, as the proposed codes could next be also implemented according to users’ wishes.

2. Numerical Study

In the present work, for all the proposed simulations, a red probe and a red laser pump are considered (Figure 2), as this basic configuration is commonly used in experimental works [8].

A $GaAs$ $\left(100\right)$ substrate is considered, as this semi-conductor can be seen as a condensed matter model in fundamental physics. No particular nitridation of the substrate surface [36], nor particular presence of $AsAs$ adsorbed ad-atoms dimers, nor $GaGa$ dimers presence [37], nor As${}_2$O${}_3$ or Ga${}_2$O${}_3$ oxidised islands [38] are considered for all the numerical developments proposed in this work. As an extension, all the proposed codes could be re-used for another medium, changing the relevant parameters.

2.1. Optical Absorption Coefficient and Optical Depth Penetration

Two expressions ${\alpha }^{\left(s\right)}$ and ${\alpha }^{\left(p\right)}$ are then introduced, for pump ($\left(p\right)$ index) and probe beam ($\left(s\right)$ index), concerning the optical absorption coefficient:

$${\alpha }^{(s,p)}=\frac{4\pi }{{\lambda }^{\left(s\right)}}\times \Im m\left(n_{GaAs}^{(s,p)}\right)$$

(1)

in which ${\lambda }^{\left(s\right)}$ corresponds to the optical probe wavelength, and if $n_{GaAs}^{(s,p)}\left({\lambda }^{\left(s\right)}\right)$ corresponds to the reference index of $GaAs$ at the probe wavelength ${\lambda }^{\left(s\right)}$. For the proposed work, $n_{GaAs}^{(s,p)}\left({\lambda }^{\left(s\right)}=800.8\mathrm{nm}\right)=3.66+0.08i$ is used [39]. In the present study, a red-red ($800.8$ nm or $1.55$ eV exact energy value) pump–probe configuration is used, and it comes ${\alpha }^{\left(s\right)}={\alpha }^{\left(p\right)}\equiv {\alpha }^{(s,p)}$.

Into the picosecond ultrasonic experiments, the first optical pulse (pump beam) is typically absorbed at the free surface of the substrate interface under the absorption length $\delta$, corresponding, in first approximation, without any supersonic diffusion of carriers [40], to the optical depth penetration $\xi$. As both pump beam and probe beam are used into the red wavelength, we have:

$${\delta }^{(s,p)}\equiv {\xi }^{(s,p)}=\frac{1}{{\alpha }^{(s,p)}}$$

(2)

Calculations concerning the $\xi$ evaluation gives nevertheless strong differences according to the wavelength values involved [39,41]. For instance, the optical depth penetrations are, therefore, numerically estimated at ≈15 nm for $400.1$ nm irradiation, and estimated at ≈400 nm for 800.8 nm laser irradiation (≈26 times higher value).

//Scilab code (part 01/13) clear all //Clear clc()    //Clear   lambdap = 800.8 * 10^(-9) //Probe optical wavelength (m) lambdas = 800.8 * 10^(-9) //Pump optical wavelength (m)   n0 = 1.0002772 //Air around the sample (refractive index)k0 = (2*%pi*n0)/lambdas //Evaluation of the wavevector for optical wave Z0 = 0.0429 * 10^(4) //Acoustic impedance of the air (kg.m-2.s-1)   //Density of the medium (kg.m-3) rhoGaAs = 5317 //5.320 g.cm-3 (reference value)   //Angle value close to zero (normal incidence for pump beam) //thetaDeg = 0 thetaDeg = 45 //for probe theta = thetaDeg * (%pi/180) //Angle (from degrees to radians)

//Scilab code (part 02/13) //GaAs bulk parameters (taken at 1.55 eV exact value) //Refraction index values at the wavelength (nm) for GaAs n2p = 3.66+%i*0.08 //1.55 eV (800.8 nm) n2s = 3.66+%i*0.08 //1.55 eV (800.8 nm) nGaAs=real(n2s)   //Optical absorption coefficient (pump and probe) alphas=4*%pi*imag(n2s)/lambdas alphap=4*%pi*imag(n2p)/lambdas       //Optical depth penetration for probe and pump xis=1/(alphas) xip=1/(alphap)   //Ratio between optical depth penetration (test, should be equal to 1) ratioxi=xip/xis

2.2. Acoustic Velocities Calculations

The different values of the acoustic velocities can be estimated from the stiffness matrix coefficient $C_{mn}$ ($m,n$ index), the anisotropy factor A and the density $\rho$. For this purpose, Burenkov relationship, involving $C_{11}$, $C_{12}$ and $C_{44}$ [42], under the melting point temperature (around 1510–1515 K [42]), are used:

$$\left\{\begin{array}{c}{C}_{11}\left(T\right)=\left(12.17-1.44\times {10}^{-3}\times T\right)\times {10}^{-1}\times {10}^{11}\\ C_{12}\left(T\right)=\left(5.46-0.64\times {10}^{-3}\times T\right)\times {10}^{-1}\times {10}^{11}\\ C_{44}\left(T\right)=\left(6.16-0.70\times {10}^{-3}\times T\right)\times {10}^{-1}\times {10}^{11}\end{array}\right.$$

(3)

//Scilab code (part 03/13) T = 298.15 //Temperature considered (K), room temperature (RT) condition   //Stiffness matrix coefficient values //Units: dyn/cm2 divided by 10 \textcolor{black}{corresponds to} N/m2 c11= ((12.17-1.44*T*1e-3)/10)*1e11  //Elastic rigidity (N/m^2) c12= ((5.46 - 0.64*T*1e-3)/10)*1e11 //Elastic rigidity (N/m^2) c44= ((6.16 - 0.70*T*1e-3)/10)*1e11 //Elastic rigidity (N/m^2)

The pure longitudinal acoustic (resp. transverse acoustic) modes LA (resp. TA) is given by:

$$V_{GaAs}^{LA}={\left(\frac{C_{11}}{\rho }\right)}^{1/2}$$

(4)

$$V_{GaAs}^{TA}={\left(\frac{C_{44}}{\rho }\right)}^{1/2}$$

(5)

The quasi-longitudinal (resp. quasi-transverse) acoustic modes QLA (resp. QTA) is given by:

$$V_{GaAs}^{QLA}={\left(\frac{C_{11}+C_{44}\times \left(1-\frac{1}{A}\right)}{\rho }\right)}^{1/2}$$

(6)

$$V_{GaAs}^{QTA}={\left(\frac{C_{44}}{\rho A}\right)}^{1/2}$$

(7)

introducing the Zener anisotropy factor A:

$$A=\frac{2C_{44}}{C_{11}-C_{12}}$$

(8)

Few numerical results are given in

Table 1. Numerical calculations of acoustic velocities and Brillouin frequency (temperature fixed at $298.15$ K and angle of incidence fixed at ${45}^{\circ }$).

Velocity	(m·s${}^{-1}$)	Brillouin Frequency	(GHz)
$V_{GaAs}^{\left(LA\right)}$	$4725.6$	$f_{GaAs}^{\left(LA\right)}$	$42.4242$
$V_{GaAs}^{\left(TA\right)}$	$3341.5$	$f_{GaAs}^{\left(TA\right)}$	$29.9984$
$V_{GaAs}^{\left(QLA\right)}$	$5233.3$	$f_{GaAs}^{\left(QLA\right)}$	$46.9824$
$V_{GaAs}^{\left(QTA\right)}$	$2231.5$	$f_{GaAs}^{\left(QTA\right)}$	$22.1895$

, concerning the calculated acoustic velocities and the related Brillouin frequencies.

A $GaAs$ $\left(100\right)$ substrate is considered for all the simulations, and $\left[100\right]$ corresponds to a propagation direction for the LA mode (involving the coefficient $C_{11}$), coupled to the two transverse modes TA1 and TA2 ($C_{44}$).

//Scilab code (part 04/13) //Anisotropy factor (adimensional factor) A=(2*c44)/(c11-c12)   //Pure longitudinal wave [100] direction VLAGaAsEstim=(c11/rhoGaAs)^0.5   //Pure shear wave [010] polarized VTAGaAsEstim=(c44/rhoGaAs)^0.5   //Quasi-longitudinal wave VQLAGaAsEstim=((c11+(c44*(1-(1/A))))/rhoGaAs)^0.5   //Quasi-shear wave VQTAGaAsEstim= (c44/(A*rhoGaAs))^0.5   //Acoustic impedance for GaAs bulk material (kg.m-2.s-1) ZGaAs = rhoGaAs * VLAGaAsEstim   //Evaluation of difference of impedance values (kg.m-2.s-1) \textcolor{black}{//Test} DeltaZ = ZGaAs-Z0 \textcolor{black} {//Z0 impedance of the air (reference level)} Diff=DeltaZ/ZGaAs*100 \textcolor{black} {//Strong or low interface)}

Considering a typical optical depth penetration $\xi$, and the LA (longitudinal acoustic) sound velocity $V_{GaAs}^{\left(LA\right)}$, the expected duration ${\tau }_{ac}$ of the acoustic pulses is given by:

$${\tau }_{ac}\equiv \frac{\xi }{V_{GaAs}^{\left(LA\right)}}$$

(9)

The characteristic frequency $f_{ac}$ of these acoustic waves can be afterwards deduced:

$$f_{ac}\equiv {\left(2\pi {\tau }_{ac}\right)}^{-1}$$

(10)

$Z_{GaAs}={\rho }_{GaAs}{V}_{GaAs}^{\left(LA\right)}$ corresponds to the acoustic impedance of the substrate for LA mode of propagation.

2.3. Brillouin Frequencies Calculations

The Brillouin frequencies $f_{GaAs}^{\left(m\right)}$, considering the different modes $m=\left\{LA,TA,QLA,QTA\right\}$, results from an interference phenomenum between the two beam coming from the incoming probe itself, as described in Figure 3 [43,44]:

$$f_{GaAs}^{\left(m\right)}=\frac{2V_{GaAs}^{\left(m\right)}}{{\lambda }^{\left(s\right)}}\times {\left(n_{GaAs}^{{\left(s\right)}_{}2}-n_0^2{\sin }^2\theta \right)}^{1/2}$$

(11)

in which ${\lambda }^{\left(s\right)}$ corresponds to the optical probe wavelength [9], and $\theta$ to the angle related to the normal incidence (above the sample surface), considering the different modes m and the index of refraction $n_{GaAs}^{\left(s\right)}$ of $GaAs$ at the wavelength ${\lambda }^{\left(s\right)}$ of the optical probe [14,39,44]. Numerical results are then given in Table 1 for an angle $\theta ={45}^{\circ }$ for the probe beam incidence, corresponding also to a typical angular value (experimental data). For instance, a $\Delta \theta \approx {10}^{\circ }$ variation of incidence angle (centered onto ${45}^{\circ }$ value), induces roughly a $\Delta f_{GaAs}^{\left(m\right)}\approx 0.3$ ps variation for the Brillouin period, as given into the numerical results (Figure 4).

//Scilab code (part 05/13) //Brillouin frequency mode value (Hz) for LA mode fBLA=((2*VLAGaAsEstim)/lambdas)*((nGaAs*nGaAs)-(sin(theta))^2)^(0.5) fBLA_GHz = fBLA * 10^(-9)   //Brillouin frequency mode value (Hz) for TA mode fBTA=((2*VTAGaAsEstim)/lambdas)*((nGaAs*nGaAs)-(sin(theta))^2)^(0.5) fBTA_GHz = fBTA * 10^(-9)   //Brillouin frequency mode value (Hz) for QLA mode fBQLA=((2*VQLAGaAsEstim)/lambdas)*((nGaAs*nGaAs)-(sin(theta))^2)^(0.5) fBQLA_GHz = fBQLA * 10^(-9)   //Brillouin frequency mode value (Hz) for QTA mode fBQTA=((2*VQTAGaAsEstim)/lambdas)*((nGaAs*nGaAs)-(sin(theta))^2)^(0.5) fBQTA_GHz = fBQTA * 10^(-9)

The impact on the Brillouin value $f_{GaAs}^{\left(m\right)}$ of the two physical parameters (angle of incidence $\theta$ and temperature T) has been simulated in Figure 4 and Figure 5, as $C_{11}$, $C_{12}$ and $C_{44}$ are temperature dependent [42]. These parameters variations can have, therefore, a significant impact onto the Brillouin frequency value.

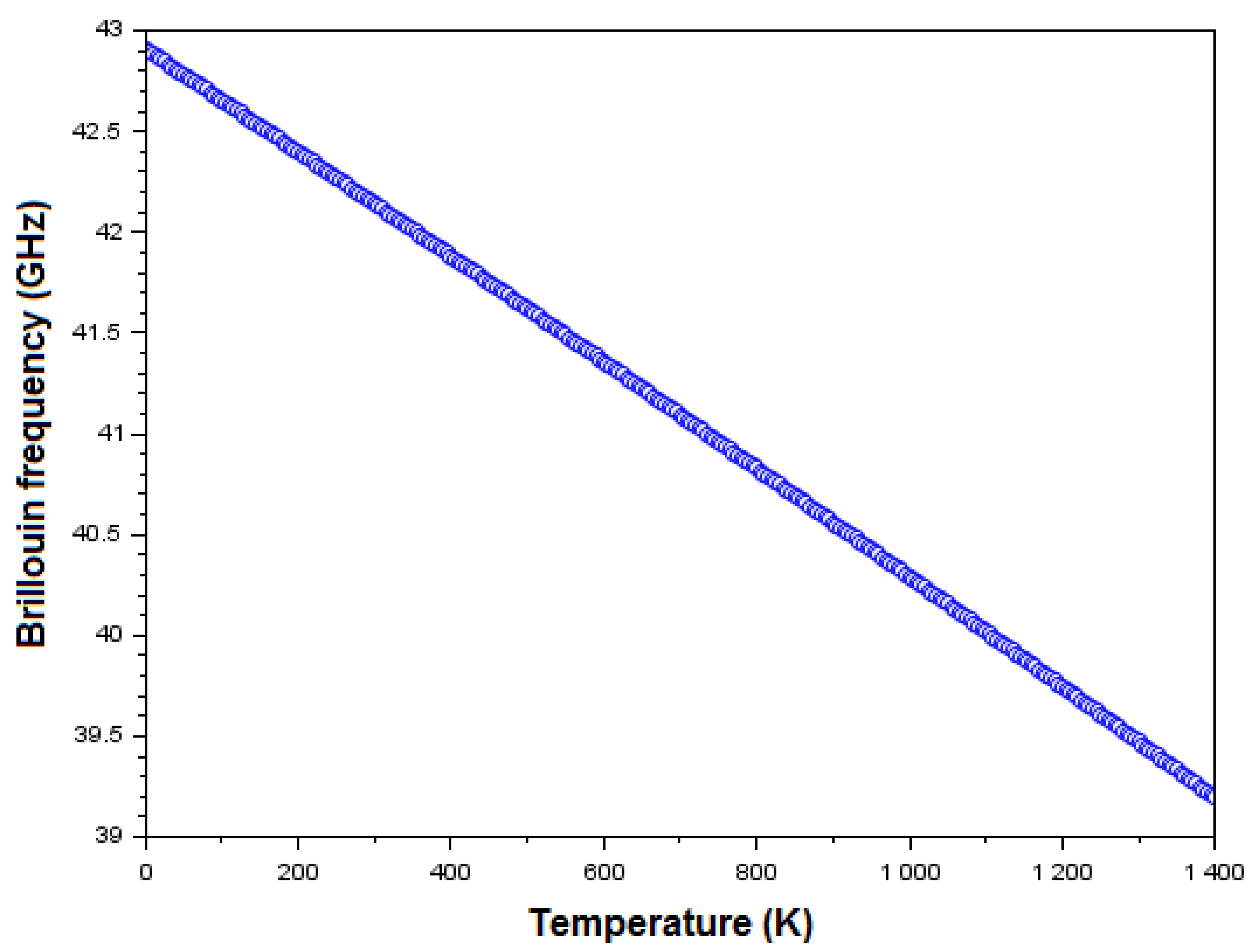
//Scilab code (part 06/13) VLAGaAsEstim=(c11/rhoGaAs)^0.5 fBLA=((2*VLAGaAsEstim)/lambdas)*((nGaAs*nGaAs)-(sin(theta))^2)^(0.5) //Brillouin frequency mode value (Hz) for LA mode fBLA_GHz = fBLA * 1e-9   scf(0) clf(0) T=0:5:1400; plot(T,fBLA_GHz,’-o’); xlabel(’Temperature (K)’) ylabel(’Brillouin frequency (GHz)’) title(’Impact of the temperature onto the Brillouin frequency, for 45 angle incidence to normal direction.’)

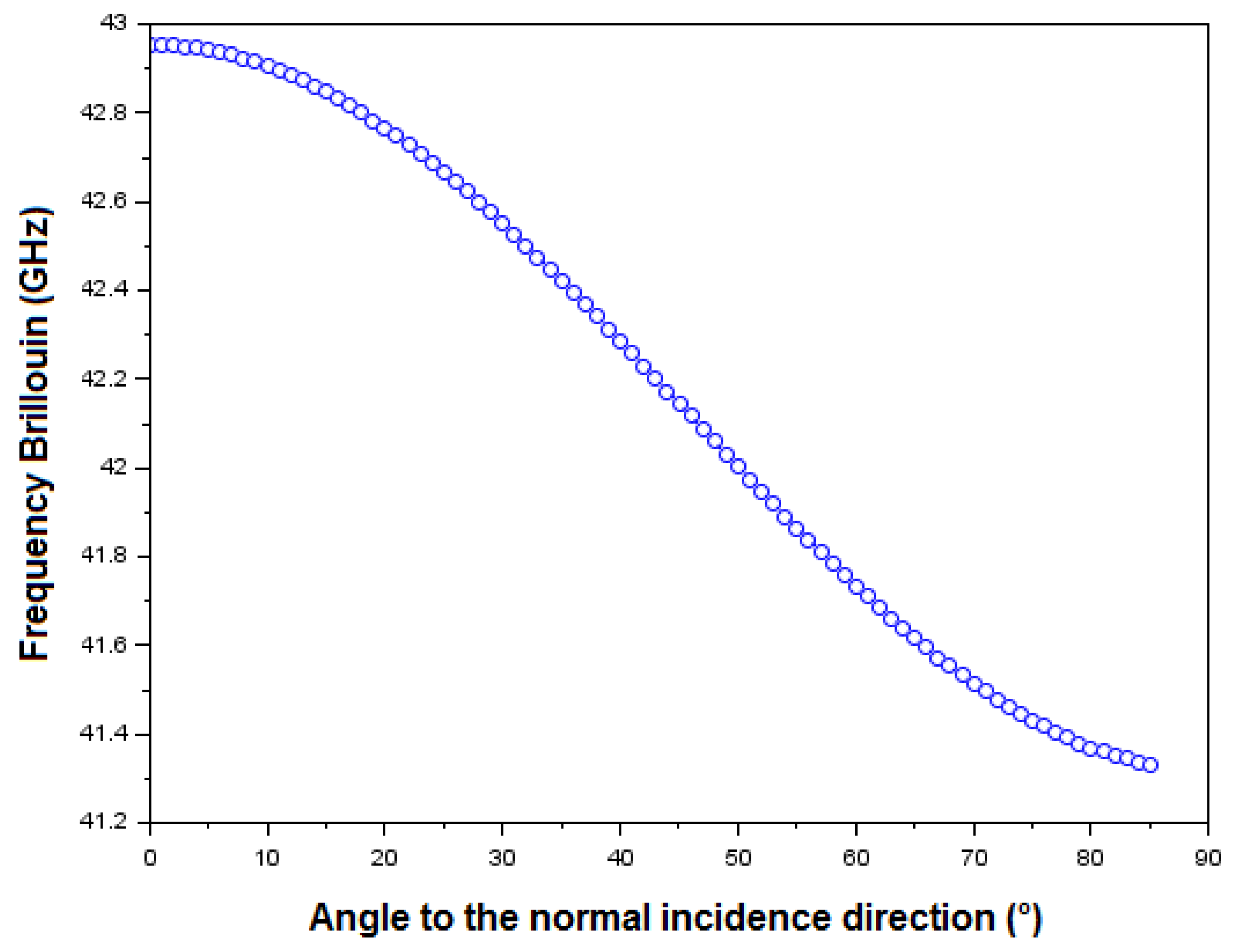
//Scilab code (part 07/13) clear all //Clear clc()     //Clear T = 298.15 //25 degrees, temperature of the medium //Elastic coefficient for GaAs (elastic rigidity expressed in N/m^2) c11= ((12.17-1.44*T*1e-3)/10)*1e11 c12= ((5.46 - 0.64*T*1e-3)/10)*1e11 c44= ((6.16 - 0.70*T*1e-3)/10)*1e11 A=(2*c44)/(c11-c12) rhoGaAs = 5317   thetaDeg=0:2:80; theta = thetaDeg * (%pi/180) VLAGaAsEstim=(c11/rhoGaAs)^0.5 fBLA=((2*VLAGaAsEstim)/lambdas)*((nGaAs*nGaAs)-(sin(theta))^2)^(0.5) fBLA_GHz = fBLA * 1e-9 scf(0) clf(0) thetaDeg=0:2:80; plot(thetaDeg,fBLA_GHz,’-o’); xlabel(’Incidence angle (degree)’) ylabel(’Brillouin frequency (GHz)’) title(’Impact of the angle incidence value onto the Brillouin frequency, for 298.15 K temperature.’)

2.4. Deformation Field Simulation

The optical wave (pump) is supposed to be absorbed beneath the interface, and the acoustic wave (optically generated acoustic ”disturbance”) is propagating into the bulk, from $z=0$ to $+\infty$ (in-depth coordinate). The probe pulse is supposed to be deflected onto the $z=0$ interface and also onto the in-depth acoustic waveplan propagating at the velocity $V_{GaAs}^{\left(LA\right)}$, inducing, therefore, typical Brillouin interference pattern (according to the Figure 3 configuration). No particular echo should be detected without any present particular bulk defects. Unidimensional configuration is considered, as $\mathsf{\Phi }>>\xi$ (typically $\mathsf{\Phi }\approx 10$$\mathsf{\mu }$m for the optical beam spot size used into typical ultrasonic experiments). A longitudinal acoustical mode $LA$ is consequently supposed to be excited into the matter.

2.5. Deformation Field

The deformation field [45] and the propagative acoustic wave present into the bulk material are modelized involving a standard Heaviside $\mathcal{H}$ step function, for spatial z and time t variables. Introducing $\phi \left(z,t\right)=z-V_{GaAs}^{\left(LA\right)}t$, the total field $\eta \left(z,t\right)$ used for the simulation is given by:

$$\eta \left(z,t\right)=\left(2-e^{-{\alpha }^{\left(p\right)}{V}_{GaAs}^{\left(LA\right)}t}\right)\times e^{-{\alpha }^{\left(p\right)}z}\times \mathcal{H}\left(z\right)-e^{-{\alpha }^{\left(p\right)}\left|\phi \left(z,t\right)\right|}\times \mathcal{H}\left(\phi \left(z,t\right)\right)$$

(12)

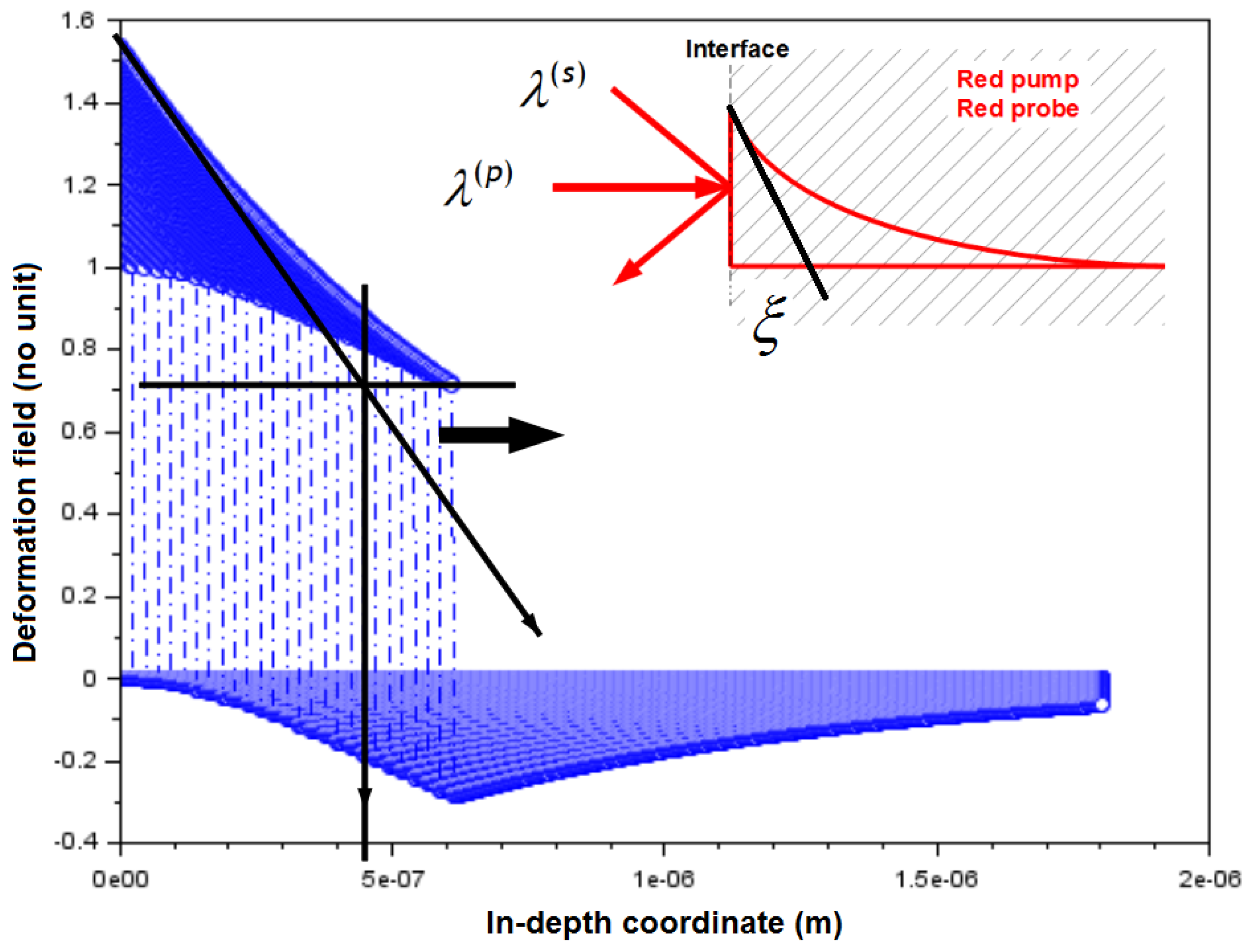
//Scilab code (part 08/13) //Heaviside step function H(z) definition deff(’y=H(x)’,’if x<0 then y=0;else y=1;end;’)   function[Sci]=defo(alphap,t,z) defs3= (2-exp(-alphap.*VLAGaAsEstim.*t))*exp(-alphap*z)*H(z)- H(z-VLAGaAsEstim*t)*exp(-alphap*abs(z-VLAGaAsEstim*t)); def=1.5*defs3; //Arbitrary scale factor Sci=def’; endfunction

The temporal evolution of the deformation field (LA mode) can be, therefore, proposed, simulating the wavefront propagation into the substrate (Figure 6). Similar results can be obtained using the $erf$ function instead an $Heaviside$ step-function.

The value of the geometrical parameter $\delta \equiv \xi$ can be then extracted (at $0^{+}$ ps) from the graphic representation given in Figure 6 and then, it is found $\xi \approx 400$ nm for a 800 nm pump laser irradiation, as physically expected.

If the simulation of the deformation field $\eta$ remains of a strong interest, the simulation of the $\frac{\Delta R}{R}$ quantity is also important, as this parameter is experimentally measured.

//Scilab code (part 09/13) //Photo-induced deformation field (red pump beam)   //Coefficient Ra20 Ra20=(-ZGaAs+Z0)/(ZGaAs+Z0)   scf(0) clf(0)   //Time between 0 ps and 100 ps, step of 1ps for t=0:5e-12:130e-12; //initial index p p=0;   //Space variable from 0.5 nm to 800 nm (bulk), step of 1 nm for z=0e-9:2.5e-9:1800e-9; p=p+1;   //Direct propagation of the wavefront into the bulk defs3(p)= (2-exp(-alphap.*VLAGaAsEstim.*t))*exp(-alphap*z)*H(z)- H((z)-VLAGaAsEstim*t)*exp(-alphap*abs((z)-VLAGaAsEstim*t)); //defor3(p)= H(z-VLAGaAsEstim*t)*exp(-alphap*abs(z-VLAGaAsEstim*t)); defs(p)=1*defs3(p);   end z=0e-9:2.5e-9:1800e-9; plot(z,defs,’-.o’) xlabel(’In-depth direction (m)’) ylabel(’Deformation field (no unit)’) title(’Spatial evolution of the deformation field for in-depth coordinate. Interface air/GaAs at 0 nm’) end

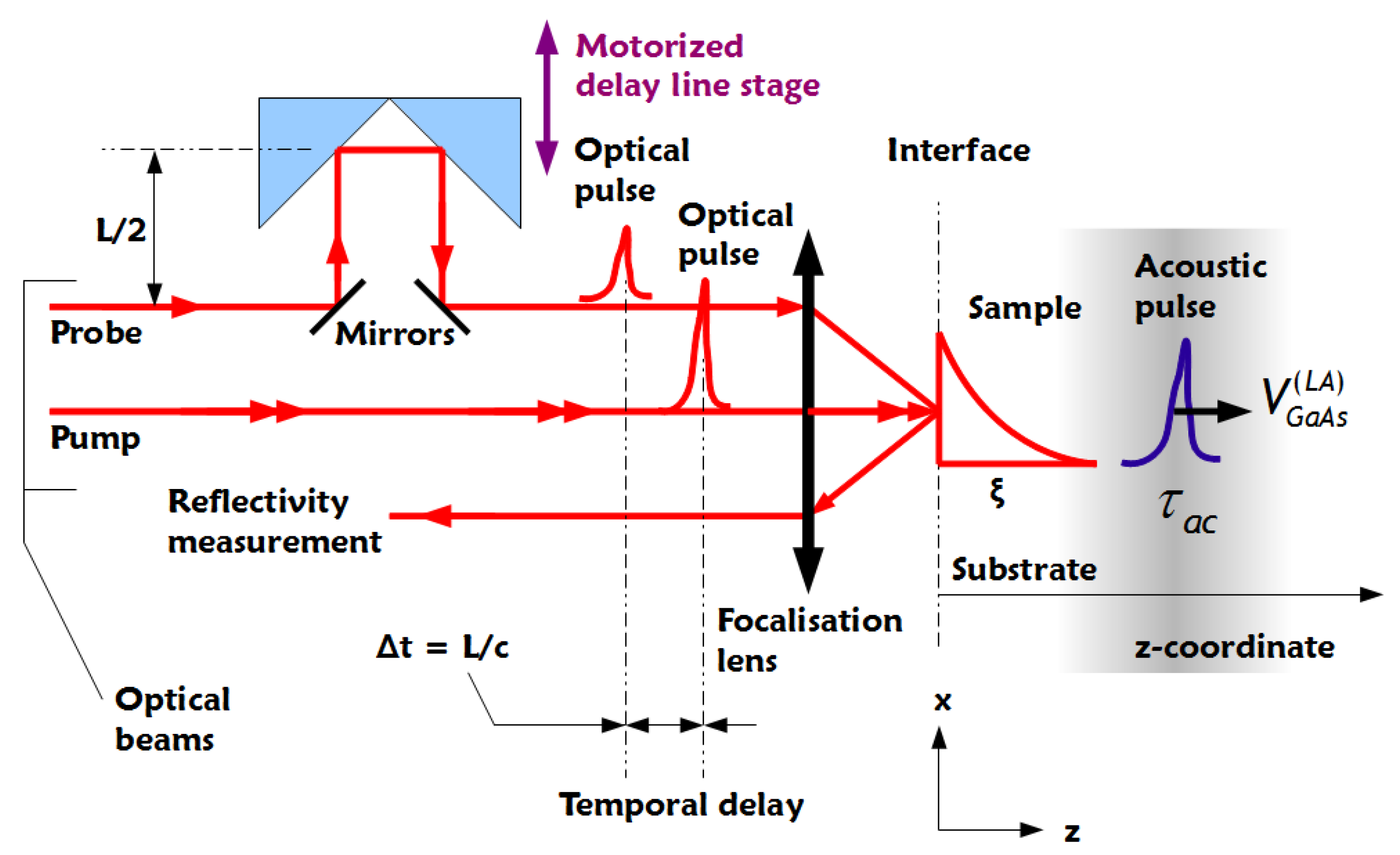
2.6. Transient Optical Reflectivity Simulation

During the experiments, the coherent acoustic phonons are photo-detected temporally monitoring the ultrafast transient changes of the detected optical reflectivity $\frac{\Delta R}{R}\left(\lambda ,t\right)$ [8], using the common optical architecture similar to the one given in Figure 2 [4,8,46]. The pump can be considered as a trigger inducing all the dynamics into the matter, under a conversion process of the optical energy of the pump beam into mechanical energy (Figure 1). The reflected laser beam (probe) intensity changes are collected by a photodiode, under the saturation laser intensity threshold. Into these typical reflectometry measurements [13], the first incident optical pulse (pump) is then absorbed beneath the substrate surface [4]. The photocreated dilatation generates a strain pulse typically within the optical depth penetration $\xi$. As the optical properties of the substrate are modified under strain (through a variation of refractive index $\Delta \tilde{n}$ or of the dielectric constant $\Delta \widetilde{ϵ}$, as given in Figure 1), the probe pulse allows to get the phase $\varphi$ and the amplitude A of the acoustic signal (through a photo-elastic coupling, as described in Figure 1). The acousto-optic interaction is found wavelength dependent [10,47,48].

The existence of acoustic waves or acoustic disturbances into the bulk of the material modifies the transient reflectivity $\frac{\Delta R}{R}\left(t\right)$, which is the physical key-quantity for monitoring acoustic wave propagating inside the medium. Either motions of the crystal surface [49,50,51] and bulk acoustic propagation phenomena [52,53,54] can be optically detected using this ultrasonic approach (Figure 1). All the simulations given into the present work are conducted considering the experimental set-up given in Figure 2 and into the conditions previously given in the text.

Photo-elastic coefficients ($p_{11}$ and $p_{12}$) [55] of the elastic tensor $p_{ij}$ and stiffness coefficients $C_{11}$ and $C_{12}$ of the reduced elastic tensor $C_{mn}$ are used to define the total photo-elastic coefficient $p{e}_{GaAs}$:

$$p{e}_{GaAs}=\frac{1}{2n_{GaAs}^{\left(s\right)}}\times \frac{2\pi }{{\lambda }^{\left(s\right)}}\times \left(p_{11}{C}_{11}+2p_{12}{C}_{12}\right)$$

(13)

in which ${\lambda }^{\left(s\right)}$ corresponds to the optical probe wavelength. The numerical result (for $800.8$ nm) is $p{e}_{GaAs}=41.2853+33.5125i$, and can be reintroduced into the simulation codes afterwards. This expression can also be described under the following derivative expression:

$$p{e}_{GaAs}=\frac{\partial k_{GaAs}}{\partial \eta }=\frac{2\pi }{{\lambda }^{\left(s\right)}}\times \frac{\partial n_{GaAs}}{\partial \eta }\equiv \frac{2\pi }{{\lambda }^{\left(s\right)}}\times pe$$

(14)

introducing the quantity $pe$ and the optical wavenumber $k_{GaAs}^{\left(s\right)}$ of the probe laser beam defined by:

$$pe=\frac{\partial n_{GaAs}}{\partial \eta }=\frac{p_{11}{C}_{11}+2p_{12}{C}_{12}}{2n_{GaAs}^{\left(s\right)}}$$

(15)

considering:

$$k_{GaAs}^{\left(s\right)}=\frac{2\pi }{{\lambda }^{\left(s\right)}}\times n_{GaAs}^{\left(s\right)}$$

(16)

Schematically, the presence of the mechanical stress into the matter generates a birefringence effect. The larger the photoelastic constant is, the stronger the birefringence signal generated by the mechanical stress. The photo-elastic coefficients ($p_{11}$, $p_{12}$ and $p_{44}$) depend on the crystal nature of the material and on the optical wavelength considered [56].

//Scilab code (part 10/13) p11=(8+%i*(3))*1e-9; //Coefficient at 800 nm p12=(-4+%i*(-3))*1e-9; //Coefficient at 800 nm   pe=(p11*c11+2*p12*c12)/(2*n2s)   //Photo-elastic coefficient (p11, p12, p44) of the photo-elastic tensor pe2=1*(2*%pi/lambdas)*(p11*c11+2*p12*c12)/(2*n2s)   //to compare with (test): //Photo-elastic coefficient (p11, p12, p44) of the photo-elastic tensor pe2=1*(2*%pi/lambdas)*pe

Considering a single interface (air-substrate), the transient complex reflectivity [7] is given by:

$$\frac{\Delta r}{r_{01}}=2i{k}_{0}u\left(0\right)+i\frac{\left(1-r_{02}^2\right)}{r_{02}}\times \frac{\partial {\tilde{k}}_{GaAs}}{\partial \eta }\times {\int }_0^{+\infty }\eta \left(z,t\right)\times e^{2i{k}_{GaAs}z}dz$$

(17)

in which $r_{02}$ corresponds to the optical reflexion coefficient at the $z=0$ interface [7] (air-substrate interface). In this expression, two contributions can be distinguished: an interface effect and a bulk effect (including a Laplace transform of the deformation field $\eta$). The interface corresponds to a mechanically free single surface. $u\left(0\right)$ corresponds to the displacement of the front surface. The probe light absorption in the surrounding air is supposed negligible during air propagation. The acousto-optical information is contained in the previously given photo-elastic coefficient expression (detection process):

$$\frac{\partial {\tilde{k}}_{GaAs}}{\partial \eta }=\frac{\partial k_{GaAs}^{{}^{\prime }}}{\partial \eta }+i\frac{\partial k_{GaAs}^{{}^{″}}}{\partial \eta }$$

(18)

in accordance with the following optical complex wavevector expression:

$${\tilde{k}}_{GaAs}=k_{GaAs}^{{}^{\prime }}+i{k}_{GaAs}^{{}^{″}}$$

(19)

The transient complex optical reflectivity is linked to the real optical transient reflectivity by the relation $R=r{r}^{*}$, if $r^{*}$ corresponds to the conjugated complex of r [1,54], and, therefore, the amplitude $A\left(t\right)$, which corresponds to the measured quantity, is given by:

$$\frac{A}{2}\left(t\right)\cong \frac{\Delta R}{2R_0}\left(t\right)=\Re e\left\{\frac{\Delta r}{r_0}\left(t\right)\right\}$$

(20)

The phase variation $\Delta \varphi$ could also be extracted, considering the imaginary part of the complexe transient reflectivity:

$$\Delta \varphi =\Im m\left(\frac{\Delta r}{r_0}\right)$$

(21)

This phase variation will not be considered for the present study, as the optically measured physical quantity is the reflectivity $\frac{\Delta R}{R_0}\left(t\right)$. From the analysis of the Brillouin oscillations (oscillating component) present into the reflectivity signal measured, all the spectral modes (frequency domain) [7,53,57,58] can be afterwards extracted, and informations onto the material itself (microcracks, velocities, attenuation, or charge carriers phenomena) can be evaluated. The initial peak (zero-time peak, and 0–5 ps temporal range) corresponds to pure electronic phenomenum and it will not be modelised into the present work, as it focuses only onto purely acoustic wave propagation phenomenum (temporal established phenomenum).

A thermal decreasing background can be superimposed to the pure transient reflectometric signal modelized, to simulate the exponential decay related to the pure thermal phenomenum. It is choosen a simple exponential decay $A\times \exp \left(-\frac{t}{\tau }\right)$. A corresponds to an arbitrary scale factor (constant), and it seems to be physically acceptable to choose $\tau \approx 20$ ps, as this value permits a relevant and good fit of real experimental case.

A FFT (Fast Fourier Transform) permits to identify the vibration modes photo-induced by the optical pump. Sampling conditions are specifically chosen (sample rate, number of samples) to match the Nyquist-Shannon criteria [59].

//Scilab code (part 11/13) k2s=2*%pi*n2s/lambdas //n2s related to the probe into GaAs   r02=(n2s-n0)/(n0+n2s) ///Reflexion coefficient //Acoustic interface air-GaAs (at normal incidence)   //Factor F for deformation integration F=(1-r02*r02)/r02   //Coefficient Ra20 (impedance ZGaAs and Z0 for air) Ra20=(-ZGaAs+Z0)/(ZGaAs+Z0)

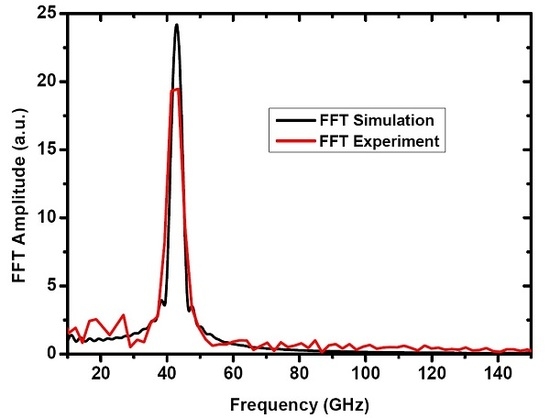
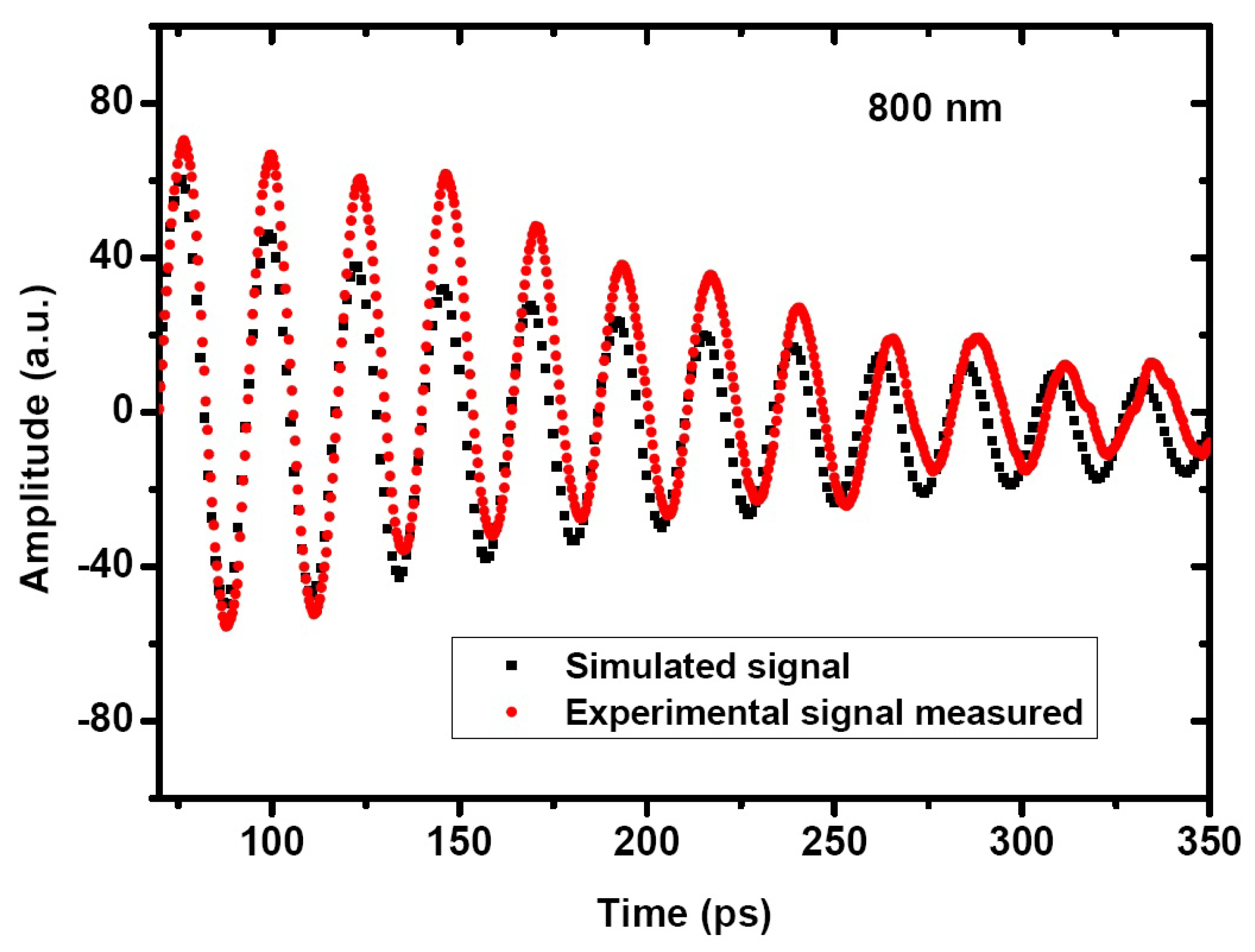
//Scilab code (part 12/13) //Transient reflectivity (integration of deformation field) intS=0; //defor1=0; //defor2=0; defor3=0; k=0; for t=0:1e-12:6000e-12; //from 0 to 6 ns (time domain) k=k+1;   r=0; for z=0:1e-9:1800e-9; //from 0 to 1800 nm (space domain) r=r+1; defor3(r)=(defo(alphap,t,z).*exp(2*%i*k2s*z))’; end z=0:1e-9:1800e-9; //from 0 to 1800 nm (space domain for integration) intS(k)=0.5*pe2*(1/r02-r02).*inttrap(z,defor3); //Trapezoidal integration end   t=0:1e-12:6000e-12; //from 0 to 6 ns (time domain) //Transient reflectivity variation (empiric exponential decay added) drr=real(intS’)+50*exp(-t/(20e-12));   scf(1) clf(1)   plot2d(t,drr);//Simulation graphic representation

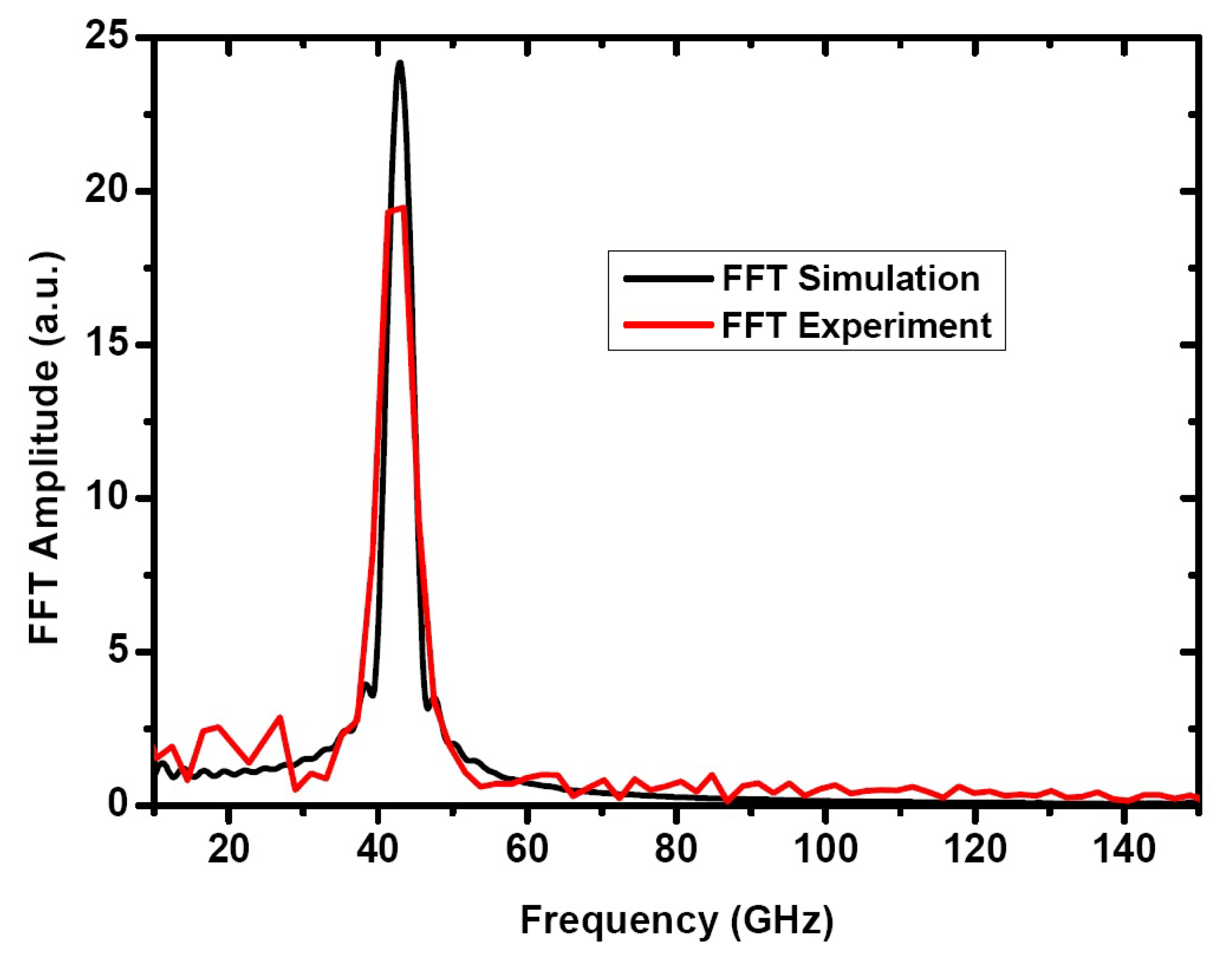
//Scilab code (part 13/13) sample_rate=1e12 t = 0e-12:1/sample_rate:6000e-12 N=size(t,’*’) //number of samples   g=fft(drr,-1)   f=sample_rate*(0:(N/2))/N;//associated frequency vector n=size(f,’*’)   scf(2) //clear the figure clf(2)   //Maximum values for frequencies [m,k]=max(f) answer=max(f) //maximum vertical axis (m)   plot(f,abs(g(1:n)));

The numerical results obtained from the simulation are in strong accordance with experimental dataset (Figure 7), considering the experimental set-up described in Figure 2. A good correlation is found concerning $FFT$ spectral components (Figure 8). Possible slight frequency shifts can be due to experimental uncertainity related to the value of the angle of incidence $\theta$ (experimental set-up), as this parameter could impact the Brillouin signal.

3. Conclusions

A complete numerical toolbox concerning photo-induced propagative acoustic wavefronts and laser ultrasonics is proposed, providing step-by-step codes. Few orders of magnitudes are calculated, such as acoustic pulse duration, acoustic typical frequency, optical absorption coefficient, and optical depth penetration. Acoustic velocities have been numerically evaluated, taking into account angular laser beam incidence dependence and temperature impact. Brillouin frequencies have been evaluated for LA, TA, QLA and QTA acoustical modes into a commonly used red pump–red-probe configuration. A deformation field simulation is given. The complex transient reflectivity is numerically described. The reflectivity signal with/without an empiric superimposed background thermal decay is also given. Numerical calculations of FFT give the opportunity to extract the mode of vibration in GHz, which can be easily compared to experimentally measured datasheets (under good matching).