An Expectation–Maximization-Based IVA Algorithm for Speech Source Separation Using Student’s t Mixture Model Based Source Priors
Abstract
:1. Introduction
2. Related Work
3. Proposed Method
3.1. Maximum Likelihood Estimation of SMM
3.2. The Expectation-Maximization Algorithm
3.3. The Expectation Step
3.4. The Maximization Step
| Algorithm 1 EM algorithm for Student’s t Mixtures |
Require: Given a Student’s t mixture model, the aim is to maximize the log likelihood function with respect to the parameters .
|
4. Experimentations and Results
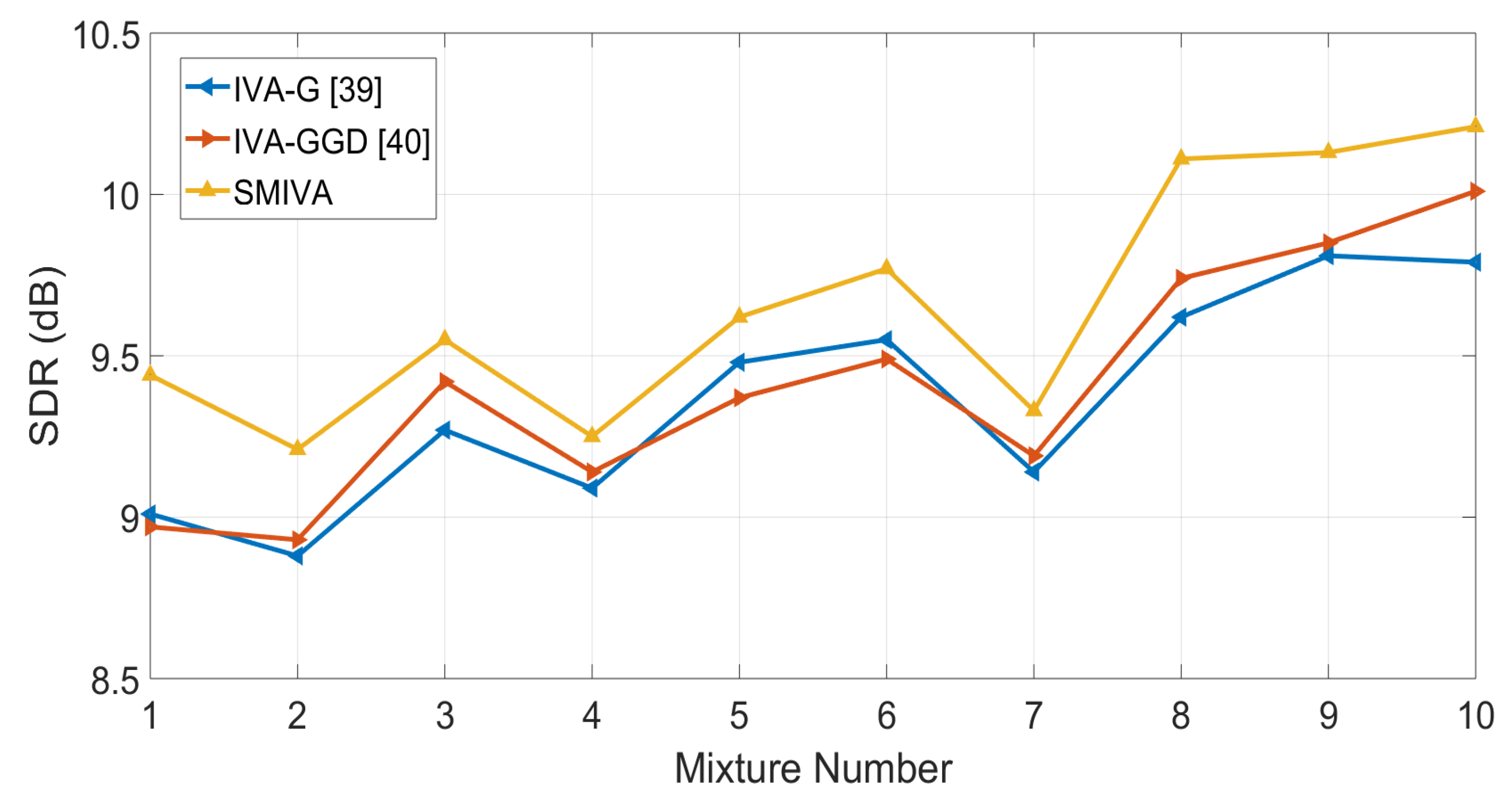
4.1. Case I: Simulations with the Image Method
4.2. Case II: Simulations with Real RIRs
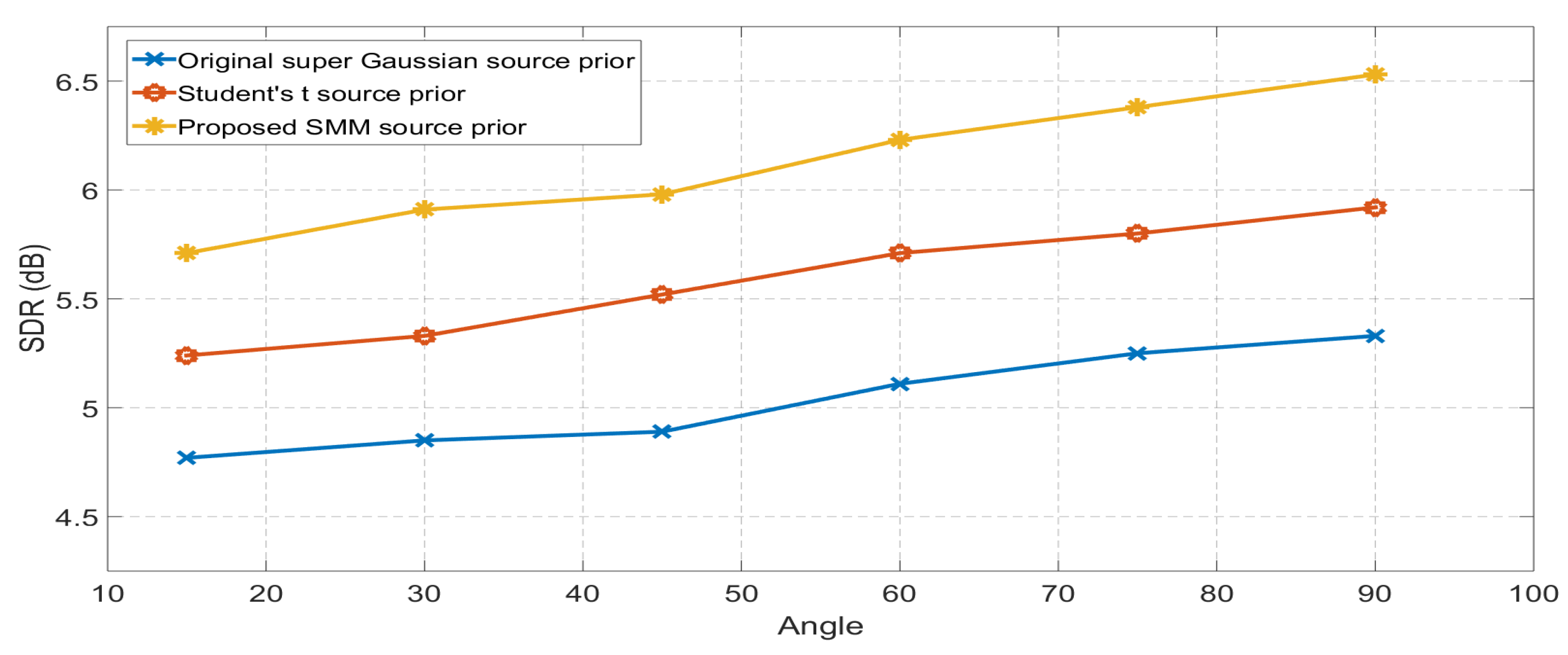
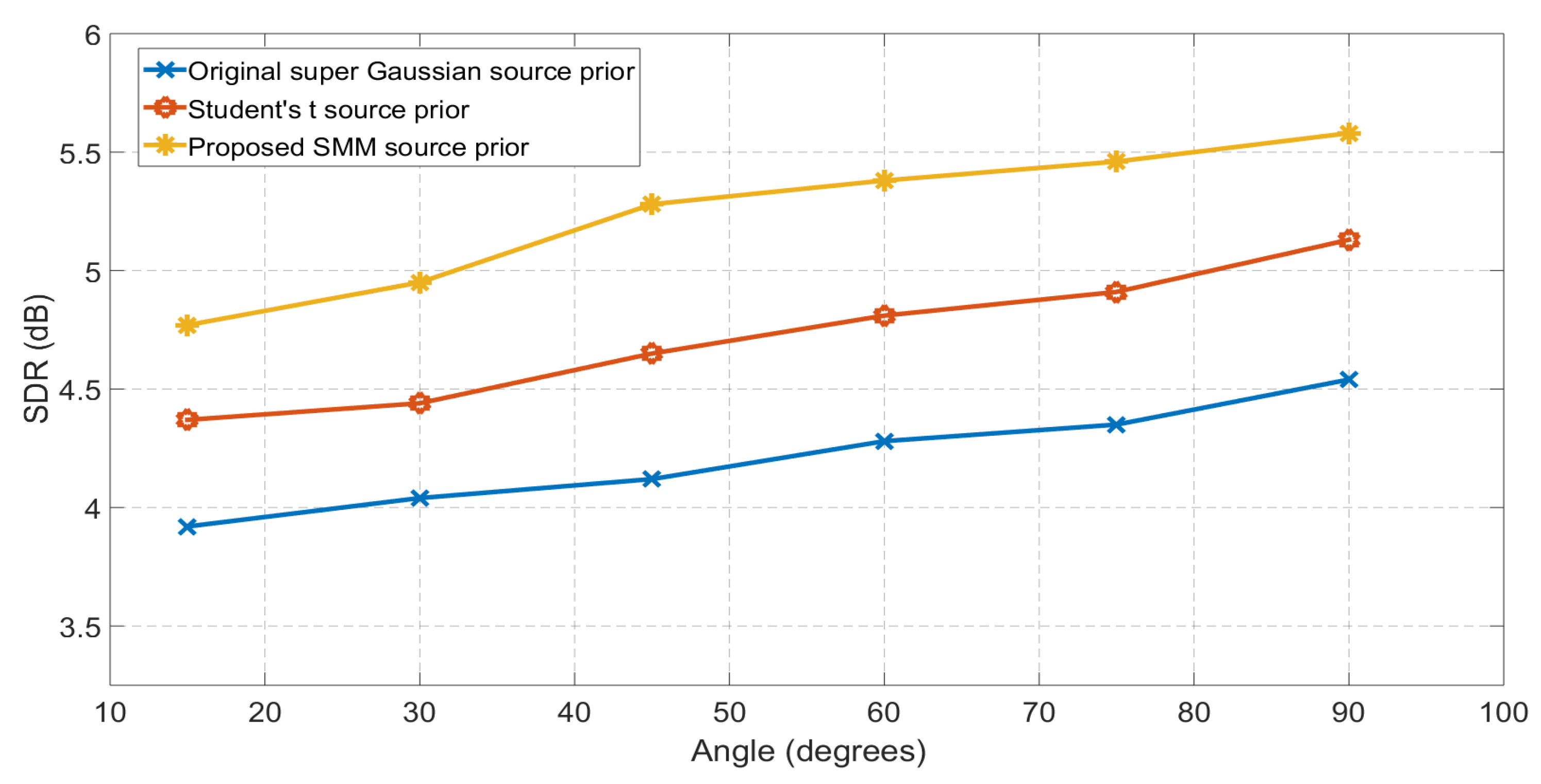
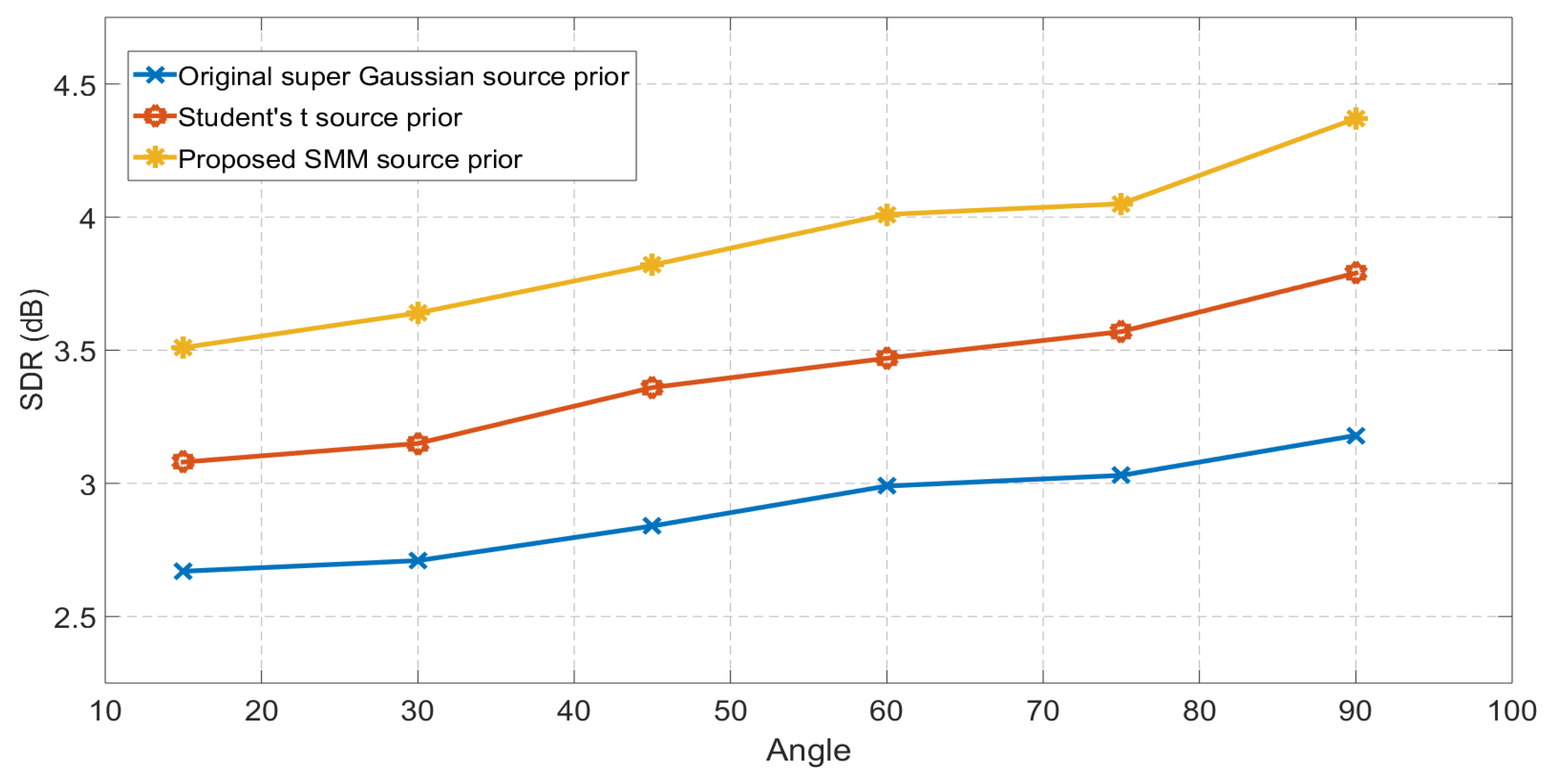
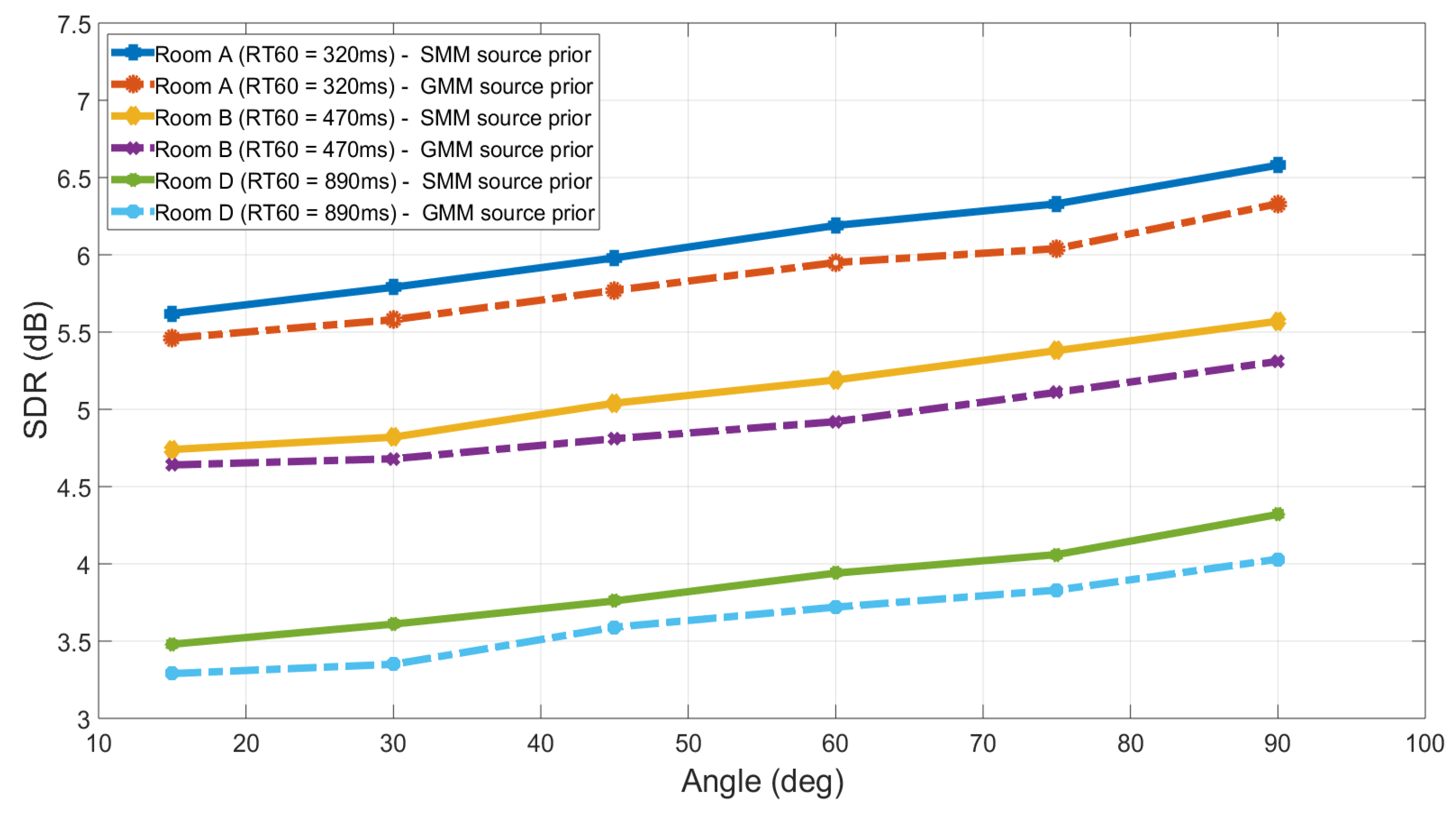
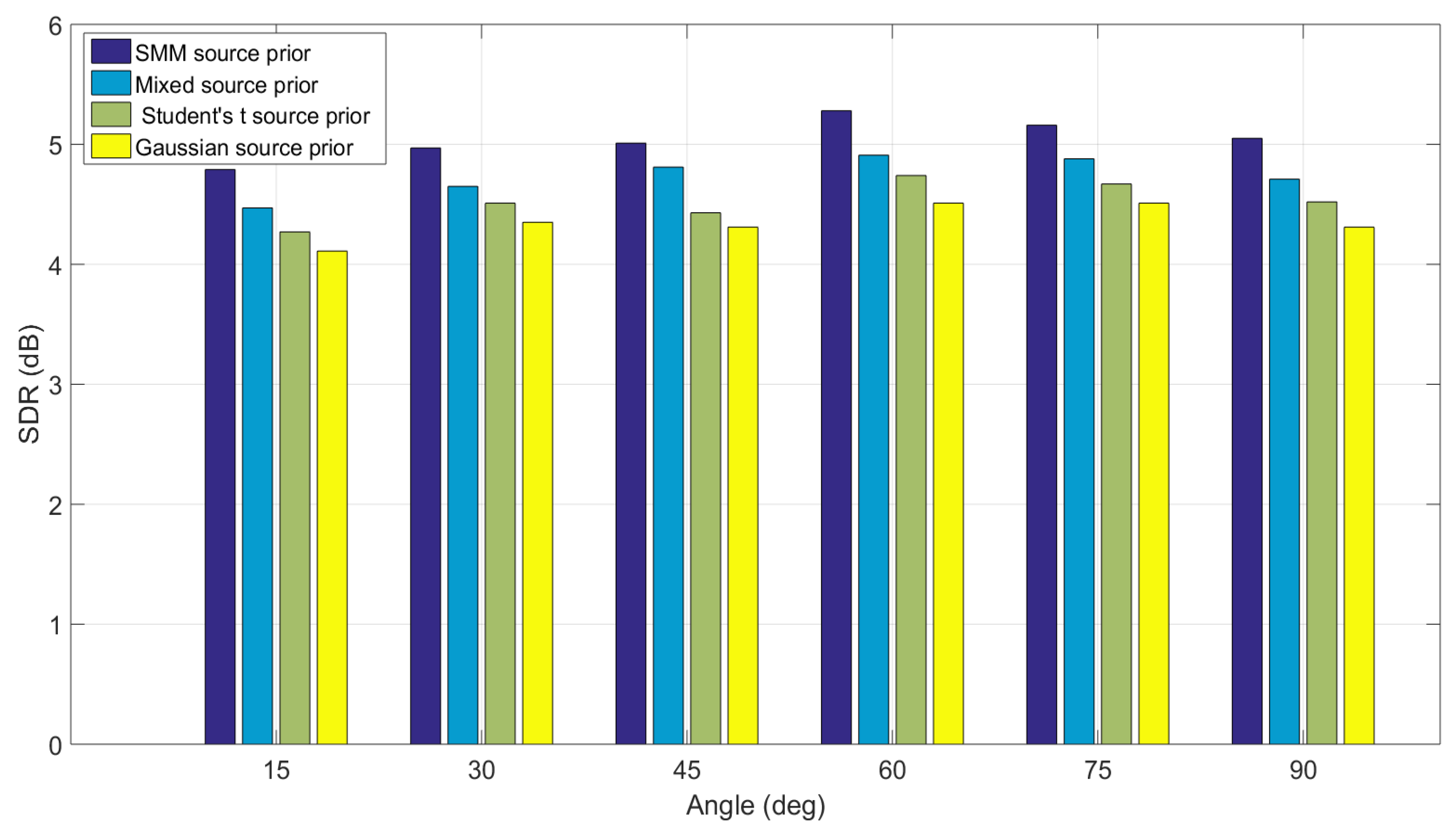
4.3. Case III: Simulations with Binaural Room Impulse Responses
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. The EM framework for SMIVA
References
- Haykin, S. Unsupervised Adaptive Filtering (Volume I: Blind Source Separation); Wiley: Hoboken, NJ, USA, 2000. [Google Scholar]
- Cherry, C. Some experiments on the recognition of speech, with one and with two ears. J. Acoust. Soc. Am. 1953, 25, 975–979. [Google Scholar] [CrossRef]
- Haykin, S.; Chen, Z. The cocktail party problem. Neural Comput. 2005, 17, 1875–1902. [Google Scholar] [CrossRef] [PubMed]
- Cichocki, A.; Amari, S. Adaptive Blind Signal and Image Processing; John Wiley: Hoboken, NJ, USA, 2002. [Google Scholar]
- McDermott, J.H. The cocktail party problem. Curr. Biol. 2009, 19, R1024–R1027. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, D.; Brown, G. Fundamentals of computational auditory scene analysis. In Computational Auditory Scene Analysis: Principles, Algorithms and Applications; John Wiley and Sons: Hoboken, NJ, USA, 2006; pp. 1–44. [Google Scholar]
- Adali, T.; Anderson, M.; Geng-Shen, F. Diversity in independent component and vector analyses: Identiability, algorithms, and applications in medical imaging. IEEE Signal Process. Mag. 2014, 31, 18–33. [Google Scholar] [CrossRef]
- Parra, L.; Alvino, C. Geometric source separation: merging convolutive source separation with geometric beamforming. IEEE Trans. Speech Audio Process. 2002, 10, 352–362. [Google Scholar] [CrossRef]
- Pedersen, M.S.; Larsen, J.U.; Kjems, U.; Parra, L.C. A survey of convolutive blind source separation methods. Springer Handb. Speech Process. Speech Commun. 2007, 8, 1–34. [Google Scholar]
- Jutten, C.; Herault, J. Blind Seperation of sources, part I: An adaptive algorithm based on neuromimetic architecture. Signal Process. 1991, 24, 1–10. [Google Scholar] [CrossRef]
- Jutten, C.; Comon, P. Handbook of Blind Source Separation: Independent Component Analysis and Applications; Academic Press: Cambridge, MA, USA, 2010. [Google Scholar]
- Lee, T.W. Independent Component Analysis: Theory and Applications; Kluwer Academic: Norwell, MA, USA, 2000. [Google Scholar]
- Hyvrinen, A. Fast and robust fixed-point algorithms for independent component analysis. IEEE Trans. Neural Netw. 1999, 10, 626–634. [Google Scholar] [CrossRef] [Green Version]
- Parra, L.; Spence, C. Convolutive blind separation of non-stationary sources. IEEE Trans. Speech Audio Process. 2000, 8, 320–327. [Google Scholar] [CrossRef]
- Kim, T.; Attias, H.; Lee, S.; Lee, T. Blind source separation exploiting higher-order frequency dependencies. IEEE Trans. Audio Speech Lang. Process. 2007, 15, 70–79. [Google Scholar] [CrossRef]
- Kim, T.; Lee, I.; Lee, T.W. Independent vector analysis: Definition and algorithms. In Proceedings of the Fortieth Asilomar Conference on Signals, Systems and Computers, Pacific Grove, CA, USA, 29 October–1 November 2006. [Google Scholar]
- Simonyan, K.; Ackermann, H.; Chang, E.F.; Greenlee, J.D. New developments in understanding the complexity of human speech production. J. Neurosci. 2016, 36, 11440–11448. [Google Scholar] [CrossRef] [PubMed]
- Cooke, M.; Ellis, D. The auditory orgnization of speech and other sources in listeners and computational models. Speech Commun. 2001, 35, 141–177. [Google Scholar] [CrossRef]
- Sun, Y.; Rafique, W.; Chambers, J.A.; Naqvi, S.M. Underdetermined source separation using time-frequency masks and an adaptive combined Gaussian-Student’s t probabilistic model. In Proceedings of the 2017 IEEE ICASSP, New Orleans, LA, USA, 5–9 March 2017; pp. 4187–4191. [Google Scholar]
- Sundar, H.; Seelamantula, C.S.; Sreenivas, T. A mixture model approach for formant tracking and the robustness of Student’s t distribution. IEEE Trans. Audio Speech Lang. Process. 2012, 20, 2626–2636. [Google Scholar] [CrossRef]
- Rafique, W.; Naqvi, S.M.; Jackson, P.J.B.; Chambers, J.A. IVA algorithms using a multivariate Student’s t source prior for speech source separation in real room environments. In Proceedings of the IEEE ICASSP, South Brisbane, QLD, Australia, 19–24 April 2015; pp. 474–478. [Google Scholar]
- Rafique, W. Enhanced Independent Vector Analysis for Speech Separation in Room Environments. Ph.D. Thesis, Newcastle University, Newcastle upon Tyne, UK, 2017. [Google Scholar]
- Bishop, C.M. Pattern Recognition and Machine Learning; Springer-Verlag: Secaucus, NJ, USA, 2006. [Google Scholar]
- Hao, J.; Lee, I.; Lee, T.W.; Sejnowski, T.J. Independent Vector Analysis for Source Separation Using a Mixture of Gaussians Prior. Neural Comput. 2010, 22, 1646–1673. [Google Scholar] [CrossRef] [Green Version]
- Rafique, W.; Erateb, S.; Naqvi, S.M.; Dlay, S.S.; Chambers, J.A. Independent vector analysis for source separation using an energy driven mixed Student’s t and super Gaussian source prior. In Proceedings of the 2016 24th European Signal Processing Conference (EUSIPCO), Budapest, Hungary, 29 August–2 September 2016. [Google Scholar]
- Liang, Y. Enhanced Independent Vector Analysis for Audio Separation in a Room Environment. Ph.D. Thesis, Loughborough University, Loughborough, UK, 2013. [Google Scholar]
- Peel, D.; McLachlan, G.J. Robust mixture modelling using the t distribution. Stat. Comput. 2000, 10, 339–348. [Google Scholar] [CrossRef]
- Rafique, W.; Naqvi, S.M.; Chambers, J.A. Speech source separation using the IVA algorithm with multivariate mixed super Gaussian Student’s t source prior in real room environment. In Proceedings of the IET Conference Proceedings, London, UK, 1–2 December 2015. [Google Scholar]
- Rafique, W.; Naqvi, S.M.; Chambers, J.A. Mixed source prior for the fast independent vector analysis algorithm. In Proceedings of the IEEE Sensor Array and Multichannel Signal Processing Workshop (SAM), Rio de Janeiro, Brazil, 10–13 July 2016; pp. 1–5. [Google Scholar]
- Aroudi, A.; Veisi, H.; Sameti, H.; Mafakheri, Z. Speech signal modeling using multivariate distributions. EURASIP J. Audio Speech Music Process. 2015, 2015, 35. [Google Scholar] [CrossRef]
- Bauchau, O.A.; Trainelli, L. The vectorial parametrization of rotation. J. Nonlinear Dyn. 2003, 32, 71–92. [Google Scholar] [CrossRef]
- Dragmor, S.S.; Goh, C.J. Some counterpart inequalities in for a functional associated with Jensen’s inequality. J. Inequal. Appl. 1997, 1, 311–325. [Google Scholar] [CrossRef]
- Garofolo, J.S.; Lamel, L.F.; Fisher, W.M.; Fiscus, J.G.; Pallett, D.S.; Dahlgren, N.L.; Zue, V. TIMIT Acoustic-Phonetic Continuous Speech Corpus; Linguistic Data Consortium: Philadelphia, PA, USA, 1993. [Google Scholar]
- Vincent, E.; Fevotte, C.; Gribonval, R. Performance measurement in blind audio source separation. IEEE Trans. Audio Speech Lang. Process. 2006, 14, 1462–1469. [Google Scholar] [CrossRef] [Green Version]
- Allen, J.B.; Berkley, D.A. Image method for efficiently simulating small-room acoustics. J. Acoust. Soc. Am. 1979, 65, 943–950. [Google Scholar] [CrossRef]
- Andreson, M.; Adali, T.; Li, X.L. Joint blind source separation with multivariate Gaussian model: Algorithms and performance analysis. IEEE Trans. Signal Process. 2012, 60, 1672–1682. [Google Scholar] [CrossRef]
- Boukouvalas, Z.; Fu, G.-S.; Adali, T. An efficient multivariate generalized Gaussian distribution estimator: Application to IVA. In Proceedings of the 2015 49th Annual Conference on Information Sciences and Systems (CISS), Baltimore, MD, USA, 18–20 March 2015. [Google Scholar]
- Hummersone, C. A Psychopsychoacoustic Engineering Approach to Machine Sound Source Separation in Reverberant Environments. Ph.D. Thesis, University of Surrey, Guildford, UK, 2011. [Google Scholar]
- ISO 3382-2: 2008. Acoustics. Measurements of Room Acoustics Parameters, Part 2; ISO: Geneva, Switzerland, 2008. [Google Scholar]
- Shinn-Cunningham, B.; Kopco, N.; Martin, T. Localizing nearby sound sources in a classroom: Binaural room impulse responses. J. Acoust. Soc. Am. 2005, 117, 3100–3115. [Google Scholar] [CrossRef]
- Hu, Y.; Loizou, P.C. Evaluation of Objective Quality Measures for Speech Enhancement. IEEE Trans. Audio Speech Lang. Process. 2008, 16, 229–238. [Google Scholar] [CrossRef]
| Sampling rate | 8 kHz |
| STFT frame length | 1024 |
| Reverberation time | 200 ms |
| Room dimensions | 7 m × 5 m × 3 m |
| Source signal duration | 4 s (TIMIT) |
| Room impulse responses | Image method |
| Objective measure | Signal to Distortion Ratio (SDR) |
| Original Super Gaussian | Student’s t Distribution | SMM Source Prior | |
|---|---|---|---|
| Set-1 | 9.09 | 9.84 | 10.27 |
| Set-2 | 8.98 | 9.72 | 10.24 |
| Set-3 | 9.26 | 10.11 | 10.87 |
| Set-4 | 9.02 | 9.95 | 10.49 |
| Set-5 | 9.53 | 10.21 | 10.62 |
| Set-6 | 9.51 | 10.14 | 10.74 |
| Set-7 | 8.91 | 9.67 | 10.09 |
| Set-8 | 9.86 | 10.48 | 11.05 |
| Set-9 | 9.94 | 10.66 | 11.24 |
| Set-10 | 10.02 | 10.56 | 11.01 |
| Sampling rate | 8 kHz |
| STFT frame length | 1024 |
| Velocity of sound | 343 m/s |
| Reverberation time | 565 ms (BRIRs) |
| Room dimensions | 9 m × 5 m × 3.5 m |
| Source signal duration | 3.5 s (TIMIT) |
| GMM Source Prior | SMM Source Prior | Percentage Improvement | |
|---|---|---|---|
| Angle- | 4.51 | 4.82 | 6.87% |
| Angle- | 4.62 | 4.97 | 7.56% |
| Angle- | 4.77 | 5.09 | 6.70% |
| Angle- | 4.97 | 5.32 | 7.04% |
| Angle- | 4.91 | 5.28 | 7.73% |
| Angle- | 4.77 | 5.12 | 7.34% |
| GMM Source Prior | SMM Source Prior | |
|---|---|---|
| Set-1 | 1.85 | 2.02 |
| Set-2 | 1.98 | 2.11 |
| Set-3 | 1.96 | 2.13 |
| Set-4 | 2.02 | 2.19 |
| Set-5 | 1.93 | 2.14 |
| Set-6 | 2.08 | 2.21 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rafique, W.; Chambers, J.; Sunny, A.I. An Expectation–Maximization-Based IVA Algorithm for Speech Source Separation Using Student’s t Mixture Model Based Source Priors. Acoustics 2019, 1, 117-136. https://doi.org/10.3390/acoustics1010009
Rafique W, Chambers J, Sunny AI. An Expectation–Maximization-Based IVA Algorithm for Speech Source Separation Using Student’s t Mixture Model Based Source Priors. Acoustics. 2019; 1(1):117-136. https://doi.org/10.3390/acoustics1010009
Chicago/Turabian StyleRafique, Waqas, Jonathon Chambers, and Ali Imam Sunny. 2019. "An Expectation–Maximization-Based IVA Algorithm for Speech Source Separation Using Student’s t Mixture Model Based Source Priors" Acoustics 1, no. 1: 117-136. https://doi.org/10.3390/acoustics1010009
APA StyleRafique, W., Chambers, J., & Sunny, A. I. (2019). An Expectation–Maximization-Based IVA Algorithm for Speech Source Separation Using Student’s t Mixture Model Based Source Priors. Acoustics, 1(1), 117-136. https://doi.org/10.3390/acoustics1010009





