Enhanced Prediction of Bond Strength in Corroded RC Structures Using Advanced Feature Selection and Ensemble Learning Framework

Abstract

Bond behavior between steel bars and concrete is fundamental to the structural integrity and durability of reinforced concrete. However, corrosion-induced deterioration severely impairs bond performance, highlighting the need for advanced and reliable assessment methods. This paper pioneers an algorithm for an advanced ensemble learning framework to predict bond strength between corroded steel bars and concrete. In this framework, a novel Stacked Boosted Bond Model (SBBM) is developed, in which a Fusion-Based Feature Selection (FBFS) strategy is integrated to optimize input variables, and SHapley Additive exPlanations (SHAP) are employed to enhance interpretability. A merit of the framework is that it can effectively identify critical factors such as crack width, transverse confinement, and corrosion level, which have often been neglected by traditional models. The proposed SBBM achieves superior predictive performance, with a coefficient of determination (R²) of 0.94 and a mean absolute error (MAE) of 1.33 MPa. Compared to traditional machine learning and analytical models, it demonstrates enhanced accuracy, generalization, and interpretability. This paper provides a reliable and transparent tool for structural performance evaluation, service life prediction, and the design of strengthening measures for corroded reinforced concrete structures, contributing to safer and more durable concrete structures.

1. Introduction

Reinforced concrete (RC) is an essential material in civil engineering, widely used in structures like bridges, buildings, and dams. The bond behavior between steel bars and concrete is critical to the structural load-bearing capacity, failure mechanisms, and durability [1,2,3]. The bond performance at the steel–concrete interface is governed by multiple factors, including concrete cover, steel bar diameter, surface smoothness (e.g., deformed), transverse reinforcement (stirrups), concrete properties (e.g., concrete strength and cementitious materials type), load, and exposure conditions (e.g., freeze–thaw cycles) [4,5,6,7,8,9,10]. Among these factors, steel corrosion is one of the most severe deterioration mechanisms for bond loss in RC structures, especially for low-strength concrete with plain round steel bars [11]. Corrosion not only weakens the steel–concrete bond but also degrades the mechanical properties of both materials. The volumetric expansion of corrosion products generates radial pressure around the steel bars, which subsequently induces cracks in the surrounding concrete and further accelerates bond deterioration [1].

Research on bond behavior can be broadly categorized into three groups [12,13]: (i) Experimental studies explore bond degradation under different corrosion conditions using laboratory methods such as accelerated electrochemical corrosion and simulated climate conditions [4,7]. These studies aim to establish correlations between corrosion levels and bond performance but are often limited by dataset scale and generalizability. (ii) Analytical studies develop models based on elasticity, fracture mechanics, and damage mechanics to describe the stress transfer mechanism and cracking behavior induced by corrosion expansion [13,14]. However, these models often struggle to incorporate environmental complexities and inevitable simplifications. (iii) Numerical simulations apply finite element methods to model the damage process caused by corrosion product expansion and stress redistribution. While effective for localized analysis, these approaches require extensive computational resources and are sensitive to parameter assumptions [6,15].

Despite extensive studies on corrosion-induced bond degradation, significant research gaps remain, particularly in developing predictive models. Traditional methods, often rely on regression analysis to establish mathematical relationships. While computationally efficient, these methods fail to capture complex nonlinear interactions between corrosion parameters, concrete properties, steel bar configuration, and confinement conditions. Constitutive models attempt to describe the stress transfer mechanism at the steel–concrete interface from the perspective of material mechanics, and hence struggle with the randomness of corrosion processes and environmental influences, which may limit their practical applicability [2,13].

The rapid advancement of machine learning (ML) has enabled the development of data-driven models that can capture nonlinear and high-dimensional relationships in engineering problems. Recent studies have shown that [16,17,18,19] ML techniques outperform conventional methods in terms of accuracy and efficiency. However, several challenges hinder their full potential: (i) Limited dataset construction and insufficient consideration of key influencing factors (e.g., corrosion-induced crack and confinement) restrict model generalization. (ii) Suboptimal feature selection methods. Current ML research applies single feature selection techniques, such as correlation-based filtering or tree-based importance analysis. This may result in the exclusion of critical variables or the inclusion of redundant ones. (iii) Inconsistent target variable selection. Some models predict relative bond strength with uncorroded bond strength as a reference [18,19], which may not fully reflect the full extent of corrosion effects on bond degradation. (iv) Limited model fusion and interpretability. The majority of previous work focuses on individual ML algorithms without adopting ensemble strategies, which restricts predictive accuracy. Additionally, ML models often function as “black boxes” [17], offering minimal interpretive value regarding the driving factors behind bond strength. This lack of transparency reduces confidence and hinders practical application in engineering structures.

To overcome these issues, this paper develops an algorithm for an advanced feature selection and ensemble learning framework to predict bond strength. The framework is systematically compared with analytical models for its accuracy and generalization. The main contributions of this paper are as follows: (i) Development of a high-quality dataset. A comprehensive data mining was conducted to establish a robust dataset that incorporates a wide range of influential variables. Particular attention was given to corrosion-induced cracking and transverse confinement, which have often been neglected previously. (ii) Fusion-Based Feature Selection (FBFS) method. A novel multi-strategy feature selection technique was developed by integrating Feature Correlation Analysis (FCA), Random Forest Feature Importance (RFFI), and Backward Feature Elimination (BFE) into a unified framework to enhance model stability. (iii) Stacked Boosted Bond Model (SBBM). It integrates five high-performing base learners, each previously validated for bond strength prediction, with Categorical Boosting (CatBoost) as the meta-learner. Comparative evaluation confirms the superior accuracy of SBBM over individual ML models. (iv) SHapley Additive exPlanations (SHAP)-based interpretability analysis. The application of SHAP enables the quantification of feature contributions and interactions, which improves the model’s interpretability and clarity.

The originality of this research lies in the development of an efficient, interpretable, and engineering-oriented ML framework for predicting the degradation of bond strength between steel rebars and concrete. Unlike previous methods, this framework explicitly incorporates high-quality, corrosion-representative data—including corrosion-induced cracking and transverse confinement, which are often overlooked—together with a fusion-based feature selection strategy and SHAP-driven interpretability. This holistic integration not only enhances predictive performance but also provides clear mechanistic insights aligned with structural engineering principles. Numerical results demonstrate that the newly developed AI-based algorithm surpasses existing models in terms of predictive accuracy, stability, and interpretability. This work provides a robust scientific foundation for performance evaluation, service life prediction, and structural strengthening of corroded RC structures, contributing to safer and more durable RC structures.

2. Bond Strength of Corroded RC Structures

2.1. Influencing Factors

Bond strength is a critical parameter in assessing the behavior of corroded RC structures. It is defined as the average bond stress along the bonded length, typically determined through pullout or beam tests and expressed as follows [20]:

$${\tau }_u=P_u/(\pi d_b{l}_b)$$

(1)

where τ_u is the average bond stress (MPa); P_u is the pullout load (N); d_b is the steel bar diameter (mm); and l_b is the bond length between steel bars and concrete (mm).

Previous studies have consistently identified concrete strength, concrete cover, stirrups, steel bar diameter, bond (embedded) length, and rebar position as key determinants of bond strength [4,5,6,7,8,9,10]. Specifically, bond strength is positively correlated with the concrete strength, particularly for deformed rebars, where mechanical interlocking is a dominant mechanism. The surface characteristics also play a crucial role, with deformed rebars exhibiting higher strength than plain ones due to enhanced mechanical interlock. Variations in rib size and angle further influence the interlocking effect. Additionally, larger diameters tend to reduce bond strength per unit area, while longer bond lengths may lead to non-uniform stress distribution, lowering average bond strength. Concrete cover contributes to confinement, delaying crack formation and maintaining bond performance even under corrosive conditions. Once cracking occurs, stirrups provide transverse constraint, improving anchorage capacity [4,13,19].

Rebar corrosion affects bond strength by altering the steel–concrete interface. At early stages, corrosion products increase surface roughness, which may temporarily enhance frictional resistance. However, as corrosion progresses, interlock loss and corrosion products’ expansion induce radial pressure on the surrounding concrete. This process often results in cover cracking and spalling. In the absence of sufficient confinement, such deterioration accelerates, leading to a reduction in bond strength. Furthermore, corrosion degrades the mechanical properties of the steel rebars, impairs load transfer efficiency, and further weakens the bond performance.

2.2. Existing Analytical Models

To quantify the degradation of bond strength due to steel corrosion, the relative bond strength, R_τ(η), is widely used and defined as [19]:

$$R_{\tau }(\eta )={\tau }_u(\eta )/{\tau }_{u,0}$$

(2)

where τ_u(η) and τ_u,0 denote the bond strength of corroded and uncorroded steel bars (MPa), respectively, and $\eta$ is corrosion level (%).

A summary of representative analytical models for bond strength as a function of corrosion level is provided in

Table 1. Existing analytical models for determining bond strength with corrosion effects.

Literature	Analytical Model
Cabrera (1996) [25]	$R_{\tau }(\eta )=1-5.6\eta$
Stanish et al. (1999) [26]	$R_{\tau }(\eta )=1-3.5\eta$
Yuan et al. (1999) [27]	$R_{\tau }(\eta )=1-(10.544-1.586{\displaystyle \frac{c}{d}})\eta$
Lee et al. (2002) [28]	${\tau }_u(\eta )=5.21e^{-5.61\eta }$, $R_{\tau }(\eta )=e^{-5.61\eta }$
Chung et al. (2004) [21]	$R_{\tau }(\eta )=\left\{\begin{array}{ll}1,& \eta \le 2.0\%\\ 2.09{\eta }^{-1.06},& \eta >2.0\%\end{array}\right.$
Bhargava et al. (2008) [22]	$R_{\tau }(\eta )=\left\{\begin{array}{ll}1.0,& \eta \le 1.5\%\\ 1.192e^{-0.117(\eta -1.5)},& \eta >1.5\%\end{array}\right.\hspace{1em}(\mathrm{Pullout} \mathrm{test})$ $R_{\tau }(\eta )=\left\{\begin{array}{ll}1.0,& \eta \le 1.5\%\\ 1.346e^{-0.198(\eta -1.5)},& \eta >1.5\%\end{array}\right.\hspace{1em}(\mathrm{Flexural} \mathrm{test})$
Kivell et al. (2012) [23]	$R_{\tau }(\eta )=\left\{\begin{array}{ll}1,& \eta \le 2.4\%\\ 1.2e^{-0.076(\eta -2.4)},& \eta >2.4\%\end{array}\right.$
Lin and Zhao (2016) [4]	$\begin{array}{l}{R}_{\tau }(\eta )=\left\{\begin{array}{ll}1,& \eta \le 1.5\%\\ e^{-\delta (\eta -1.5\%)},& \eta >1.5\%\end{array}\right.\\ \mathrm{where} \delta ={\displaystyle \frac{13.28-0.57c/d}{43.54A_{st}/(n\cdot d\cdot s)+1}}\end{array}$
Zhang et al. (2016) [29]	$R_{\tau }(\eta )=1-\left[\left(10.544-1.586{\displaystyle \frac{c}{d}}\right)-5.61\right]\eta$
Ma et al. (2017) [24]	$R_{\tau }(\eta )=\left\{\begin{array}{ll}1,& \eta \le 2.41\%\\ 1.68{\eta }^{-0.59},& \eta >2.41\%\end{array}\right.$
Guo (2022) [30]	${\tau }_{u,0}=1.06{\left(f_c\right)}^{0.588}$, ${\tau }_u(\eta )=1.06\cdot {\left(f_c\right)}^{0.588}\cdot e^{-3\eta }$

. As shown, most models adopt either linear or exponential relationships to characterize bond degradation trends. Due to discrepancies in experimental setups, specimen geometries, and corrosion acceleration methods, the critical corrosion threshold, typically associated with the onset of corrosion-induced surface cracking, varies significantly among studies, ranging from 1.5% to 2.41% [4,21,22,23,24]. This threshold often aligns with the onset of a visible crack on the concrete surface and is influenced by multiple factors, such as concrete cover, concrete strength, rebar diameter, and applied current density.

$$\delta ={\delta }_c\cdot {\delta }_{\xi }\cdot {\delta }_i=\left\{\begin{array}{ll}{\displaystyle \frac{k_1+k_2(c/d)}{k_4{\xi }_{st}+1}},& i\le 200 \mu {\mathrm{A}/\mathrm{cm}}^2\\ {\displaystyle \frac{k_1+k_2(c/d)}{k_4{\xi }_{st}+1}}\left[k_3\ln \left({\displaystyle \frac{i}{200}}\right)+1.0\right],& i>200 \mu {\mathrm{A}/\mathrm{cm}}^2\end{array}\right.$$

(3)

$${\xi }_{st}={\displaystyle \frac{A_{st}}{n_b{s}_{st}{d}_b}}$$

(4)

where k₁, k₂, k₃, and k₄ are empirical parameters; c/d is the cover-to-diameter ratio; i is the current density (μA/cm²); A_st is the total stirrup area at the splitting plane (mm²); n_b is the number of tensile steel bars; and s_st is the stirrup spacing (mm).

While some models [21,22,23,24,25,26,28] focus exclusively on the direct relationship between corrosion level and bond strength loss, others [4,27,29,30] attempt to account for additional parameters such as concrete cover, rebar size, cover-to-diameter ratio, and stirrup confinement. Notably, Lin et al. [4] introduced a degradation coefficient δ (Equation (3)) that explicitly incorporates such parameters. Their model quantifies the confinement effect through a stirrup confinement index, ξ_st, and introduces a correction factor, δ_i, to capture the influence of corrosion current density during accelerated corrosion testing. This method offers a more theoretical and practical formulation for engineering applications.

Despite decades of research, existing models remain constrained by several fundamental shortcomings that hinder their applicability to complex and realistic scenarios. Most notably, the reliance on oversimplified linear or exponential formulations limits their ability to capture the inherently nonlinear and progressive nature of bond degradation, especially under advanced stages of corrosion and cracking. Furthermore, the strong empirical dependence of these models on narrowly defined experimental conditions, such as fixed concrete strength ranges, specific rebar types, or controlled corrosion levels, significantly reduces their generalizability. The coupled influence of key structural and environmental parameters, such as stirrup confinement, concrete cover, corrosion-induced cracking, and current density, is seldom quantified in a unified framework. Moreover, current analytical models remain disconnected from emerging data-driven methods, overlooking the potential of machine learning and hybrid modeling to enhance predictive performance and adaptability.

To bridge these critical gaps, this paper develops an innovative algorithm for a framework that synthesizes mechanistic insights with data-driven techniques, with the objective of delivering more accurate, robust, and broadly applicable predictions of bond strength deterioration in corroded RC structures.

3. Methodology for Algorithm Development

To address the limitations in current models for bond strength, this paper develops an algorithm for an advanced ensemble learning framework to predict bond strength between corroded steel bars and concrete, as illustrated in Figure 1. This framework incorporates data-driven techniques into a structured pipeline that includes data preparation, feature selection, model development, and interpretability analysis. The process begins with data preprocessing and the implementation of a Fusion-Based Feature Selection (FBFS) method to extract the most informative variables and eliminate redundancy. This step facilitates the development of the Stacked Boosted Bond Model (SBBM), which integrates multiple high-performing base learners through a hierarchical ensemble strategy to enhance predictive performance. For improved model transparency, the SHAP technique is employed to quantify the importance and interaction of input variables. Finally, the model’s performance is evaluated against traditional analytical approaches. The following subsections provide a detailed description of each component in this framework.

3.1. Data Preparation

To develop a reliable bond strength prediction model, a high-quality dataset is essential. In this paper, 386 experimental results were collated from carefully selected, peer-reviewed sources [4,12,31,32,33,34,35,36,37,38,39,40]. The selection criteria for these references include: (i) comprehensive experimental setups providing detailed and reliable measurements related to corroded steel–concrete bond behavior; (ii) the inclusion of key variables critical to corrosion effects, such as corrosion level, confinement coefficient, and corrosion-induced crack width; and (iii) well-documented and diverse test conditions. These data form a comprehensive dataset comprising nineteen input variables and one output variable, as summarized in

Table 2. Statistical summary of variables for bond slip specimens.

Features	Symbol	Unit	Type	Mean	Std	Max	Min	Category Distribution
Input variables
Water-to-cement ratio	w/c	-	Numeric	0.50	0.10	0.70	0.35	-
Concrete compressive strength	fc	MPa	Numeric	32.9	5.3	40.0	19.8	-
Bottom cover	c1	mm	Numeric	56.13	25.82	112.5	12.00	-
Side cover	c2	mm	Numeric	61.93	23.57	112.5	12.00	-
Rebar type	BT	-	Categorical	-	-	-	-	Plain: 8%; Deformed: 92%
Bond length	la	mm	Numeric	124.50	88.61	300.00	28.00	-
Number of steel bars	nb	-	Numeric	1.30	0.43	2.00	1.00	-
Steel bar diameter	db	-	Numeric	17.04	4.28	25.00	10.00	-
Bond length-to-diameter ratio	la/db	-	Numeric	7.84	6.61	25.00	2.00	-
Bottom cover-to-diameter ratio	c1/db	-	Numeric	3.36	1.37	4.85	1.00	-
Side cover-to-diameter ratio	c2/db	-	Numeric	3.66	1.13	4.85	1.00	-
Stirrup diameter	dst	mm	Numeric	3.04	3.26	8.00	0.00 *	-
Stirrup spacing	sst	mm	Numeric	31.32	38.81	150.00	0.00 *	-
Total stirrup area	Ast	mm2	Numeric	31.22	35.32	100.50	0.00 *	-
Transverse confinement coefficient	Kst	-	Numeric	0.027	0.037	0.157	0.00 *	-
Stirrup yield strength	fyt	MPa	Numeric	147.9	171.2	400.0	0.00 *	-
Corrosion current density	i	mA/cm2	Numeric	1122	3629	200	0.00 #	-
Corrosion level	CL	%	Numeric	6.63	6.85	36.95	0.00 #	-
Mean corrosion crack width	wavg	mm	Numeric	0.55	0.92	7.59	0.00 #	-
Output variable
Bond strength	τu	MPa	Numeric	12.77	8.94	40.10	0.50	-

Note: The superscript ‘*’ indicates no stirrups and ‘#’ denotes uncorroded steel bars’ bond performance, improving the model’s robustness and its ability to capture complex degradation mechanisms at the steel–concrete interface.

. Key variables include corrosion level, concrete strength, rebar diameter, bond length, confinement coefficient, and corrosion-induced crack width. Special attention is devoted to confinement and corrosion-induced cracking, which have often been overlooked in previous research. Their inclusion enables a more comprehensive representation of corrosion effects on bond performance, improving the model’s robustness and its ability to capture complex degradation mechanisms at the steel–concrete interface.

To further understand the dataset, Figure 2 visualizes the distribution of these variables. Specifically, Figure 2j shows that about 60% of the samples have a confinement coefficient of 0, indicating a balanced representation of both confined and unconfined cases. Figure 2l illustrates a wide range of corrosion levels, covering mild to severe deterioration. The relative frequency gradually decreases with increasing corrosion, which aligns with real-world observations. Figure 2k indicates that most corrosion-induced crack widths fall within 0–2 mm, remaining below the thresholds of typical durability design. These distributions will enable that the model is trained on representative structural conditions and can effectively capture corrosion-induced bond degradation.

Although Figure 2 includes fitted curves (red dashed lines) to visually illustrate the distribution patterns, these curves are intended solely for illustrative purposes and are not applied for inferential statistical modeling. Certain variables, such as crack width or number of rebars, appear concentrated within specific ranges. Thus, efforts were made to ensure that the dataset reflects a representative spectrum of corrosion scenarios and structural configurations. This was achieved by integrating data from various experimental sources, which helps reduce potential biases caused by the predominance of individual variables.

3.2. Fusion-Based Feature Selection (FBFS) Method

To achieve an optimal feature subset, a Fusion-Based Feature Selection (FBFS) strategy was developed to integrate multiple feature selection techniques. The purpose of this hybrid method is to eliminate redundant or irrelevant variables while retaining those with significant predictive power. The FBFS framework comprises the following three components: (i) Feature Correlation Analysis (FCA) [41]. Pearson correlation coefficients were computed to detect multicollinearity between input features. Features exhibiting strong correlation (|r| > threshold) were considered redundant, and one from each correlated pair was removed. This step ensures statistical independence among features, improving model stability and reducing overfitting risks. (ii) Random Forest Feature Importance (RFFI) [42]. A random forest model was utilized to evaluate the relative importance of each feature based on impurity reduction (e.g., Gini importance or MSE decrease). Features consistently showing low importance were flagged as noise and excluded. This non-parametric, nonlinear method captures complex interactions that traditional metrics might overlook. (iii) Backward Feature Elimination (BFE) [43]. Starting from the full feature set, this wrapper-based method recursively removes the least contributing feature (evaluated via cross-validated performance metrics such as Negative Mean Squared Error, NMSE). The process stops when model performance no longer improves or begins to decline. BFE provides a task-specific refinement tailored to the learning algorithm.

By integrating these three strategies, the FBFS ensures that only the most relevant and informative features are retained, leading to a more robust, efficient, and interpretable feature subset. Moreover, it mitigates the risk of overfitting and preserves essential predictive information, which enhances reliability across various datasets and scenarios.

3.3. Development of Stacked Boosted Bond Model (SBBM)

In this paper, the output variable is the bond strength (denoted by τ_u in Table 2), which is predicted based on selected input features obtained through the FBFS optimization process. To effectively capture the complexity and nonlinearity of the corrosion–bond relationship in concrete, a Stacked Boosted Bond Model (SBBM) is developed. Instead of relying solely on off-the-shelf software tools, the model is built through a structured and optimized ensemble learning pipeline that integrates algorithmic diversity, structural domain knowledge, and systematic optimization.

The SBBM employs a two-layer architecture. In the first layer, five diverse base learners, i.e., Random Forest (RF), Extreme Gradient Boosting (XGBoost), Light Gradient Boosting Machine (LightGBM), Gradient Boosting Regression Tree (GBRT), and Adaptive Boosting (AdaBoost) [16,17,18,19], are trained independently using k-fold cross-validation to ensure generalization. Each base model receives the same preprocessed feature set and is trained to capture different aspects of the data distribution. Their out-of-fold predictions are then collected to form a new feature matrix, which serves as input to the second-layer meta-learner. At the second layer, Categorical Boosting (CatBoost) [16] is adopted as the meta-learner due to its robustness against overfitting, ability to capture high-order interactions, and efficiency in handling heterogeneous feature types. This stacking mechanism allows the model to leverage the strengths of individual learners while minimizing their weaknesses. To further improve model performance and avoid manual tuning, Bayesian optimization is used to fine-tune the hyperparameters of both base learners and the meta-learner. This probabilistic optimization strategy efficiently navigates the hyperparameter space, resulting in improved convergence, reduced training time, and superior prediction accuracy.

Overall, the proposed SBBM demonstrates not only enhanced predictive accuracy but also strong generalizability across varying corrosion levels and specimen configurations. The modular design of the stacking framework allows for future integration of domain-specific knowledge and additional feature interactions, providing a scalable and adaptable tool for bond strength prediction under corrosion conditions.

3.4. Explainability and Evaluation of Stacked Boosted Bond Model (SBBM)

Although a machine learning model can achieve excellent performance in predicting the bond strength, its high complexity renders it a “black box”, making it challenging to interpret its outputs. Some methods have been proposed to enhance the interpretability of ML-based models, one of which is the SHAP technique, introduced by Lundberg and Lee [44]. SHAP is developed based on game theory and calculates an importance score or SHAP value for each input variable. Moreover, SHAP values enable ranking input variables in descending order of their impact on the response variable, where features with higher SHAP values are considered more influential and those with lower values contribute less. Therefore, this paper employs SHAP to interpret the output results and rank input features based on their contributions to model output, providing deeper insights into the underlying mechanisms governing bond behavior in corroded RC structures.

Moreover, to assess the effectiveness of the developed ML model, its performance is compared against five base learners, as well as existing formulas. The criteria for evaluation include accuracy, robustness, and prediction stability, using key metrics such as R², RMSE, MAE, and MAPE. R² measures the proportion of variance explained by the model, with values closer to 1 indicating better predictive power. RMSE and MAE assess the magnitude of prediction errors, with lower values signifying higher accuracy, while MAPE expresses errors as a percentage of actual values, allowing for a scale-independent comparison. Their formulas are as follows [12,17,19]:

$$MAE={\displaystyle \frac{1}{N}}{\displaystyle \sum _{i=1}^N\left|y_i-{\widehat{y}}_i\right|}$$

(5)

$$RMSE=\sqrt{{\displaystyle \frac{1}{N}}{\displaystyle \sum _{i=1}^N{(y_i-{\widehat{y}}_i)}^2}}$$

(6)

$$MAPE={\displaystyle \frac{1}{N}}{\displaystyle \sum _{i=1}^N\left|(y_i-{\widehat{y}}_i)/y_i\right|}$$

(7)

$$R^2=1-{\displaystyle \sum _{i=1}^N{\left({\widehat{y}}_i-y_i\right)}^2}/{\displaystyle \sum _{i=1}^N{\left({\overline{y}}_i-y_i\right)}^2}$$

(8)

where N represents the number of samples; ${[y_1, \dots , y_N]}^T$ and ${[{\widehat{y}}_1, \dots , {\widehat{y}}_N]}^T$ denote the actual output values from the dataset and the predicted value from the model, respectively; and $\overline{y}$ is the mean of actual values.

In contrast to black-box applications, the developed framework reflects an interpretable, scalable, and domain-informed modeling strategy for bond strength deterioration under reinforcement corrosion.

4. Numerical Results and Analysis

4.1. Feature Engineering

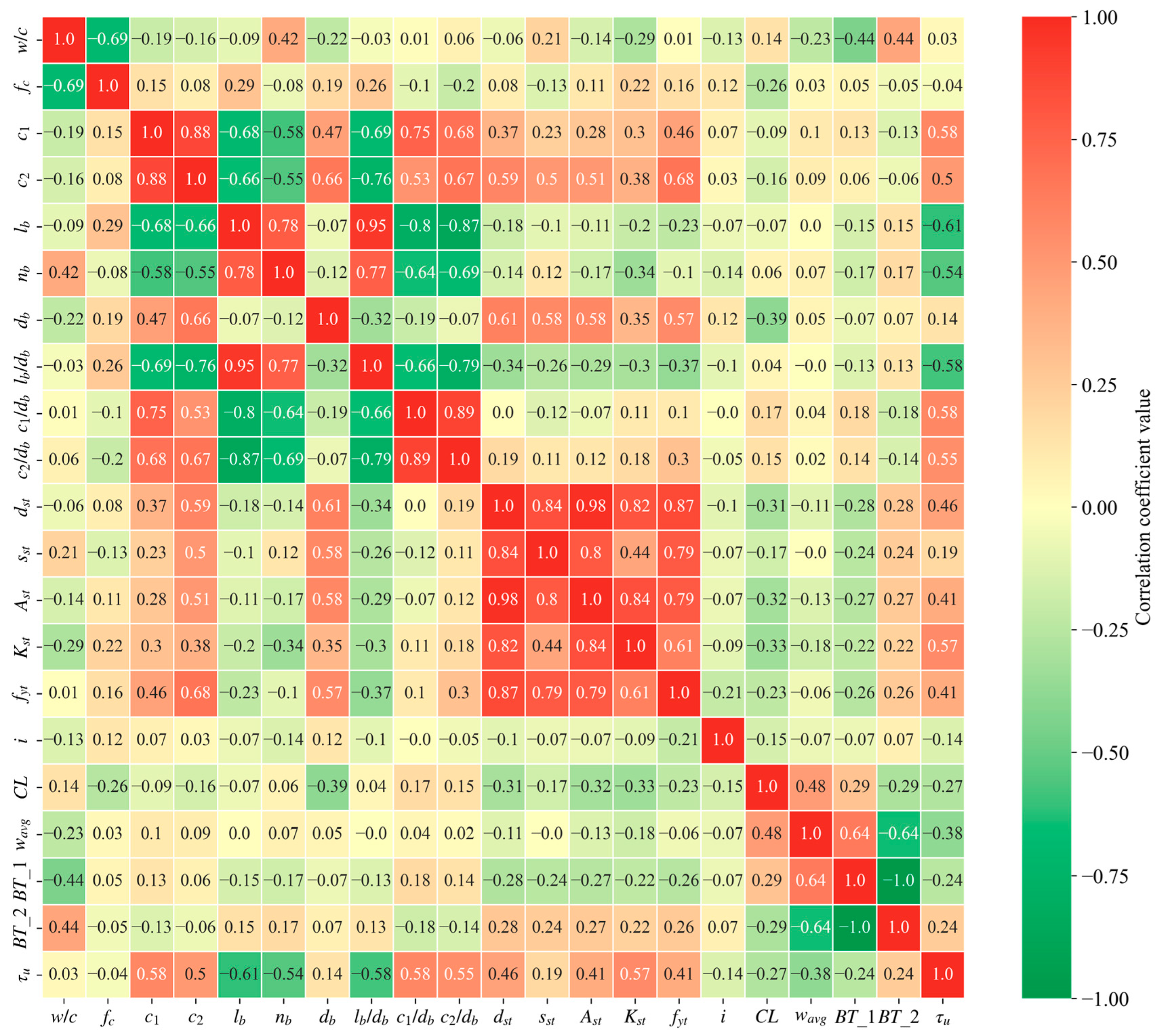
Feature selection is a critical step for model performance, redundancy, and interpretability. The process begins with Feature Correlation Analysis (FCA), which calculates the correlation matrix to identify highly correlated features (Pearson correlation coefficient |r|> 0.80). Figure 3 shows the correlation among input features. A strong correlation appears between bottom cover (c₁) and side cover (c₂), largely due to the inclusion of many central pullout specimens where c₁ equals c₂. Similarly, bond length (l_b) and its ratio to rebar diameter (l_b/d_b) also exhibit high correlation, indicating the need to exclude one of them in later steps to reduce multicollinearity. Notably, the features related to transverse confinement, such as stirrup diameter (d_st), stirrup spacing (s_st), stirrup area (A_st), stirrup yield strength (f_yt), and transverse confinement coefficient (K_st), also show significant correlation. This highlights the importance of identifying the most representative indicator for transverse confinement in the feature selection process.

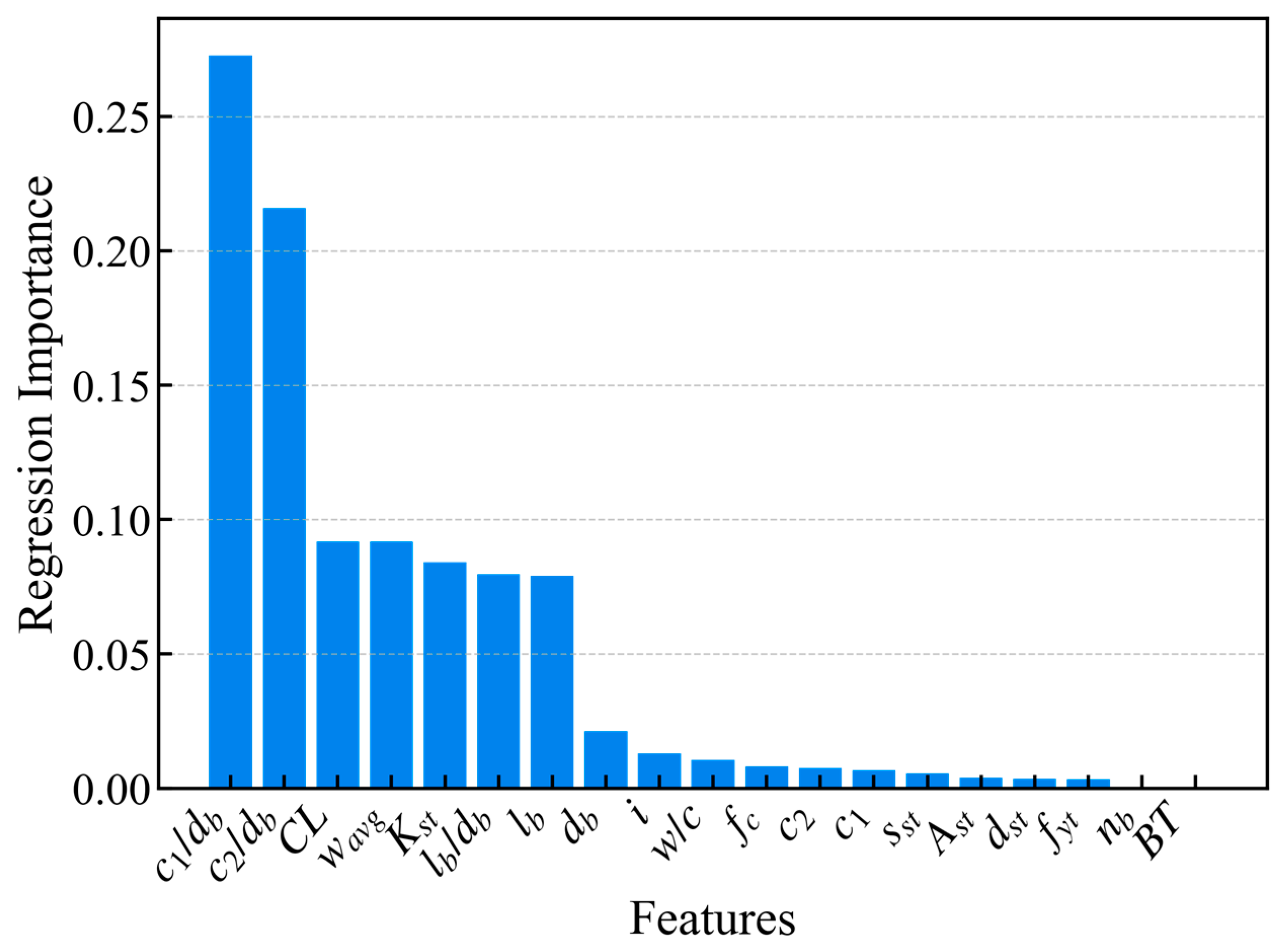
Next, the Random Forest Feature Importance (RFFI) method computes the importance score of each feature and ranks them accordingly. As shown in Figure 4, ten features demonstrate high importance (importance score > 0.01). In addition to commonly used features such as bottom cover-to-diameter ratio (c₁/d_b), corrosion level (CL), bond length to rebar diameter ratio (l_b/d_b), and rebar diameter (d_b), the newly introduced features of corrosion crack width (w_avg) and transverse confinement coefficient (K_st) also show a high importance score, underscoring their significant role in predicting bond strength.

The Backward Feature Elimination (BFE) method is then applied to recursively removes less influential features. The final optimal subset includes only the most relevant inputs. Figure 5 illustrates the variation in model performance with different feature sets. The results indicate that model performance stabilizes once the number of retained features exceeds thirteen.

Finally, FBFS integrates the outcomes from all three methods, effectively removing redundant features and selecting the most relevant variables based on their importance and model performance. The optimized feature subset includes w/c, f_c, c₁, n_b, d_b, l_b/d_b, c₁/d_b, c₂/d_b, s_st, K_st, i, CL, and w_avg. Obviously, the transverse confinement coefficient (K_st) and corrosion crack width (w_avg), which have rarely been considered in previous studies, are found to significantly affect bond strength. The inclusion of these critical variables not only improves the model’s accuracy but also deepens the understanding of the factors related to bond strength. This, in turn, enhances the model’s applicability in engineering.

4.2. Performance of Stacked Boosted Bond Model (SBBM)

This section compares the performance of the SBBM with five base learners: RF, XGBoost, LightGBM, GBRT, and AdaBoost. As shown in Figure 6, the scatter plots illustrate the predicted versus actual bond strength values across all models, with a ±25% error margin iso-line for reference. The data points are more densely concentrated along the 45° line, indicating better accuracy and less dispersion. It can be found that except for AdaBoost, which tends to overestimate bond strength when it is below 5 MPa, the other five models accurately capture the variation patterns of bond strength across the input parameter space. Furthermore, the SBBM exhibits the smallest difference in R² values between the training and testing sets and smallest value in MAE, indicating its superior generalization capability and reduced risk of overfitting. This indicates their strong predictive capabilities, with SBBM demonstrating the most consistent and accurate performance.

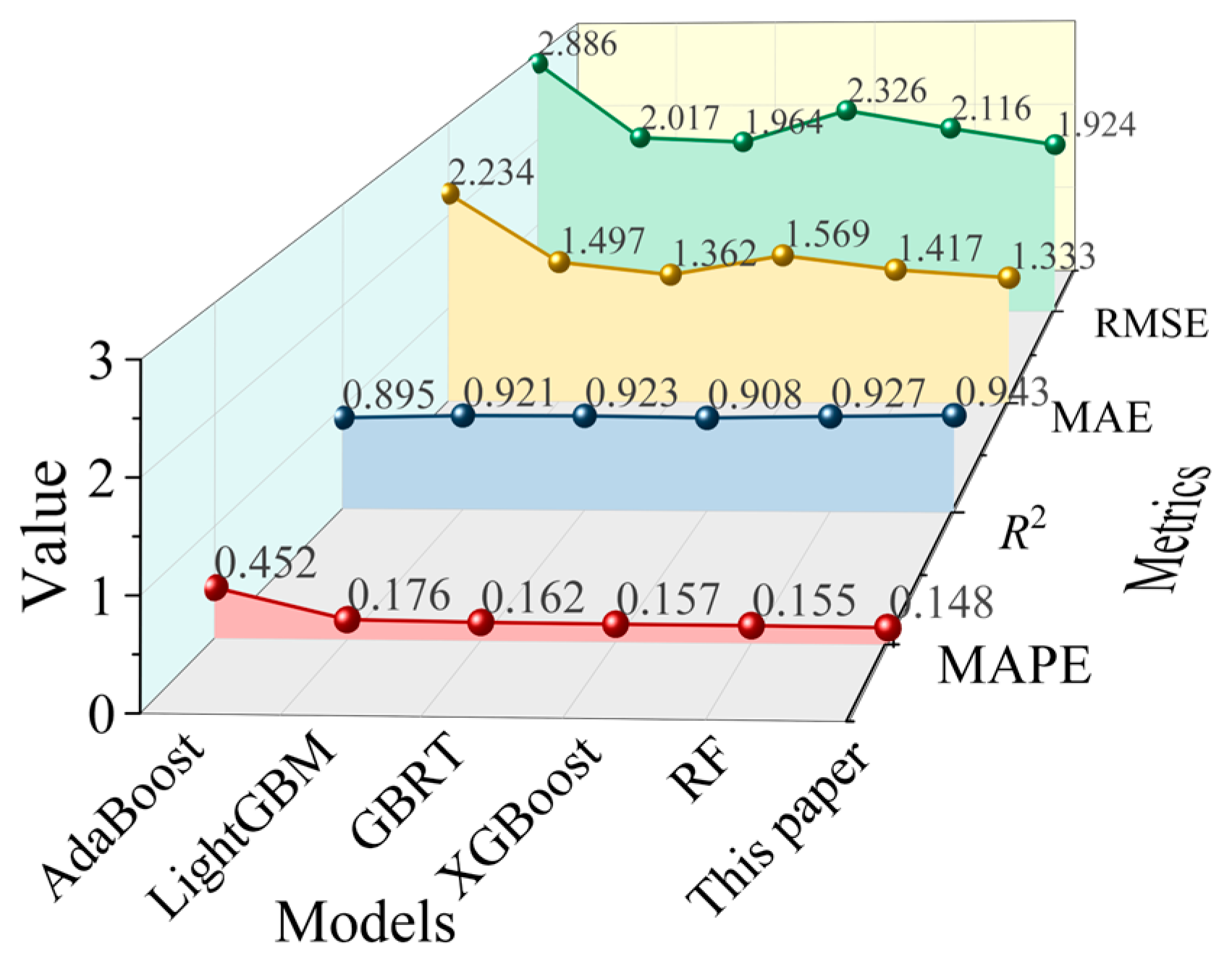
Figure 7 presents the metrics comparing the models on the testing set. All six models exhibit strong predictive capabilities, with R² values exceeding 89% for both training and testing sets, and the majority of data points fall within acceptable error margins. Clearly, these results are consistent with expectations, as the five base learners have been validated in previous studies [16,17,18,19,20], which justifies their selection as base learners in this paper. However, the SBBM still outperforms all individual base learners on the testing set, with the lowest RMSE, MAE, and MAPE values, as well as the highest R² value. This further confirms the SBBM’s superior ability to predict the bond strength of corroded concrete.

4.3. Interpretation of Stacked Boosted Bond Model (SBBM)

Figure 8 illustrates the interpretability results derived from the SHAP method. In Figure 8a, the y-axis ranks the input features in descending order based on their contribution to bond strength, with the most influential feature displays at the top. The x-axis represents the SHAP values, quantifying each feature’s impact on the model output. A color gradient is used to indicate the magnitude of features, where blue denotes lower values and red to pink represent higher values. This visualization enables a clear and intuitive understanding of how different feature magnitudes influence bond strength predictions. Figure 8b presents the mean absolute SHAP values for each input variable, thereby reflecting their global importance. The x-axis represents the mean absolute SHAP values, while the y-axis lists the variables ranked by importance. Longer bars signify a greater overall influence on bond strength prediction.

As shown, the bottom cover-to-diameter ratio (c₁/d_b) and transverse confinement coefficient (K_st) are identified as the most influential feature, both contributing positively to bond strength. Specifically, an increased bottom cover-to-diameter ratio enhances the concrete’s crack resistance and improves stress transfer efficiency, while greater transverse confinement mitigates crack propagation, reinforces mechanical interlocking, and increases interfacial shear stiffness. Notably, the corrosion level (CL) and corrosion-induced crack width (w_avg) are found to have a profound negative impact. This is consistent with mechanical theory, as higher corrosion levels result in expansive stresses that induce cracking and reduce friction, mechanical interlocking, and confinement efficiency. It is also worth noting that the relationship between corrosion and bond strength is non-monotonic. Mild corrosion can enhance bond strength through increased roughness and mechanical interlock, as reported in previous experimental studies. Although SHAP values show a generally negative trend for corrosion-related features, localized red points with positive SHAP values for low corrosion levels (CL) can be observed in Figure 8a. These subtle positive contributions reflect the initial strengthening effect of light corrosion, which is later offset as degradation progresses.

Collectively, the SHAP-based interpretability is consistent with structural mechanics, providing a physically meaningful explanation of how corrosion-related and structural parameters influence bond behavior. This enhances the model’s credibility and offers insight for practical engineering applications.

4.4. Comparison with Analytical Models

As previously discussed, the SBBM demonstrates the highest prediction accuracy in estimating bond strength. To further assess its practical applicability, a comparative analysis was conducted between the SBBM and analytical models listed in Table 1. The comparison highlights the advantages of data-driven machine learning approaches over conventional empirical formulations. As illustrated in Figure 9, for bond strength values below 10 MPa, most analytical models perform relatively well with predictions closely clustered around the 45° line. However, as bond strength increases, the data points progressively deviate downward from the 45° line, which indicates a rise in prediction errors at higher strength levels. Among the evaluated analytical models, only those proposed by Kivell et al. [23] and Lin and Zhao [4] achieve R² values exceeding 0.60, while the others fall below this threshold. This discrepancy can be attributed to two primary factors: (i) the small dataset size and narrow variable range used during model development; and (ii) heavy reliance on relative bond strength assumptions, which are inherently sensitive to baseline model accuracy for uncorroded specimens.

Figure 10 provides a comprehensive comparison between the SBBM and analytical models, with relative values of four metrics. These metrics, R², RMSE, MAE, and MAPE, are normalized such that the SBBM is set to a baseline of 1, with a total sum of 4. Compared to analytical models, the SBBM consistently yields the lowest RMSE, MAE, and MAPE values and the highest R² value, with superior predictive performance. As a result, the SBBM is represented by the lower bar heights in Figure 10, further highlighting its minimal prediction error and enhanced generalization capability.

The remarkable ability of the SBBM to process large-scale, heterogeneous datasets allows it to capture complex nonlinear relationships and intricate interactions among multiple parameters, such as corrosion-induced crack width, transverse confinement coefficient, and corrosion level. In contrast, traditional analytical models, typically developed from small-scale experimental data, are inherently limited by the narrow scope of input variables and testing conditions. This makes it challenging for such models to capture the intricate and coupled effects of corrosion-related parameters. These findings underscore the superior robustness and practical applicability of the SBBM in predicting the bond strength of corroded RC structures.

5. Conclusions

This paper develops an advanced ensemble learning framework integrating the Stacked Boosted Bond Model (SBBM) with a novel Fusion-Based Feature Selection (FBFS) strategy to predict the bond strength between corroded steel bars and concrete. The proposed SBBM achieved high predictive accuracy, with R² exceeding 94% and significant reductions in RMSE, MAE, and MAPE compared to individual base learners and analytical models. The use of SHapley Additive exPlanations (SHAP) enhanced the model’s transparency, identifying critical factors such as corrosion crack width, transverse confinement, and corrosion level, which are often overlooked by traditional approaches. The main contributions of the paper are: (i) the incorporation of corrosion-related features into a robust prediction framework, (ii) the development of an effective feature selection method, balancing feature importance and redundancy, and (iii) improved interpretability, clarifying the mechanisms of bond degradation due to corrosion.

Furthermore, although the current model is trained on experimental data derived from ordinary concrete, the proposed framework is inherently data-driven and not limited by specific concrete types. This makes it readily extensible to alternative concrete systems, including those incorporating recycled aggregates, steel slag, or supplementary cementitious materials (SCMs), all of which are increasingly relevant for sustainable construction. Nevertheless, extending the model’s applicability to such materials requires careful consideration of their distinct physicochemical properties and their influence on bond degradation mechanisms. Future research should focus on compiling representative datasets and, where necessary, introducing material-specific descriptors to ensure accurate generalization across diverse concrete types.