Abstract
In 2022, a working party (fib TG 8.9.3) was formed to try and better develop critical chloride (Ccrit) distributions for use in modelling new structures and assessing existing structures. The authors of this paper are leading TG 8.9.3. and are in the process of writing a Bulletin (the Bulletin) that will detail how Ccrit values have been developed since the 1970s. The Bulletin notes that chloride-induced corrosion initiation modelling based on Ccrit is not intended as a sole durability assessment tool for structures exposed to chloride. It is recognized that voids and moisture at the bar can control corrosion activation virtually independent of chloride content, but in most cases sufficient voids and moisture are present so that the arrival of adequate chloride triggers corrosion activation of the reinforcement. So, durability verification by modelling restriction of chloride penetration, so that the concentration at the bar is less than that commonly found to cause corrosion, seems appropriate. This empirical approach was first fully detailed in fib Bulletin 34 A key part in the empirical model is the ‘adequate chloride to trigger corrosion activation’ Ccrit. Although Ccrit has a wide distribution and has different distributions in different environments and concrete compositions, its use in modelling provides greater design flexibility and improved confidence compared to the Deemed-to-Satisfy (DtS) rules included in most codes. Because of the limitations in DtS provisions, modelling provides more effective designs by incorporating specific criteria for a broad range of exposures, materials, and construction methods. This paper proposes that a lower bound for Ccrit distributions for a range of materials and exposures can be developed from published papers. This paper includes Ccrit distributions for steel fibres, carbon steel (above and below water), high tensile steel, galvanized steel, and stainless steels. These are expected to be recommended in the Bulletin.
1. Introduction
National codes for chloride exposure typically provide limited Deemed-to-Satisfy (DtS) requirements. These standards are conservative by nature, assuming worst-case conditions—such as the highest temperatures, most severe chloride levels, poorest diffusion properties, and lowest Ccrit distributions. While this approach ensures safety, it often results in overly cautious designs. In some cases, however, selecting poor-performing materials—despite meeting code requirements—has led to premature deterioration.
Because DtS provisions do not adequately account for variability in key factors like surface chloride content, diffusion coefficients, Ccrit, and temperature, modelling is increasingly used to enable more consistent and tailored designs. Modelling also supports the development of a wider range of DtS requirements for scenarios where full modelling is not feasible.
Durability modelling has developed in three stages:
- 1960–1980: Design life began to be split into initiation and propagation phases (T0 + T1 model by Tuutti [1]), with chloride-induced corrosion understood to initiate once Ccrit is reached.
- 1980–2005: Empirical models emerged, evolving to express key variables—such as Ccrit—as statistical distributions.
- 2005 onwards: Research further refined these distributions, with Ccrit identified as a key parameter.
The fib Model Code for Service Life Design (fib 34 [2]) introduced a probabilistic, performance-based framework. It is now the approach used in fib Model Code 2020 [3]), ISO 16204 [4]), EN 1992-1-1 [5]). This framework accounts for all major factors influencing chloride-induced corrosion and enables project-specific durability designs.
This paper proposes a set of lower-bound Ccrit distributions—based on published data—for different reinforcement types. These distributions can be directly applied in the MC2020 framework, allowing for broader material choices and more reliable, tailored durability designs.
2. Importance of Durability Modelling and Background to WP 8.9.3
It is essential to drastically reduce the environmental cost of construction as it is one of the major sources of greenhouse gas emissions; the rate of construction is increasing, and serious climate change is already on us. It requires a step change in thinking, one that increases the life of our structures. Better tools to help select materials, life cycles that give optimum performance in terms of pollution, and more efficient use of resources are essential if we are not to fly blindly into this storm. Appropriate selection of cement systems, admixtures, rebar, concrete cover, and mix design all have the potential to significantly increase the life of concrete structures, but we cannot optimize their use without better tools to predict life cycle performance.
Modelling has the potential to unlock the appropriate use of materials. Full probabilistic models are available and are being further developed, but as yet, input variables are far from well described. A large proportion of our infrastructure is in coastal regions and in areas where de-icing salts are used. Both lead to aggressive chloride environments, yet one of the biggest unknowns in our models is the appropriate Ccrit distribution to use in design. MC 2010 [6] provides no information on Ccrit distributions for different concretes or steels. A 2010 CSIRO report [7] on climate change indicated a likely increase of up to 3.5% in chloride-induced corrosion initiation around the coasts of Australia. So, both the extent of buildings in severe exposure areas and the proportion deteriorating is increasing. Clearly, the proportion of structures in chloride environments that prematurely deteriorate needs to be drastically reduced.
The scope of TG 8.9.3 is as follows:
- Discuss the subject of corrosion onset due to chlorides and to update the knowledge through fib.
- Gather information on corrosion-resistant bars as a means for the avoidance of corrosion.
- Derive revised design rules and recommended cover depths for the different types of bar.
- Make examples and case studies of applications.
The objectives are as follows:
- Provide background to the range of Ccrit distributions that should be used in design.
- Identify limitations on the use of the Ccrit distributions provided.
- Provide other corrosion protection design guidance that is critical to using the critical chloride levels (e.g., cracking, galvanic cells, exposures, pitting).
- Identify any issues with steel/galvanizing composition.
- Provide QA recommendations when using the materials discussed.
3. Ccrit and Its Measurement
If a reproducible distribution of Ccrit is to be developed, then there needs to be a consistent definition. Regarding this, the group agreed that Ccrit can be defined as the concentration of chloride in concrete required to break down the passive layer (i.e., depassivate) of the reinforcement, which may lead to corrosion initiation. Hence, to evaluate the critical chloride threshold, there are two critical issues: the detection of the depassivation time and the (immediate) measurement of the chloride content near the steel surface.
Andrade [8] suggests that “…depassivation is considered when in a delimited surface of steel (let’s say of 1 cm2) the corrosion current density during a sustained period of time is higher than 0.1–0.2 µA/cm2”. Even with a precise definition and a consistent method of measurement by polarisation resistance, the authors found a high degree of scatter.
Apart from the measuring method it is also important to define Ccrit statistically, i.e.:
- For full probabilistic modelling purposes, it shall be defined as a distribution.
- Deterministic calculation, without partial factors, only yields results of known reliability (50% chance of corrosion at reliability of 0) when the mean value is used. A safe value for Ccrit and other variables could be used, but that would be overly conservative.
- Partial factors would need to be based on a specific distribution for Ccrit.
The Ccrit distribution for carbon steel in atmospheric zones is quoted by fib 34 [2] as BetaD(0.60/0.15/0.02/2): 0.6 is the mean critical chloride level as Weight Percent Cement (WPC), 0.15 is the standard deviation, and 0.02 and 0.2 are the maximum and minimum values corresponding to 0 and 1 in a beta distribution. This distribution has a 95% probability that Ccrit will exceed 0.38 WPC, a little different to 0.35 WPC for a normal distribution of the same mean and standard deviation.
The measurement of Ccrit is easy to standardize in laboratory conditions as the corrosion behaviour of the bar can be constantly monitored through electrochemical measurements. For existing structures, constant monitoring is not usually performed, and it is less feasible. In research on structures, a different method may be appropriate.
In the Bulletin, only the general principles of measuring Ccrit are reviewed. Referring to research on structures, it might be convenient to define it as the chloride level when visible corrosion is seen on the reinforcement, when cracking occurs, when the potential is a certain value, or when the polarisation resistance reaches a certain amount. All these methods would yield different results. Figure 1 a from Papworth [9] shows a theoretical T0 + T1 graph showing corrosion degree with time for concrete with a long propagation period. This could be representative of a dry coastal region that only has <30 rain days/year. Overlain is a graph of chloride concentration at the reinforcement depth with time (in blue colour). The shape is typical of that from a mean Ccrit of 0.6 WPC when corrosion initiates. The intention is to relate the chloride level to the progress of corrosion.
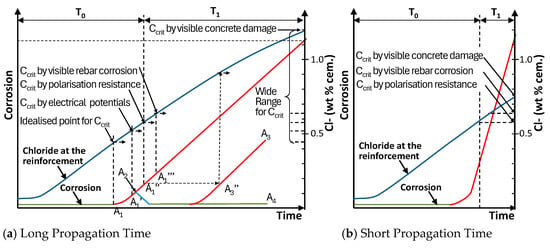
Figure 1.
Variations of T0 + T1 corrosion model incorporating chloride level at reinforcement and various possible depassivation measurements.
Shown on this graph are potential points when different measurement methods might detect corrosion (A1 to A1′′′) and demonstrates why different measurement methods might lead to significant differences in measured Ccrit, particularly if methods based on visible concrete damage are included. Clearly, if design life is to be assessed based on initiation plus propagation, the measurement of corrosion onset in relation to these periods is critical.
Figure 1a also shows various other important considerations in relation to detecting ongoing corrosion. Melchers [10] noted that corrosion might start (A1) and then the reinforcement might re-passivate (A2) permanently (A4) or temporarily (A3). The point here is that any method of measurement should not suggest corrosion before these points may have been reached. Andrade’s view is that the polarisation resistance method with a corrosion current set sufficiently high (A1′′ and A3′′) would achieve that goal.
In splash zones or wet coastal areas, the T0 + T1 diagram might look like Figure 1b. Papworth [9] notes that these graphs show that the chloride ingress rate and corrosion rate are not directly linked, as the latter is more dependent on moisture content than on chloride content. This means that, where the propagation period is long, there will also be a high buildup of chlorides at the bar between initiation and first crack. Hence, Ccrit distributions based on concrete damage (first crack) will be significantly higher than Ccrit distributions obtained by non-destructive testing. Conversely, where the propagation period is short, the difference in Ccrit for any of the measurement method will be insignificant Rin terms of modelling errors.
In fib and EuroCode 2, the “Corrosion (condition) limit state” (CLS) has been adopted. This CLS falls between the first depassivation and the appearance of a crack and has been, by agreement (nominally), ascribed to a pit depth of 500 microns (and to a uniform corrosion of 50 microns).
This is achieved quickly in submerged or tidal exposures, but it may take longer in atmospheric zones.
4. Carbon Steel
4.1. Historical Ccrit Distributions
A common discrete value quoted in the literature for Ccrit is 0.4 WPC. Generally, it is not noted what statistic this represents, but it is consistent with distributions given in fib 34 [2] when considered as a characteristic value with a 5–10% chance of structures corroding at this value, i.e., it is a safe design value. It has been reported that reinforcements in some structures show no signs of corrosion long after the 0.4 WPC Ccrit is reached. This may be largely because 95% of structures should show no corrosion of reinforcements at this chloride level. However, there are other reasons why the Ccrit value could be higher than the current values in fib 34.
Gulikers [11] reviewed the critical chlorides giving in fib 34 [2] and 76 [12] and those given in Duracrete [13]. The fib values were as proposed by Gehlen [14]. Originally, values for the mean (0.5% WPC) and standard deviation (0.15%) came from the experimental work by Breit [15] on ‘lollipop’ samples. However, Gehlen considered 0.5% too conservative/unrealistic for practice. Therefore, he increased the mean from 0.5% to 0.6% but maintained the same value for the standard deviation. The limits on the beta distribution are 0.2 and 2 WPC. Gehlen gave no further support or experimental evidence for the increase by 0.1%, although various papers by authors he associated with suggest that much higher values occur. The only limitation given for Ccrit is that it applies to mild steel only.
Gulikers [11] also notes that Duracrete [13] had Ccrit distributions for different exposures and w/c, as shown in Table 1. These were values based on visible concrete damage. This raises the question as to why different values were not published in fib for different concrete qualities and exposures. Given the low Ccrit for concrete with a w/c of 0.5, and that in practice concrete with a w/c ratio of 0.5 should not be used for concrete in splash zones, it might be reasonable to propose Ccrit for splash zones for high performance and moderate performance concrete, coinciding with w/c ratios of 0.3–0.35 and 0.35–0.4, at a much higher mean value than currently given in fib 34 [2].

Table 1.
Ccrit from Duracrete R9 based on time to concrete damage.
Notably, no values are given for coastal concrete.
Even before the publication of fib 34 [2], there had been extensive research on values for Ccrit. Since fib 34, there has been much more research, yet there has been no unifying research.
Among other older values, it is important to emphasize that Melchers [16] gives examples where chloride concentrations at the bar were much higher than fib Ccrit, with no corrosion. This is consistent with other research where the chlorides needed for depassivation were much higher than those given in fib 34 [2]. This raises concern that using the MC Model with fib Ccrit distributions might lead to overly conservative designs, and that chloride ingress may not be the most appropriate modelling approach.
The European perspective was very much on the need for far better guidance on the use of Ccrit now that modelling is finding wide usage amongst engineers with little research background. It was necessary to ensure designs were safe, but not overly conservative. However, there was still concern that factors other than chlorides at the bar were not adequately accounted for in determining if corrosion would occur.
One of the lead Ccrit researchers, Ueli Angst, in one paper [17] within the work of RILEM TC 235, gave a review of factors at the steel–concrete interface that affect Ccrit. Angst et al. summarized these as follows:
- The degree to which steel is polished, the steel metallurgy, and the moisture content at the Steel–Concrete Interface (SCI) are by far the most dominant influencing characteristics.
- Cement type and w/b ratio have comparatively small effects.
- Corrosion at macroscopic interfacial voids depends on the moisture states, with partially filled voids representing the worst case.
- The relative degree of corrosion sometime after initiation can be affected by propagation as well as initiation. Reported advanced corrosion at bleed lenses, for example, are more a function of high propagation rates than low Ccrit.
In another Angst paper [18], also with coworkers, it is proposed that, rather than continuing to focus on corrosion as T0 + T1, with Ccrit related to T0, the corrosion process be considered as one continuum including initiation and propagation. In determining whether to use a Ccrit related to depassivation or first crack, the modeler would have to consider the appropriate target reliability for the different limit states. For depassivation and first crack, target reliabilities of 1.3 and 1.5, respectively, may be appropriate.
The Bulletin draws the conclusion that it is not possible at this stage to provide a relationship between all the factors affecting Ccrit. The best that can be expected is to place limits of application of the Ccrit distributions proposed. The lack of application limitations is seen as a flaw in the fib 34 [2] Ccrit distribution. The Bulletin will give insight into the issues of developing a Ccrit for different situations. Also, the Bulletin, in accordance with MC 2020 [3], will support the addition of a propagation period to the time to depassivation to provide the service life. In the same way as modelling service life using a Ccrit for first crack, adding a propagation period to time of depassivation gives the Corrosion Limit State (CLS), while time to depassivation is a Depassivation Limit State (DLS). In certain exposure classes, this adds a significant propagation period to the time to depassivation because the expected corrosion rate is low and the pit depth is limited for a sustained period of time.
4.2. Recent Research on Ccrit
This adoption of the CLS was deeply discussed by an ad hoc group when preparing MC 2020 [3], and they decided to apply it not only to chloride-induced corrosion but also to carbonation and other types of attack or damage. This concept of condition limit states can be applied to other deterioration mechanisms. In the particular case of chloride attack, Andrade (Figure 2) showed that fib 34 [2] Ccrit distributions were supported by other authors, and hence fib 34 could be used even though other distributions are found in the literature (Figure 2). In some cases, the reasons for the higher standard deviation values for other distributions are unclear because they come from site measurements (Angst) where perhaps the concrete moisture content is variable, while in others it is known (Izquierdo < −200 mv) because they are the result of laboratory well controlled testing.
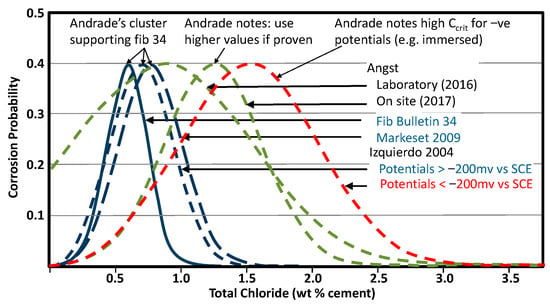
Figure 2.
Different chloride distributions by different researchers. Colours are only to help highlight different lines.
Conversely, Angst [19] highlights three studies shown in red, three in yellow, and two in blue (Figure 3) showing different clusters for higher Ccrit distributions. This suggest three consistent studies cannot be randomly picked as agreeing to give a universal Ccrit distribution. That is, even though higher Ccrit distributions may be used by engineers in specific and well-defined cases, the criteria published for general use must be a lower bound, i.e., fib 34 [2] values.
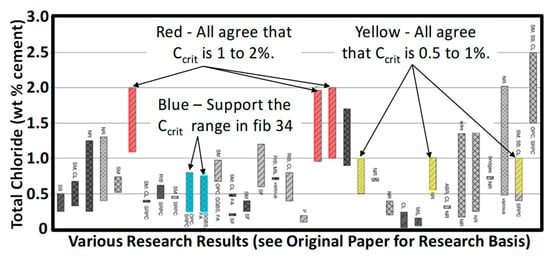
Figure 3.
Different chloride distribution clusters not identifying causes for difference [19].
4.3. Different Ccrit for Different Circumstances
The TG 8.9.3 working party had considerable discussions on the fib 34 [2] Ccrit distribution. Papworth [9] considered how the wide distribution in fib 34 could be reasonably applied for all concrete types. His Figure 4a shows five distributions based on a single contrived data set for Ccrit. The whole data set fits the distribution given in fib 34. The other four distributions take a portion of the whole date set, splitting the data into four sets, potentially representing different qualities.
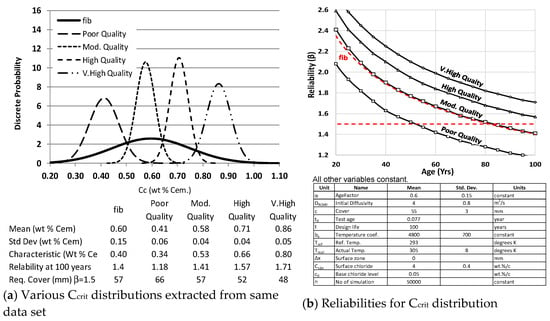
Figure 4.
Comparison of data giving fib’s Ccrit with the same data as four different quality concretes.
The meaning of quality is deliberately not defined and could be an aspect of the interface and/or the mix. This was so that an assessment of the influence of quality on Ccrit could be made by using the various distributions to assess the reliability of a structure where all the other inputs were held constant in a full probabilistic analysis (Figure 4b). It must be born in mind that these distributions are only for values making up the fib 34 [2] Ccrit distribution. Higher distributions would give even higher reliability than shown here.
Figure 4b shows the fib 34 [2] distribution gives a reliability of 1.4 at 100 years, and this might be taken as just acceptable where a target reliability of 1.3 was required for time to depassivation. If the distribution represents concrete at the poor and high end of the quality spectrums, the reliability was around 1.1 and 1.7, respectively. That represents a significant difference in cover required. As noted earlier, there was already concern that the fib 34 Ccrit distribution underestimated the resistance to chloride in some situations, and this strengthened the idea that different distributions should be used for different qualities, if those qualities could be defined.
4.4. Application Limits for Ccrit
Possible Ccrit values were tabled, together with potential limitations of use, in Table 2 for TG 8.9.3 consideration.

Table 2.
Circular for TG8.9.3 members on Ccrit and its limitations.
The diffusion coefficient was included as a general measure of quality as it is a test likely to be required for chloride environments as a measure of chloride ingress rate. The requirement for testing on representative trial blocks and first pours was an attempt to ensure that assessment was based on site concrete rather than on laboratory samples. Voids and porosity were intended to give some measure of voidage at the SCI, while steel composition and surface condition were an attempt to include other SCI properties.
Strong responses to the possible limits in Table 2 were as follows:
- (a)
- It is the SCI that is responsible for Ccrit, and the measures in Table 2 mainly consider the concrete’s general quality; they would not deal adequately with qualifying the interface.
- (b)
- In terms of general concrete quality, the normal requirements for concrete for each exposure were adequate. No additional restrictions are required.
- (c)
- Any measure for Ccrit needed to be based on the real, as placed, concrete and not on laboratory samples.
On the other hand, an attempt to classify the concrete quality with respect to reinforcement corrosion is being made in CEN TC 104-Concrete related to the new EN-206, and it is based on classifying the concretes in relation to their carbonation rate or chloride diffusion coefficient obtained in tests at early ages and as already standardized. The values of the rates of ingress are classified from lower to higher in Exposure Resistance Classes (ERCs).
It is clear that the influencing factors have to be drawn from the SCI, and proxy measures of concrete mix or the in-situ performance of the bulk concrete would not provide realistic limitations. A detailed report [20] on the methods of characterizing the SCI outlines “current methods (laboratory or field-based) for characterizing local properties of the SCI that have been identified as governing factors affecting corrosion initiation. These properties include characteristics of the steel such as mill scale and rust layers, and characteristics of the concrete such as interfacial voids, microstructure and moisture content.” It notes various limitations for a full characterization of the SCI, but more positively notes “established techniques are available for direct quantitative characterization of selected features, namely mill scale and rust layers on the steel surface, and the interfacial voids and microstructure of the cementitious matrix at the SCI”.
While SCI characterization is as yet imperfect, some of the key aspects for which tests are available might at least be available to better define Ccrit distributions. These might include pH, interface voids, potentials, temperature, and relative humidity.
4.5. The Influence of Cracks
The treatment of Ccrit in this report is focused on uncracked concrete. The corrosion of reinforcements at cracks is a subject in its own right. Typically, design considers that corrosion at cracks in chloride exposures does not occur where the crack width is less than 0.3 mm [21]. Activation may occur, initially giving rapid corrosion rates, but if the crack self-heals the corrosion stops as the bar passivates. However, this has not been related to chloride levels, and the reason the bar stops corroding has not been fully identified.
4.6. Underwater Corrosion
The corrosion of steel in immersed concrete is not well understood. It is often stated that oxygen starvation of the cathodic areas in underwater concrete means corrosion is not an issue. Papworth [22] notes that this might not be the cause of the lack of corrosion. It might be that, in pores saturated with highly alkaline seawater, the high pH leads to a high critical chloride level consistent with Pourbaix. Various authors [23,24,25] report mean critical chloride levels of around 2% by weight cement in immersed zones compared to 0.6% by weight cement given in fib 34 [2] for zones where air is available at the bar. Also, this is deduced from the work by Angst [19].
The chloride profiles of concrete in immersed seawater-exposed structures differ significantly to those of above-water structures. Browne [26] showed a flatter chloride profile for immersed concrete than splash-zone concrete (Figure 5a). Even though the surface chloride in the underwater zone was less than half that in the splash zone, the chloride level at 150 mm depth was higher after 34 years. The chloride levels found by Walsh [27] after 60 years (Figure 5b) were virtually flat, having reached a maximum at 9–12 kg/m3.
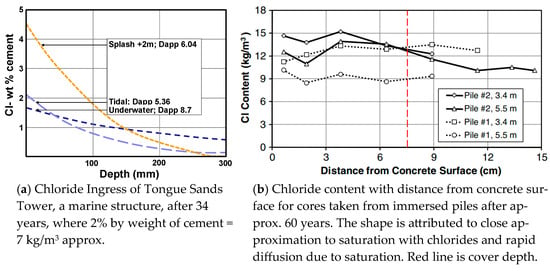
Figure 5.
Chloride profiles for immersed marine concrete. Marine structures are taken as being in or over water. Immersed concrete is taken to be concrete that will be underwater at all times. Figure (a) is from Browne [26] and figure (b) is from Walsh [27].
The chloride profiles and critical chloride levels are significant as they show the care required when applying the MC Model.
Walsh [27] reports that he examined sections from submerged piles in the laboratory, and there was extensive localised corrosion on the face of many bars that faced the exposed surface (Figure 6a). The corrosion products had not caused spalling but had migrated away from the bar (Figure 6b). The resulting perimeter-averaged values for the corroding regions typically ranged from 5 μm/y to 35 μm/y and were randomly distributed and considered to occur at local concrete deficiencies. In Walsh’s piles, corrosion was limited to 6% and 12% of the bar lengths in two piles. Walsh notes that Beaton’s results were similar.

Figure 6.
Localised corrosion and corrosion product distribution in underwater structures.
The importance of this is that it shows that, where concrete is locally deficient, such as in honeycombing, corrosion can occur, but the corrosion rate will be low. However, in honeycombed concrete corrosion, initiation would be expected to occur in the early life, and hence the corrosion rate would apply over virtually the whole design life. The corrosion rate can be taken to be 5–35 μm/y. Over a 160-year design life, this would translate to 0.8–5.6 mm averaged around the bar (i.e., thicker loss expected but only on one side) and would apply to limited areas of honeycombing. The corrosion will not result in spalling but in the migration of iron ions away from the reinforcement.
As Walsh [27] states, “Consequently, if corrosion at a spot in the submerged region started relatively early in the life of the structure, e.g., as a result of a local concrete deficiency, that spot may tend to remain a relatively stable feature over a long period of time. Such a situation would be consistent with the field observations noted … where relatively small, localized corroding regions were found to be surrounded by large amounts of non-corroding steel, much of which exhibited an undisturbed surface appearance”.
Although slow, the corrosion in immersed zones may lead to significant localised corrosion over a 100-year design life. Because the corrosion rate will be slow, and the corrosion products are not expansive, this is not likely to be a structural issue for many decades. The Bulletin proposes that the MC Model is not an appropriate tool for immersed concrete analysis, but rather, an allowance for localised corrosion should be applied.
5. Galvanized Reinforcement
Galvanized reinforcement has been used in concrete for well over 50 years. Guides produced in 1970 [28] and 1981 [29] provide extensive information on field experience and laboratory tests that validates the use of galvanized reinforcement. Unfortunately, other pieces of research using accelerated tests inappropriately cast doubt on the performance benefits of using galvanized reinforcement in marine exposures.
The use of galvanized reinforcement in marine exposures is less extensive than it should be as many specifiers, even durability engineers, often reject its use due to the bad impressions created by inappropriate accelerated tests in the 1970s. In 1979, the FHWA recommended against using galvanized reinforcement after a series of accelerated laboratory experiments questioned its ability to prevent corrosion. However, the agency rescinded this recommendation in 1983 [28]. There are many examples of Hot Dip Galvanizing’s (HDG) successful use in a wide range of exposures, some of which are summarised by Yeomans [30]. While these prove improved corrosion resistance, the poor Ccrit values in some cases are suspected to be due to poor galvanising.
An example of galvanised steel’s excellent performance is in Bermuda. Bermuda pioneered galvanized reinforcement use in hot saline environments for a number of critical structures in the 1950s. This proved extremely successful. The 1953 Longbird bridge is a prime example. In 1981 [29], an assessment showed no deterioration of the galvanized reinforcements, even though the chloride level at the reinforcement was 1.2 WPC, i.e., three times the Ccrit often quoted for conventional reinforcement. The reduced maintenance cost of structures using galvanized reinforcement compared to conventional reinforcement led the Bermuda government to use galvanized reinforcement in all structures in a USD 300 million infrastructure program in the 1990s [31].
Examples of the performance of galvanised reinforcement by SHRP2 [32] are shown in Table 3.

Table 3.
Summary of reported data on Ccrit for galvanised reinforcement by SHRP2 [32].
Lollini [33] reviewed various papers on Ccrit for HDG, as shown in Table 4.

Table 4.
Ccrit-HDG for concrete by various researchers (Lollini [33]).
The Bulletin is expected to recommend a beta distribution of (1.2, 0.3, 0.6, 3.0) for Ccrit of HDG steel, where quality is maintained at a high level. The 1.2 mean is twice that of carbon steel. The values were largely based on Table 5.

Table 5.
Papers used to define Ccrit-HDG.
6. Stainless Steel
Moser [36] notes that alloys, e.g., Cr, Ni, Mo, and N, provide corrosion resistance by the formation of a highly stable passive film. In stainless steels, Cr additions lead to a chromium oxide (Cr2O3) passive film. If the passive film is broken down and corrosion pits nucleate, the presence of alloyed Ni, Mo, and N aid in the re-passivation of the pits. Different alloying compositions defined for different grades of stainless-steel leads to stainless steel’s different levels of resistance to chloride-induced passivation, i.e., different Ccrit’s.
While the use of stainless steel may seem expensive, if used only in critical areas it may not add significantly to construction cost. This should be carefully evaluated, through a proper LCC analysis, to define the most suitable solution that on one hand guarantees the durability requirement and on the other hand allows one to save money. For example, its use in dowel bars may cost very little, where the likelihood and consequence of corrosion at bridge deck joints is high and makes their use almost obligatory. The electrical connection between stainless steel and carbon steel was shown, in various studies quoted by Perez-Quiroz [37], not to lead to galvanic corrosion; if the steels remained passive, a reasonable underlying premise for durability design as the propagation phase is unlikely to be significant in aggressive chloride environments.
A more global use of stainless steel may also be appropriate where realistic modelling shows carbon steel will not give the required reliability. Moser [36] notes that Progreso Pier, located on Mexico’s Yucatan Peninsula and built in 1939 with poor quality concrete and a cover thickness of 25 mm, is over 70 years old and remains in excellent condition, although with some pits, while a companion pier built in 1979 with normal ferritic mild steel reinforcement had to be demolished due to corrosion damage after two decades of service.
The Bulletin refers to many other papers showing the high corrosion resistance of stainless steel, including data from Lollini [38] and SHRP [32], as shown in Figure 7.
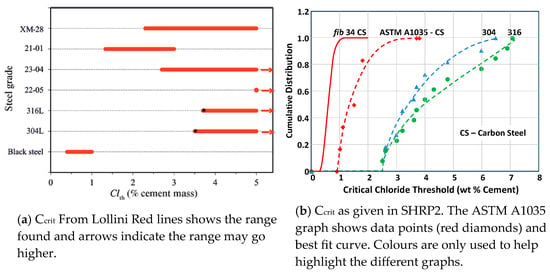
Figure 7.
Corrosion of stainless steel.
Based on the various research papers discussed in the Bulletin, Ccrit for the various stainless-steel grades has been proposed as shown in Table 6. These are the basis of recommendations in the Bulletin.

Table 6.
Grades of stainless steel.
7. Steel Fibres
The T0 + T1 model can be used to assess the design life of steel-fibre-reinforced concrete. However, because it takes only very little corrosion to make the fibre performance insignificant, only T0 should be used in design.
Corrosion of the fibres does not cause spalling, and the structural damage is limited to loss of toughness over the section where the fibres have corroded; the design allows for a sacrificial thickness at the surface, which is considered as unreinforced. The MC Model can be used to determine the sacrificial thickness based on the Ccrit for steel fibres.
Mangat [39,40] investigated the corrosion of fibres in more corrosive marine exposures. He found that, after 300 marine spray cycles, low carbon steel fibre corroded at the surface and none of the fibre corroded when embedded in concrete, even though chloride levels were as high as four times the often-quoted steel corrosion threshold of 0.4 wt.% cement. Nemegeer [41] showed that the corrosion of low carbon steel fibre in samples exposed to wet–dry cycling in chloride-infiltrated samples did not occur, except within the thin carbonated surface zone. Dauberschmidt [42] concluded that, depending on the quality of the concrete-to-fibre interface, the critical chloride content may be in the range of 3% chloride by weight of cement.
It is concluded that Ccrit for steel fibres is considerably higher than fib 34′s [2] for carbon steel reinforcement. The principal reasons postulated are as follows:
- In general, each fibre is electrically discontinuous, whereas reinforcement is interconnected. Hence, macro cells are likely to be less significant with steel fibres. However, pitting corrosion of fibres would quickly make the fibre redundant.
- With conventional reinforcement, a porous interface between the reinforcement and the concrete can lead to a low chloride activation level. This interface layer is generally absent with steel fibres.
In conventional reinforced concrete, spalling at anchorages zones is an issue due to the loss of bond. The analogy in fibre-reinforced concrete is that corrosion that separates the hooked or enlarged ends that form the fibre’s anchorage could mean the whole fibre is redundant. This is an important consideration at load transfer across cracks and joints.
Kosa [43] and Mangat [39] considered the critical crack width for fibre concrete by testing beams for toughness after severe exposure. They independently concluded that there was no reduction in load capacity for cracks less than 0.15 mm and proposed this as maximum allowable crack width.
8. Conclusions and Recommendations
The Ccrit for low carbon steel has a wide distribution due to the range of factors that effect it. The fib 34’s [2] beta distribution, with a mean value of 0.6 wt% binder and standard deviation of 0.15 wt% binder for total chloride, or any other of the statistical distributions given in fib Bulletin 112 [44], should be used in probabilistic modelling when nothing else is known about the concrete. Modelers may decide to reduce the standard deviation or use a characteristic value with a safety factor, based on other information, but it has been shown that this range may occur within one structure and hence the perceptions of bar/paste interface ‘quality’ may not be a good reason to vary it. If there is information that the pH is low, it may be sensible to lower the Ccrit, but the distribution already allows that the competing effects of low pH and higher chloride binding mean the distribution applies where fly ash and slag are used. As shown, Ccrit may be affected by exposure; it might be reasonable to increase the mean value for coastal structures and reduce it for marine structures.
The fib 34’s [2] distribution for Ccrit gives a lower characteristic value of around 0.35 wt% binder. This is what many refer to as the critical chloride content when no distribution is considered. It is important to understand that this is not a mean value. When used in the fib chloride model as a discrete value, it is often considered to give a conservative design life, but the actual probability of failure will not be known. It may be better to use the mean value of 0.6 wt% binder and other mean values for variables and know that the predicted design life has a 50% probability of failure. This may be a suitable probability for some structures (e.g., under a wharf).
At this stage, there is no agreed method to establish the realistic/practical long-term critical chloride content for a structure. It would be useful if agreement could be reached on the criteria to be used to determine corrosion depassivation as this would reduce the variability when measuring Ccrit.
The Bulletin is likely to recommend the Ccrit values shown in Table 7. Modelling using these values will enable those involved in durability design to provide options for reinforcement and concrete that will achieve the same reliability over the design life. It will also provide the basis for achieving target reliabilities not covered by the DtS requirements in codes.

Table 7.
TG 8.9.3 recommended lowest Ccrit distributions.
The Ccrit values in Table 7 are lower bounds. Various authors have established much higher values. It is clear from these, and examples of real structures, that in some circumstances much higher values of Ccrit are applicable. However, without a clear understanding of the reasons for using higher values, and as a means of ensuring those reasons apply to a structure, it is appropriate to use these lower bounds.
Author Contributions
Original draft preparation by F.P. F.P., C.A. and F.L. contributed to its development throughout. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
All data available is either presented or included in the referenced papers.
Acknowledgments
The author thanks all fib TG 8.8.3 members (Perdix, U. Angst, E. Bernhard, S. Burtscher, M. Gastaldi, J. Gullikers, M. Kurtay, G. Markeset, R. Newby, R. Pollai, J. Sanchez, F. Moro, M. Raupach, and A. Rahimi) on ‘Critical Chloride Content’ for their input to the discussions aimed at resolving this difficult topic. The views of the author expressed in this paper may differ to those of other committee members.
Conflicts of Interest
Author Frank Papworth was employed by the company Building and Construction Research and Consulting Pty Ltd. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| Ccrit | Critical chloride level. Typically, the level at which reinforcement is depassivated, as measured by non-destructive tests. However, it can be defined relative to any measurement method (e.g., time to concrete damage). It can be quoted as a distribution (Ccrit distribution), a lower 95 percent confidence level (Ccrit value), or as a general term (Ccrit) |
| CLS | Corrosion Limit State |
| DtS | Deemed to Satisfy |
| HDG | Hot Dipped Galvanized |
| LCC | Life Cycle Cost |
| SCI | Steel–Concrete Interface |
| WPC | Weight Percent Cement |
| µA/cm2 | Micro Amps per square centimetre |
| µm/y | Micro meters per year |
References and Note
- Tuutti, K. Corrosion of Steel in Concrete. Doctoral Thesis, KTH Royal Institute of Technology, Stockholm, Sweeden, 1982. [Google Scholar]
- fib Bulletin 34. Model Code for Service Life Design; fib: Lausanne, Switzerland, 2006. [Google Scholar]
- fib Model Code for Concrete Structures (2020); International Federation for Structural Concrete (fib) Switzerland: Lausanne, Switzerland, 2024.
- ISO 16204; Durability—Service Life Design of Concrete Structures. International Organisation for Standards: Geneva, Switzerland, 2012.
- EN 1992-1-1; Eurocode 2: Design of Concrete Structures. European Committee for Standardisation: Brussels, Belgium, 2023.
- fib Model Code for Concrete Structures (2010); International Federation for Structural Concrete (fib) Switzerland: Lausanne, Switzerland, 2013.
- CSIRO State of the Climate. CSIRO & Bureau of Meteorology Joint Report; CSIRO: Canberra, Australia, 2010. [Google Scholar]
- Andrade, C.; Garces, P.; Martinez, I. Galvanic currents and corrosion rates of reinforcements measured in cells simulating different pitting areas caused by chloride attack in sodium hydroxide. Corros. Sci. 2008, 50, 2959–2964. [Google Scholar] [CrossRef]
- Papworth, F. Modelling for improved durability design. In Background to Critical Chloride Level Establishment and Proposal for Further Refinement; Concrete Institute of Australia, Concrete: Perth, Australia, 2023. [Google Scholar]
- Melchers, R.E. Modelling durability of reinforced concrete structures. Corros. Eng. Sci. Technol. 2020, 55, 171–181. [Google Scholar] [CrossRef]
- Gulikers, J. Communication to WP 8.9.3 Overview of selected literature on Ccrit for interpretation and verification of fib 34-values. Personal communication, 26 April 2023
- fib Bulletin 76. Benchmarking of Deemed to Satisfy Provisions in Standards; fib: Lausanne, Switzerland, 2015. [Google Scholar]
- Duracrete Final Technical Report; Probabilistic performance-based durability design of concrete structures—Statistical quantification of the variables in the limit state functions. The European Union–Brite EuRam III Contract BRPR-CT95-0132, Project BE95-1347/R9; The European Union: Brussels, Belgium, 2000; ISBN 90 376 0374.
- Gehlen, C. Probabilistische Lebensdauerbemessung von Stahlbetonbauwerken Zuverlässigkeitsbetrachtungen zur Wirksamen Vermeidung von Bewehrungskorrosion; Deutscher Ausschuss fuer Stahibeton, Issue 510; Wilhelm & Sohn: Hessen, Germany, 2000. [Google Scholar]
- Breit, W. Critical Chloride Content—Investigations of Steel in Alkaline Chloride Solutions. Mater. Corros. 1998, 49, 539–550. [Google Scholar] [CrossRef]
- Melchers, R.E.; Chaves, I.A. Reinforcement Corrosion in Marine Concretes—1: Initiation. ACI Mater. J. Sept 2019, 116, 57–66. [Google Scholar] [CrossRef]
- Angst, U.M.; Isgor, O.B.; Hansson, C.M.; Sagüés, A.; Geiker, M.R. Beyond the chloride threshold concept for predicting corrosion of steel in concrete. Appl. Phys. Rev. 2022, 9, 011321. [Google Scholar] [CrossRef]
- Angst, U.M. The effect of the steel–concrete interface on chloride induced corrosion initiation in concrete: A critical review by RILEM TC 262-SCI. Mater. Struct. 2019, 52, 1–25. [Google Scholar] [CrossRef]
- Angst, U.; Elsener, B.; Larsen, C.K.; Vennesland, O. Critical chloride content in reinforced concrete—A review. Cem. Concr. Res. 2009, 39, 1122–1138. [Google Scholar] [CrossRef]
- Wong, H.S.; Angst, U.M.; Geiker, M.R.; Isgor, O.B.; Elsener, B.; Michel, A.; Alonso, M.C.; Correia, M.J.; Pacheco, J.; Gulikers, J. Methods of characterizing the steel-concrete interface to enhance understanding of reinforcement corrosion: A critical review by RILEM TC 262-SCI. Mater. Struct. May 2022, 55, 124. [Google Scholar] [CrossRef]
- Bamforth, P. CIRIA C766. In Control of Cracking Caused by Restrained Deformation in Concrete; CIRIA: London, UK, 2018. [Google Scholar]
- Papworth, F. Durability design for concrete immersed in seawater or brine. In Proceedings of the Australasian Corrosion Association Conference, Adelaide, Australia, 11–14 November 2018. [Google Scholar]
- Sandberg, P. Systematic collection of field data for service life prediction of concrete structures. In Durability of Concrete in Saline Environment; CEMENTA: Danderyd, Sweden, 1996. [Google Scholar]
- Izquierdo, D.; Alonso, C.; Andrade, C.; Castellote, M. Potentiostatic determination of chloride threshold values for rebar depassivation. Exp. Stat. Study-Electrochim. Acta 2004, 49, 2731–2739. [Google Scholar] [CrossRef]
- Pedeferri, P. Cathodic protection and cathodic prevention. Constr. Build. Mater. 1996, 10, 391–402. [Google Scholar] [CrossRef]
- Browne, R.D.; Blundell, R.; Domone, P.L.J.; Papworth, F.; Geoghegan, M.P.; Baker, A.F. Marine Durability Survey of the Tongue Sands Tower; Concrete in the Oceans Technical Report No 5; Cement and Concrete Association: Slough, UK, 1980. [Google Scholar]
- Walsh, M.; Sagues, A. Steel Corrosion in Submerged Concrete Structures—Part 2: Modelling of Corrosion Evolution and Control. Corrosion 2016, 72, 665–678. [Google Scholar] [CrossRef] [PubMed]
- Galvanized Reinforcement for Concrete; International Lead and Zinc Research Organisation Inc.: New York, NY, USA, 1970.
- Galvanized Reinforcement for Concrete—II. International Lead and Zinc Research Organisation Inc.: New York, NY, USA, 1981.
- Yeomans, S.R. Galvanized Steel Reinforcement in Concrete; Elsevier: Amsterdam, The Netherlands, 2004. [Google Scholar]
- Allan, N.D. The Bermuda outdoor experience: Leading the way on Galvanized Reinforcement. In Galvanized Steel Reinforcement in Concrete; Yeomans, S.R., Ed.; Elsevier: Amsterdam, The Netherlands, 2004. [Google Scholar]
- SHRP2 Solutions Service Life Design of Concrete Bridges (R19A); Appendix C. Chloride threshold for Various Reinforcement Steel Types; American Association of State Highway and Transportation Officials: Washington, DC, USA, 2019.
- Lollini, F.; Carsana, M.; Gastaldi, M.; Redaelli, E.; Bertolini, L. The challenge of the performance-based approach for the design of reinforced concrete structures in chloride bearing environment. Constr. Build. Mater. 2015, 79, 245–254. [Google Scholar] [CrossRef]
- Srimahajariyaphong, Y.; Niltawach, S. Corrosion prevention of rebar in concrete due to chloride. J. Met. Mater. Miner. 2011, 21, 57–66. [Google Scholar]
- Bertolini, L.; Elsener, B.; Pedeferri, P.; Redaelli, E.; Polder, R.B. Corrosion of Steel in Concrete: Prevention, Diagnosis, Repair; Wiley: Hoboken, NJ, USA, 2004; ISBN 3-527-30800-8. [Google Scholar]
- Moser, R.; Singh, P.; Khan, L.; Kurtis, K. Durability of Precast Prestressed Concrete Piles in Marine Environment, Part 1 & 2. Georgia Institute of Technology. Project No. 10-26. Task Order No 02-78. 2011 and 2012. Available online: https://rosap.ntl.bts.gov (accessed on 27 April 2025).
- Perez-Quiroz, J.T.; Teran, J.; Herrera, M.J.; Martinez, M.; Genesca, J. Assessment of stainless steel reinforcement for concrete structures rehabilitation. J. Constr. Steel Res. 2008, 64, 1317–1324. [Google Scholar] [CrossRef]
- Lollini, F.; Carsana, M.; Gastaldi, M.; Redaelli, E. Corrosion behavior of stainless steel reinforcement in concrete. De Gruyter Brill. Corros. Rev. 2018, 37, 3–19. [Google Scholar] [CrossRef]
- Mangat, P.S.; Gurausamy, K. Steel fibre reinforced concrete for marine applications. In Proceedings of the 4th International Conference on Behaviour of Offshore Structures, Delft, The Netherlands, 1–5 July 1985; pp. 867–879. [Google Scholar]
- Mangat, P.S.; Gurusamy, K. Permissible crack widths in steel fibre reinforced marine concrete. Cem. Concr. Res. 1987, 17, 734–742. [Google Scholar] [CrossRef]
- Nemegeer, D.; Vanbrabant, J.; Stang, H. Durability of Steel Fibre Reinforced Concrete. European Community Brite Euram III project Report. RILEM Technical Committee 162, TDF Workshop, Proceedings Pro 31. 2003; pp. 47–66. Available online: https://www.rilem.net/publication/publication/36?id_papier=894 (accessed on 27 April 2025).
- Dauberschmidt, C.T. Investigations on the Corrosion Mechanisms of Steel Fibres in Concrete Containing Chlorides; RWTH: Aachen, Germany, 2005. [Google Scholar]
- Kosa, K. Corrosion of Fibre Reinforced Concrete. Ph.D. Thesis, University of Michigan, Ann Arbour, MI, USA, 1988. [Google Scholar]
- fib Bulletin 112. fib Model Code 2020 Complementary Guidance on Concrete Durability; fib: Lausanne, Switzerland, 2006. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).