Epitaxial Growth of Ni-Mn-Ga on Al2O3(
Abstract
1. Introduction
2. Materials and Methods
3. Results
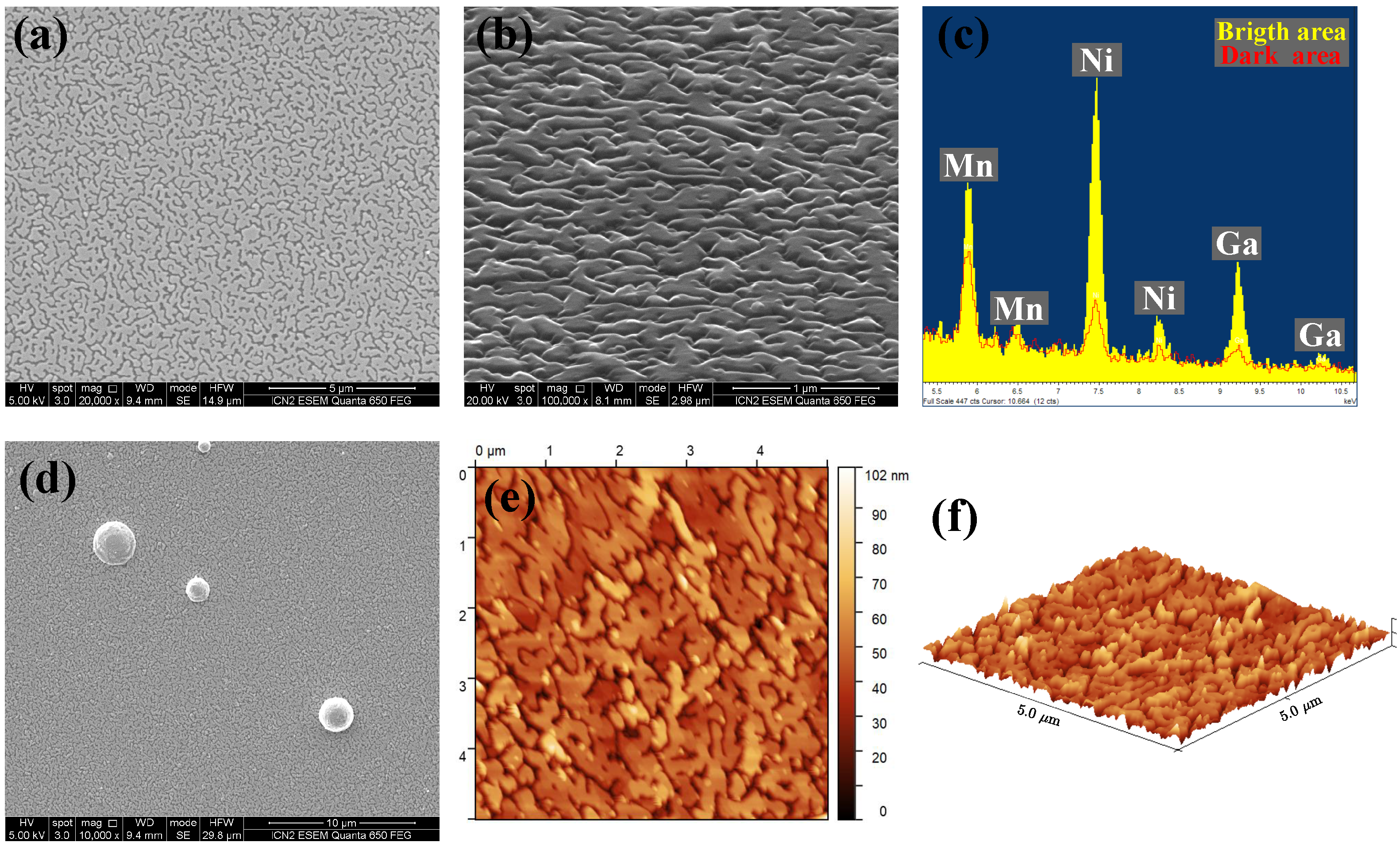
3.1. Film Growth Characteristics
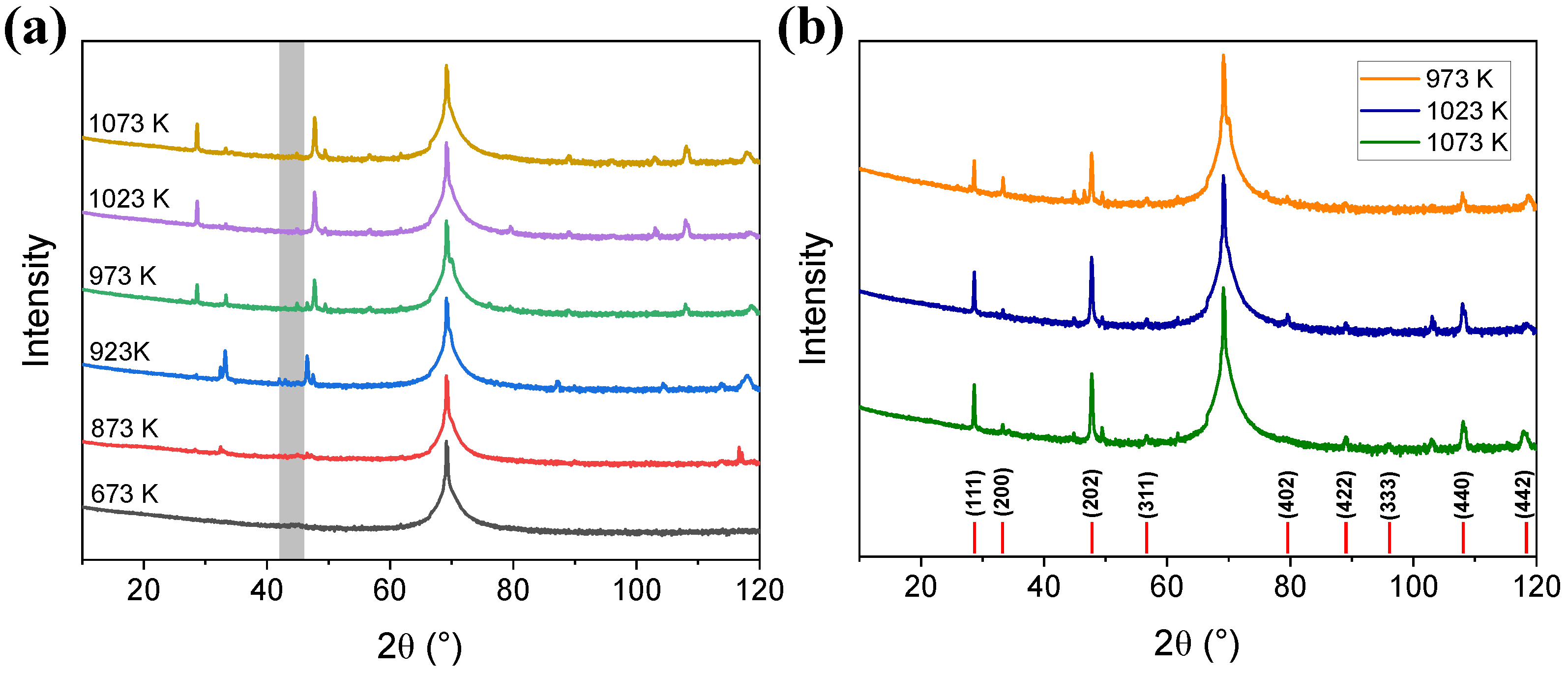
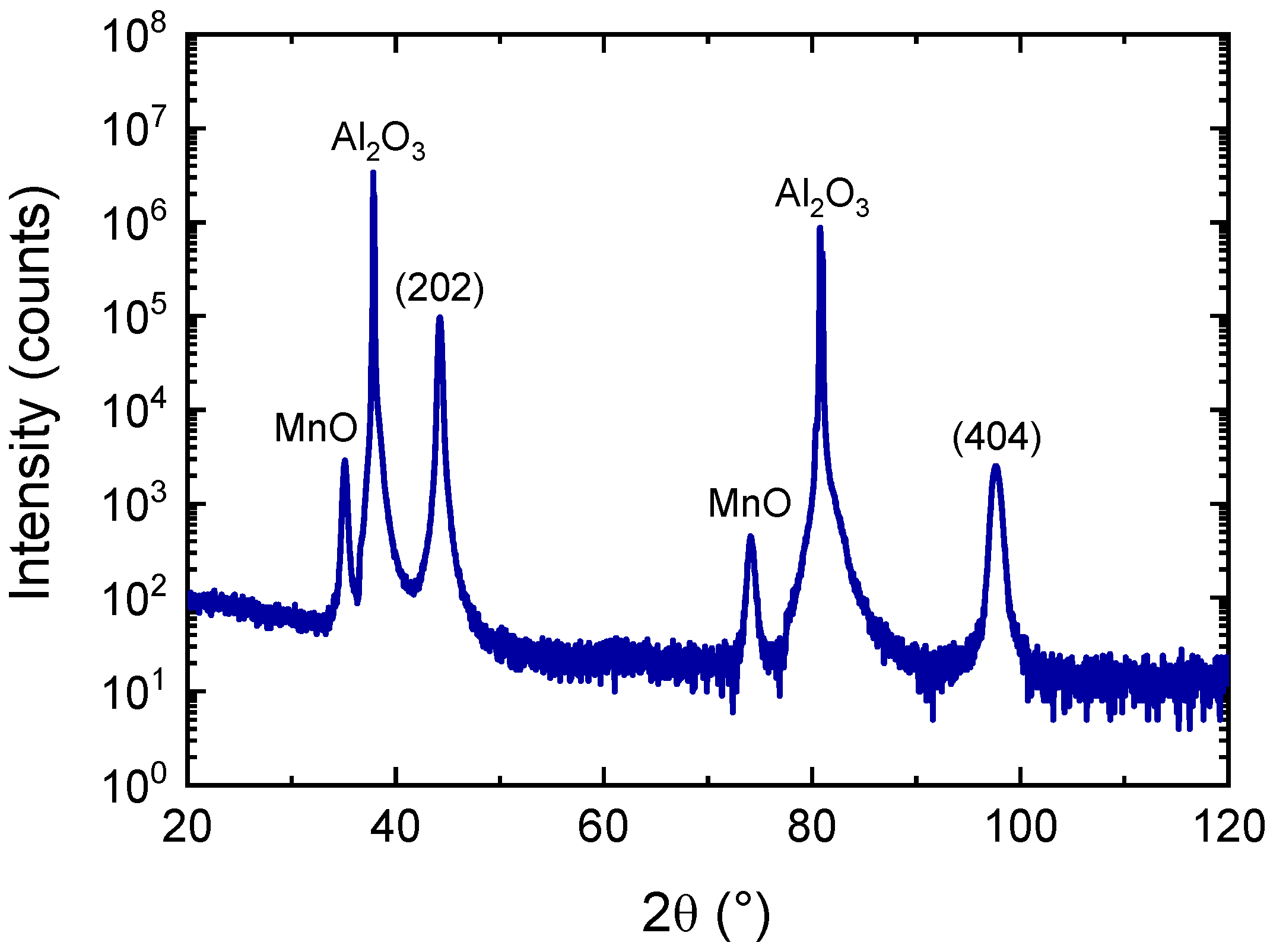
3.2. Determination of Crystalline Structure by X-Ray Diffraction
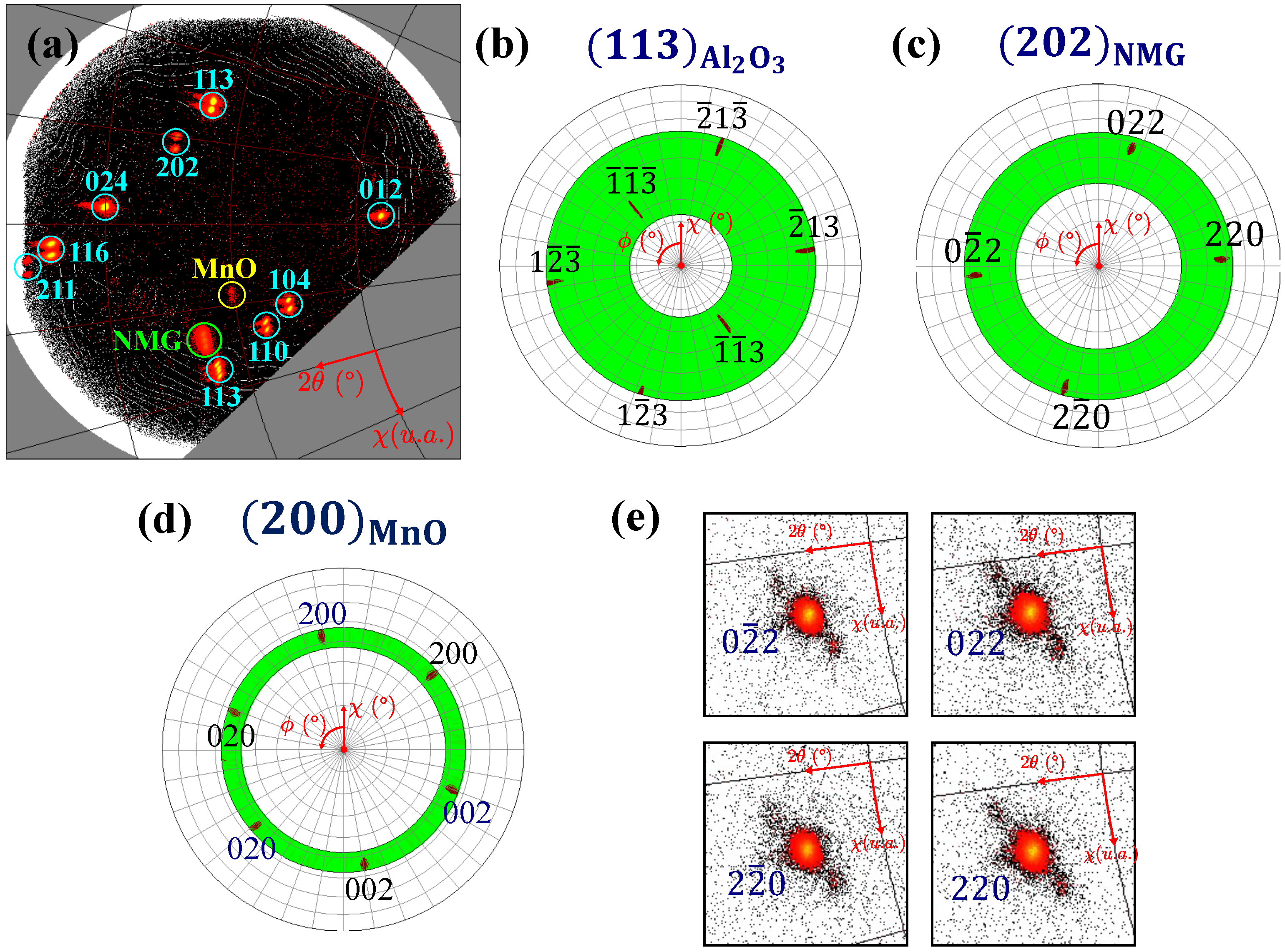
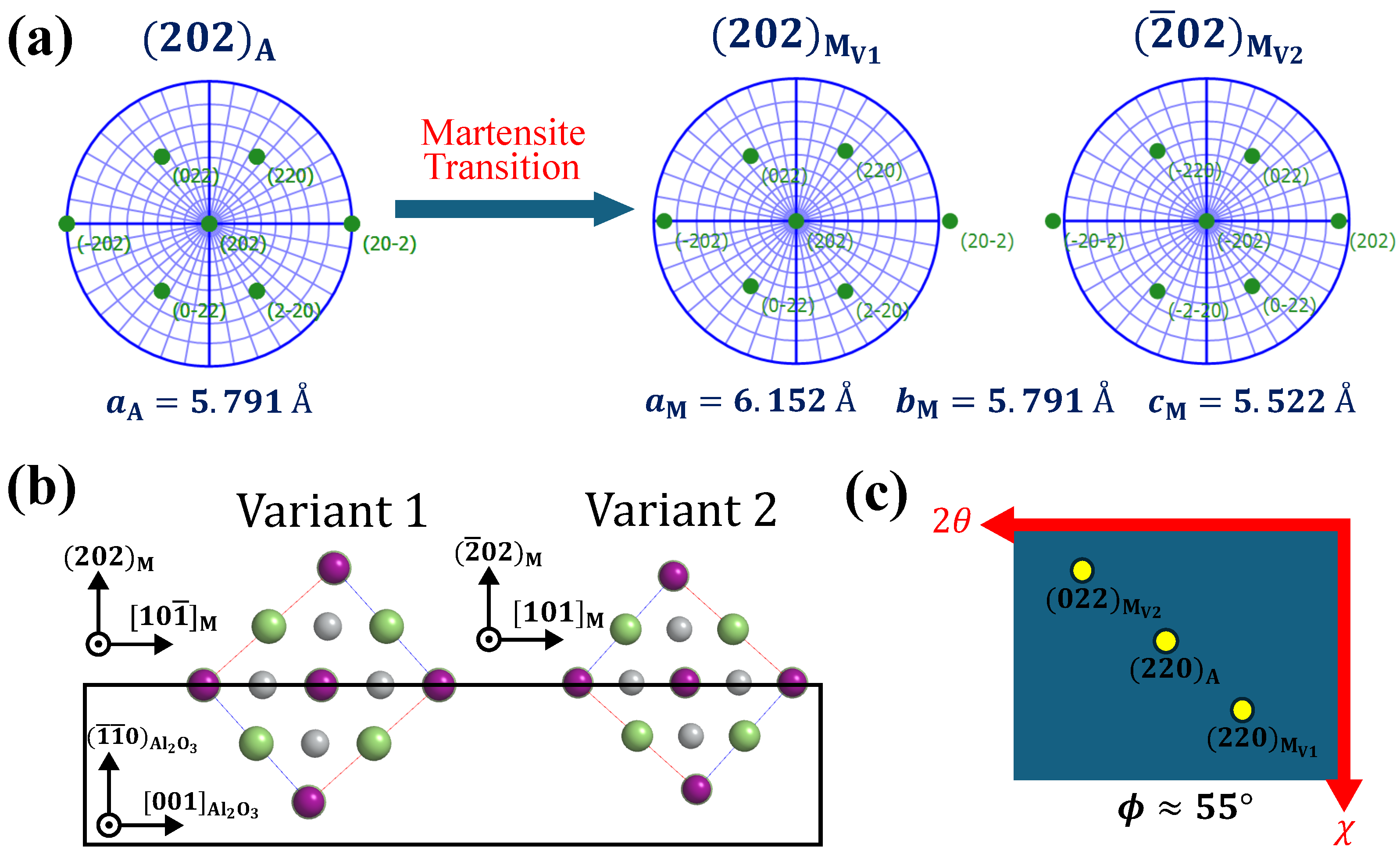
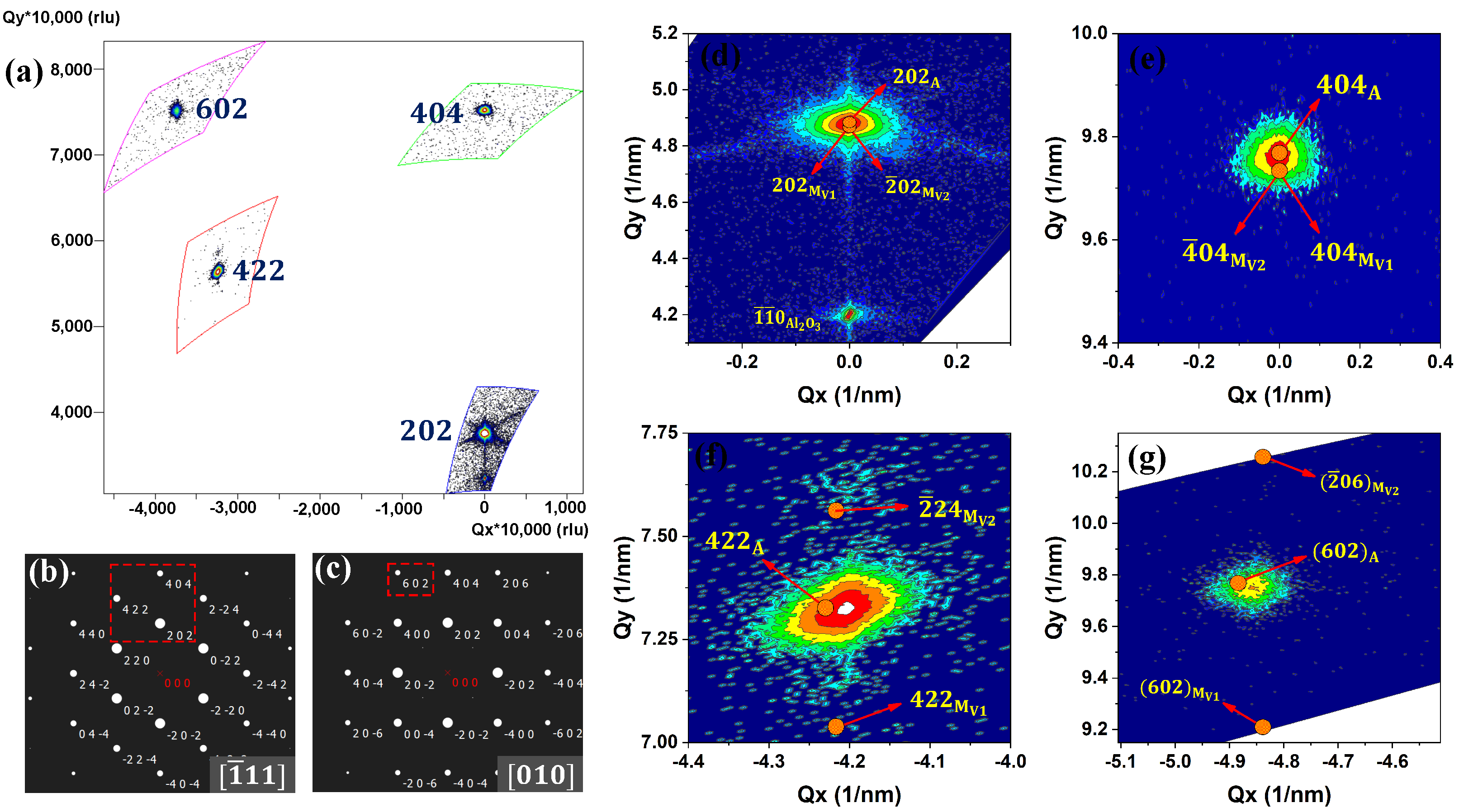
3.3. Microstructure Observed by Transmission Electron Microscopy
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| MSMA | Magnetic Shape Memory Alloy |
| PLD | Pulsed Laser Deposition |
| NMG | Ni-Mn-Ga |
| HR-(S)TEM | High-Resolution Scanning Transmission Electron Microscopy |
| SEM | Scanning Electron Microscopy |
| XRD | X-ray Diffraction |
| RSMs | Reciprocal Space Maps |
Appendix A. Sample Optimisation
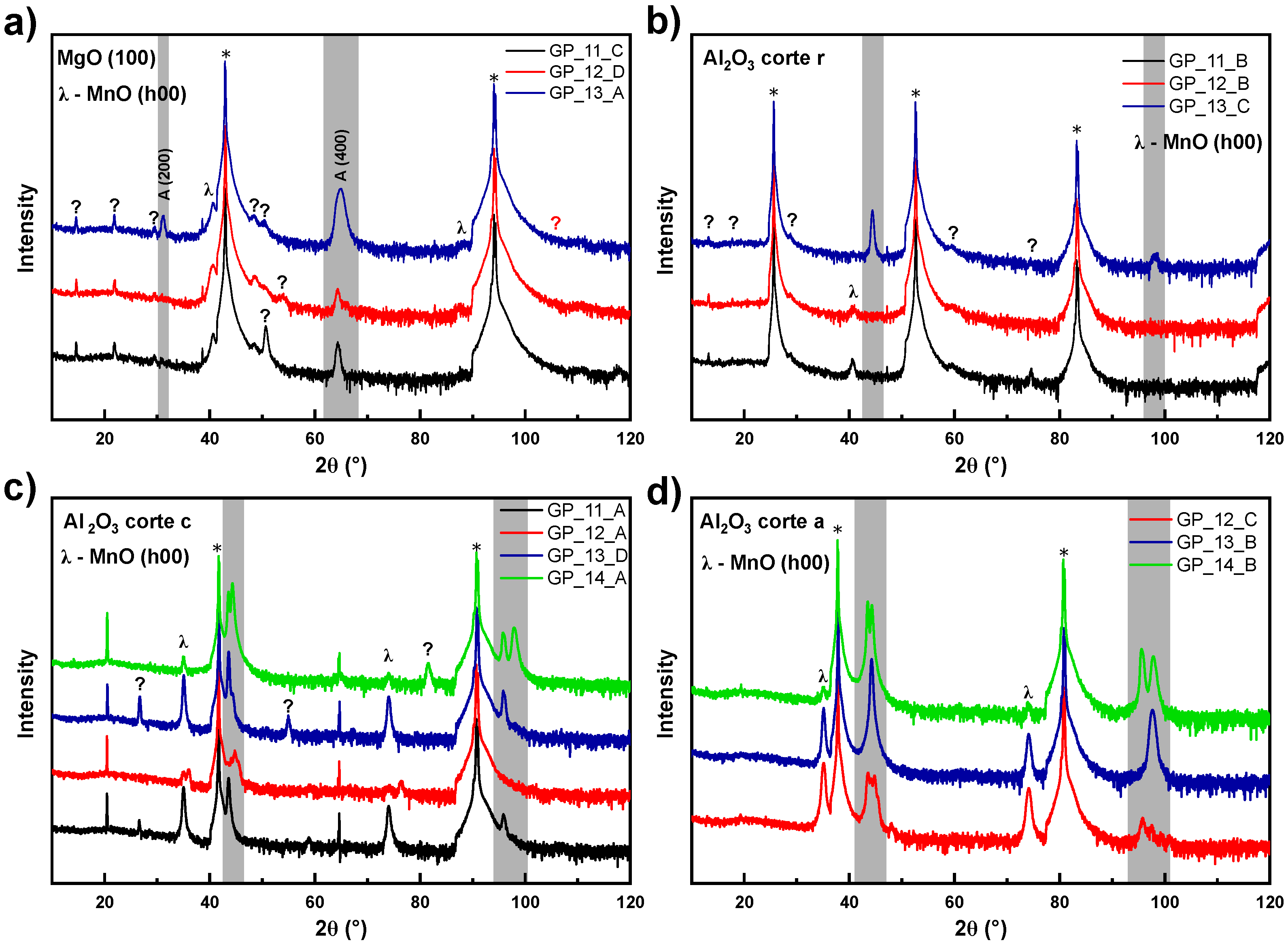
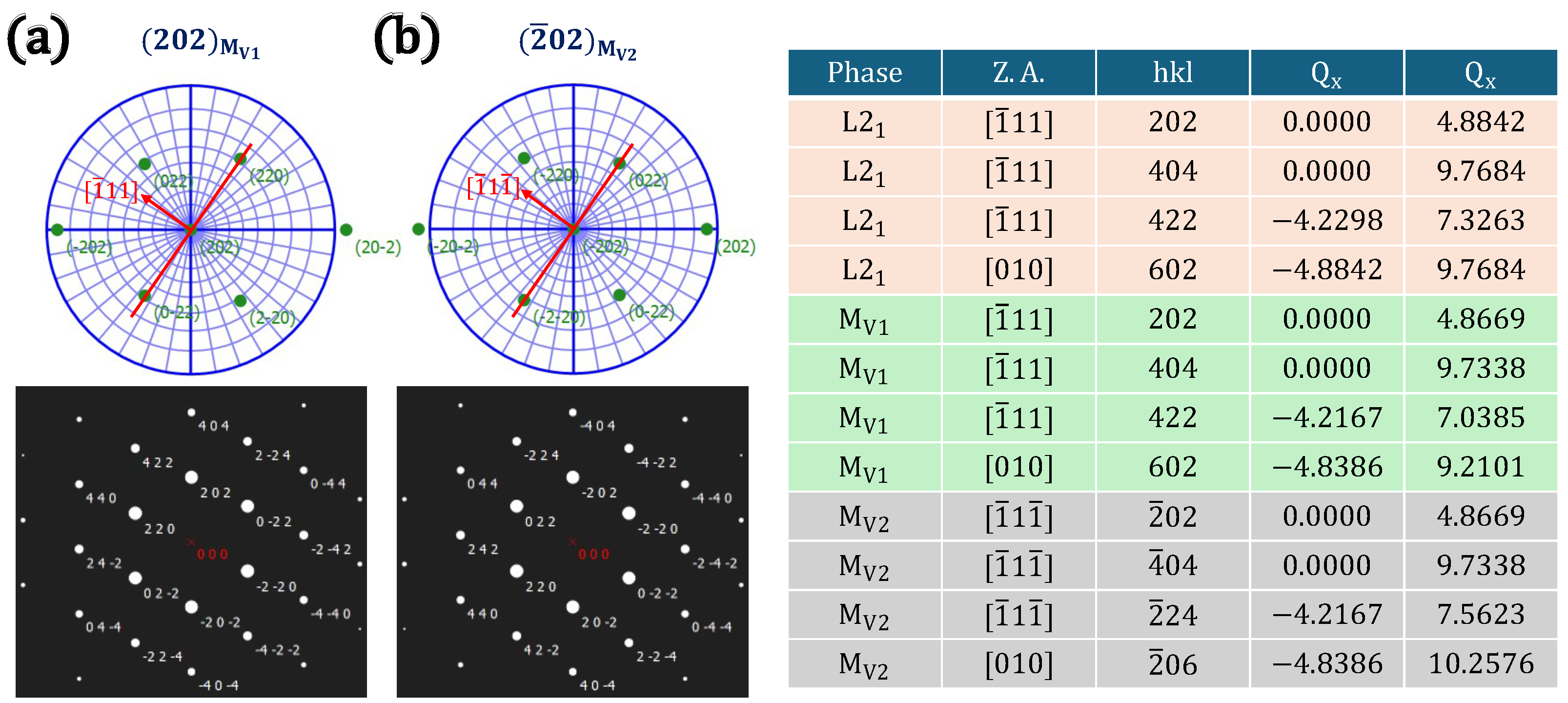
Appendix B. RSM for Martensite Variants
References
- Yu, G.H.; Xu, Y.L.; Liu, Z.H.; Qiu, H.M.; Zhu, Z.Y.; Huang, X.P.; Pan, L.Q. Recent progress in Heusler-type magnetic shape memory alloys. Rare Met. 2015, 34, 527–539. [Google Scholar] [CrossRef]
- Karaca, H.; Karaman, I.; Basaran, B.; Lagoudas, D.; Chumlyakov, Y.; Maier, H. On the stress-assisted magnetic-field-induced phase transformation in Ni2MnGa ferromagnetic shape memory alloys. Acta Mater. 2007, 55, 4253–4269. [Google Scholar] [CrossRef]
- Ullakko, K.; Huang, J.K.; Kantner, C.; O’Handley, R.C.; Kokorin, V.V. Large magnetic-field-induced strains in Ni2MnGa single crystals. Appl. Phys. Lett. 1996, 69, 1966–1968. [Google Scholar] [CrossRef]
- Kainuma, R.; Imano, Y.; Ito, W.; Sutou, Y.; Morito, H.; Okamoto, S.; Kitakami, O.; Oikawa, K.; Fujita, A.; Kanomata, T.; et al. Magnetic-field-induced shape recovery by reverse phase transformation. Nature 2006, 439, 957–960. [Google Scholar] [CrossRef]
- Ranzieri, P.; Campanini, M.; Fabbrici, S.; Nasi, L.; Casoli, F.; Cabassi, R.; Buffagni, E.; Grillo, V.; Magén, C.; Celegato, F.; et al. Achieving Giant Magnetically Induced Reorientation of Martensitic Variants in Magnetic Shape-Memory Ni–Mn–Ga Films by Microstructure Engineering. Adv. Mater. 2015, 27, 4760–4766. [Google Scholar] [CrossRef]
- Murray, S.J.; Marioni, M.A.; Kukla, A.M.; Robinson, J.; O’Handley, R.C.; Allen, S.M. Large field induced strain in single crystalline Ni–Mn–Ga ferromagnetic shape memory alloy. J. Appl. Phys. 2000, 87, 5774–5776. [Google Scholar] [CrossRef]
- Sozinov, A.; Likhachev, A.A.; Lanska, N.; Ullakko, K. Giant magnetic-field-induced strain in NiMnGa seven-layered martensitic phase. Appl. Phys. Lett. 2002, 80, 1746–1748. [Google Scholar] [CrossRef]
- Ullakko, K.; Ezer, Y.; Sozinov, A.; Kimmel, G.; Yakovenko, P.; Lindroos, V. Magnetic-field-induced strains in polycrystalline Ni-Mn-Ga at room temperature. Scr. Mater. 2001, 44, 475–480. [Google Scholar] [CrossRef]
- Chmielus, M.; Zhang, X.X.; Witherspoon, C.; Dunand, D.C.; Müllner, P. Giant magnetic-field-induced strains in polycrystalline Ni–Mn–Ga foams. Nat. Mater. 2009, 8, 863–866. [Google Scholar] [CrossRef]
- Brown, P.J.; Crangle, J.; Kanomata, T.; Matsumoto, M.; Neumann, K.U.; Ouladdiaf, B.; Ziebeck, K.R.A. The crystal structure and phase transitions of the magnetic shape memory compound Ni2MnGa. J. Phys. Condens. Matter 2002, 14, 10159–10171. [Google Scholar] [CrossRef]
- Cong, D.Y.; Wang, Y.D.; Zetterström, P.; Peng, R.L.; Delaplane, R.; Zhao, X.; Zuo, L. Crystal structures and textures of hot forged Ni48Mn30Ga22alloy investigated by neutron diffraction technique. Mater. Sci. Technol. 2005, 21, 1412–1416. [Google Scholar] [CrossRef]
- Glavatskyy, I.; Glavatska, N.; Urubkov, I.; Hoffman, J.U.; Bourdarot, F. Crystal and magnetic structure temperature evolution in Ni–Mn–Ga magnetic shape memory martensite. Mater. Sci. Eng. A 2008, 481–482, 298–301. [Google Scholar] [CrossRef]
- Sozinov, A.; Likhachev, A.A.; Lanska, N.; Soderberg, O.; Ullakko, K.; Lindroos, V.K. Effect of crystal structure on magnetic-field-induced strain in Ni-Mn-Ga. In Smart Structures and Materials 2003: Active Materials: Behavior and Mechanics; Lagoudas, D.C., Ed.; SPIE: Bellingham, WA, USA, 2003; Volume 5053, p. 586. [Google Scholar] [CrossRef]
- Gruner, M.E.; Niemann, R.; Entel, P.; Pentcheva, R.; Rößler, U.K.; Nielsch, K.; Fähler, S. Modulations in martensitic Heusler alloys originate from nanotwin ordering. Sci. Rep. 2018, 8, 8489. [Google Scholar] [CrossRef]
- Wei, Z.Y.; Liu, E.K.; Li, Y.; Han, X.L.; Du, Z.W.; Luo, H.Z.; Liu, G.D.; Xi, X.K.; Zhang, H.W.; Wang, W.H.; et al. Magnetostructural martensitic transformations with large volume changes and magneto-strains in all-d-metal Heusler alloys. Appl. Phys. Lett. 2016, 109, 071904. [Google Scholar] [CrossRef]
- Dunand, D.C.; Müllner, P. Size Effects on Magnetic Actuation in Ni-Mn-Ga Shape-Memory Alloys. Adv. Mater. 2010, 23, 216–232. [Google Scholar] [CrossRef]
- Ranzieri, P.; Fabbrici, S.; Nasi, L.; Righi, L.; Casoli, F.; Chernenko, V.A.; Villa, E.; Albertini, F. Epitaxial Ni–Mn–Ga/MgO(100) thin films ranging in thickness from 10 to 100 nm. Acta Mater. 2013, 61, 263–272. [Google Scholar] [CrossRef]
- Sharma, A.; Mohan, S.; Suwas, S. Structural transformations in highly oriented seven modulated martensite Ni–Mn–Ga thin films on an Al2O3 substrate. J. Mater. Res. 2016, 31, 3016–3026. [Google Scholar] [CrossRef]
- Sharma, A.; Mohan, S.; Suwas, S. Evidence of adaptive modulation and magnetic field induced reorientation of variants in epitaxially grown Ni-Mn-Ga thin film on Al2O3 (11-20) substrate. Mater. Sci. Eng. B 2019, 242, 6–16. [Google Scholar] [CrossRef]
- Yang, B.; Soldatov, I.; Chen, F.; Zhang, Y.; Li, Z.; Yan, H.; Schäfer, R.; Wang, D.; Esling, C.; Zhao, X.; et al. Observation of magnetic domain evolution in constrained epitaxial Ni–Mn–Ga thin films on MgO(0 0 1) substrate. J. Mater. Sci. Technol. 2022, 102, 56–65. [Google Scholar] [CrossRef]
- Kar, S.; Ikeda, Y.; Lünser, K.; Woodcock, T.G.; Nielsch, K.; Reith, H.; Maaß, R.; Fähler, S. Growth Twins and Premartensite Microstructure in Epitaxial Ni-Mn-Ga Films. Acta Mater. 2023, 252, 118902. [Google Scholar] [CrossRef]
- Tello, P.G.; Castaño, F.J.; O’Handley, R.C.; Allen, S.M.; Esteve, M.; Castaño, F.; Labarta, A.; Batlle, X. Ni–Mn–Ga thin films produced by pulsed laser deposition. J. Appl. Phys. 2002, 91, 8234–8236. [Google Scholar] [CrossRef]
- Hakola, A.; Heczko, O.; Jaakkola, A.; Kajava, T.; Ullakko, K. Pulsed laser deposition of NiMnGa thin films on silicon. Appl. Phys. A 2004, 79, 1505–1508. [Google Scholar] [CrossRef]
- Zhang, Y.; Hughes, R.; Preston, J.; Botton, G.; Niewczas, M. Texture and Microstructure Studies on Films of Ni-Mn-Ga Produced by R. F. Sputtering and Pulsed Laser Deposition. In State-of-the-Art Research and Application of SMAs Technologies; Trans Tech Publications Ltd.: Bäch, Switzerland, 2008; Volume 59, pp. 11–17. [Google Scholar] [CrossRef]
- Yoshitake, T.; Shiraishi, G.; Nagayama, K. Elimination of droplets using a vane velocity filter for pulsed laser ablation of FeSi2. Appl. Surf. Sci. 2002, 197–198, 379–383. [Google Scholar] [CrossRef]
- Aziz, M.J. Film growth mechanisms in pulsed laser deposition. Appl. Phys. A 2008, 93, 579–587. [Google Scholar] [CrossRef]
- Seto, Y.; Ohtsuka, M. ReciPro: Free and open-source multipurpose crystallographic software integrating a crystal model database and viewer, diffraction and microscopy simulators, and diffraction data analysis tools. J. Appl. Crystallogr. 2022, 55, 397–410. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pinedo-Cuba, M.G.; Caicedo-Roque, J.M.; Padilla-Pantoja, J.; Quispe-Marcatoma, J.; Landauro, C.V.; Peña-Rodríguez, V.A.; Santiso, J.
Epitaxial Growth of Ni-Mn-Ga on Al2O3(
Pinedo-Cuba MG, Caicedo-Roque JM, Padilla-Pantoja J, Quispe-Marcatoma J, Landauro CV, Peña-Rodríguez VA, Santiso J.
Epitaxial Growth of Ni-Mn-Ga on Al2O3(
Pinedo-Cuba, Manuel G., José M. Caicedo-Roque, Jessica Padilla-Pantoja, Justiniano Quispe-Marcatoma, Carlos V. Landauro, Víctor A. Peña-Rodríguez, and José Santiso.
2025. "Epitaxial Growth of Ni-Mn-Ga on Al2O3(
Pinedo-Cuba, M. G., Caicedo-Roque, J. M., Padilla-Pantoja, J., Quispe-Marcatoma, J., Landauro, C. V., Peña-Rodríguez, V. A., & Santiso, J.
(2025). Epitaxial Growth of Ni-Mn-Ga on Al2O3(





