Design of Deterministic Microstructures as Substrate Pre-Treatment for CVD Diamond Coating
Abstract
1. Introduction
- In their report, Seewig et al. introduced the 3D standard DIN EN ISO 25178, which claims to make the best possible use of the potential of topography evaluation [13]. The measuring chain, consisting of measurement data acquisition, measurement data preparation, and available characteristic operators, was described. The application limits of the ISO were also considered and alternative methods presented and compared with each other.
- In the book “Characterization of Areal Surface Texture”, Leach recognized the growing need for three-dimensional (area) measurement and characterization techniques with the increasing need to control the functionality of surfaces [14]. Therefore, he presented an areal framework adopted by the international community. Unlike many other contributions that often address the measurement aspects, the book focused on the characterization techniques. The interpretation of the measured data was to decide importance in order to generate suitable (functional) information for a given task.
- In his PhD thesis, Hartmann concluded that conventional tolerance concepts for the specification and verification of geometric features (e.g., ISO GPS) are limited for applications in the micro- and nanometer range [15]. This can be explained by the insufficient mapping of functional relationships between geometrical and non-geometrical features, which significantly influence the functionality of a workpiece. In the design-oriented verification process, only standardized parameters are recorded and evaluated independently of each other. A holistic, multi-dimensional assessment of acquired measurement data with respect to a function-oriented conformity decision is missing. In his work, Hartmann provides an approach for solving this deficiency by means of a transferable method for the predicative assessment of the degree of expected functionality of structured workpiece surfaces. The models are based on real surface measurement data.
2. Materials and Methods
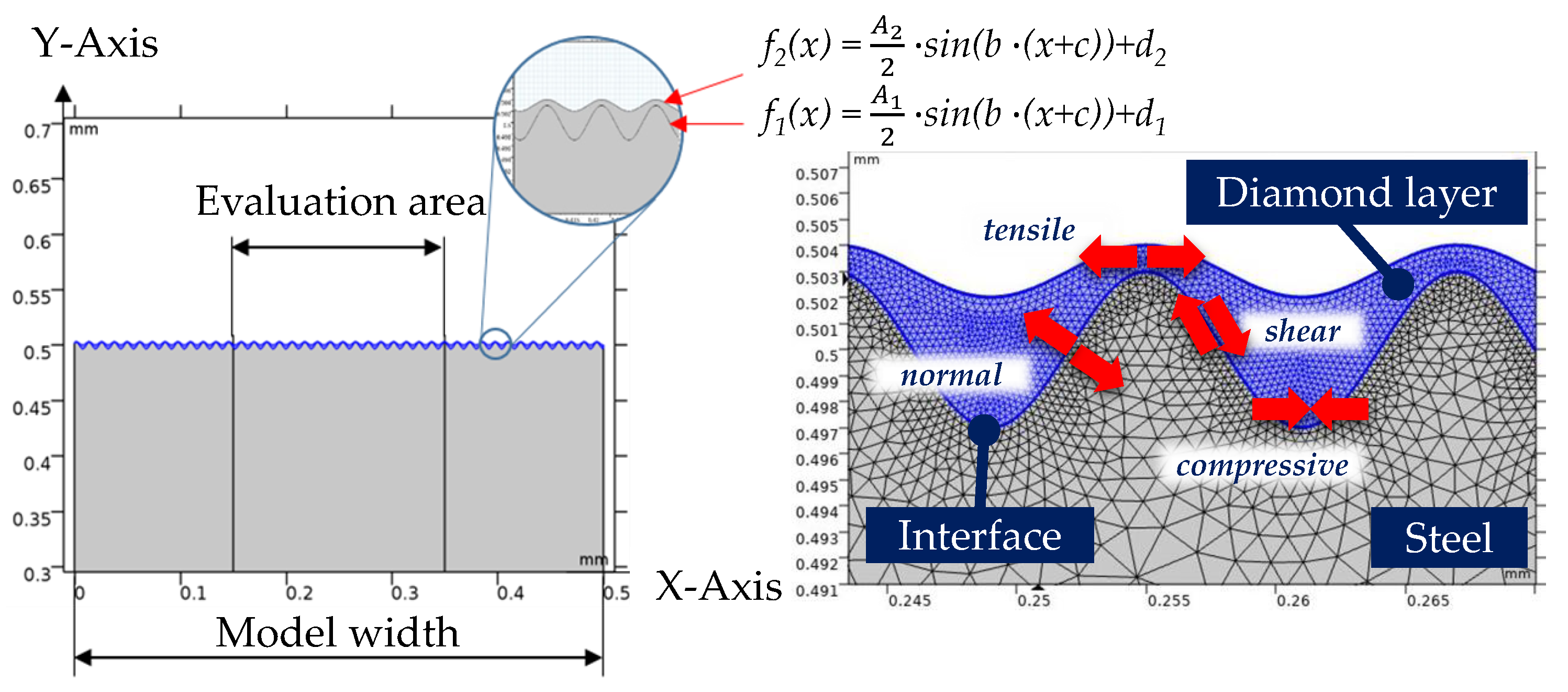
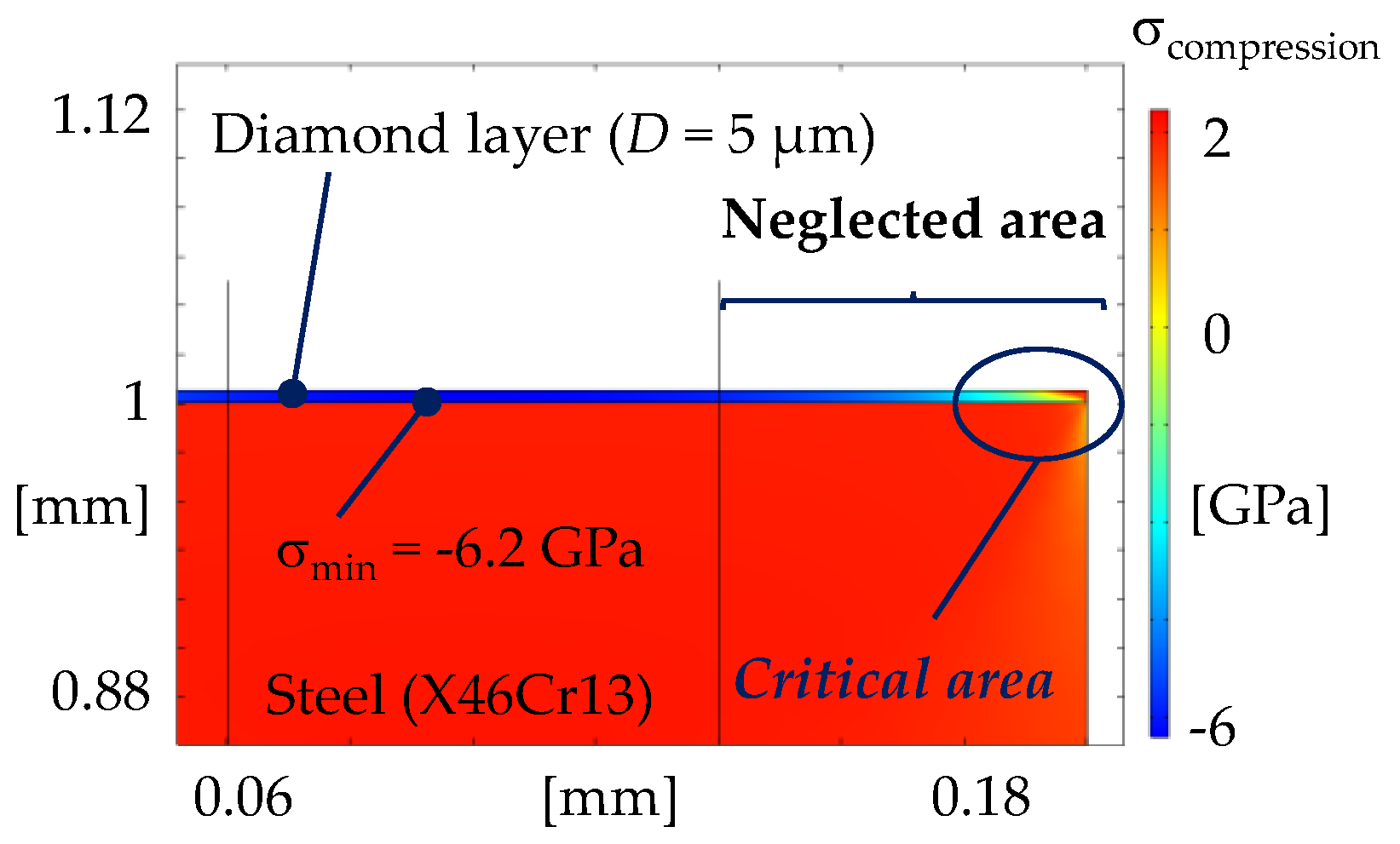
2.1. Cooling Simulation Model
- a chemically necessary intermediate layer including its geometric and material-specific properties;
- the variability of the thermal expansion coefficient of the materials considered in relation to the temperature;
- the phase transformation of the steel material as well as its associated volume change;
- the cooling rate; and
- the grain size of the diamond layer: micro or nano crystalline.
2.2. Kinematic Surface Simulation Model
2.3. Ultrasonic Vibration Superimposed Machining
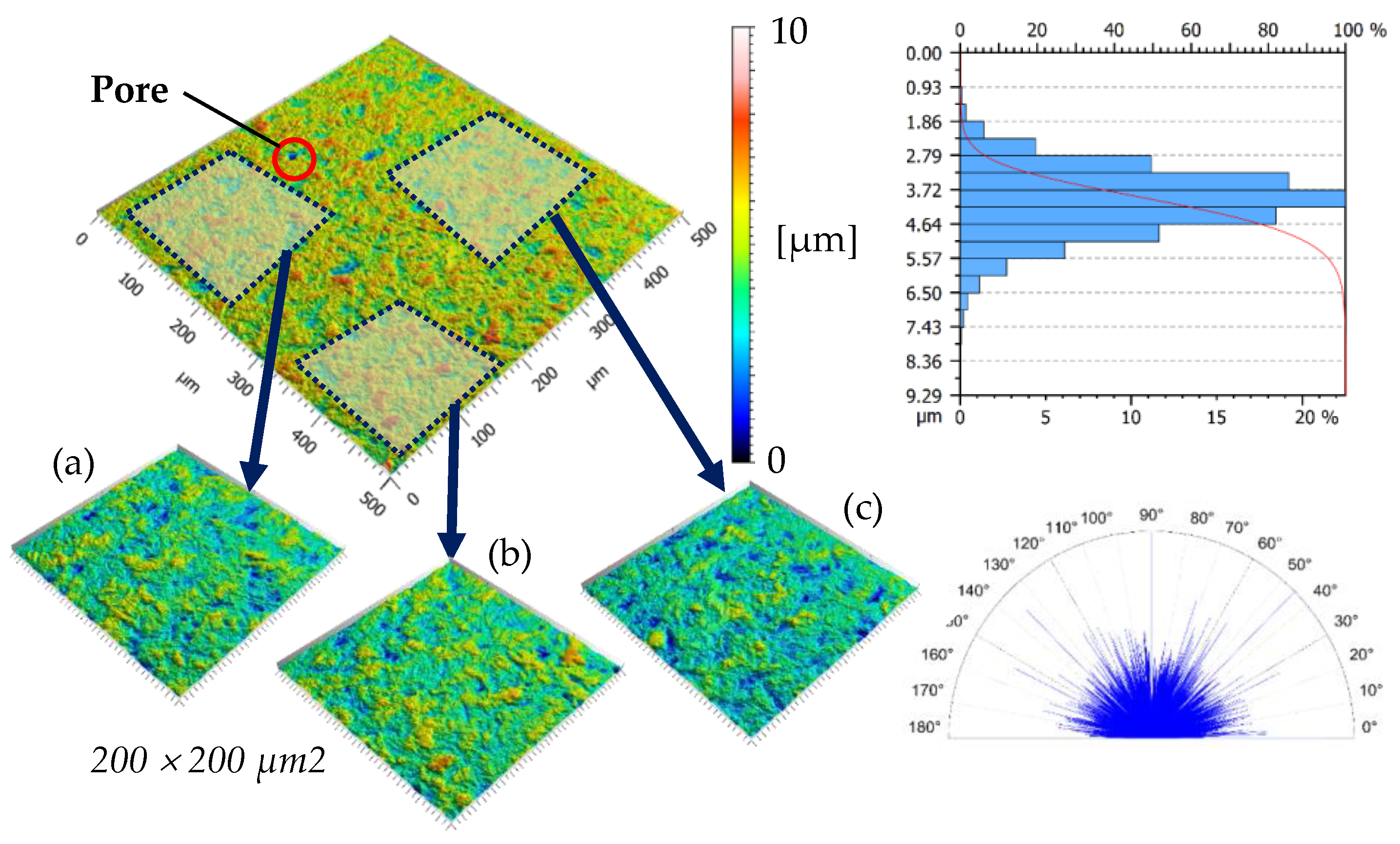
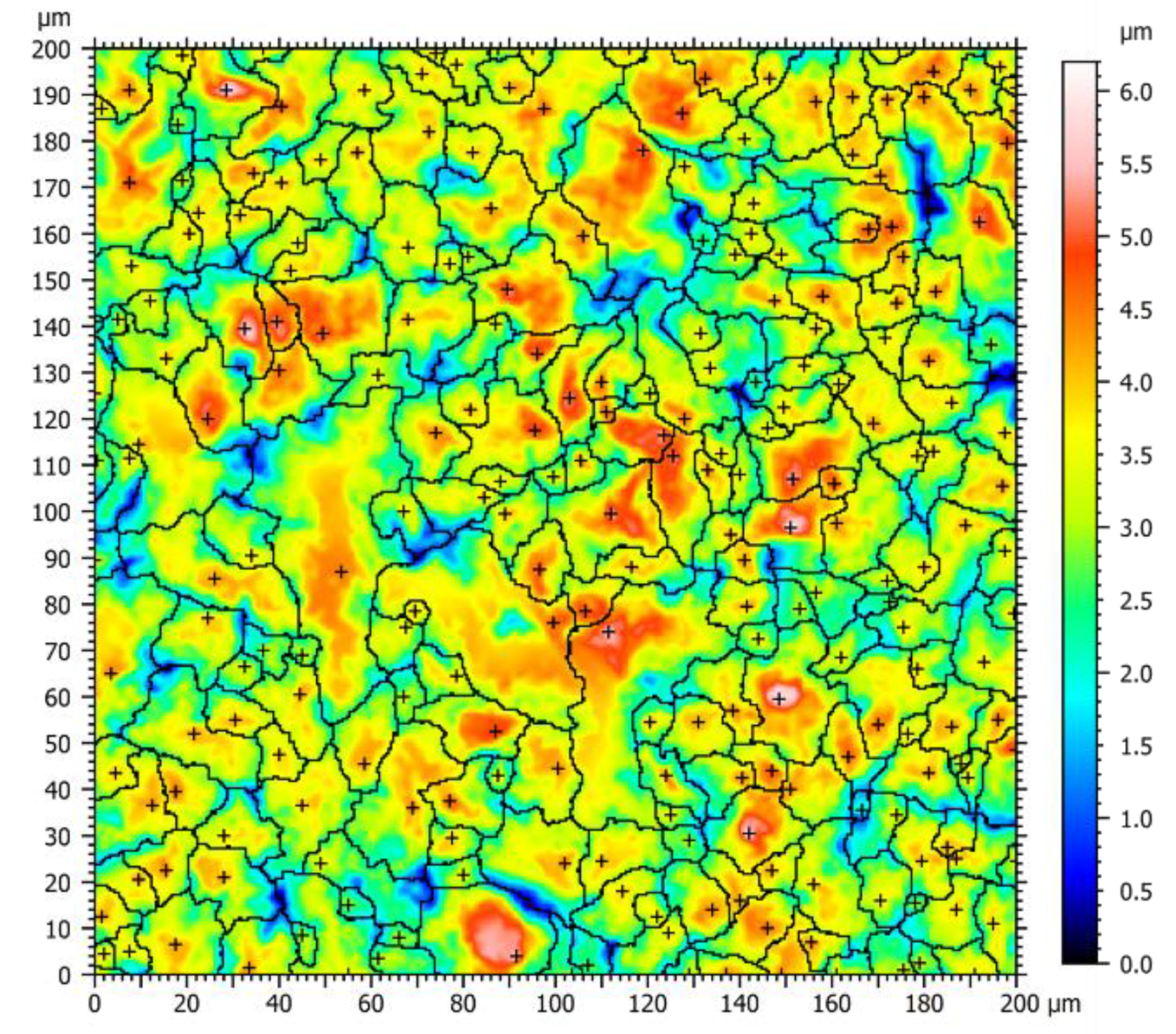
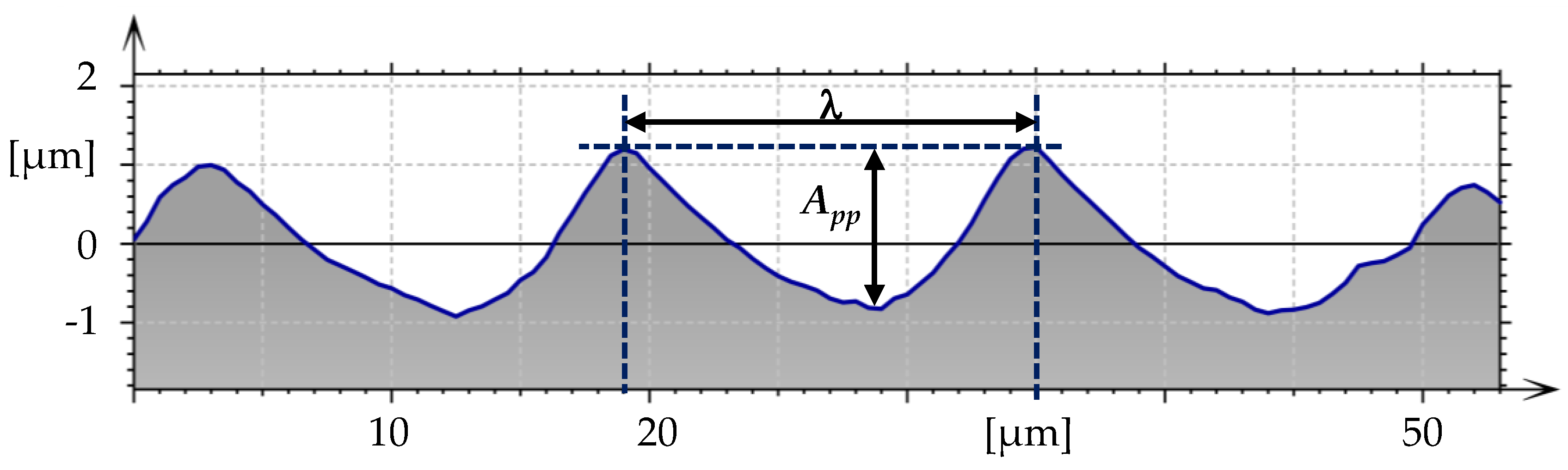
2.4. Surface Measurement and Analysis
3. Results
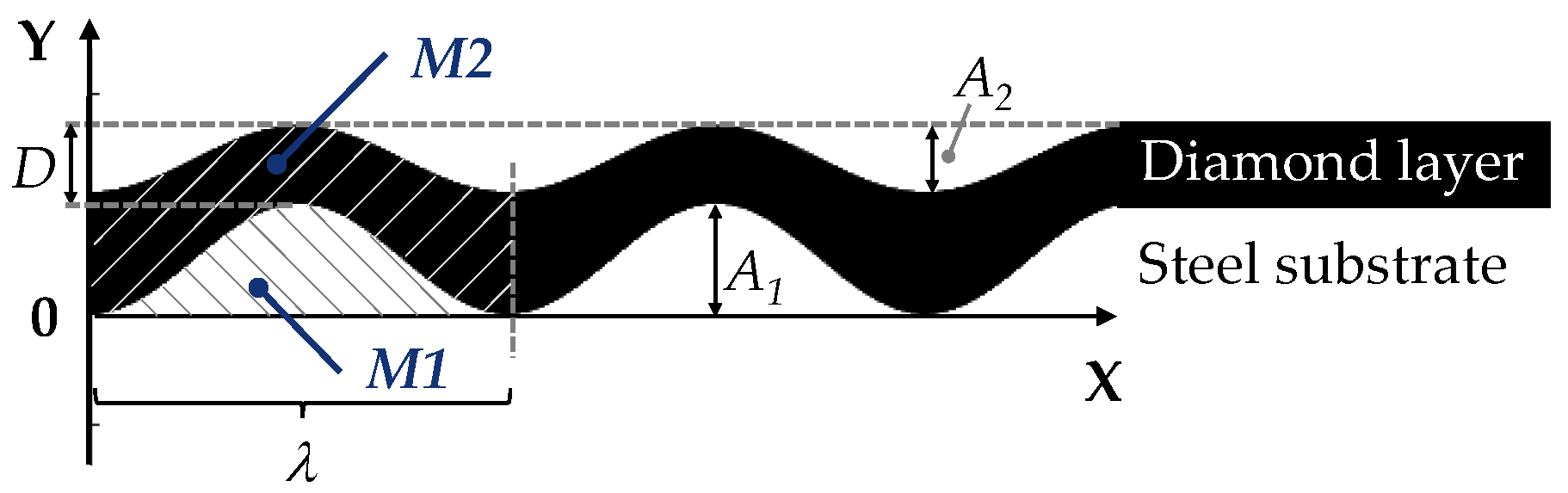
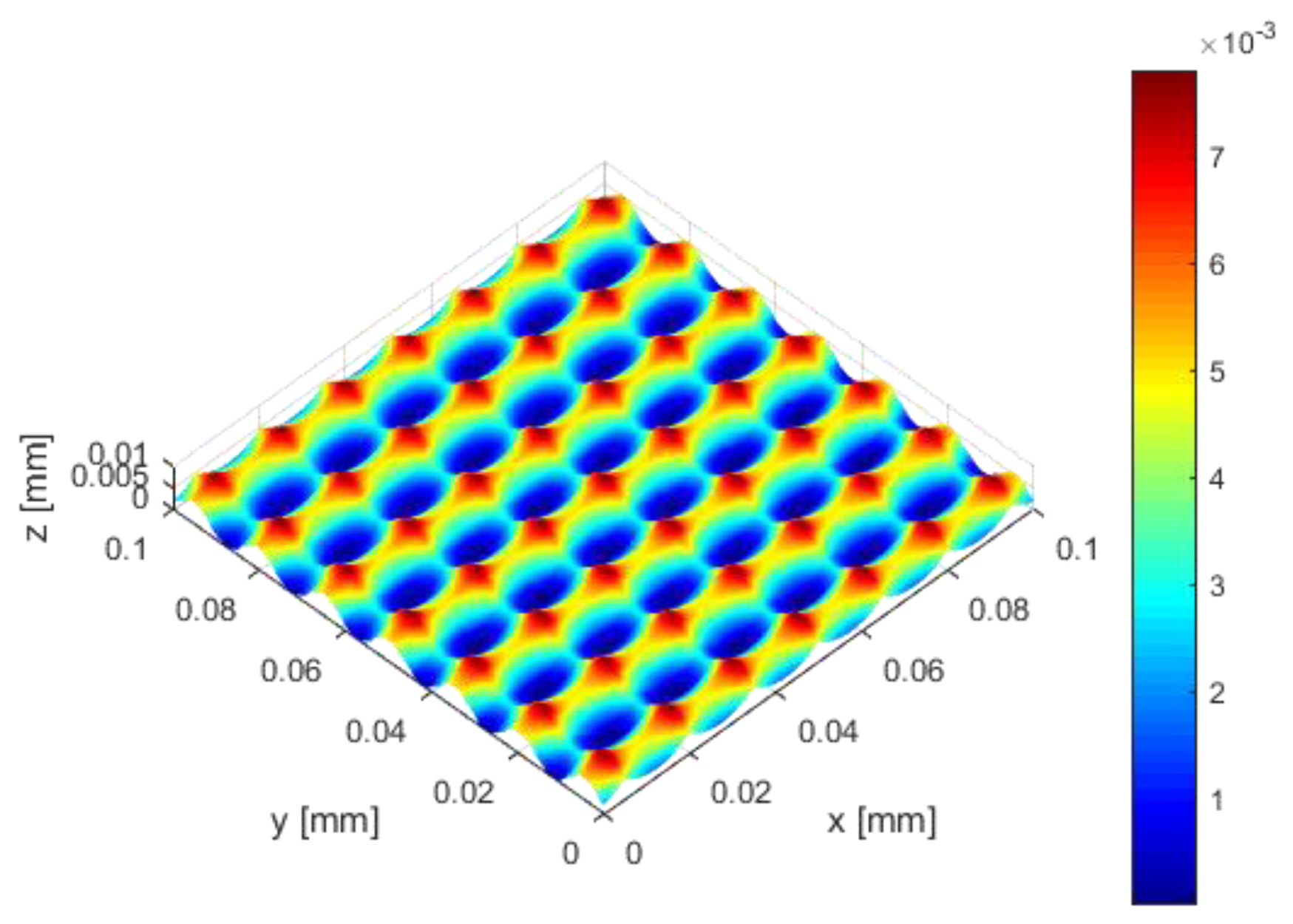
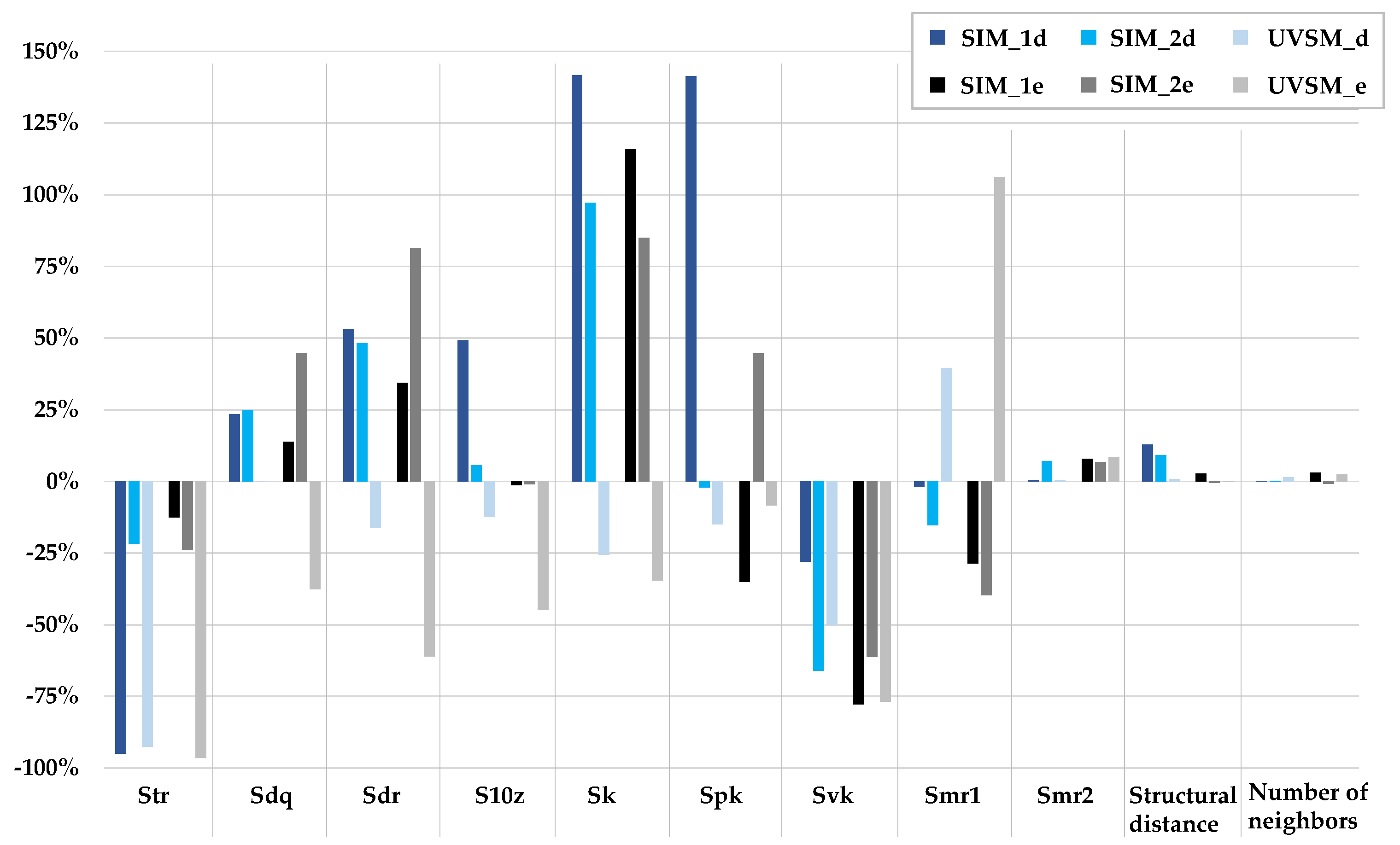
3.1. Surface Derivation
- Profile height: approx. 5 μm
- Distance between motifs: approx. 15–16 μm
- Number of motif neighbors: 5–6
- Furthermore, the following features are desired:
- ⚬
- an isotropic surface or a distribution of the microstructures without preferential direction, respectively;
- ⚬
- an even material distribution; and
- ⚬
- more steep than flat microstructures.
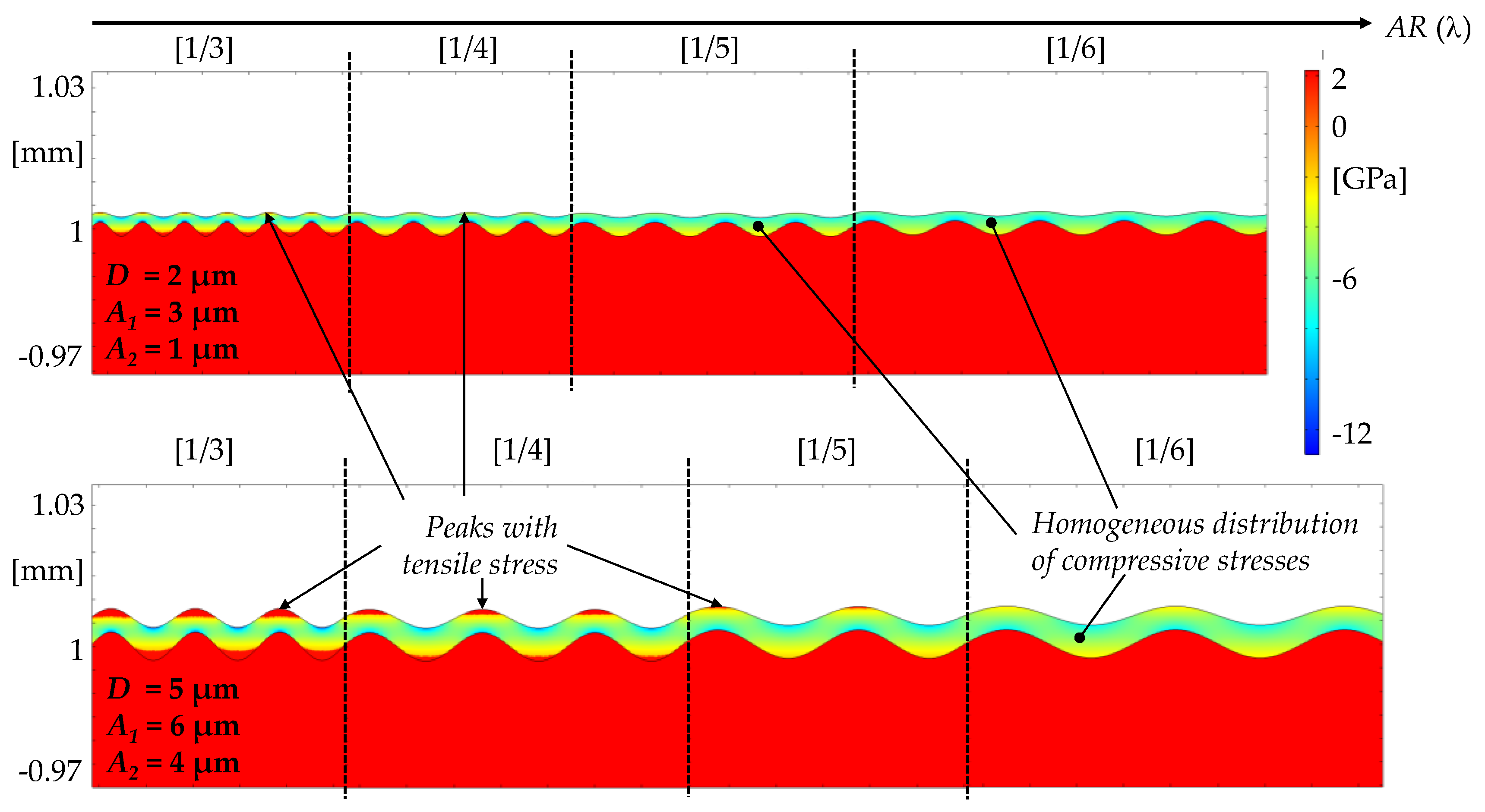
3.2. Results of the Cooling Simulation
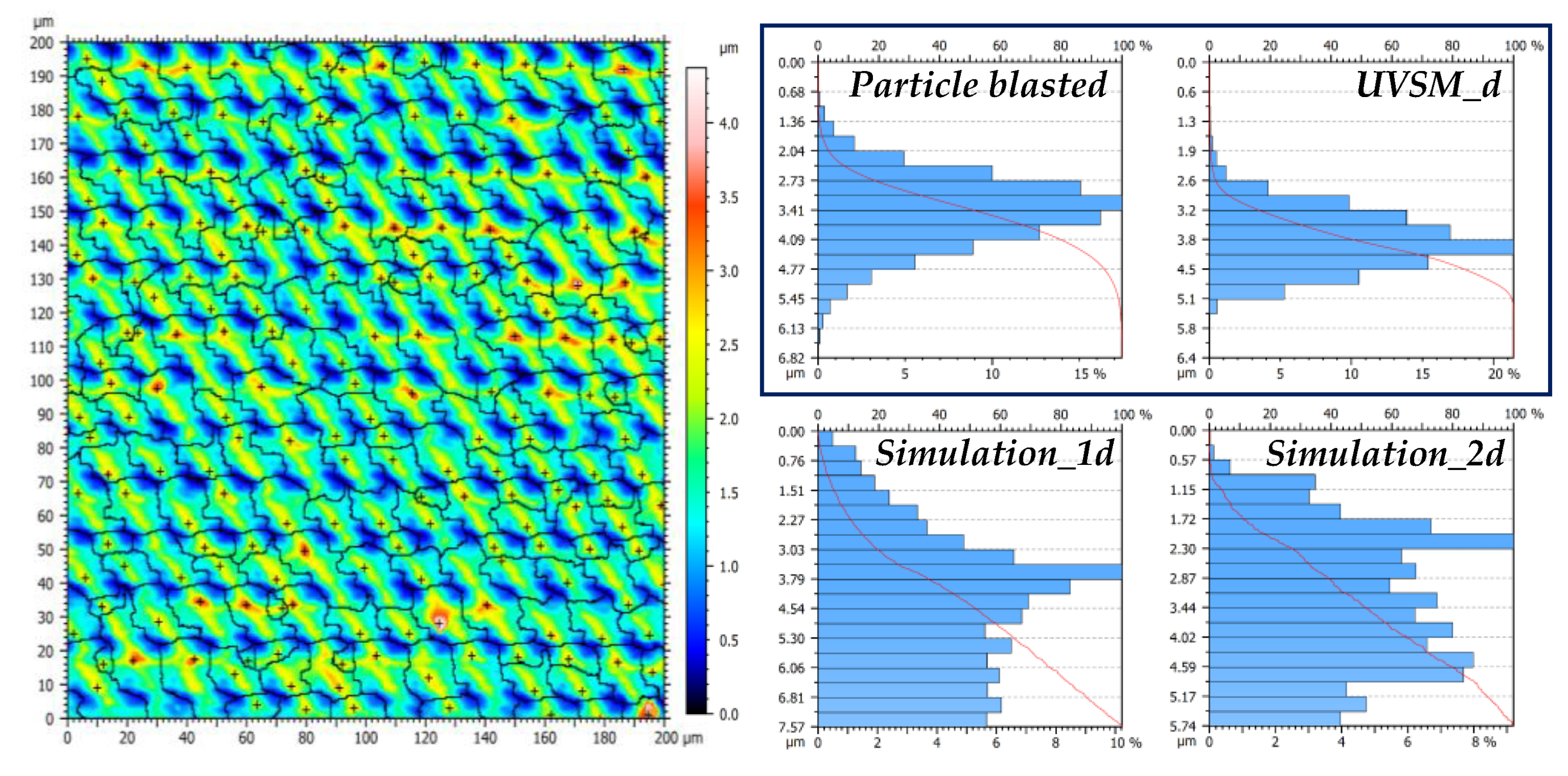
3.3. Surface Simulation and Manufacturing via UVSM
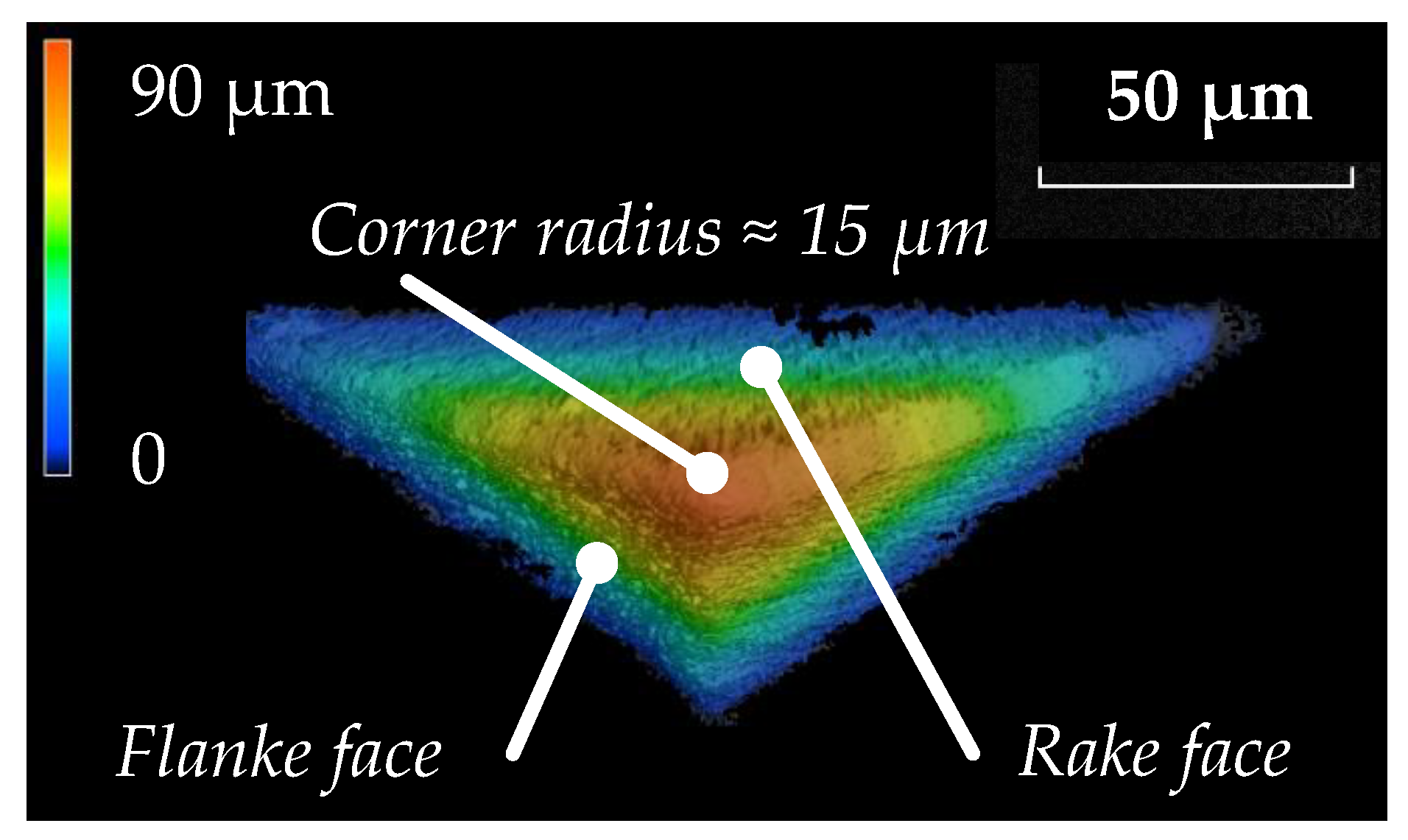
3.4. Tool Wear Behavior
4. Discussion
5. Summary and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviation
| Symbol | Definition |
| A1 | Amplitude of the substrate microstructure: peak–peak (µm) |
| A2 | Amplitude of the diamond layer: peak–peak (µm) |
| Afz | Aspect ratio in the direction of the feed velocity |
| AP | Mathematical amplitude (μm) |
| App | Measured ultrasonic amplitude: peak-peak (μm) |
| AR | Aspect ratio |
| AUS | Ultrasonic amplitude: peak-peak (μm) |
| CAD | Computer-aided design |
| CR | Contour mapping ratio |
| CS | Cooling simulation |
| CVD | Chemical vapor deposition |
| D | Diamond layer thickness (µm) |
| Dtool | Tool diameter (mm) |
| fsim | Sampling rate (s−1) |
| fUS | Ultrasonic frequency (kHz) |
| fz | Feed per tooth (μm) |
| HSS | High speed steel |
| LR | Layer thickness ratio |
| MR | Material ratio |
| M1 | Material of the substrate of a period (µm2) |
| M2 | Material of the diamond layer of a period (µm2) |
| n | Integer |
| ntool | Rotational speed (min−1) |
| N | Number of intersections per period |
| rtool, eff | Effective tool radius (mm) |
| rε | Corner radius (µm) |
| Rfz | Ratio of the feed per tooth in relation to the wavelength of the oscillation |
| Rrε | Ratio of the corner radius in relation to the wavelength of the oscillation |
| Rzcalc | Maximum possible structure height |
| Rλ | Ratio of the ultrasonic frequency in relation to the rotational speed |
| S10z | Ten-point height (µm) |
| Sdq | Root mean square gradient |
| Sdr | Surface magnification (%) |
| Sk | Core roughness depth (μm) |
| Smr1 | Peak material portion (%) |
| Smr2 | Valley material portion (%) |
| Spk | Reduced peak height (μm) |
| STL | CAD-file format (Standard Triangulation/Tesselation Language) |
| Str | Isotropy (%) |
| Svk | Reduced valley depth (μm) |
| Sz | Maximum height (µm) |
| tsim | Minimum temporal resolution (s) |
| UVSM | Ultrasonic vibration superimposed machining |
| vf | Feed velocity (mm/min) |
| κ | Angle of the major cutting edge (1°) |
| κ’ | Angle of the minor cutting edge (1°) |
| λ | Wavelength of the oscillation/structural distance in direction of the cutting speed (μm) |
| σμιν | Minimum principal stress (GPa) |
| ΔXY | Distance of neighboring dexels in X and Y direction (µm) |
| Δσcompression | (absolute) Difference of the compressive stresses (GPa) |
Appendix A
References
- Amaral, M.; Almeida, F.; Fernandes, A.; Costa, F.; Oliveira, F.; Silva, R.; Costa, F.; Oliveira, F. The role of surface activation prior to seeding on CVD diamond adhesion. Surf. Coat. Technol. 2010, 204, 3585–3591. [Google Scholar] [CrossRef]
- Singh, R.K.; Gilbert, D.R.; Fitz-Gerald, J.; Harkness, S.; Lee, D.G. Engineered Interfaces for Adherent Diamond Coatings on Large Thermal-Expansion Coefficient Mismatched Substrates. Science 1996, 272, 396–398. [Google Scholar] [CrossRef]
- Wako, H.; Abe, T.; Takagi, T.; Ikohagi, T. Comparison of diamond film adhesion on molybdenum substrates with different surface morphologies. Appl. Surf. Sci. 2009, 256, 1466–1471. [Google Scholar] [CrossRef]
- Xu, Z.; Lev, L.; Lukitsch, M.; Kumar, A. Effects of surface pretreatments on the deposition of adherent diamond coatings on cemented tungsten carbide substrates. Diam. Relat. Mater. 2017, 16, 461–466. [Google Scholar] [CrossRef]
- Gomez, H.; Durham, D.; Xiao, X.; Lukitsch, M.; Lu, P.; Chou, K.; Sachdev, A.; Kumar, A. Adhesion analysis and dry machining performance of CVD diamond coatings deposited on surface modified WC-Co turning inserts. J. Mater. Process. Technol. 2012, 212, 523–533. [Google Scholar] [CrossRef]
- Lee, D.; Gilbert, D.; Lee, S.; Singh, R. Surface composites: A novel method to fabricate adherent interfaces in thermal-mismatched systems. Compos. Part B Eng. 1999, 30, 667–674. [Google Scholar] [CrossRef]
- Grögler, T.; Zeiler, E.; Horner, A.; Rosiwal, S.; Singer, R. Microwave-plasma-CVD of diamond coatings onto titanium and titanium alloys. Surf. Coat. Technol. 1998, 98, 1079–1091. [Google Scholar] [CrossRef]
- Grögler, T.; Franz, A.; Klaffke, D.; Rosiwal, S.M.; Singer, R.F. Tribological optimization of CVD diamond coated Ti-6Al-4V1. Diam. Relat. Mater. 1998, 7, 1342–1347. [Google Scholar] [CrossRef]
- Grögler, T.; Plewa, O.; Rosiwal, S.; Singer, R. CVD diamond films as protective coatings on titanium alloys. Int. J. Refract. Met. Hard Mater. 1998, 16, 217–222. [Google Scholar] [CrossRef]
- Zeiler, E.; Klaffke, D.; Hiltner, K.; Grögler, T.; Rosiwal, S.; Singer, R. Tribological performance of mechanically lapped chemical vapor deposited diamond coatings. Surf. Coat. Technol. 1999, 116, 599–608. [Google Scholar] [CrossRef]
- Lim, P.; Lin, F.; Shih, H.; Ralchenko, V.; Varnin, V.; Pleskov, Y.; Hsu, S.; Chou, S.; Hsu, P. Improved stability of titanium based boron-doped chemical vapor deposited diamond thin-film electrode by modifying titanium substrate surface. Thin Solid Films 2008, 516, 6125–6132. [Google Scholar] [CrossRef]
- Damm, D.D.; Contin, A.; Barbieri, F.C.; Trava-Airoldi, V.J.; Barquete, D.M.; Corat, E.J. Interlayers Applied to CVD Diamond Deposition on Steel Substrate: A Review. Coatings 2017, 7, 141. [Google Scholar] [CrossRef]
- Seewig, J.; Wiehr, C.; Gröger, S. Charakterisierung Technischer Bauteiloberflächen, Arbeitskreis 3D-Rauheitsmesstechnik; VDI Wissensforum GmbH: Düsseldorf, Germany, 2012. [Google Scholar]
- Leach, R. Characterisation of Areal Surface Texture; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Hartmann, W.D. Mess- und Auswertestrategien zur Modellbasierten Bewertung Funktionaler Eigenschaften Mikrostrukturierter Oberflächen. Ph.D. Thesis, Friedrich-Alexander-Universität, Erlangen, Germany, 2014. [Google Scholar]
- Börner, R.; Winkler, S.; Junge, T.; Titsch, C.; Schubert, A.; Drossel, W.-G. Generation of functional surfaces by using a simulation tool for surface prediction and micro structuring of cold-working steel with ultrasonic vibration assisted face milling. J. Mater. Process. Technol. 2018, 255, 749–759. [Google Scholar] [CrossRef]
- Prieske, M.; Börner, R.; Schubert, A. Influence of the surface microstructure on the adhesion of a CVD-diamond coating on steel with a CrN interlayer. MATEC Web Conf. 2018, 190, 14008. [Google Scholar] [CrossRef][Green Version]
- Kellermann, K.; Bareiß, C.; Rosiwal, S.M.; Singer, R.F. Well Adherent Diamond Coatings on Steel Substrates. Adv. Eng. Mater. 2008, 10, 657–660. [Google Scholar] [CrossRef]


| Constant Parameter | rtool, eff [mm] | κ [°] | κ’ [°] | AUS [µm] | fUS [kHz] |
|---|---|---|---|---|---|
| value | 9 | 45 | 45 | 4 | 19 |
| Variable Parameter | ntool [min−1] | fz [µm] | rε [µm] |
|---|---|---|---|
| value | 523.056/523.176 | 12.97/25.95/51.89 | 6.49/12.97/25.95 |
| Rλ = X.5 | |||
|---|---|---|---|
| Rfz | Rrε = 0.5 | Rrε = 1 | Rrε = 2 |
| 0.5 |  |  |  |
| 1 |  |  |  |
| 2 |  |  |  |
| Rλ = X.0 | |||
|---|---|---|---|
| Rfz | Rrε = 0.5 | Rrε = 1 | Rrε = 2 |
| 0.5 | 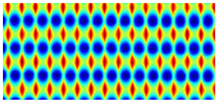 |  |  |
| 1 |  |  | 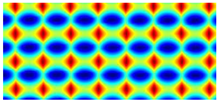 |
| 2 |  |  | 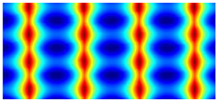 |
| Surface Parameter | Value (a/b/c) | Average |
|---|---|---|
| S10z [µm] | 4.46/5.00/5.71 | 5.1 |
| Sdr in % | 16.1/16.9/16.8 | 16.6 |
| Str in % | 88/83/84 | 85 |
| Sdq | 0.62/0.64/0.64 | 0.63 |
| Abbott curve | ||
| 2.04/1.93/1.95 0.62/0.61/0.75 0.81/0.82/0.87 8.32/9.79/9.83 89.6/88.4/89.1 | 1.97 0.66 0.83 9.3 89 |
| Averaged motif distance [µm] | 15.2/15.0/17.1 | 15.8 |
| Number of neighbors | 5.33/5.47/5.35 | 5.4 |
| Designation | Calculation | Description |
|---|---|---|
| AR | A1/λ | Aspect ratio |
| CR | A2/A1 | Contour mapping ratio |
| LR | D/A1 | Layer thickness ratio |
| MR | Terms (9–11) | Material ratio |
| Parameter | Unit | Value |
|---|---|---|
| Substrate amplitude A1 | [µm] | 2; 3; 4; 5; 6 |
| Layer amplitude A2 | [µm] | A1-2*n (0 ≤ n ≤ A1/2) |
| Layer thickness D | [µm] | 2; 5 |
| Aspect ratio AR | - | 1/3; 1/4; 1/5; 16 |
| Thickness Diamond Layer | D = 2 µm | D = 5 µm | |||||||
|---|---|---|---|---|---|---|---|---|---|
| A1 | A2 | Aspect Ratio AR (A1/λ) | |||||||
| [µm] | 1/3 | 1/4 | 1/5 | 1/6 | 1/3 | 1/4 | 1/5 | 1/6 | |
| 2 | 0 | 5.23 | 4.09 | 3.28 | 2.68 | 4.13 | 3.01 | 2.23 | 1.68 |
| 2 | 2 | 6.42 | 4.84 | 3.80 | 3.00 | 8.87 | 7.07 | 5.82 | 4.84 |
| 3 | 1 | 5.34 | 3.86 | 2.91 | 2.29 | 4.94 | 3.79 | 2.93 | 2.26 |
| 3 | 3 | 3.05 | 2.45 | 1.92 | 1.51 | 8.84 | 6.62 | 5.11 | 4.04 |
| 4 | 0 | 5.57 | 4.39 | 3.61 | 3.13 | 4.30 | 3.20 | 2.41 | 1.84 |
| 4 | 2 | 3.38 | 2.38 | 1.76 | 1.39 | 5.22 | 3.77 | 2.70 | 1.93 |
| 4 | 4 | 1.40 | 1.21 | 0.98 | 0.74 | 7.32 | 5.26 | 3.90 | 2.97 |
| 5 | 1 | 4.81 | 3.67 | 3.01 | 2.62 | 4.66 | 3.36 | 2.43 | 1.75 |
| 5 | 3 | 1.75 | 1.24 | 0.95 | 0.80 | 4.70 | 3.14 | 2.09 | 1.35 |
| 5 | 5 | 0.51 | 0.54 | 0.45 | 0.30 | 5.49 | 3.90 | 2.85 | 2.06 |
| 6 | 0 | 5.49 | 4.48 | 3.88 | 3.53 | 4.16 | 3.04 | 2.23 | 1.65 |
| 6 | 2 | 3.57 | 2.80 | 2.37 | 2.15 | 4.56 | 3.11 | 2.12 | 1.43 |
| 6 | 4 | 0.67 | 0.51 | 0.44 | 0.43 | 3.97 | 2.35 | 1.41 | 0.77 |
| 6 | 6 | 0.00 | 0.14 | 0.11 | 0.02 | 3.96 | 2.84 | 2.01 | 1.37 |
| Step | Variant (d) | Variant (e) |
|---|---|---|
| Technical adjustment: | ||
| - AUS - fz/λ - Rλ | 4 µm 16 µm/16 µm X.0 | 5 µm 10 µm/20 µm X.5 |
| Simulation 1 | 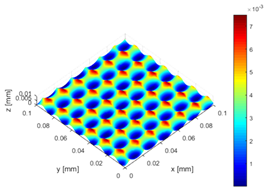 | 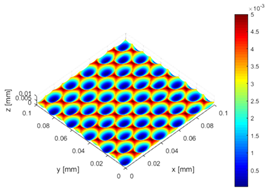 |
| Realistic adaption | Measured cutting tip (HSS, new condition); Rλ = X.5 | Measured cutting tip (HSS, new condition) |
| Simulation 2 | 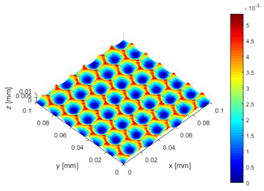 | 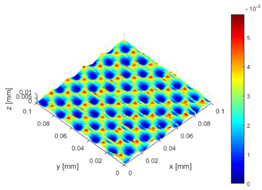 |
| UVSM |  | 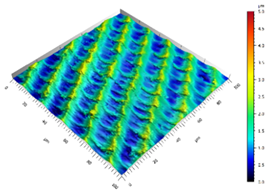 |
| Surface | Form Filter | Gaussian Filter | Sz-Filter |
|---|---|---|---|
| Particle blasted | ✓ | ✓ | 5% |
| Simulation_1d | - | - | 5% |
| Simulation_1e | - | - | 5% |
| Simulation_2d | - | - | 10% |
| Simulation_2e | - | - | 10% |
| UVSM_1d | ✓ | ✓ | 10% |
| UVSM_1e | ✓ | ✓ | 5% |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Börner, R.; Penzel, M.; Junge, T.; Schubert, A. Design of Deterministic Microstructures as Substrate Pre-Treatment for CVD Diamond Coating. Surfaces 2019, 2, 497-519. https://doi.org/10.3390/surfaces2030037
Börner R, Penzel M, Junge T, Schubert A. Design of Deterministic Microstructures as Substrate Pre-Treatment for CVD Diamond Coating. Surfaces. 2019; 2(3):497-519. https://doi.org/10.3390/surfaces2030037
Chicago/Turabian StyleBörner, Richard, Michael Penzel, Thomas Junge, and Andreas Schubert. 2019. "Design of Deterministic Microstructures as Substrate Pre-Treatment for CVD Diamond Coating" Surfaces 2, no. 3: 497-519. https://doi.org/10.3390/surfaces2030037
APA StyleBörner, R., Penzel, M., Junge, T., & Schubert, A. (2019). Design of Deterministic Microstructures as Substrate Pre-Treatment for CVD Diamond Coating. Surfaces, 2(3), 497-519. https://doi.org/10.3390/surfaces2030037





