Abstract
The Roman town of Ostia offers a unique opportunity to study a wide range of structural damage affecting different types of ancient buildings. In the Piccolo Mercato, potential seismic effects are visible in the masonry walls and in some of the masonry pillars that in ancient times supported an arcade. This paper, with the aim of providing insight into the causes of the observed damage on one of these pillars, reports and discusses some results of an interdisciplinary study. The damaged pillar under consideration, in particular, is today broken with the upper part rotated about 12 degrees counterclockwise from the lower part. Numerical simulations of this pillar have been performed using finite element models, and incremental nonlinear time-history analyses were carried out for quite a large number of seismic input ground motions. From the obtained results, it appears that a rotation, similar to that exhibited by the upper part of the pillar, can be attributed to seismic action with Peak Ground Acceleration (PGA) values ranging from medium to high.
1. Introduction
The investigation and study of potential seismic damage in historical buildings and archaeological sites can provide valuable insights into past earthquakes, including hypotheses about their intensity, direction, and other parameters. A building’s response to an earthquake depends on various factors related to its structural characteristics, such as design flaws, materials used, craftsmanship, and many others. Additionally, a building’s dynamic response during an earthquake is influenced by the site’s geology, which may amplify ground shaking.
Ancient buildings exhibit damage patterns similar to those observed in modern constructions during recent earthquakes [1,2]. However, these are not always easily recognizable as being caused by earthquakes. The archaeological restoration choices carried out in past centuries were rarely focused on preserving the proper readability of damage due to earthquakes, and restoration interventions—that included anastylosis and integration—over time have modified the original structures [3,4]. Moreover, the complexity of the formation of a damage pattern, which may have undergone a temporal evolution involving both static factors and seismic events, can make the interpretation of earthquake traces a real challenge [5]. Indeed, the interpretation of seismic-induced damage on archaeological remains should be carried out with extreme caution, following a methodological and multidisciplinary approach.
In recent years, archaeoseismology has experienced significant developments, providing concrete contributions in methodology and instrumentation [6,7]. Quantitative methods and a multidisciplinary approach have been recognized as of fundamental importance by many researchers in this field [8]. In this regard, methodologies supporting the results of archaeological and historical studies have used innovative photogrammetry techniques and data acquisition methods, enabling three-dimensional (3D) reconstructions and the creation of Digital Elevation Models [9,10,11,12]. Engineering approaches and mechanical analysis methods have been increasingly used to understand failure mechanisms and damage scenarios [13,14]. Among numerical models, discrete-element models (DEM) are often adopted [15,16,17], but also accurate finite element models (FEM) are sometimes used to perform numerical simulations [18,19,20]. In some research, advanced time-history analyses have been carried out using harmonic and impulsive actions or accelerometer recordings [21,22,23,24]. Of course, the architectural layout of the building and its resistance capabilities, at the time of the earthquake, should be known and adequately represented in the mechanical model used in the numerical simulations, to obtain reliable results.
To foster the knowledge of the historical seismic activity, the archaeological site of Ostia Antica represents a unique opportunity thanks to a wide range of structural damages affecting different types of ancient buildings. At the interdisciplinary workshop “Ostia and Portus Between Hypothesis and Reality”, held in Ostia in June 2022 [25], various research and analytical studies were shared and discussed. These studies focused on historic damage and collapses of structures, abandonments, and restorations possibly related to strong earthquakes in the past. The authors presented some initial results, as part of an interdisciplinary study, to interpret the damage observed on one of the pillars in the Piccolo Mercato (“Little Market”) (see Figure 1) in the archaeological area of Ostia [26]. Some preliminary numerical simulations, including a few nonlinear time-history analyses, were performed to validate the interpretation of the pillar’s damage and establish a possible timeframe. Specifically, two configurations of the pillar were investigated to determine whether a potential seismic event that caused the damage occurred before the abandonment of the town of Ostia. The first configuration considered the free-standing pillar as it appears today, isolated after the loss of the vaulted arcade that once covered the market area; conversely, the second configuration considered the presence of the vaults that rested on the pillar itself. The comparison of the obtained numerical results with the observed damage suggested that today’s observed pillar damage could be attributable to a past seismic event, and that this seismic event occurred when the complex was already abandoned.
This paper conducts an additional comprehensive numerical investigation on the same pillar of the Piccolo Mercato. The purpose is to obtain some quantitative results on the extent of the possible seismic shaking at the pillar’s base, compatible with the damage pattern visible today. Only the free-standing configuration of the pillar was considered, and nonlinear time-history analyses were performed to represent the free-standing pillar through finite element models and by applying a set of seven spectrum-compatible natural earthquake records.
2. Materials
2.1. The Ancient Roman City of Ostia
The history of Ostia Antica dates back to the 4th century B.C. when it was established as the port of Rome. It served as a crucial supply and trading hub for the city of Rome, allowing Ostia to play a vital role in Mediterranean trade and in providing grain and other goods to Rome over the centuries. The settlement flourished during the Roman Empire era, leading to the construction of many of its most notable buildings.
During Late Antiquity, the decline of Ostia Antica began as the Roman Empire faced economic and political crises. This significantly impacted on the importance of Ostia as a commercial port. Due to political instability and the weakening of central authority, trade declined, and the city lost its prosperity. Over time, the slow buildup of sediments and the shifting course of the Tiber River caused the port of Ostia to fill with silt [27]. This natural process diminished the city’s suitability as a port and commercial center.

Figure 1.
(a) Aerial view of the Piccolo Mercato in Ostia Antica with the location of the case study (the white circle) (from [26]); (b) The angular position of the pillar within the arcade around the courtyard; (c) Damage of the pillar, with the counterclockwise rotation of the upper part.
The decline of Ostia as an active settlement happened gradually over many centuries and was well underway by the 3rd century. Over time, the city was covered by river sediments until it was unearthed and excavated in modern times. Although there are no direct records of specific earthquakes in Ostia Antica in the 4th and 5th centuries, the city likely experienced them due to its geological location. Ostia was built on unstable ground, and changes in the relationship between land, river, and sea affected not only construction and urban development, but also contributed to the city’s decay. The ground conditions likely caused many damages and collapses in public and private buildings [13], in addition to earthquakes and other natural disasters. Today, Ostia Antica, along with Pompeii, with an area of about 150 hectares, is the largest archaeological site in Italy and one of the largest in the planet. In 2019 it received the European Heritage Label [28]. The ruins of the city were excavated from the beginning of the 19th century: numerous dwelling houses and productive structures have been preserved along with public monuments, making it an important testimony to ancient daily life. Currently only 40% of the site has been unearthed, thus more than half of the city is still buried.
2.2. The Piccolo Mercato and the Damaged Pillar
The name Piccolo Mercato (I, VIII, 1) refers to a complex excavated in the early 1870s in the North-Western part of the Forum near the riverbank. It was a large horreum covering an area of approximately 46 hectares, consisting of a series of rooms arranged around a central courtyard. It was constructed around 120 A.D. using the Opus mixtum construction technique. It was part of a predetermined master plan, which included neighboring structures like Horrea (I, VIII, 2), Caseggiato dei Misuratori del Grano (I, VII, 1), and Horrea Epagathiana. This complex was designed during Hadrian’s reign and played a key role in the development of the Tiber docks district, concurrent with the construction of Claudius’ and Trajan’s ports.
Figure 1c shows an aerial view of the Piccolo Mercato as it is today, while Figure 1b,c show the pillar investigated in this paper. In Figure 1c, the location of this pillar is shown with a white circle.
As can be inferred from Figure 1a,b, in ancient times the pillar belonged to an arcade. It was a corner element where two internal corridors intersected, with a width of 4.70 m and 4.40 m. The typology of the vaulted corridors can be deduced from similar cases, such as the one in the Insula degli Aurighi (III, X, 1). It is possible to hypothesize the original presence of a barrel vault with lateral lunettes oriented toward the cross, compatible with rectangular structural modules. Looking at the construction technique, it is noticeable that bonding (or leveling) courses of bipedales layers (large bricks approximately 58 cm side) are present at about two-fifths of the current height of the pillar, providing both an aesthetic interval and a better load distribution.
The pillar analyzed here is broken and rotated counterclockwise at an angle of about 12°. As seen in Figure 1c, the fracture and rotation around its vertical axis occurred at the level of the bipedals. Other pillars of the Piccolo Mercato and the Portici di Pio IX, having the same construction technique and materials, exhibit similar damage, though less pronounced. As early as 1918, Lanciani provided a detailed description of the pillar’s geometry, weight, and damage, attributing the latter to a seismic shock with a whirling effect, i.e., “iscossa vorticosa” [29].
3. Methods
3.1. The Seismic Activity of Ostia Antica
Beyond a limited amount of direct historical evidence, much of the information about the seismic activity of Ostia Antica comes from modern studies based on archaeological, geological, and seismic data. Several historical photos of archaeological excavations preserved at the archive in Ostia together with diaries, inscriptions, and other sources help to reconstruct the placements of ruins and interpret the possible causes of the variation from their original positions.
The first scholar to tackle this type of investigation was the archaeologist and engineer Rodolfo Lanciani, who can be considered a forerunner in archaeoseismology. His writing dating back to 1918, “Signs of Earthquakes in the Buildings of Ancient Rome”, testifies to his efforts to interpret the damage and failure of some monuments in Ostia and to support the earthquake hypothesis [29].
Recently, more modern tools have allowed for obtaining new evidence on the ancient seismicity of the site. In 2017 and 2020, seismic surveys were carried out by placing sensors in some areas of the ancient city and in Portus. Seismic noise measurements and a review of the available stratigraphic logs in the investigated area have provided insights into subsurface geology and have generated two interesting hypotheses regarding potential earthquakes. Overall, it was hypothesized the occurrence of a W-SW/E-NE fault located on the Northern boundary of the city (Figure 2). It suggested that this activity was accompanied by seismogenic phenomena, which may be responsible for the damage to the buildings, causing local earthquakes as an alternative hypothesis to their Apennine origin [13,30].
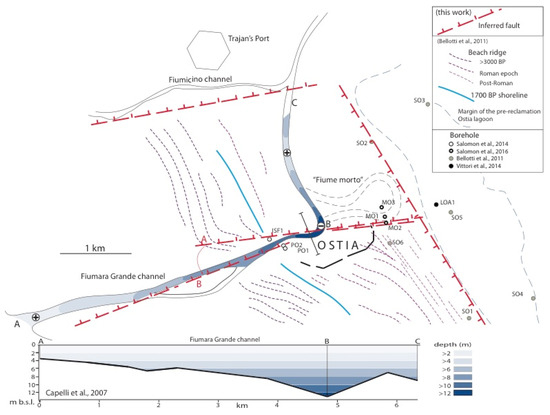
Figure 2.
Structural-geomorphological map of Ostia Antica (from [30]).
3.2. Nonlinerar Time-History Analyses
Free-standing masonry columns and other vertical monuments are likely to be subjected to intense rocking, sliding, and overturning under strong ground motions. Many descriptions of stone and masonry objects dislocated by earthquakes can be found in literature, serving as a remarkable part of macroseismic observations [31]. If their three-dimensional motion is observed, such objects may also exhibit wobbling and spinning, leading to severe displacements in the block under motion [32].
Numerical models using Discrete Element Methods (DEM) are mainly employed in archaeoseismology, as they are suitable for capturing the dynamic behavior of individual blocks located close to each other, typical of many vertically oriented objects such as columns, monuments, and tombstones. However, DEM models can also be conveniently applied to masonry elements made of mortar and blocks to predict their structural response when some parts become detached from the whole structure. Of course, the blocks can be modeled with varying degrees of stiffness [24].
For further information about analysis and assessment of historic masonry structures and numerical simulation through Finite Element Methods (FEM) and DEM approaches, the interested reader may refer to [33,34,35,36,37,38].
In this paper, the FEM technique has been employed to build a numerical model of the pillar and a relatively simple Finite Element (FE) model of the analyzed pillar was built using the FE code ANSYS [38]. This model was used to analyze and gain quantitative insights into the dynamic actions that may have caused the damage to the pillar. The numerical model used is a block-like model (refer to Figure 3) that represents the pillar with a series of layered rigid blocks, each composed of several brick finite elements.
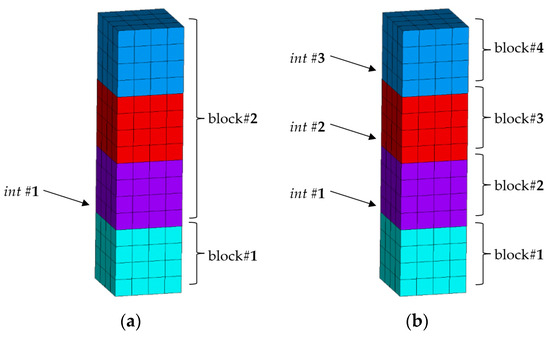
Figure 3.
Block-like models: (a) two-block model, (b) four-block model.
The blocks were discretized with 3D elements (SOLID45), defined by eight nodes having three translation degrees of freedom (DOF) at each node, and each rigid block was connected to adjacent blocks with monolateral interface elements (CONTAC52).
These interface elements are spatial, point-to-point contact elements, that can bear compressive loads (in the direction normal to the surfaces) while not transferring tensile loads; they also ensure the transfer of shear actions according to an attritive Coulomb model. The use of these elements to analyze contact problems is fairly widespread. In the scientific literature, these types of elements have been used, e.g., to model the contact between steel wall and concrete core for concrete-filled tubular columns [39], to investigate the load-bearing mechanism of steel bifurcation (combined with concrete anchor block) [40], or to investigate damage propagation in historic masonry domes under seismic loads [41].
Two different FE models were constructed and utilized for the numerical analyses. The first FE model, depicted in Figure 3a, consists of two rigid blocks identified based on the present fracture observed in the bipedales layer. In order to facilitate comparison, a second model comprising of four rigid blocks of equal dimensions was also taken into account (see Figure 3b).
Numerical simulations, presented below, were performed by simultaneously applying the two horizontal components of real earthquakes in the x- and the y-directions (i.e., two horizontal directions in the plane of the pillar’s cross-section). More specifically, a combination of seven pairs of historically recorded accelerograms, whose main characteristics are listed in Table 1, was used as seismic input.

Table 1.
Earthquake records used as input on ground motion.
They were selected through Rexel [42] from the European Strong Motion Database and the ITACA Database to comply with the 5% damped elastic response spectrum, provided by the Italian Building Code NTC2018 for a return period of 975 years (Collapse prevention) in Ostia. Figure 4 shows the pseudo-acceleration spectra of the primary component of all the input ground notions used, together with the reference response spectrum. To perform the numerical analyses, for all the used seismic records, the horizontal component with the highest PGA value was always applied in the x-direction.
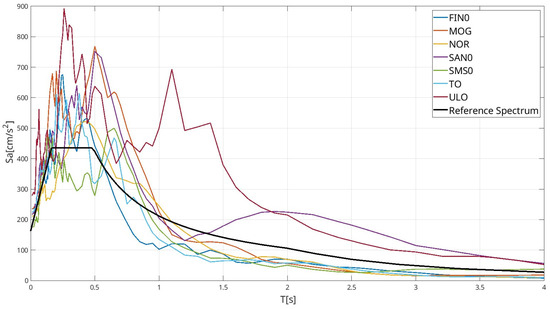
Figure 4.
Elastic spectra of the earthquake records used (primary components).
Each ground motion was applied several times, scaling its amplitude in order to have the PGA of the primary component (denoted in the following as sc-PGA) ranging from 3.0 to 9.0 m/s2. Time-history analyses were performed by applying the scaled accelerograms for 15 s, after which the pillar oscillated in free vibrations for another 5 s. Each input time-history was sampled at 1000 Hz, and a Rayleigh damping of 2% on the first three modes was assumed. The damping ratio for brick masonry structures can vary depending on several factors including material properties, geometry, boundary conditions, loading modes etc., and typically ranges from 2% to 5%. The lower damping of 2% was here assumed to be common for unreinforced masonry, such as walls that are not tied to other structural elements that might contribute to its increase.
4. Results and Discussion
Figure 5a (two-block model) and Figure 5b (four-block model) illustrate the deformed configurations obtained at the time steps t = 5.4 s and t = 20 s obtained by applying the earthquake denoted as FIN0 (see Table 1), amplified to have a maximum amplitude of scaled acceleration sc-PGA = 4 m/s2. The figure provides, as an example, a qualitative picture of the behavior of the two models under these seismic records.
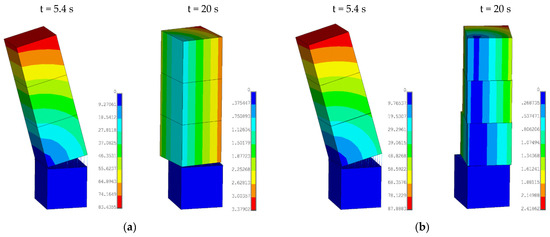
Figure 5.
Block-like models (a) two-block model; (b) four-block model and their deformed configurations at t = 5.4 s and t = 20 s, under the FIN0 record for a sc-PGA = 4 m/s2.
The time step t = 5.4 s corresponds to the step at which the maximum acceleration value is reached (in the seismic record FIN0); the instant t = 20 s corresponds to the end of the seismic event and reports the final configuration assumed by the pillar as a consequence of the seismic loading. What is illustrated in Figure 5, for the case of the seismic record FIN0, is quite general and occurs, though with different values, for all the other seismic records. Substantially, it is observed that the displacement configuration obtained at the end of the analyses shows a residual rotation of the upper part of the pillar with respect to the base (which is slightly different between the two-block and four-block model while still maintaining consistency over orders of magnitude of displacements and rotations).
For the same input on ground motion (i.e., the FIN0 record), selected time histories are shown in Figure 6 and Figure 7 for the two-block and four-block models, respectively.
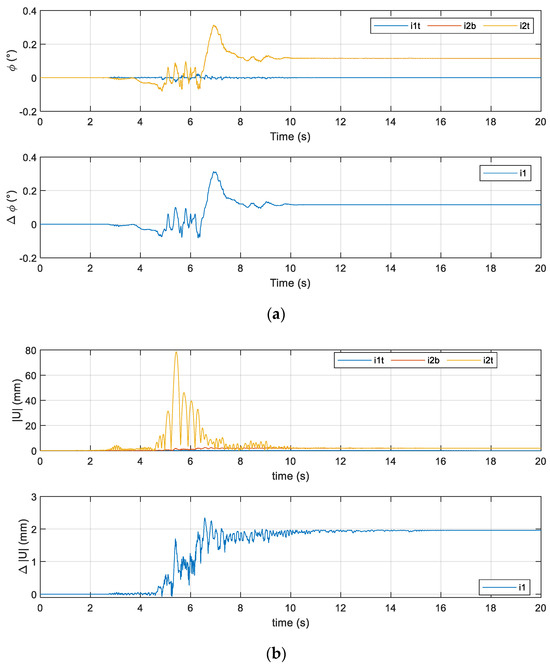
Figure 6.
Two−block model under the FIN0 record for a sc-UPGA = 4 m/s2: (a) time histories of absolute (ϕ) and relative (Δϕ) rotations at each interface, and (b) norm of the absolute () and relative () displacement at each interface.
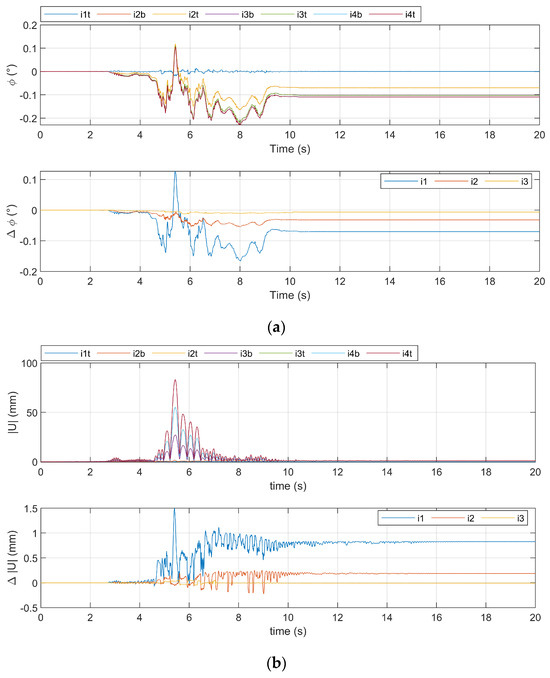
Figure 7.
Four−block model under the FIN0 record for a sc-PGA = 4 m/s2: (a) time histories of absolute (ϕ) and relative () rotations at each interface, and (b) norm of the absolute () and relative () displacement at each interface.
Going into details, denoting the interfaces between rigid blocks in the models with “i#”, numbered incrementally from the bottom to the top of the pillar (see Figure 3), any generalized displacement measured at the top of the lower block and at the bottom of the upper block will be referred to as “i#t” and “i#b” (where “#” denotes the number of the block with respect to the notation reported in Figure 3), respectively. With reference to this notation, Figure 6a shows the time histories of absolute (ϕ) and relative (Δϕ) rotations at each interface, while Figure 6b illustrates the time histories of the norm of the absolute () and relative () displacements at each interface. The term relative rotation (/displacement) refers to the difference (calculated at the interface between the blocks) between the rotation (/displacement) of the base of the upper block and the rotation (/displacement) of the top of the lower block.
Focusing on the two-block model, and analyzing the relative rotation (Δϕ) at the first interface (which is, for this model, also the only one), Figure 6a shows how the upper block, during the seismic loading, rotates with respect to the lower one, alternating between clockwise and counterclockwise. The maximum value of the relative rotation is approximately 0.31°, while the residual rotation (i.e., the one at the end of the analysis) is approximately 0.12°. If the absolute displacements () are considered (Figure 6b), the maximum value obtained at the top of the pillar (i.e., at the top of the block #2) is 78.6 mm and this value is recorded at t = 5.4 s (the value whose deformed configuration is illustrated in Figure 5a). This displacement at the end of the analysis is approximately 2 mm, and this is the value of the relative displacement () obtained at the end of the analysis between the two blocks.
The analogous results for the four-blocks model are reported in Figure 7a,b. Similar considerations can be developed for Figure 7 as for Figure 6. Overall, the values recorded at the top of the pillar at the end of the analysis are consistent with those obtained with the two-block model, although the values of relative rotations () and relative displacements () are, in this case, spread over different interfaces. However, the maximum values of these relative displacements and rotations are always drawn on the first interface (int#1 in Figure 3b).
Besides the reasonable and expected differences in the seismic response time-history provided by the two models, a coherent residual rotation and displacement can be observed at the first interface (i1), where the fracture of the pillar is actually located. This observation holds true even in the model with more interfaces (see Figure 5b and Figure 7). In addition, the results obtained by means of the two models are quantitatively similar, in terms of both maximum amplitude of rotations and displacements. For this reason, only the results obtained with the two-block model are reported hereinafter.
The maximum values of relative rotations () at the interface i1, during the whole time-history for selected values of the scaled PGA for all of the applied inputs on ground motions is summarized in Table 2. Table 3 reports the absolute top displacements () (at the level i2t), still attained during the whole time-history, as the PGA of each record was increased.

Table 2.
Maximum values of relative rotations (two−block model).

Table 3.
Absolute value of top displacements (two−block model).
In Figure 8, the graph of such values as a function of the sc-PGA’s values is reported for all the sets of considered earthquakes (Table 1). The results provided by the two-block model are considered. Figure 8 summarizes the maximum value of the relative rotation () at the interface i1 for a sc-PGA, varying between 3 and 9 m/s2. In addition this figures also reports the maximum value of the absolute displacement () at the top of the FE model, i.e., the displacement of the level i2t.
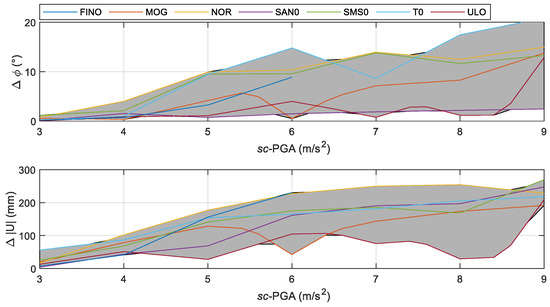
Figure 8.
Two−block model: maximum value of the relative rotation at the interface i1 () and maximum value of the absolute rotation at the top of the model ().
Even if with a quite simple family of FEM numerical models, and despite the uncertainties that may arise from the division of the pillar into a different number of blocks, the numerical results of the nonlinear time-history analyses confirm that a seismic event can be compatible as a trigger of the observed damage on the pillar, both as typology and as amount of damage. Figure 8, in particular, suggests that an earthquake with a PGA ranging from medium to high (starting from about 5 m/s2) can be considered consistent with a pillar rotation with a value close to the one recorded by Rodolfo Lanciani in [29].
5. Concluding Remarks
Earthquake damage to structures at archaeological sites documents the effects of seismic shaking. Numerical models and innovative engineering approaches can help quantitatively identify certain ranges of ground motion parameters and date seismic events.
This paper reports several numerical nonlinear time-history analyses that were conducted to investigate the possible seismic damage of a pillar of the Piccolo Mercato in Ostia Antica. The pillar displays earthquake-like damage, characterized by a residual vertical rotation of the upper part with respect to the lower one. The first documented evidence of damage, that could be attributed to the effects of an earthquake, dates back to 1918 and is due to the archaeologist and engineer Rodolfo Lanciani. He hypothesized that the damage on the pillar was caused by a seismic event triggered by one of the historical earthquakes that affected the site of Ostia Antica.
The numerical simulations were performed using block-like finite element models, applying a set of seven spectrum-compatible historically recorded accelerograms. They aimed to obtain some quantitative results on the extent of the possible seismic shaking at the base of the pillar compatible with the present damage pattern.
The results of the numerical analyses confirm that a seismic event can be compatible as a trigger of the observed damage on the pillar, both in typology and amount of damage. In fact, the primary outcome of this study suggests that the rotation of approximately 12 degrees in the upper three-fifths of the pillar (relative to the remaining lower third), today visible, may be compatible with peak ground acceleration values ranging from medium to high (in particular, according to the results obtained with the considered set of earthquakes, starting from about 5 m/s2).
Author Contributions
Conceptualization, L.P., B.P. and M.B.; methodology, L.P., B.P. and M.B.; software, B.P. and M.B.; validation, L.P., B.P. and M.B.; investigation, L.P.; writing—original draft preparation, L.P., B.P. and M.B.; writing—review and editing, L.P., B.P. and M.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The raw data supporting the conclusions of this study will be made available by the authors on request.
Acknowledgments
We appreciate the continuous support of the Ostia Antica Archaeological Park and the Gerda Henkel Foundation, which is crucial for the progress of our research.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Rodríguez-Pascua, M.A.; Pèrez Lòpez, R.; Giner-Robles, J.L.; Silva, P.G.; Garduño-Monroy, V.H.; Reicherter, K. A comprehensive classification of Earthquake Archaeological Effects (EAE) in archaeoseismology: Application to ancient remains of Roman and Mesoamerican cultures. Quat. Int. 2011, 242, 20–30. [Google Scholar] [CrossRef]
- Kázmér, M. Damage to Ancient Buildings from Earthquakes. In Encyclopedia of Earthquake Engineering; Beer, M., Kougioumtzoglou, I., Patelli, E., Au, I.K., Eds.; Springer: Berlin/Heidelberg, Germany, 2014; pp. 1–7. [Google Scholar] [CrossRef]
- Pecchioli, L. Problematiche connesse al restauro archeologico, The Cultural heritage protection in Italy. In Mediterraneum, La Tutela dei Beni Culturali in Italia; Maniscalco, F., Ed.; Massa Editore: Napoli, Italy, 2003; pp. 61–63. [Google Scholar]
- Marino, L. Material for an Atlas of Pathologies in Archaeological Areas and Ruined Buildings; Alinea Editore: Firenze, Italy, 2009. [Google Scholar]
- Arrighetti, A. L’archeosismologia in Architettura. Per un Manuale. Strumenti per la Didattica e la Ricerca; Firenze University Press: Firenze, Italy, 2015. [Google Scholar] [CrossRef]
- Galadini, F.; Hinzen, K.G.; Stiros, S.C. Archaeoseismology: Methodological issues and procedure. J. Seismol. 2006, 10, 395–414. [Google Scholar] [CrossRef]
- Hinzen, K.G. Archaeoseismology. In Encyclopedia of Solid Earth Geophysics; Gupta, H.K., Ed.; Springer: Berlin/Heidelberg, Germany, 2011; pp. 11–15. [Google Scholar] [CrossRef]
- Hinzen, K.G.; Fleischer, C.; Reamer, S.K.; Schreiber, S.; Schütteet, S.; Yerli, B. Quantitative methods in archaeoseismology. Quat. Int. 2011, 242, 31–41. [Google Scholar] [CrossRef]
- Forlin, P.; Valente, R.; Kázmér, M. Assessing earthquake effects on archaeological sites using photogrammetry and 3D model analysis. Digit. Appl. Archaeol. Cult. Herit. 2018, 9, e00073. [Google Scholar] [CrossRef]
- Meghraoui, M.A.; Hinzen, K.G.; Malik, J.N. Paleoseismology, Archeoseismology and Paleotsunami Studies. In Encyclopedia of Geology, 2nd ed.; Alderton, D., Elias, S.A., Eds.; Academic Press: London, UK, 2021; pp. 636–655. [Google Scholar] [CrossRef]
- Sánchez-Sánchez, Y.; Elez, J.; Silva, P.G.; Santos-Delgado, G.; Giner-Robles, J.L.; Reicherter, K. 3D Modelling of Archaeoseismic Damage in the Roman Site of Baelo Claudia (Gibraltar Arc, South Spain). Appl. Sci. 2022, 12, 5223. [Google Scholar] [CrossRef]
- Arrighetti, A.; Repole, M. Expeditious archaeoseismological analysis of a medieval town centre. The case of Siena and the PROTECT project. Eur. J. Post-Class. Archaeol. 2024, 14, 303–324. [Google Scholar]
- Pecchioli, L.; Cangi, G.; Marra, F. Evidence of seismic damages on ancient Roman buildings at Ostia: An arch mechanics approach. J. Archaeol. Sci. Rep. 2018, 21, 117–127. [Google Scholar] [CrossRef]
- Stiros, S.C. Monumental articulated ancient Greek and Roman columns and temples and earthquakes: Archaeological, historical, and engineering approaches. J. Seismol. 2020, 24, 853–881. [Google Scholar] [CrossRef]
- Ambraseys, N.; Psycharis, I.N. Assessment of the long-term seismicity of Athens from two classical columns. Bull. Earthq. Eng. 2012, 10, 1635–1666. [Google Scholar] [CrossRef]
- Hinzen, K.G.; Cucci, L.; Tertulliani, A. Rotation of Objects during the 2009 L’Aquila Earthquake Analyzed with 3D Laser Scans and Discrete-Element Models. Seismol. Res. Lett. 2013, 84, 745–751. [Google Scholar] [CrossRef]
- Mordanova, A.; de Felice, G. Seismic Assessment of Archaeological Heritage Using Discrete Element Method. Int. J. Archit. Herit. 2020, 14, 345–357. [Google Scholar] [CrossRef]
- Caputo, R.; Hinzen, K.G.; Liberatore, D.; Schreiber, S.; Helly, B.; Tziafalias, A. Quantitative archaeoseismological investigation of the Great Theatre of Larissa, Greece. Bull. Earthq. Eng. 2011, 9, 347–366. [Google Scholar] [CrossRef]
- Lorenzoni, F.; Valluzzi, M.R.; Modena, C. Seismic assessment and numerical modelling of the Sarno Baths, Pompeii. J. Cult. Herit. 2019, 40, 288–298. [Google Scholar] [CrossRef]
- Aita, D.; Beatini, V.; Garavaglia, E.; Paris, V.; Pizzigoni, A.; Sgambi, L. The stone roof of the tholos of Athena Pronaia in Delphi: Structural hypotheses starting from fragments of marble tiles. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2023, XLVIII-M-2-2023, 59–66. [Google Scholar] [CrossRef]
- Volant, P.; Levret, A.; Carbon, D.; Scotti, O.; Comberscure, D.; Verdel, T.; Piant, A.; Laurent, P. An archaeo-seismological study of the Nîmes Roman aqueduct, France: Indirect evidence for an M > 6 seismic event? Nat. Hazards 2009, 49, 53–77. [Google Scholar] [CrossRef]
- Kim, J.; Lorenzoni, F.; Salvalaggio, M.; Valluzzi, M.R. Seismic vulnerability assessment of free-standing massive masonry columns by the 3D Discrete Element Method. Eng. Struct. 2021, 246, 113004. [Google Scholar] [CrossRef]
- Tabbara, M.R.; Karam, G.N. Experimental, Numerical, and Theoretical Investigation of the Rocking Response of Baalbek Columns under Harmonic Excitations. J. Earthq. Eng. 2022, 26, 887–910. [Google Scholar] [CrossRef]
- Hinzen, K.G.; Meghraoui, M.; Bahrouni, N.; Reamer, S.K. Testing the earthquake damage and vulnerability of the Cherichira aqueduct bridge, Kairouan (Tunisia) with discrete element modeling. Mediterr. Geosci. Rev. 2022, 4, 495–516. [Google Scholar] [CrossRef]
- Available online: https://www.ostiaantica.beniculturali.it/en/events/hazard-and-disaster-risk-ostia-and-portus-between-hypothesis-and-reality-conference-live-streaming (accessed on 2 September 2024).
- Pecchioli, L.; Betti, M.; Pintucchi, B. Archaeoseismological project in Ostia: Tracking evidence on seismic damage by nonlinear numerical simulations. Dev. Built Environ. 2022, 10, 100073. [Google Scholar] [CrossRef]
- Lanciani, R.A. The Ruins and Excavations of Ancient Rome; A Companion Book for Students and Travelers; The Riverside Press: Cambridge, UK, 1897. [Google Scholar]
- Available online: https://culture.ec.europa.eu/cultural-heritage/initiatives-and-success-stories/european-heritage-label/european-heritage-label-sites/archaeological-area-of-ostia-antica-italy (accessed on 2 September 2024).
- Lanciani, R.A. Segni di terremoti negli edifizi di Roma antica. Bull. Comm. Archeol. Comunale Roma 1918, 45, 3–28. (In Italian) [Google Scholar]
- Marra, F.; Milana, G.; Pecchioli, L.; Roselli, P.; Cangi, G.; Famiani, D.; Mercuri, A.; Carlucci, G. Historical faulting as the possible cause of earthquake damages in the ancient Roman port city of Ostia. J. Seismol. 2020, 24, 833–851. [Google Scholar] [CrossRef]
- Hinzen, K.G. Rotation of vertically oriented objects during earthquakes. J. Seismol. 2012, 16, 797–814. [Google Scholar] [CrossRef]
- Pradhan, C.; Banerjee, A.; Roy, R. Evolution of a 3D model for free-standing rigid blocks and its behavior under base excitations. Int. J. Non-Linear Mech. 2022, 142, 103992. [Google Scholar] [CrossRef]
- Asteris, P.G.; Sarhosis, V.; Mohebkhah, A.; Plevris, V.; Papaloizou, L.; Komodromos, P.; Lemos, J.V. Numerical Modeling of Historic Masonry Structures. In Handbook of Research on Seismic Assessment and Rehabilitation of Historic Structures; Asteris, P.G., Plevris, V., Eds.; IGI Global: Hershey, PA, USA, 2015; pp. 213–256. [Google Scholar] [CrossRef]
- D’Altri, A.M.; Sarhosis, V.; Milani, G.; Rots, J.; Cattari, S.; Lagomarsino, S.; Sacco, E.; Tralli, A.; Castellazzi, G.; de Miranda, S. A review of numerical models for masonry structures. In Numerical Modeling of Masonry and Historical Structures; Ghiassi, B., Milani, M., Eds.; Elsevier: Amsterdam, The Netherlands, 2019; pp. 3–53. [Google Scholar] [CrossRef]
- Betti, M.; Galano, L.; Vignoli, A. Finite element modelling for seismic assessment of historic masonry buildings. In Earthquakes and Their Impact on Society; D’Amico, S., Ed.; Springer Natural Hazards: Cham, Switzerland, 2016; pp. 377–415. [Google Scholar] [CrossRef]
- Theodossopoulos, D.; Sinha, B. A review of analytical methods in the current design processes and assessment of performance of masonry structures. Constr. Build. Mater. 2013, 41, 990–1001. [Google Scholar] [CrossRef]
- Schiavoni, M.; Giordano, E.; Roscini, F.; Clementi, F. Numerical modeling of a majestic masonry structure: A comparison of advanced techniques. Eng. Fail. Anal. 2023, 149, 107293. [Google Scholar] [CrossRef]
- Bartoli, G.; Betti, M.; Biagini, P.; Borghini, A.; Ciavattone, A.; Girardi, M.; Lancioni, G.; Marra, A.M.; Ortoloani, B.; Pintucchi, B.; et al. Epistemic uncertainties in structural modelling: A blind benchmark for seismic assessment of slender masonry towers. ASCE’s J. Perform. Constr. Facil. 2017, 31, 04017067. [Google Scholar] [CrossRef]
- Abedi, K.; Ferdousi, A.; Afshin, H. A novel steel section for concrete-filled tubular columns. Thin-Walled Struct. 2008, 46, 310–319. [Google Scholar] [CrossRef]
- Su, K.; Zhu, H.Z.; Shi, Y.A.; Wei, Y.J.; Wu, H.G.; Shi, C.Z. Loads bearing mechanism of steel bifurcation combined with concrete anchor block. Eng. Struct. 2019, 194, 251–2619. [Google Scholar] [CrossRef]
- Bartoli, G.; Betti, M.; Borri, C. Numerical modelling of the structural behaviour of Brunelleschi’s Dome of Santa Maria del Fiore. Int. J. Archit. Herit. 2015, 9, 408–429. [Google Scholar] [CrossRef]
- Iervolino, I.; Galasso, C.; Cosenza, E. REXEL: Computer aided record selection for code-based seismic structural analysis. Bull. Earthq. Eng. 2010, 8, 339–362. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).