A Study of the Accuracy of a 3D Indoor Camera for Industrial Archaeology Applications
Abstract
:1. Introduction
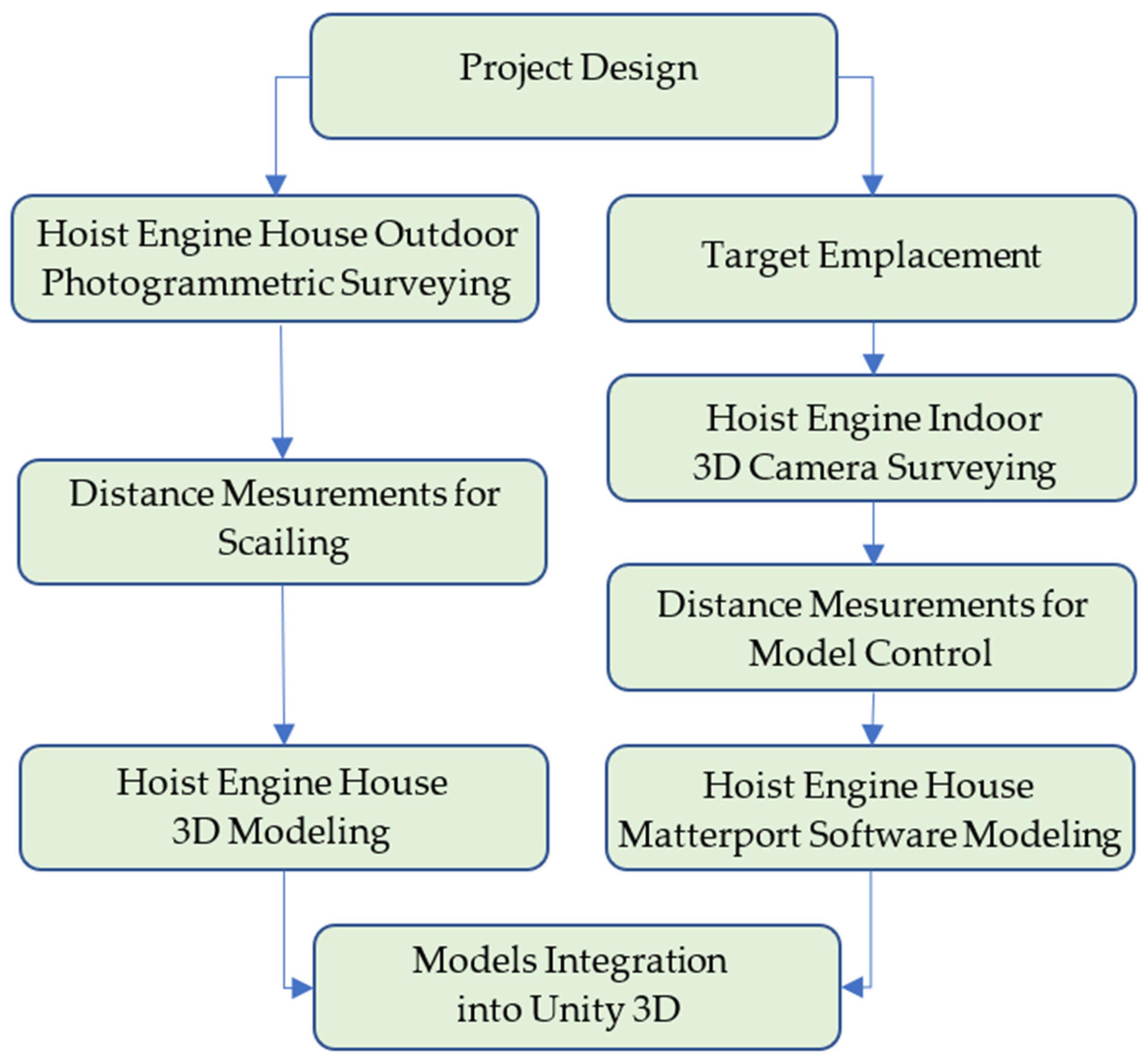
2. Materials and Methods
2.1. Data for Accuracy Check and Calibration Method
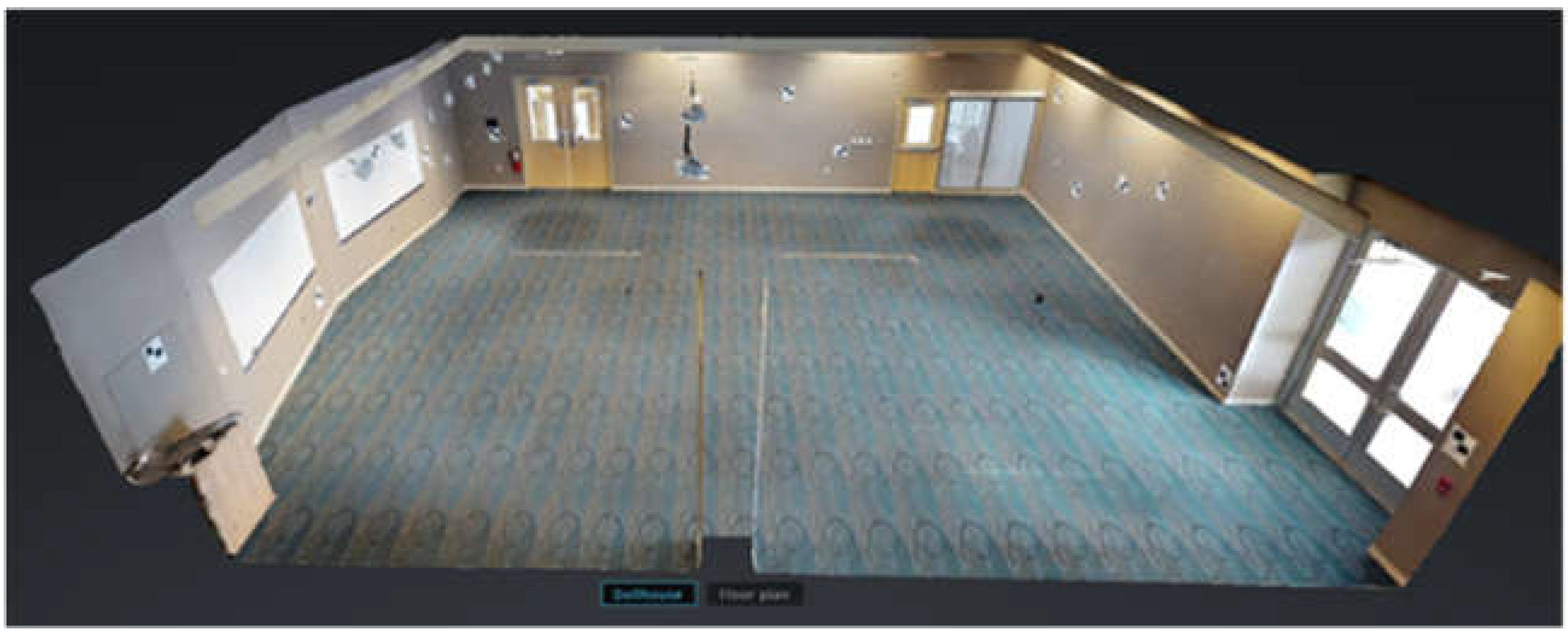
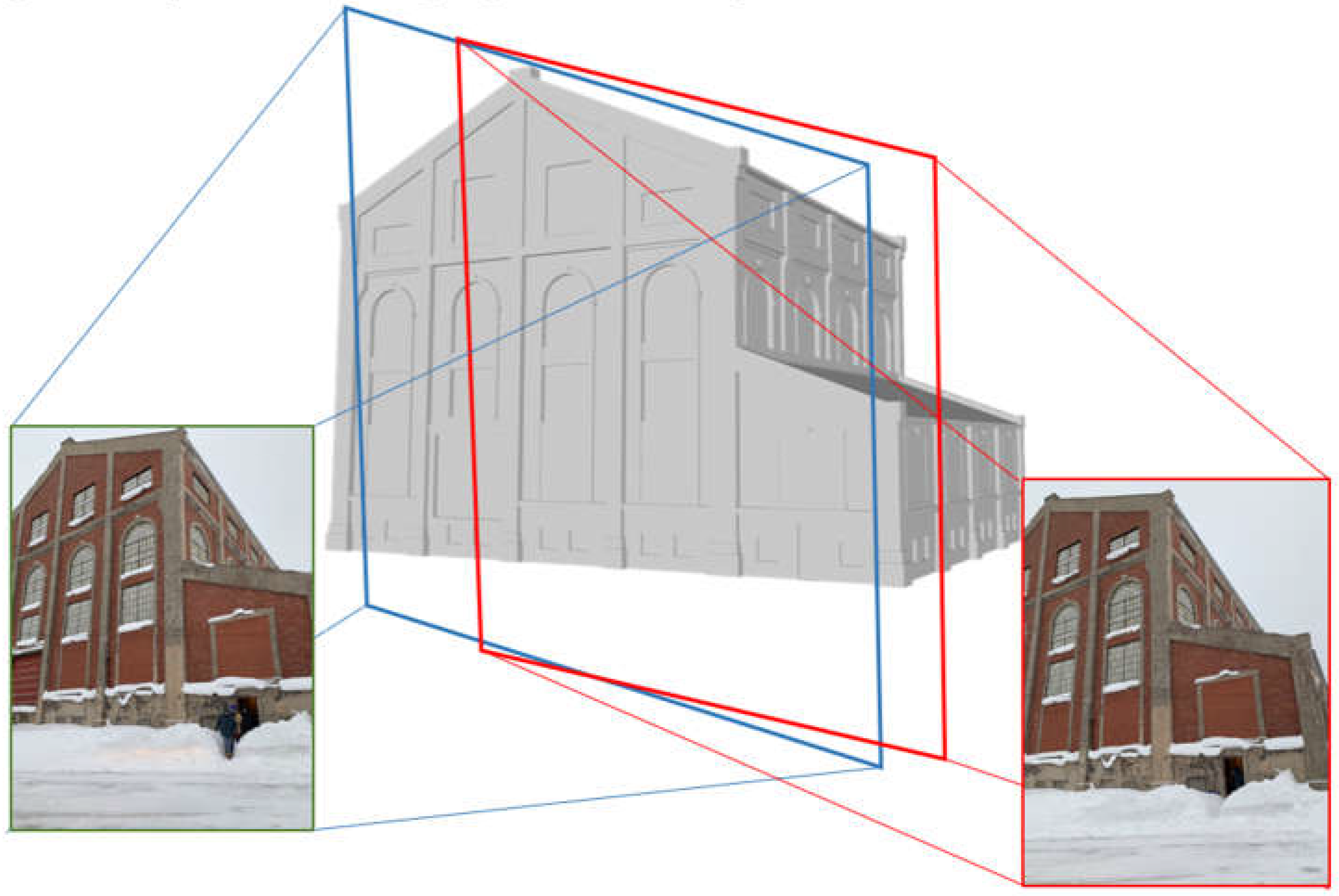
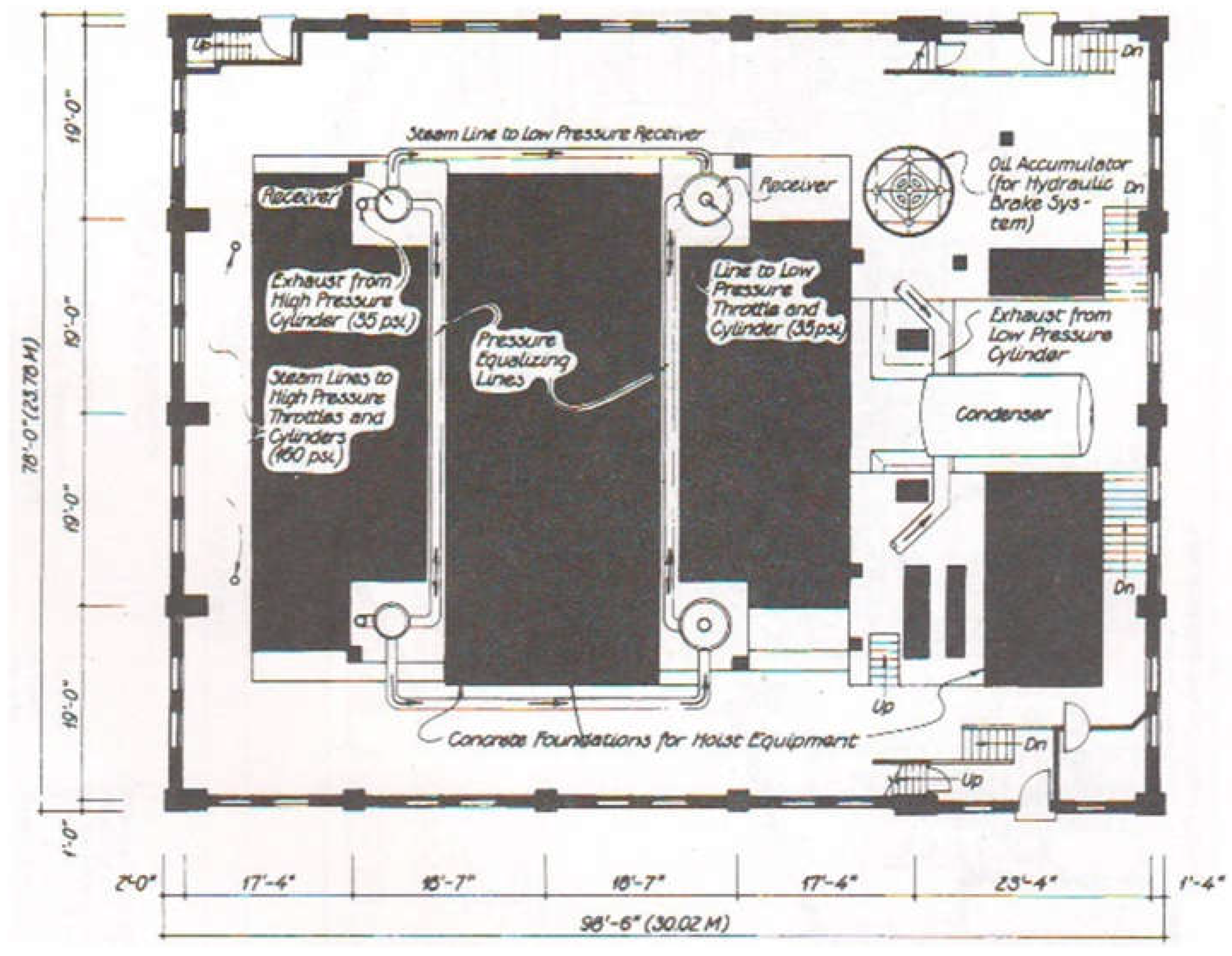
2.2. Study Object and Data for Modeling
3. Results
3.1. Accuracy Check—Distance Comparison
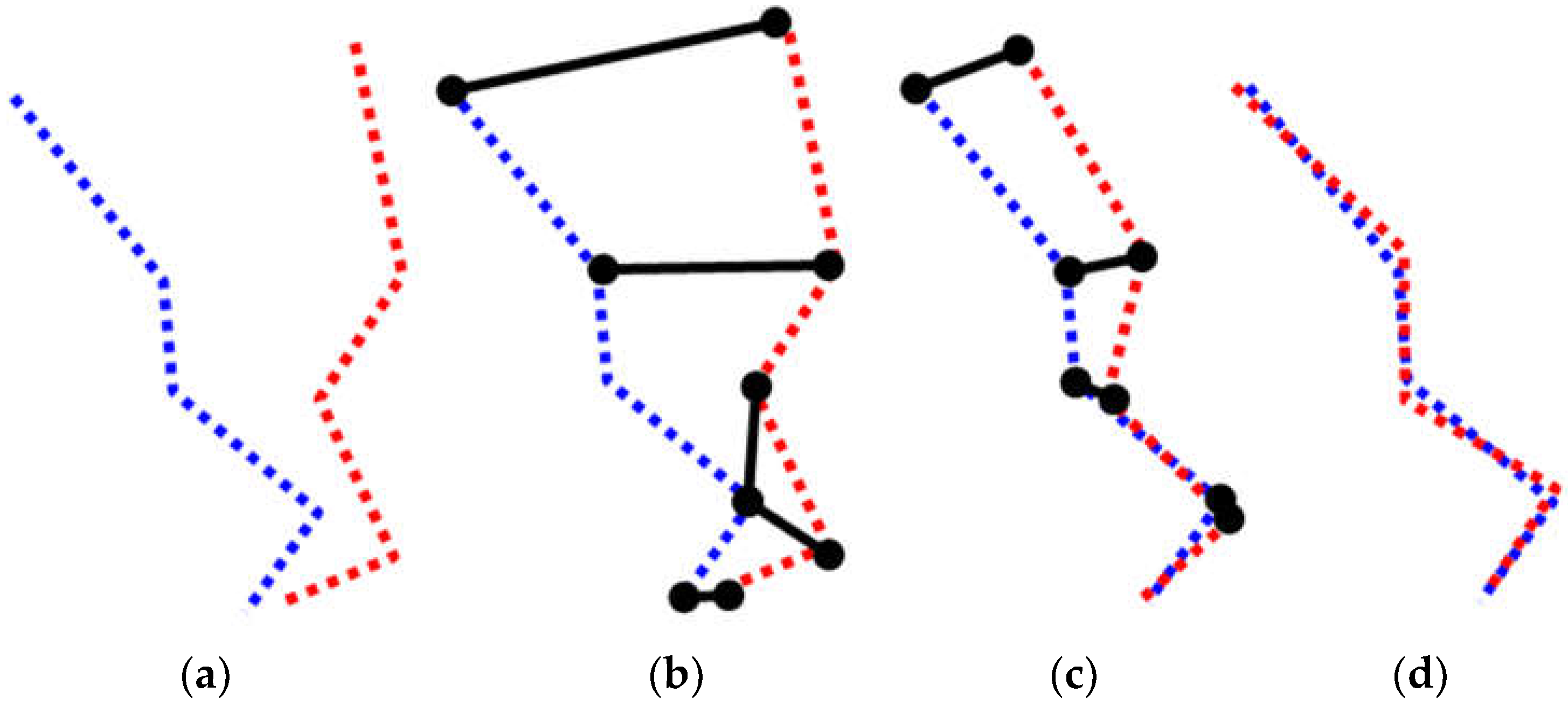
3.2. Accuracy Check—Clouds Comparison
3.3. Calibration
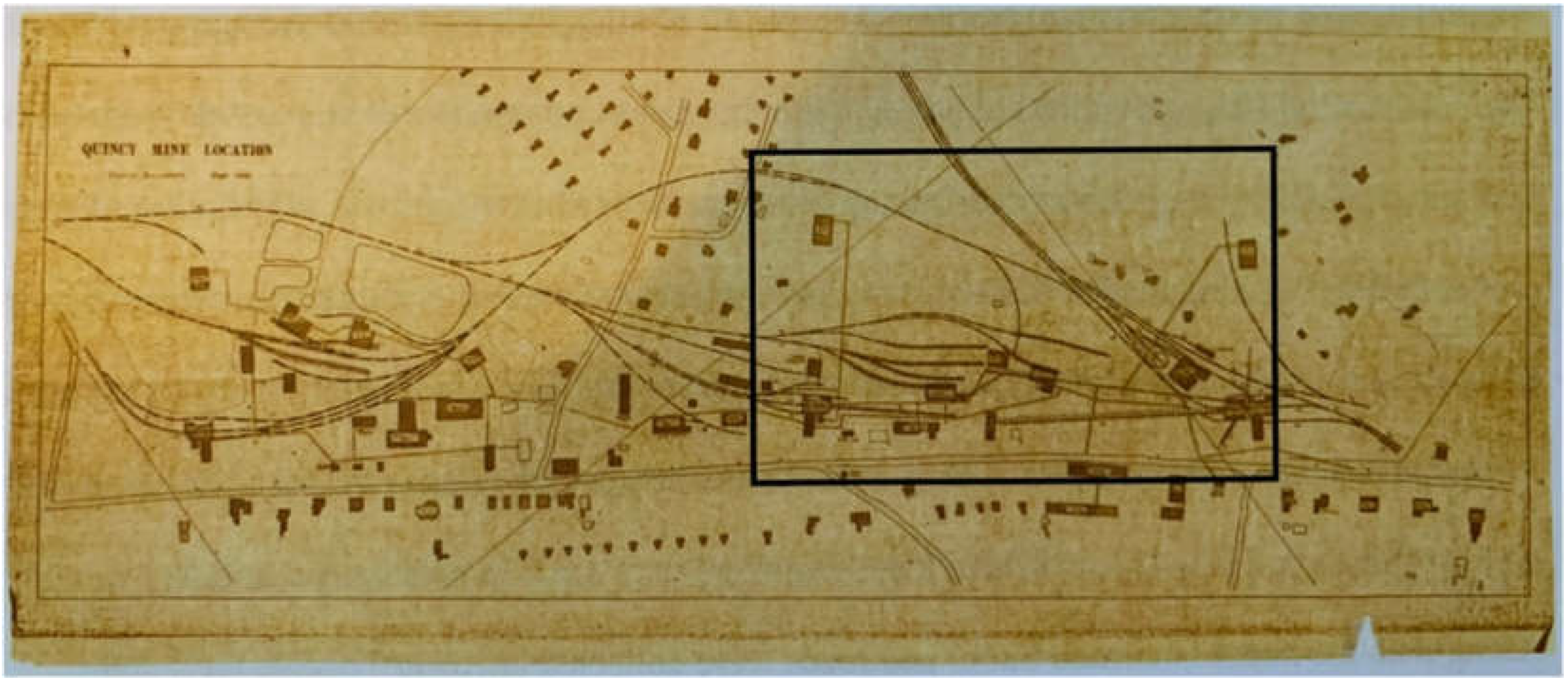
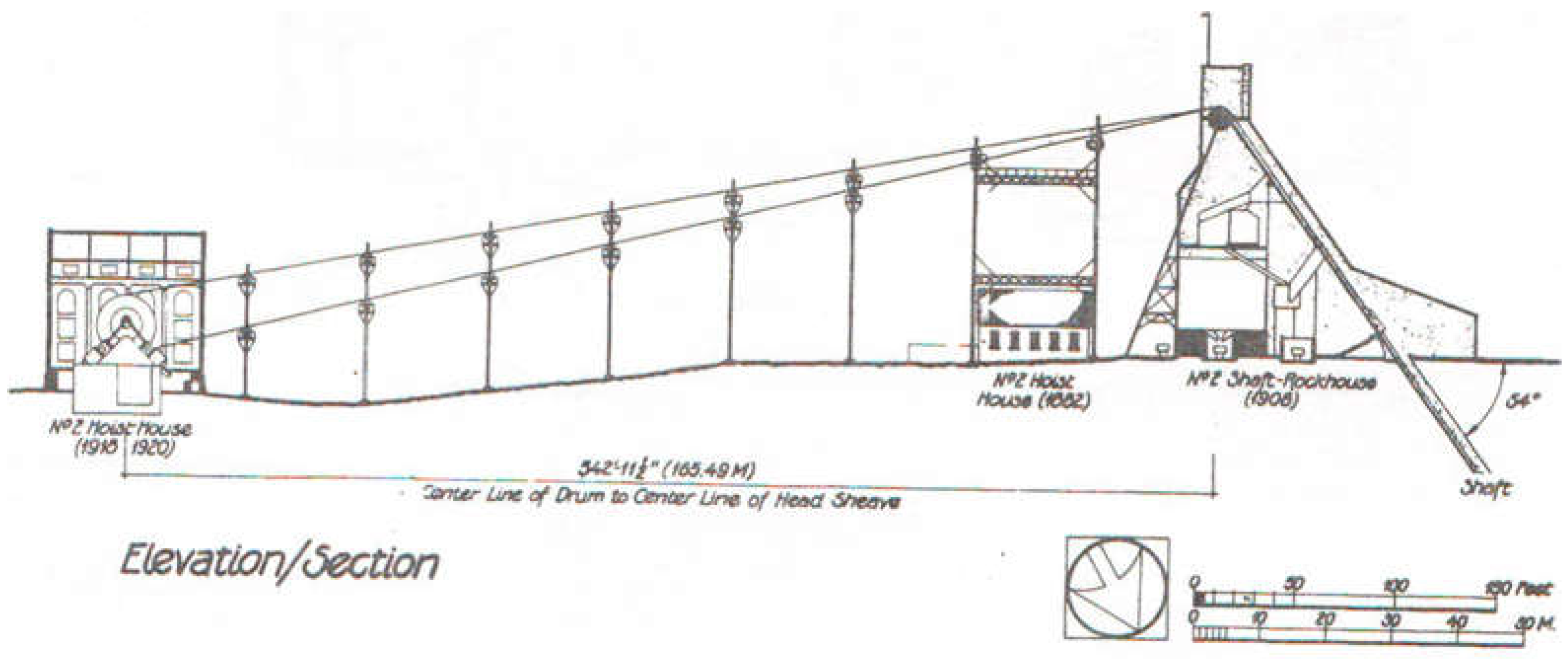
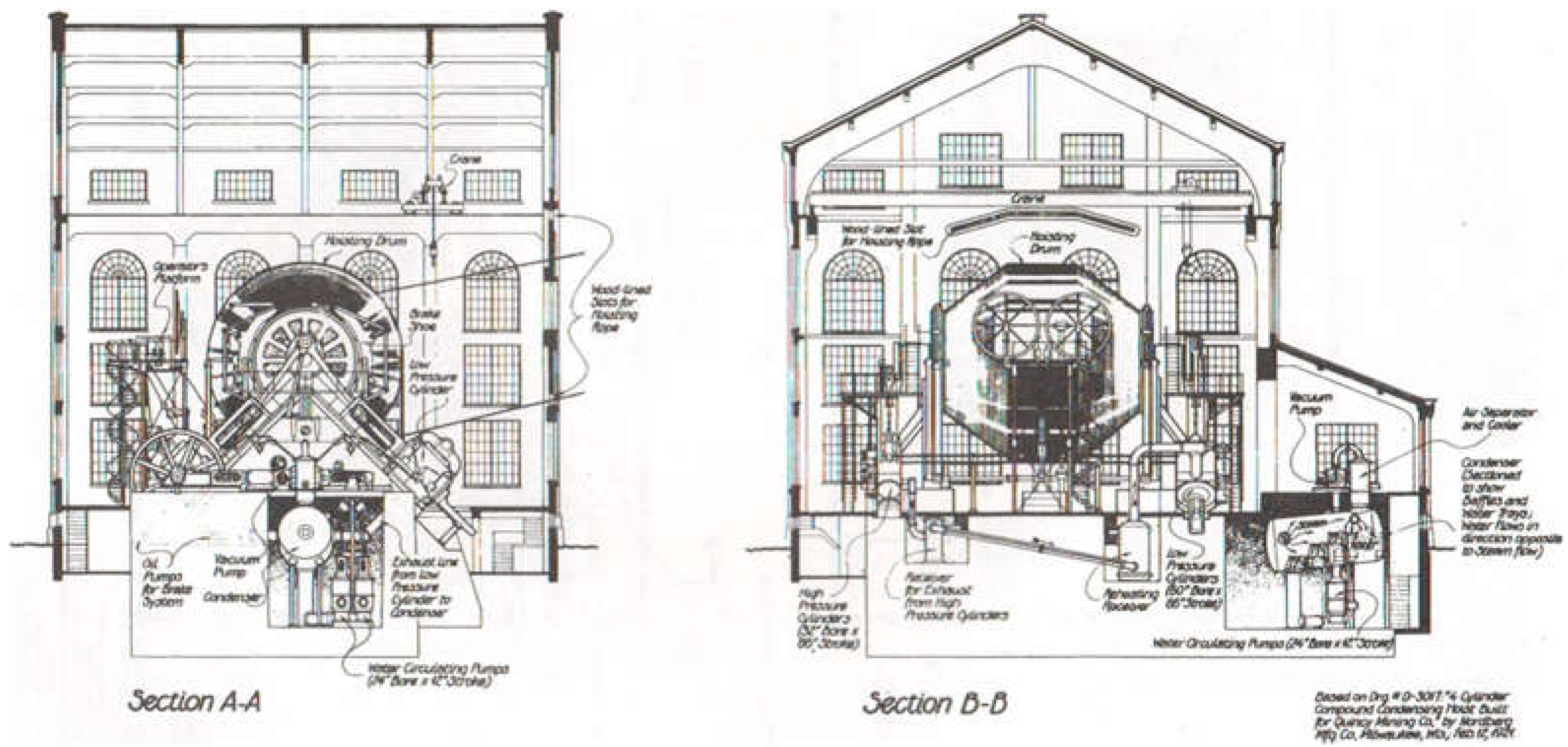
3.4. Quincy Mine Hoist Engine: Outdoor and Indoor Surveying and Modeling
4. Discussion
- (1)
- Try to ensure high data redundancy, increase the number of surveying stations, and use the camera field of view to be sure that each part of the object was captured six to eight times.
- (2)
- Place and capture the artificial targets with known coordinates. After the cloud generation, these targets will serve as an additional source of control and correction.
- (3)
- Perform camera calibration. It is preferable to calibrate the camera in the field conditions using targets with known coordinates.
- (4)
- Mark the points of interest.
- (1)
- Pre-surveying design should be performed based on a preliminary sketch of the surveying object. Industrial objects have a very complex geometry, and to grasp all the features of the object, the preliminary design of the scanning stations must be developed.
- (2)
- The study has shown the high reliability of the Matterport Pro 3D camera in adverse conditions, e.g., low temperature and high humidity. These conditions go hand in hand with industrial archaeology objects. Anyway, the control of the environmental parameters is highly recommended before and during surveying.
- (3)
- These cameras operate in visual bands, and good lighting conditions must be ensured. This recommendation is crucial for industrial archaeology that deals with objects and rooms full of industrial equipment and “dead zones”.
- (4)
- The Matterport Pro 3D data processing is only possible with Matterport software. The surveyor has to bear this fact in mind. The further processing and integration of the Matterport Pro 3D data is only possible after pre-processing in Matterport-based software and export of surveying data into the point cloud.
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Palmer, M.; Neaverson, P. Industrial Archaeology. Principles and Practice, 2nd ed.; Routledge: London, UK, 1998. [Google Scholar]
- Conlin Casella, E.; Symonds, J.I. Industrial Archaeology. Future Directions; Springer: New York, NY, USA, 2005. [Google Scholar]
- Leon, I.; Pérez, J.J.; Senderos, M. Advanced Techniques for Fast and Accurate Heritage Digitisation in Multiple Case Studies. Sustainability 2020, 12, 6068. [Google Scholar] [CrossRef]
- Marín-Buzón, C.; Pérez-Romero, A.; López-Castro, J.L.; Ben Jerbania, I.; Manzano-Agugliaro, F. Photogrammetry as a New Scientific Tool in Archaeology: Worldwide Research Trends. Sustainability 2021, 13, 5319. [Google Scholar] [CrossRef]
- Huggett, J. Challenging Digital Archaeology. Open Archaeol. 2015, 1, 79–85. [Google Scholar] [CrossRef]
- Opitz, R.; Limp, F.W. Recent developments in high-density survey and measurement (HDSM) for archaeology: Implications for practice and theory. Annu. Rev. Anthropol. 2015, 44, 347–376. [Google Scholar] [CrossRef]
- Photogrammetry is the New Archaeological Photography: 3D Modeling at Abydos. Available online: https://abydos.org/blog/2019/3/13/photogrammetry-is-the-new-archaeological-photography-3d-modeling-at-abydos (accessed on 28 July 2023).
- Trepal, D.; Lafreniere, D.; Stone, T. Mapping Historical Archaeology and Industrial Heritage: The Historical Spatial Data Infrastructure. J. Comput. Appl. Archaeol. 2021, 4, 202–213. [Google Scholar] [CrossRef]
- Trepal, D.; Lafreniere, D.; Gilliland, J. Historical Spatial Data Infrastructures for Archaeology: Towards a Spatio-Temporal Big data Approach to Studying the Post-Industrial City. Hist. Archaeol. 2020, 54, 424–452. [Google Scholar] [CrossRef]
- Barazzetti, L.; Previtali, M.; Roncoroni, F. Can we use Low-Cost 360 Degree Cameras to create accurate 3D models? Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2018, 42, 69–75. [Google Scholar] [CrossRef]
- Soria, G.; Ortega, L.; Feito, F.R.; Barroso, I. Procesamiento de imágenes panorámicas en patrimonio. Catedral de Jaén (Processing panoramic images in heritage. Jaen Cathedral). Virtual Archaeol. Rev. 2015, 6, 28–34. [Google Scholar] [CrossRef]
- Galizia, M.; Santagati, C. Low cost image-based modeling techniques for archaeological heritage digitalization: More than just a good tool for 3d visualization? Virtual Archaeol. Rev. 2013, 4, 123–129. [Google Scholar] [CrossRef]
- Chodoronek, M. The Use and Application of Photogrammetry for the In-Field Documentation of Archaeological Features: Three Case Studies from the Great Plains and Southeastern Alaska. Master Thesis, University of Nebraska, Lincoln, NE, USA, 2015. Available online: http://digitalcommons.unl.edu/anthrotheses (accessed on 20 July 2023).
- Shults, R. New Opportunities of Low-Cost Photogrammetry for Culture Heritage Preservation. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2017, 42, 481–486. [Google Scholar] [CrossRef]
- Pulcrano, M.; Scandurra, S.; Minin, G.; di Luggo, A. 3D cameras acquisitions for the documentation of cultural heritage. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2019, 42, 639–646. [Google Scholar] [CrossRef]
- Khoshelham, K.; Elberink, S.O. Accuracy and resolution of Kinect depth data for indoor mapping applications. Sensors 2012, 12, 1437–1454. [Google Scholar] [CrossRef] [PubMed]
- Costantino, D.; Angelini, M.G.; Caprino, G. Laser scanner survey of an archaeological site—Scala Di Furno (Lecce, Italy). Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2010, 38, 178–183. [Google Scholar]
- Muhammed, Q.Q.; Saluh, M.M.; Al-Azawi, R.J.; Kadhim, A.C.; Shaker, R.M. Remote Sensing and Terrestrial Laser Scanning Techniques for Archaeological Site Analysis. In Proceedings Frontiers in Optics + Laser Science 2022 (FIO, LS), Technical Digest Series, Paper JW5A.92, Rochester, NY, USA, 17–20 October 2022; Available online: https://opg.optica.org/abstract.cfm?URI=FiO-2022-JW5A.92 (accessed on 20 July 2023).
- Marín-Buzón, C.; Pérez-Romero, A.M.; León-Bonillo, M.J.; Martínez-Álvarez, R.; Mejías-García, J.C.; Manzano-Agugliaro, F. Photogrammetry (SfM) vs. Terrestrial Laser Scanning (TLS) for Archaeological Excavations: Mosaic of Cantillana (Spain) as a Case Study. Appl. Sci. 2021, 11, 11994. [Google Scholar] [CrossRef]
- Chiabrando, C.; Spanò, A.; Sammartano, G.; Losè, L.T. UAV oblique photogrammetry and LiDAR data acquisition for 3D documentation of the Hercules fountain. Virtual Archaeol. Rev. 2017, 8, 83–96. [Google Scholar] [CrossRef]
- Fiz, J.I.; Martín, P.M.; Cuesta, R.; Subías, E.; Codina, D.; Cartes, A. Examples and Results of Aerial Photogrammetry in Archeology with UAV: Geometric Documentation, High Resolution Multispectral Analysis, Models and 3D Printing. Drones 2022, 6, 59. [Google Scholar] [CrossRef]
- Gärdin, D.; Jimenez, A. Optical Methods for 3D-Reconstruction of Railway Bridges Infrared Scanning, Close Range Photogrammetry and Terrestrial Laser Scanning. Master’s Thesis, Luleå University of Technology, Luleå, Sweeden, 2018. Available online: http://ltu.diva-portal.org/smash/get/diva2:1184613/FULLTEXT01.pdf (accessed on 20 July 2023).
- Thermal Imaging and “Seeing the Unseen” at Industrial Heritage Sites. Available online: https://www.linkedin.com/pulse/thermal-imaging-seeing-unseen-industrial-heritage-sites-scarlett (accessed on 28 July 2023).
- Gruenkemeier, A. 3D-documentation technologies for use in industrial archaeology applications. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2008, 37, 291–296. [Google Scholar]
- Monego, M.; Fabris, M.; Menin, A.; Achilli, V. 3-D survey applied to industrial archaeology by TLS methodology. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2017, 42, 449–455. [Google Scholar] [CrossRef]
- Agostinelli, M.; Clini, P.; Lancioni, N.; Quattrini, R.; Sabbatini, G. The Volponi’s Kiln in Urbino. Industrial archaeology and historic landscape in the cradle of the Renaissance. Documentation, survey and drawing. In Proceedings of the XXI International CIPA Symposium, Athens, Greece, 1–6 October 2007. [Google Scholar]
- Lobb, M.; Brown, T.; Leyland, J.; Bernard, V.; Daire, M.-Y.; Langouët, L. An estuarine tidescape of production: Terrestrial laser scanning of fixed fishing structures and a tide mill in the Léguer Estuary, Brittany. Antiquity 2020, 94, 1296–1313. [Google Scholar] [CrossRef]
- Pérez-Martín, E.; Herrero-Tejedor, T.R.; Gómez-Elvira, M.Á.; Rojas-Sola, J.I.; Conejo-Martin, M.Á. Graphic study and geovisualization of the old windmills of La Mancha (Spain). Appl. Geogr. 2011, 31, 941–949. [Google Scholar] [CrossRef]
- Rojas-Sola, J.I.; Galán-Moral, B.; la Morena-De la Fuente, D. Agustín de Betancourt’s Double-Acting Steam Engine: Geometric Modeling and Virtual Reconstruction. Symmetry 2018, 10, 351. [Google Scholar] [CrossRef]
- Bitelli, G.; Gatta, G.; Girelli, A.V.; Vittuari, L.; Zanutta, A. Integrated methodologies for the 3D survey and the structural monitoring of industrial archaeology: The case of the Casalecchio di Reno Sluice, Italy. Int. J. Geophys. 2011, 2011, 874347. [Google Scholar] [CrossRef]
- Rojas-Sola, J.I.; Porras-Galán, J.; García-Ruesgas, L. Reconstrucción digital 3D del patrimonio histórico de agustín de betancourt: La máquina para cortar hierba en canales navegables (Digital 3D reconstruction of agustin de betancourt’s historical heritage: The machine for cutting grass in waterways). Virtual Archaeol. Rev. 2016, 7, 20–30. [Google Scholar] [CrossRef]
- Sproat, D.; Toolis, R.; Hepher, J.; Rankin, D. Town and factory: An historic building survey of 200 years of Jhon Paton’s Kilncraigs woollen mill in Alloa, Clackmannanshire. Ind. Archaeol. Rev. 2004, 26, 21–36. [Google Scholar] [CrossRef]
- Pietroni, E.; Pescarin, S. VR cooperative environments for the interpretation and reconstruction of the archaeological landscape. Virtual Archaeol. Rev. 2010, 1, 25–29. [Google Scholar] [CrossRef]
- Barrilea, V.; Fotiaa, A.; Bilottaa, G.; De Carlo, D. Integration of geomatics methodologies and creation of a cultural heritage App using augmented reality. Virtual Archaeol. Rev. 2019, 10, 40–51. [Google Scholar] [CrossRef]
- Matterport. Matterport Pro2 3D Camera Specifications. Available online: https://support.matterport.com/s/article/Matterport-Pro2-3D-Camera-Specifications?language=en_US (accessed on 28 July 2023).
- Matterport. Scanning a Job Site for Construction Documentation. Available online: https://support.matterport.com/s/article/Scanning-a-Job-Site-for-Construction-Documentation?language=en_US&ardId=kA05d000001DWyYCAW (accessed on 28 July 2023).
- Society for Industrial Archeology (SIA). Available online: https://www.sia-web.org (accessed on 26 January 2023).
- Lehtola, V.V.; Kaartinen, H.; Nuchter, A.; Kaijaluoto, R.; Kukko, A.; Litkey, P.; Honkavaara, E.; Rosnell, T.; Vaaja, M.T.; Virtanen, J.P.; et al. Comparison of the selected state-of-the-art 3D indoor scanning and point cloud generation methods. Remote Sens. 2017, 9, 796. [Google Scholar] [CrossRef]
- Virtanen, J.-P.; Kurkela, M.; Turppa, T.; Vaaja, M.T.; Julin, A.; Kukko, A.; Hyyppa, J.; Ahlavuo, M.; von Numers, J.E.; Haggren, H.; et al. Depth camera indoor mapping for 3D virtual radio play. Photogramm. Rec. 2018, 33, 171–195. [Google Scholar] [CrossRef]
- Shults, R.; Levin, E.; Habibi, R.; Shenoy, S.; Honcheruk, O.; Hart, T.; An, Z. Capability of Matterport 3d Camera for Industrial Archaeology Sites Inventory. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2019, 42, 1059–1064. [Google Scholar] [CrossRef]
- Chen, Y.; Tang, J.; Jiang, C.; Zhu, L.; Lehtomäki, M.; Kaartinen, H.; Kaijaluoto, R.; Wang, Y.; Hyyppä, J.; Hyyppä, H.; et al. The Accuracy Comparison of Three Simultaneous Localization and Mapping (SLAM)-Based Indoor Mapping Technologies. Sensors 2018, 18, 3228. [Google Scholar] [CrossRef]
- Roe, M. Recording mining landscapes in the Yorkshire Dales: The Contribution of the Northern Mine Research Society. Ind. Archaeol. Rev. 2006, 28, 117–122. [Google Scholar] [CrossRef]
- Photogrammetry in Industrial Heritage: Remote Sensing at the Quincy Smelter, Part 2. Available online: https://www.linkedin.com/pulse/photogrammetry-industrial-heritage-remote-sensing-quincy-scarlett (accessed on 28 July 2023).
- He, Y.; Liang, B.; Yang, J.; Li, S.; He, J. An Iterative Closest Points Algorithm for Registration of 3D Laser Scanner Point Clouds with Geometric Features. Sensors 2017, 17, 1862. [Google Scholar] [CrossRef] [PubMed]
- Estépar, R.S.J.; Brun, A.; Westin, C.F. Robust Generalized Total Least Squares Iterative Closest Point Registration. In Medical Image Computing and Computer-Assisted Intervention—MICCAI 2004; MICCAI 2004. Lecture Notes in Computer Science; Barillot, C., Haynor, D.R., Hellier, P., Eds.; Springer: Berlin/Heidelberg, Germany, 2004; Volume 3216. [Google Scholar] [CrossRef]
- Besl, P.J.; McKay, N.D. A Method for Registration of 3D Shapes. IEEE Trans. Pattern Anal. Mach. Intell. TPAMI 1992, 14, 239–255. [Google Scholar] [CrossRef]
- Quincy Mining Company HAER. A Look at the Architecture and Communities of the Quincy Mining Company; Quincy Mine Hoist Association (QMHA): Houghton, MI, USA, 2019. [Google Scholar]
- Quincy Mine Hoist Association (QMHA). Available online: https://quincymine.com (accessed on 26 January 2023).
- JAG3D. Java·Applied·Geodesy·3D. Available online: https://software.applied-geodesy.org (accessed on 26 January 2023).









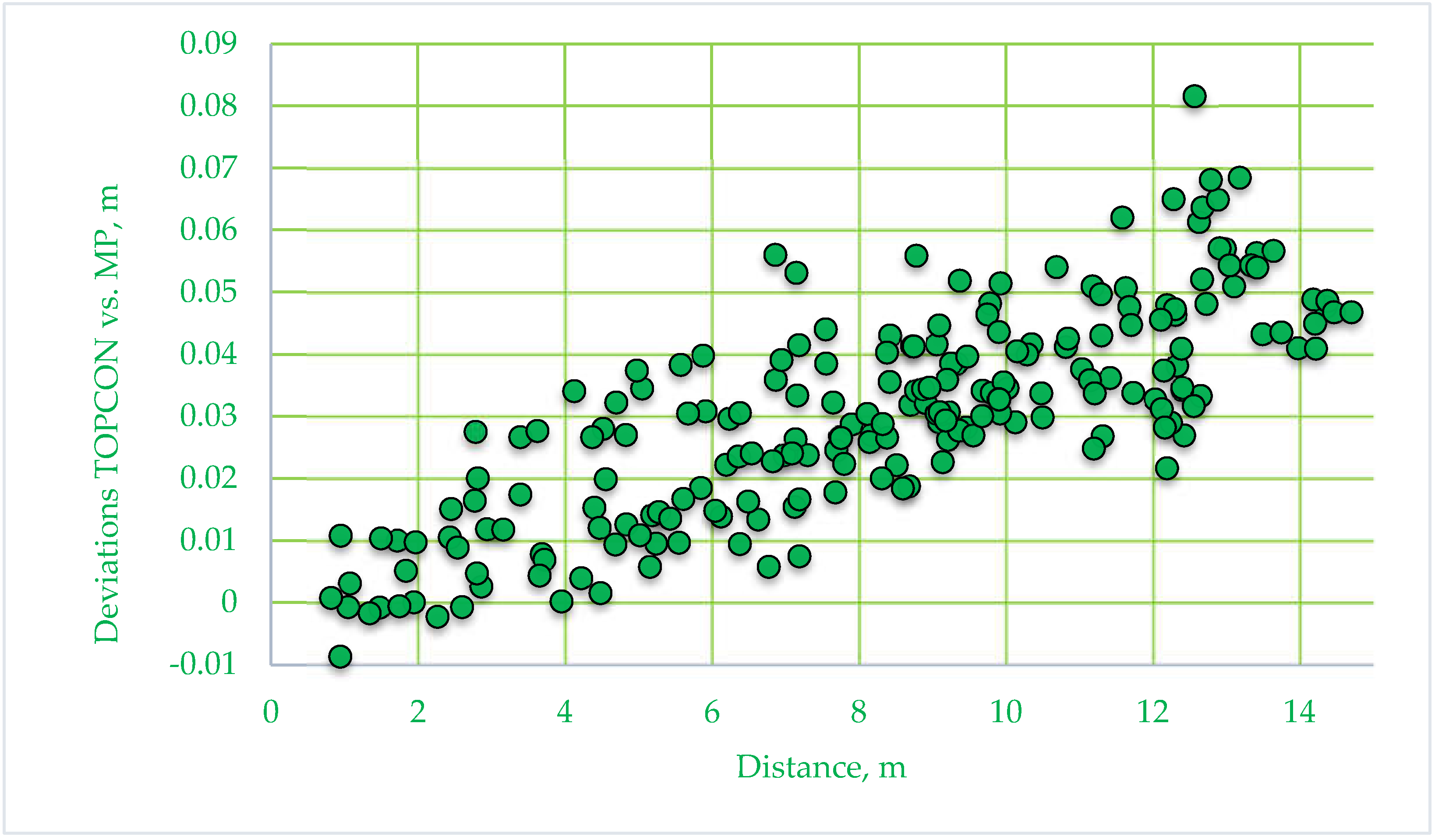
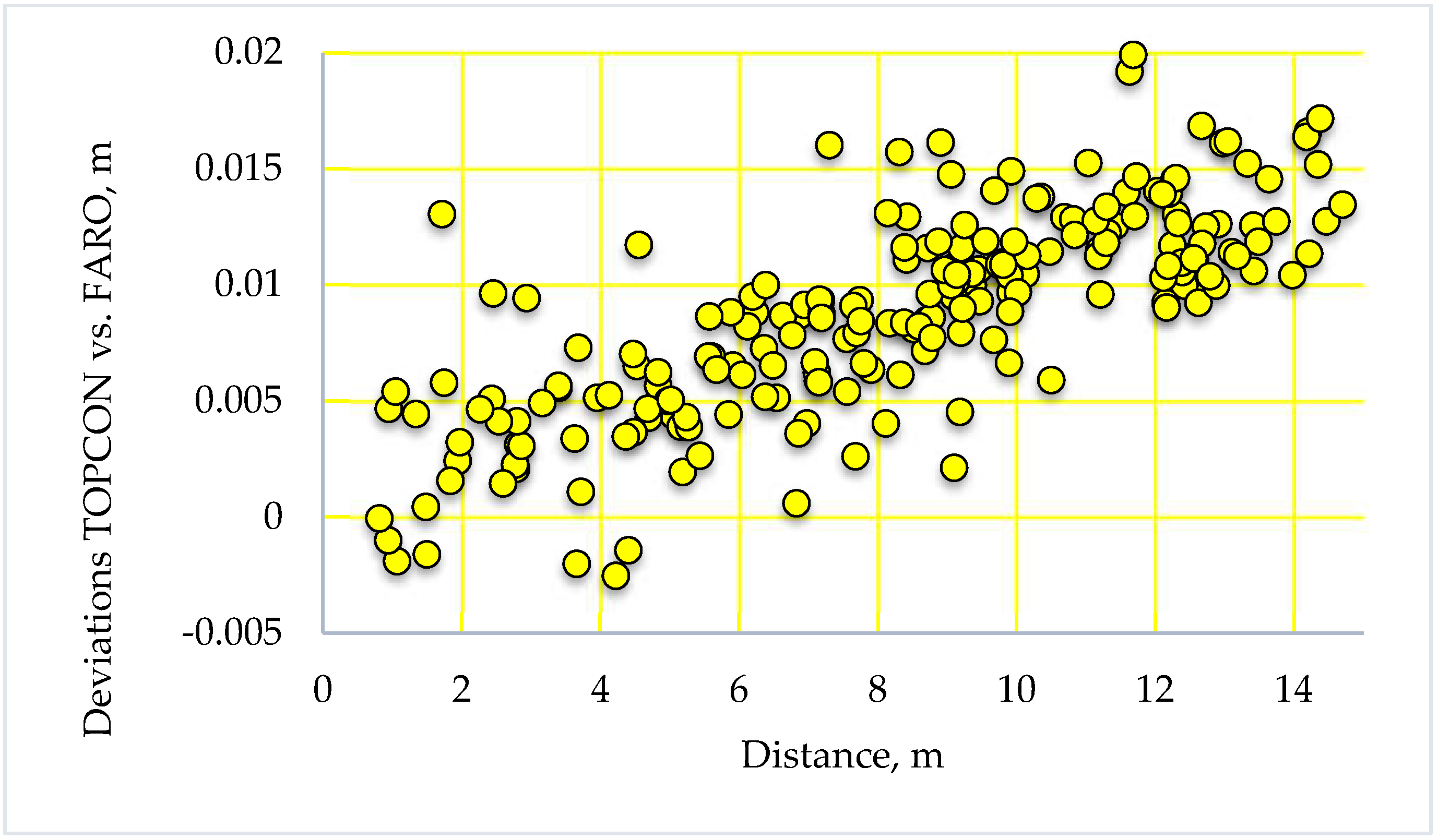
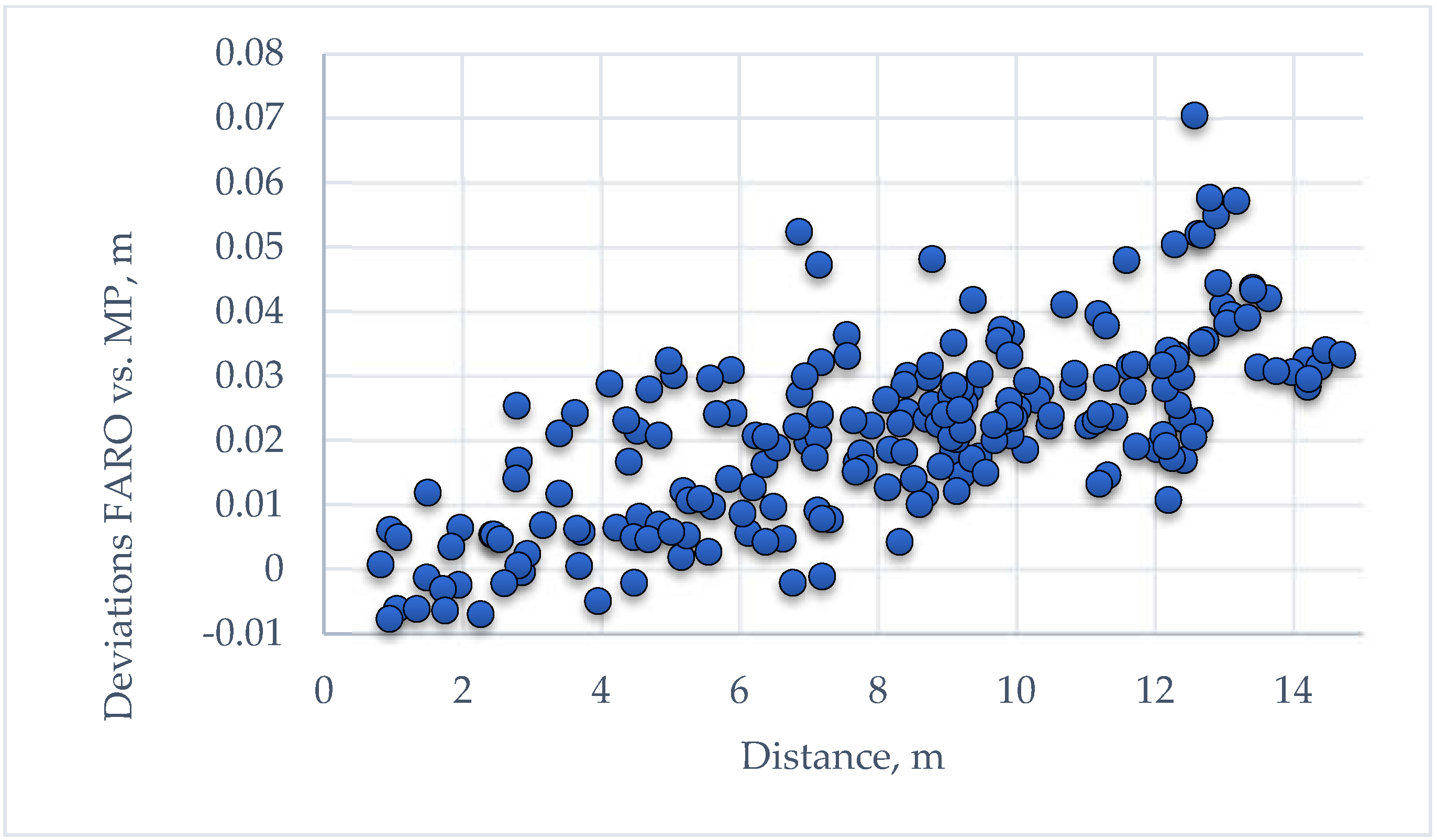

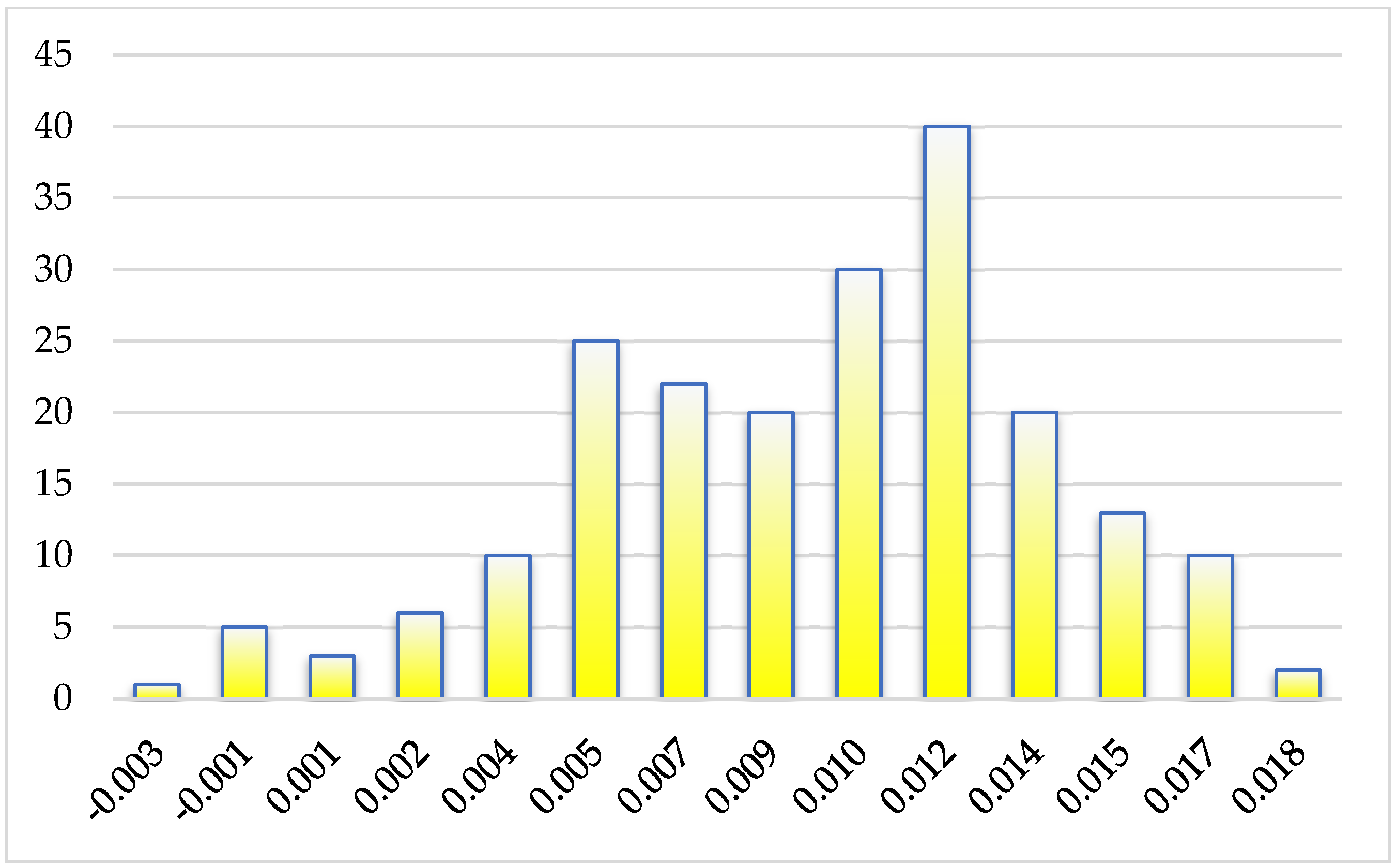
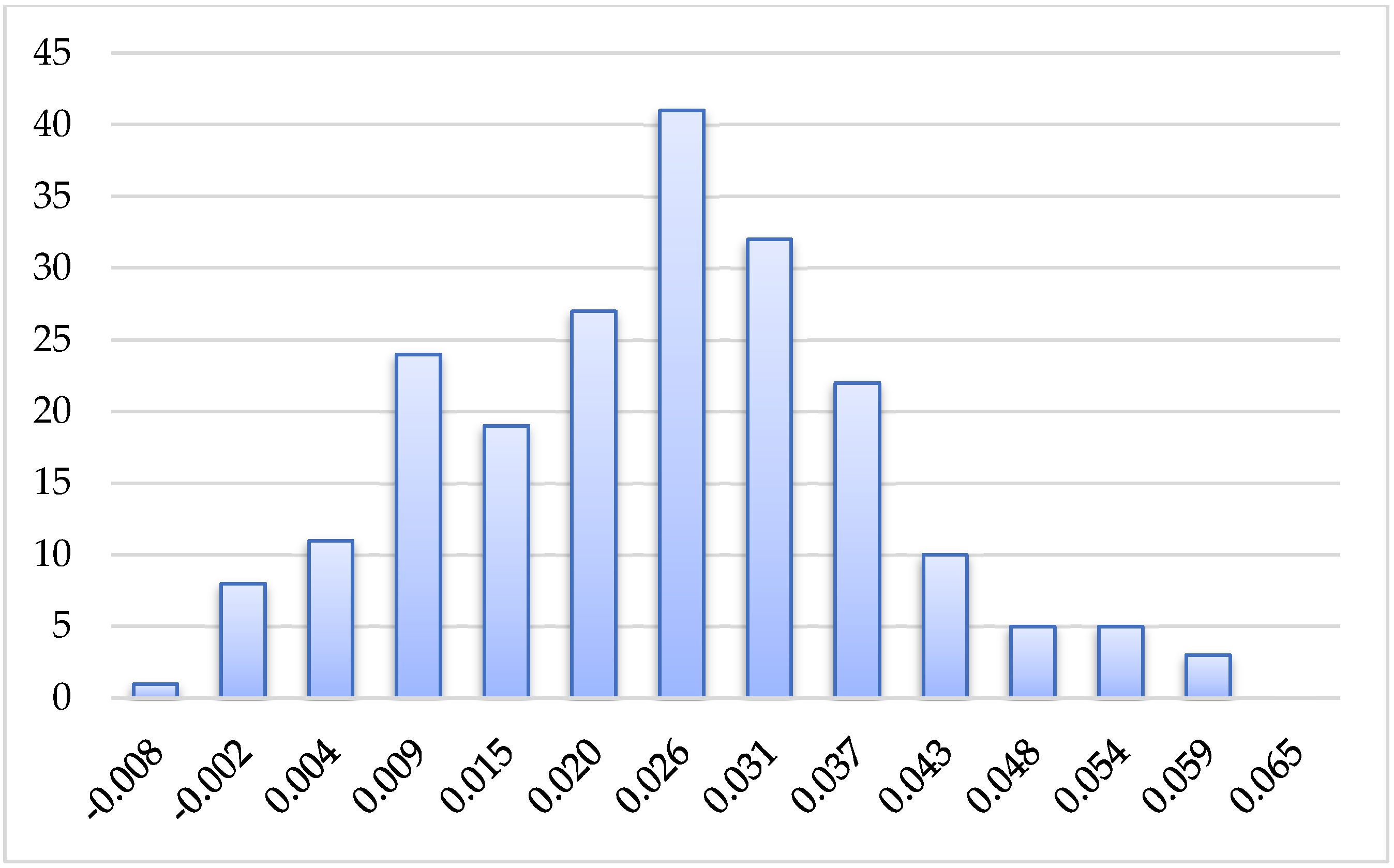
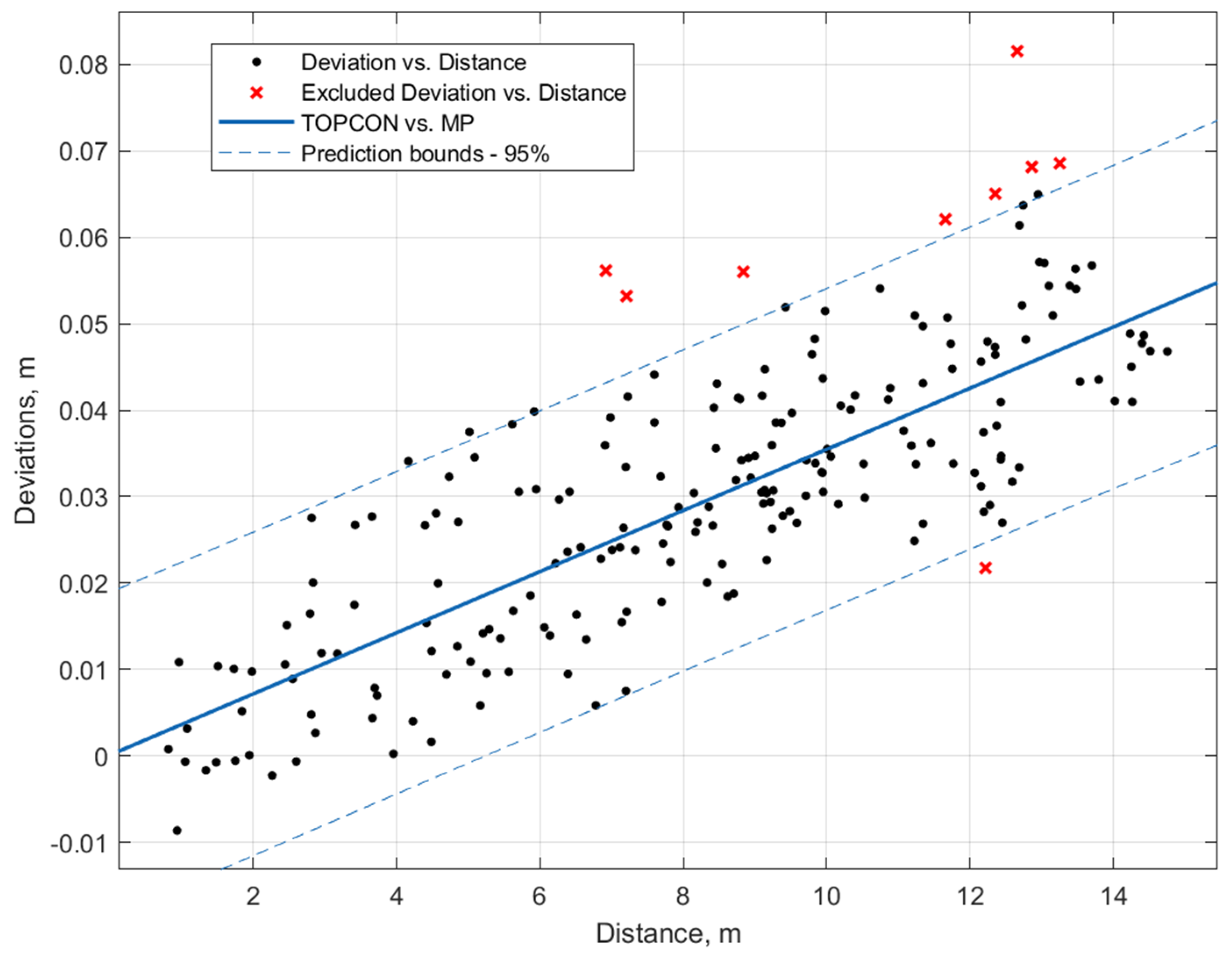




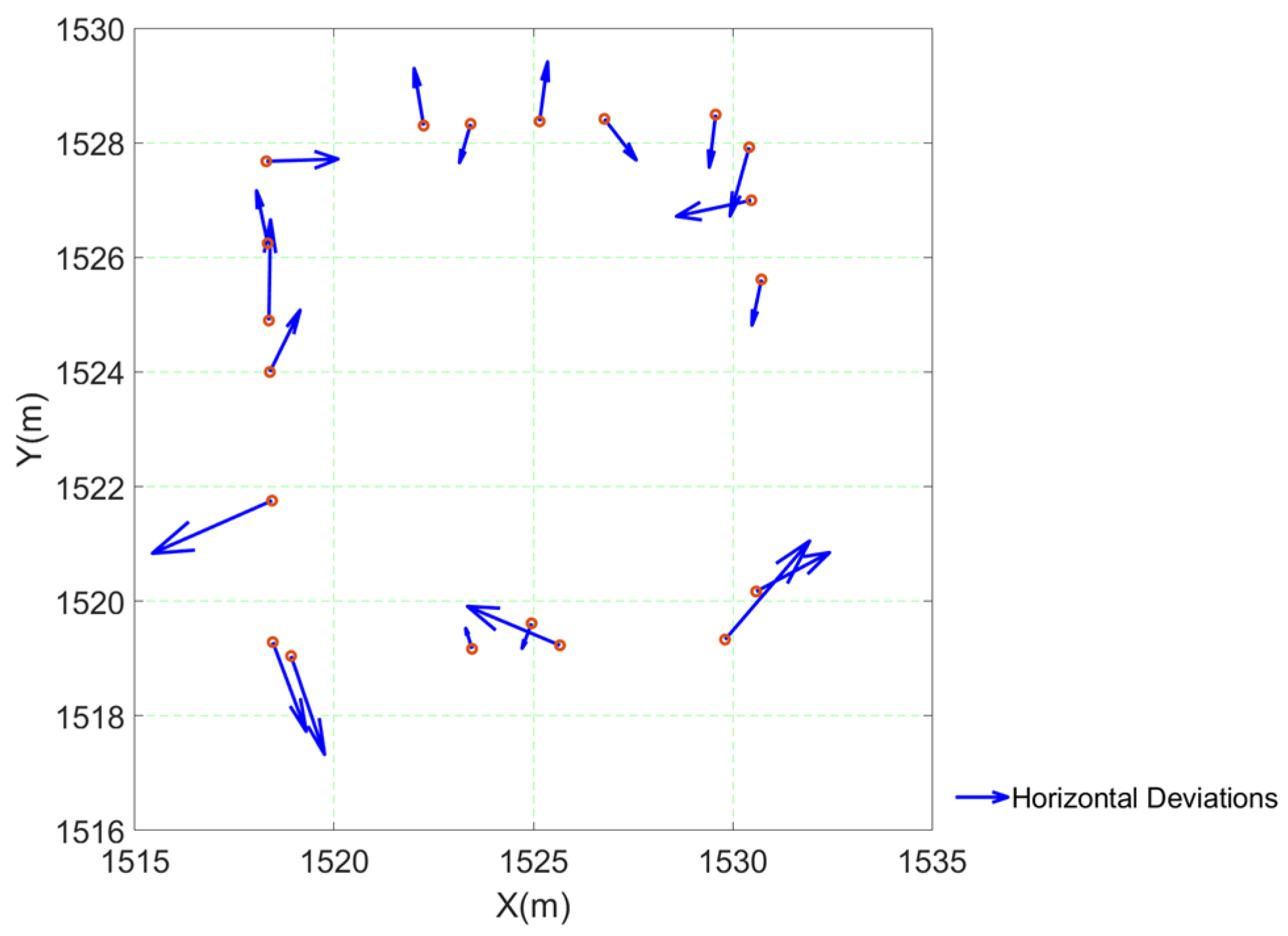









| Parameters, m | FARO Scanner vs. Matterport, m | Total Station vs. Matterport, m | Total Station vs. FARO Scanner, m |
|---|---|---|---|
| Mean | 0.0216 | 0.0305 | 0.0088 |
| Median | 0.0224 | 0.0306 | 0.0093 |
| Standard Deviation | 0.0141 | 0.0166 | 0.0044 |
| Range | 0.0782 | 0.0903 | 0.0224 |
| Minimum | −0.0077 | −0.0086 | −0.0025 |
| Maximum | 0.0705 | 0.0816 | 0.0199 |
| Count | 210 | 210 | 210 |
| Points | Orientation RMSE, m | No Scale Adjust, m | Orientation RMSE, m | Scale Adjust, m | |||
|---|---|---|---|---|---|---|---|
| C2C Mean | C2C RMS | C2C Mean | C2C RMSE | Scale | |||
| Original clouds | 0.0104 | 0.0129 | 0.0093 | 0.0072 | 0.0062 | 0.0041 | 1.003381 |
| 2M | 0.0092 | 0.0134 | 0.0142 | 0.0087 | 0.0084 | 0.0079 | 1.000630 |
| 1M | 0.0119 | 0.0064 | 0.0055 | 0.0121 | 0.0063 | 0.0046 | 0.999946 |
| 500K | 0.0157 | 0.0064 | 0.0055 | 0.0161 | 0.0063 | 0.0046 | 0.999891 |
| 200K | 0.0236 | 0.0071 | 0.0064 | 0.0240 | 0.0064 | 0.0046 | 0.999767 |
| Parameter | Value | σPar | T ≤ Φ − 1|H0 |
|---|---|---|---|
| Tx | 1527.4054 m | 1.7 mm | ✘ |
| Ty | 1521.7045 m | 1.8 mm | ✘ |
| Tz | 28.8318 m | 3.9 mm | ✘ |
| q0 | −0.99991764 | 0.00000139 | ✘ |
| q1 | 0.00139630 | 0.00017123 | ✘ |
| q2 | 0.00016900 | 0.00013625 | ✔ |
| q3 | −0.01275706 | 0.00010727 | ✘ |
| dsx | 3268.3 mm/km | 273.0 mm/km | ✘ |
| dsy | 3898.6 mm/km | 346.4 mm/km | ✘ |
| dsz | 5574.1 mm/km | 2376.8 mm/km | ✔ |
| Rx | 0.17749 gon | 21.77 mgon | ✘ |
| Ry | 0.02378 gon | 17.38 mgon | ✔ |
| Rz | 398.37571 gon | 13.66 mgon | ✘ |
| Point | X, m | Y, m | Z, m | σX mm | σY mm | σZ mm | εX mm | εY mm | εZ mm |
|---|---|---|---|---|---|---|---|---|---|
| A01 | 1518.4487 | 1521.7556 | 29.1297 | 3.1 | 3.1 | 3.4 | −7.5 | −2.3 | −2.6 |
| A02 | 1518.3932 | 1524.0000 | 30.8259 | 3.1 | 3.1 | 3.2 | 1.9 | 2.7 | 3.4 |
| A03 | 1518.3698 | 1524.8976 | 30.4800 | 3.1 | 3.1 | 3.1 | 0.1 | 4.4 | −1.9 |
| A04 | 1518.3388 | 1526.2446 | 29.8643 | 3.1 | 3.1 | 3.2 | −0.7 | 2.3 | 1.9 |
| A05 | 1518.3044 | 1527.6758 | 31.1795 | 3.1 | 3.2 | 3.4 | 4.5 | 0.1 | −2.2 |
| A06 | 1522.2479 | 1528.2988 | 29.7896 | 3.1 | 3.1 | 3.2 | −0.6 | 2.5 | 0.9 |
| A07 | 1523.4266 | 1528.3300 | 31.0545 | 3.0 | 3.1 | 3.2 | −0.7 | −1.7 | 2.7 |
| A08 | 1525.1567 | 1528.3728 | 29.2959 | 3.0 | 3.1 | 3.3 | 0.5 | 2.6 | 0.9 |
| A09 | 1526.7790 | 1528.4166 | 30.4297 | 3.1 | 3.1 | 3.1 | 2.0 | −1.8 | 0.5 |
| A10 | 1529.5683 | 1528.4910 | 30.1051 | 3.1 | 3.1 | 3.2 | −0.4 | −2.3 | −1.4 |
| A11 | 1530.4093 | 1527.9206 | 29.7500 | 3.2 | 3.1 | 3.2 | −1.2 | −3.0 | −0.9 |
| A12 | 1530.4640 | 1526.9962 | 30.2438 | 3.1 | 3.1 | 3.2 | −4.7 | −0.7 | −1.6 |
| A13 | 1530.7169 | 1525.6147 | 30.7894 | 3.1 | 3.1 | 3.2 | −0.6 | −2.0 | −0.8 |
| A15 | 1530.5836 | 1520.1693 | 30.7696 | 3.2 | 3.2 | 3.3 | 4.6 | 1.7 | 2.3 |
| A16 | 1529.8039 | 1519.3302 | 30.0777 | 3.2 | 3.2 | 3.3 | 5.3 | 4.3 | 5.2 |
| A17 | 1525.6651 | 1519.2302 | 30.4983 | 3.1 | 3.1 | 3.1 | −5.8 | 1.7 | −3.5 |
| A18 | 1524.9542 | 1519.6144 | 30.0243 | 3.1 | 3.1 | 3.1 | −0.6 | −1.1 | −1.5 |
| A19 | 1523.4613 | 1519.1684 | 31.0058 | 3.1 | 3.1 | 3.2 | −0.4 | 0.9 | −2.3 |
| A20 | 1518.9253 | 1519.0448 | 29.8003 | 3.1 | 3.2 | 3.2 | 2.1 | −4.3 | 1.5 |
| A21 | 1518.4664 | 1519.2857 | 30.4297 | 3.1 | 3.2 | 3.2 | 2.1 | −3.9 | −0.6 |
| Distances | Control Distances from Map, m | Matterport Distances, m | Differences, m | Corrected Matterport Distances, m | Corrected Differences, m |
|---|---|---|---|---|---|
| 1 | 5.81 | 5.79 | −0.02 | 5.81 | 0.003 |
| 2 | 5.81 | 5.77 | −0.04 | 5.79 | −0.018 |
| 3 | 5.81 | 5.7 | −0.11 | 5.72 | −0.088 |
| 4 | 5.81 | 5.83 | 0.02 | 5.85 | 0.043 |
| 5 | 5.73 | 5.66 | −0.07 | 5.68 | −0.048 |
| 6 | 2 | 1.97 | −0.03 | 1.98 | −0.024 |
| 7 | 2 | 1.97 | −0.03 | 1.98 | −0.024 |
| 8 | 2 | 1.97 | −0.03 | 1.98 | −0.024 |
| 9 | 23.16 | 22.87 | −0.29 | 22.96 | −0.201 |
| 10 | 23.16 | 22.83 | −0.33 | 22.92 | −0.241 |
| 11 | 23.16 | 22.79 | −0.37 | 22.88 | −0.281 |
| 12 | 29 | 28.82 | −0.18 | 28.91 | −0.086 |
| 13 | 29 | 28.88 | −0.12 | 28.97 | −0.026 |
| 14 | 29 | 28.89 | −0.11 | 28.98 | −0.016 |
| 15 | 28.4 | 28.24 | −0.16 | 28.33 | −0.068 |
| Mean | 14.66 | −0.125 | 14.58 | −0.073 | |
| RMS | 0.120 | 0.094 | |||
| Relative | 1:122 (0.82%) | 1:155 (0.64%) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shults, R.; Levin, E.; Aukazhiyeva, Z.; Pavelka, K.; Kulichenko, N.; Kalabaev, N.; Sagyndyk, M.; Akhmetova, N. A Study of the Accuracy of a 3D Indoor Camera for Industrial Archaeology Applications. Heritage 2023, 6, 6240-6267. https://doi.org/10.3390/heritage6090327
Shults R, Levin E, Aukazhiyeva Z, Pavelka K, Kulichenko N, Kalabaev N, Sagyndyk M, Akhmetova N. A Study of the Accuracy of a 3D Indoor Camera for Industrial Archaeology Applications. Heritage. 2023; 6(9):6240-6267. https://doi.org/10.3390/heritage6090327
Chicago/Turabian StyleShults, Roman, Eugene Levin, Zhanar Aukazhiyeva, Karel Pavelka, Nataliia Kulichenko, Naiman Kalabaev, Maral Sagyndyk, and Nagima Akhmetova. 2023. "A Study of the Accuracy of a 3D Indoor Camera for Industrial Archaeology Applications" Heritage 6, no. 9: 6240-6267. https://doi.org/10.3390/heritage6090327
APA StyleShults, R., Levin, E., Aukazhiyeva, Z., Pavelka, K., Kulichenko, N., Kalabaev, N., Sagyndyk, M., & Akhmetova, N. (2023). A Study of the Accuracy of a 3D Indoor Camera for Industrial Archaeology Applications. Heritage, 6(9), 6240-6267. https://doi.org/10.3390/heritage6090327








