Modelling the Alteration of Medieval Stained Glass as a Function of Climate and Pollution: Comparison between Different Methodologies
Abstract
1. Introduction
2. Materials and Methods
2.1. Data
2.2. Dose–Response Functions
2.3. Kinetic Laws
3. Results and Discussion
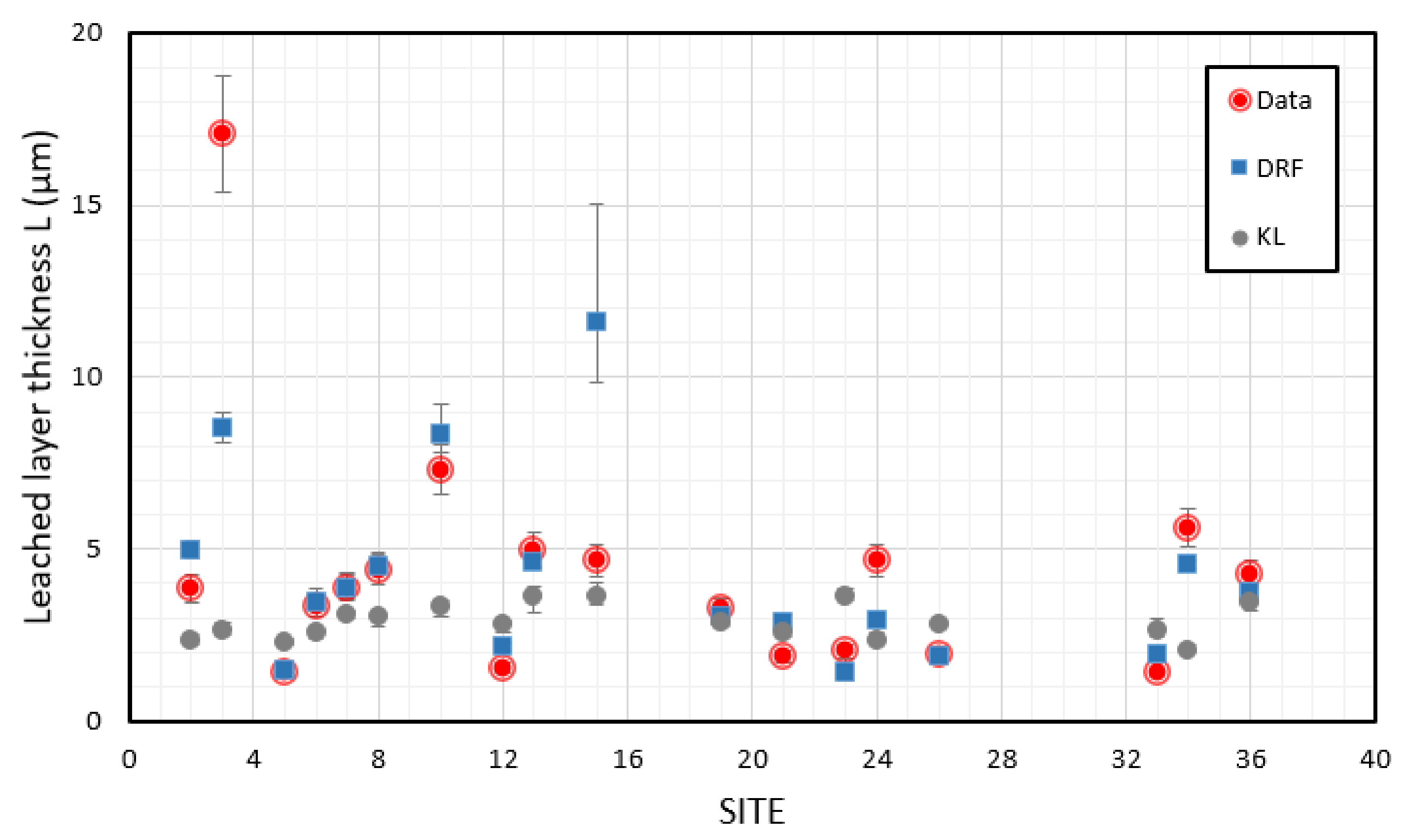
3.1. Leached Layer Thickness in Model Glass
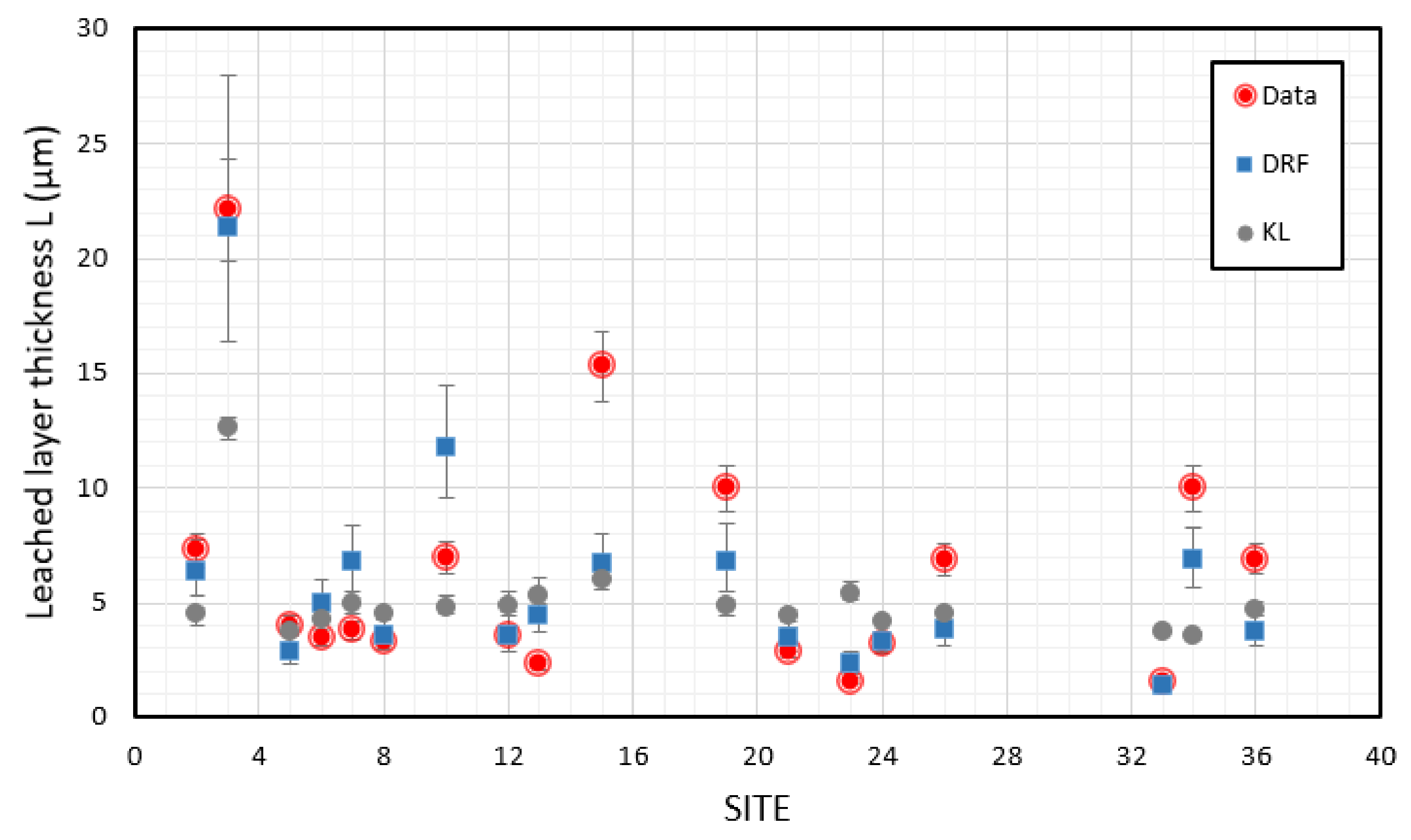
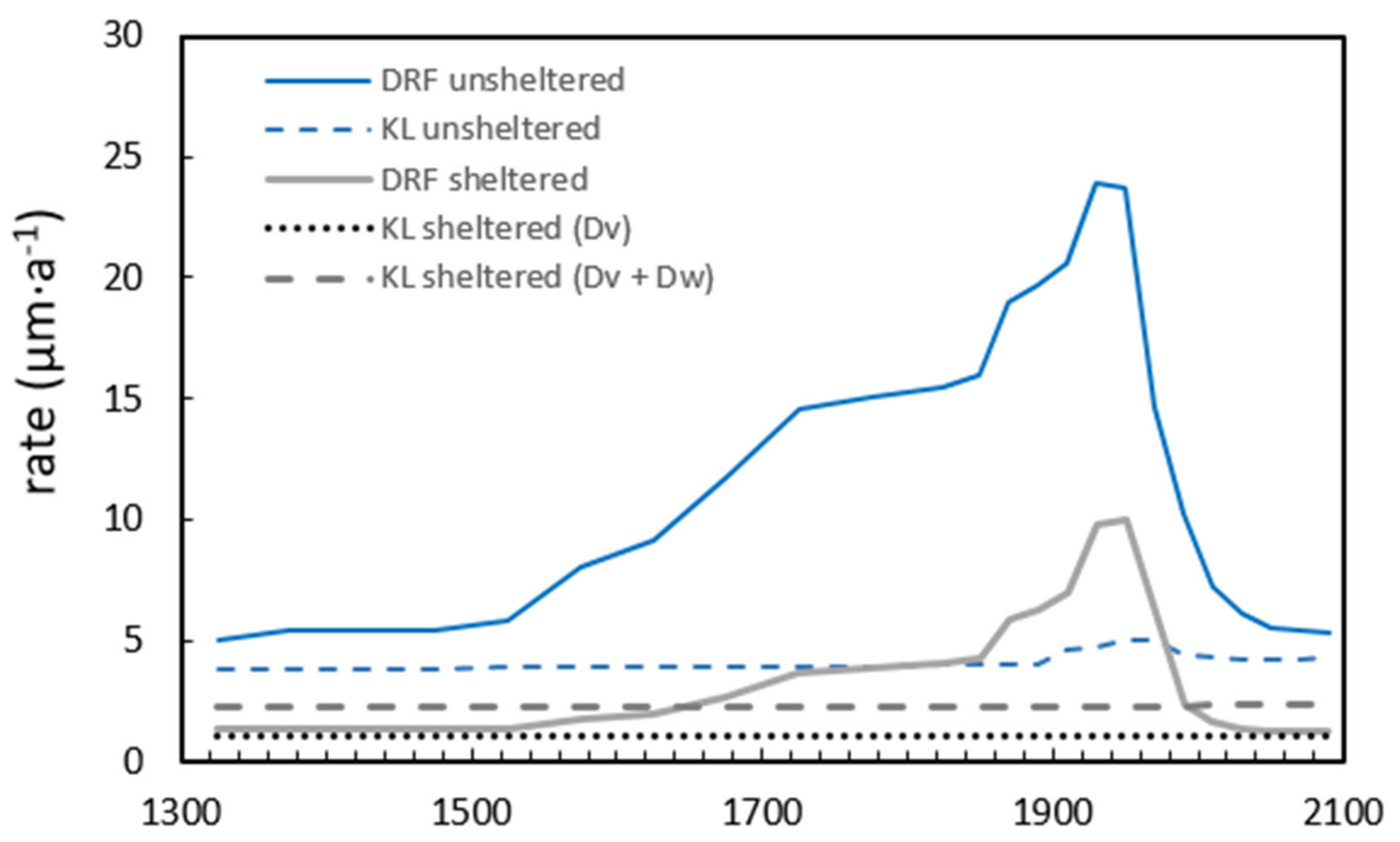
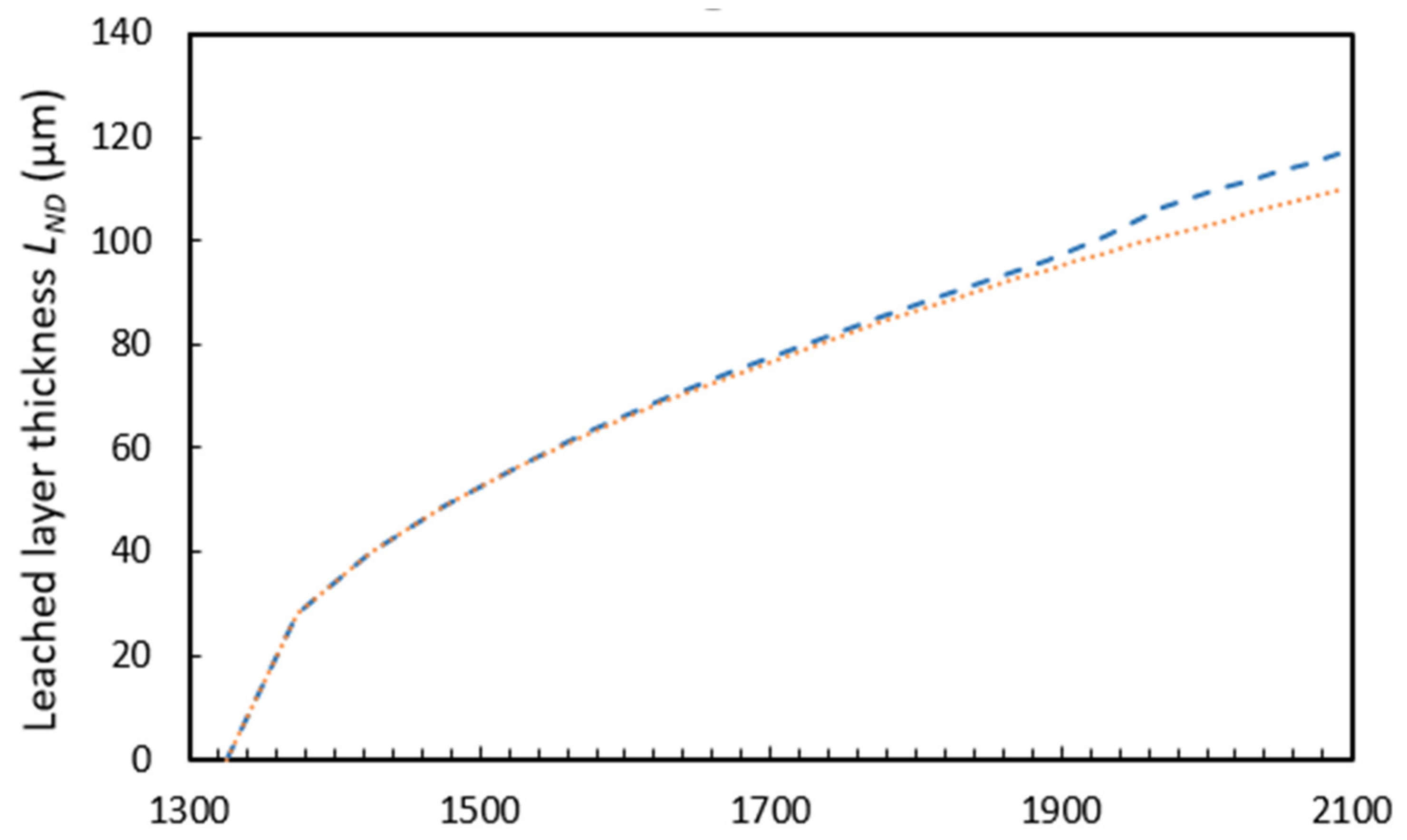
3.2. Long-Term Alteration Rate of Historic Glass in Paris
3.3. Advantages and Drawbacks of the Models
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Adlington, L.W.; Freestone, I.C.; Kunicki-Goldfinger, J.J.; Ayers, T.; Gilderdale Scott, H.; Eavis, A. Regional Patterns in Medieval European Glass Composition as a Provenancing Tool. J. Archaeol. Sci. 2019, 110, 104991. [Google Scholar] [CrossRef]
- Verney-Carron, A.; Sessegolo, L.; Chabas, A.; Lombardo, T.; Rossano, S.; Perez, A.; Valbi, V.; Boutillez, C.; Muller, C.; Vaulot, C.; et al. Alteration of Medieval Stained Glass Windows in Atmospheric Medium: Review and Simplified Alteration Model. NPJ Mater. Degrad. 2023. under review. [Google Scholar]
- Sterpenich, J.; Libourel, G. Using Stained Glass Windows to Understand the Durability of Toxic Waste Matrices. Chem. Geol. 2001, 174, 181–193. [Google Scholar] [CrossRef]
- Bräutigam, U.; Bürger, H.; Völksch, G. Investigations into Structure and Composition of Gel Layers on Medieval Window Glasses of the Katharinenkirche, Oppenheim (Germany), and the Cathedral St. Gatien, Tours (France). Glastech. Ber. Glass Sci. Technol. 1995, 68, 29–33. [Google Scholar]
- Carmona, N.; García-Heras, M.; Gil, C.; Villegas, M.A. Vidrios y Grisallas Del s. XV de La Cartuja de Miraflores (Burgos): Caracterización y Estado de Conservación. Bol. Soc. Esp. Ceram. Vidr. 2005, 44, 251–258. [Google Scholar] [CrossRef]
- Carmona, N.; Laiz, L.; Gonzalez, J.M.; Garcia-Heras, M.; Villegas, M.A.; Saiz-Jimenez, C. Biodeterioration of Historic Stained Glasses from the Cartuja de Miraflores (Spain). Int. Biodeterior. Biodegrad. 2006, 58, 155–161. [Google Scholar] [CrossRef]
- Garcia-Vallès, M.; Vendrell-Saz, M. The Glasses of the Transept’s Rosette of the Cathedral of Tarragona: Characterization, Classification and Decay. Bol. Soc. Esp. Ceram. Vidr. 2002, 41, 217–224. [Google Scholar]
- Gillies, K.J.S.; Cox, A. Decay of Medieval Stained Glass at York, Canterbury and Carlisle. I: Composition of the Glass and Its Weathering Products. Glastech. Ber. 1988, 61, 75–84. [Google Scholar]
- Lombardo, T.; Loisel, C.; Gentaz, L.; Chabas, A.; Verita, M.; Pallot-Frossard, I. Long Term Assessment of Atmospheric Decay of Stained Glass Windows. Corros. Eng. Sci. Technol. 2010, 45, 420–424. [Google Scholar] [CrossRef]
- Marchesi, V.; Messiga, B.; Riccardi, M.P. Window Panes of the Certosa Di Pavia: Chemical Composition, Microstructure and Alteration. Surf. Eng. 2005, 21, 397–401. [Google Scholar] [CrossRef]
- Messiga, B.; Riccardi, M.P. Alteration Behaviour of Glass Panes from the Medieval Pavia Charterhouse (Italy). J. Cult. Herit. 2006, 7, 334–338. [Google Scholar] [CrossRef]
- Perez y Jorba, M.; Dallas, J.P.; Bauer, C.; Bahezre, C.; Martin, J.C. Deterioration of Stained Glass by Atmospheric Corrosion and Micro-Organisms. J. Mater. Sci. 1980, 15, 1640–1647. [Google Scholar] [CrossRef]
- Piñar, G.; Garcia-Valles, M.; Gimeno-Torrente, D.; Fernandez-Turiel, J.L.; Ettenauer, J.; Sterflinger, K. Microscopic, Chemical, and Molecular-Biological Investigation of the Decayed Medieval Stained Window Glasses of Two Catalonian Churches. Int. Biodeterior. Biodegrad. 2013, 84, 388–400. [Google Scholar] [CrossRef]
- Schreiner, M. Deterioration of Stained Medieval Glass by Atmospheric Attack. Part 1. Scanning Electron Microscopic Investigations of the Weathering Phenomena. Glastech. Ber. 1988, 61, 197–204. [Google Scholar]
- Schreiner, M. Deterioration of Stained Medieval Glass by Atmospheric Attack. Part 2. Secondary Ion Mass Spectrometry Analysis of the Naturally Weathered Glass Surfaces. Glastech. Ber. 1988, 61, 223–229. [Google Scholar]
- Sessegolo, L.; Verney-Carron, A.; Saheb, M.; Remusat, L.; Gonzalez-Cano, A.; Nuns, N.; Mertz, J.-D.; Loisel, C.; Chabas, A. Long-Term Weathering Rate of Stained-Glass Windows Using H and O Isotopes. NPJ Mater. Degrad. 2018, 2, 17. [Google Scholar] [CrossRef]
- Lefèvre, R.-A.; Grégoire, M.; Derbez, M.; Ausset, P. Origin Of Sulphated Grey Crusts On Glass In Polluted Urban Atmosphere: Stained Glass Windows Of Tours Cathedral (France). Glastech. Ber. Glass Sci. Technol. 1998, 71, 75–80. [Google Scholar]
- Lombardo, T.; Gentaz, L.; Verney-Carron, A.; Chabas, A.; Loisel, C.; Neff, D.; Leroy, E. Characterisation of Complex Alteration Layers in Medieval Glasses. Corros. Sci. 2013, 72, 10–19. [Google Scholar] [CrossRef]
- Verney-Carron, A.; Sessegolo, L.; Saheb, M.; Valle, N.; Ausset, P.; Losno, R.; Mangin, D.; Lombardo, T.; Chabas, A.; Loisel, C. Understanding the Mechanisms of Si–K–Ca Glass Alteration Using Silicon Isotopes. Geochim. Cosmochim. Acta 2017, 203, 404–421. [Google Scholar] [CrossRef]
- Gentaz, L. Simulation et Modélisation de l’altération Des Verres de Composition Médiévale Dans L’atmosphère Urbaine. Ph.D. Thesis, Université Paris-Est, Marne-la-Vallée, France, 2011. [Google Scholar]
- Gentaz, L.; Lombardo, T.; Loisel, C.; Chabas, A.; Vallotto, M. Early Stage of Weathering of Medieval-like Potash-Lime Model Glass: Evaluation of Key Factors. Environ. Sci. Pollut. Res. Int. 2011, 18, 291–300. [Google Scholar] [CrossRef]
- Geotti-Bianchini, F.; Nicola, C.; Preo, M.; Vallotto, M.; Verita, M. MicroIRRS and EPMA Study of the Weathering of Potash-Lime-Silicate Glasses. Riv. Stn. Sper. Vetro 2005, 35, 49–61. [Google Scholar]
- Melcher, M.; Schreiner, M. Evaluation Procedure for Leaching Studies on Naturally Weathered Potash-Lime-Silica Glasses with Medieval Composition by Scanning Electron Microscopy. J. Non-Cryst. Solids 2005, 351, 1210–1225. [Google Scholar] [CrossRef]
- Melcher, M.; Schreiner, M. Leaching Studies on Naturally Weathered Potash-Lime–Silica Glasses. J. Non-Cryst. Solids 2006, 352, 368–379. [Google Scholar] [CrossRef]
- Melcher, M.; Schreiner, M. Quantification of the Influence of Atmospheric Pollution on the Weathering of Low-Durability Potash-Lime-Silica Glasses. Pollut. Atmos. 2007, 49, 13–22. [Google Scholar]
- Melcher, M.; Schreiner, M. Results from the Multipollutant Programme: Evaluation of the Decay to Glass Samples of Medieval Composition after 3, 4, 5 and 6 Years of Exposure. Part B: Results of the Unsheltered Exposure; UNECE International Co-Operative Programme on Effects on Materials, Including Historic and Cultural Monuments; Institute of Sciences and Technologies in Art, Academy of Fine Arts: Vienna, Austria, 2004; p. 136. [Google Scholar]
- Munier, I.; Lefèvre, R.; Geotti-Bianchini, F.; Verità, M. Influence of Polluted Urban Atmosphere on the Weathering of Low Durability Glasses. Glass Technol. 2002, 43, 225–237. [Google Scholar]
- Tidblad, J.; Kucera, V.; Ferm, M.; Kreislova, K.; Brüggerhoff, S.; Doytchinov, S.; Screpanti, A.; Grøntoft, T.; Yates, T.; de la Fuente, D.; et al. Effects of Air Pollution on Materials and Cultural Heritage: ICP Materials Celebrates 25 Years of Research. Int. J. Corros. 2012, 2012, e496321. [Google Scholar] [CrossRef]
- Gentaz, L.; Lombardo, T.; Chabas, A.; Loisel, C.; Neff, D.; Verney-Carron, A. Role of Secondary Phases in the Scaling of Stained Glass Windows Exposed to Rain. Corros. Sci. 2016, 109, 206–216. [Google Scholar] [CrossRef]
- Melcher, M.; Schreiner, M. Statistical Evaluation of Potash-Lime-Silica Glass Weathering. Anal. Bioanal. Chem. 2004, 379, 628–639. [Google Scholar] [CrossRef]
- Woisetschläger, G.; Schreiner, M. Evaluation of Decay to Glass Samples after 1 and 2 Years of Exposure; UNECE International Co-Operative Programme on Effects on Materials, Including Historic and Cultural Monumentsicp Materials; Institute of Chemistry, Academy of Fine Arts: Vienna, Austria, 1998; p. 68. [Google Scholar]
- Sessegolo, L.; Verney-Carron, A.; Ausset, P.; Nowak, S.; Triquet, S.; Saheb, M.; Chabas, A. Alteration Rate of Medieval Potash-Lime Silicate Glass as a Function of PH and Temperature: A Low PH-Dependent Dissolution. Chem. Geol. 2020, 550, 119704. [Google Scholar] [CrossRef]
- Boehm, T. The Influence of Temperature, Relative Humidity and SO2 Concentration on Weathering of Glass. In Proceedings of the 5th ESG Conference, Prague, Czech Republic, 21–24 June 1999; pp. 49–55. [Google Scholar]
- Carmona, N.; Villegas, M.A.; Fernández Navarro, J.M. Corrosion Behaviour of R2O–CaO–SiO2 Glasses Submitted to Accelerated Weathering. J. Am. Ceram. Soc. 2005, 25, 903–910. [Google Scholar] [CrossRef]
- Sessegolo, L.; Verney-Carron, A.; Valle, N.; Ausset, P.; Narayanasamy, S.; Nowak, S.; Fourdrin, C.; Saheb, M.; Chabas, A. Alteration of Potash-Lime Silicate Glass in Atmospheric Medium: Study of Mechanisms and Kinetics Using 18O and D Isotopes. J. Non-Cryst. Solids 2021, 570, 121020. [Google Scholar] [CrossRef]
- Brimblecombe, P.; Lefèvre, R.-A. Weathering of Materials at Notre-Dame from Changes in Air Pollution and Climate in Paris, 1325–2090. J. Cult. Herit. 2021, 50, 88–94. [Google Scholar] [CrossRef]
- Tidblad, J.; Kreislová, K.; Faller, M.; de la Fuente, D.; Yates, T.; Verney-Carron, A.; Grøntoft, T.; Gordon, A.; Hans, U. ICP Materials Trends in Corrosion, Soiling and Air Pollution (1987–2014). Materials 2017, 10, 969. [Google Scholar] [CrossRef]
- Tidblad, J.; Kucera, V.; Mikhailov, A.A.; Henriksen, J.; Kreislova, K.; Yates, T.; Stöckle, B.; Schreiner, M. UN ECE ICP Materials: Dose-Response Functions on Dry and Wet Acid Deposition Effects After 8 Years of Exposure. Water Air Soil Pollut. 2001, 130, 1457–1462. [Google Scholar] [CrossRef]
- Melcher, M.; Schreiner, M. Results from the Multipollutant Programme: Evaluation of the Decay to Glass Samples of Medieval Composition after 3, 4, 5 and 6 Years of Exposure. Part A: Results of the Sheltered Exposure; UNECE International Co-Operative Programme on Effects on Materials, Including Historic and Cultural Monuments; Institute of Sciences and Technologies in Art, Academy of Fine Arts: Vienna, Austria, 2003; p. 167. [Google Scholar]
- Doremus, R. Interdiffusion of Hydrogen and Alkali Ions in a Glass Surface. J. Non-Cryst. Solids 1975, 19, 137–144. [Google Scholar] [CrossRef]
- Chave, T.; Frugier, P.; Ayral, A.; Gin, S. Solid State Diffusion during Nuclear Glass Residual Alteration in Solution. J. Nucl. Mater. 2007, 362, 466–473. [Google Scholar] [CrossRef]
- Grambow, B. A General Rate Equation for Nuclear Waste Glass Corrosion. MRS Online Proc. Libr. Arch. 1984, 44, 15–27. [Google Scholar] [CrossRef]
- Ionescu, A.; Lefèvre, R.-A.; Brimblecombe, P.; Grossi, C.M. Long-Term Damage to Glass in Paris in a Changing Environment. Sci. Total Environ. 2012, 431, 151–156. [Google Scholar] [CrossRef]
- Brimblecombe, P. London Air Pollution, 1500–1900. Atmos. Environ. 1977, 11, 1157–1162. [Google Scholar] [CrossRef]
- Brimblecombe, P.; Grossi, C.M. Millennium-Long Recession of Limestone Facades in London. Environ. Geol. 2008, 56, 463–471. [Google Scholar] [CrossRef]
- Richards, J.; Brimblecombe, P. The Transfer of Heritage Modelling from Research to Practice. Herit. Sci. 2022, 10, 17. [Google Scholar] [CrossRef]
- Di Turo, F.; Proietti, C.; Screpanti, A.; Fornasier, M.F.; Cionni, I.; Favero, G.; De Marco, A. Impacts of Air Pollution on Cultural Heritage Corrosion at European Level: What Has Been Achieved and What Are the Future Scenarios. Environ. Pollut. 2016, 218, 586–594. [Google Scholar] [CrossRef]
- Grøntoft, T. Maintenance Costs for European Zinc and Portland Limestone Surfaces Due to Air Pollution since the 1980s. Sustain. Cities Soc. 2018, 39, 1–15. [Google Scholar] [CrossRef]
- Grøntoft, T. Conservation-Restoration Costs for Limestone Façades Due to Air Pollution in Krakow, Poland, Meeting European Target Values and Expected Climate Change. Sustain. Cities Soc. 2017, 29, 169–177. [Google Scholar] [CrossRef]
- Grøntoft, T.; Verney-Carron, A.; Tidblad, J. Cleaning Costs for European Sheltered White Painted Steel and Modern Glass Surfaces Due to Air Pollution Since the Year 2000. Atmosphere 2019, 10, 167. [Google Scholar] [CrossRef]
- Spezzano, P. Mapping the Susceptibility of UNESCO World Cultural Heritage Sites in Europe to Ambient (Outdoor) Air Pollution. Sci. Total Environ. 2021, 754, 142345. [Google Scholar] [CrossRef]
| Glass | SiO2 | K2O | CaO | P2O5 | Na2O | MgO | Al2O3 | MnO | Fe2O3 |
|---|---|---|---|---|---|---|---|---|---|
| M1 | 48.0 | 25.5 | 15.0 | 4.0 | 3.0 | 3.0 | 1.5 | ||
| M3 | 60.0 | 15.0 | 25.0 | ||||||
| SG3 | 51.3 | 19.2 | 16.8 | 3.8 | 1.1 | 4.0 | 1.8 | 1.0 | 1.2 |
| 6-Month Exposure (October 1993–April 1994) | 12-Month Exposure (October 1993–October 1994) | |||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Environmental Data | L6U | Environmental Data | L12U | |||||||||||||||
| Site | T | RH | SO2 | NO2 | r | pH | Data | DRF | KL | T | RH | SO2 | NO2 | r | pH | Data | DRF | KL |
| °C | % | µg·m−3 | mm | µm | µm | µm | °C | % | µg·m−3 | mm | µm | µm | µm | |||||
| Kaperske Hory (Czech Rep.) | 1.5 | 77 | 20.2 | 8.5 | 124.7 | 4.6 | 3.9 | 5.0 | 2.3 | 7.3 | 73 | 16.7 | 7.1 | 1006.7 | 5.1 | 7.3 | 6.4 | 4.5 |
| Kopisty (Czech Rep.) | 3.4 | 80 | 52.2 | 32.9 | 252.4 | 4.9 | 17.1 | 8.5 | 2.6 | 9.8 | 74 | 51.1 | 28.5 | 1343.5 | 0.5 | 22.1 | 21.4 | 12.6 |
| Ähtari (Finland) | −6.2 | 87 | 2.2 | 5.4 | 230.5 | 4.5 | 1.4 | 1.5 | 2.3 | 2.0 | 80 | 1.3 | 4 | 529.1 | 4.6 | 4.0 | 2.9 | 3.8 |
| Helsinki (Finland) | −2.4 | 84 | 9.5 | 37.8 | 253.7 | 4.4 | 3.4 | 3.5 | 2.6 | 5.0 | 76 | 6.8 | 36.3 | 621.5 | 4.4 | 3.5 | 5.0 | 4.3 |
| Waldhof-Langenbrügge (Germany) | 2.9 | 90 | 11.5 | 13.3 | 392.6 | 4.6 | 3.9 | 3.9 | 3.1 | 8.9 | 82 | 7.3 | 9.5 | 723.3 | 4.5 | 3.8 | 6.8 | 5.0 |
| Aschaffenburg (Germany) | 5.4 | 70 | 16.2 | 41.8 | 403 | 4.8 | 4.4 | 4.5 | 3.1 | 11.4 | 64 | 11.7 | 40.2 | 749 | 4.8 | 3.3 | 3.6 | 4.5 |
| Bottrop (Germany) | 5.8 | 83 | 45.8 | 40.7 | 439.5 | 4.7 | 7.3 | 8.3 | 3.3 | 11.1 | 79 | 35.8 | 37.9 | 764.6 | 4.8 | 7.0 | 11.8 | 4.8 |
| Garmisch-Partenkirchen (Germany) | 2.2 | 83 | 4.7 | 17.3 | 391.1 | 5.2 | 1.5 | 2.2 | 2.8 | 9.8 | 80 | 2.1 | 10.7 | 1195.1 | 5.2 | 3.6 | 3.6 | 4.9 |
| Rome (Italy) | 15.3 | 72 | 18.5 | 26.8 | 662 | 5.9 | 5.0 | 4.6 | 3.6 | 19.5 | 67 | 13.9 | 29.1 | 875.8 | 5.1 | 2.3 | 4.5 | 5.3 |
| Casaccia (Italy) | 10.8 | 80 | 4.7 | 12 | n.a. | 4.9 | 1.4 | n.a. | n.a. | 15.3 | 74 | 4.8 | 11.3 | n.a. | 4.9 | n.a. | 3.9 | n.a. |
| Milan (Italy) | 9 | 68 | 54.2 | 94.1 | 504.2 | 4.2 | 4.7 | 11.6 | 3.6 | 15.0 | 68 | 31.7 | 85.9 | 1202.8 | 4.3 | 15.3 | 6.7 | 6.0 |
| Vredepeel (Netherlands) | 5 | 88 | 8.8 | 30.5 | 451.1 | 5.8 | 3.2 | 3.0 | 2.9 | 10.0 | 83 | 6.7 | 27.8 | 875.2 | 5.1 | 10.0 | 6.8 | 4.9 |
| Oslo (Norway) | −1.4 | 76 | 7.2 | 59.2 | 333.6 | 4.7 | 1.9 | 2.9 | 2.6 | 6.8 | 71 | 5.1 | 54.9 | 789.4 | 4.8 | 2.9 | 3.5 | 4.4 |
| Birkenes (Norway) | −1.4 | 85 | 1.1 | 3.1 | 1046.6 | 4.4 | 2.0 | 1.4 | 3.6 | 4.9 | 79 | 0.9 | 2.3 | 1646.9 | 4.4 | 1.6 | 2.4 | 5.4 |
| Stockholm (Sweden) | 0.3 | 78 | 7.4 | 26.8 | 138.7 | 4.3 | 4.7 | 2.9 | 2.4 | 6.9 | 70 | 5.2 | 24.8 | 513.4 | 4.6 | 3.2 | 3.3 | 4.2 |
| Aspvreten (Sweden) | −0.1 | 88 | 2.8 | 4.5 | 270.1 | 4.2 | 1.9 | 1.9 | 2.8 | 5.9 | 83 | 1.8 | 3.7 | 585.3 | 4.4 | 6.9 | 3.8 | 4.5 |
| London (UK) | n.a. | n.a. | n.a. | n.a. | n.a. | n.a. | 5.8 | n.a. | n.a. | n.a. | n.a. | n.a. | n.a. | n.a. | n.a. | 14.1 | n.a. | n.a. |
| Wells (UK) | n.a. | n.a. | n.a. | n.a. | n.a. | n.a. | 3.5 | n.a. | n.a. | n.a. | n.a. | n.a. | n.a. | n.a. | n.a. | 4.3 | n.a. | n.a. |
| Toledo (Spain) | 8.3 | 69 | 3.9 | 20.8 | 362.6 | 5.8 | 1.4 | 1.9 | 2.6 | 13.9 | 58 | 2.5 | 19.1 | 487.3 | 5.9 | 1.6 | 1.4 | 3.8 |
| Moscow (Russia) | −3.9 | 80 | 18.3 | 26.9 | 324.1 | 6.2 | 5.6 | 4.5 | 2.1 | 4.4 | 74 | 17.6 | 31.3 | 717.2 | 6 | 10.0 | 6.8 | 3.6 |
| Lisbon (Portugal) | 15.4 | 68 | 12.5 | 37 | 561.5 | 5.5 | 4.3 | 3.7 | 3.4 | 18.2 | 64 | 12.5 | 37 | 808.2 | 5.6 | 6.9 | 3.7 | 4.7 |
| Dorset (Canada) | −6.1 | 81 | 17.8 | n.a. | n.a. | n.a. | 2.0 | n.a. | n.a. | 3.4 | 81 | 13.8 | n.a. | n.a. | n.a. | 1.7 | n.a. | n.a. |
| Steubenville (USA) | 2.8 | 62 | 51.5 | 44.3 | 468.5 | n.a. | 2.9 | n.a. | n.a. | 10.6 | 68 | 43.8 | 40.6 | 1072.4 | n.a. | 2.6 | n.a. | n.a. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Verney-Carron, A.; Sessegolo, L.; Lefèvre, R.-A.; Brimblecombe, P. Modelling the Alteration of Medieval Stained Glass as a Function of Climate and Pollution: Comparison between Different Methodologies. Heritage 2023, 6, 3074-3088. https://doi.org/10.3390/heritage6030164
Verney-Carron A, Sessegolo L, Lefèvre R-A, Brimblecombe P. Modelling the Alteration of Medieval Stained Glass as a Function of Climate and Pollution: Comparison between Different Methodologies. Heritage. 2023; 6(3):3074-3088. https://doi.org/10.3390/heritage6030164
Chicago/Turabian StyleVerney-Carron, Aurélie, Loryelle Sessegolo, Roger-Alexandre Lefèvre, and Peter Brimblecombe. 2023. "Modelling the Alteration of Medieval Stained Glass as a Function of Climate and Pollution: Comparison between Different Methodologies" Heritage 6, no. 3: 3074-3088. https://doi.org/10.3390/heritage6030164
APA StyleVerney-Carron, A., Sessegolo, L., Lefèvre, R.-A., & Brimblecombe, P. (2023). Modelling the Alteration of Medieval Stained Glass as a Function of Climate and Pollution: Comparison between Different Methodologies. Heritage, 6(3), 3074-3088. https://doi.org/10.3390/heritage6030164







