Thermography Investigation and Seismic Vulnerability Assessment of a Historical Vaulted Masonry Building
Abstract
:1. Introduction
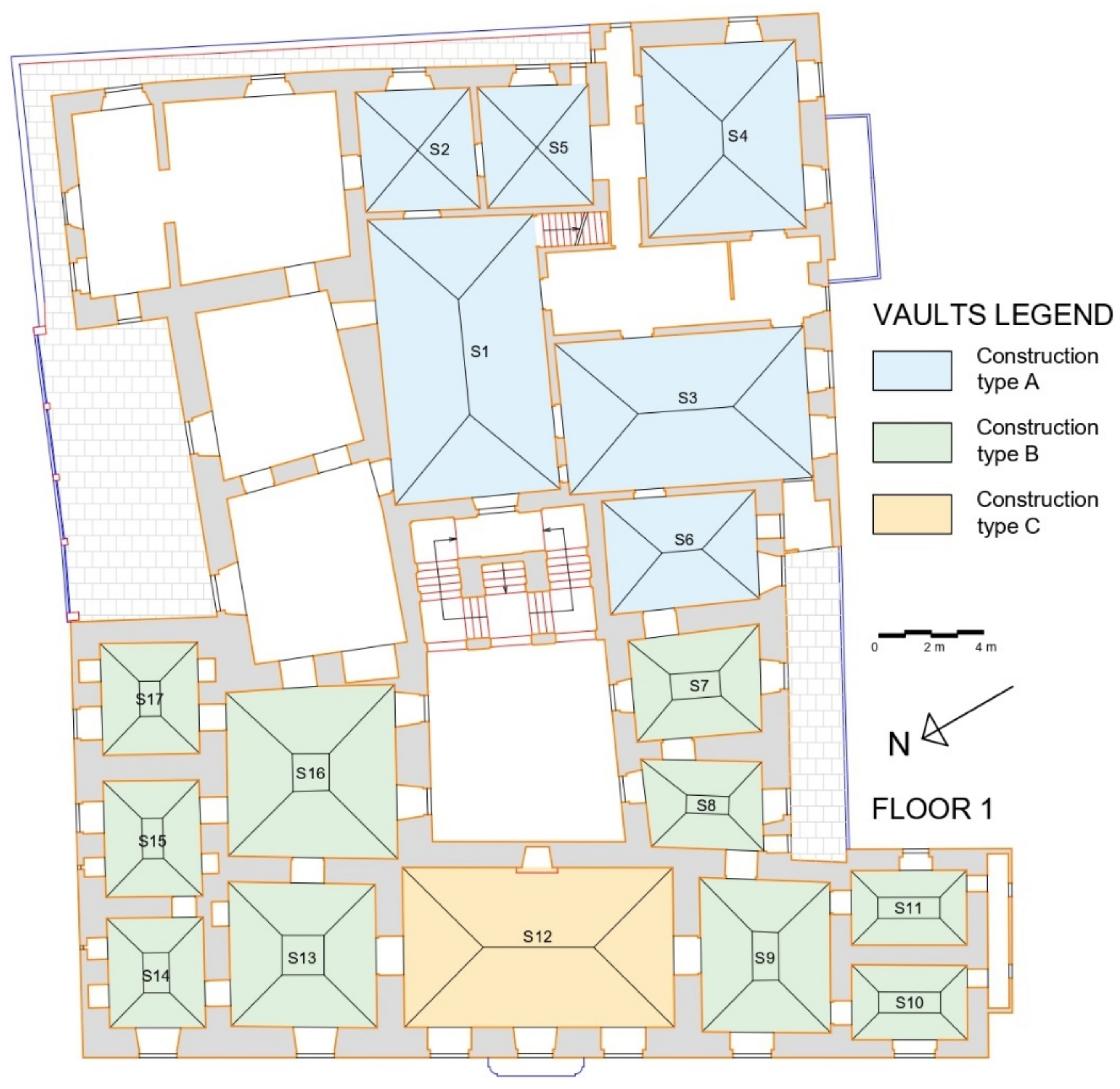
2. Description of the Building
- Modest or null clamping between the perimeter walls and, as well as, between the transversal walls;
- Modest or null transversal connection between three masonry leafs which are separated by internal cores with negligible mechanical properties;
- Non-uniform floor stiffness in reference to the top floor, where masonry cross vaults alternate with ceramic tube vaults—so-called ribbed vault (therefore without floor rigidity)—wooden floor, steel floor and a large skylight.

Historic Context
3. Diagnostic Campaign
3.1. InfraRed Thermography (IRT)
3.2. SonReb
3.3. Boroscopy
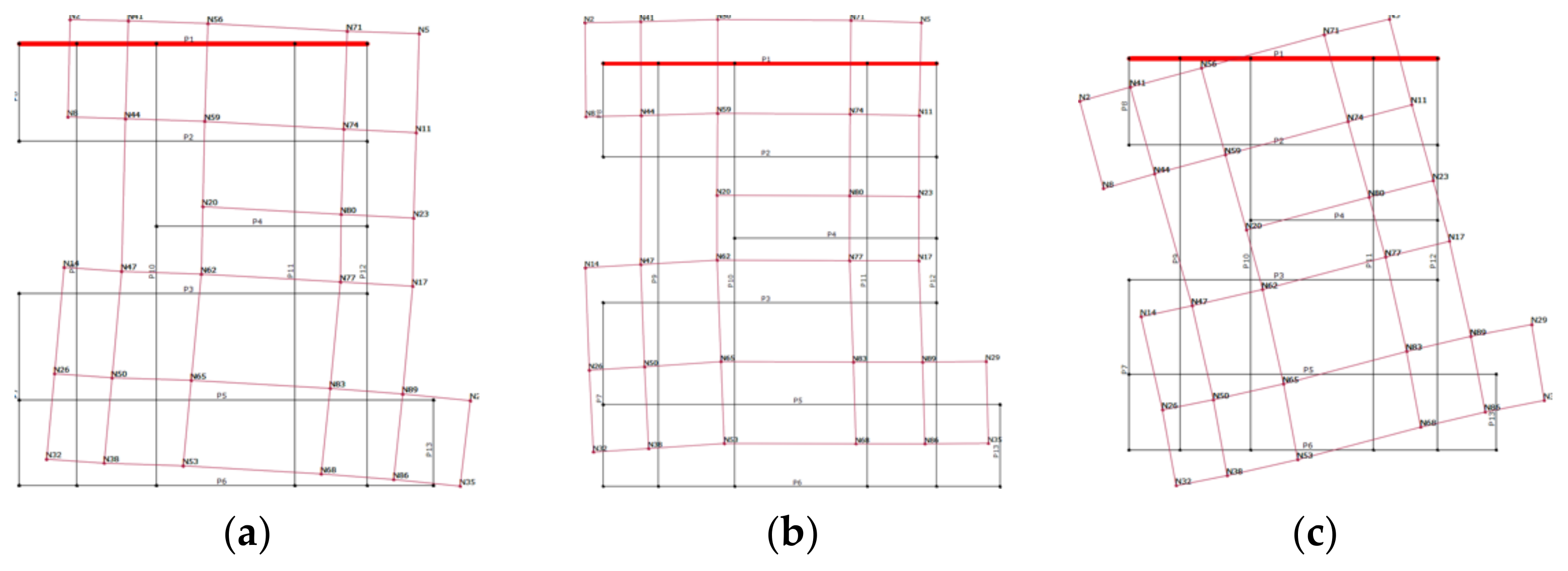
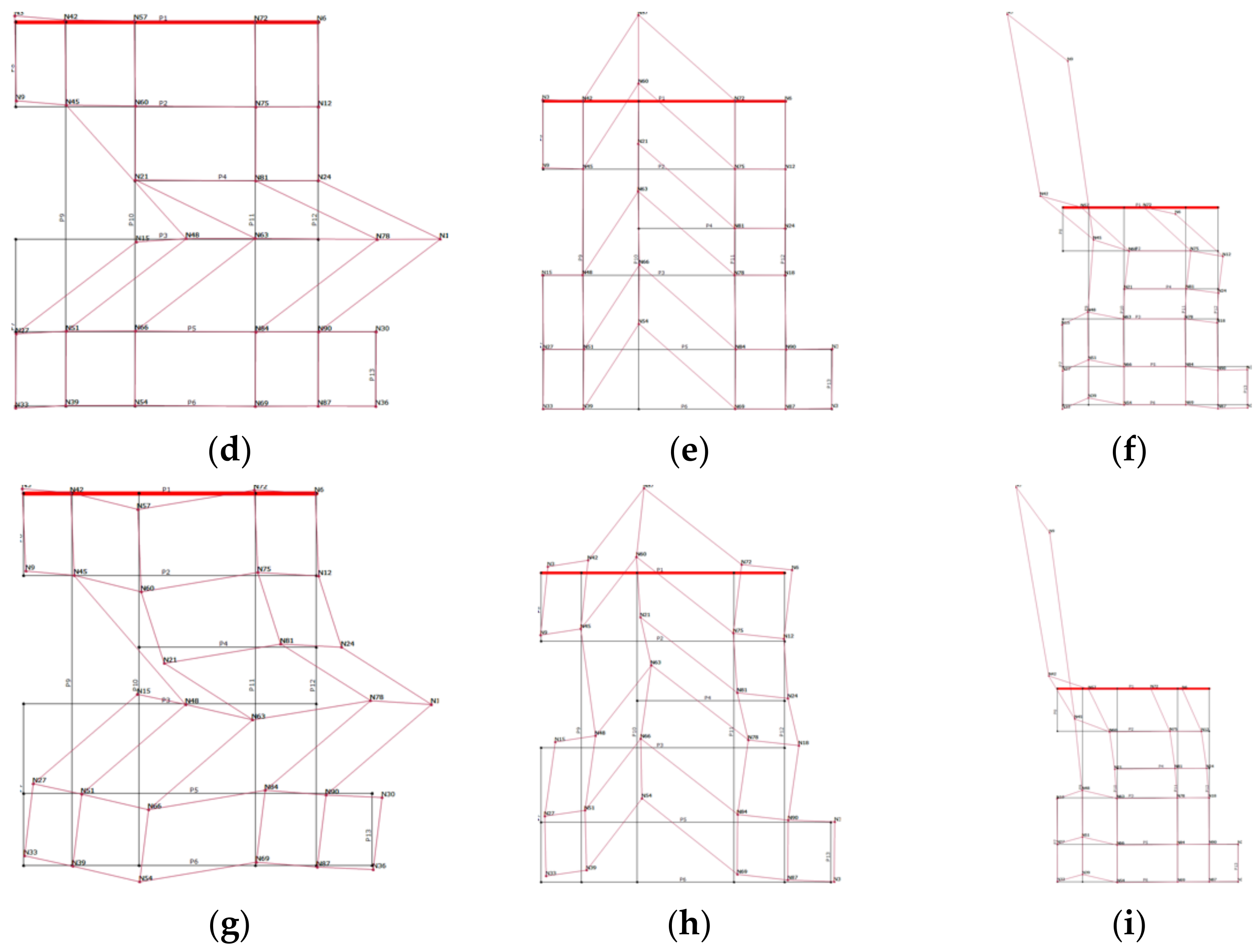
4. Structural Analysis
- Just two floors were modeled, or rather the basement and mezzanine floor were neglected (due to the absence of vaulted floors and seismic forces, respectively);
- All the balconies (i.e., cantilevered slabs) were modeled, only considering their seismic mass to avoid local vibration modes;
- Fixed support at the ground level was considered;
- To avoid numerical convergence issues, the masonry walls were assumed to be perpendicular to each other.

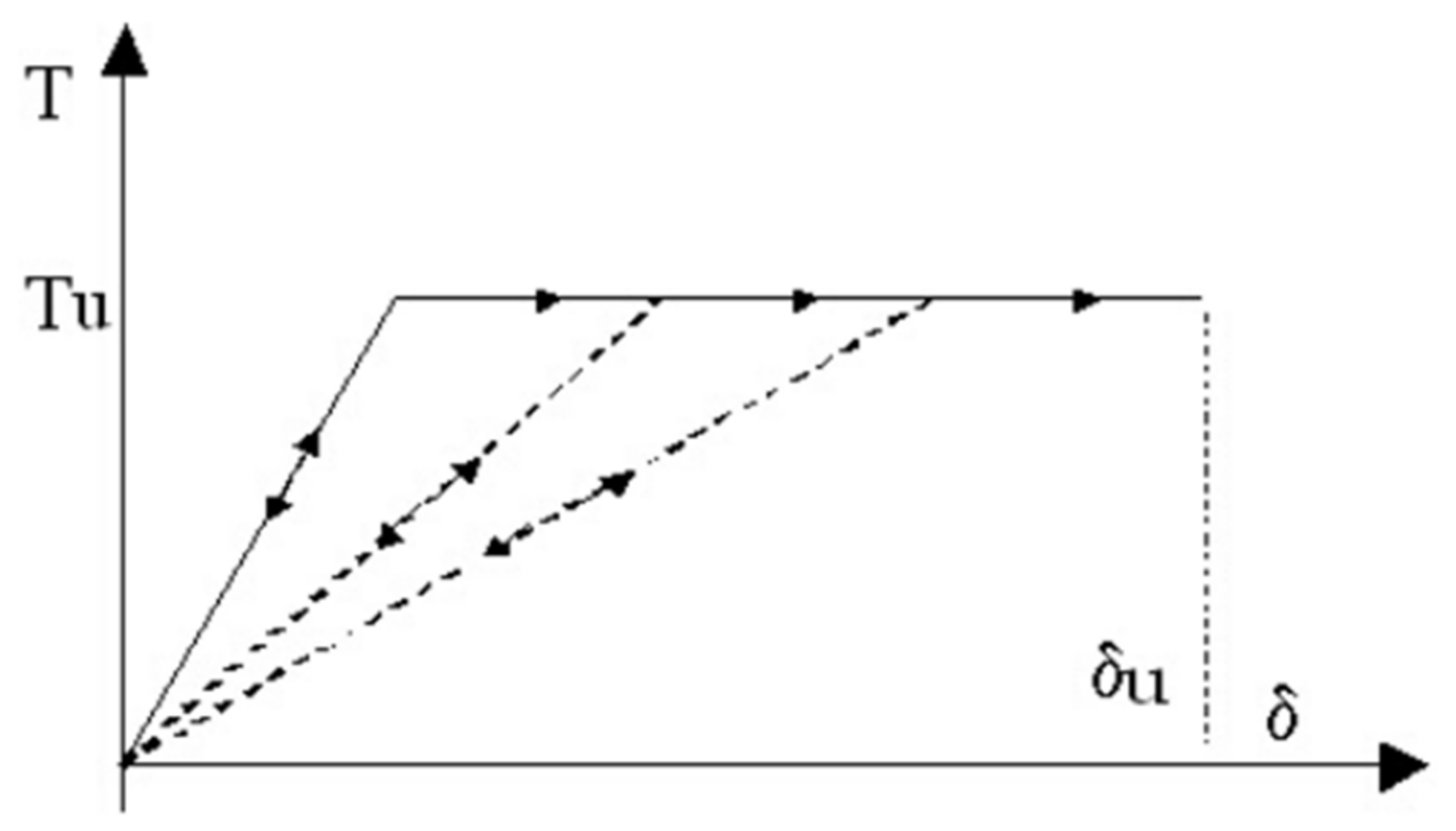
- (1)
- Initial stiffness given by elastic (cracked) properties;
- (2)
- Bilinear behavior with maximum values of shear and bending moment as calculated in ultimate limit states;
- (3)
- Redistribution of the internal forces according to the element equilibrium;
- (4)
- Detection of damage limit states, considering global and local damage parameters;
- (5)
- Stiffness degradation in the plastic range;
- (6)
- Ductility control by the definition of maximum drift (δu) based on the failure mechanism, according to the Italian seismic code and Eurocode 8;
- (7)
- Element discarded from analysis at ultimate drift reached without interruption of global analysis.
4.1. Modal Analysis
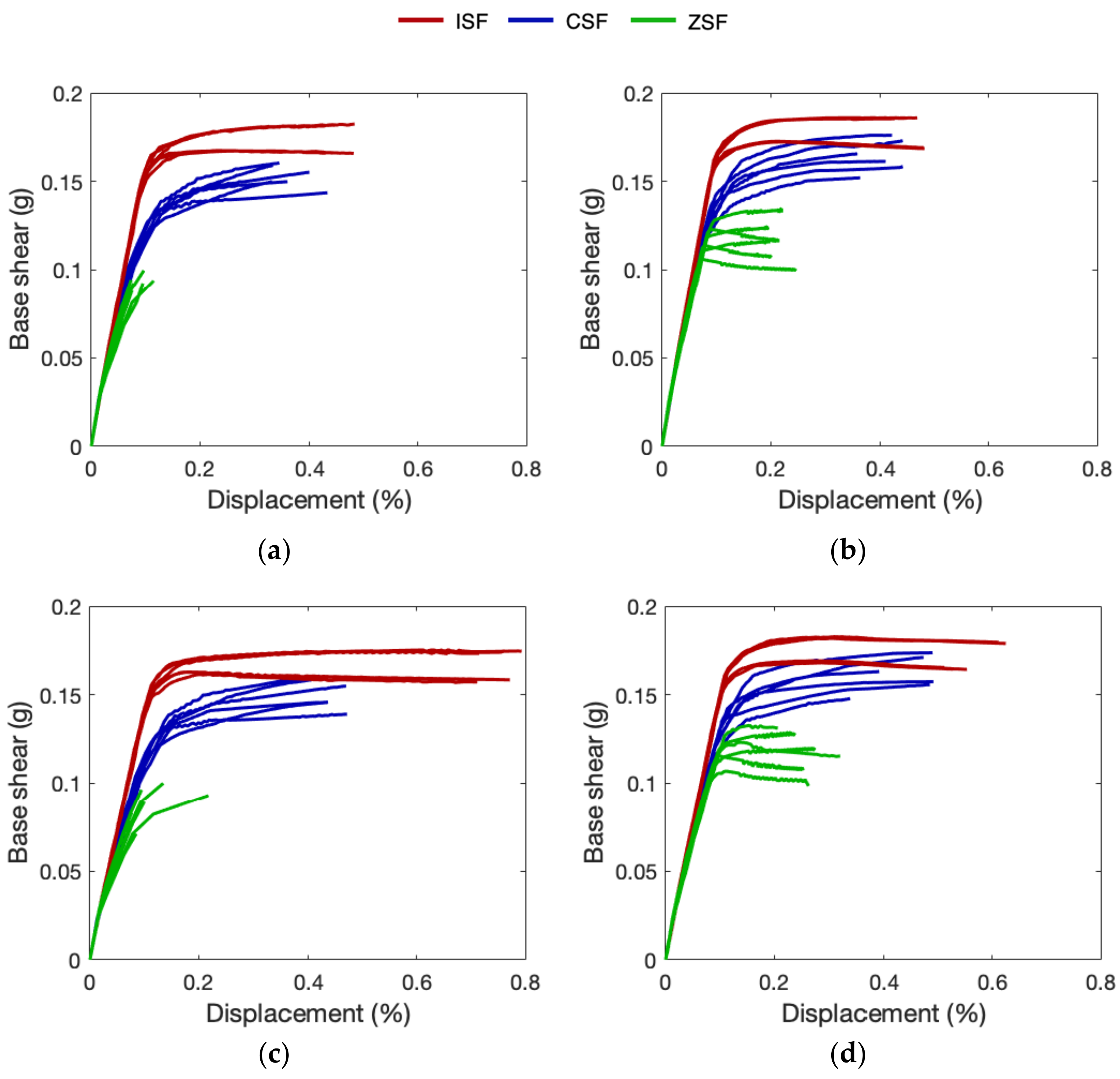
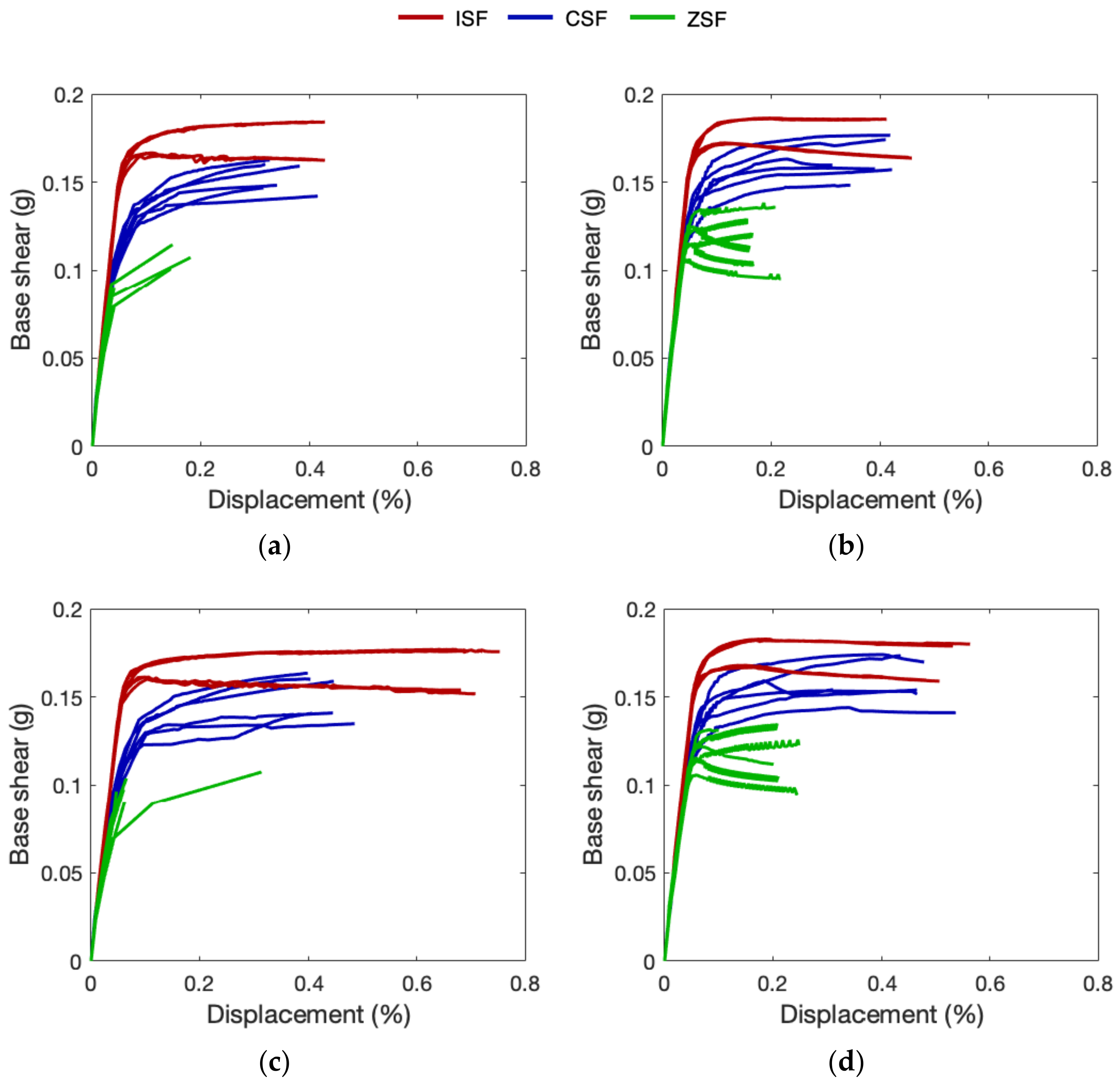
4.2. Pushover Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Barbieri, G.; Biolzi, L.; Bocciarelli, M.; Fregonese, L.; Frigeri, A. Assessing the seismic vulnerability of a historical building. Eng. Struct. 2013, 57, 523–535. [Google Scholar] [CrossRef]
- Croci, G. General methodology for the structural restoration of historic buildings: The cases of the Tower of Pisa and the Basilica of Assisi. J. Cult. Herit. 2000, 1, 7–18. [Google Scholar] [CrossRef]
- Micelli, F.; Cascardi, A.; Marsano, M. Seismic strengthening of a theatre masonry building by using active FRP wires. In Brick and Block Masonry: Proceedings of the 16th International Brick and Block Masonry Conference; CRC Press: Padova, Italy, 2016; pp. 753–761. [Google Scholar]
- Micelli, F.; Cascardi, A. Structural assessment and seismic analysis of a 14th century masonry tower. Eng. Fail. Anal. 2020, 107, 104198. [Google Scholar] [CrossRef]
- Cascardi, A.; Micelli, F.; Aiello, M.A.; Funari, M. Structural analysis of a masonry church with variable cross-section dome. In Brick and Block Masonry-From Historical to Sustainable Masonry; CRC Press: Boca Raton, FL, USA, 2020; pp. 220–226. [Google Scholar]
- Micelli, F.; Cascardi, A.; Aiello, M.A. Seismic capacity estimation of a masonry bell-tower with verticality imperfection detected by a drone-assisted survey. Infrastructures 2020, 5, 72. [Google Scholar] [CrossRef]
- ICOMOS/Iscarsah Committee. Recommendations for the Analysis, Conservation and Structural Restoration of Architectural Heritage. 2005. Available online: www.icomos.org (accessed on 7 July 2022).
- Lourenço, P.B. Computations on historic masonry structures. Prog. Struct. Eng. Mater. 2000, 4, 301–319. [Google Scholar] [CrossRef]
- Ceroni, F.; Pecce, M.; Sica, S.; Garofano, A. Assessment of seismic vulnerability of a historical masonry building. Buildings 2012, 2, 332–358. [Google Scholar] [CrossRef]
- Saccucci, M.; Cima, V.; Grande, E.; Imbimbo, M.; Pelliccio, A. The Knowledge Process in the Seismic Assessment of Masonry Building Aggregates–An Italian Case Study. In International Conference on Critical Thinking in Sustainable Rehabilitation and Risk Management of the Built Environment; Springer: Cham, Switzerland, 2019; pp. 330–347. [Google Scholar]
- Lourenço, P.B.; Mendes, N.; Ramos, L.F.; Oliveira, D.V. Analysis of masonry structures without box behavior. Int. J. Archit. Herit. 2011, 5, 369–382. [Google Scholar] [CrossRef]
- Aşıkoğlu, A.; Vasconcelos, G.; Lourenço, P.B. Overview on the nonlinear static procedures and performance-based approach on modern unreinforced masonry buildings with structural irregularity. Buildings 2021, 11, 147. [Google Scholar] [CrossRef]
- Pagano, M. Teoria Degli Edifici, Edifi in Muratura; Liguori: Napoli, Italy, 1968; Volume 1. (In Italian) [Google Scholar]
- Binda, L.; Anzani, A.; Saisi, A. Failures due to long-term behaviour of heavy structures. Learn. Fail. Long-Term Behav. Heavy Mason. Struct. 2008, 23, 1–28. [Google Scholar]
- Heyman, J. The stone skeleton. Int. J. Solids Struct. 1996, 2, 249–279. [Google Scholar] [CrossRef]
- Heyman, J. The safety of masonry arches. Int. J. Mech. Sci. 1969, 11, 363–385. [Google Scholar] [CrossRef]
- Oliveira, D.V.; Lourenço, P.B. Repair of Stone Masonry Arch Bridges; International Center for Numerical Methods in Engineering: Barcelona, Spain, 2004. [Google Scholar]
- De Santis, S.; De Felice, G. Seismic analysis of masonry arches. In Proceedings of the Fifteenth World Conference on Earthquake Engineering, Lisbon, Portugal, 24–28 September 2012. [Google Scholar]
- Sisti, R.; Di Ludovico, M.; Borri, A.; Prota, A. Damage assessment and the effectiveness of prevention: The response of ordinary unreinforced masonry buildings in Norcia during the Central Italy 2016–2017 seismic sequence. Bull. Earthq. Eng. 2019, 17, 5609–5629. [Google Scholar] [CrossRef]
- Circolare 21 Gennaio 2019, n. 7 C.S.LL.PP. Istruzioni per l’Applicazione dell’ «Aggiornamento delle “Norme Tecniche per le Costruzioni”» di Cui al Decreto Ministeriale 17 Gennaio. 2018. Available online: https://www.gazzettaufficiale.it/eli/id/2019/02/11/19A00855/sg (accessed on 7 July 2022).
- Vollmer, M.; Klaus-Peter, M.Ã. Infrared Thermal Imaging: Fundamentals, Research and Applications; John Wiley & Sons: Hoboken, NJ, USA, 2010. [Google Scholar]
- UNI EN 12504-2:2021; Testing Concrete in Structures-Part 2: Non-Destructive Testing-Determination of Rebound Number. British Standards Institution: London, UK, 2021.
- UNI EN 12504-4:2021; Testing concrete in structures-Part 4: Determination of Ultrasonic Pulse Velocity. British Standards Institution: London, UK, 2021.
- Aliabdo, A.A.E.; Elmoaty, A.E.M.A. Reliability of using non-destructive tests to estimate compressive strength of building stones and bricks. Alex. Eng. J. 2012, 51, 193–203. [Google Scholar] [CrossRef] [Green Version]
- D.M. 17/01/2018. Aggiornamento delle “Norme Tecniche per le Costruzioni” (NTC 2018). Supplemento Ordinario alla “Gazzetta Ufficiale”, n. 42 del 20/02/2018. Available online: https://www.gazzettaufficiale.it/eli/id/2018/2/20/18A00716/sg (accessed on 7 July 2022). (In Italian).
- 3MURI. Seismic Calculation of Masonry Structures According to M.D.14/01/2018; 3MURI: Torino, Italy, 2009. [Google Scholar]
- Lagomarsino, S.; Penna, A.; Galasco, A.; Cattari, S. TREMURI program: An equivalent frame model for the non-linear seismic analysis of masonry buildings. Eng. Struct. 2013, 56, 1787–1799. [Google Scholar] [CrossRef]
- Marseglia, P.S.; Micelli, F.; Leone, M.; Aiello, M.A. Modeling of masonry vaults as equivalent diaphragms. In Key Engineering Materials; Trans Tech Publications Ltd.: Freienbach, Switzerland, 2015; Volume 628, pp. 185–190. [Google Scholar]
- Marseglia, P.S.; Micelli, F.; Aiello, M.A. Analysis of equivalent diaphragm vault structures in masonry construction under horizontal forces. Heritage 2020, 3, 989–1017. [Google Scholar] [CrossRef]
- Capanna, I.; Aloisio, A.; Di Fabio, F.; Fragiacomo, M. Sensitivity Assessment of the Seismic Response of a Masonry Palace via Non-Linear Static Analysis: A Case Study in L’Aquila (Italy). Infrastructures 2021, 6, 8. [Google Scholar] [CrossRef]
- Giongo, I.; Piazza, M.; Tomasi, R. Pushover analysis of traditional masonry buildings: Influence of refurbished timber-floors stiffness. In Proceedings of the International Conference on Structural Health Assessment of Timber Structure, Lisbon, Portugal, 16–17 June 2011; pp. 1–13. [Google Scholar]


















| Floor ID | Young’s Modulus(GPa) | Tangential Modulus (GPa) | Thickness (cm) |
|---|---|---|---|
| Camorcanna vault | Zero stiffness | ||
| Wooden floor | Zero stiffness | ||
| Masonry vault | 0.855 | 0.285 | 15 |
| “Bubbole” vault | 0.427 | 0.142 | 15 |
| Steel beams floor | Infinite stiffness | ||
| Model ID | Mode Number | Frequency (Hz) | % of Mass Excited along X | % of Mass Excited along Y |
|---|---|---|---|---|
| ISF_50 | 1 | 4.477 | 77.46 | 12.00 |
| 2 | 4.508 | 11.53 | 81.86 | |
| 3 | 5.152 | 4.38 | 0.00 | |
| ZSF_50 | 1 | 3.297 | 28.89 | 0.00 |
| 2 | 3.687 | 0.00 | 37.01 | |
| 3 | 4.232 | 1.30 | 2.10 | |
| CSF_50 | 1 | 4.367 | 34.61 | 0.64 |
| 2 | 4.444 | 0.63 | 50.13 | |
| 3 | 5.076 | 1.01 | 0.50 | |
| ISF_100 | 1 | 6.269 | 77.95 | 11.78 |
| 2 | 6.296 | 11.64 | 81.83 | |
| 3 | 7.208 | 3.59 | 0.07 | |
| ZSF_100 | 1 | 4.628 | 28.76 | 0.00 |
| 2 | 5.186 | 0.00 | 37.00 | |
| 3 | 5.870 | 1.24 | 2.19 | |
| CSF_100 | 1 | 4.909 | 35.04 | 0.64 |
| 2 | 5.429 | 1.43 | 45.38 | |
| 3 | 6.099 | 1.87 | 3.00 |
| Model ID | Force Distribution | Capacity PGA (g) | Demand PGA (g) | Capacity/Demand |
|---|---|---|---|---|
| ISF_50 | x_u | 0.312 | 0.083 | 3.78 |
| y_u | 0.330 | 3.99 | ||
| x_fs | 0.325 | 3.93 | ||
| y_fs | 0.330 | 3.98 | ||
| CSF_50 | x_u | 0.262 | 3.16 | |
| y_u | 0.310 | 3.75 | ||
| x_fs | 0.342 | 4.14 | ||
| y_fs | 0.260 | 3.14 | ||
| ZSF_50 | x_u | 0.152 | 1.84 | |
| y_u | 0.161 | 1.94 | ||
| x_fs | 0.168 | 2.03 | ||
| y_fs | 0.172 | 2.08 | ||
| ISF_100 | x_u | 0.409 | 4.94 | |
| y_u | 0.419 | 5.07 | ||
| x_fs | 0.394 | 4.76 | ||
| y_fs | 0.406 | 4.91 | ||
| CSF_100 | x_u | 0.364 | 4.40 | |
| y_u | 0.400 | 4.84 | ||
| x_fs | 0.419 | 5.06 | ||
| y_fs | 0.370 | 4.47 | ||
| ZSF_100 | x_u | 0.234 | 2.83 | |
| y_u | 0.189 | 2.29 | ||
| x_fs | 0.259 | 3.13 | ||
| y_fs | 0.213 | 2.58 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cascardi, A.; Longo, F.; Perrone, D.; Lassandro, P.; Aiello, M.A. Thermography Investigation and Seismic Vulnerability Assessment of a Historical Vaulted Masonry Building. Heritage 2022, 5, 2041-2061. https://doi.org/10.3390/heritage5030107
Cascardi A, Longo F, Perrone D, Lassandro P, Aiello MA. Thermography Investigation and Seismic Vulnerability Assessment of a Historical Vaulted Masonry Building. Heritage. 2022; 5(3):2041-2061. https://doi.org/10.3390/heritage5030107
Chicago/Turabian StyleCascardi, Alessio, Fabio Longo, Daniele Perrone, Paola Lassandro, and Maria Antonietta Aiello. 2022. "Thermography Investigation and Seismic Vulnerability Assessment of a Historical Vaulted Masonry Building" Heritage 5, no. 3: 2041-2061. https://doi.org/10.3390/heritage5030107
APA StyleCascardi, A., Longo, F., Perrone, D., Lassandro, P., & Aiello, M. A. (2022). Thermography Investigation and Seismic Vulnerability Assessment of a Historical Vaulted Masonry Building. Heritage, 5(3), 2041-2061. https://doi.org/10.3390/heritage5030107










