Abstract
In this paper, the city of Matera is described from a mathematical point of view. Previous papers on this subject have concentrated on seeing Matera as a fractal city. Here, this analysis is also dealt with as an extension of Euclidean dimensions. The idea is to create a double presentation narrative which is useful for the promotion of cultural heritage and also for the popularizing of mathematics. Those who like geometrical vision will discover some aspects of one of the most ancient cities in Italy. Those who like travelling will have new words to describe the wonders of this country. We reach this objective by using a combinatoric puzzle and suitable story telling.
1. Introduction
Recently, a certain number of papers, books and scientific blogs have given a vision of mathematics in the promotion of cultural heritage (see Reference [1]). The connection between mathematics and art as well as mathematics and nature is appreciated from the tourist point of view. We suggest an itinerary in Matera (Italy) to see its peculiar forms from a mathematical point of view. This attempt also leads to research results. See References [2,3,4] as refereed papers and References [5,6] as popularizing versions of these ideas. In particular, in Reference [3] we gave a qualitative description of Matera by means of fractals sets; in Reference [4] we carried out quantitative computation to support the thesis that Matera has fractal geometry. In Reference [2], a comparison between the shape of Matera and Petra is illustrated. It is possible to compare these works with the definition of fractal city given in References [7,8], concluding that Matera is another example in which the application of fractal tools to urbanistic is possible and fruitful.
In this paper, we present another point of view: We try to explain a mathematical concept by seeing a city that contains its representation. The mathematical concept is the dimension and the city is still Matera. In Section 2, we describe some places in this city where the guest can see Euclidean suggestions. In Section 3, we briefly go back to the observations of References [3,4,6] by fractal analysis and include these in the information that a touristic guide can give. In Section 4, we suggest an application. In Section 5, we present a combinatoric puzzle decorated with some pictures of Matera. This enables us to create a story explaining the concepts given in Section 2 and Section 3.
2. Going for a Walk in Euclidean Dimensions
In Matera, different stories of dimensions can be suggested starting from different points of observation. For example, the Museum of Contemporary Sculpture in Matera, called MUSMA, is the ideal point to observe the fourth dimension. Some interesting installations can be seen by mathematicians as three-dimensional projections of four-dimensional objects. On the other hand, speaking to a curious tourist who likes scientific language, the guides must point out that this museum exhibits space–time. Not just space. Nor only time. Indeed, though Palazzo Pomarici was built in the 16th Century, today it houses a collection of modern works which concern the future. The proximity of the Sassi zone, with houses dug into limestone rock hundreds of years ago and contemporary sculpture, tell us about the ancient world. The stone itself gives this space–time shock, and one piece of evidence is Alberto Viani’s sculpture, see Figure 1, and the way in which it collects rays of light and shadows as a physical universe. Indeed, it was inspired by a collection of mathematical surfaces used by scientists at the beginning of the 20th Century when a new cosmological vision appeared. See Reference [9]. From our point of view, MUSMA is the place in Matera where space and time are intertwined.

Figure 1.
Alberto Viani’s sculpture in MUSMA.
Almost all installations in MUSMA are sculptures. Observing them in detail, we go down from the four dimensions to three dimensions. Sculpure mainly plays with depth. We can see this, for example, in the facial expressions of the small Birichino by Menardo Rosso (see Figure 2). Without depth, we cannot see the core of the work. The same artist said that “Nothing is material in space, we are nothing but plays of light”. From a mathematical point of view, this statement refers to the theories on light paths (therefore shorter ones) in curved space. In this museum, there are also installations that realize the games of light deviated from more or less curved obstacles.

Figure 2.
Menardo Rosso’s sculpture in MUSMA.
In MUSMA, the light flows on marble, bronze, iron, steel, terracotta, plaster, ceramic, papier-mâché, tuff, and wood, and it reveals by drawing the shadow. On the contrary, in many cases, two dimensions are sufficient for an image. Lucania 61, a large mural by Carlo Levi in Palazzo Lanfranchi shows the inhabitants of Basilicata in 1961. In this mural, the artist neglects depth, leaving to the viewer the task of finding it. See a detail in Figure 3.

Figure 3.
A detail of Lucania 61 by Carlo Levi.
Let’s move to “Casa di Ortega”. The Spanish painter Josè Ortega tried to bring out the scream of pain in papier mache (see Figure 4).

Figure 4.
Ortega’s polychrome bas-relief.
This technique allows the viewer to remain in the middle between the two dimensions of an image and the three dimensions of sculpture. On the contrary, the artisans who live in Matera filled the ceiling of Ortega’s house with a ceramic sky (see Figure 5). For a mathematician, the crosses on these tiles suggest the tessellations of a surface but also the only two coordinates that are sufficient to find a point on a surface.

Figure 5.
Ceramic covering Casa Ortega ceiling.
To reach Ortega’s house and MUSMA we pass stairs and slopes. The city of Matera is perched on a hill, it has an elevation of 401 m above sea level. In order to bring water into all houses, an underground city was needed. In Reference [10], Pietro Laureano wrote that this city has an inverted pyramid, a sort of mirror of the tetrahedron of the Civita, the higher part of the city (see Figure 6).

Figure 6.
Matera center and higher part: Civita.
Matera and its water system appear as a complex multi-dimensional world. As in the Gauss-2D complex space, we have four multi-quadrants. The origin of this complex system is in Piazza Vittorio Veneto where we can cross the horizontal and real plane of the city level. In addition, we can also think of an imaginary vertical plane between the populated city and the natural landscape (see Figure 7). The canyon, here called “gravina”, is a thin line between rocks without humans and populated rocks. In all the other parts of the vision, human building and natural scenery are intertwined.

Figure 7.
Gravina (canyon) as an imaginary plane.
A tourist guide has to underline the ingenuity of those who used the empty spaces of nature to protect themselves from the cold and built empty spaces in the rock to save themselves from thirst. Mathematics was as always unconsciously allied with urban planning choices.
Going back to Piazza Vittorio Veneto, we can go down into Palombaro Lungo, the giant ancient cistern, (see Figure 8). It is natural to ask about the aqueduct, observing that a water network and the way in which length, amplitude and number of conduits are settled. From the mathematical point of view, this is a graph: A set of points (called vertex) and lines (called arches) that eventually connect the point. In the Matera aqueduct, all vertices are connected and all arches are weighted by parameters that enable the water to be wisely dosed.

Figure 8.
Palombaro Lungo, aqueduct graph from Reference [2].
There is also an abstract graph in the city: The underground connections of the canals become the connections of the houses made by clothes lines or simply by citizens gazing at each other. The one dimensional concept is always present in Matera here, since an apparently chaotic city increases relations. A convex set is a set in which any two points are connected by a line which remains in the set. It is important to notice that any square is convex since it is the place of relations. In the Sassi zone, the houses were distributed in small groups of almost 10 which had a courtyard in common in which the life of everyone was controlled. This yard has a local name of “vicinato”. Like a theatre, it is convex. Any convex set is a connected set. This is a very important mathematical inclusion that is translated in any human agorà!
There are sets without connections and their dimension is less than one. For example, a point has zero dimension. However, very complicated sets of “separated” points are also zero-dimensional: The set of lights in Matera nights is one of these.
What is the best point to see the geometry of Matera? Everywhere around the Sassi zone and in every different point we can see different shapes.
Can a good definition of dimension become a tale for a tourist? We believe so. The guide is in dialogue with those who follow him. For example, after observing the sculptures, we show a cube and ask how we can break it into two equal parts. The visitor will tell us to do it through a plane. We will point out that we have divided a three dimensional object by a two dimensional object. Then, we show a sheet and ask how it can be broken into two equal parts. The visitor will tell us it can be done using a line. We will point out that we have divided a two dimensional object with an object of one dimension. Now, let us show a thread. It will be the same for a visitor to understand how a point, zero dimensional, is enough to divide an object of dimension one. In this descent, the visitor may wonder if the point can be divided. Mathematicians define negative dimension as that of the empty set. It would be nice to give to the tourist this explanation on the balcony of Ortega’s house that overlooks two vacuums: the canyon, the void dug by water and the stone gardens, the void dug by the wind. See Reference [11].
Then, one can come back from negative to zero, one, two, three, four dimensions and ask about higher ones. This is difficult to understand and we can only sketch that the higher dimension is related to groups of symmetry. The wheel of of the Cathedral of the city is a rare element of symmetry. Palazzo del Sedile, on the contrary, presents a symmetry broken by the absence of a clock (see Figure 9). A good narrator can also explain the infinite dimension by opening the windows of Ortegas’s house and mentioning that spaces with infinite coordinates are the right ones to study the motion of the flight of the nibbio.

Figure 9.
Broken symmetry, Palazzo del Sedile.
3. Taking a Photo of a Fractal City
Fractional dimensions appeared in mathematics during the 20th Century. It was necessary to understand the measure of irregular surfaces or the length of irregular curves. Irregular means full of tips and cusps. For a surface and the volume in which its contained, not being regular means being full of voids. It is important in various contexts to understand the degree of regularity of a surface and if it is increasing or not during its evolution. The most irregular things that can be seen in Matera are the canyon and the rocks above it. Water and wind continuously act there. In Reference [3], by means of a graphics program, we realized a fractal on an aerial picture of the canyon. We get a sequence of Julia sets, very complicated and unstable fractals, obtaining a figure that seems to runs along the gravina like a river. The comprehension of the rule that generates it and the computation of its fractal dimension is not easy, indeed it changes from point to point.
It is better to present to the visitor with something simpler, though chaotic. The inhabitants of Matera, from ancient times, have also acted by continuously excavating the rock. The Sassi zone is itself irregular, but “self-similar”.
Imagine many people in Matera each taking one photo of the Sassi zone from different points, for example our Figure 6. Each photo would be different. Imagine putting these photos together and asking someone extraneous to this game to extract one of them. He or she would guess that the selected photo has been taken in the city of Matera. This possibility to go from local vision to the global one is only given in particular contexts. The same game would not be possible in Milan for example, since only images of particular monuments are characteristic of the city.
In order to explain why Matera is a fractal city, to speak about its topological and fractal dimension, we have to observe this “self-similarity”. The same form repeats many times but on a different scale, and it offers the pleasant effect that trees give us when passing from the trunks to the branches, (see Figure 10). The same harmony that sea sponges have has been recreated in the magical continuous passage of concave and convex spaces especially in Sasso Caveoso (one of the two sections of the Sassi zone).

Figure 10.
Self-similarity. From an empty doorway we can see many smaller doorways.
Here, we want to suggest to a tourist guide how to explain this comparison between Matera and a mathematical sponge in a better way. To do this, we draw attention to the continuous succession of edges. The number and disposition of edges determine whether a polyhedron is a cube or a prism. Looking at its edges, we claim that Matera has the shape of a children’s book! First of all, it must be clear that what we mean by “book form” is overlapping sheets of the same size to create a volume. This definition only applies to cities or skyscrapers. The request that the sheets be of equal size in a volume is not necessary. When the sheets were made from dried plants, the shape of the sheet varied according to the humidity of the air. Even an ancient book in which the pages are cut to separate them has different-shaped pages. Finally, some books for children that fill our bookcases today have recesses and holes and images printed on the edge that make each page a different shape from the previous one. Matera is a book of the latter kind. Its stone pages all have different shapes and this influences the volume of its houses, the number and the position of its edges, and therefore, its story. The word “volume” is used in publishing and in geometry: These multiple meanings hide a secret. In the history of mathematics, it took thousands of years to formalize the process that leads from the superimposition of very thin (two-dimensional) sheets to the concept of volume (three-dimensional). Likewise, if we write on a single page with lowercase, infinite lines (one-dimensional), we would fill the whole sheet. Mathematicians also know a special book in which the sheets are pierced so differently that the overlapping pages give zero volume. It is like leafing through those books in which you can see images moving very quickly. The images are replaced by appropriately distributed voids and the result is the so-called Menger Sponge (see Reference [12] and Figure 11). It can be seen as a book of blank pages with its infinite margins all annotated. It is an object of infinite perimeter and null volume. Among other things, for mathematicians this is the universal model of a one-dimensional whole (see Reference [13] Section 4.4). It is a kind of continuous story to which all stories can be matched. This is a limiting process, we will never see it complete. Like the model of Matera, which can be seen at Palazzo Lanfranchi, it is nothing but an approximation of the city, so we can imagine figures closer and closer to that of the sponge.

Figure 11.
The Menger sponge and its face: the Sierpinski carpet.
After this informal description, let us detail the geometrical rule that gives this form starting from a cube. We make a triadic decomposition of the cube (this means it looks like a Rubiks Cube). If it has 27 smaller cubes and we remove 7: the central one and the 6 joined to its faces. There are 20 cubes left, on each one we can repeat this passage. You can then reapply the rule to the remaining 400 even smaller cubes. The resulting figure increases in complexity. The Fractal Menger Sponge is the limit figure of this process. One of the reasons why Matera is a fractal city is that the Sassi zone is obtained like this figure by repeating the same procedure on a different scale. Matera was born from excavated stone layers, the dwellings in the Sassi are the removed cubes whose floor-ceiling dividers are these stone pages impregnated with steps from remote and recent eras.
A Menger Sponge has a fractal dimension of ln(20)/ln 3 ≈ 2.7268, i.e., it is intermediate between two dimensions and three dimensions. For self-similar fractals, the dimension corresponds to the logarithm of the number of equal parts by which an object is subdivided and the logarithm of the scale factor that determines this division. The box-counting dimension can be used for a more complicated figure. In particular, using Benoit fractal analysis software, we can take a photo of Matera, transform it into a binary image and then trace a series of cross-links with ever closer meshes; the algorithm counts the number of boxes containing at least one element of the object. From the bi-logarithmic graph of the box number as a function of their width, the fractal dimension is determined as the slope of the regression line. One more dimension has to be added since we are starting from an image, while the object is in space. For Sasso Barisano (the other part of the Sassi zone), this gives 2.80, which is sufficiently close to that of an abstract Menger sponge, (for more details see Reference [4]).
Now, let us imagine taking a photo at night. We would see a diffusion of lights from doors and windows. It corresponds to putting a light in every hole of the Menger sponge. If we asked for a name for this distribution we would invoke a Sierpinski carpet, that in Figure 11 corresponds to a side of the Menger sponge.
Coming this time from global to local, we can concentrate on a very small zone of Matera, for example a wall. It is made of tuff. We can restrict our vision. Again, we see that it is full of emptiness. If we see a small part of tuff we soon understand that this rock is tuff. This kind of rock is described by a fractal called the Apollonius’ gasket. Therefore, Matera is contained in a fractal (the canyon), has a fractal urban structure (Peano curve for the map, see Reference [4], Menger Sponge for the buildings) and contains fractals (the tuff and the distribution of light).
4. Applications
There is still a lot to do, going from the global to local vision and vice versa. For example, in Matera we move towards the rock churches, (see Figure 12). A deep study of the cave type and morphology by means of fractal dimensions was carried out in Reference [14]. In general, the computation of the fractal dimension is related to the empty/full ratio. It allows us to describe and study the evolving natural phenomena. We can describe the shape of the cavities in a geometrical way; the natural ceilings like the floors are full of rock roots. In turn, we can use the powerful fractal technique to calculate the ruinous work of time on frescos. If a mildew appears some cave-crypt, we can take a photo of its expansion and compute the fractal dimension; repeating the data survey, we can see that if the fractal dimension is increasing, then the mold is expanding. In conclusion, we can plan the schedule of interventions. Telling this to the tourists, we are sure they will appreciate the usefulness of the fractional dimension.

Figure 12.
Frescos on limestone in rock cave churches.
Leonardo Sinisgalli was a poet and popularizer of science from Basilicata. He wrote in a tale “Limestone roughness ripens in salt and in the sun”, in less than 10 words that we have the secret of the evolution of Matera rocks. This also tells us about the future. This evolution has not stopped and we have to remember this when we plan to convert a house into a hotel or to propose a renovation. Nothing stops the sun and salts.
5. A Living Lab Experience
We must not worry about tourists getting scared. We can make this mathematical description together with a graphic representation by means of combinatoric puzzles on which we can paste images of Matera. After the tour for summarizing the itinerary, the guide can again pose the question: how can you divide a cube into two equal parts, but now without using a plane? The cube of Yoshimoto n. 1 was made in 1971, demonstrating that a cube decomposes into two starred rhombic dodecahedra. This puzzle is itself something surprising, so much so as to be exhibited at the Museum of Modern Art in New York in a gold and silver version (see Figure 13).
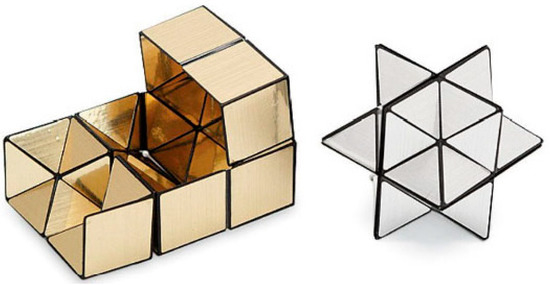
Figure 13.
Yoshimoto cube n.1.
During the Living Lab of the YOCOCU 2018 Congress, the author presented this object covered with images of the Sassi zone (see Figure 14). The two aspects that come together are the shape of the city dictated by nature and man’s chosen urban planning. Mathematical study and knowledge of the cultural heritage contained in Matera were necessary to understand which images to put in the various recesses of the cube (for further details see Reference [15]). At the same moment, each movement of the cube corresponds to a part of the itinerary purpose in this paper.

Figure 14.
Matera images on Yoshimoto cubes.
6. Conclusions
A tourist guide and visitor will be really satisfied by the use of three languages in Matera: the graphic-artistic language, the scientific-mathematical language and the literary one. Combining this story telling with the images on the Yoshimoto cube n. 1, we give the tourist new words to describe the harmony between natural and human work on the rocks. The Author has presented this experience with success at some Science Festivals, in a national radio program of popularization of science, and in many schools—achieving the goal of creating a narrative double presentation which is useful for the promotion of cultural heritage and also for the divulgation of mathematics.
Acknowledgments
The Author thanks the organizer of 6th international YOCOCU conference for the kind invitation and for encouraging her to try a Living Lab. She is particularly grateful to two anonymous referees of this paper for their comments. The Author is also grateful to Carlo Cardinale for permission to use his photos, (Figure 1, Figure 4, Figure 5, Figure 6, Figure 8 and Figure 12). The other images were taken by the Author.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Lucente, S. Itinerari Matematici in Puglia; Giazira Scritture: Noicattaro, Italy, 2016. [Google Scholar]
- Lucente, S. Matter built, excaved, split: A journey through fractal cities. Lett. Mat. Int. 2017, 5, 279–286. [Google Scholar] [CrossRef]
- D’Alessio, L.; Lucente, S. Matera: A wonderfully chaotic city. In Proceedings of the VIth Conference Diagnosis, Conservation and Valorization of Cultural Heritage, Napoli, Italy, 10–11 December 2015; Aracne Editrice: Napoli, Italy, 2015; pp. 185–191. [Google Scholar]
- D’Alessio, L.; Lucente, S. Matera frattale. In Proceedings of the VIIth Conference Diagnosis, Conservation and Valorization of Cultural Heritage, Napoli, Italy, 15–16 December 2016; Aracne Editrice: Napoli, Italy, 2016; pp. 126–134. [Google Scholar]
- Laureano, P. Matera, la sfida della memoria, Architettura della fusione. Lett. Internazionale 2013, 118, 44–47. [Google Scholar]
- Lucente, S. Il senso di Matera per la geometria: Una Città a Forma Di Libro Per Bambini, La Repubblica. Available online: https://rep.repubblica.it/pwa/locali/2018/04/10/news/il_senso_di_matera_per_la_geometria_una_citta_a_forma_di_libro_per_bambini-193510417/ (accessed on 10 April 2018).
- Batty, M.; Longley, P. Fractal Cities: A Geometry of form and Function; Academic Press: Cambridge, MA, USA, 1994. [Google Scholar]
- Frankhauser, P. The fractal approach. A new tool for the spatial analysis of urban agglomerations. Popul. Engl. Sel. 1998, 10, 205–240. [Google Scholar]
- Campedelli, L. Fantasia e Logica Nella Matematica; Feltrinelli: Milan, Italy, 1966. [Google Scholar]
- Laureano, P. La Piramide Rovesciata. Il Modello Dell’Oasi per il Pianeta Terra; Bollati Boringhieri: Torino, Italy, 1995. [Google Scholar]
- Laureano, P. Giardini di Pietra, I Sassi di Matera e la Civiltà Mediterranea; Bollati Boringhieri: Torino, Italy, 2003. [Google Scholar]
- Mandelbrot, B. The Fractal Geometry of Nature; Henry Holt and Company: New York, NY, USA, 1977. [Google Scholar]
- Edgar, G.A. Measure, Topology and Fractal Geometry; Springer: New York, NY, USA, 1999. [Google Scholar]
- Kambesis, P.N.; Larson, E.B.; Mylroie, J.E. Morphometric analysis of cave patterns using fractal indices, in Caves and Karst across Time. Geol. Soc. Am. Spec. Pap. 2015, 516, 67–86. [Google Scholar]
- D’Alessio, L.; Lucente, S. Forme dinamiche per conoscere tesori invisibili. In Proceedings of the IXth Conference Diagnosis, Conservation of Cultural Heritage, Napoli, Italy, 13–14 December 2018; Cervino Edizioni: Giugliano in Campania, Italy, 2018; pp. 170–178. [Google Scholar]
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).