Abstract
The growing demand for efficient energy management has become essential for achieving sustainable development across social, economic, and environmental sectors. Accurate energy demand forecasting plays a pivotal role in energy management. However, energy demand data present unique challenges due to their complex characteristics, such as multi-seasonality, hidden structures, long-range dependency, irregularities, volatilities, and nonlinear patterns, making energy demand forecasting challenging. We propose a hybrid dimension reduction deep learning algorithm, Temporal Variational Residual Network (TVRN), to address these challenges and enhance forecasting performance. This model integrates variational autoencoders (VAEs), Residual Neural Networks (ResNets), and Bidirectional Long Short-Term Memory (BiLSTM) networks. TVRN employs VAEs for dimensionality reduction and noise filtering, ResNets to capture local, mid-level, and global features while tackling gradient vanishing issues in deeper networks, and BiLSTM to leverage past and future contexts for dynamic and accurate predictions. The performance of the proposed model is evaluated using energy consumption data, showing a significant improvement over traditional deep learning and hybrid models. For hourly forecasting, TVRN reduces root mean square error and mean absolute error, ranging from 19% to 86% compared to other models. Similarly, for daily energy consumption forecasting, this method outperforms existing models with an improvement in root mean square error and mean absolute error ranging from 30% to 95%. The proposed model significantly enhances the accuracy of energy demand forecasting by effectively addressing the complexities of multi-seasonality, hidden structures, and nonlinearity.
1. Introduction
Energy is crucial for a nation’s economic growth, quality of life, and environmental sustainability. According to the U.S. Energy Information Administration, global energy consumption is projected to increase by 34% from 2022 to 2025, reaching 855 quadrillion BTUs [1]. Population growth and economic expansion have been the main drivers of increasing energy usage over the past decades [2]. Interestingly, AI-driven energy demand is expected to double by 2030 [3]. In response to this trend, many countries enforce energy codes and regulations to mitigate energy usage, promote energy efficiency, and reduce CO2 emissions [4]. Accurate energy demand forecasting is essential for sustainable resource allocation, informed policymaking, and minimizing waste, thereby ensuring economic stability and environmental sustainability [5,6].
Energy demand forecasting is typically structured across different time horizons, each serving distinct needs. The National Renewable Energy Laboratory (NREL) categorizes energy demand forecasting into short-term (e.g., minutes to several days), medium-term (e.g., a week to several months), and long-term (e.g., annual and beyond) predictions, which are defined as follows [7]. Short-term forecasting supports operational decisions, such as real-time grid management and handling demand fluctuations resulting from unexpected events. Medium-term forecasting is used for tactical planning, including maintenance scheduling, fuel procurement, and financial forecasting. Long-term forecasting is crucial in strategic decision-making, as it guides infrastructure investments, capacity expansion, and policy development. Each horizon employs different modeling approaches and addresses specific needs within the energy planning ecosystem. Since exogenous shocks influence tactical planning and strategic decision-making in energy demand time series, this study focuses on short-term energy demand (or consumption) forecasting to enhance operational efficiency and market responsiveness.
Energy demand forecasting has been extensively studied using various statistical and machine learning methods, including traditional ARIMA and its variants such as ARMAX, GARCH, ARX, and TARX [8,9,10,11,12], which serve as foundational tools due to their simplicity. However, these models are constrained by their inherent assumptions of linearity and stationarity, which limit their ability to model complex real-world energy demand behavior. Specifically, they struggle to capture nonlinear fluctuations, abrupt changes, and the presence of multiple overlapping seasonal cycles in energy consumption. To address these challenges, machine learning techniques such as Support Vector Machines (SVM) [13], Artificial Neural Networks (ANNs) [14], random forests [15], and gradient boosting [16] have been explored, improving forecast accuracy. While these techniques can capture nonlinearity and enhance forecasting accuracy, they typically rely on shallow architectures that struggle to model temporal dependencies and hierarchical time dynamics, particularly in long-term sequences. This restricts their capacity to grasp complex energy demand patterns, which involve multi-seasonality, hidden structures, long-range dependencies, and irregularities. Deep learning models, including Recurrent Neural Networks (RNNs) [17], Convolutional Neural Networks (CNNs) [18], and Long Short-Term Memory (LSTM) networks [19], have demonstrated significant improvements by automatically extracting nonlinear features and modeling sequential dependencies. Nevertheless, these models are not without limitations: vanilla RNNs suffer from vanishing gradient issues; CNNs, while effective at capturing local spatial patterns, lack temporal awareness; and LSTMs, though more robust, can still struggle with multi-seasonality and long-term irregularities in volatile demand patterns. To overcome the limitations of standalone deep learning models, various hybrid frameworks have been proposed in the energy forecasting domain. These architectures aim to leverage spatial and temporal learning via combinations such as CNN-LSTM [20], CNN-GRU [21], and attention-based CNN-LSTM-BiLSTM [22]. Despite their success in integrating localized feature extraction with sequence modeling, these hybrid models exhibit critical shortcomings. Specifically, CNNs are inherently optimized for grid-like image data and often fail to capture irregular temporal dynamics in time series without extensive customization [20]. LSTMs and GRUs, while compelling for sequential modeling, struggle with learning deep hierarchical representations, particularly under multivariate, multi-seasonal, and volatile energy demand conditions. Furthermore, existing VAE-BiLSTM hybrids [23] enhances probabilistic forecasting but suffers from gradient degradation in deep architectures and limited feature reuse across scales. Notably, none of these models incorporates residual connections within variational frameworks, a gap our proposed method directly addresses.
Dimensionality reduction (DR) techniques are increasingly integrated with deep learning to enhance energy demand forecasting, particularly for feature extraction and noise reduction. Traditional DR methods such as Principal Component Analysis (PCA) [24], Linear Discriminant Analysis (LDA), Singular Value Decomposition (SVD), and Non-Negative Matrix Factorization (NMF) [25] have been employed for preprocessing energy datasets before deep learning applications. To overcome the limitations of traditional DR techniques, autoencoders (AEs) and their variants, such as sparse autoencoders (SAEs) and variational autoencoders (VAEs), have been widely adopted. These unsupervised deep learning models leverage nonlinear transformations for feature extraction in deep neural networks [26,27,28,29]. SAEs introduce sparsity constraints to prevent overfitting and improve interpretability by selectively activating neurons. On the other hand, VAEs enhance traditional autoencoders by introducing a probabilistic framework where the encoder produces a distribution instead of a fixed vector and by including a Kullback–Leibler (KL) divergence term in the loss function. This enables generative modeling, smooth latent space interpolation, and greater robustness against overfitting [28,29]. These DR techniques have been combined with deep learning algorithms, e.g., complementary ensemble empirical mode decomposition with PCA and LSTM (CEEMD-PCA-LSTM) will be referred to as CPL [30], multilevel wavelet decomposition networks (MWDNs) [31], variational mode decomposition (VMD) [32], and VAE-BiLSTM [23]. However, these methods often struggle to capture the complex low-dimensional structures inherent in energy data, partially due to their linear reduction. Furthermore, these methods struggle to capture local temporal patterns, seasonality, and long-term dependencies in energy data [33]. However, VAEs often experience training instability and degraded performance in deeper networks, especially when attempting to capture layered temporal abstractions. To mitigate this, we embed a ResNet into the VAE encoder, ensuring gradient stability and enabling hierarchical representation learning.
In deep learning model architectures such as Convolutional Neural Networks (CNNs) and VAEs, the depth of the hidden network layers, defined by the number of layers, plays a critical role in determining model performance. However, increasing the depth of the neural network often leads to a degradation problem, where the model’s accuracy decreases. Residual Neural Networks (ResNets), initially proposed for image analysis [34], address this issue by introducing a residual learning framework that facilitates the training of deep networks. ResNets achieve this by incorporating identity shortcut connections that bypass one or more layers, allowing gradients to propagate more effectively during backpropagation. These skip connections are implemented through residual blocks that perform element-wise addition between the input and output of convolutional layers. This mechanism addresses problems such as vanishing gradients, enabling the efficient training of deeper models. Furthermore, ResNets enhance the extraction of complex and abstract features by preserving historical information and reducing feature loss, allowing the model to learn more expressive and discriminative representations [34]. While ResNets have revolutionized deep vision tasks, their application as embedded encoders in time series VAEs, particularly for energy data, remains unexplored. This adaptation allows us to exploit residual connections to stabilize training and extract temporal features at multiple abstraction levels.
We propose a novel deep learning architecture, the Temporal Variational Residual Network (TVRN), which is the first to integrate ResNet-embedded VAEs with BiLSTM networks for energy demand forecasting. This design uniquely addresses key challenges in modeling multi-seasonality, long-range dependencies, and nonlinear temporal fluctuations. The model begins with a ResNet-embedded VAE, where residual blocks mitigate vanishing gradients and promote hierarchical feature extraction during encoding [35]. This allows the encoder to effectively learn multiscale patterns from short-term irregularities to long-term structural trends while preserving gradient flow. The VAE maps input sequences into a low-dimensional probabilistic latent space using a multivariate Gaussian distribution, with Kullback–Leibler divergence regularization to encourage smoothness and generalizability [29]. Subsequently, BiLSTM layers model temporal dependencies bidirectionally, leveraging both historical and forward-looking patterns to enhance predictive performance. TVRN presents a new hybrid architecture that combines residual-enhanced probabilistic encoding with bidirectional temporal inference, an approach not previously explored in energy forecasting. This multiscale framework integrates feature extraction, dimensionality reduction, and sequential learning, effectively addressing significant limitations of earlier hybrid models. Showing strong empirical results, TVRN pushes the boundaries of current technology and paves the way for new directions in deep learning for complex time series forecasting.
The major contributions of this work are summarized as follows:
- We propose TVRN, a novel hybrid architecture that combines a ResNet-embedded VAE with a BiLSTM network to address nonlinearities, irregular seasonality, and deep latent structure in energy demand forecasting.
- To the best of our knowledge, this is the first application of a ResNet-embedded VAE for time series forecasting. While ResNet has primarily been applied in image recognition, our adaptation enables deeper VAE structures without gradient degradation, enhancing the model’s capacity to extract local, seasonal, and global features from complex energy data.
- The TVRN model integrates ResNet-embedded VAEs with BiLSTM to improve forecasting by combining denoising, deep residual learning, and bidirectional temporal modeling.
- We conduct extensive evaluations of TVRN on both hourly and daily energy consumption data, comparing it against a suite of strong baselines, including traditional statistical models (ARIMA), deep learning models (DNN, CNN, BiLSTM), and hybrid solutions (PCA-BiLSTM, CPL). Results consistently show that TVRN outperforms all benchmarks in RMSE and MAE, showing significant performance gains across all forecasting horizons.
The remainder of this paper is organized as follows: Section 2 introduces the hybrid ResNet-embedded VAE-BiLSTM architecture. Section 3 outlines the experimental setup and details the hourly and daily energy consumption data used. Section 4 describes the result of the data analysis experiment. Section 5 provides a comprehensive discussion of the analytical results. Finally, Section 6 concludes with the main findings.
2. Methodology
Consider a time series , representing energy consumption recorded at regular intervals from time to T. This sequence often exhibits multi-seasonality, hidden structures, nonlinear dependencies, abrupt irregularities, and high volatility challenges that conventional models struggle to handle effectively. In this section, we present the architecture and data flow of the proposed TVRN and elaborate on how its components jointly enhance forecasting performance.
2.1. TVRN Algorithm Architecture
We propose a novel hybrid framework, TVRN, that combines a ResNet-embedded VAE with a BiLSTM network for accurate energy demand forecasting. The overall structure is illustrated in Figure 1. The process begins with data preprocessing, where raw energy demand signals undergo logarithmic transformation and normalization to stabilize variance and scale features. The core innovation lies in the ResNet-embedded VAE encoder, which performs hierarchical multiscale feature extraction while simultaneously reducing dimensionality and suppressing noise. ResNet starts its hierarchical extraction with the initial layers, which detect local features such as short-term fluctuations, spikes, sudden changes, and irregularities. The intermediate layers capture seasonal and cyclical patterns, while the deeper layers identify global features, including long-term trends and notable correlation patterns in energy consumption data. Unlike conventional VAEs that rely on standard feedforward encoders, our model embeds residual blocks within the VAE encoder, which allows the network to train deeper layers without degradation. These skip connections enable efficient gradient propagation and better preservation of both local and long-range feature dynamics in the latent representation. These latent sequences are then fed into a BiLSTM, which leverages both forward and backward temporal dependencies. This allows the model to contextualize each time step using both past and future patterns, particularly beneficial for forecasting complex energy demand signals with multi-seasonal and irregular characteristics. Finally, the BiLSTM’s output is passed through a dense layer and denormalized to produce the final predicted energy consumption values. The TVRN framework thus unifies deep residual feature encoding, probabilistic dimensionality reduction, and bidirectional temporal inference in an end-to-end architecture optimized for energy forecasting.
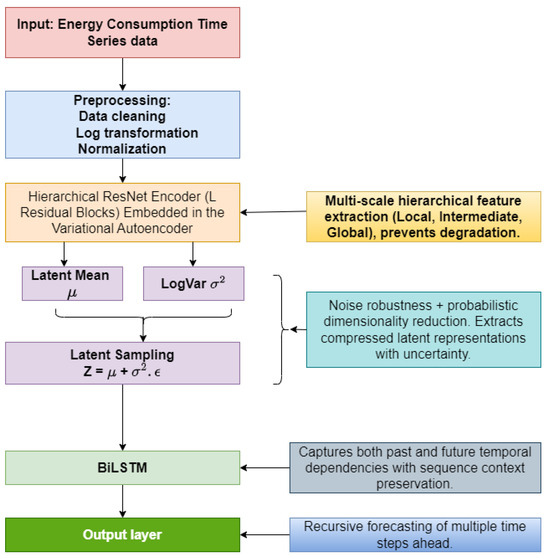
Figure 1.
Proposed TVRN model architecture comprising ResNet encoder, latent representation, and BiLSTM layer for time series forecasting.
Consider energy demand data , is represented as follows:
where f is a measurable function that can be either linear or nonlinear, and error meets the following criteria:
The autoregressive lag, p, will be determined through experimental trials of model training to capture all past energy information effectively. Before conducting the main analytical steps, we standardize the time series data described in (1). Standardization is favored over alternative scaling methods, such as min-max normalization, due to its effectiveness in enhancing model performance [36], improving numerical stability [37], and accelerating convergence [38].
Step 1: Residual Block Integration into VAE Encoder
A core innovation of the proposed TVRN framework lies in the integration of a ResNet within the encoder of VAE, as illustrated in Figure 1, Figure 2 and Figure 3. Unlike traditional VAE encoders, which typically rely on shallow or feedforward architectures, our design incorporates stacked residual blocks to enable deeper hierarchical feature learning while mitigating gradient vanishing and degradation issues common in deep networks. The ResNet-enhanced encoder initiates multiscale feature abstraction by progressively capturing patterns across different temporal levels. Specifically, Shallow residual blocks learn short-term, localized phenomena such as fluctuations, spikes, and abrupt changes. Intermediate layers capture medium-range seasonal and cyclical patterns. Deeper blocks extract long-term dependencies and global correlation structures embedded in the energy demand time series. Each residual block, as illustrated in Figure 2, leverages skip connections and convolutional transformations, enhancing the encoder’s capacity to extract meaningful representations without information loss or training instability.
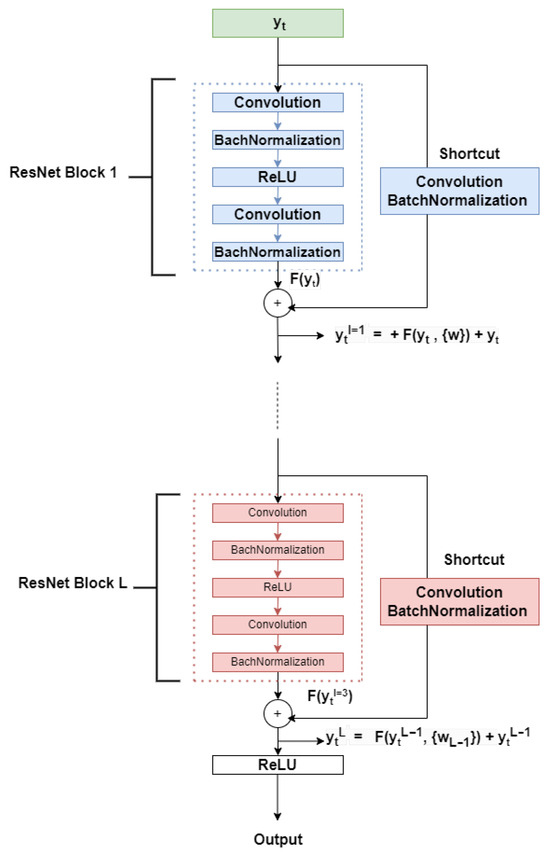
Figure 2.
Illustration of Residual Neural Network Block Architecture.
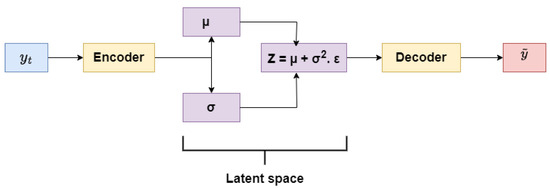
Figure 3.
Variational autoencoder (VAE) network architecture.
For a given an input sequence , the output of the residual block in the encoder is defined as:
where is the input to the block, denotes the trainable parameters (weights and biases), and is the residual mapping comprising convolutional, normalization, and activation operations.
In practice, each residual mapping performs:
followed by batch normalization and a nonlinear activation (e.g., ReLU). These operations are repeated across residual blocks to refine hierarchical abstractions.
The cumulative output of the entire ResNet encoder after L residual blocks is given by:
where is the original input, and the summation captures the accumulated feature transformations at each depth level.
This ResNet-VAE encoder provides a robust latent representation that reflects both fine-grained and long-range temporal structures, forming a compressed yet expressive input for the downstream BiLSTM forecaster.
Step 2: Probabilistic Latent Encoding
Given the deep feature representation from the ResNet encoder (Equation (3)), the VAE encodes this sequence into a lower-dimensional latent space. Unlike standard Autoencoders that produce deterministic embeddings, the VAE formulates the latent representation z as a random variable governed by a multivariate Gaussian distribution [28]. This probabilistic approach enhances generalization by encouraging smooth latent manifolds and regularized feature spaces. The prior distribution over the latent variables is defined as , where denotes the model parameters [39].
The encoder network learns to approximate the true posterior by predicting the mean and variance of the latent Gaussian distribution [28,29]:
where represents the trainable parameters of the ResNet-based encoder.
The ResNet encoder then maps input features to this distribution via:
where denotes the parameters of the residual encoder network.
To enable gradient-based training through stochastic layers, we adopt the reparameterization trick [28], which samples z using:
This formulation ensures that backpropagation can proceed despite the stochastic nature of the latent space.
The decoder network reconstructs the input from the latent vector z, producing a conditional Gaussian output distribution:
where are the decoder parameters, and denote the learned reconstruction statistics.
To optimize the VAE, we maximize the Evidence Lower Bound (ELBO), which balances two objectives: (1) accurate reconstruction of the input sequence , and (2) regularization of the latent space via Kullback–Leibler (KL) divergence between the approximate posterior and the prior:
This ensures that the latent space is both informative and smooth, supporting better generalization and downstream forecasting accuracy.
The use of a ResNet-embedded encoder within a probabilistic VAE structure, as used here, has not been explored in prior time series literature. This design allows the model to encode multiscale features from complex energy demand into a robust latent representation that preserves uncertainty, enables generative modeling, and supports superior sequential inference in later stages.
Step 3: Modeling a BiLSTM to Capture Energy Demand Dependencies Using a Latent Space Representation
The latent space vector produced by the ResNet-embedded VAE encoder, along with the latent representation described in (Steps 1 and 2), forms the combined latent variable z, which serves as input to a BiLSTM for sequential modeling. These representations capture multiscale temporal features derived from the original energy consumption data. In the final forecasting stage of the TVRN framework, a BiLSTM network is employed to model both historical and future dependencies from this latent space, enabling accurate energy demand predictions. BiLSTM networks [40] extend traditional LSTM architectures by incorporating two parallel layers: a forward layer that processes the sequence chronologically and a backward layer that scans it in reverse. This bidirectional design allows the model to more effectively capture long-range dependencies, thereby enhancing predictive performance, particularly under conditions of multi-seasonal patterns and irregular demand fluctuations [41].
The BiLSTM forecast for a latent vector z at time t is computed as:
where represents the parameters of both forward and backward LSTM layers.
Table 1 illustrates the forward and backward processes, as shown in (7). BiLSTM captures long-range dependencies through the forward cell states , which process past patterns, and the backward cell state , which processes information from future time steps to the current cells [41]. This process is managed through BiLSTM components, including the input gate (i), forget gate (f), and output gate (o) equations for the forward LSTM, as provided in [40] and shown in Table 1.

Table 1.
Comparison of Forward and Backward LSTM Gate Operations.
The BiLSTM network’s hidden state at each time step is obtained by concatenating the forward and backward hidden vectors:
which allows the network to incorporate information from both past and future contexts when predicting energy demand.
The complete end-to-end TVRN forecasting process from raw time series to prediction is summarized by:
where and denote the trainable parameters of the ResNet-embedded encoder and the BiLSTM, respectively. The function encodes the input into the latent space using the ResNet-VAE, and BiLSTM subsequently forecasts the future value.
Finally, since the input time series is normalized during preprocessing, the predicted output is rescaled to its original scale using the anti-standardization formula:
where and are the sample standard deviation and mean, respectively.
The integration of a variational latent space with bidirectional sequence modeling, in TVRN, enables the model to learn complex dynamics from both past and future contexts. This architectural hybrid between probabilistic deep encoding (ResNet-embedded VAE) and temporal sequence inference (BiLSTM) sets TVRN apart from conventional hybrid forecasting models.
2.2. Out-of-Sample Energy Demand Forecasting Using Recursive Algorithms and Evaluation Metrics
Once the TVRN is built and trained, as described in the methodology section, we apply it to forecast the test data. We adopt a recursive forecasting approach, where the trained model generates multi-step predictions using each forecasted value as an input for predicting the next step [42]. This iterative process enables the model to forecast all h future values at time t by leveraging previously predicted outputs [43]. On the other hand, direct multi-step forecasting predicts each time horizon independently, without relying on prior forecasted values, as demonstrated in [44]. The recursive multi-step forecasting approach relies on the trained model. At time t, the forecast for (where ) is iteratively generated through the recursive process.
As described in Figure 4, a critical aspect of the recursive forecasting process is using forecasted values as inputs when actual observations are unavailable at time t. For instance, the forecast is derived from the trained ’Model’ based on past observations . However, since the one-step ahead time series value is unknown at time t, it is replaced with its forecasted counterpart, . As the forecasting horizon h extends, the reliance on previously predicted values increases, potentially amplifying forecasting variance.
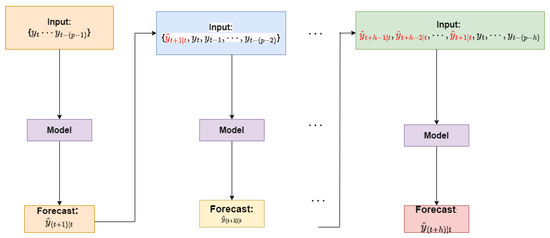
Figure 4.
Recursive algorithm for multi-step ahead forecasting.
The final stage of model evaluation involves assessing its performance using various statistical metrics, including mean squared error (MSE), root mean square error (RMSE), and mean absolute error (MAE). These metrics, which are influenced by the data scale, quantify the accuracy of predictions on test datasets. While there is no universal consensus regarding the optimal metric for forecasting evaluation, the mean squared error (MSE) is frequently preferred due to its strong theoretical foundation in statistical modeling. MAE and MSE offer valuable insights into forecasting accuracy and the magnitude of prediction errors. However, MAE assigns equal weight to all errors, whereas MSE places greater emphasis on more significant errors, making it more sensitive to outliers [45]. This characteristic renders MSE particularly useful in scenarios where penalizing substantial deviations is crucial. The assessment metrics are expressed as follows.
where indicates the actual values while signifies the predicted values for both in-sample and out-of-sample forecasting. Furthermore, T refers to the total number of observations for either in-sample or out-of-sample data.
3. Data Descriptions
We analyzed hourly and daily power consumption data from PJM Interconnection LLC (PJM), a regional transmission organization (RTO) in the United States that oversees the electric transmission system across the Eastern region. The dataset spans 2002 to 2018 and contains 145,336 hourly and 6,057 daily records. Although our study focuses on short-term energy demand forecasting, using a long-span dataset (2002–2018) is essential. DL models benefit from extensive, diverse historical data, especially in energy forecasting, where seasonal patterns, trends, and irregular events are prominent. A more extended dataset enhances the DL model’s ability to generalize and adapt to varying future conditions. The dataset is publicly available at https://www.kaggle.com/datasets/robikscube/hourly-energy-consumption?select=PJME_hourly.csv (accessed on 21 April 2023).
Figure 5 illustrates these complexities: strong seasonal trends with high variability and consumption spikes are evident in Figure 5a,c. The Hurst exponent (0.9109 for hourly, 0.8880 for daily) indicates persistence, while spectral entropy values (3.0579 for hourly, 4.0530 for daily) suggest significant noise. Autocorrelation functions (Figure 5b,d) show strong correlations across multiple lags with a sinusoidal pattern, reflecting seasonality. Squared coherence plots (Figure 5f,h) reveal a complex energy distribution across frequencies. Frequency domain analysis (Figure 5e,g) identifies dominant frequencies, with a primary 24 h cycle (0.0417 Hz), intermediate 10 h and 8 h periodicities, and additional peaks at 0.1429 Hz (weekly cycle), 0.3 Hz, and 0.412 Hz (bi-daily fluctuations). These complex properties in energy demand underscore the need for advanced forecasting techniques.
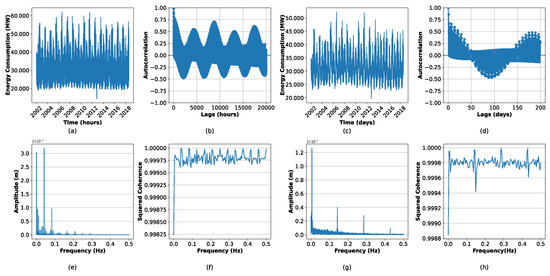
Figure 5.
Complex properties of energy consumption: (a) Hourly energy consumption. (b) Autocorrelation of hourly energy consumption. (c) Daily energy consumption. (d) Autocorrelation of daily energy consumption. (e) Fourier transform of hourly energy consumption. (f) Squared coherence of hourly energy consumption. (g) Fourier transform of daily energy consumption. (h) Squared coherence of daily energy consumption.
We conduct the Augmented Dickey-Fuller (ADF) test [46] on both hourly and daily energy consumption data, reporting test statistics, p-values, and critical values at the 1%, 5%, and 10% significance levels. The analysis considers three regression specifications: ‘c’ (constant), ‘ct’ (constant and linear trend), and ’ctt’ (constant, linear, and quadratic trends). In all cases, the p-values are significantly below 0.05, firmly rejecting the null hypothesis of a unit root. Additionally, the KPSS test [47] does not reject the null hypothesis of stationarity, with a p-value (0.1 > 0.05), which reinforces that the data is stationary. A log transformation applied before model training offers key advantages: normalizing the data scale, mitigating outliers, and enhancing pattern recognition. Stabilizing variance is critical in energy data, where higher variability is observed at larger values, which supports models that usually assume distributed errors. Additionally, it simplifies modeling by converting multiplicative relationships into additive ones, improving the handling of seasonal variations in forecasting.
Design and Optimization of Hyperparameters
The dataset includes 145,336 hourly energy consumption records, divided as follows: the first 145,012 h (from 1 January 2002, 01:00:00 to 19 July 2018, 06:00:00) for training, the next 300 h (from 19 July 2018, 07:00:00 to 31 July 2018, 18:00:00) for validation, and the last 24 h (from 31 July 2018, 19:00:00 to 1 August 2018, 18:00:00) for testing. The TVRN hybrid model was trained using optimized hyperparameters and demonstrated superior predictive performance. The optimal autoregressive order for hourly energy consumption is 96 h. The latent space dimensionality is set to 8, with the encoder utilizing dense layers to compute the mean and log variance, followed by a sampling layer incorporating the Gaussian reparameterization trick. The BiLSTM component of the hybrid model consisted of multiple Bidirectional LSTM layers. The first layer contained 32 units with tanh activation and returning sequences, a dropout rate of 0.2, and batch normalization. Subsequent layers consisted of 16 and 8 units, respectively, employing kernel regularization with an L2 penalty of 0.0001. The fourth layer included four units with tanh activation, while the final output layer comprised a single unit with the same activation function. The TVRN model trains using a composite loss function that combines binary cross-entropy for reconstruction loss and KL divergence for regularization. The Adam optimizer minimizes the total loss using a batch size of 64 over 30 epochs, with the mean squared error (MSE) as the primary loss function. A comprehensive summary of the ResNet parameters used in the hybrid model is provided in Table 2. The entire model is implemented in Python 3.12.7. The ResNet-embedded VAE with BiLSTM is developed using the TensorFlow and Keras frameworks. Additionally, various machine learning and deep learning algorithms are utilized through the scikit-learn library.

Table 2.
Hyperparameters ResNet component used in the hybrid model training.
Empirically assess the denoising ability of our VAE-based framework; we compare the signal-to-noise ratio (SNR) of the original energy consumption time series with that of the latent representations generated by the encoder. Before applying the VAE, the SNR of the standardized hourly and daily energy signals was about 14.09 dB and 16.80 dB, respectively, indicating strong signals relative to noise. After encoding with the VAE, the average SNR across latent dimensions dropped to 0.1313 dB for hourly data and 0.059 dB for daily data. This notable decrease shows the VAE’s capacity to compress and regularize the signal by diminishing high-variance noise components. Importantly, this does not imply loss of information; instead, it highlights the VAE’s function as a probabilistic filter that preserves key structural features while reducing noise, resulting in more robust and generalizable latent representations for forecasting.
4. Results
Based on the dataset described in Section 3 and the hyperparameter settings detailed in the Design and Optimization of Hyperparameters subsection, we present the results summarized in Table 3 and Table 4, as well as Figure 6 and Figure 7.

Table 3.
The performance of hourly energy forecasting, assessed using RMSE and MAE across different forecasting horizons (h-ahead), with the best results in each row highlighted in bold.

Table 4.
Forecast performance of daily energy data, evaluated using RMSE and MAE across various models and forecasting horizons. Bold indicates the best result in each row.
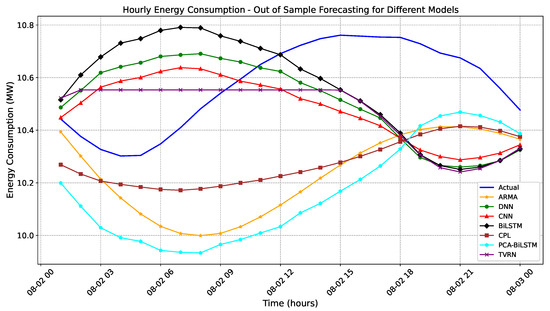
Figure 6.
Visualization of hourly energy consumption forecasting across various models for the next 24 h.
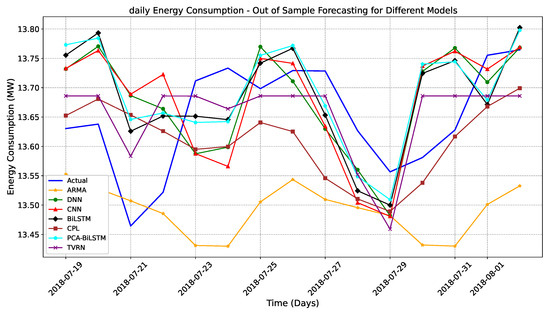
Figure 7.
Visualization of 15-day-ahead daily energy consumption forecasting across various models.
Table 3 presents the performance metrics of the forecasting model for hourly energy consumption based on the in-sample data, along with three different out-of-sample forecasting horizons: h = 1 h, 12 h, and 24 h. The results indicate that the proposed TVRN model consistently outperforms ARIMA, standard deep learning methods such as DNN, BiLSTM, and CNN, as well as hybrid models like CPL and PCA-BiLSTM across the selected forecasting horizons. For example, the TVRN hybrid model shows significant improvements in RMSE compared to PCA-BiLSTM by 86%, 48%, and 19%, and similarly, improvements compared to CPL are 99%, 41%, and 12% for h = 1 h, 12 h, and 24 h, respectively. Improvements are also noted in the MAE metrics. The traditional ARIMA model performs worse than all other models for 12 and 24 h forecasting horizons. Although TVRN shows a slightly higher training, for example, in RMSE (0.076) than BiLSTM (0.024) and PCA-BiLSTM (0.015), it consistently outperforms them on test data across all forecasting horizons. This highlights a key generalization tradeoff: TVRN’s use of variational regularization and residual skip improves robustness and prevents overfitting, leading to better performance on unseen data. While BiLSTM and PCA-BiLSTM achieve lower training errors, they overfit and degrade on longer horizons. Its latent representation learning also captures complex nonlinear and seasonal patterns, making it more effective for real-world energy forecasting.
Figure 6 presents a comparative visualization of hourly energy consumption forecasts from various models against actual observed values. The proposed TVRN model exhibits superior performance in accurately capturing temporal trends and structures. Unlike ARIMA and ARMA, which struggle with nonlinearity and consistently underestimate energy demand, or CPL, which tends to produce flat-line predictions, TVRN effectively models the 24 h cycle, including midday peaks and evening declines. Compared to the erratic oscillations of DNN and CNN, TVRN provides smoother and more stable forecasts, reflecting improved generalization. A minor limitation is observed between 08-02 03:00 and 08-02 15:00, where the forecast slightly underestimates the rising demand, likely due to latent space compression or recursive error accumulation. Nevertheless, TVRN closely tracks actual consumption throughout the 24 h horizon, underscoring its robustness, low bias, and adaptability for short-term energy forecasting.
The total daily energy consumption data for 6057 days is divided into three parts: the first 5842 days (from 2 January 2002, to 30 December 2017) for training, the next 200 days (from 1 January 2018, to 18 July 2018) for validation, and the last 15 days (from 19 July 2018 to 2 August 2018) for the test dataset. The hyperparameters used for model training are identical to those employed for training on hourly energy data, with an autoregressive order of 30.
Table 4 presents the performance metrics of the forecasting model for daily energy consumption, based on in-sample data, alongside three different out-of-sample forecasting horizons: h = 1 day, 7 days, and 15 days. The results show that the proposed TVRN hybrid model consistently outperforms ARIMA, standard deep learning methods, CPL, and PCA-BiLSTM across the selected forecasting horizons. For instance, the TVRN demonstrates a notable improvement in RMSE compared to PCA-BiLSTM by 95%, 35%, and 30%, and similarly, improvements compared to CPL are 92%, 61%, and 66% for h = 1 day, 7 days, and 15 days, respectively. Enhancements are also evident in the MAE metrics. The traditional ARIMA model performs worse for h = 7 and 15 days ahead of the forecast horizons.
Figure 7 illustrates the 15-day-ahead daily energy consumption forecasting results, where the proposed TVRN model (purple line) consistently tracks the actual trend (blue line) more closely than all other baseline models. The ARIMA (orange) and CPL (brown) models exhibit rigid, low-variance predictions, failing to adapt to day-to-day fluctuations, characteristics especially evident around inflection points. Both DNN (green) and CNN (red) capture some variation but tend to overshoot or oscillate erratically, particularly near 22 July and 26 July, reflecting instability in their short-term sensitivity. The BiLSTM model (black) performs significantly better by effectively modeling both peaks and troughs, while PCA-BiLSTM (cyan) offers moderate improvement by integrating dimensionality reduction with sequential learning. Among all, TVRN demonstrates the best alignment with the actual series by preserving both magnitude and directionality of sharp and gradual changes. This performance reflects its ability to integrate multiscale temporal features through residual-enhanced variational encoding. However, slight flattening is observed in TVRN’s forecasts between 30 July and 1 August, potentially due to latent space saturation or recursive inference drift. Despite this minor limitation, TVRN maintains the most accurate and coherent trajectory across the 15-day horizon, reinforcing its effectiveness for medium-range energy forecasting in dynamic environments.
5. Discussion
This study presents the TVRN, a novel hybrid deep learning framework that integrates residual learning, probabilistic dimensionality reduction, and bidirectional temporal modeling for energy demand forecasting. The key innovation of TVRN lies in the architectural coupling of a ResNet-embedded VAE with a BiLSTM. This configuration enables the model to hierarchically extract features from raw energy demand data, encode them probabilistically, and model sequential dependencies bidirectionally, a combination not previously explored in energy forecasting literature. This layered design effectively addresses core challenges in energy consumption time series prediction, including long-range dependencies, multi-seasonality, hidden structural patterns, and data irregularities.
Empirical studies demonstrate that the proposed TVRN model consistently outperforms traditional statistical models, standard deep learning approaches, and existing hybrid models in terms of RMSE and MAE. We evaluated TVRN on hourly and daily energy consumption data, comparing its predictive accuracy across multiple forecasting horizons against various benchmark models, as presented in Table 3 and Table 4. The results indicate that TVRN achieves superior forecasting accuracy compared to traditional models, such as ARIMA, deep learning models, including DNN, BiLSTM, and CNN, and hybrid models, including PCA-BiLSTM and CPL. For instance, for hourly forecasting, the hybrid TVRN model reduces root mean square error and mean absolute error, ranging from 19% to 86% compared to other models. Similarly, for daily energy consumption forecasting, it outperforms existing models with improvements in root mean square error and mean absolute error ranging from 30% to 95%. Additionally, the forecasting plots for hourly and daily energy consumption, presented in Figure 6 and Figure 7, demonstrate that TVRN effectively maintains close forecasting performance across energy data studies. In contrast, alternative models, such as ARIMA and CPL, exhibit deviations from actual values, as shown in Figure 7. To further validate the comparative performance, we conducted paired t-tests on pointwise forecast errors using hourly prediction data. The results show that TVRN significantly outperforms the baseline models: ARIMA (p = 0.000098), DNN (p = 0.001060), BiLSTM (p = 0.000991), CNN (p = 0.001080), and PCA-BiLSTM (p = 0.000054), with all p-values well below the 0.05 significance threshold. For instance, in the 24-step-ahead forecast, TVRN achieves a lower RMSE and MAE than all competitors with statistically significant differences. Although CPL performs slightly better during early hours (1:00–5:00 AM), its p-value of 0.139 indicates that the performance difference is not statistically significant. Furthermore, by analyzing RMSE and MAE across increasing forecast horizons using both hourly and daily energy datasets (Table 3 and Table 4). Models such as CPL and PCA-BiLSTM show minimal change in error over time, reflecting static extrapolation and a high-bias regime. In contrast, TVRN exhibits a consistent and gradual increase in error, maintaining the lowest RMSE and MAE at all horizons from short-term (h = 1) to long-term (h = 24 hourly, h = 15 daily). This pattern indicates TVRN’s superior ability to capture both short-and long-range dependencies.
The superior performance of the proposed TVRN architecture can be attributed to several key factors. First, VAEs, as a class of deep generative models, learn latent representations of energy consumption instead of directly modeling raw data, which enhances forecasting accuracy [48]. By capturing the underlying generative process of energy consumption data through latent random variables, VAEs facilitate a more precise representation of essential temporal patterns in time series data [49]. Second, integrating ResNet into the VAE framework significantly enhances the encoder’s feature extraction capability, resulting in a more informative representation of the latent space. In TVRN, ResNet plays a pivotal role in mitigating the vanishing gradient problem through skip connections while enhancing the learning of residual representations. This architecture enables effective multiscale feature extraction, capturing local patterns such as short-term fluctuations and abrupt changes, intermediate structures such as seasonal and cyclic variations, and global trends characterized by long-range dependencies. ResNet improves stability and efficiency in feature learning by preserving gradient flow in deep networks, thereby increasing the model’s capacity to extract hierarchical temporal dependencies and enhancing predictive accuracy in complex time series forecasting. This integration between VAE’s generative modeling and ResNet’s hierarchical feature extraction reinforces the model’s superior forecasting performance.
We compare the computational complexity of models, for example, for daily energy consumption forecasting, which varies considerably regarding training time, parameter count, and inference efficiency. These factors significantly influence both forecasting accuracy and deployment feasibility. An evaluation of the computational complexity measured by training time per epoch, inference time per sample, and the number of trainable parameters reveals necessary trade-offs associated with daily energy demand forecasting. Lightweight models, such as CNN and DNN, provide the fastest training times (1.05 s and 1.73 s per epoch) and low inference latency (approximately 17–18 ms), alongside modest parameter counts (15,315 and 5549, respectively). This makes them suitable for swift deployment in constrained environments. On the other hand, BiLSTM and PCA-BiLSTM, featuring around 22,600 parameters and training times of approximately 3.05–3.06 s per epoch, offer enhanced sequence modeling capabilities while still ensuring efficient inference (about 17–20 ms). These models are particularly effective for time series forecasting where temporal dependencies are essential. In contrast, CPL and TVRN, which have larger architectures (46,353 and 75,929 parameters, respectively), demonstrate longer training times (2.37 s and 3.15 s) and, in the case of TVRN, higher inference latency (around 33 ms per sample). This increased complexity stems from its hybrid architecture that combines ResNet, VAE, and BiLSTM. Although TVRN has higher computational complexity compared to conventional deep learning models due to its integration of ResNet, VAE, and BiLSTM, it provides significantly better forecasting accuracy. While training takes more time and uses more parameters, inference latency stays within practical limits (~33 ms), making deployment in real-world applications feasible. This trade-off is justified when forecast accuracy is critically important economically or operationally, as even minor improvements can enhance grid reliability and resource management.
Our findings highlight the advantages of a hybrid dimension reduction-based deep learning framework over single deep learning models, emphasizing the importance of dimension reduction through multilevel feature extraction using ResNet, as described in reference [50]. This study further confirms the effectiveness of hybrid deep learning approaches over single-model architectures, as supported by the existing literature [20,51]. This discovery reinforces the benefits of hybrid frameworks in capturing complex temporal dependencies, thereby improving the accuracy of energy demand forecasting. The latent vector derived from the ResNet encoder follows a multi-Gaussian distribution, playing a vital role in hierarchical feature extraction. This facilitates a flexible and probabilistic representation of latent space, effectively capturing the intricate and nonlinear characteristics of energy consumption data capabilities that PCA-based methods and VAEs alone lack.
PCA-based hybrid models, such as PCA-BiLSTM and CPL [30], utilize linear transformations for dimensionality reduction. However, these models struggle to capture the complex patterns inherent in energy consumption data. While PCA-BiLSTM outperforms single deep learning models at h = 1 h, CPL shows superior performance at h = 1 day ahead forecasting. However, both models exhibit significant underperformance compared to single deep learning models at longer-term forecasting horizons. Specifically, in the hourly energy consumption study, PCA-based models perform poorly for h = 12 and h = 24 h. In the daily energy study, they underperform for h = 7 and h = 15 days, as shown in Table 3 and Table 4. These findings suggest that PCA-based hybrid models are insufficient for capturing the intricate dynamics of energy consumption forecasting. In contrast, the TVRN model consistently delivers superior forecasting performance across empirical studies of energy consumption, as shown in Section 3. This improvement can be attributed to ResNet’s ability to extract local, intermediate, and global features, thereby effectively capturing the inherent complexities of energy consumption data, including multi-seasonality, long-range dependencies, nonlinearity, and hidden structures.
While the hybrid TVRN model shows promising improvements in energy consumption forecasting, it has limitations that need further exploration. First, although it achieves higher forecast performance based on RMSE and MAE, it does not include prediction intervals, which are essential for understanding uncertainty. Second, the constraints imposed on the VAE latent space by the multivariate Gaussian distribution. Moreover, our model outperformed other approaches in terms of root mean square error (RMSE) and mean absolute error (MAE) in both cases. However, some segments of the hourly forecast visualizations in Figure 6 exhibit flat, straight-line predictions. This behavior may be attributed to possible factors: (1) the VAE may have learned a latent representation with limited variation or dynamic range in those intervals, resulting in nearly identical outputs, and (2) due to the recursive forecasting approach, where predicted values are fed back as inputs, early-stage errors or latent space saturation can propagate, leading to a sequence of flat predictions.
6. Conclusions
In this paper, we develop an innovative hybrid model called TVRN to address the challenges inherent in energy demand data, including multi-seasonality, hidden structures, irregular patterns, and nonlinearity. The proposed hybrid model integrates a VAE for dimensionality reduction, local feature extraction, and noise filtering. Simultaneously, the ResNet embedded within the VAE captures local, intermediate, and global features at shallow, mid-level, and deep levels, thereby addressing the vanishing gradient problem that often occurs in deeper networks. The BiLSTM component, on the other hand, captures sequential information through forward and backward propagation. Through the analysis of hourly and daily energy consumption, the results demonstrate that TVRN outperforms ARIMA, deep learning models (DNNs, BiLSTM, CNNs), and hybrid models (PCA-BiLSTM, CPL) in out-of-sample forecasting, achieving better accuracy in both RMSE and MAE. Our findings indicate that TVRN, which embeds a ResNet architecture into a variational autoencoder, shows promise in improving the accuracy of energy consumption forecasting, particularly in capturing nonlinear patterns and complex seasonal structures in temporal dynamics.
Future research could enhance the capabilities of the proposed TVRN framework in several directions. First, research on TVRN could extend its capabilities by exploring alternative latent space distributions beyond the standard multivariate Gaussian assumption, thereby enhancing representation learning. These approaches may enable the model to capture better complex and multimodal features inherent in energy demand data. Second, to address the limitations of point forecasting, future work will incorporate uncertainty quantification by constructing prediction intervals around forecast outputs. This enhancement would allow the model to account for predictive uncertainty, enabling more informed decision-making and increasing the robustness and interpretability of the forecasting system under real-world variability. Finally, we plan to assess the generalizability of TVRN across diverse climatic and socio-economic contexts by extending our analysis to include datasets from additional regions, such as the Electric Reliability Council of Texas (ERCOT) and the New York Independent System Operator (NYISO). Evaluating the model on these geographically distinct datasets will help test its adaptability, transferability, and overall robustness across heterogeneous energy consumption patterns and policy environments.
Author Contributions
Conceptualization, S.A. and S.K.; methodology, S.A.; software, S.A.; validation, S.A. and S.K.; formal analysis, S.A.; investigation, S.A.; resources, S.A. and S.K.; data curation, S.A.; writing—original draft preparation, S.A.; writing—review and editing, S.K.; visualization, S.A.; supervision, S.K.; project administration, S.A.; funding acquisition, S.K. All authors have read and agreed to the published version of the manuscript.
Funding
This work was partly supported by the Alfred P. Sloan Foundation Grant #G-2020-1392 and NSF DMS-EiR Grant #2100729.
Data Availability Statement
The dataset is publicly available at https://www.kaggle.com/datasets/robikscube/hourly-energy-consumption?select=PJME_hourly.csv, accessed on 21 April 2023.
Acknowledgments
During the preparation of this manuscript/study, the authors used ChatGPT 4o and Grammarly to edit and enhance the grammar of the manuscript. The authors have reviewed and edited the output and take full responsibility for the content of this publication.
Conflicts of Interest
The authors declare that there are no conflicts of interest regarding the publication of this paper.
Abbreviations
The following abbreviations are used in this manuscript:
| TVRN | Temporal Variational Residual Network |
| ARIMA | Autoregressive Integrated Moving Average |
| ARMAX | Autoregressive Moving Average with eXogenous |
| GARCH | Generalized Autoregressive Conditional Heteroskedasticity |
| ARX | Autoregressive with eXtra Input |
| TARX | Threshold Autoregressive with eXogenous |
| SVM | Support Vector Machine |
| ANN | Artificial Neural Network |
| RNN | Recurrent Neural Network |
| CNN | Convolutional Neural Network |
| LSTM | Long Short-Term Memory |
| BiLSTM | Bidirectional Long Short-Term Memory |
| GRU | Gated Recurrent Unit |
| PCA | Principal Component Analysis |
| CEEMD | Complementary Ensemble Empirical 81 Mode Decomposition |
| AE | Autoencoder |
| VAE | Variational Autoencoder |
| MWDN | Multilevel Wavelet Decomposition Network |
| (SVD) | Singular Value Decomposition |
References
- US Energy Information Administration (EIA). International Energy Outlook 2013; US Energy Information Administration (EIA): Washington, DC, USA, 2013; p. 25.
- Suganthi, L.; Samuel, A.A. Energy models for demand forecasting—A review. Renew. Sustain. Energy Rev. 2012, 16, 1223–1240. [Google Scholar] [CrossRef]
- Chen, S. Data centres will use twice as much energy by 2030—Driven by AI. Nature 2025. [Google Scholar] [CrossRef]
- Zhao, H.X.; Magoulès, F. A review on the prediction of building energy consumption. Renew. Sustain. Energy Rev. 2012, 16, 3586–3592. [Google Scholar] [CrossRef]
- Wei, N.; Li, C.; Peng, X.; Zeng, F.; Lu, X. Conventional models and artificial intelligence-based models for energy consumption forecasting: A review. J. Pet. Sci. Eng. 2019, 181, 106187. [Google Scholar] [CrossRef]
- Klyuev, R.V.; Morgoev, I.D.; Morgoeva, A.D.; Gavrina, O.A.; Martyushev, N.V.; Efremenkov, E.A.; Mengxu, Q. Methods of forecasting electric energy consumption: A literature review. Energies 2022, 15, 8919. [Google Scholar] [CrossRef]
- Zhou, E.; Gadzanku, S.; Hodge, C.; Campton, M.; Can, S.d.R.d.; Zhang, J. Best Practices in Electricity Load Modeling and Forecasting for Long-Term Power System Planning; National Renewable Energy Laboratory (NREL): Golden, CO, USA, 2023.
- Cuaresma, J.C.; Hlouskova, J.; Kossmeier, S.; Obersteiner, M. Forecasting electricity spot-prices using linear univariate time-series models. Appl. Energy 2004, 77, 87–106. [Google Scholar] [CrossRef]
- Bakhat, M.; Rosselló, J. Estimation of tourism-induced electricity consumption: The case study of the Balearic Islands, Spain. Energy Econ. 2011, 33, 437–444. [Google Scholar] [CrossRef]
- Garcia, R.C.; Contreras, J.; Van Akkeren, M.; Garcia, J.B.C. A GARCH forecasting model to predict day-ahead electricity prices. IEEE Trans. Power Syst. 2005, 20, 867–874. [Google Scholar] [CrossRef]
- Moghram, I.; Rahman, S. Analysis and evaluation of five short-term load forecasting techniques. IEEE Trans. Power Syst. 1989, 4, 1484–1491. [Google Scholar] [CrossRef]
- Weron, R.; Misiorek, A. Forecasting spot electricity prices: A comparison of parametric and semiparametric time series models. Int. J. Forecast. 2008, 24, 744–763. [Google Scholar] [CrossRef]
- Dong, B.; Cao, C.; Lee, S.E. Applying support vector machines to predict building energy consumption in tropical region. Energy Build. 2005, 37, 545–553. [Google Scholar] [CrossRef]
- Rodrigues, F.; Cardeira, C.; Calado, J.M.F. The daily and hourly energy consumption and load forecasting using artificial neural network method: A case study using a set of 93 households in Portugal. Energy Procedia 2014, 62, 220–229. [Google Scholar] [CrossRef]
- Lahouar, A.; Slama, J.B.H. Day-ahead load forecast using random forest and expert input selection. Energy Convers. Manag. 2015, 103, 1040–1051. [Google Scholar] [CrossRef]
- Taieb, S.B.; Hyndman, R.J. A gradient boosting approach to the Kaggle load forecasting competition. Int. J. Forecast. 2014, 30, 382–394. [Google Scholar] [CrossRef]
- Shi, H.; Xu, M.; Li, R. Deep learning for household load forecasting—A novel pooling deep RNN. IEEE Trans. Smart Grid 2017, 9, 5271–5280. [Google Scholar] [CrossRef]
- Wang, H.Z.; Li, G.Q.; Wang, G.B.; Peng, J.C.; Jiang, H.; Liu, Y.T. Deep Learning-Based Ensemble Approach for Probabilistic Wind Power Forecasting. Appl. Energy 2017, 188, 56–70. [Google Scholar] [CrossRef]
- Bedi, J.; Toshniwal, D. Deep Learning Framework for Forecasting Electricity Demand. Appl. Energy 2019, 238, 1312–1326. [Google Scholar] [CrossRef]
- Kim, T.Y.; Cho, S.B. Predicting residential energy consumption using CNN-LSTM neural networks. Energy 2019, 182, 72–81. [Google Scholar] [CrossRef]
- Wang, X.; Wang, X.; Zhao, Q.; Wang, S.; Fu, L. A multi-energy load prediction model based on deep multi-task learning and an ensemble approach for regional integrated energy systems. Int. J. Electr. Power Energy Syst. 2021, 126, 106583. [Google Scholar]
- Wu, K.; Wu, J.; Feng, L.; Yang, B.; Liang, R.; Yang, S.; Zhao, R. An attention-based CNN-LSTM-BiLSTM model for short-term electric load forecasting in an integrated energy system. Int. Trans. Electr. Energy Syst. 2021, 31, e12637. [Google Scholar] [CrossRef]
- Kim, T.; Lee, D.; Hwangbo, S. A deep-learning framework for forecasting renewable demands using variational auto-encoder and bidirectional long short-term memory. Sustain. Energy Grids Netw. 2024, 38, 101245. [Google Scholar] [CrossRef]
- Maćkiewicz, A.; Ratajczak, W. Principal components analysis (PCA). Comput. Geosci. 1993, 19, 303–342. [Google Scholar] [CrossRef]
- Lee, D.; Seung, H.S. Algorithms for non-negative matrix factorization. Adv. Neural Inf. Process. Syst. 2001, 13, 556–562. [Google Scholar]
- Hinton, G.E.; Salakhutdinov, R.R. Reducing data dimensionality with neural networks. Science 2006, 313, 504–507. [Google Scholar] [CrossRef]
- Ng, A. Sparse autoencoder. Cs294a Lect. Notes 2011, 72, 1–19. [Google Scholar]
- Kingma, D.P.; Welling, M. Auto-Encoding Variational Bayes. arXiv 2013, arXiv:1312.6114. [Google Scholar] [PubMed]
- Kingma, D.P.; Welling, M. An introduction to variational autoencoders. Found. Trends Mach. Learn. 2019, 12, 307–392. [Google Scholar] [CrossRef]
- Zhang, Y.; Yan, B.; Aasma, M. A novel deep learning framework: Prediction and analysis of financial time series using CEEMD and LSTM. Expert Syst. Appl. 2020, 159, 113609. [Google Scholar] [CrossRef]
- Wang, J.; Wang, Z.; Li, J.; Wu, J. Multilevel Wavelet Decomposition Network for Interpretable Time Series Analysis. In Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, London, UK, 19–23 August 2018; pp. 2437–2446. [Google Scholar]
- Dragomiretskiy, K.; Zosso, D. Variational mode decomposition. IEEE Trans. Signal Process. 2013, 62, 531–544. [Google Scholar] [CrossRef]
- Cai, B.; Yang, S.; Gao, L.; Xiang, Y. Hybrid variational autoencoder for time series forecasting. Knowl.-Based Syst. 2023, 281, 111079. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Chen, K.; Chen, K.; Wang, Q.; He, Z.; Hu, J.; He, J. Short-term load forecasting with deep residual networks. IEEE Trans. Smart Grid 2018, 10, 3943–3952. [Google Scholar] [CrossRef]
- Orr, G.B.; Müller, K.R. (Eds.) Neural Networks: Tricks of the Trade; Springer: Berlin/Heidelberg, Germany, 1998. [Google Scholar]
- Goodfellow, I.; Bengio, Y.; Courville, A.; Bengio, Y. Deep Learning; MIT Press: Cambridge, UK, 2016; Volume 1, No. 2. [Google Scholar]
- Ioffe, S.; Szegedy, C. Batch normalization: Accelerating deep network training by reducing internal covariate shift. In Proceedings of the International Conference on Machine Learning, Lille, France, 6–11 June 2015; pp. 448–456. [Google Scholar]
- Doersch, C. Tutorial on variational autoencoders. arXiv 2016, arXiv:1606.05908. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Siami-Namini, S.; Tavakoli, N.; Namin, A.S. The performance of LSTM and BiLSTM in forecasting time series. In Proceedings of the 2019 IEEE International Conference on Big Data (Big Data), Los Angeles, CA, USA, 9–12 December 2019; pp. 3285–3292. [Google Scholar]
- Cheng, H.; Tan, P.N.; Gao, J.; Scripps, J. Multistep-ahead time series prediction. In Advances in Knowledge Discovery and Data Mining, Proceedings of the 10th Pacific-Asia Conference, PAKDD 2006, Singapore, 9–12 April 2006; Proceedings 10; Springer: Berlin/Heidelberg, Germany, 2006; pp. 765–774. [Google Scholar]
- Sorjamaa, A.; Hao, J.; Reyhani, N.; Ji, Y.; Lendasse, A. Methodology for long-term prediction of time series. Neurocomputing 2007, 70, 2861–2869. [Google Scholar] [CrossRef]
- Chevillon, G. Direct multi-step estimation and forecasting. J. Econ. Surv. 2007, 21, 746–785. [Google Scholar] [CrossRef]
- Aras, S.; Kocakoç, İ.D. A new model selection strategy in time series forecasting with artificial neural networks: IHTS. Neurocomputing 2016, 174, 974–987. [Google Scholar] [CrossRef]
- Dickey, D.A.; Fuller, W.A. Distribution of the estimators for autoregressive time series with a unit root. J. Am. Stat. Assoc. 1979, 74, 427–431. [Google Scholar]
- Kwiatkowski, D.; Phillips, P.C.; Schmidt, P.; Shin, Y. Testing the null hypothesis of stationarity against the alternative of a unit root: How sure are we that economic time series have a unit root? J. Econom. 1992, 54, 159–178. [Google Scholar] [CrossRef]
- Ullah, S.; Xu, Z.; Wang, H.; Menzel, S.; Sendhoff, B.; Bäck, T. Exploring clinical time series forecasting with meta-features in variational recurrent models. In Proceedings of the 2020 International Joint Conference on Neural Networks (IJCNN), Glasgow, UK, 19–24 July 2020; pp. 1–9. [Google Scholar]
- Chen, W.; Tian, L.; Chen, B.; Dai, L.; Duan, Z.; Zhou, M. Deep variational graph convolutional recurrent network for multivariate time series anomaly detection. In Proceedings of the International Conference on Machine Learning, Baltimore, MD, USA, 17–23 June 2022; pp. 3621–3633. [Google Scholar]
- Choi, H.; Ryu, S.; Kim, H. Short-term load forecasting based on ResNet and LSTM. In Proceedings of the 2018 IEEE International Conference on Communications, Control, and Computing Technologies for Smart Grids (SmartGridComm), Aalborg, Denmark, 29–31 October 2018; pp. 1–6. [Google Scholar]
- Wu, Z.; Huang, N.E. Ensemble Empirical Mode Decomposition: A Noise-Assisted Data Analysis Method. Adv. Adapt. Data Anal. 2009, 1, 1–41. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).