Enhancing Neural Architecture Search Using Transfer Learning and Dynamic Search Spaces for Global Horizontal Irradiance Prediction
Abstract
1. Introduction
- Dynamic adaptation of the search spaces (DSS): In this study, we progressively refine the search space based on interim best models, preventing the exploration of redundant architectures and speeding up convergence;
- Reduction of exploration time via transfer learning (TL) and extrapolation techniques applied to the learning curve: The knowledge gained by high-performing architectures in initial phases is reused in subsequent generations, thus reducing time and resources, and training for unpromising candidate models is terminated early;
- The design of high-performance architectures through intelligent adaptive exploration.
2. Neural Architecture Search
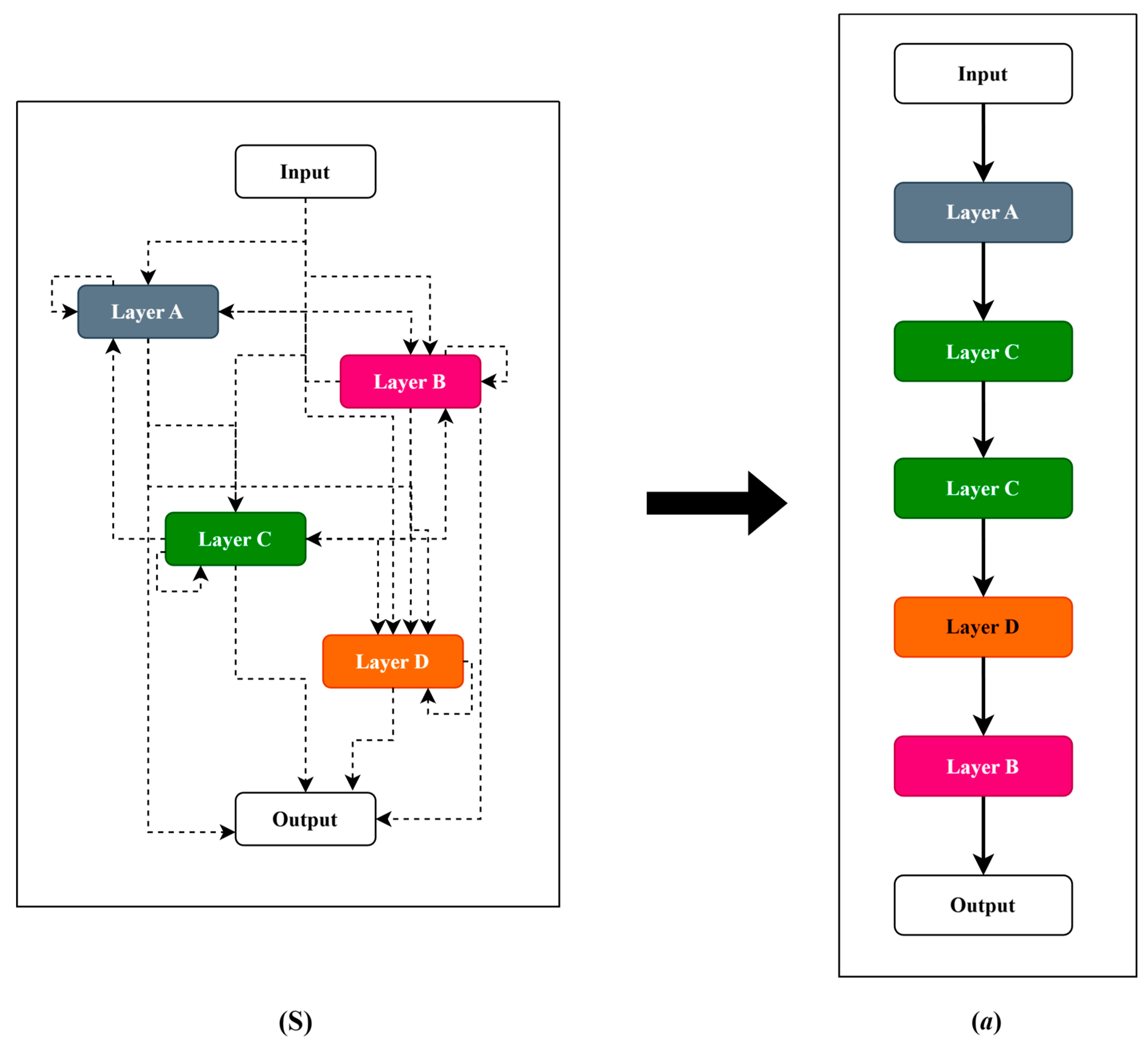
2.1. Architecture Search Space
2.2. Search Strategy
2.3. Performance Estimation Strategy
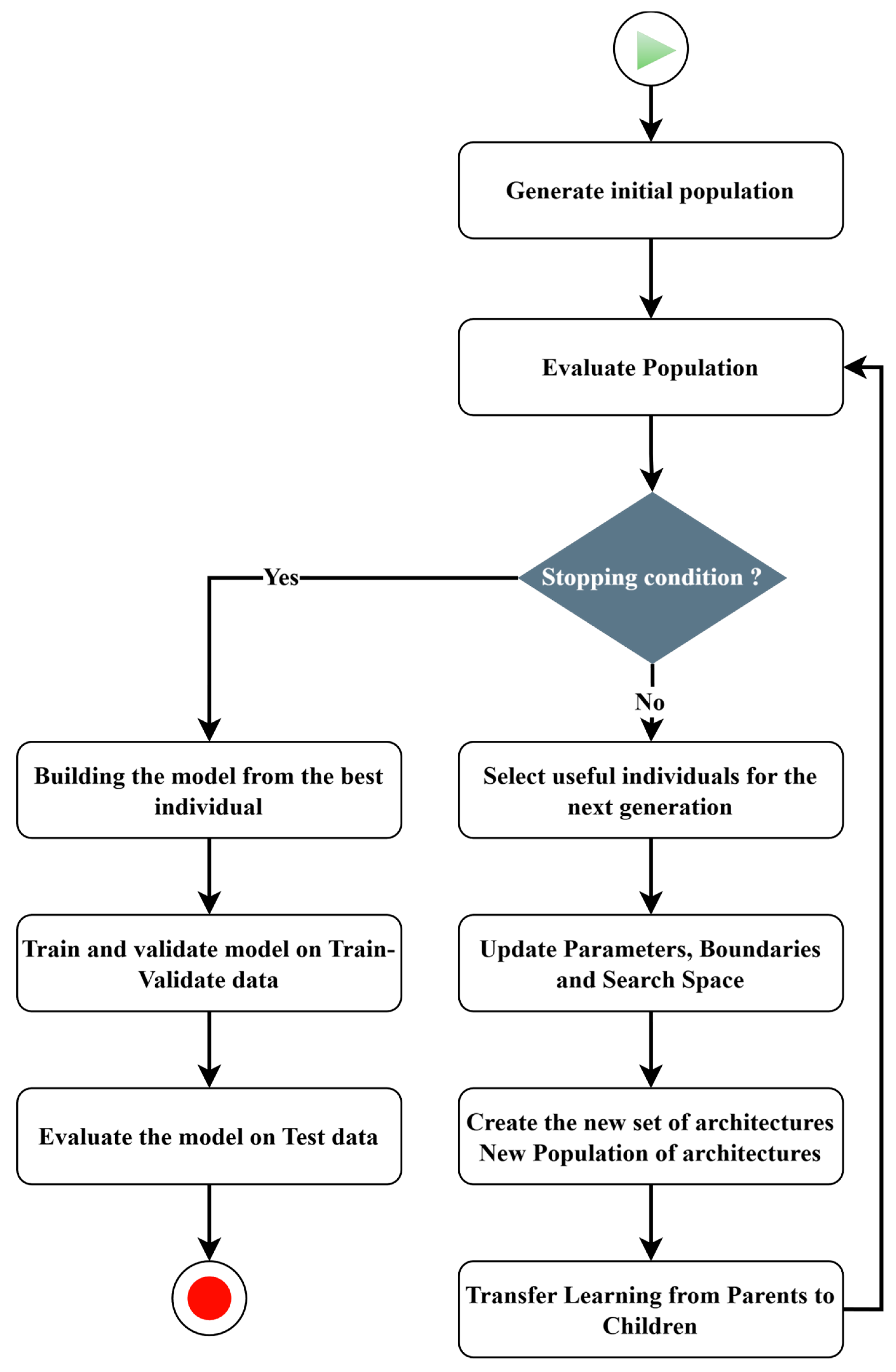
3. Proposed Approach of NAS Application
3.1. LSTM Model
3.2. Metaheuristic Algorithms
3.2.1. Artificial Bee Colony
3.2.2. Genetic Algorithm
3.2.3. Differential Evolution Algorithm
3.2.4. Particle Swarm Optimization
3.2.5. Hyperparameter Encoding and Tuning
- Neurons per input, hidden, and output layer (integer value): Governs model capacity and the bias-variance trade-off;
- Activation function (categorized as ReLU, Sigmoid, or Tanh): Affects nonlinearity, convergence speed, and gradient stability;
- Learning rate (continuous value): Controls weight update magnitude, balancing convergence speed and oscillations;
- Number of stacked LSTM units (integer): Adjusts temporal depth and sequential dependency modeling.
3.3. Solution Approach
| Algorithm 1 Hybrid NAS with Transfer Learning and Dynamic Search Space |
|
Dynamic Search Space (DSS)
3.4. Application and Evaluation
4. Results and Discussion
4.1. Data Acquisition and Modeling
4.1.1. Data Acquisition
4.1.2. Data Modeling
4.2. General Architecture Definition Parameters
4.3. Detailed Results of Four Approaches
4.3.1. Grid Search Results
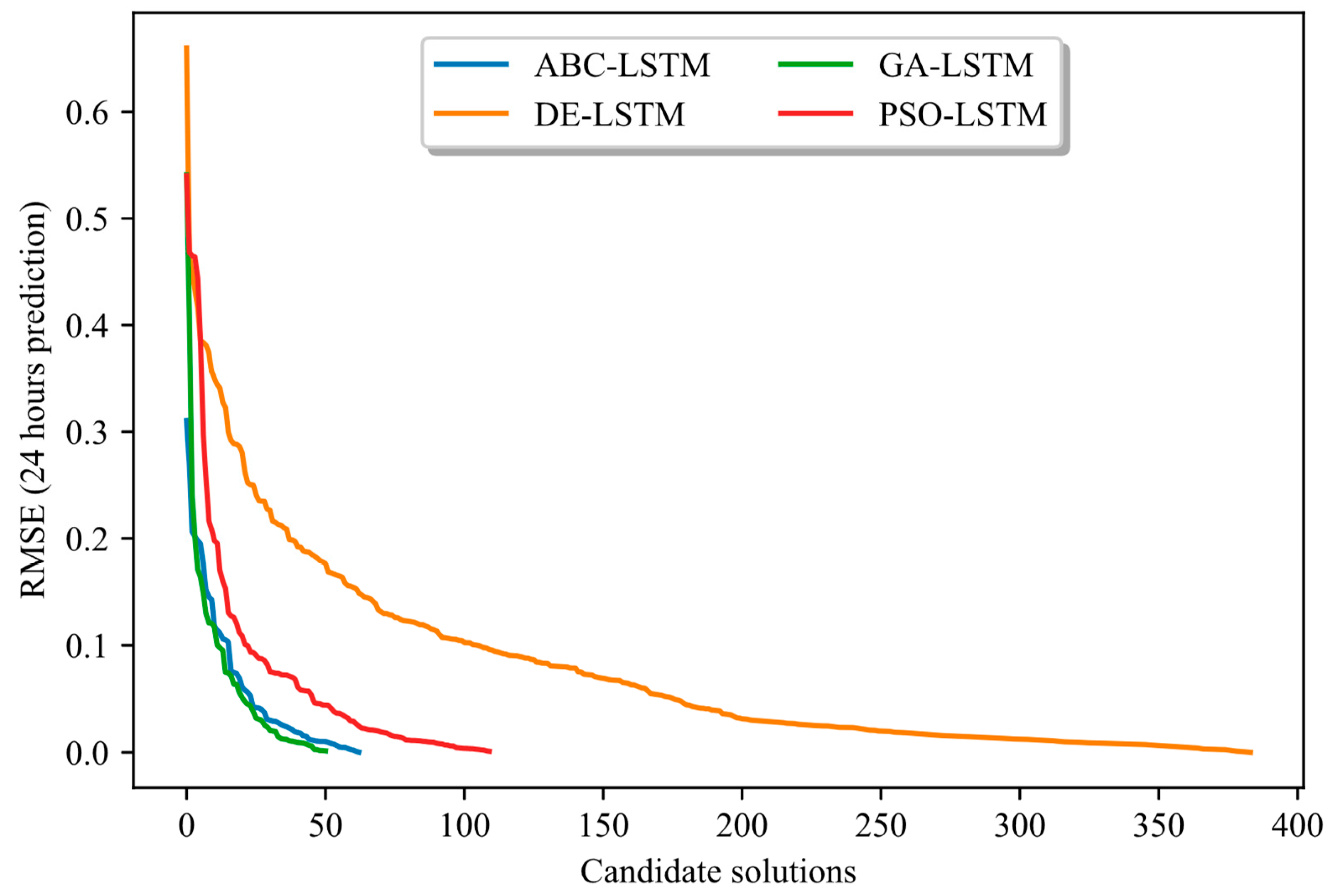
4.3.2. Metaheuristics Results Without TL and DSS
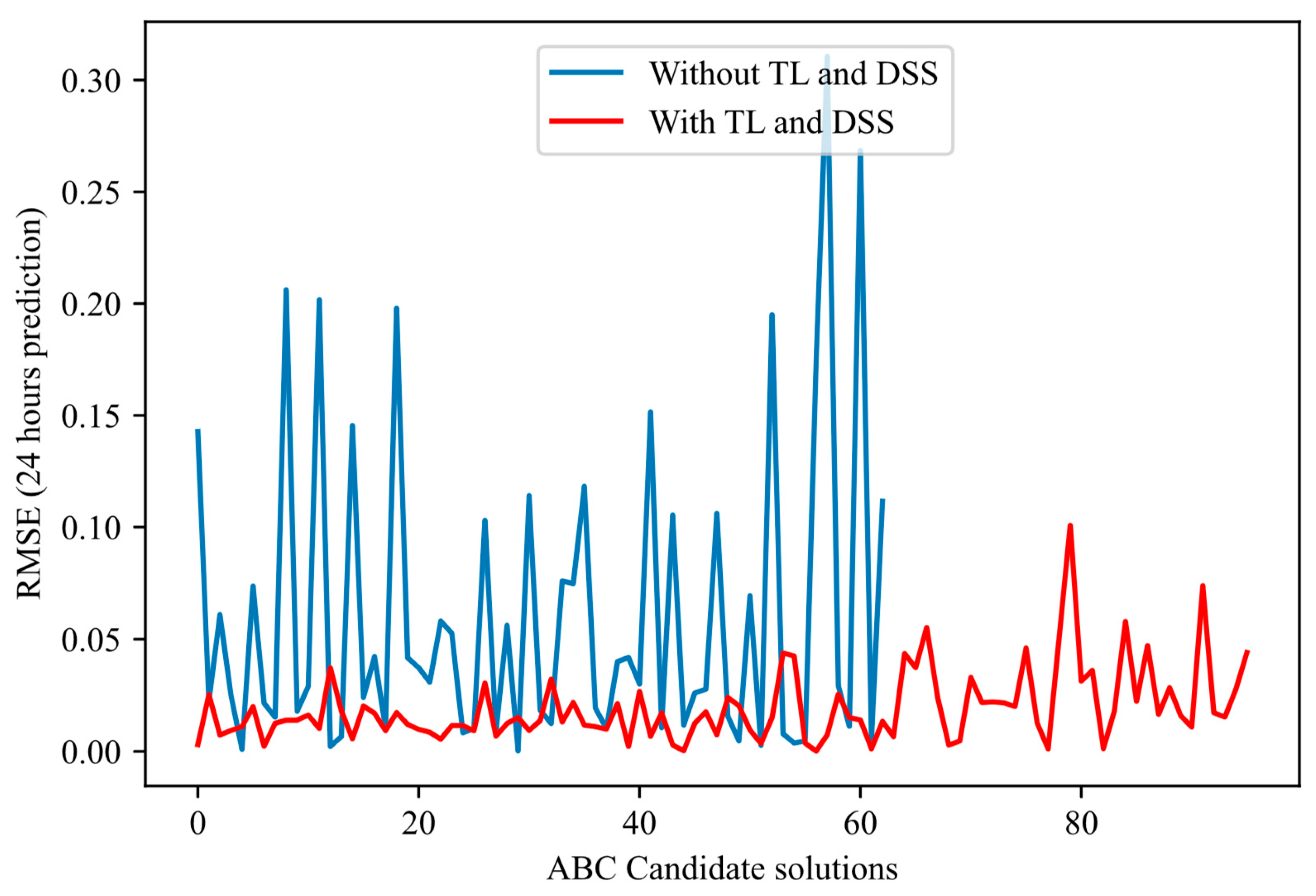
4.3.3. Metaheuristics Results with TL and DSS
4.3.4. Comparison of the Results
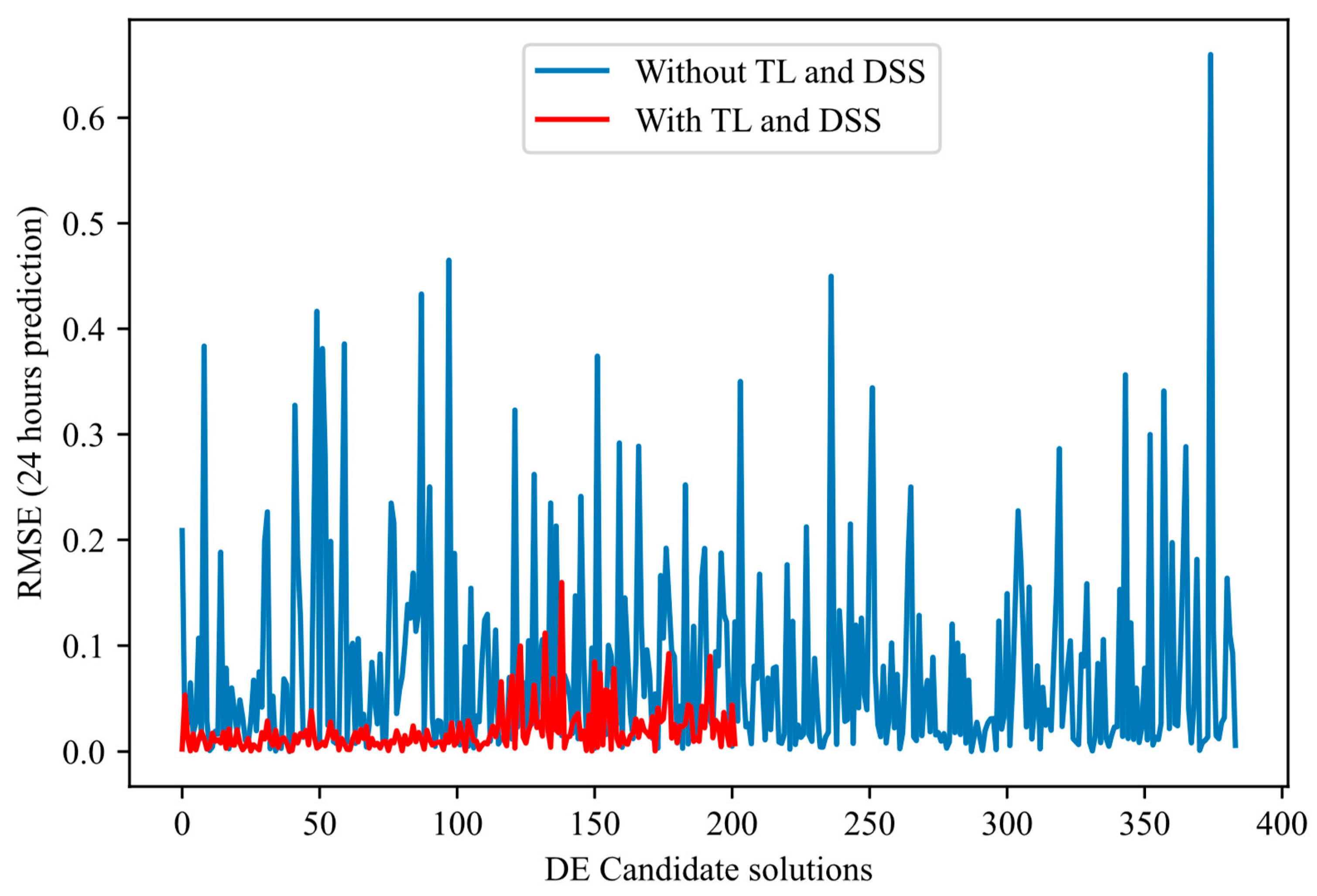
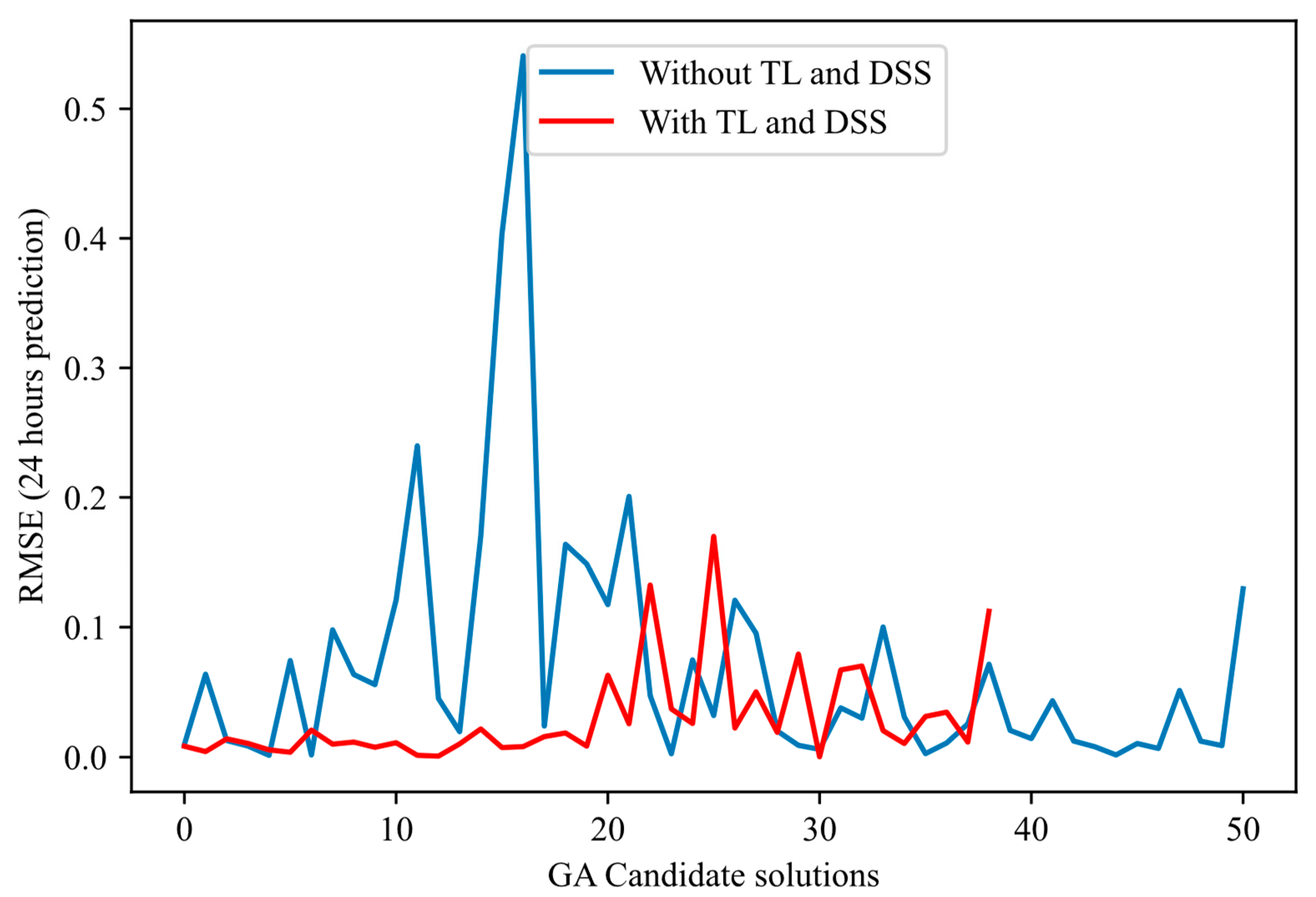
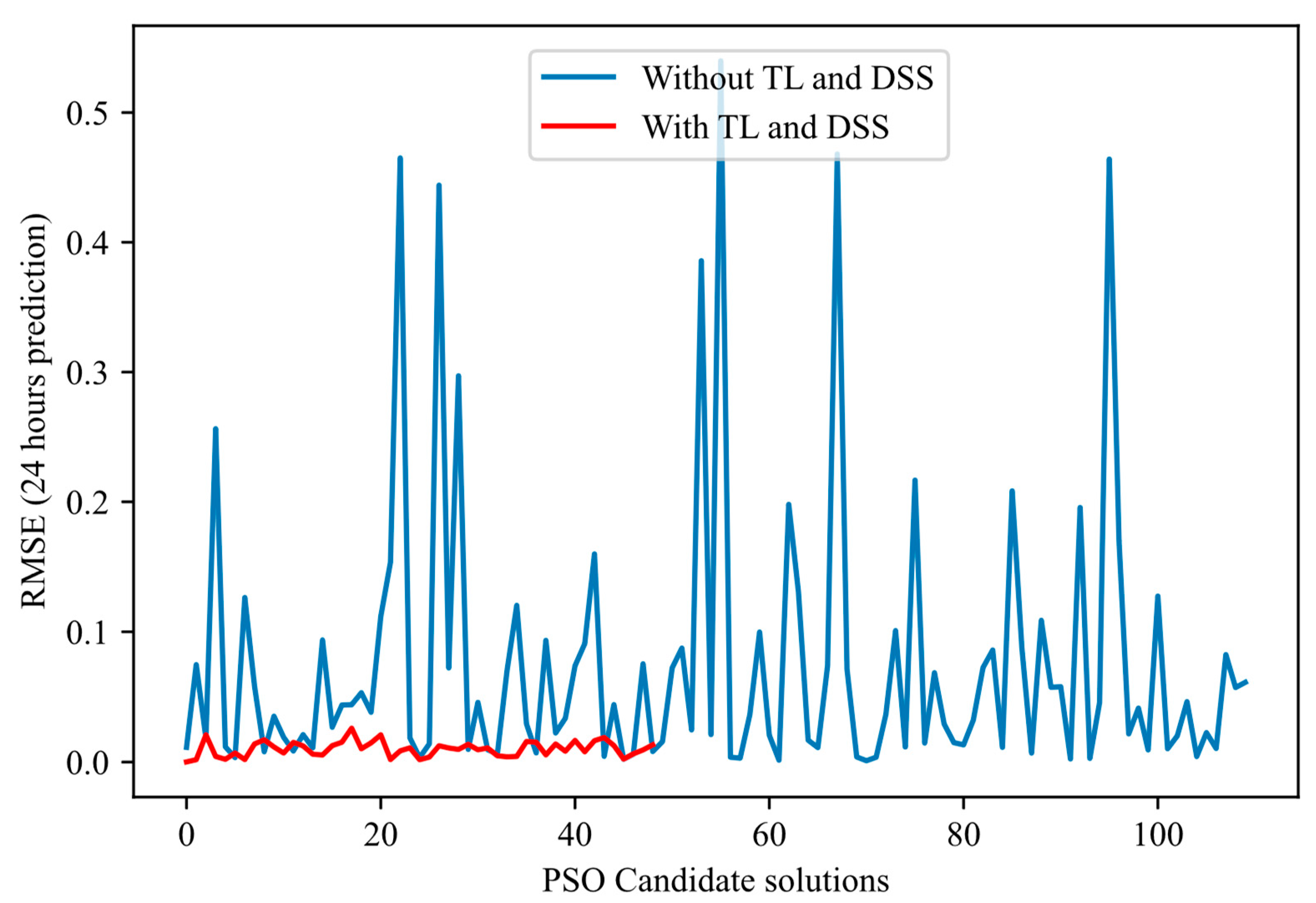
- Converges more quickly: Most of the error reduction occurs within the first 20–30 iterations for the proposed method. In contrast, the basic method often requires more than 50 iterations or even double that to achieve a comparable level of performance.
- Presents reduced variance: The red curves fluctuate much less and have a narrower envelope, reflecting more controlled and reliable progress. In contrast, the blue curves (approach without TL-DSS) frequently show declines and peaks of degradation, indicating ineffective evaluation.
- Achieves a more reliable final RMSE: In each of the figures, the end point of the red curve (approach with TL-DSS) is below that of the blue curve (approach without TL-DSS). This result shows that TL-DSS not only speeds up the search but also produces a more accurate architecture.
4.4. Comparison with Other Research
5. Conclusions
- Dynamic search space (DSS): Progressively refining the search space based on interim best models;
- Speed-up via transfer learning (TL) and learning curve extrapolation: Significantly reducing the NAS run time;
- High-performance architecture design through intelligent adaptive exploration: Balancing speed and predictive accuracy.
- Extending dynamic NAS to Transformer-based time-series models, leveraging their self-attention mechanisms for long-range dependencies;
- Investigating conditional NAS for hybrid CNN–RNN or GNN architectures, allowing the search to jointly select model families and hyperparameters.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| DNN | Deep Neural Network |
| NAS | Neural Architecture Search |
| GHI | Global Horizontal Irradiance |
| TL | Transfer Learning |
| DSS | Dynamic Search Spaces |
| RMSE | Root Mean Squared Error |
| MAE | Mean Absolute Error |
| MSE | Mean Squared Error |
| ABC | Artificial Bee Colony |
| GA | Genetic Algorithm |
| DE | Differential Evolution |
| PSO | Particle Swarm Optimization |
| RNN | Recurrent Neural Network |
| SOTA | State Of The Art |
| MSTL | Multi-seasonal Trend decomposition of Time-Series |
| MCAR | Missing Completely at Random |
| PMM | Predictive Mean Matching |
| SGD | Stochastic Gradient Descent |
| GS | Grid Search |
| MERRA-2 | Modern Era Retrospective Analysis for Research and Applications, Version 2 |
| CPU | Central Processing Unit |
References
- Shawki, N.; Nunez, R.R.; Obeid, I.; Picone, J. On Automating Hyperparameter Optimization for Deep Learning Applications. In Proceedings of the 2021 IEEE Signal Processing in Medicine and Biology Symposium (SPMB), Philadelphia, PA, USA, 4 December 2021; pp. 1–7. [Google Scholar] [CrossRef]
- Sharifi, A.A.; Zoljodi, A.; Daneshtalab, M. TrajectoryNAS: A Neural Architecture Search for Trajectory Prediction. Sensors 2024, 24, 5696. [Google Scholar] [CrossRef]
- Elsken, T.; Metzen, J.H.; Hutter, F. Neural architecture search: A survey. J. Mach. Learn. Res. 2019, 20, 1997–2017. [Google Scholar]
- Liang, J.; Zhu, K.; Li, Y.; Li, Y.; Gong, Y. Multi-Objective Evolutionary Neural Architecture Search with Weight-Sharing Supernet. Appl. Sci. 2024, 14, 6143. [Google Scholar] [CrossRef]
- Chitty-Venkata, K.T.; Emani, M.; Vishwanath, V.; Somani, A.K. Neural Architecture Search Benchmarks: Insights and Survey. IEEE Access 2023, 11, 25217–25236. [Google Scholar] [CrossRef]
- Xie, S.; Zheng, H.; Liu, C.; Lin, L. SNAS: Stochastic neural architecture search. arXiv 2018, arXiv:1812.09926v3. [Google Scholar]
- Niu, R.; Li, H.; Zhang, Y.; Kang, Y. Neural Architecture Search Based on Particle Swarm Optimization. In Proceedings of the 2019 3rd International Conference on Data Science and Business Analytics (ICDSBA), Istanbul, Turkey, 11–12 October 2019; pp. 319–324. [Google Scholar] [CrossRef]
- Mandal, A.K.; Sen, R.; Goswami, S.; Chakraborty, B. Comparative Study of Univariate and Multivariate Long Short-Term Memory for Very Short-Term Forecasting of Global Horizontal Irradiance. Symmetry 2021, 13, 1544. [Google Scholar] [CrossRef]
- OpenWeather. History Bulk weather data—OpenWeatherMap. Available online: https://openweathermap.org/history-bulk (accessed on 9 June 2023).
- Haider, S.A.; Sajid, M.; Sajid, H.; Uddin, E.; Ayaz, Y. Deep learning and statistical methods for short-and long-term solar irradiance forecasting for Islamabad. Renew. Energy 2022, 198, 51–60. [Google Scholar] [CrossRef]
- Chinnavornrungsee, P.; Kittisontirak, S.; Chollacoop, N.; Songtrai, S.; Sriprapha, K.; Uthong, P.; Yoshino, J.; Kobayashi, T. Solar irradiance prediction in the tropics using a weather forecasting model. Jpn. J. Appl. Phys. 2023, 62, SK1050. [Google Scholar] [CrossRef]
- Ranmal, D.; Ranasinghe, P.; Paranayapa, T.; Meedeniya, D.; Perera, C. ESC-NAS: Environment Sound Classification Using Hardware-Aware Neural Architecture Search for the Edge. Sensors 2024, 24, 3749. [Google Scholar] [CrossRef]
- Chitty-Venkata, K.T.; Emani, M.; Vishwanath, V.; Somani, A.K. Neural Architecture Search for Transformers: A Survey. IEEE Access 2022, 10, 108374–108412. [Google Scholar] [CrossRef]
- Jwa, Y.; Ahn, C.W.; Kim, M.J. EGNAS: Efficient Graph Neural Architecture Search Through Evolutionary Algorithm. Mathematics 2024, 12, 3828. [Google Scholar] [CrossRef]
- Baker, B.; Gupta, O.; Raskar, R.; Naik, N. Accelerating neural architecture search using performance prediction. arXiv 2017, arXiv:1705.10823. [Google Scholar]
- Best, N.; Ott, J.; Linstead, E.J. Exploring the efficacy of transfer learning in mining image-based software artifacts. J. Big Data 2020, 7, 59. [Google Scholar] [CrossRef]
- Viering, T.; Loog, M. The Shape of Learning Curves: A Review. IEEE Trans. Pattern Anal. Mach. Intell. 2023, 45, 7799–7819. [Google Scholar] [CrossRef]
- Adriaensen, S.; Rakotoarison, H.; Müller, S.; Hutter, F. Efficient bayesian learning curve extrapolation using prior-data fitted networks. Adv. Neural Inf. Process. Syst. 2024, 36, 19858–19886. [Google Scholar]
- Chandrashekaran, A.; Lane, I.R. Speeding up Hyper-parameter Optimization by Extrapolation of Learning Curves Using Previous Builds. In Proceedings of the Joint European Conference on Machine Learning and Knowledge Discovery in Databases, Skopje, Macedonia, 18–22 September 2017; Springer International Publishing: Cham, Switzerland, 2017; pp. 477–492. [Google Scholar] [CrossRef]
- Zhou, G.; Moayedi, H.; Bahiraei, M.; Lyu, Z. Employing artificial bee colony and particle swarm techniques for optimizing a neural network in prediction of heating and cooling loads of residential buildings. J. Clean. Prod. 2020, 254, 120082. [Google Scholar] [CrossRef]
- Telikani, A.; Tahmassebi, A.; Banzhaf, W.; Gandomi, A.H. Evolutionary machine learning: A survey. ACM Comput. Surv. (CSUR) 2021, 54, 1–35. [Google Scholar] [CrossRef]
- Karaboga, D.; Basturk, B. On the performance of artificial bee colony (ABC) algorithm. Appl. Soft Comput. 2008, 8, 687–697. [Google Scholar] [CrossRef]
- Civicioglu, P.; Besdok, E. A conceptual comparison of the Cuckoo-search, particle swarm optimization, differential evolution and artificial bee colony algorithms. Artif. Intell. Rev. 2013, 39, 315–346. [Google Scholar] [CrossRef]
- Sossa, H.; Garro, B.A.; Villegas, J.; Avilés, C.; Olague, G. Automatic Design of Artificial Neural Networks and Associative Memories for Pattern Classification and Pattern Restoration. In Proceedings of the 2012 Mexican Conference on Pattern Recognition, Huatulco, Mexico, 27–30 June 2012; Springer: Berlin/Heidelberg, Germany, 2012; pp. 23–34. [Google Scholar] [CrossRef]
- Li, G.; Yang, N. A Hybrid SARIMA-LSTM Model for Air Temperature Forecasting. Adv. Theory Simul. 2023, 6, 2200502. [Google Scholar] [CrossRef]
- de Campos Souza, P.V. Fuzzy neural networks and neuro-fuzzy networks: A review the main techniques and applications used in the literature. Appl. Soft Comput. 2020, 92, 106275. [Google Scholar] [CrossRef]
- Grollier, J.; Querlioz, D.; Camsari, K.Y.; Everschor-Sitte, K.; Fukami, S.; Stiles, M.D. Neuromorphic spintronics. Nat. Electron. 2020, 3, 360–370. [Google Scholar] [CrossRef] [PubMed]
- Gao, Y.; Yin, D.; Zhao, X.; Wang, Y.; Huang, Y. Prediction of Telecommunication Network Fraud Crime Based on Regression-LSTM Model. Wirel. Commun. Mob. Comput. 2022, 2022, 3151563. [Google Scholar] [CrossRef]
- Legrene, I.; Wong, T.; Dessaint, L.A. Horizontal Global Solar Irradiance Prediction Using Genetic Algorithm and LSTM Methods. In Proceedings of the 2024 IEEE 19th Conference on Industrial Electronics and Applications (ICIEA), Kristiansand, Norway, 5–8 August 2024; pp. 1–5. [Google Scholar] [CrossRef]
- Dokeroglu, T.; Sevinc, E.; Cosar, A. Artificial bee colony optimization for the quadratic assignment problem. Appl. Soft Comput. 2019, 76, 595–606. [Google Scholar] [CrossRef]
- Yang, Y.; Liu, D. A Hybrid Discrete Artificial Bee Colony Algorithm for Imaging Satellite Mission Planning. IEEE Access 2023, 11, 40006–40017. [Google Scholar] [CrossRef]
- Mehboob, U.; Qadir, J.; Ali, S.; Vasilakos, A. Genetic algorithms in wireless networking: Techniques, applications, and issues. Soft Comput. 2016, 20, 2467–2501. [Google Scholar] [CrossRef]
- Katoch, S.; Chauhan, S.S.; Kumar, V. A review on genetic algorithm: Past, present, and future. Multimed. Tools Appl. 2021, 80, 8091–8126. [Google Scholar] [CrossRef] [PubMed]
- Singsathid, P.; Puphasuk, P.; Wetweerapong, J. Adaptive differential evolution algorithm with a pheromone-based learning strategy for global continuous optimization. Found. Comput. Decis. Sci. 2023, 48, 243–266. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95—International Conference on Neural Networks, Perth, Australia, 27 November–1 December 1995; IEEE: Piscataway, NJ, USA, 1995; Volume 4, pp. 1942–1948. [Google Scholar] [CrossRef]
- Liu, Y.; Sun, Y.; Xue, B.; Zhang, M.; Yen, G.G.; Tan, K.C. A Survey on Evolutionary Neural Architecture Search. IEEE Trans. Neural Netw. Learn. Syst. 2023, 34, 550–570. [Google Scholar] [CrossRef]
- Akmam, E.F.; Siswantining, T.; Soemartojo, S.M.; Sarwinda, D. Multiple Imputation with Predictive Mean Matching Method for Numerical Missing Data. In Proceedings of the 2019 3rd International Conference on Informatics and Computational Sciences (ICICoS), Semarang, Indonesia, 29–30 October 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Bandara, K.; Hyndman, R.J.; Bergmeir, C. MSTL: A Seasonal-Trend Decomposition Algorithm for Time Series with Multiple Seasonal Patterns. arXiv 2021, arXiv:2107.13462. [Google Scholar] [CrossRef]

| Loopback | Batch Size | Optimizer | Activation Function |
|---|---|---|---|
| 12 | 32 | Adam | Sigmoid |
| Method | Iterations | Population Size | Search Time Limit CPU Time (h) |
|---|---|---|---|
| Metaheuristics | 5 and 3 | 10 | – |
| Grid Search | – | 100 |
| Parameters | Boundaries | ||
|---|---|---|---|
| Metaheuristics Without DSS and TL | Metaheuristics with DSS and TL | Grid Search | |
| Number of LSTM layers | 1–3 | – | 1–3 |
| Number of LSTM units | 64–128 | ||
| Learning rate | 0.0001–0.01 | ||
| Dropout rate | 0.0–0.5 | ||
| Method | Test Case | Architecture Depth | Learning Rate | Dropout Rate | RMSE-24 |
|---|---|---|---|---|---|
| GS-LSTM | 1 | 1 | 0.005 | 0.0 | 0.0005 |
| 2 | 1 | 0.0042 | 0.0 | 0.0015 |
| Test Case | Criteria | Forecasting Window (h) | ||||
|---|---|---|---|---|---|---|
| 6 | 12 | 24 | 48 | 72 | ||
| 1 | RMSE | 0.0002 | 0.0003 | 0.0005 | 0.0008 | 0.0011 |
| MAE | 0.0002 | 0.0003 | 0.0004 | 0.0007 | 0.0010 | |
| 2 | RMSE | 0.0006 | 0.0009 | 0.0015 | 0.0027 | 0.0039 |
| MAE | 0.0006 | 0.0009 | 0.0014 | 0.0025 | 0.0035 | |
| Methods | Evaluation Without Transfer Learning and Dynamic Search Space | |||||
|---|---|---|---|---|---|---|
| Depth | Learning Rate | Dropout Rate | RMSE 24 h | MAE 24 h | Relative CPU Time (%) | |
| ABC-LSTM | 3 | 0.0008 | 0.02 | 0.0002 | 0.0002 | 9.12 |
| DE-LSTM | 3 | 0.0066 | 0.3 | 0.0001 | 0.0001 | 100.0 |
| GA-LSTM | 2 | 0.0059 | 0.36 | 0.0014 | 0.0012 | 5.66 |
| PSO-LSTM | 2 | 0.0049 | 0.00 | 0.0010 | 0.0009 | 23.35 |
| Methods | Evaluation with Transfer Learning and Dynamic Search Space | |||||
|---|---|---|---|---|---|---|
| Depth | Learning Rate | Dropout Rate | RMSE 24 h | MAE 24 h | Relative CPU Time (%) | |
| ABC-LSTM | 2 | 0.0054 | 0.07 | 0.0001 | 0.0001 | 37.73 |
| DE-LSTM | 1 | 0.0039 | 0.00 | 0.0005 | 0.0004 | 100.0 |
| GA-LSTM | 2 | 0.0039 | 0.30 | 0.0003 | 0.0003 | 25.72 |
| PSO-LSTM | 1 | 0.0033 | 0.00 | 0.0001 | 0.0001 | 13.42 |
| Methods | Comparison Between GS and DE Without TL and DSS | Comparison Between GS and DE with TL and DSS | ||
|---|---|---|---|---|
| Relative CPU Time (%) | RMSE | Relative CPU Time (%) | RMSE | |
| ABC-LSTM | 9.12 | 0.0002 | 37.73 | 0.0001 |
| DE-LSTM | 100.0 | 0.0001 | 100.0 | 0.0005 |
| GA-LSTM | 5.66 | 0.0014 | 25.72 | 0.0003 |
| PSO-LSTM | 23.35 | 0.0010 | 13.42 | 0.0001 |
| GA-LSTM | 11.94 | 0.0005 | 62.85 | 0.0005 |
| 0.0015 | 0.0015 | |||
| Methods | Comparison Between Approaches Without TL and DSS and Approaches with TL and DSS | ||||
|---|---|---|---|---|---|
| Without | with | CPU Time Reduction (%) | |||
| Relative CPU Time (%) | RMSE | Relative CPU Time (%) | RMSE | ||
| ABC-LSTM | 100.0 | 0.0002 | 78.56 | 0.0001 | 21.44 |
| DE-LSTM | 100.0 | 0.0001 | 18.99 | 0.0005 | 81.01 |
| GA-LSTM | 100.0 | 0.0014 | 86.25 | 0.0003 | 13.75 |
| PSO-LSTM | 100.0 | 0.0010 | 10.91 | 0.0001 | 89.09 |
| Article/Method | Field of Application | NAS Method/Main Algorithm | Major Innovations | Efficiency/Main Performance |
|---|---|---|---|---|
| ESC-NAS [12] | Classification of environmental sounds on the edge | NAS hardware-aware, Bayesian search | Cell search optimized for edge, taking into account hardware constraints | 85.78% (FSC22), 81.25% (UrbanSound8K), compact models for edge |
| EGNAS [14] | Graph Neural Networks (GNN) | Evolutionary NAS, parameter sharing | Fast evolutionary algorithm, weight sharing, step training | Up to 40× faster than SOTA methods, better accuracy on Cora, Citeseer, PubMed |
| Multi-Objective Evolutionary NAS [4] | Image classification (generalized) | Multi-lens evolutionary NAS, supernet | Weight-sharing supernet, MOEA/D bi-population, inter-population communication | Outperforms SOTA on various datasets, increasing diversity and efficiency |
| TrajectoryNAS [2] | Trajectory prediction (autonomous vehicles) | Multi-objective NAS, metaheuristics | End-to-end optimization, precision/latency function, NAS on each component | +4.8% precision, 1.1× less latency on NuScenes compared to SOTA |
| The proposed approach: ENAS-TL-DSS | Time series prediction | Enhanced NAS, evolutionary algorithms, LSTM | Dynamic Search space, learning transfer, learning curve extrapolation | Up to 89.09% of search time reduction, up to 99% prediction accuracy, increasing efficiency |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Legrene, I.; Wong, T.; Dessaint, L.-A. Enhancing Neural Architecture Search Using Transfer Learning and Dynamic Search Spaces for Global Horizontal Irradiance Prediction. Forecasting 2025, 7, 43. https://doi.org/10.3390/forecast7030043
Legrene I, Wong T, Dessaint L-A. Enhancing Neural Architecture Search Using Transfer Learning and Dynamic Search Spaces for Global Horizontal Irradiance Prediction. Forecasting. 2025; 7(3):43. https://doi.org/10.3390/forecast7030043
Chicago/Turabian StyleLegrene, Inoussa, Tony Wong, and Louis-A. Dessaint. 2025. "Enhancing Neural Architecture Search Using Transfer Learning and Dynamic Search Spaces for Global Horizontal Irradiance Prediction" Forecasting 7, no. 3: 43. https://doi.org/10.3390/forecast7030043
APA StyleLegrene, I., Wong, T., & Dessaint, L.-A. (2025). Enhancing Neural Architecture Search Using Transfer Learning and Dynamic Search Spaces for Global Horizontal Irradiance Prediction. Forecasting, 7(3), 43. https://doi.org/10.3390/forecast7030043






