SegmentedCrossformer—A Novel and Enhanced Cross-Time and Cross-Dimensional Transformer for Multivariate Time Series Forecasting

Abstract

Multivariate Time Series Forecasting (MTSF) has been innovated with a series of models in the last two decades, ranging from traditional statistical approaches to RNN-based models. However, recent contributions from deep learning to time series problems have made huge progress with a series of Transformer-based models. Despite the breakthroughs by attention mechanisms applied to deep learning areas, many challenges remain to be solved with more sophisticated models. Existing Transformers known as attention-based models outperform classical models with abilities to capture temporal dependencies and better strategies for learning dependencies among variables as well as in the time domain in an efficient manner. Aiming to solve those issues, we propose a novel Transformer—SegmentedCrossformer (SCF), a Transformer-based model that considers both time and dependencies among variables in an efficient manner. The model is built upon the encoder–decoder architecture in different scales and compared with the previous state of the art. Experimental results on different datasets show the effectiveness of SCF with unique advantages and efficiency.

1. Introduction

Multivariate time series consisting of multiple univariates in different dimensions are of importance in many real-life scenarios. Each univariate represents one specific domain or attribute such as temperature, daily number of passengers in an airport, and so on. As a representative and critical problem in time series, MTSF aims to effectively predict future patterns within a certain period given past time series. In today’s digital era, extensive time series data is ubiquitous in almost every industry, including traffic, retail supply, energy, healthcare, and weather forecasting. Utilization of large-scale time series data enables reasonable forecasting using large deep learning models.

Success in deep learning tasks such as Natural Language Processing (NLP) and Computer Vision (CV) motivates innovations in time series domains along with the launch of models with intricate architectures. Recent generations of Large Language Models (LLMs) capable of NLP tasks such as generating long text [1,2] and machine translation [3] inspire constructions of large models in time series tasks. Derivatives of Transformer architectures with attention mechanisms are on the rise due to the success of Vision Transformer [4] in machine translation. Compared to the classical models like RNNs, Transformers are prominent in recognizing relations among segments given long sequences of text. Furthermore, the influence of positional information is also considered by attention mechanisms, so that the relationships among segments in any position can be extracted.

Inspired by the classical Transformer [4] for machine translation with benchmark datasets, subsequent models attain great performances in domains including image classification [5,6], machine translation, and video processing [7] with even smaller datasets [8] under limited circumstances. However, in large models with millions of parameters, costs of attention architectures are prohibitive with gigantic datasets [9]. To alleviate computational constraints, a series of Transformer-based architectures are developed with abilities to improve performance in particular scenarios. Through thoughtful pretraining procedures, large models are expected to produce excellent results in downstream tasks with smaller datasets.

The hidden potential of Transformers promotes the boom of deep learning models. At present, Transformer-based architecture is still in the stage of inception and needs improvements in various aspects. Several popular Transformer-based models such as FEDformer [10], Autoformer [11], Reformer [12], and Informer [13] have achieved state-of-the-art performance with sophisticated architectures that replace full attention mechanisms. However, to reduce the computational complexity in large-scale models, those models do not fully consider the dependencies in both temporal domains and dimensions. Some of them, such as [14], capture only the temporal dependencies in each univariate separately. To address such problems, we propose a novel approach that captures the dependencies in both time and dimensions among variables. Compared to the preceding state of the art, our model (i) considers dependencies for time series in each time point and correlations among the univariates, (ii) contains a novel algorithm for cross-time self-attention to extract significance of a variate along with other univariates in a certain history, and (iii) proposes an efficient encoder–decoder architecture to deal with forecasting problems that is compared to previous Transformer-based models. To make comparison with baselines, we conduct experiments with benchmark datasets in state-of-the-art models, and experimental results show the effectiveness of our model in MTSF problems.

The rest of the paper is organized as follows: Section 2 gives an overall literature review for models related to time series forecasting. Section 3 elaborates details of our methods including architecture and mathematical formulas. In Section 4, we show experiments for implementation of our proposed methods including datasets, experiment setup, as well as analysis and discussions of results. Finally, we conclude our work in Section 5. In the Appendix A.1, we elaborate the pseudocode for our methods and present comprehensive results on baselines as well as ablation studies.

2. Related Work

Research on time series tasks has made significant progress through the development of various architectures, ranging from early statistical methods to deep learning approaches such as Recurrent Neural Networks (RNNs) [15,16], Graph Neural Networks (GNNs) [17], Long Short-Term Memory (LSTM) networks [18], and, more recently, Transformer-based models. To address the lack of large-scale datasets in specific domains, generative pretraining using data from various domains through Foundation Models (FMs) enables effective transfer learning by fine-tuning on limited domain-specific data. Specifically, representation learning explores the characteristic and periodicity of time series, by which the models can be applied in downstream tasks. Compared to text with long sequences, time series data are more complicated with seasonal trends and continuous values rather than linguistic long sequences consisting of vocabularies with semantic information. To address the challenges of effective learning capabilities, a series of methods for new models along with enhanced algorithms based on existing models and optimization techniques are proposed.

Multivariate Time Series Forecasting (MTSF). Multivariate time series consist of multiple univariates, represented as sequences of numerical values for different specific dimensions over time domains. For example, an MSTF dataset of the climate consists of information about climate conditions including, but not limited to, temperatures, humidity, air pressure, wind speed, etc. over a period in a particular region, recorded in diverse time units such as minutes, hours, days, weeks, and so on. However, as mentioned earlier, MTSF over long-term history poses many challenges. Unlike text sequences in NLP and image pixels in CV, Multivariate Time Series (MTS) contain temporal dependencies over time as well as correlations between dimensions compared to univariate time series tokens. Thus, to address the challenges in MTSF tasks, novel methods proposed for representation learning explore trends in time series over the time domain and decomposition strategies that split MTS into smaller segments or patches for efficient computations [10,19].

Classical Architectures. Explorations into time series forecasting originate from the early classic methods [20]. Different from image pixels in CV or sequences of text tokens in NLP, performance of time series tasks is affected by seasonal patterns over time. To address such challenges, a variety of architectures [15,16,17,18] for time series were proposed over the last two decades. In the early stages, a series of traditional statistical methods were proposed, including Exponential Smoothing (ETS) [21] and Auto-Regressive Moving Averages (ARMA) [22]. While such classical benchmarks have been widely used in early studies, several recent works on Transformer-based time series forecasting [10,11,13] have adopted the convention of comparing only against state-of-the-art deep learning models, not statistical or naive methods. This is primarily because (i) the performance gap between statistical models and modern deep architectures on high-dimensional, non-linear, and multivariate tasks is already well-established, (ii) Transformer-based models are explicitly designed to address the shortcomings of both traditional statistical and RNN-based methods by modeling long-range dependencies and cross-variable interactions using attention mechanisms, and (iii) Statistical baselines such as ARIMA or ETS are inherently incapable of handling large-scale multivariate sequences with missing values, non-stationarity, or spatio-temporal structures, which are central to the current task formulations.

In recent years, extensive development of deep learning has led to the emergence of models in time series tasks, too. For example, a couple of recurrent-neural-network-based methods are DeepAR [23] and LSTNet [24] that are based on RNN architecture that considers recurrence of the output as the input for next time step. To address long-time recurrent backpropagation, LSTM [18] is proposed with computational complexity of $\mathcal{O}\left(1\right)$ in each time step, and subsequent variants, such as the Gated Recurrent Unit (GRU) [25], simplifies the LSTM framework and further reduces the complexity of computation. To adapt to time series, convolutional-neural-network-based methods such as TCN [25] include convolutions for learning dependencies. For graph-neural-network-based methods, MTGNN [17], StemGNN [26], AGCRN [27], etc. are proposed for long time series forecasting.

Transformers. Transformer-based methods have already made significant progress in NLP and CV tasks, following the introduction of Transformers [4] in machine translation. However, quadratic computational complexity versus sequence length for tokens over vanilla Transformers leads to prohibitively expensive computational burdens in long-term time series sequences. In addition, more effective architecture needs to handle long time series with more complicated patterns. To address such challenges, a series of enhanced Transformer-based methods are proposed for MTSF cases. For example, Autoformer [11] proposes a novel decomposition algorithm with autocorrelation for long-term forecasting, capturing dependencies and seasonal patterns with decomposition blocks within the encoder. In contrast, FEDformer [10] proposes a different seasonal-trend decomposition block with Fourier transform to solve the lack of a global view of time series caused by expensive memory costs. To deal with memory bottlenecks in full attention, recent works propose efficient models to capture intricate patterns in MTS. For example, Ref. [28] proposes a LogSparse Transformer with cost of $\mathcal{O}(L{(log L)}^2)$ with convolutional self-attention that yields queries and keys by casual convolution that enables local context incorporated into attention. Later, Informer [13] further broke the memory bottleneck by the ProbSparse self-attention mechanism, achieving $\mathcal{O}\left(L\mathit{log}L\right)$ computational complexity. Furthermore, FEDformer [10] and Pyraformer [29] achieve $\mathcal{O}\left(L\right)$ regarding sequence L. The former proposes the attention-based blocks for decomposition and capturing patterns, and the latter introduces a pyramid-based architecture called a Pyramidal Attention Module (PAM) that learns dependencies in intra- and inter-scales at different resolutions. Interestingly, PatchTST [14] splits input time series into patches and separates each channel to learn features with shared embedding and Transformer blocks. Similarly, Crossformer [30] also splits time series sequences into segments and learns dependencies with intermediate routers for efficient computations. In addition, other Transformer-based models such as [9,12] achieve state-of-the-art performance by proposed novel methods for self-attention for downstream tasks. A host of related recent architectures are found in [31].

Despite significant progress of models in time series forecasting, there are still challenges that need further improvements. For example, N-BEATS [32] handles only univariate time series forecasting with residual links and deep fully connected layers. PatchTST [14] separates multivariate time series into independent channels that share the same embedding and Transformer weights. However, independent channels are unable to interact with each other. Crossformer [30] attempts to learn relationships between segments but only with a few intermediate routers for efficient computation that cannot fully capture dependencies. Other methods such as Autoformer [11] and FEDformer [10] solve the MSTF problems with complicated algorithms for decomposition or for partial attention among all segments.

To address these challenges, we propose a new method to bridge the gap. This new method makes contributions to MSTF, including: (1) proposing an effective novel Transformer-based method for multivariate time series forecasting, (2) enhancing the performance of the state of the art by a novel strategy that captures dependencies of information in cross-time and cross-dimension efficiently, and (3) offering a foundation model for future related tasks in the time series domain.

3. Methodology

Multivariate Time Series Forecasting (MTSF) aims to make a prediction of future values for time series given a certain history. In MTSF, time series have multiple univariates, each of which represents a variable or an attribute depending on scenarios. With well-organized time series data, forecasting can be performed in different temporal granularities. In cases where long-term dependencies are necessary, time series within tiny granularities are recorded over a long history. To perform long-term forecasting, dependencies are captured, and temporary granularity varies in practice, ranging from hours in stock price to days in weather forecasting.

Problem Definition. Suppose the given history is ${\mathit{x}}_{1:T}\in {\mathbb{R}}^{T\times D}$, where T is the number of time steps for the past time and $D>1$ is the dimension in each time step. The goal of MTSF is to predict future values of time series ${\mathit{x}}_{T+1:T+\tau }\in {\mathbb{R}}^{\tau \times D}$ where $\tau$ is the number of time steps in the future. Specifically, in MTSF, $D$ is greater than 1.

To process multivariate time series, we first split the input time series into segments and then perform embedding operations for each segment in the embedded dimension. Then, inspired by Crossformer [30], we propose a new enhanced Two-Stage Attention (TSA) that considers dependencies for one dimension in history and for the other dimensions. Like the classical Transformer [4], our model is also an encoder-and-decoder structure with enhanced TSA equipped. Like the Hierarchical Encoder-and-Decoder (HED) structure constructed in [30], our model captures information in Multivariate Time Series (MTS) in different scales with multiple blocks of encoders and decoders before final forecasting.

Figure 1 above depicts the overall architecture of our model with the main components, each of which is expanded and further illustrated in subsequent sections.

Figure 1. Overall architecture of our Method: (a) Segment-Wise Embedding, (b) Positional Embedding, (c) Hierarchical Encoder–Decoder (HED), (d) MLP Head.

3.1. Time Series Segment-Wise Embedding

A multivariate time series in a time step is represented by a $T\times D$ vector ${\mathit{x}}_{1:T}\in {\mathbb{R}}^{T\times D}$ where T is the number of time steps for history and D is the dimension or number of univariates for MTS. Like Transformers for the previous state of the art [5,8,9,10,11,12,13,14], MTS is embedded into large dimensions before the stage of attentions that capture dependencies across time. That is, given input MTS ${\mathit{x}}_{1:T}\in {\mathbb{R}}^{T\times D}$ in a time step T, the algorithm embeds the time series point at each time step into an embedded vector: ${\mathit{x}}_t\to {\mathit{h}}_t$, ${\mathit{x}}_t\in {\mathbb{R}}^D$, ${\mathit{h}}_t\in {\mathbb{R}}^{d_{model}}$ where $1<t<T$, ${\mathit{x}}_t$ and ${\mathit{h}}_t$ represent the vector for time series and embedded vector at time t. Thus, an MTS ${\mathit{x}}_{1:T}\in {\mathbb{R}}^{T\times D}$ is embedded into T vectors $\left\{ {\mathit{h}}_1,{\mathit{h}}_2,{\mathit{h}}_3,\dots ,{\mathit{h}}_T \right\}$. Figure 2 below shows the process of segmentation for embedded vectors.

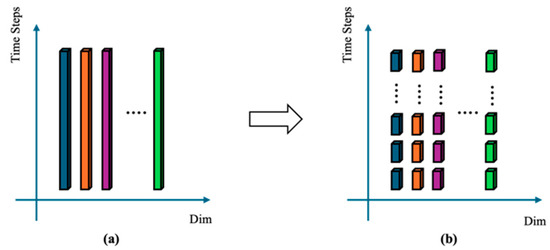
Figure 2. Segment-Wise Embedding: (a) Embedded vectors for input time series after embedding layer, (b) Segmented embedded vectors: Embedded vectors are further split into small segments given segment length $L_{seg}$. Vectors in different color represent different dimensions.

Dimension-Wise Segmentation. We propose a segment-wise method that embeds time series in segments. That is, given input MTS ${\mathit{x}}_{1:T}\in {\mathbb{R}}^{T\times D}$ in a time step T and a segment length $L_{seg}$, our method first transposes and represents the input time series in a D-dimensional vector ${\mathit{x}}_{1:T}= \left\{{\mathit{x}}_1,{\mathit{x}}_2,{\mathit{x}}_3,\dots ,{\mathit{x}}_D\right\}$, where ${\mathit{x}}_d\in {\mathbb{R}}^T$ and $1\le d\le D$, and contains all values of the same dimension across the time step T.

Then, given the segment length $L_{seg}$, each vector ${\mathit{x}}_d\in {\mathbb{R}}^T$ is divided into ${\displaystyle \frac{T}{L_{seg}}}$ segments, assuming that T is divisible by $L_{seg}$. Mathematical representation of segments in each dimension is shown in Equation (1):

$${\mathbf{x}}_{1:T}={\mathbf{x}}_{1:D}=\left\{{\mathbf{x}}_{i,s} | 1\le i\le D,1\le s\le {\displaystyle \frac{T}{L_{seg}}}\right\},$$

(1)

where $i$ denotes the i-th dimension in the MTS and s represents the s-th segment in the dimension $i$ so the set ${\mathbf{x}}_{i,s}$ aggregates all $s$ temporal segments of a particular dimension $i$ over all dimensions. Mathematically, ${\mathbf{x}}_{1:D}$ is the transpose of ${\mathbf{x}}_{1:T}$.

Cross-time Dimension Embedding. With the segmentation of input MTS, all segments are then embedded into vectors with a higher dimension as defined in $d_{model}$, represented as an embedded dimension. For each ${ \mathit{x}}_{i,s} \in {\mathbb{R}}^{L_{seg}}$, which is the s-th segment in i-th dimension, we follow the same embedding algorithm in [30] to embed each segment into the vector by linear projection followed by a position embedding, as shown in Equation (2),

$${\mathbf{h}}_{i,s}=\mathbf{E}{\mathbf{x}}_{i,s}+{\mathbf{E}}_{i,s}^{\left(pos\right)},$$

(2)

In Equation (2), $\mathbf{E}\in {\mathbb{R}}^{d_{model}\times L_{seg}}$ is the learnable embedding vector for linear projection and ${\mathbf{E}}_{i,s}^{\left(pos\right)}\in {\mathbb{R}}^{d_{model}}$ is the learnable vector for position embedding for each segment in position $(i,s)$. After the stage of embedding, input MTS is embedded into a 2D vector $\mathbf{H}=\{{\mathbf{h}}_{i,s}\in {\mathbb{R}}^{d_{model}}|1\le i\le D,1\le s\le {\displaystyle \frac{T}{L_{seg}}}\}$, where ${\mathbf{h}}_{i,s}$ represents the univariate embedding vector for each segment ${\mathbf{x}}_{i,s}$ that denotes a segment of multivariate time series for the i-th dimension over the time segment of length $L_{seg}$, and $\mathbf{H}\in {\mathbb{R}}^{T\times d_{model}}$ is the embedding vector of MTS in segments.

3.2. Two-Stage Attention

Embedded 2D vectors obtained from embedding are utilized for self-attention in Transformers [5] with various algorithms for attention in encoder and decoder blocks. Given a 2D embedding vector, classical Transformers like ViT [5] and Swin Transformer [33] flatten 2D arrays into a 1D vector and feed it into Transformer blocks. However, simply flattening an embedding array for long-term time series data into a 1D array is prohibitive for the attention stage, causing computational cost $\mathcal{O}\left(N^2\right)$ for input length N.

We propose a novel enhanced Two-Stage Attention (TSA) consisting of a multistep process with Multihead Attention (MSA) by considering attention for both the univariate itself in the past time domain and influences on other univariates. Compared to TSA proposed in [30], our method consists of two stages to capture dependencies in both cross-time and cross-dimension by segments of embedding vectors instead of intermediate routers to collect information to reduce complexity. The overall architecture of TSA is shown in Figure 3.

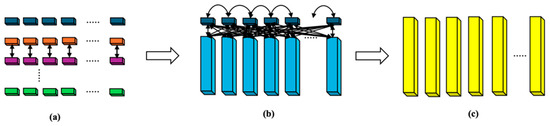
Figure 3. Architecture of TSA for one dimension: (a) Cross-time Stage, (b) Cross-dimension Stage, (c) Output of TSA Stage. Vectors in different color represent different dimensions.

Attention. Attention [4] is the function of mapping the query and key–value pairs to output as the weighted sum of values, with query, key, and values all in vectors. Given query Q, together with keys and values K and V, the output of attention is computed as:

$$\mathrm{A}\mathrm{t}\mathrm{t}\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}\left(Q,K,V\right)=\mathrm{s}\mathrm{o}\mathrm{f}\mathrm{t}\mathrm{m}\mathrm{a}\mathrm{x}({\displaystyle \frac{Q{K}^T}{\sqrt{d_k}}})V,$$

(3)

To use attention in our method, we follow the operations in [4] for the attention function. For more information, one can also find details in [4].

Multi-head Self-Attention. To perform multiple attention functions with queries, keys, and values simultaneously, MSA deploys the group of queries, keys, and values with learnable linear projections with dimensions $d_k$, $d_k$, and $d_v$, respectively. Each attention function has its own version of queries, keys, and values and produces output values in dimension $d_v$. With $h$ attention functions working in parallel, the output of each is concatenated and further projected to form the result value.

Instead of single attention, MSA allows attention for information with more interpretations of information in different positions. Given $h$ attention functions in parallel, the mathematical representation of MSA is described as follows:

$$\mathrm{M}\mathrm{u}\mathrm{l}\mathrm{t}\mathrm{i}\mathrm{H}\mathrm{e}\mathrm{a}\mathrm{d}\left(Q,K,V\right)=\mathrm{C}\mathrm{o}\mathrm{n}\mathrm{c}\mathrm{a}\mathrm{t}\left({\mathrm{h}\mathrm{e}\mathrm{a}\mathrm{d}}_1,{\mathrm{h}\mathrm{e}\mathrm{a}\mathrm{d}}_2,\dots ,{\mathrm{h}\mathrm{e}\mathrm{a}\mathrm{d}}_h\right)W^O,$$

(4)

$$\mathrm{w}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{e} {\mathrm{h}\mathrm{e}\mathrm{a}\mathrm{d}}_{\mathrm{i}}=\mathrm{A}\mathrm{t}\mathrm{t}\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}\left(Q{W}_i^Q,K{W}_i^K,V{W}_i^V\right),$$

(5)

where $W_i^Q\in {\mathbb{R}}^{d_{model}\times d_k}$, $W_i^K\in {\mathbb{R}}^{d_{model}\times d_k}$, $W_i^V\in {\mathbb{R}}^{d_{model}\times d_v}$, and $W^O\in {\mathbb{R}}^{h{d}_v\times d_{model}}$ are weights of matrices for query Q, key K, and value V for linear projections and h is the number of parallel attention functions or heads. In general cases, one uses $d_k=d_v=d_{model}/h$ for dimensions in weights of Q, K, and V, respectively, for each head.

Cross-Time Stage. Embedded vectors in segments from the embedding layer are evaluated in TSA operations in an encoder and decoder structure with multiple stages. Instead of using intermediate routes with MSA in Crossformer [30], we propose a novel two-stage attention that performs cross-time dimensions by MSA with embeddings for a univariate with its history and with other univariates in order. Given a 2D embedding in sequences of length $L_{seg}$, in the first stage, our method performs MSA in segments for each univariate separately. Suppose the 2D embedding vector is given in $\mathbf{H}=\{{\mathit{h}}_{i,s}\in {\mathbb{R}}^{d_{model}}| 1\le i \le D, 1\le s\le {\displaystyle \frac{T}{L_{seg}}} \}$, the output vector of MSA for each dimension is shown in Equation (6) below:

$${\mathit{c}\mathit{r}\mathit{o}\mathit{s}\mathit{s}\mathit{t}\mathit{i}\mathit{m}\mathit{e}}_i=\mathrm{M}\mathrm{S}\mathrm{A}\left({\mathbf{h}}_{i,:}{\mathbf{h}}_{i,:},{\mathbf{h}}_{i,:}\right)\mathrm{where} 1\le i\le D,$$

(6)

Specifically, ${\mathrm{h}}_{i:}$ denotes the embedded vectors of the i-th dimension in segments, where ${\mathit{h}}_i=\{{\mathbf{h}}_{i,s}\in {\mathbb{R}}^{d_{model}}|1\le s\le {\displaystyle \frac{T}{L_{seg}}}\}$ for each $i$ between 1 and D.

By MSA, we follow a similar structure for the cross-time stage in [30] but with our method to deal with attention for each univariate with its given history:

$${\tilde{\mathbf{Y}}}_{i,:}^{time}=\mathrm{L}\mathrm{a}\mathrm{y}\mathrm{e}\mathrm{r}\mathrm{N}\mathrm{o}\mathrm{r}\mathrm{m}\left({\mathit{h}}_{i,:}+{\mathit{c}\mathit{r}\mathit{o}\mathit{s}\mathit{s}\mathit{t}\mathit{i}\mathit{m}\mathit{e}}_i\right),$$

(7)

$${\mathbf{Y}}_{i,:}^{time}=\mathrm{L}\mathrm{a}\mathrm{y}\mathrm{e}\mathrm{r}\mathrm{N}\mathrm{o}\mathrm{r}\mathrm{m}\left({\tilde{\mathbf{Y}}}_{i,:}^{time}+\mathrm{M}\mathrm{L}\mathrm{P}\left({\tilde{\mathbf{Y}}}_{i,:}^{time}\right)\right)$$

(8)

Equation (8) produces the output of the stage for each univariate. To get the final output of the cross-time stage, all ${\mathbf{Y}}_{i,:}^{time}$ are concatenated as follows:

$${\mathbf{Y}}^{time}=\mathrm{C}\mathrm{o}\mathrm{n}\mathrm{c}\mathrm{a}\mathrm{t}({\mathbf{Y}}_{1,:}^{time},{\mathbf{Y}}_{2,:}^{time},\dots ,{\mathbf{Y}}_{D,:}^{time}),$$

(9)

The output of this stage is in the same dimension as the 2D input embedding vector $\mathbf{H}$ such that ${\mathbf{Y}}^{time}\in {\mathbb{R}}^{D\times d_{model}}$.

Cross-Dimension Stage. In our method, the second stage in TSA captures dependencies between one univariate and other univariates in the time domain. Instead of a small number of intermediate routers, we apply MSA in ${\mathit{Y}}^{time}$ from the cross-time stage with embedded vectors of other univariates. To reduce the complexity of computation, groups of segments for other univariates are linearly projected from dimension $\left(D-1\right)$ to a 1-dimensional vector, resulting in computational complexity of $\mathcal{O}\left(D\right)$ instead of $\mathcal{O}\left(D^2\right)$.

The stage consists of two sub-stages. The first sub-stage takes 2D embedding vector $\mathbf{H}$ and extracts the segments of the embedding vector for other univariates. That is, for the i-th dimension, segments of embedding vectors for other dimensions except $i$ are extracted for the attention function as follows:

$${\mathbf{H}}_i^{\ast }=\left\{h_{d,s}\in \mathbf{H}|1\le d\le D,d\ne i,1\le s\le {\displaystyle \frac{T}{L_{seg}}}\right\},$$

(10)

On the other hand, ${\mathbf{H}}_i^{\ast }$ consists of all segments in the embedding vector $\mathbf{H}$ except those in i-th dimension such that ${\mathbf{H}}_i^{\ast }\in {\mathbb{R}}^{(D-1)\times d_{model}}$ and, for each $i$, $h_{i,1},h_{i,2},\dots ,h_{i,s}$ are omitted from ${\mathbf{H}}_i^{\ast }$, where $1\le s\le {\displaystyle \frac{T}{L_{seg}}}$. To reduce the complexity, we apply linear projection with learnable weights in ${\mathbf{H}}_i^{\ast }$ for MSA in the next sub-stage. Suppose ${\mathbf{H}}_i^{\ast }\in {\mathbb{R}}^{(D-1)\times d_{model}}$ for each $i$, the linear projection is described in the following equation:

$${\overline{\mathbf{Y}}}_i=W_i{\mathbf{H}}_i^{\ast }+b,$$

(11)

where $W_i\in {\mathbb{R}}^{d_{model}\times (D\dot{-}1)}$ and $b\in {\mathbb{R}}^{d_{model}}$ represent the weight matrix and bias for each ${\mathbf{H}}_i^{\ast }$.

The second sub-stage takes the linear projection of ${\mathit{H}}_i^{\ast }$ as input with the output of cross-time stage ${\mathit{Y}}^{time}$ and applies MSA to capture dependencies for other univariates in the time domain. With the final output of the previous stage ${\overline{\mathit{Y}}}_i$ as input for each $i$, we propose a similar structure in Crossformer with our method for MSA. The mathematical representation of this stage is described below:

$${\mathbf{T}}_i=\mathrm{M}\mathrm{S}\mathrm{A}({\mathbf{Y}}_{i,:}^{time},{\overline{\mathbf{Y}}}_i,{\overline{\mathbf{Y}}}_i),$$

(12)

$${{\tilde{\mathbf{Y}}}_i}^{dim}=\mathrm{L}\mathrm{a}\mathrm{y}\mathrm{e}\mathrm{r}\mathrm{N}\mathrm{o}\mathrm{r}\mathrm{m}({\mathbf{Y}}_{i,:}^{time}+{\mathbf{T}}_i),$$

(13)

$${\mathbf{Y}}_i^{dim}=\mathrm{L}\mathrm{a}\mathrm{y}\mathrm{e}\mathrm{r}\mathrm{N}\mathrm{o}\mathrm{r}\mathrm{m}({{\tilde{\mathbf{Y}}}_i}^{dim}+\mathrm{M}\mathrm{L}\mathrm{P}({{\tilde{\mathbf{Y}}}_i}^{dim})),$$

(14)

${\mathbf{Y}}_i^{dim}$ is the output of the cross-dimension stage for each dimension $i$. By concatenating all ${\mathbf{Y}}_i^{dim}$, the final output of TSA is obtained, as shown below:

$$\mathbf{T}\mathbf{S}\mathbf{A}\left(\mathbf{H}\right)={\mathbf{Y}}^{dim}=Concat({\mathbf{Y}}_1^{dim},{\mathbf{Y}}_2^{dim},\dots ,{\mathbf{Y}}_i^{dim}),$$

(15)

where ${\mathbf{Y}}^{dim}\in {\mathbb{R}}^{D\times d_{model}}$ and $1\le i\le D$.

3.3. Hierarchical Encoder–Decoder

The encoder–decoder structure is adopted in Transformer and its state of the art [3,5,10,12,13,14,29,30] in MTSF to capture dependencies from the information in different scales. We also follow the Hierarchical Encoder–Decoder (HED) structure in [30] based on our method for TSA. With the use of HED blocks, information at different scales is used for forecasting from a fine level to a coarse scale.

Encoder. To construct the encoder for our model, we propose a simple algorithm by using TSA for each layer. Each layer output is modeled as ${\mathit{Y}}^{enc,l}=\mathrm{E}\mathrm{n}\mathrm{c}\mathrm{o}\mathrm{d}\mathrm{e}\mathrm{r}\left({\mathit{Y}}^{enc,l-1}\right)$ and represented as:

$${\mathbf{Y}}^{enc,l}=\left\{\begin{array}{c}\mathbf{H}, l=1\\ \mathrm{TSA}\left({\mathbf{Y}}^{enc,l-1}\right), l>1\end{array}\right.,1\le l\le L,$$

(16)

where H denotes the embedding vector after dimension-wise segmentation and L refers to the number of layers in the encoder. As the equation shows, if $l=1$, the output is simply the value of H; if $l>1$, the input of layer at l is the TSA value of the layer at $l-1$.

Decoder. Following the HED structure, we construct the decoder for forecasting with the same number of layers as in the encoder. The input of the decoder at layer $l$ depends on the output of both the encoder at layer $l$ and the decoder at layer $l-1$ so the process of the decoder at layer l could be modeled as ${\mathit{Y}}^{dec,l}=\mathrm{D}\mathrm{e}\mathrm{c}\mathrm{o}\mathrm{d}\mathrm{e}\mathrm{r}({\mathit{Y}}^{enc,l},{\mathit{Y}}^{dec,l-1})$ and the mathematical representation is shown below:

$${\tilde{\mathbf{Y}}}^{dec,l}=\left\{\begin{array}{c}\mathrm{T}\mathrm{S}\mathrm{A}\left({\mathbf{E}}^{dec}\right), l=1\\ \mathrm{T}\mathrm{S}\mathrm{A}\left({\tilde{\mathbf{Y}}}^{dec,l-1}\right), l>1\end{array}\right.,$$

(17)

$${\overline{\mathbf{Y}}}_d^{dec,l}=\mathrm{M}\mathrm{S}\mathrm{A}\left({\tilde{\mathbf{Y}}}_d^{dec,l},{\mathbf{Y}}_d^{enc,l},{\mathbf{Y}}_d^{enc,l}\right),1\le d\le D,$$

(18)

$${\overline{\mathbf{Y}}}^{dec,l}=\mathrm{C}\mathrm{o}\mathrm{n}\mathrm{c}\mathrm{a}\mathrm{t}\left({\overline{\mathbf{Y}}}_1^{dec,l},{\overline{\mathbf{Y}}}_2^{dec,l},\dots ,{\overline{\mathbf{Y}}}_D^{dec,l}\right),$$

(19)

$${\widehat{\mathbf{Y}}}^{dec,l}=\mathrm{L}\mathrm{a}\mathrm{y}\mathrm{e}\mathrm{r}\mathrm{N}\mathrm{o}\mathrm{r}\mathrm{m}({\tilde{\mathbf{Y}}}^{dec,l}+{\overline{\mathbf{Y}}}^{dec,l}),$$

(20)

$${\mathbf{Y}}^{dec,l}=\mathrm{L}\mathrm{a}\mathrm{y}\mathrm{e}\mathrm{r}\mathrm{N}\mathrm{o}\mathrm{r}\mathrm{m}({\widehat{\mathbf{Y}}}^{dec,l}+\mathrm{M}\mathrm{L}\mathrm{P}({\widehat{\mathbf{Y}}}^{dec,l})),$$

(21)

Specifically, ${\mathbf{E}}^{dec}\in {\mathbb{R}}^{D\times \frac{\tau }{L_{seg}}\times d_{model}}$ is the learnable position embedding vector as the input of the decoder with $l=1$, and at layer $1<l\le L$, ${\tilde{\mathbf{Y}}}^{dec,l}$ is the output of TSA that takes ${\tilde{\mathbf{Y}}}^{dec,l-1}$ as input. Then, ${\tilde{\mathbf{Y}}}^{dec,l}$ is processed dimension-wise by MSA with ${\mathbf{Y}}_d^{enc,l}$ as the key and value, which connects relations with the corresponding vector for dimension $d$ at encoder layer $l$. Afterwards, each ${\mathbf{Y}}_d^{enc,l}$ is concatenated for residual connection and MLP in two LayerNorms.

The prediction of the model is produced by the sum of prediction of each decoder layer by using linear projections with learnable weights. Suppose for each layer $l$ the weight of vector is denoted by ${\mathit{W}}_l$, the prediction of MTSF for future $\tau$ time steps ${\mathit{x}}_{T+1:T+\tau }$ given history of T time steps is represented as:

$$\mathbf{p}\mathbf{r}\mathbf{e}\mathbf{d}\left({\mathbf{x}}_{1:T}\right)={\mathbf{x}}_{T+1:T+\tau }={\sum }_{l=1}^L{\mathit{W}}_l{\mathbf{Y}}^{dec,l},{\mathit{W}}_l\in {\mathbb{R}}^{L_{seg}\times d_{model}},$$

(22)

The Multivariate Time Series (MTS) in our method is processed in segments, allowing the prediction of future $\tau$ steps to also be represented in segmented form as: ${\mathbf{x}}_{T+1:T+\tau }=\left\{{\mathbf{x}}_{i,d}\in {\mathbb{R}}^{L_{seg}\times d_{model}}|1\le i\le {\displaystyle \frac{\tau }{L_{seg}}},1\le d\le D\right\}$. Specifically, for each layer $l$, ${\mathbf{x}}_{T+1:T+\tau }^l=\left\{{\mathbf{x}}_{i,d}^l\in {\mathbb{R}}^{L_{seg}\times d_{model}}|1\le i\le {\displaystyle \frac{\tau }{L_{seg}}},1\le d\le D,1\le l\le L\right\}$.

4. Experiments

The proposed model is implemented with four real-world time series datasets widely used in baseline models, comparing the results with state-of-the-art Transformers. The performance of the proposed model is recorded along with the results of the state-of-the-art Transformers for MTSF.

In our experiments, we demonstrate the model configurations, present the results of its implementation in forecasting tasks using benchmark datasets, and validate the effectiveness of the proposed method. Like previous baselines, we use Mean Square Error (MSE) and Mean Absolute Error (MAE) as evaluation metrics in our case.

4.1. Datasets

We choose four MTS datasets as real-world benchmark datasets widely used in the state of the art [15,16,17] to evaluate the proposed model and present the performance results using the same metrics: (1) Electricity Transformer Temperature (ETT-small), (2) Weather (WTH), (3) Influenza-Like Illness (ILI), (4) Exchange-Rate. However, unlike [30], we split all chosen datasets with the ratio of 0.6:0.2:0.2. Configurations and details of all used datasets are shown in Table 1.

Table 1. Detailed information for real-world datasets in our experiment.

Dataset Name	Dimensions	Total	Training	Validation	Testing
ETTh1	7	17,420	10,443	3481	3481
ETTh2	7	17,420	10,405	3461	3461
ETTm1	7	69,680	41,671	13,913	13,913
ETTm2	7	69,680	41,797	13,931	13,931
WTH	21	52,696	31,570	10,517	10,517
Exchange-Rate	8	7588	4545	1516	1516
ILI	7	966	532	171	170

Electricity Transformer Temperature (ETT-small). ETT-small consists of four groups of datasets called ETTh1, ETTh2, ETTm1, and ETTm2. It records the data for an electricity transformer in two years with seven attributes in each time step including load, oil temperature in hours (ETTh1, ETTh2) and minutes (ETTm1, ETTm2). Full versions of datasets and details are also available in [11].

Weather (WTH). WTH contains the meteorological information of weather in over 1600 locations in the US in 4 years between 2010 and 2013. It consists of over 10 features including temperature, humidity, wind velocity, wind degree, and so on, every hour.

Influenza-Like Illness (ILI). ILI contains information about influenza patients in multiple states in the United States recorded by the Centers for Disease Control (CDC) from 2002 to 2020. It includes patients’ personal information, outpatient illness, and viral surveillance at national, regional, and state levels. The latest information and visualization about influenza tests in various areas can be viewed in [16].

Exchange-Rate. The Exchange-Rate dataset includes daily exchange of currencies from eight countries between 1990 and 2010. More information can be found in [11].

4.2. Setup

We conduct experiments with the proposed method using real-world MTS datasets on a machine with multi-GPUs that process inputs in batches. To evaluate the performance of our method, we choose the Mean Square Error (MSE) and Mean Absolute Error (MAE) as evaluation metrics. The model is implemented on a machine consisting of 4 GPUs, each with 24 GB memory.

Baselines. To show the effectiveness of our method, we use the recent models for MTSF as baseline methods, including (1) LSTnet, (2) Transformer, (3) Autoformer, (4) Informer, (5) Reformer, (6) FEDformer, (7) Pyraformer.

Model Parameters. With four real-world benchmark datasets, we follow similar configurations for the Crossformer model [30] along with segment length, input length, and prediction length. By default, in our method, input time series data is processed in batches with batch size $B=32$, the number of encoder layers is 3, the number of MSA heads is 4, $d_{model}=256$. In ECL and Traffic, $d_{model}$ is also set to be 64. Specifically, for datasets ETTh1, ETTh2, WTH, and ECL and Traffic, the input length is set to be in $\left\{24,48,96,168,336,720\right\}$; for datasets ETTm1 and ETTm2, the input length would be $\left\{24,48,96,192,288,672\right\}$; for dataset ILI, the input length is in $\left\{24,36,48,60\right\}$; for dataset Exchange-Rate, input length is in $\left\{ 24,36,48,60,96,168,336,720\right\}$. By default, the segment length is set to be $\left\{6,4,24\right\}$ and batch size is 32. The learning rate is in $\left\{5\times {10}^{-3},{10}^{-3},5\times {10}^{-4}, {10}^{-4},5\times {10}^{-5},{10}^{-5}\right\}$ and ${10}^{-4}$ by default. In short-term prediction, the prediction length is set to be in $\left\{4,6,24,48\right\}$ whereas, in a long-term case, it is set to be larger than 48 in $\left\{168,336,720\right\}$. The epoch number is 20.

4.3. Model Results

We show the results of our new method with configurations under four real-world datasets as well as the performance of the state of the art including traditional models and Transformer-based methods. The full list of results is presented in the Appendix A.3.

Table 2 presents the results of our proposed model for different prediction lengths, using MSE and MAE as evaluation metrics. Configurations for models including other parameters such as input length, segment length, batch size, and so on are followed based on Section 4.2. In this section, we only show the results of short-term forecasting in different prediction lengths for four datasets. For each prediction length with different model configurations, we choose and show the best one among all experimental results. Detailed information about performance versus model parameters for all configurations is shown in the Appendix A.2.

Table 2. Results of MTSF Task for our method with small prediction length with different datasets.

Dataset	ETTh1		ETTh2		ETTm1		ETTm2		WTH		Exchange		ILI
Metrics	MSE	MAE	MSE	MAE	MSE	MAE	MSE	MAE	MSE	MAE	MSE	MAE	MSE	MAE
4	0.273	0.342	0.111	0.217	0.117	0.209	0.109	0.202	0.050	0.084	0.228	0.290	1.641	0.777
6	0.343	0.379	0.126	0.236	0.158	0.244	0.140	0.240	0.060	0.096	0.324	0.342	2.305	0.917
12	0.453	0.447	0.179	0.282	0.258	0.324	0.152	0.245	0.078	0.127	0.577	0.492	2.835	1.097
24	0.464	0.496	0.259	0.338	0.342	0.377	0.211	0.289	0.132	0.172	1.413	0.791	4.287	1.406
48	0.583	0.561	0.427	0.405	0.454	0.472	0.222	0.303	0.222	0.264	2.048	1.109	5.901	1.704

To show the effectiveness of our method, Table 3 lists the results of the state-of-the-art baselines including Transformers and typical traditional methods; the results of our methods are shown under SCF. In this case, long-term forecasting with longer prediction lengths is additionally implemented in our method to coordinate with others and for comparisons. For more details about specific baselines, refer to [31]. A comprehensive list of results is also presented in the Appendix A.3.

Table 3. Results of MTSF Task with different Prediction Lengths. Bold indicates the best. Results of our method are shown in the SCF column. Figures in bold indicate the best results.

Models		Crossformer		FEDformer		Transformer		Informer		Autoformer		Pyraformer		SCF		LSTMa		MTGNN
Metric		MSE	MAE	MSE	MAE	MSE	MAE	MSE	MAE	MSE	MAE	MSE	MAE	MSE	MAE	MSE	MAE	MSE	MAE
ETTh1	24	0.464	0.496	0.318	0.384	0.620	0.577	0.577	0.549	0.384	0.425	0.493	0.507	0.464	0.496	0.650	0.624	0.336	0.393
	48	0.583	0.561	0.342	0.396	0.692	0.671	0.685	0.625	0.392	0.419	0.554	0.544	0.583	0.561	0.702	0.675	0.386	0.429
	168	0.410	0.441	0.412	0.449	0.947	0.797	0.931	0.752	0.490	0.481	0.781	0.675	0.464	0.496	1.212	0.867	0.466	0.474
	336	0.440	0.461	0.456	0.474	1.094	0.813	1.128	0.873	0.505	0.484	0.912	0.747	0.531	0.529	1.424	0.994	0.736	0.643
	720	0.519	0.524	0.521	0.515	1.241	0.917	1.215	0.896	0.498	0.500	0.993	0.792	0.913	0.695	1.960	1.322	0.916	0.750
ETTm1	24	0.211	0.293	0.290	0.364	0.306	0.371	0.323	0.369	0.383	0.403	0.310	0.371	0.342	0.380	0.621	0.629	0.260	0.324
	48	0.300	0.352	0.342	0.396	0.465	0.470	0.494	0.503	0.454	0.453	0.465	0.464	0.457	0.444	1.392	0.939	0.386	0.408
	96	0.320	0.373	0.366	0.412	0.681	0.612	0.678	0.614	0.481	0.463	0.520	0.504	0.342	0.377	1.339	0.913	0.428	0.446
	288	0.404	0.427	0.398	0.433	1.162	0.879	1.056	0.786	0.634	0.528	0.729	0.657	0.365	0.396	1.740	1.124	0.469	0.488
	672	0.569	0.528	0.455	0.464	1.231	1.103	1.192	0.926	0.606	0.542	0.980	0.678	0.340	0.400	2.736	1.555	0.620	0.571
WTH	24	0.294	0.343	0.357	0.412	0.349	0.397	0.335	0.381	0.363	0.396	0.301	0.359	0.132	0.172	0.546	0.570	0.307	0.356
	48	0.370	0.411	0.428	0.458	0.386	0.433	0.395	0.459	0.456	0.462	0.376	0.421	0.203	0.256	0.829	0.677	0.388	0.422
	168	0.473	0.494	0.564	0.541	0.613	0.582	0.608	0.567	0.574	0.548	0.519	0.521	0.298	0.323	1.038	0.835	0.498	0.512
	336	0.495	0.515	0.533	0.536	0.707	0.634	0.702	0.620	0.600	0.571	0.539	0.543	0.388	0.376	1.657	1.059	0.506	0.523
	720	0.526	0.542	0.562	0.557	0.834	0.741	0.831	0.731	0.587	0.570	0.547	0.553	0.456	0.429	1.536	1.109	0.510	0.527
ILI	24	3.041	1.186	2.687	1.147	3.954	1.323	4.588	1.462	3.101	1.238	3.970	1.338	4.287	1.406	4.220	1.335	4.265	1.387
	36	3.406	1.232	2.887	1.160	4.167	1.360	4.845	1.496	3.397	1.270	4.377	1.410	5.417	1.631	4.771	1.427	4.777	1.496
	48	3.459	1.221	2.297	1.155	4.476	1.463	4.865	1.516	2.947	1.203	4.811	1.503	5.901	1.704	4.945	1.462	5.333	1.592
	60	3.640	1.305	2.809	1.163	5.219	1.553	5.212	1.576	3.019	1.202	5.204	1.588	7.005	1.898	5.176	1.504	5.070	1.552

4.4. Analysis and Discussion

Table 2 and Table 3 show the results of our method and its comparison with other baselines. As shown in the tables, our method generates excellent results with many benchmark datasets as expected. As explained in the previous section, our method has the advantage of fully considering all dimensions in two stages for cross-time and cross-dimension. Unlike LogSparse Transformer [28], our method takes $\mathcal{O}\left(L\right)$ of computational complexity but goes through all univariates at each time point. Table 3 shows that our method generates the best results with the WTH dataset compared to other baseline models, showing the effectiveness of our method with long-term multivariate time series. As mentioned in Section 4.1, the WTH dataset contains more types of univariates that record more information over a long history. On the other hand, the advantage of our method with two-stage attention is reflected with long-term time series. With two-stage attention, our method fully captures dependencies and patterns by self-attention between segments for all dimensions across time. In addition, with a large-scale time series dataset, our method is better for long predictions. For example, as shown in Table 2, our method generates the best results for long-term prediction, with prediction lengths of 288 and 672 for ETTm1, implying that, with sufficient historical information, our method could be more powerful for forecasting in long horizons.

However, in some datasets, the method does not provide the best results due to a few reasons. First, for efficient computation, our method applies simple linear projection in TSA, assuming linear relations for weights after each stage in TSA, but complex irregular distributions over various multivariate time series data are not the case for linear relationships. To address non-linear relationships in time series, a new algorithm is needed in future work. Secondly, only MSA is performed in dimensions and time in order which may neglect to learn dependencies between segments of two different dimensions at different time steps. Thirdly, the setup for parameters such as input length and segment length may affect performance of our methods. For example, a short input length is unable to make long predictions due to insufficient historical information. According to experimental results, although our method does not achieve the best results on all datasets, it consistently either outperforms other state-of-the-art baselines or performs comparably, demonstrating the effectiveness of our novel approach over existing methods.

5. Conclusions

We propose a novel Transformer-based method for multivariate time series forecasting and demonstrate its effectiveness over previous state-of-the-art approaches using commonly used benchmark datasets. We deploy models with our method in different configurations and record detailed results in this work. As discussed in the previous section, our method outperforms baseline models by the strategy that captures dependencies on dimensions in its past information and other dimensions across history by multi-head self-attention and connects with a simple linear projection in a hierarchical encoder–decoder structure for predictions. Our method has a significant impact on time series forecasting and motivates improvements in models for specific domains. With the success of our method, our novel architecture could be applied across key domains such as weather forecasting, energy systems, environmental monitoring, healthcare, and so on, contributing to reliable long-term forecasting.

However, there are a few issues that limit the performance of our method and achieving better results with some datasets. First, we assume all dimensions are in linear relationships, so linear projections are used for weights after the stage of two-stage attention; however, irregular patterns for time series data may have more complex relations where linear projection is not effective in such conditions. Secondly, for computation simplicity, our method does not focus on seasonal trends depending on types of data so that seasonality for samples is not clear for forecasting. In future work, it is necessary to visualize the seasonal trends in our method. Thirdly, the decomposition method needs to be further considered for better representation of input time series. We would concentrate on addressing these problems and improve our method for better performance as a foundation model in future work.

Appendix A.1. Algorithms

The section provides the pseudocodes for algorithms of each component for our model architecture, which is represented mathematically in Section 3. As elaborated in the Methodology, we present algorithms including dimension-wise segmentation, cross-time dimension embedding, two-stage attention, and an encoder and decoder in a HED structure for our method.

Algorithm A1 SegmentedCrossformer

1: Inputs: 2:     Multivariate Time Series ${\mathit{x}}_{1:T}\in {\mathbb{R}}^{T\times D}$ with D dimensions in time step T, 3:     Segment Length: ${\mathit{L}}_{\mathit{s}\mathit{e}\mathit{g}}$ 4:     Embedded Dimension ${\mathit{d}}_{\mathit{m}\mathit{o}\mathit{d}\mathit{e}\mathit{l}}$ 5:     Learnable Embedding Vector $\mathbf{E}\in {\mathbb{R}}^{d_{model}\times L_{seg}}$ 6:     Learnable Position Embedding Vector ${\mathit{E}}_{pos}$ $\in {\mathbb{R}}^{d_{model}}$ 7:     Number of Heads in MSA: $\mathbf{h}$ 8:     Number of Current Encoder and Decoder Layers: $\mathit{l}$ 9:     Learnable Position Embedding Vector: ${\mathit{E}}^{dec}$ 10: Procedure SegmentedCrossformer(${\mathit{x}}_{1:T}$, ${\mathit{L}}_{\mathit{s}\mathit{e}\mathit{g}}$, ${\mathit{d}}_{\mathit{m}\mathit{o}\mathit{d}\mathit{e}\mathit{l}}$, $\mathbf{h}$, $\mathit{l}$): 11:      # Initialization 12:   Set Query Q, Key K and Value V 13:   Set Learnable Embedding Vector $\mathbf{E}\in {\mathbb{R}}^{d_{model}\times L_{seg}}$ 14:   Set Learnable Position Embedding Vector ${\mathit{E}}_{pos}$ $\in {\mathbb{R}}^{d_{model}}$ 15:   Set Learnable Position Embedding Vector: ${\mathit{E}}^{dec}$ 16:   # Implementation Starts from here 12:   Set ${\mathit{x}}_D=$ DimWiseEmbedding(${\mathit{x}}_{1:T}$, ${\mathit{L}}_{\mathit{s}\mathit{e}\mathit{g}}$) 13:   Set ${\mathit{H}}_T=CrossTimeEmbedding({\mathit{x}}_D,{\mathit{d}}_{\mathit{m}\mathit{o}\mathit{d}\mathit{e}\mathit{l}},\mathbf{E},{\mathit{E}}_{pos})$ 14:   Set $\mathbf{H}=TwoStageAttn\left({\mathit{H}}_T\right)$ 15:   # Hierarchical Encoder-Decoder to make the prediction 16:   Set $\mathbf{Y}=HED(\mathbf{H},\mathit{l}, {\mathit{E}}^{dec},\mathbf{D})$ 17:   return Y

Algorithm A2 Dimension-Wise Embedding

1: Inputs: 2:     Multivariate Time Series ${\mathit{x}}_{1:T}\in {\mathbb{R}}^{T\times D}$ with D dimensions in time step T 3.     Segment Length: ${\mathit{L}}_{\mathit{s}\mathit{e}\mathit{g}}$ 4: Procedure DimWiseEmbedding(${\mathit{x}}_{1:T},{\mathit{L}}_{\mathit{s}\mathit{e}\mathit{g}}$): 6:     Reshape ${\mathit{x}}_{1:T}\in {\mathbb{R}}^{T\times D}$ into ${\mathit{x}}_{1:D}\in {\mathbb{R}}^{\left(T/L_{seg}\right)\times L_{seg}\times D}$ 7.     Set x = ${\mathit{x}}_{1:D}$ 8.    return x

Algorithm A3 Cross-Time Embedding

1: Input: 2:    Segmented Multivariate Time Series ${\mathit{x}}_{1:D}\in {\mathbb{R}}^{\left(T/L_{seg}\right)\times L_{seg}\times D}$ 3.    Embedded Dimension ${\mathit{d}}_{\mathit{m}\mathit{o}\mathit{d}\mathit{e}\mathit{l}}$ 3:    Learnable Embedding Vector $\mathbf{E}\in {\mathbb{R}}^{d_{model}\times L_{seg}}$ 4:    Learnable Position Embedding Vector ${\mathit{E}}_{pos}$ $\in {\mathbb{R}}^{d_{model}}$ 5: Procedure CrossTimeEmbedding(${\mathit{x}}_{1:D}$, ${\mathit{d}}_{\mathit{m}\mathit{o}\mathit{d}\mathit{e}\mathit{l}}$, E, ${\mathit{E}}_{pos}$): 6:    Set Embedding Vector H = {} 7:    Set ${\mathit{E}}_{i,s}^{\left(pos\right)}$ = ${\mathit{E}}_{pos}$ where $1\le i \le D$ and $1\le s\le T/L_{seg}$ 7:    for each segment ${\mathit{x}}_{i,s}$ in ${\mathit{x}}_{1:D}$ do: 8:       Set ${\mathit{h}}_{i,s}=\mathbf{E}{\mathit{x}}_{i,s}+{\mathit{E}}_{i,s}^{\left(pos\right)}$ 9:       Set H = Concat(H, ${\mathit{h}}_{i,s}$) 10:   end for 11:   return H

Algorithm A4 Multihead Self-Attention (MSA)

1: Require: Query: Q, Key: K, Value: V 2: Input:   3:    Number of Heads in MSA: $\mathbf{h}$ 4:    Query: Q, Key: K, Value: V 5:    Embedded Dimension: ${\mathit{d}}_{\mathit{m}\mathit{o}\mathit{d}\mathit{e}\mathit{l}}$ 6: Procedure MSA(Q, K, V, $\mathbf{h}$, ${\mathit{d}}_{model}$): 7:    Set Y = {} 8:    for $\mathit{i}\leftarrow 0 \mathbf{t}\mathbf{o} \mathbf{h}$ do: 9:        Set ${\mathit{d}}_k={\mathit{d}}_v={\mathit{d}}_h={\mathit{d}}_{model}/\mathit{h}$ 10:      Set ${\mathit{W}}_i^Q\in {\mathbb{R}}^{d_{model}\times d_k}$, ${\mathit{W}}_i^K\in {\mathbb{R}}^{d_{model}\times d_k}$, ${\mathit{W}}_i^V\in {\mathbb{R}}^{d_{model}\times d_v}$ and ${\mathit{W}}^O\in {\mathbb{R}}^{h{d}_v\times d_{model}}$ 11:      Set ${\mathit{h}\mathit{e}\mathit{a}\mathit{d}}_i=softmax({\displaystyle \frac{\mathit{Q}{\mathit{W}}_i^Q{\left(\mathit{K}{\mathit{W}}_i^K\right)}^T}{\sqrt{{\mathit{d}}_k}}})$ 12:      Set Y = Concat(Y, ${\mathit{h}\mathit{e}\mathit{a}\mathit{d}}_i$) 13:    end for 14:    return Y

Algorithm A5 Two-Stage Attention

1: Input: 2:    2D Embedding Vector $\mathbf{H}=\{{\mathit{h}}_{i,s}\in {\mathbb{R}}^{d_{model}}| 1\le i \le D, 1\le s\le {\displaystyle \frac{T}{L_{seg}}} \}$ 3:    Require Query Q, Key K, Value V for Multi-head Self-Attention (MSA) 4:    Number of Heads in MSA: $\mathbf{h}$ 5:    Embedded Dimension ${\mathit{d}}_{\mathit{m}\mathit{o}\mathit{d}\mathit{e}\mathit{l}}$ 6: 7: Procedure CrossTimeStage(H): 8:   Set ${\mathit{Y}}^{time}$= {} 9:   for $\mathit{i}\leftarrow 0 \mathbf{t}\mathbf{o} \mathit{D}$ do: 10:      Set ${\mathit{h}}_{i,:}=\mathbf{H}\left[i\right]$ 11:      Set ${\mathit{c}\mathit{r}\mathit{o}\mathit{s}\mathit{s}\mathit{t}\mathit{i}\mathit{m}\mathit{e}}_i=MSA({\mathit{h}}_{i,:},{\mathit{h}}_{i,:},{\mathit{h}}_{i,:},\mathbf{h},{\mathit{d}}_{\mathit{m}\mathit{o}\mathit{d}\mathit{e}\mathit{l}})$ 12:      Set ${\tilde{\mathit{Y}}}_{i,:}^{time}=LayerNorm({\mathit{h}}_{i,:}+{\mathit{c}\mathit{r}\mathit{o}\mathit{s}\mathit{s}\mathit{t}\mathit{i}\mathit{m}\mathit{e}}_i)$ 13:      Set ${\mathit{Y}}_{i,:}^{time}=LayerNorm\left({\tilde{\mathit{Y}}}_{i,:}^{time}+MLP\left({\tilde{\mathit{Y}}}_{i,:}^{time}\right)\right)$ 14:      Set ${\mathit{Y}}^{time}=Concat({\mathit{Y}}^{time}, {\mathit{Y}}_{i,:}^{time})$ 15:   end for 16:   return ${\mathit{Y}}^{time}$ 17: 18: Procedure CrossDimStage(H): 19.   Set ${\mathit{Y}}^{dim}$ = {} 19:   for $i\leftarrow 0 \mathbf{t}\mathbf{o} \mathit{D}$ do: 20:      Set ${\mathit{H}}_i^{\ast }=\left\{ h_{d,s}\in \mathit{H} | 1\le d\le D,d\ne i, 1\le s\le {\displaystyle \frac{T}{L_{seg}}}\right\}$ 21:      Set learnable weight for linear projection ${\mathit{W}}_i$ and bias $\mathbf{b}\in {\mathbb{R}}^{d_{model}}$ 22:      Set ${\overline{\mathit{Y}}}_i=W_i{\mathit{H}}_i^{\ast }+\mathbf{b}$ 23:      Set ${\mathit{T}}_i=MSA({\mathit{Y}}_{i,:}^{time},\overline{{\mathit{Y}}_i},\overline{{\mathit{Y}}_i})$ 24:      Set ${{\tilde{\mathit{Y}}}_i}^{dim}=LayerNorm({\mathit{Y}}_{i,:}^{time}+{\mathit{T}}_i)$ 25:      Set ${\mathit{Y}}_i^{dim}=\mathrm{L}\mathrm{a}\mathrm{y}\mathrm{e}\mathrm{r}\mathrm{N}\mathrm{o}\mathrm{r}\mathrm{m}({{\tilde{\mathit{Y}}}_i}^{dim}+\mathrm{M}\mathrm{L}\mathrm{P}({{\tilde{\mathit{Y}}}_i}^{dim}))$ 26:      Set ${\mathit{Y}}^{dim}=Concat({\mathit{Y}}^{dim},{\mathit{Y}}_i^{dim})$ 27:   end for 28:   return ${\mathit{Y}}^{dim}$ 29: 30: Procedure TwoStageAttn(H): 31:   Set ${\mathit{H}}_{temp}=crossTimeStage\left(\mathbf{H}\right)$ 32:   Set $\mathbf{Y}=crossDimStage\left({\mathit{H}}_{temp}\right)$ 33:   return Y

Algorithm A6 Hierarchical Encoder–Decoder (HED)

1: Inputs: 2:    Embedded Vector from TSA: H 3:    Number of Current Encoder and Decoder Layers: $\mathit{l}$ 4:    Learnable Position Embedding Vector: ${\mathit{E}}^{dec}$ 5: Procedure Encoder(H, l): 6:    if $\mathit{l}=1$ then: Set ${\mathit{Y}}^{enc}=\mathbf{H}$ 9:    else: Set ${\mathit{Y}}^{enc}=TSA(\mathbf{H})$ 8:    end if 9:    return ${\mathit{Y}}^{enc}$ 10: 11: Procedure Decoder(H,l, ${\mathit{E}}^{dec}$): 12:   if $\mathit{l}$ = 1 then: Set ${\tilde{\mathit{Y}}}^{dec}=TSA\left({\mathit{E}}^{dec}\right)$ 13:   else: Set ${\tilde{\mathit{Y}}}^{dec}= TSA\left(\mathit{H}\right)$ 14:   end if 15:   return ${\tilde{\mathit{Y}}}^{dec}$ 16: 17: Procedure HED(H,L, ${\mathit{E}}^{dec}$,$\mathbf{D}$): 18:   Set Y = 0 19:   for $l\leftarrow 1 \mathbf{t}\mathbf{o} \mathbf{L}+1$do: 20:       Set ${\mathit{H}}_{enc}=\mathbf{H}$, ${\mathit{H}}_{dec}=\mathbf{H}$ 21:       Set ${\mathit{Y}}^{enc,l}=Encoder({\mathit{H}}_{enc},\mathit{i})$, ${\tilde{\mathit{Y}}}^{dec,l}=Decoder({\mathit{H}}_{dec},l,{\mathit{E}}^{dec})$ 22:       # update output for each encoder and decoder layer to be the input for next iteration 23:       Set ${\mathit{H}}_{enc}= {\mathit{Y}}^{enc,l}$, ${\mathit{H}}_{dec}={\tilde{\mathit{Y}}}^{dec,l}$ 24:       Set ${\overline{\mathit{Y}}}^{dec,l}$ = {} 25:       for $\mathit{i}\leftarrow 0 \mathbf{t}\mathbf{o} \mathbf{D}$ do: 26:         Set ${\tilde{\mathit{Y}}}_d^{dec,l}$= ${\tilde{\mathit{Y}}}^{dec,l}[i]$, ${\mathit{Y}}_d^{enc,l}={\mathit{Y}}^{enc,l}[i]$ 27:         Set ${\overline{\mathit{Y}}}_d^{dec,l}=MSA({\tilde{\mathit{Y}}}_d^{dec,l},{\mathit{Y}}_d^{enc,l},{\mathit{Y}}_d^{enc,l},\mathbf{h},{\mathit{d}}_{model})$ 28:         Set ${\overline{\mathit{Y}}}^{dec,l}=Concat({\overline{\mathit{Y}}}^{dec,l},{\overline{\mathit{Y}}}_d^{dec,l})$ 29:       end for 30:       Set ${\widehat{\mathit{Y}}}^{dec,l}=LayerNorm({\tilde{\mathit{Y}}}^{dec,l}+{\overline{\mathit{Y}}}^{dec,l})$ 31:       Set ${\mathit{Y}}^{dec,l}=LayerNorm({\widehat{\mathit{Y}}}^{dec,l}+MLP({\widehat{\mathit{Y}}}^{dec,l}))$ 32:       # make the prediction for by the sum for each layer $l$ 33:       # Make inference for time series 34:       Set ${\mathit{W}}_l\in {\mathbb{R}}^{L_{seg}\times d_{model}}$ 35:       Set $\mathbf{Y}={\mathit{Y}+\mathit{W}}_l{\mathit{Y}}^{dec,l}$ 36:    end for 37:    return Y

Appendix A.2. Ablation Study

By default, we set up experiments for our model with parameters in Section 4, showing results of performance and comparing with the state of the art. To show the effectiveness of our methods, we conduct ablation studies with more configurations with hyperparameter tuning.

Input Length. The input length represents the size of the look-back window that contains historical information for inference. Based on different datasets, we set up input length depending on the size of the time series in each dataset. By default, we set up a short input length in {24, 48, 96}. In the ablation study, we set up input length based on datasets. For ETTh1, ETTh2, WTH, ECL, and Traffic, we set the input length to be {24, 48, 96, 168, 336, 720}. For ETTm1, ETTm2, and Exchange-Rate, we set up input length with {24, 48, 96, 192, 288, 672}. For ILI, we set the input length to be {24, 36, 48, 60}. The tables below show results of our methods for four real-world benchmark datasets with different input lengths.

Table A1. Results of our method with various input lengths with Datasets ETTh1, ETTh2, and WTH.

Datasets	Metrics	Input Length
		24	48	96	168	336	720
ETTh1	MSE	0.551	0.593	0.538	0.464	0.531	0.913
	MAE	0.510	0.534	0.529	0.496	0.529	0.695
ETTh2	MSE	0.118	0.111	0.526	1.057	0.913	1.957
	MAE	0.220	0.217	0.445	0.705	0.684	1.137
WTH	MSE	0.139	0.132	0.127	0.303	0.388	0.456
	MAE	0.172	0.172	0.178	0.318	0.376	0.429

Table A1. Results of our method with various input lengths with Datasets ETTh1, ETTh2, and WTH.

Datasets	Metrics	Input Length
		24	48	96	168	336	720
ETTh1	MSE	0.551	0.593	0.538	0.464	0.531	0.913
	MAE	0.510	0.534	0.529	0.496	0.529	0.695
ETTh2	MSE	0.118	0.111	0.526	1.057	0.913	1.957
	MAE	0.220	0.217	0.445	0.705	0.684	1.137
WTH	MSE	0.139	0.132	0.127	0.303	0.388	0.456
	MAE	0.172	0.172	0.178	0.318	0.376	0.429

Table A2. Results of our method for various input lengths with Dataset ETTm1, ETTm2, and Exchange-Rate.

Datasets		ETTm1		ETTm2		Exchange-Rate
Metrics		MSE	MAE	MSE	MAE	MSE	MAE
Input length	24	0.454	0.431	0.199	0.286	0.271	0.313
	48	0.388	0.394	0.222	0.303	0.361	0.364
	96	0.342	0.377	0.338	0.382	2.335	1.161
	192	0.345	0.391	0.456	0.424	3.156	1.364
	288	0.365	0.396	0.690	0.544	2.464	1.281
	672	0.340	0.390	1.113	0.724	1.927	1.145

Table A2. Results of our method for various input lengths with Dataset ETTm1, ETTm2, and Exchange-Rate.

Datasets		ETTm1		ETTm2		Exchange-Rate
Metrics		MSE	MAE	MSE	MAE	MSE	MAE
Input length	24	0.454	0.431	0.199	0.286	0.271	0.313
	48	0.388	0.394	0.222	0.303	0.361	0.364
	96	0.342	0.377	0.338	0.382	2.335	1.161
	192	0.345	0.391	0.456	0.424	3.156	1.364
	288	0.365	0.396	0.690	0.544	2.464	1.281
	672	0.340	0.390	1.113	0.724	1.927	1.145

Table A3. Results of our method for various input lengths with Dataset ILI.

Datasets		ILI
Metrics		MSE	MAE
Input length	24	1.790	0.875
	36	5.417	1.631
	48	2.679	1.020
	60	7.004	1.898

Table A3. Results of our method for various input lengths with Dataset ILI.

Datasets		ILI
Metrics		MSE	MAE
Input length	24	1.790	0.875
	36	5.417	1.631
	48	2.679	1.020
	60	7.004	1.898

Table A1, Table A2 and Table A3 show the best results for model configurations with different input lengths for four real-world datasets with MSE and MAE as metrics.

Appendix A.3. Comprehensive Results

To show the effectiveness of our model, we collect comprehensive results of the state-of-the-art methods which were implemented with a variety of datasets from past research. In this section, we record the comprehensive results of both our method and state-of-the-art methods including Transformer-based models and classical architecture like RNN-based methods.

Table A5 and Table A6 below show comprehensive results of MTSF models for different prediction lengths for four real-world datasets.

Table A4. Results of models with different prediction length for Datasets ETTh1, ETTm1, WTH, and ILI. The best results are highlighted in bold.

Models		MTGNN		DLinear		LSTNet		LSTMa		STformer		SCF
Metric		MSE	MAE	MSE	MAE	MSE	MAE	MSE	MAE	MSE	MAE	MSE	MAE
ETTh1	24	0.336	0.393	0.312	0.355	1.293	0.901	0.650	0.624	0.368	0.441	0.464	0.496
	48	0.386	0.429	0.352	0.383	1.456	0.960	0.702	0.675	0.445	0.465	0.582	0.561
	168	0.466	0.474	0.416	0.430	1.997	1.214	1.212	0.867	0.652	0.608	0.972	0.725
	336	0.736	0.643	0.450	0.452	2.655	1.369	1.424	0.994	1.069	0.806	0.979	0.734
	720	0.916	0.750	0.486	0.501	2.143	1.380	1.960	1.322	1.071	0.817	0.985	0.758
ETTm1	24	0.260	0.324	0.217	0.289	1.968	1.170	0.621	0.629	0.278	0.348	0.342	0.377
	48	0.386	0.408	0.278	0.330	1.999	1.215	1.392	0.939	0.445	0.458	0.465	0.453
	96	0.428	0.446	0.310	0.354	2.762	1.542	1.339	0.913	0.420	0.455	0.550	0.510
	288	0.469	0.488	0.369	0.386	1.257	2.076	1.740	1.124	0.733	0.597	0.745	0.613
	672	0.620	0.571	0.416	0.417	1.917	2.941	2.736	1.555	0.777	0.625	0.973	0.730
WTH	24	0.307	0.356	0.357	0.391	0.615	0.545	0.546	0.570	0.307	0.359	0.127	0.178
	48	0.388	0.422	0.425	0.444	0.660	0.589	0.829	0.677	0.381	0.416	0.203	0.256
	168	0.498	0.512	0.515	0.516	0.748	0.647	1.038	0.835	0.497	0.502	0.298	0.323
	336	0.506	0.523	0.536	0.537	0.782	0.683	1.657	1.059	0.566	0.564	0.388	0.376
	720	0.510	0.527	0.582	0.571	0.851	0.757	1.536	1.109	0.589	0.582	0.456	0.429
ILI	24	4.265	1.387	2.940	1.205	4.975	1.660	4.220	1.335	3.150	1.232	4.287	1.406
	36	4.777	1.496	2.826	1.184	5.322	1.659	4.771	1.427	3.512	1.243	5.417	1.631
	48	5.333	1.592	2.677	1.155	5.425	1.632	4.945	1.462	3.499	1.234	5.901	1.704
	60	5.070	1.552	3.011	1.245	5.477	1.675	5.176	1.504	3.715	1.316	7.005	1.898

Table A4. Results of models with different prediction length for Datasets ETTh1, ETTm1, WTH, and ILI. The best results are highlighted in bold.

Models		MTGNN		DLinear		LSTNet		LSTMa		STformer		SCF
Metric		MSE	MAE	MSE	MAE	MSE	MAE	MSE	MAE	MSE	MAE	MSE	MAE
ETTh1	24	0.336	0.393	0.312	0.355	1.293	0.901	0.650	0.624	0.368	0.441	0.464	0.496
	48	0.386	0.429	0.352	0.383	1.456	0.960	0.702	0.675	0.445	0.465	0.582	0.561
	168	0.466	0.474	0.416	0.430	1.997	1.214	1.212	0.867	0.652	0.608	0.972	0.725
	336	0.736	0.643	0.450	0.452	2.655	1.369	1.424	0.994	1.069	0.806	0.979	0.734
	720	0.916	0.750	0.486	0.501	2.143	1.380	1.960	1.322	1.071	0.817	0.985	0.758
ETTm1	24	0.260	0.324	0.217	0.289	1.968	1.170	0.621	0.629	0.278	0.348	0.342	0.377
	48	0.386	0.408	0.278	0.330	1.999	1.215	1.392	0.939	0.445	0.458	0.465	0.453
	96	0.428	0.446	0.310	0.354	2.762	1.542	1.339	0.913	0.420	0.455	0.550	0.510
	288	0.469	0.488	0.369	0.386	1.257	2.076	1.740	1.124	0.733	0.597	0.745	0.613
	672	0.620	0.571	0.416	0.417	1.917	2.941	2.736	1.555	0.777	0.625	0.973	0.730
WTH	24	0.307	0.356	0.357	0.391	0.615	0.545	0.546	0.570	0.307	0.359	0.127	0.178
	48	0.388	0.422	0.425	0.444	0.660	0.589	0.829	0.677	0.381	0.416	0.203	0.256
	168	0.498	0.512	0.515	0.516	0.748	0.647	1.038	0.835	0.497	0.502	0.298	0.323
	336	0.506	0.523	0.536	0.537	0.782	0.683	1.657	1.059	0.566	0.564	0.388	0.376
	720	0.510	0.527	0.582	0.571	0.851	0.757	1.536	1.109	0.589	0.582	0.456	0.429
ILI	24	4.265	1.387	2.940	1.205	4.975	1.660	4.220	1.335	3.150	1.232	4.287	1.406
	36	4.777	1.496	2.826	1.184	5.322	1.659	4.771	1.427	3.512	1.243	5.417	1.631
	48	5.333	1.592	2.677	1.155	5.425	1.632	4.945	1.462	3.499	1.234	5.901	1.704
	60	5.070	1.552	3.011	1.245	5.477	1.675	5.176	1.504	3.715	1.316	7.005	1.898

Table A5. Results of models with different prediction length for Datasets ETTh2 and ETTm2. The best results are highlighted in bold.

Models		SCF		Informer		LogTrans		Reformer		LSTNet		LSTMa
Metric		MSE	MAE	MSE	MAE	MSE	MAE	MSE	MAE	MSE	MAE	MSE	MAE
ETTh2	24	0.259	0.338	0.720	0.665	0.828	0.750	1.531	1.613	2.742	1.457	1.143	0.813
	48	0.427	0.405	1.457	1.001	1.806	1.034	1.871	1.735	3.567	1.687	1.671	1.221
	168	1.057	1.057	3.489	1.515	4.070	1.681	4.660	1.846	3.242	2.513	4.117	1.674
	336	0.913	0.684	2.723	1.340	3.875	1.763	4.028	1.688	2.544	2.591	3.434	1.549
	720	1.957	1.957	3.467	1.473	3.913	1.552	2.015	4.625	4.625	3.709	3.963	1.788
ETTm2	24	0.199	0.286	0.173	0.301	0.211	0.332	0.333	0.429	1.101	0.831	0.580	0.572
	48	0.223	0.303	0.303	0.409	0.427	0.487	0.558	0.571	2.619	1.393	0.747	0.630
	168	0.346	0.377	0.365	0.453	0.768	0.642	0.658	0.619	3.142	1.365	2.041	1.073
	336	0.712	0.550	1.056	0.804	1.090	0.806	2.441	1.190	2.856	1.329	0.969	0.742
	720	1.043	0.679	3.126	1.302	2.397	1.214	1.328	3.409	3.409	1.420	2.541	1.239

Table A5. Results of models with different prediction length for Datasets ETTh2 and ETTm2. The best results are highlighted in bold.

Models		SCF		Informer		LogTrans		Reformer		LSTNet		LSTMa
Metric		MSE	MAE	MSE	MAE	MSE	MAE	MSE	MAE	MSE	MAE	MSE	MAE
ETTh2	24	0.259	0.338	0.720	0.665	0.828	0.750	1.531	1.613	2.742	1.457	1.143	0.813
	48	0.427	0.405	1.457	1.001	1.806	1.034	1.871	1.735	3.567	1.687	1.671	1.221
	168	1.057	1.057	3.489	1.515	4.070	1.681	4.660	1.846	3.242	2.513	4.117	1.674
	336	0.913	0.684	2.723	1.340	3.875	1.763	4.028	1.688	2.544	2.591	3.434	1.549
	720	1.957	1.957	3.467	1.473	3.913	1.552	2.015	4.625	4.625	3.709	3.963	1.788
ETTm2	24	0.199	0.286	0.173	0.301	0.211	0.332	0.333	0.429	1.101	0.831	0.580	0.572
	48	0.223	0.303	0.303	0.409	0.427	0.487	0.558	0.571	2.619	1.393	0.747	0.630
	168	0.346	0.377	0.365	0.453	0.768	0.642	0.658	0.619	3.142	1.365	2.041	1.073
	336	0.712	0.550	1.056	0.804	1.090	0.806	2.441	1.190	2.856	1.329	0.969	0.742
	720	1.043	0.679	3.126	1.302	2.397	1.214	1.328	3.409	3.409	1.420	2.541	1.239

Table A6. Results of models with different prediction length for Datasets ETTh1, ETTh2, ETTm1, and ETTm2. The best results are highlighted in bold.

Models	Metric	Datasets
		ETTh1				ETTh2				ETTm1				ETTm2
		96	192	336	720	96	192	336	720	96	192	336	720	96	192	336	720
SCF	MSE	0.771	1.136	0.979	0.985	0.905	1.007	0.913	1.957	0.538	0.701	0.756	1.033	0.316	0.456	0.712	1.043
	MAE	0.658	0.794	0.734	0.758	0.650	0.698	0.684	1.137	0.496	0.597	0.622	0.752	0.458	0.424	0.550	0.679
FEDformer	MSE	0.376	0.420	0.459	0.506	0.346	0.429	0.496	0.463	0.379	0.426	0.445	0.543	0.203	0.269	0.325	0.421
	MAE	0.419	0.448	0.465	0.507	0.388	0.439	0.487	0.474	0.419	0.441	0.459	0.490	0.287	0.328	0.366	0.415
Autoformer	MSE	0.449	0.500	0.521	0.514	0.358	0.456	0.482	0.515	0.505	0.553	0.621	0.671	0.255	0.281	0.339	0.422
	MAE	0.459	0.482	0.496	0.512	0.397	0.452	0.486	0.511	0.475	0.496	0.537	0.561	0.339	0.340	0.372	0.419
Informer	MSE	0.865	1.008	1.107	1.181	3.755	5.602	4.721	3.647	0.672	0.795	1.212	1.166	0.365	0.533	1.363	3.379
	MAE	0.713	0.792	0.809	0.865	1.525	1.931	1.835	1.625	0.571	0.669	0.871	0.823	0.453	0.563	0.887	1.338
LogTrans	MSE	0.878	1.037	1.238	1.135	2.116	4.315	1.124	3.118	0.600	0.837	1.124	1.153	0.768	0.989	1.334	3.048
	MAE	0.740	0.824	0.932	0.852	1.197	1.635	1.604	1.540	0.546	0.700	0.832	0.820	0.642	0.757	0.872	1.328
Reformer	MSE	0.837	0.923	1.097	1.257	2.626	11.12	9.323	3.874	0.538	0.658	0.898	1.102	0.658	1.078	1.549	2.631
	MAE	0.728	0.766	0.832	0.889	1.317	2.979	2.769	1.697	0.528	0.592	0.721	0.841	0.619	0.827	0.972	1.242

Table A6. Results of models with different prediction length for Datasets ETTh1, ETTh2, ETTm1, and ETTm2. The best results are highlighted in bold.

Models	Metric	Datasets
		ETTh1				ETTh2				ETTm1				ETTm2
		96	192	336	720	96	192	336	720	96	192	336	720	96	192	336	720
SCF	MSE	0.771	1.136	0.979	0.985	0.905	1.007	0.913	1.957	0.538	0.701	0.756	1.033	0.316	0.456	0.712	1.043
	MAE	0.658	0.794	0.734	0.758	0.650	0.698	0.684	1.137	0.496	0.597	0.622	0.752	0.458	0.424	0.550	0.679
FEDformer	MSE	0.376	0.420	0.459	0.506	0.346	0.429	0.496	0.463	0.379	0.426	0.445	0.543	0.203	0.269	0.325	0.421
	MAE	0.419	0.448	0.465	0.507	0.388	0.439	0.487	0.474	0.419	0.441	0.459	0.490	0.287	0.328	0.366	0.415
Autoformer	MSE	0.449	0.500	0.521	0.514	0.358	0.456	0.482	0.515	0.505	0.553	0.621	0.671	0.255	0.281	0.339	0.422
	MAE	0.459	0.482	0.496	0.512	0.397	0.452	0.486	0.511	0.475	0.496	0.537	0.561	0.339	0.340	0.372	0.419
Informer	MSE	0.865	1.008	1.107	1.181	3.755	5.602	4.721	3.647	0.672	0.795	1.212	1.166	0.365	0.533	1.363	3.379
	MAE	0.713	0.792	0.809	0.865	1.525	1.931	1.835	1.625	0.571	0.669	0.871	0.823	0.453	0.563	0.887	1.338
LogTrans	MSE	0.878	1.037	1.238	1.135	2.116	4.315	1.124	3.118	0.600	0.837	1.124	1.153	0.768	0.989	1.334	3.048
	MAE	0.740	0.824	0.932	0.852	1.197	1.635	1.604	1.540	0.546	0.700	0.832	0.820	0.642	0.757	0.872	1.328
Reformer	MSE	0.837	0.923	1.097	1.257	2.626	11.12	9.323	3.874	0.538	0.658	0.898	1.102	0.658	1.078	1.549	2.631
	MAE	0.728	0.766	0.832	0.889	1.317	2.979	2.769	1.697	0.528	0.592	0.721	0.841	0.619	0.827	0.972	1.242