Bootstrapping Long-Run Covariance of Stationary Functional Time Series
Abstract
1. Introduction
2. Estimation of Long-Run Covariance Function
2.1. Notation
2.2. Estimation of Long-Run Covariance Function
3. Bootstrap Methods
3.1. Sieve Bootstrap
3.2. Functional Autoregressive Bootstrap
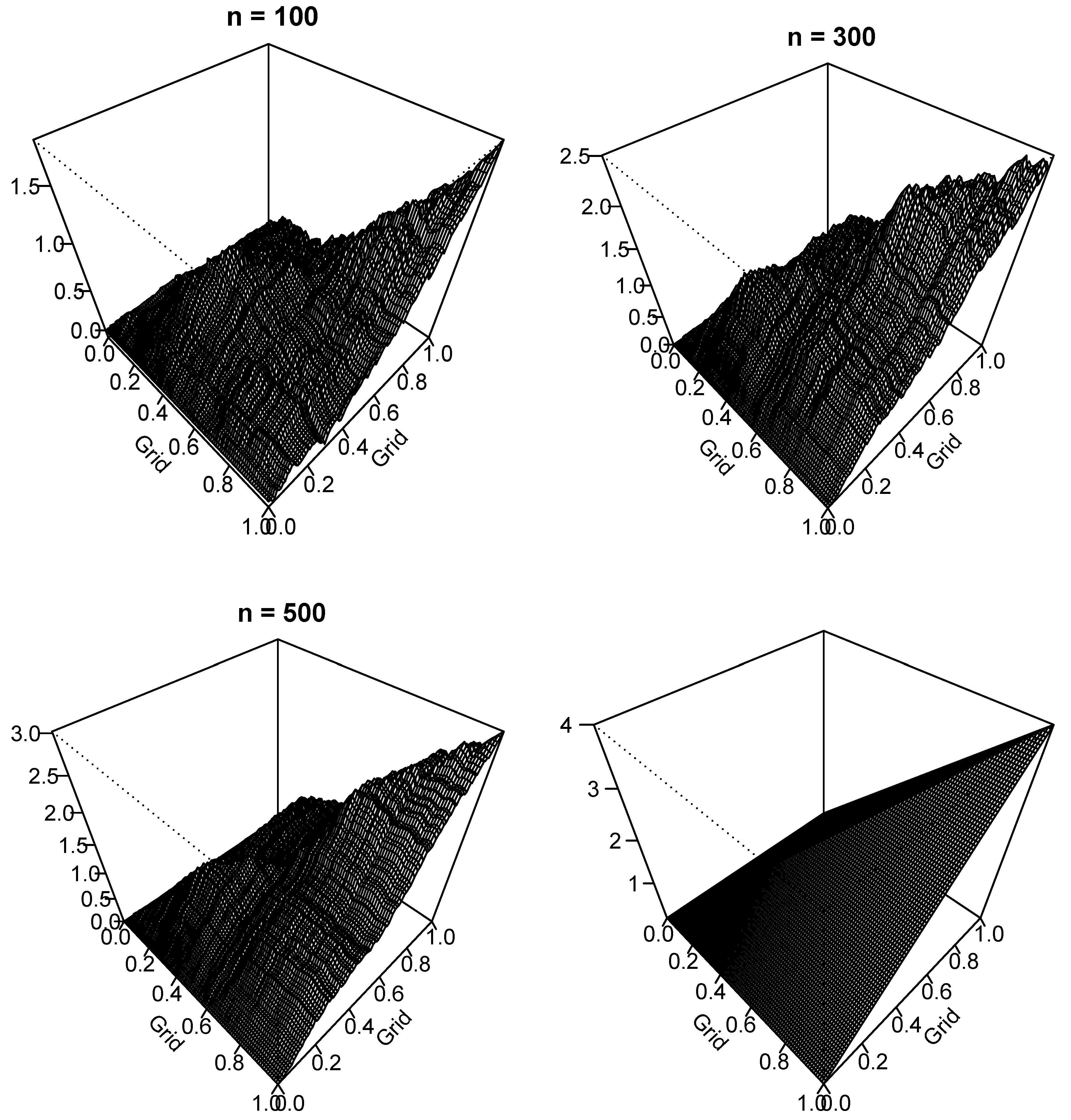
4. Simulation Study
4.1. Simulation Data Generating Processes (DGPs)
4.2. Simulation Evaluation Metrics
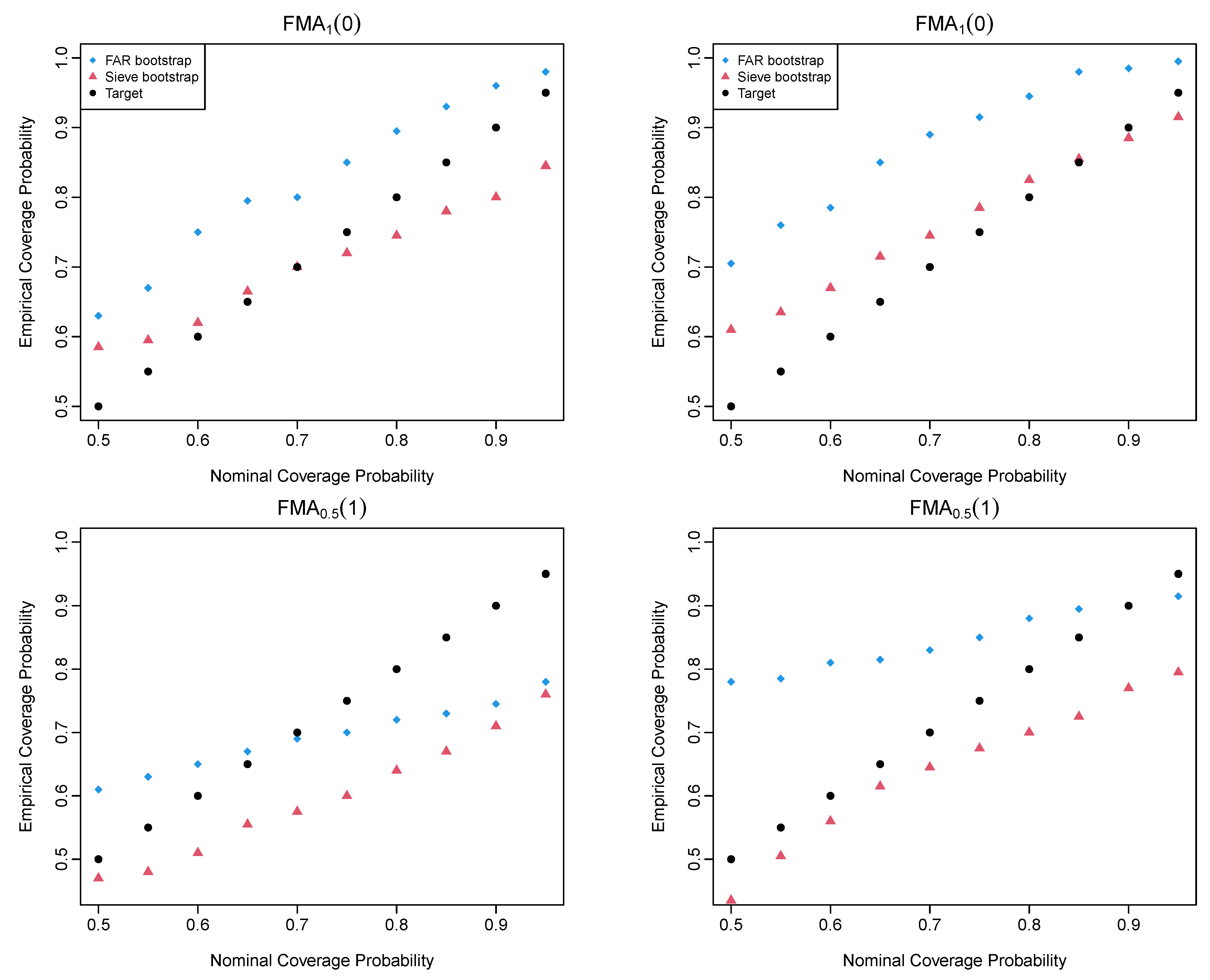
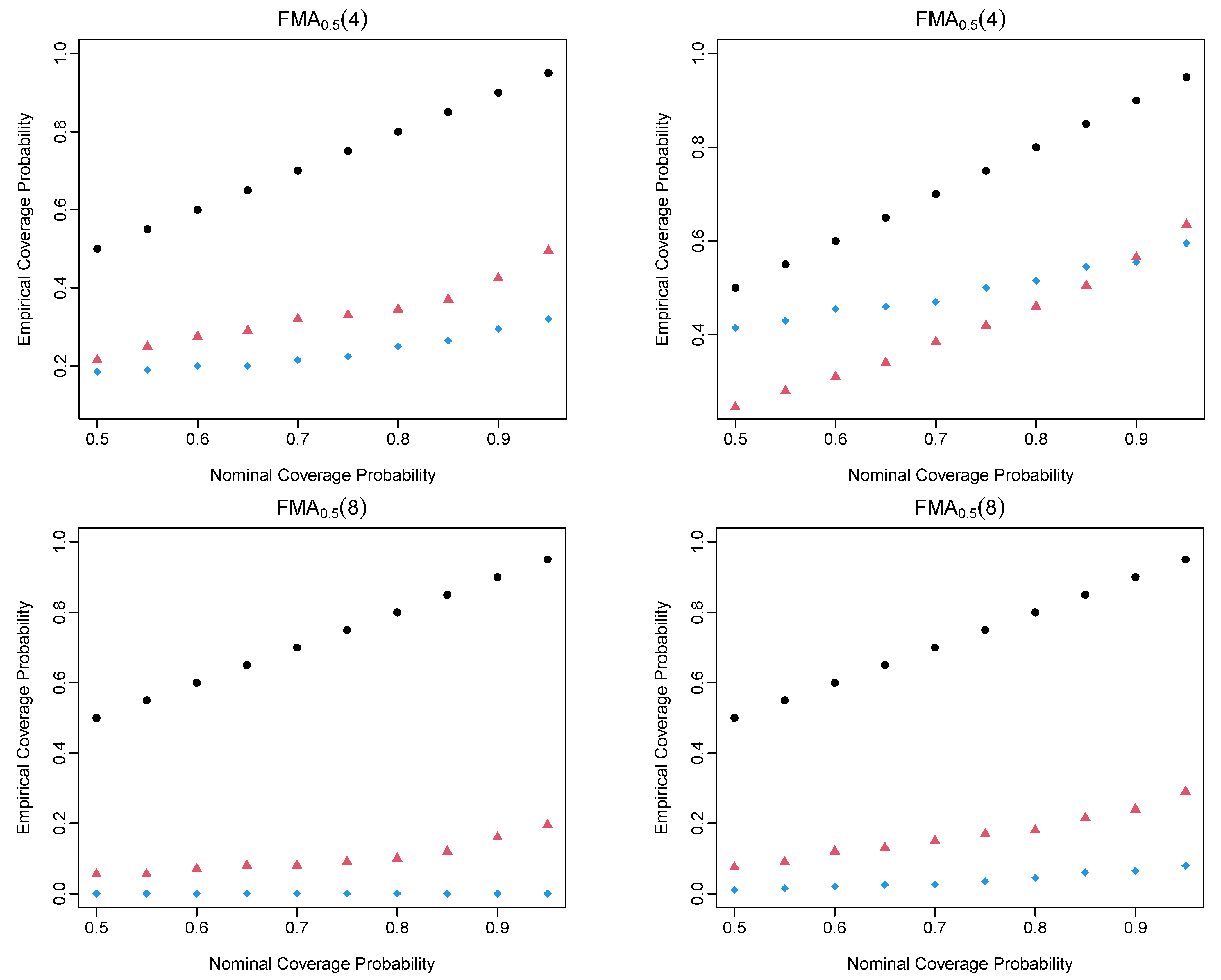
4.3. Simulation Results of the FMA Processes
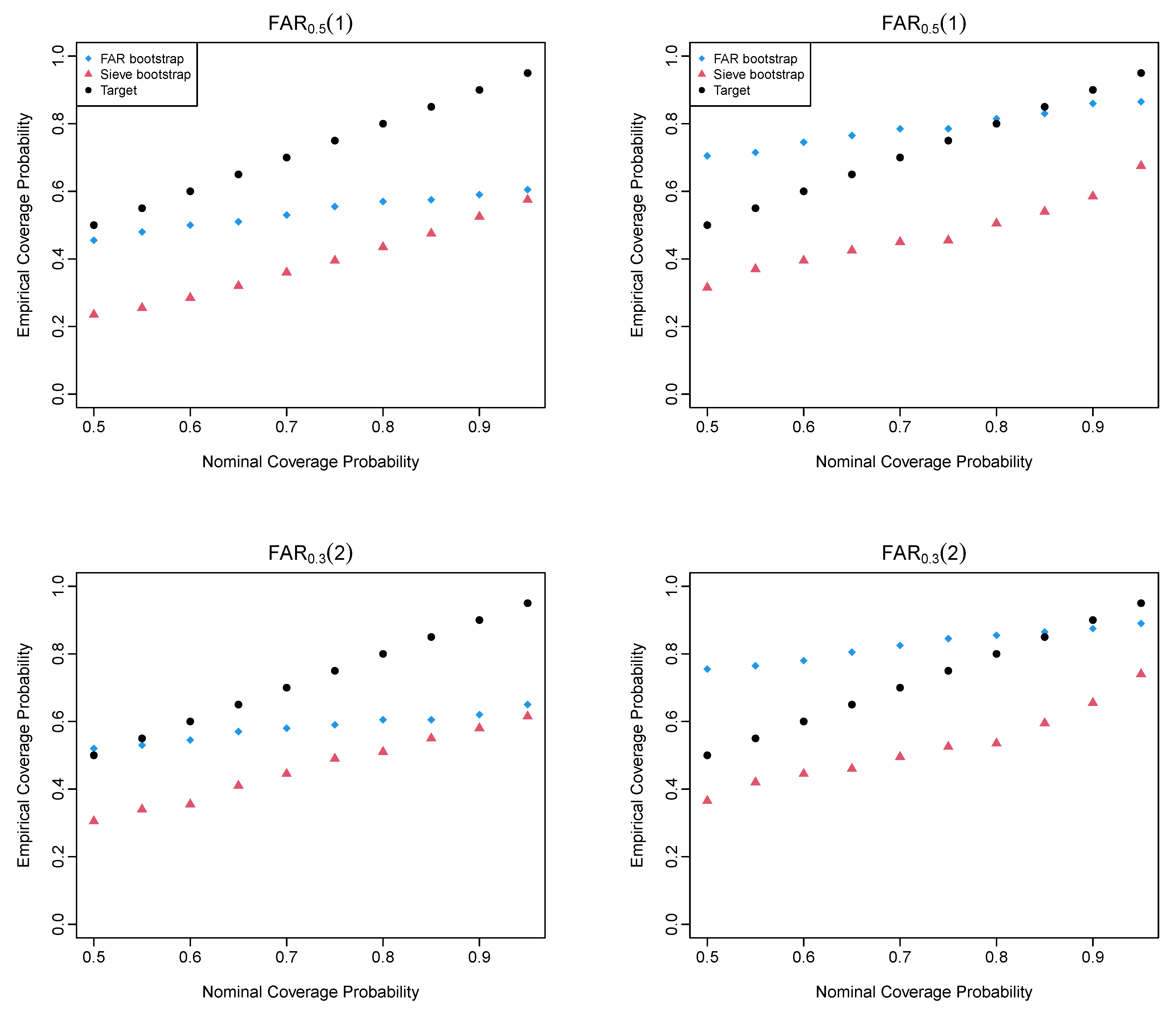
4.4. Simulation Results of the FAR Processes
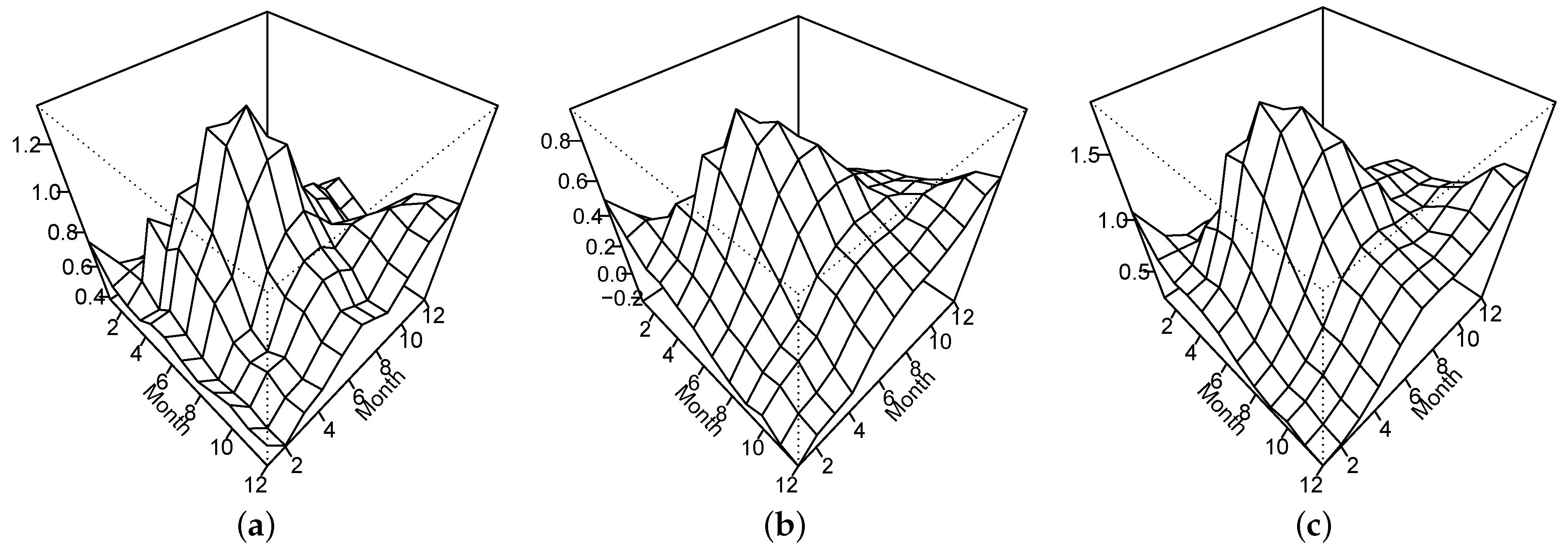
5. Monthly Sea Surface Temperature
6. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hörmann, S.; Kokoszka, P. Functional time series. In Handbook of Statistics; Rao, T.S., Rao, S.S., Eds.; Elsevier: Amsterdam, The Netherlands, 2012; Volume 30, pp. 157–186. [Google Scholar]
- Kokoszka, P.; Rice, G.; Shang, H.L. Inference for the autocovariance of a functional time series under conditional heteroscedasticity. J. Multivar. Anal. 2017, 162, 32–50. [Google Scholar] [CrossRef]
- Andersen, T.G.; Su, T.; Todorov, V.; Zhang, Z. Intraday periodic volatility curves. J. Am. Stat. Assoc. Theory Methods 2023, in press. [Google Scholar] [CrossRef]
- Ferraty, F.; Vieu, P. Nonparametric Functional Data Analysis: Theory and Practice; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Ramsay, J.O.; Silverman, B.W. Functional Data Analysis; Springer: New York, NY, USA, 2005. [Google Scholar]
- Kokoszka, P.; Reimherr, M. Introduction to Functional Data Analysis; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Peña, D.; Tsay, R.S. Statistical Learning for Big Dependent Data; Wiley: Hoboken, NJ, USA, 2021. [Google Scholar]
- Politis, D.N. The impact of bootstrap methods on time series analysis. Stat. Sci. 2003, 18, 219–230. [Google Scholar] [CrossRef]
- Hörmann, S.; Kidzinski, L.; Hallin, M. Dynamic functional principal components. J. R. Stat. Soc. Ser. B 2015, 77, 319–348. [Google Scholar] [CrossRef]
- Franke, J.; Nyarige, E.G. A residual-based bootstrap for functional autoregressions. Working paper, Technische Universität Kaiserslautern. arXiv 2019, arXiv:abs/1905.07635. [Google Scholar]
- Nyarige, E.G. The Bootstrap for the Functional Autoregressive Model FAR(1). Ph.D. Thesis, Technische Universität Kaiserslautern, Kaiserslautern, Germany, 2016. Available online: https://kluedo.ub.uni-kl.de/frontdoor/index/index/year/2016/docId/4410 (accessed on 31 January 2023).
- Pilavakis, D.; Paparoditis, E.; Sapatinas, T. Moving block and tapered block bootstrap for functional time series with an application to the K-sample mean problem. Bernoulli 2019, 25, 3496–3526. [Google Scholar] [CrossRef]
- Shang, H.L. Bootstrap methods for stationary functional time series. Stat. Comput. 2018, 28, 1–10. [Google Scholar] [CrossRef]
- Paparoditis, E. Sieve bootstrap for functional time series. Ann. Stat. 2018, 46, 3510–3538. [Google Scholar] [CrossRef]
- Ferraty, F.; Vieu, P. Kernel regression estimation for functional data. In The Oxford Handbook of Functional Data Analysis; Ferraty, F., Ed.; Oxford University Press: Oxford, UK, 2011; pp. 72–129. [Google Scholar]
- Zhu, T.; Politis, D.N. Kernel estimates of nonparametric functional autoregression models and their bootstrap approximation. Electron. J. Stat. 2017, 11, 2876–2906. [Google Scholar] [CrossRef]
- Paparoditis, E.; Shang, H.L. Bootstrap prediction bands for functional time series. J. Am. Stat. Assoc. Theory Methods 2023, 118, 972–986. [Google Scholar] [CrossRef]
- Rice, G.; Shang, H.L. A plug-in bandwidth selection procedure for long run covariance estimation with stationary functional time series. J. Time Ser. Anal. 2017, 38, 591–609. [Google Scholar] [CrossRef]
- Franke, J.; Hardle, W. On bootstrapping kernel spectral estimate. Ann. Stat. 1992, 20, 121–145. [Google Scholar] [CrossRef]
- Politis, D.N.; Romano, J.P. On flat-top spectral density estimators for homogeneous random fields. J. Stat. Plan. Inference 1996, 51, 41–53. [Google Scholar] [CrossRef]
- Li, D.; Robinson, P.M.; Shang, H.L. Long-range dependent curve time series. J. Am. Stat. Assoc. Theory Methods 2020, 115, 957–971. [Google Scholar] [CrossRef]
- Ahn, S.C.; Horenstein, A.R. Eigenvalue ratio test for the number of factors. Econometrica 2013, 81, 1203–1227. [Google Scholar]
- Hurvich, C.M.; Tsai, C.-L. A corrected Akaike information criterion for vector autoregressive model selection. J. Time Ser. Anal. 1993, 14, 271–279. [Google Scholar] [CrossRef]
- Bosq, D. Linear Processes in Function Spaces; Lecture notes in Statistics; Springer: New York, NY, USA, 2000. [Google Scholar]
- Lahiri, S.N. Resampling Methods for Dependent Data; Springer: New York, NY, USA, 2003. [Google Scholar]
- Mestre, G.; Portela, J.; Rice, G.; Roque, A.M.S.; Alonso, E. Functional time series model identification and diagnosis by means of auto- and partial autocorrelation analysis. Comput. Stat. Data Anal. 2021, 155, 107108. [Google Scholar] [CrossRef]
- Cardot, H.; Mas, A.; Sarda, P. CLT in functional linear regression models. Probab. Theory Relat. Fields 2007, 138, 325–361. [Google Scholar] [CrossRef]
- Horváth, L.; Kokoszka, P.; Rice, G. Testing stationarity of functional time series. J. Econom. 2014, 179, 66–82. [Google Scholar] [CrossRef]
- Kokoszka, P.; Reimherr, M. Determining the order of the functional autoregressive model. J. Time Ser. Anal. 2013, 34, 116–129. [Google Scholar] [CrossRef]
- Kreiss, J.-P.; Paparoditis, E.; Politis, D.N. On the range of validity of the autoregressive sieve bootstrap. Ann. Stat. 2011, 39, 2103–2130. [Google Scholar]
- Paparoditis, E.; Meyer, M.; Kreiss, J.-P. Extending the validity of frequency domain bootstrap methods to general stationary processes. Annals of Statistics 2020, 48, 2404–2427. [Google Scholar]
- Górecki, T.; Hörmann, S.; Horváth, L.; Kokoszka, P. Testing normality of functional time series. J. Time Ser. Anal. 2018, 39, 471–487. [Google Scholar] [CrossRef]

| DGP | |||||
|---|---|---|---|---|---|
| 0.3979 | 0.1967 | 0.1298 | 0.1172 | 0.1112 | |
| 0.4396 | 0.1914 | 0.1242 | 0.1178 | 0.1140 | |
| 0.0923 | 0.0930 | 0.0912 | 0.0922 | 0.0959 | |
| 0.3961 | 0.1123 | 0.1113 | 0.1107 | 0.1153 | |
| 0.6365 | 0.4647 | 0.3055 | 0.1849 | 0.1653 | |
| 0.7068 | 0.5986 | 0.4974 | 0.4024 | 0.3134 |
| FAR Bootstrap | Sieve Bootstrap | FAR Bootstrap | Sieve Bootstrap | |
| 0.1010 | 0.0525 | 0.1560 | 0.0490 | |
| 0.0845 | 0.1280 | 0.1280 | 0.0825 | |
| 0.4905 | 0.3935 | 0.2310 | 0.3105 | |
| 0.7250 | 0.6245 | 0.6870 | 0.5590 | |
| FAR Bootstrap | Sieve Bootstrap | FAR Bootstrap | Sieve Bootstrap | |
|---|---|---|---|---|
| 0.1880 | 0.3390 | 0.0910 | 0.2535 | |
| 0.1475 | 0.2650 | 0.1180 | 0.2015 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shang, H.L. Bootstrapping Long-Run Covariance of Stationary Functional Time Series. Forecasting 2024, 6, 138-151. https://doi.org/10.3390/forecast6010008
Shang HL. Bootstrapping Long-Run Covariance of Stationary Functional Time Series. Forecasting. 2024; 6(1):138-151. https://doi.org/10.3390/forecast6010008
Chicago/Turabian StyleShang, Han Lin. 2024. "Bootstrapping Long-Run Covariance of Stationary Functional Time Series" Forecasting 6, no. 1: 138-151. https://doi.org/10.3390/forecast6010008
APA StyleShang, H. L. (2024). Bootstrapping Long-Run Covariance of Stationary Functional Time Series. Forecasting, 6(1), 138-151. https://doi.org/10.3390/forecast6010008






