Abstract
Standard time-series modeling requires the stability of model parameters over time. The instability of model parameters is often caused by structural breaks, leading to the formation of nonlinear models. A state-dependent model (SDM) is a more general and flexible scheme in nonlinear modeling. On the other hand, time-series data often exhibit multiple frequency components, such as trends, seasonality, cycles, and noise. These frequency components can be optimized in forecasting using Singular Spectrum Analysis (SSA). Furthermore, the two most widely used approaches in SSA are Linear Recurrent Formula (SSAR) and Vector (SSAV). SSAV has better accuracy and robustness than SSAR, especially in handling structural breaks. Therefore, this research proposes modeling the SSAV coefficient with an SDM approach to take structural breaks called SDM-SSAV. SDM recursively updates the SSAV coefficient to adapt over time and between states using an Extended Kalman Filter (EKF). Empirical results with Indonesian Export data and simulation studies show that the accuracy of SDM-SSAV outperforms SSAR, SSAV, SDM-SSAR, hybrid ARIMA-LSTM, and VARI.
1. Introduction
Over the years, Indonesian economic conditions have experienced various uncertain turmoils, which are associated with the monetary crisis in Indonesia in 1997–1998. Others include the financial crisis of America in 2008–2009, which was triggered by the bankruptcy of Lehman Brothers [1,2], the economic slowdown of America and China in 2015–2016 [3], the outbreak of COVID-19 in early 2020 [4], and the Russian invasion of Ukraine in early 2022 [5]. These occurrences led to uncontrollable fluctuations in time-series patterns, including financial data and economic indicators, making them challenging to predict and often showing nonlinear behavior. Indonesian export is one of the economic indicators indicated to be affected by some of these phenomena, so the pattern becomes erratic fluctuations that tend to form nonlinear patterns.
Reference [6] stated that there are three methods for analyzing data with a nonlinear pattern, namely bilinear [7,8], threshold autoregressive [9,10], and exponential autoregressive models [11,12]. Each model class has a different procedure for determining the type of nonlinearity. Still, in practice, it may be challenging to decide which kind of nonlinearity best fits the characteristics of the dataset. This led to the proposal of the state-dependent model (SDM), which is more flexible and a general nonlinear model class [6]. SDM is the state space model that jumps from one segment of the state space to another. Meanwhile, nonlinear patterns are generally divided into two types, including structural breaks and time-varying. Several methods are used to model structural breaks, each offering unique advantages. These include Markov Switching, the threshold model, adaptive group lasso, time-varying parameters, and a combination of Realised Volatility and Heterogeneous Autoregressive methods, as implemented by [13,14,15,16,17,18,19].
However, this study focused on structural breaks characterized by breakpoints associated with the pattern of change over a certain period to ensure that the overall time-series data are divided into segments. Structural breaks refer to points at which a sudden shift in a time-series pattern or behavior occurs. A structural break implies that the parameters of the statistical model generating the time-series data change at specific points in time. The instability of model parameters is often caused by structural breaks, leading to the formation of nonlinear models [20,21,22]. The parameters of the model before and after the change point of the structural break are different, such that a single model cannot represent the whole data. Furthermore, a single model cannot describe the entire data if the change point occurs more than once. Various factors, including policy changes, economic crises, technological innovations, natural disasters, or market conditions, can cause structural breaks.
The concept of structural breaks was popularized by [23], who stated that the instability of model parameters often leads to forecasting failures due to a shock to a time-series dataset. According to [24], structural breaks are time-series data that fluctuate between the equilibrium and recovery state after a disturbance. This process is also defined as the result of a limited natural cycle in the economic system. Structural breaks in the economic system can cause model specifications to become nonlinear, posing a risk of producing less accurate predictions when modeled with standard linear time-series methods [25]. Therefore, using a method that accommodates this behavior of the data becomes crucial for obtaining more accurate results.
The other problem that must be considered in the time-series data analysis is the frequency element, comprising trends, seasonality, cycles, and noise, due to its significant influence on the investigation conclusion. Singular Spectrum Analysis (SSA) [26] presents a solution for optimizing the presence of the frequency element in time-series data. SSA is a nonparametric time-series method that does not rely on parametric assumptions, such as linearity, normality, and stationarity [27,28]. SSA has been implemented for various purposes besides reducing noise and forecasting. These include smoothing, handling missing data, identifying trends, decomposing seasonal components and periodicity, detecting structural changes, etc. SSA has also been used in various fields, such as geophysics and climate [29,30,31,32], engineering [33,34], medicine [35,36], and economics [37,38,39]. One method that can handle structural breaks and optimize the presence of frequency components in the data is SSA. A preliminary study has been carried out on the use of structural-break modeling with SSA by [37,38,40,41,42,43]. The results showed that in modeling structural breaks, the linear recurrent formulae (LRF) form recurrent equations in the SSA framework, leading to a biased conclusion. Therefore, to address this limitation, the LRF-form recurrent equation was modified to be an adaptive recurrent equation using SDM-SSAR [43].
Furthermore, structural break modeling with SDM is intended to handle the parameter shift observed in time-series data as it transitions from one segment to another due to a shock. Reference [43] utilized SDM in a recurrent SSA method, more specifically, using the Extended Kalman Filter (EKF) for state vector estimation. The EKF represents a nonlinear version of the Kalman filter, using the concept that nonlinear models can be approximated through local linearization. The EKF’s filtering process is based on a Taylor series approximation as a transition function between states, rendering it well-suited for nonlinear modeling [44].
SSA comprises three forecasting schemes, namely SSA-Recurrent (SSAR), SSA-Vector (SSAV), and SSA-Simultaneous [45]. However, SSAR [46] and SSAV [47] are the most widely used, where studies by [42,45,48] found that SSAV is more robust and has better accuracy than SSAR, particularly in handling structural breaks. Therefore, this study proposed using novel methods to obtain a robust model in the presence of a structural break through the development of a modified SSAV coefficient with SDM, called SDM-SSAV. By proposing this method, adequate knowledge about the business processes needed to model structural breaks that are more robust than the existing method, such as SDM-SSAR, is provided. Furthermore, this study has practical implications for business and government, particularly in predicting Indonesian exports.
2. Materials and Methods
2.1. Dataset
The empirical and simulation studies were used to implement the proposed method. The empirical study examined the data collected by Indonesia’s Central Bureau of Statistics (BPS), such as the monthly export value from 1993 to 2022, recorded in millions of US dollars. In addition, this study used export data because they significantly influence Indonesia’s economic performance. According to an analysis by [49], exports statistically positively affect economic growth. Moreover, preliminary studies by [50] and [51] reported that exports could impact the increase in investment, production, and overall economic growth. Considering Indonesian export data as an essential indicator in the economy, several researchers have modeled Indonesian export data, such as [52], who used the hybrid ARIMA-Long Short Term Memory (LSTM), and [53], who used the Vector Autoregressive Integrated (VARI) method.
The Monte Carlo simulation generated time-series data with structural breaks, trends, seasonality, noise, and a nonlinear pattern. The following equation generates the data:
with and t = 1, …, n. The τ is vertical movement or shifts that affect the mean level of the signal, is a constant, is the growth rate of the signal used to illustrate the trend element, and are the amplitude, and are the angular frequency utilized to describe the seasonal elements. The data generated in the simulation study were divided into two groups, namely small (n ≤ 300) and large samples (n > 300) [42].
2.2. Singular Spectrum Analysis (SSA)
The SSA process starts by assuming the presence of time-series data , where n > 2, with no zero or missing observation, a fixed integer called the window length (L) in the range , and [45]. SSA comprises two main stages, namely decomposition and reconstruction. Decomposition starts with embedding compiling time-series data into a trajectory matrix measuring L × K. Suppose the trajectory matrix is denoted as Z, then the formula is obtained as follows:
The Singular Value Decomposition (SVD) is the next step in the decomposition process. This step begins with the construction of a matrix to calculate three components, known as eigentriples: the eigenvalue, eigenvector, and principal component. The eigenvalues (λ1, λ2, …, λL) are obtained in descending order (λ1 ≥ λ2 ≥ … ≥ λL ≥ 0) using the equation , where I is an identity matrix. The eigenvector (U) is calculated with the equation . The eigenvector matrix consists of vectors (u1, u2, …, uL), which form an orthonormal system of the eigenvectors of matrix S corresponding to the eigenvalues. The principal components , are calculated using the following formula:
The G matrix is the sum of the matrix, where , d = L* with L* = min {L, K}. The SVD of the G trajectory matrix is formulated as follows:
The SVD of the complete trajectory matrix can be described using Equation (5):
The matrix G has a rank denoted by d = max{i, where λi > 0}, hence, when d = L, then the matrix G = Z. The second stage is reconstruction, which starts with grouping eigentriples according to patterns or frequency characteristics, such as trends, seasonality, cyclicality, and noise. This process partitions the matrix into m subsets of disjoints I1, I2, …, Im, and Equation (4) can be written as follows:
Grouping is used to construct a matrix in (4); suppose m = 2, then I1 = I = {i1, …, ir} and I2 = {1, …, d}\I, where 1 ≤ i1, …, ir ≤ d. The next step in the reconstruction is to diagonal average each GIm matrix into new time-series data of n denoted as follows:
The process of diagonal averaging of the G matrix uses the following Formula [54]:
where L* = min(L, K), K* = max(L, K), and . Meanwhile when L < K and for others, and hence, the reconstruction method used to obtain the new time-series data is denoted by . The LRF forecasting process utilizes the last (L − 1) observations from new time-series data multiplied by the LRF parameter coefficient . To obtain the LRF coefficient, U = [u1:…:ur], where ui is a vector that has an element (L − 1) of vector ui, then for i = 1, the first component of eigenvector u1, i.e., (u1,1, u2,1, …, uL-1,1). When , with is the last component of vector ui with , then the LRF parameter coefficients is formulated as follows.
Meanwhile, the time-series data of the last forecasting result at point L of the new time-series data is formulated as follows.
The new time-series data of the LRF forecasting result for the h-th point is defined as follows.
In this study, the LRF coefficient is used to develop structural-break modeling. The LRF coefficient is important for understanding time-series data dynamics and enables optimal forecasting at multiple stages (multi-step) [43].
2.3. SSA Parameter Coefficient Mofdeling Using SDM
In the SDM method, the LRF parameter coefficient is used to change the data pattern. Assuming are the state vector of the time-series data, then according to the proposed concept by [6], the propagation of the LRF parameter coefficient is defined as a function of Yn, and Equation (10) is formulated as follows.
The SDM method treats the parameter coefficient change according to the dynamics of state and time. Where , with u = 1, 2, …, (L − 1) is assumed to be an analytic function that changes slowly over time and is elaborated on through the expansion of the Taylor series.
where , is the gradient, and d is the length of the seasonal period of the time-series data. The gradient parameter is an unknown hyperparameter and is assumed to change slowly in the random walk as follows:
where and are the sequence of random variables valued at independent matrics, such that . Additionally, Equation (12) is expressed in state space format, where the state vector is changed from to the state-dependent coefficient added with the gradient, as follows:
where is a vector that represents the model parameter with functions of . Replace in Equation (12) with in Equation (15), this produces the state-space model as follows:
is an innate characteristic of the system used to capture the system’s movement, is a transition matrix for the state shift characterized by the shape of diagonal blocks developed over time. Meanwhile, is the measurement noise, and is the process noise. The next step is estimating the vector state using the EKF procedure.
The stages of estimating the vector state using EKF are as follows [43]:
where is formulated as follows:
is a Kalman gain matrix formulated as follows:
where represents the next step forecasting error’s variance–covariance matrix, which can be expressed as follows:
is a forecasting error variance on one step later , where the error is formulated as follows:
is a variance–covariance matrix of , and hence, the order of values can be calculated as follows using the conventional Kalman filter:
The initial values of , , and are calculated using the bootstrap SSA algorithm [28,55] and establishing , , and , where and are a variance–covariance matrix of .
2.4. SSA Vector Parameter Coefficient Modeling Using SDM
In this section, we develop the SSAV coefficient using the SDM method from being fixed over time to being adaptable to shocks over time. The process of the SDM-SSAV forecasting algorithm starts by continuing the sequence of vectors in matrix G in Equation (7) to ensure the forecasting algorithm generates time-series data with h points in the next period as follows:
- Form a matrix that is a linear operator showing orthogonal projections c , where , and is a modified LRF parameter coefficient based on the EKF in Equation (17).where , and is a vector of parameter coefficients that is a function of and has a component , estimated using the EKF.
- Forming SSAV operator , which is formulated as follows:
- The matrix is a combination of matrices G and , where the matrix , for i = K + 1, …, K + h + L − 1. The vectors that make up the matrix are denoted as follows:The matrix has the following structure: .
- Applying a diagonal averaging process to the matrix to obtain prediction in the 1st to n-th and the next h-th point prediction, . Therefore, the forecasting results in the next h period are denoted as follows: .
2.5. Accuracy Evaluation
The present study assessed the performance of the proposed forecasting methods with two commonly used metrics, namely the Root Mean Square Error (RMSE) [56], as stated in Equation (25).
Where is the h-th next step predicted value of out-of-sample data, is the h-th true value of out-of-sample, and m is the total length of the out-of-sample data. In the accuracy evaluation, we compare our proposed method, SDM-SSAV, with SSAV, SSAR, SDM-SSAR, hybrid ARIMA-LSTM, and VARI. Meanwhile, in the simulation study, we compare our proposed method with an existing method that considers structural breaks, namely SDM-SSAR.
3. Results and Discussion
This section is divided into two subsections, namely the analysis of the empirical case and simulation study, which were obtained using the proposed methods for modeling structural breaks.
3.1. Modeling Indonesian Export Data Using SSAR, SSAV, SDM-SSAR, SDM-SSAV, Hybrid ARIMA-LSTM, and VARI
To ensure the appropriateness of the analysis method, it is important to identify the characteristics of the observed data. The characteristics include measured critical characteristics, such as the mean, standard deviation, normality, stationarity, nonlinearity, decomposition, and structural breaks. A visual representation of Indonesia’s monthly export data from January 1993 to December 2022 is shown in Figure 1.
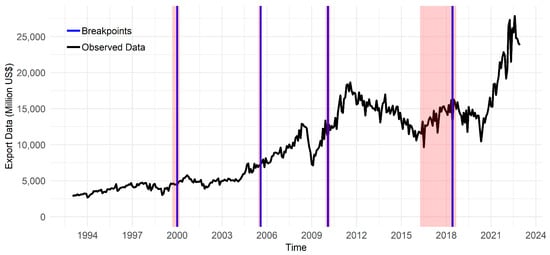
Figure 1.
Indonesian monthly export value during January 1993–December 2022 (million US$).
The black line in Figure 1 depicts Indonesia’s export data from January 1993 to December 2022. In the 1990s, exports were generally stable, except from mid-1997 to 1998, when there was a monetary crisis. Furthermore, in the 2000s, exports continued to increase steadily, with a temporary decrease from July 2008 to February 2009. This decrease was due to the global financial crisis, which started on 15 September 2008, when one of the largest companies in the United States, Lehman Brothers, went bankrupt. Despite this challenge, the Indonesian economy recovered immediately, as showed by an upward trend until its peak in August 2011. Export performance remained highly volatile during the subsequent decade from 2010 to 2022. This volatility was influenced by the economic slowdown of several trading partner countries in 2015 and 2016, specifically America and China, in addition to the outbreak of COVID-19 in early 2020. The development of Indonesian exports during that period showed a stochastic upward trend despite the numerous turmoils from 1993 to 2022.
Four breakpoints, identified based on the results of the Bai-Perron test, are shown in Figure 1 as blue lines, marking significant shifts in January 2001, August 2005, February 2010, and June 2018. Meanwhile, the red area in Figure 1 shows the confidence interval of the estimated breakpoint. In addition, the detailed information about the Bai-Perron test operation is stated in [57]. These structural breaks show that specific points in time have experienced substantial shifts in the underlying data-generating process. Such shifts could be attributed to various factors, including changes in economic conditions, policy interventions, or external events. Consequently, these structural breaks introduced changes in statistical properties, like the mean, effectively illustrating the sensitivity of the data to external shocks or shifts in trends.
The Teräsvirta test [56] showed a p-value of 0.0342 with a nonlinear pattern because it is less than the 5% level. Additionally, the nonstationary nature is indicated by the Zivot-Andrews test [58], with a statistic of −5.5793 exceeding the critical value of −5.08. The Shapiro-Wilks test [59] further supports non-Gaussian distribution, yielding a p-value of 1.398 × 10−13, less than the 5% level. The Zivot-Andrew test was selected due to its consideration of structural changes in time-series data, consistent with the expected characteristics in Indonesian export data. The test was used to determine the presence of a unit root. Indonesian export data have considerable variability, evidenced by a substantial standard deviation of 5627.53 million US$. In addition, it had a reasonably large average of 9983 million US$. Table 1 shows a comprehensive overview of the characteristics of Indonesian export data.

Table 1.
Statistics descriptive of Indonesian export for the period 1993–2022.
Figure 2 shows various patterns in the components of Indonesia’s export data, black line shows the observed data, trends (blue line), seasonality (red line), and noise components (purple line). The trend component reflects the long-term direction or pattern of the data, showing a consistent upward movement in Indonesia’s export values. Meanwhile, the seasonal component showed recurring patterns or fluctuations at specific intervals, depicting a slowdown in exports towards the end of each year. This slowdown was attributed to extended holidays, commonly known as holiday blues, impacting trade activities during that period.
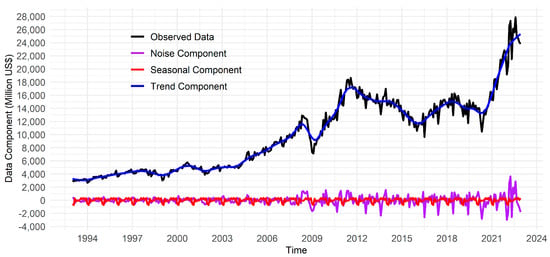
Figure 2.
Decomposition of Indonesian exports in January 1993–December 2022.
This analysis evaluating the predictive accuracy of the SDM-SSAV method compared to SSAR, SSAV, SDM-SSAR, hybrid ARIMA-LSTM, and VARI, using Indonesian export data. A more detailed operation of hybrid ARIMA-LSTM can be seen in [52], while a more detailed operation of the VARI method can be seen in [53]. Furthermore, in this comparison, we group SDM-SSAV, SSAV, SSAR, and SDM-SSAR in the frequency domain method group, while the hybrid ARIMA-LSTM and VARI methods are in the non-frequency domain group. Experiments were conducted with the training data concerning this evaluation, exploring several parameter combinations sensitive to forecasting accuracy. From these experiments, the optimal parameters are a window length (L) of 12, a grouping effect (r) of one, and a horizon of 26, representing the testing data’s size. The training data size is the total sample minus the horizon. Meanwhile, to determine the initial values of , , and using Bootstrap SSA, the optimum smoothing factor is 0.05 and 9.0 × 10−6. For effectiveness, only the experimental results with the optimum parameters that yield the highest accuracy are shown in Table 2, Table 3, Table 4, Table 5 and Table 6.

Table 2.
RMSE of SDM-SSAV and SSAR.

Table 3.
RMSE of SDM-SSAV and SSAV.

Table 4.
RMSE of SDM-SSAV and SDM-SSAR.

Table 5.
RMSE of SDM-SSAV and Hybrid ARIMA-LSTM.

Table 6.
RMSE of SDM-SSAV and VAR(2,1).
Table 2 shows a comprehensive assessment of the performance of SDM-SSAV and SSAR standards across various forecasting points (h = 1 to 12). In addition, RRMSE was less than one for every forecasting point, showing the superior accuracy of the SDM-SSAV method in comparison to the SSAR method. The obtained p-values of the Diebold-Mariano test, which were consistently less than the 5% significance level for all forecasting points, signified a statistically significant difference in the performance between the SDM-SSAV and SSAR methods. A detailed operation of the Diebold-Mariano test is reported in the research provided in [60]. This result suggested that modeling the SSAV coefficient parameters with the SDM method statistically significantly impacts the SSAV standard performance, particularly in handling structural breaks.
Table 3 shows that the RRMSE at forecasting points h = 2 to 12 has a value less than one, while at h = 1, both methods illustrate similar performances. All p-values from the Diebold-Mariano test were less than the 5% significance level except at h = 1 and 2. These results showed that although the SDM-SSAV had smaller RMSE values at all forecasting points, its statistical superiority in accuracy was explicitly observed at h = 3 to 12.
Table 4 shows that the SDM-SSAV method outperformed the SDM-SSAR regarding forecasting accuracy, as illustrated by the RRMSE values consistently being less than one for all forecasting points (h = 1 to 12). This result implied a better performance and accuracy of the SDM-SSAV method across the forecast horizon. However, the p-value obtained from the Diebold-Mariano test shows that the forecasting points from h = 1 to 10 are statistically significant at the 10% level. This result indicates that the SDM-SSAV and SDM-SSAR forecasting results are statistically different, at least up to the 10-month forecasting point. Furthermore, it was concluded that the SDM-SSAV method was statistically superior to the SDM-SSAR in terms of accuracy for the next ten months.
Table 5 shows that the SDM-SSAV method outperformed the Hybrid ARIMA-LSTM, as illustrated based on the RRMSE values of less than one for all forecasting points (h = 1 to 12). This result implied a better performance and accuracy of the SDM-SSAV method across the forecast horizon. The p-value obtained from the Diebold-Mariano test showed that the forecasting points from h = 1 to 12 are statistically significant at the 5% level. This result indicates that statistically, SDM-SSAV has accuracy differences and outperforms the Hybrid ARIMA-LSTM for the next one to 12 months.
Table 6 shows that the SDM-SSAV method outperformed the VAR(2,1), as illustrated based on the RRMSE values of less than one for all forecasting points (h = 1 to 12). This result implied a better performance and accuracy of the SDM-SSAV method across the forecast horizon. The p-value obtained from the Diebold-Mariano test showed that the forecasting points from h = 1 to 12 are statistically significant at the 5% level. Despite the statistical significance within this range, it was concluded that the SDM-SSAV method was statistically different and superior to the VAR(2,1) in terms of accuracy for the next one to 12 months. Based on the RMSE value in Table 2, Table 3, Table 4, Table 5 and Table 6 the closest to the accuracy of the SDM-SSAV method is SDM-SSAR. This result implies that approaches that consider structural breaks—sudden variations in time-series data—are typically more accurate than those that do not.
3.2. Simulation Study
In the simulation study, we generated several data using Monte Carlo simulation according to Equation (1) and setting parameter values in four scenarios as shown in Table 7 below.

Table 7.
Parameter values in the study simulation.
To assess the consistent pattern accuracy of the forecasting models, this simulation study performed 100 replications in each scenario. The results of data generation from one of the replications are then examined for several characteristics, such as stationarity, linearity, and the presence of structural breaks, shown in Table 8 below. Table 8 shows that the generated data in all scenarios showed nonstationary based on test statistics of the Zivot-Andrews test of −5.57, smaller than the critical value of −5.08. Moreover, nonlinear characteristics are confirmed through the p-value of the Teräsvirta test, which is smaller than the 5% significance level. This result highlights the complexity of the data; thus, modeling with a linear model may not be sufficient to capture the underlying pattern. Therefore, modeling with nonlinear methods might be more appropriate. In addition, the presence of structural breaks in the data was detected based on the Bai-Perron test. The existence of structural breaks suggested changes in statistical properties, specifically a shift in the mean over time due to external shocks. Identifying these breaks is crucial for accurate modeling and forecasting, as ignoring them could lead to biased or misleading results, as demonstrated by [43]. These results indicated that the data-generating process aligned with the proposed method’s specifications, especially in linearity and the presence of structural breaks.

Table 8.
Characteristic identification of generated data.
In Figure 3, a series of time-series plots was generated using Equation (1) and the parameters according to Table 7. A dashed black line depicts the breakpoints, and the red line indicates the confidence interval of the breakpoint estimate. Breakpoints are significant changes or shifts in a data series that delineate one segment from another, often indicating a change in trend or behavior in the time series data. Each subfigure in Figure 3 showed distinct characteristics of the generated data. Figure 3a,b, and c show 157, 207, and 365 time-series data points generated with four breakpoints, thus dividing the data into five segments. Furthermore, Figure 3d shows 405 time series data points with five breakpoints, thus dividing the data into six segments.
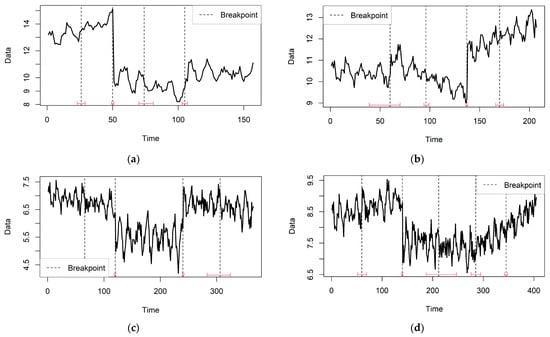
Figure 3.
(a) Data generated in the first scenario (n = 157); (b) data generated in the second scenario (n = 207); (c) data generated in the third scenario (n = 365); (d) data generated in the fourth scenario (n = 405).
Figure 3 is a visual representation of the essential data components, namely the trend, seasonality, and noise, that motivate the use of the SSA method for forecasting. In Figure 3b,d, an upward trend was observed, while Figure 3a,c showed a downward trend. Similarly, the four plots in Figure 3 depict different seasonal periods, representing distinct seasonal elements. This variation in seasonal periods allows for testing the effectiveness of the forecasting methods in handling data with diverse seasonal patterns. The noise element was generated through a normal distribution and with a distinct average value in each subsample (ni), while the parameter π was also set differently for each scenario. However, the deliberate decision to maintain a constant variance value of 0.2 across all scenarios aims to generate data with structural breaks solely in the mean, with no consideration given to those in the variance.
As Table 4 shows, the method with the closest accuracy to SDM-SSAV is SDM-SSAR; in this simulation study, we focus on comparing the accuracy of only these two methods. These methods are applied to predict the out-sample data, divided into 12 forecast points labeled as h = 1 to 12. The accuracy of both methods is then assessed using the RMSE based on the predicted data. The results of this comparative evaluation are visually presented through a boxplot. The data simulation process depends on several parameters, such as the Window Length (L) and Grouping Effect (r), and configuration of the parameters detailed in Section 2.1. The SDM-SSAR and SDM-SSAV methods were applied with alternative parameter values, and the optimal ones were selected based on minimizing the RMSE at each out-sample prediction point (h = 1 to 12). The process was replicated 100 times in each scenario to determine a consistent accuracy pattern. In addition, the simulation process is applied to small sample sizes (n < 300), namely n1 = 157 and n2 = 207, and large sample sizes (n ≥ 300), such as n3 = 365 and n4 = 405.
Figure 4 compares the SDM-SSAV and SDM-SSAR models across various scenarios, considering forecasting points from h = 1 to 12, each with 100 replications. However, the median RMSE of the SDM-SSAV is consistently less than that of the SDM-SSAR across all scenarios and forecasting points. These simulation results align with the ones shown in Table 5, where the accuracy evaluation using Indonesian export data illustrated that the RMSE of the SDM-SSAV is less than the SDM-SSAR for forecasting points ranging from h = 1 to 12. The simulations focus on the superior accuracy of the SDM-SSAV across diverse conditions, including small (n < 300) and large sample sizes (n > 300), non-stationary and nonlinear data, and scenarios with structural breaks in the data. The result showed that as the forecasting point moves further into the future, RMSE values increase. Additionally, the performance of both methods weakens with more structural breaks.
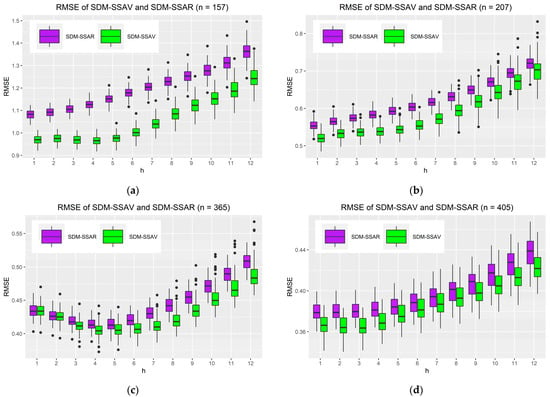
Figure 4.
(a). Boxplot RMSE of the SDM-SSAV and SDM-SSAR from the data-generating process n = 157 with L = 12, r = 1, horizon = 29, and smoothing factor = 5.0 × 10−6. (b) Boxplot RMSE of the SDM-SSAV and SDM-SSAR from the data-generating process n = 207 with L = 12, r = 1, horizon = 24, and smoothing factor = 2.0 × 10−6. (c) Boxplot RMSE of the SDM-SSAV and SDM-SSAR from the data-generating process n = 365 with L = 12, r = 1, horizon = 28, and smoothing factor = 5.0 × 10−8. (d) Boxplot RMSE of the SDM-SSAV and SDM-SSAR from the data-generating process n = 405 with L = 14, r = 1, horizon = 27, and smoothing factor = 5.0 × 10−8.
The SDM-SSAV requires a longer simulation time than the SDM-SSAR, irrespective of its superior accuracy. In the first scenario (Figure 4a), the SDM-SSAV lasts approximately 41,969.60 s, significantly longer than the SDM-SSAR, which is completed in about 14,885.68 s. The trend continues in the second scenario (Figure 4b), with the SDM-SSAV requiring approximately 17,477.22 s, while the SDM-SSAR finished in a shorter time of relatively 6554.68 s. In the third scenario (Figure 4c), the SDM-SSAV and SDM-SSAR lasted approximately 139,061.73 s and 35,522.88 s, respectively. Finally, in the fourth scenario (Figure 4d), the SDM-SSAV and SDM-SSAR require a simulation time of 166,869.03 s and 39,348.86 s, respectively.
3.3. Forecasting Indonesian Export Using SDM-SSAV
This section discusses the results of forecasting Indonesian export data for 12 months in 2023. Applying the SDM-SSAV method, with the parameters set at L = 12, r = 1, and a smoothing factor of 0.2 and 1.2 × 10−5. The actual Indonesian export, predictive, and 12-step ahead forecasting data are shown in Figure 5. The plotted forecast showed a significant decline in early 2023, followed by an improvement in export performance over the subsequent nine months, albeit with a decrease in the final three months. This decline was attributed to a seasonal factor, where exports traditionally decrease at the beginning of each year due to the holiday blues phenomenon. In addition, world geopolitical conditions have changed due to the Russian invasion of Ukraine in early 2022, which directly affected the increase in world oil prices. Uncertainty in the global geopolitical conditions has resulted in lower demand for essential export commodities from major trading partners, such as China, thereby influencing Indonesian export performance.
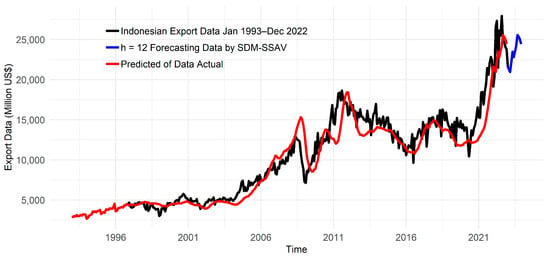
Figure 5.
The Indonesian export during January 1993–December 2022, based on predicted data (January 1993–December 2022), and the next 12-month forecasting data (January–December 2023).
4. Conclusions
In conclusion, the precision of forecasts can be compromised by structural breaks in time-series data. Therefore, this study addressed these challenges by implementing the SDM methods to develop the SSAV coefficient. The SDM method played a significant role in modeling SSAV coefficients, which were initially fixed to be adaptive according to state and time shifts. This approach allowed for flexible adjustments to the number of states when implementing the SDM method in SSAV. Additionally, the SSAV coefficients derived from SDM modeling were used in the SSAV forecasting scheme, leading to the creation of the SDM-SSAV method. Indonesian export data were used along with the conducted simulation studies to assess the effectiveness of the SDM-SSAV in consistently handling structural breaks. Based on the implementation of Indonesian export data and the simulation studies, the SDM-SSAV outperformed the existing method in frequency and non-frequency domain methods at all forecast points of h = 1 to 12 points. In addition, the SDM-SSAV proved to be efficient at handling structural breaks better than its counterpart, even in the case of data with nonlinear and nonstationary patterns without requiring transformation, like differencing. However, the SDM-SSAV needed more time for data processing compared to the SDM-SSAR. A more stable method against outlier data with a more efficient processing time is required for future investigation.
Author Contributions
Conceptualization, Y.S.; Formal analysis, Y.S. and D.D.P.; Funding acquisition, H.K.; Investigation, Y.S.; Methodology, Y.S. and D.D.P.; Project administration, H.K.; Resources, Y.S.; Software, Y.S.; Supervision, H.K. and D.D.P.; Validation, Y.S., H.K., and D.D.P.; Visualization, Y.S.; Writing—original draft, Y.S.; Writing—review and editing, H.K. and D.D.P. All authors have read and agreed to the published version of the manuscript.
Funding
This study received by the Ministry of Education, Culture, Research, and Technology, Indonesia, under Grant 0557/E5.5/AL.04/2023.
Data Availability Statement
The data in this study are available at the official Statistics of Indonesia (BPS): www.bps.go.id (accessed on 2 September 2023).
Acknowledgments
The authors are grateful to the lecturers and partners in the Doctor Degree in Statistics, Department of Statistics, Faculty of Science and Data Analytics, Institut Teknologi Sepuluh Nopember (ITS). They are also grateful to The Statistics of Indonesia (BPS) and the Ministry of Education, Culture, Research, and Technology, Indonesia.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Cao, Y.K.; Guo, H.F. The impact of global financial crisis on China’s trade in forest product and countermeasures. In Proceedings of the 2009 International Conference on Information Management, Innovation Management and Industrial Engineering, ICIII, Xi’an, China, 26–27 December 2009; Volume 4, pp. 580–583. [Google Scholar] [CrossRef]
- Afonso, A.; Blanco-Arana, M.C. Financial and economic development in the context of the global 2008-09 financial crisis. Int. Econ. J. 2022, 169, 30–42. [Google Scholar] [CrossRef]
- Cashin, P.; Mohaddes, K.; Raissi, M. China’ s slowdown and global financial market volatility: Is world growth losing out? Emerg. Mark. Rev. 2017, 31, 164–175. [Google Scholar] [CrossRef]
- Hu, S.; Gao, Y.; Niu, Z.; Jiang, Y.; Li, L.; Xiao, X.; Wang, M.; Fang, E.F.; Menpes-Smith, W.; Xia, J.; et al. Weakly Supervised Deep Learning for COVID-19 Infection Detection and Classification from CT Images. IEEE Access 2020, 8, 118869–118883. [Google Scholar] [CrossRef]
- Zgurovsky, M.; Kravchenko, M.; Boiarynova, K.; Kopishynska, K.; Pyshnograiev, I. The Energy Independence of the European Countries: Consequences of the Russia’s Military Invasion of Ukraine. In Proceedings of the 2022 IEEE 3rd International Conference on System Analysis & Intelligent Computing (SAIC), Kyiv, Ukraine, 4–7 October 2022. [Google Scholar] [CrossRef]
- Priestley, M.B. State-Dependent Models: A General Approach to Non-Linear Time Series Analysis. J. Time Ser. Anal. 1980, 1, 47–71. [Google Scholar] [CrossRef]
- Mohler, R.R. Bilinear Control Processes: With Applications to Engineering, Ecology, and Medicine; Academic Press: New York, NY, USA; London, UK, 1973; Volume 106. [Google Scholar]
- Brockett, R.W. Volterra series and geometric control theory. Automatica 1976, 12, 167–176. [Google Scholar] [CrossRef]
- Tong, H. Non-Linear Time Series: A Dynamical System Approach; Oxford University Press: New York, NY, USA, 1990. [Google Scholar]
- Tong, H.; Lim, K.S. Threshold autoregression, limit cycles and cyclical data. Journal of the Royal Statistical Society. Series B (Methodological) 1980, 42, 245–292. [Google Scholar] [CrossRef]
- Haggan, V.; Ozaki, T. Modelling Nonlinear Random Vibrations Using an Amplitude-Dependent Autoregressive Time Series Model. Biometrika 1981, 68, 189–196. [Google Scholar] [CrossRef]
- Ozaki, T. Non-Linear Time Series Models for Non-Linear Random Vibrations. Journal of Applied Probability. 1980, 17, 84–93. [Google Scholar] [CrossRef]
- Ardia, D.; Bluteau, K.; Boudt, K.; Catania, L.; Trottier, D.A. Markov-switching GARCH models in R: The MSGARCH package. J. Stat. Softw. 2019, 91, 1–38. [Google Scholar] [CrossRef]
- Davidescu, A.A.; Apostu, S.A.; Paul, A. Comparative analysis of different univariate forecasting methods in modelling and predicting the romanian unemployment rate for the period 2021–2022. Entropy 2021, 23, 325. [Google Scholar] [CrossRef]
- Behrendt, S.; Schweikert, K. A Note on Adaptive Group Lasso for Structural Break Time Series. Econ. Stat. 2021, 17, 156–172. [Google Scholar] [CrossRef]
- Ito, M. Detecting Structural Breaks in Foreign Exchange Markets by using the group LASSO technique. arXiv 2022, arXiv:2202.02988. [Google Scholar]
- Ito, M.; Noda, A.; Wada, T. An Alternative Estimation Method of a Time-Varying Parameter Model. arXiv 2017, arXiv:1707.06837. [Google Scholar] [CrossRef]
- Gong, X.; Lin, B. Structural breaks and volatility forecasting in the copper futures market. J. Futur. Mark. 2018, 38, 290–339. [Google Scholar] [CrossRef]
- De Gaetano, D. Forecast combinations in the presence of structural breaks: Evidence from U.S. equity markets. Mathematics 2018, 6, 34. [Google Scholar] [CrossRef]
- Antoch, J.; Hanousek, J.; Horváth, L.; Hušková, M.; Wang, S. Structural breaks in panel data: Large number of panels and short length time series. Econom. Rev. 2019, 38, 828–855. [Google Scholar] [CrossRef]
- Hansen, B.E. The New Econometrics of Structural Change. J. Econ. Perspect. 2001, 15, 117–128. [Google Scholar] [CrossRef]
- Kruiniger, H. Not So Fixed Effects: Correlated Structural Breaks in Panel Data; Queen Mary University: London, UK, 2008; pp. 1–33. [Google Scholar]
- Clements, M.P.; Hendry, D.F. Intercept Corrections and Structural Change. J. Appl. Econom. 1996, 11, 475–494. [Google Scholar] [CrossRef]
- Beaudry, P.; Galizia, D.; Portier, F. Reviving the Limit Cycle View of Macroeconomic Fluctuations; NBER Working Papers Series; National Bureau of Economic Research: Cambridge, MA, USA, 2015; pp. 1–23. [Google Scholar]
- Kantz, H.; Schreiber, T. Nonlinear Time Series Analysis; Cambridge University Press: Cambridge, UK, 2004; Volume 7. [Google Scholar]
- Broomhead, D.S.; King, G.P. Extracting qualitative dynamics from experimental data. Phys. D Nonlinear Phenom. 1986, 20, 217–236. [Google Scholar] [CrossRef]
- Sanei, S.; Hassani, H. Singular Spectrum Analysis of Biomedical Signals; CRC Press: Boca Raton, FL, USA, 2015. [Google Scholar]
- Golyandina, N.; Nekrutkin, V.; Zhigljavsky, A. Analysis of Time Series Structure SSA and Related Techniques, 1st ed.; Chapman & Hall/CRC: London, UK, 2001. [Google Scholar]
- Hou, Z.; Wen, G.; Tang, P.; Cheng, G. Periodicity of Carbon Element Distribution Along Casting Direction in Continuous-Casting Billet by Using Singular Spectrum Analysis. Met. Mater. Trans. B 2014, 45, 1817–1826. [Google Scholar] [CrossRef]
- Le Bail, K.; Gipson, J.M.; MacMillan, D.S. Quantifying the Correlation Between the MEI and LOD Variations by Decomposing LOD with Singular Spectrum Analysis BT. In Earth on the Edge: Science for a Sustainable Planet; Springer: Berlin/Heidelberg, Germany, 2014; pp. 473–477. [Google Scholar]
- Chang, Y.W.; Van Bang, P.; Loh, C.H. Identification of Basin Topography Characteristic Using Multivariate Singular Spectrum Analysis: Case Study of the Taipei Basin. Eng. Geol. 2015, 197, 240–252. [Google Scholar] [CrossRef]
- Ghil, M.; Allen, M.R.; Dettinger, M.D.; Ide, K.; Kondrashov, D.; Mann, M.E.; Robertson, A.W.; Saunders, A.; Tian, Y.; Varadi, F.; et al. Advanced spectral methods for climatic time series. Rev. Geophys. 2002, 40, 3-1–3-41. [Google Scholar] [CrossRef]
- Chao, S.H.; Loh, C.H. Application of singular spectrum analysis to structural monitoring and damage diagnosis of bridges. Struct. Infrastruct. Eng. 2014, 10, 708–727. [Google Scholar] [CrossRef]
- Liu, K.; Law, S.S.; Xia, Y.; Zhu, X.Q. Singular spectrum analysis for enhancing the sensitivity in structural damage detection. J. Sound Vib. 2014, 333, 392–417. [Google Scholar] [CrossRef]
- Thuraisingham, R.A. Use of SSA and MCSSA in the Analysis of Cardiac RR Time Series. J. Comput. Med. 2013, 2013, 231459. [Google Scholar] [CrossRef]
- Bureneva, O.; Safyannikov, N.; Aleksanyan, Z. Singular Spectrum Analysis of Tremorograms for Human Neuromotor Reaction Estimation. Mathematics 2022, 10, 1794. [Google Scholar] [CrossRef]
- Silva, E.S.; Hassani, H.; Heravi, S. Modeling European industrial production with multivariate singular spectrum analysis: A cross-industry analysis. J. Forecast. 2018, 37, 371–384. [Google Scholar] [CrossRef]
- Silva, E.S.; Hassani, H. On the use of singular spectrum analysis for forecasting U.S. trade before, during and after the 2008 recession. Int. Econ. 2015, 141, 34–49. [Google Scholar] [CrossRef]
- Hassani, H.; Rua, A.; Silva, E.S.; Thomakos, D. Monthly forecasting of GDP with mixed-frequency multivariate singular spectrum analysis. Int. J. Forecast. 2019, 35, 1263–1272. [Google Scholar] [CrossRef]
- Hassani, H.; Webster, A.; Silva, E.S.; Heravi, S. Forecasting U.S. Tourist arrivals using optimal Singular Spectrum Analysis. Tour. Manag. 2015, 46, 322–335. [Google Scholar] [CrossRef]
- Rahmani, D.; Heravi, S.; Hassani, H.; Ghodsi, M. Forecasting time series with structural breaks with Singular Spectrum Analysis, using a general form of recurrent formula. arXiv 2016, arXiv:1605.02188. [Google Scholar] [CrossRef]
- Ghodsi, M.; Hassani, H.; Rahmani, D.; Silva, E.S. Vector and recurrent singular spectrum analysis: Which is better at forecasting? J. Appl. Stat. 2017, 45, 1872–1899. [Google Scholar] [CrossRef]
- Rahmani, D.; Fay, D. A state-dependent linear recurrent formula with application to time series with structural breaks. J. Forecast. 2021, 41, 43–63. [Google Scholar] [CrossRef]
- Sarkka, S. Bayesian Filtering and Smoothing; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar]
- Golyandina, N.; Zhigljavsky, A. Singular Spectrum Analysis for Time Series, 2nd ed.; Springer: Berlin, Germany, 2020; Volume 28. [Google Scholar]
- Danilov, D.L. Principal components in time series forecast. J. Comput. Graph. Stat. 1997, 6, 112–121. [Google Scholar] [CrossRef]
- Nekrutkin, V. Approximation Spaces and Continuation of Time Series. In Statistical Models with Applications in Econometrics and Neibouring Fields; Ermakov, S.M., Kashtanov, Y., Eds.; University of St. Petersburg: St. Petersburg, Russia, 1999; pp. 3–32. [Google Scholar]
- Sasmita, Y.; Kuswanto, H.; Prastyo, D.D.; Otok, B.W. Performance evaluation of Bootstrap-Linear recurrent formula and Bootstrap-Vector singular spectrum analysis in the presence of structural break. AIP Conf. Proc. 2023, 2556, 050004. [Google Scholar] [CrossRef]
- Ginting, A.M. An Analysis of Export Effect on the Economic Growth of Indonesia. Bul. Ilm. Litbang Perdagang. 2017, 11, 1–21. [Google Scholar] [CrossRef]
- Xie, C.; Liu, Z.; Liu, L.; Zhang, L.; Fang, Y.; Zhao, L. Export rebate and export performance: From the respect of China’s economic growth relying on export. In Proceedings of the 2010 Third International Conference on Business Intelligence and Financial Engineering, Hong Kong, China, 13–15 August 2010; pp. 432–436. [Google Scholar] [CrossRef]
- Kalaitzi, A.S.; Chamberlain, T.W. Exports and Economic Growth: Some Evidence from the GCC. Int. Adv. Econ. Res. 2020, 26, 203–205. [Google Scholar] [CrossRef]
- Dave, E.; Leonardo, A.; Jeanice, M.; Hanafiah, N. Forecasting Indonesia Exports Using a Hybrid Model ARIMA-LSTM. Procedia Comput. Sci. 2021, 179, 480–487. [Google Scholar] [CrossRef]
- Djara, V.A.D.; Dewi, D.D.; Hananti, H.; Qisthi, N.; Rosmanah, R.; HM, Z.; Toharudin, T.; Ruchjana, B.N. Prediction of Export and Import in Indonesia Using Vvector Autoregressive Integrated (VARI). J. Math. Comput. Sci. 2022, 12, 105. [Google Scholar] [CrossRef]
- Pham, M.H.; Nguyen, M.N.; Wu, Y.K. A Novel Short-Term Load Forecasting Method by Combining the Deep Learning with Singular Spectrum Analysis. IEEE Access 2021, 9, 73736–73746. [Google Scholar] [CrossRef]
- Rahmani, D. A forecasting algorithm for Singular Spectrum Analysis based on bootstrap Linear Recurrent Formula coefficients. Int. J. Energy Stat. 2014, 02, 287–299. [Google Scholar] [CrossRef]
- Liu, F.; Lu, Y.; Cai, M. A hybrid method with adaptive sub-series clustering and attention-based stacked residual LSTMs for multivariate time series forecasting. IEEE Access 2020, 8, 62423–62438. [Google Scholar] [CrossRef]
- Bai, J.; Perron, P. Computation and analysis of multiple structural change models. J. Appl. Econom. 2003, 18, 1–22. [Google Scholar] [CrossRef]
- Zivot, E.; Andrews, D.W.K. the the Great Crash, the and Unit-Root. J. Bus. Econ. Stat. 1992, 10, 251–270. [Google Scholar]
- Royston, P. Remark AS R94: A remark on Algorithm AS 181: The W test for normality. Appl. Stat. 1995, 44, 547–551. [Google Scholar] [CrossRef]
- Diebold, F.X.; Mariano, R.S. Comparing predictive accuracy. J. Bus. Econ. Stat. 1995, 13, 253–263. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).