Abstract
Forecasters have been using various criteria to select the most appropriate model from a pool of candidate models. This includes measurements on the in-sample accuracy of the models, information criteria, and cross-validation, among others. Although the latter two options are generally preferred due to their ability to tackle overfitting, in univariate time-series forecasting settings, limited work has been conducted to confirm their superiority. In this study, we compared such popular criteria for the case of the exponential smoothing family of models using a large data set of real series. Our results suggest that there is significant disagreement between the suggestions of the examined criteria and that, depending on the approach used, models of different complexity may be favored, with possible negative effects on the forecasting accuracy. Moreover, we find that simple in-sample error measures can effectively select forecasting models, especially when focused on the most recent observations in the series.
1. Introduction
The “no free lunch” theorem [1] suggests that “...for any algorithm, any elevated performance over one class of problems is offset by performance over another class”. This theorem also holds true in time-series forecasting settings, meaning that no model can optimally forecast all series and, consequently, that the most appropriate model should be identified per case to improve the overall forecasting accuracy. Indeed, if model selection could be carried out perfectly, then the accuracy gains would be substantial [2]. Unfortunately, due to the uncertainty involved in the process [3], the task of model selection has been proven to be very challenging in practice, especially when performed for numerous series [4] or for data that involve anomalies, outliers, and shifts [5]. To that end, the forecasting literature has developed various criteria, rules, and methods to improve model selection and automate forecasting.
Early attempts at model selection involved utilizing information criteria, such as Akaike’s information criterion (AIC; [6]) and the Bayesian information criterion (BIC; [7]), and choosing the most appropriate model by comparing their ability to fit the historical observations with the number of parameters used to produce forecasts. Other attempts include rule-based selections [8], i.e., using a set of heuristics to define when a model should be preferred over another. These rules, which typically build on time-series features (e.g., strength of trend and seasonality), can also be determined analytically by processing the forecast errors of various models across different series of diverse features [9]. The rise of machine learning has facilitated the development of such feature-based model selection algorithms, also called “meta-learners” [10]. Another promising alternative is to select models judgmentally, thereby allowing the incorporation of human experience [11] and avoiding making unreasonable choices [12]. In any case, particular emphasis should be placed on the pool of candidate models considered for making selections [13].
Another direction for selecting forecasting models is based on cross-validation [14], which is specifically designed to overcome issues related to overfitting and to enhance the generalization of the forecasting methods used. In time-series forecasting applications, cross-validation variants include blocked approaches that mitigate the problem of serial correlations [15,16] and techniques that omit data close to the period used to evaluate performance [17]. Therefore, along with information criteria, cross-validation is among the most popular approaches used nowadays for effective model selection [18].
Despite the development of several model selection approaches, researchers and practitioners have been relatively indecisive about the criteria that they should use in practice for identifying the most accurate forecasting models. Each criterion comes with particular advantages and limitations, often rendering their use subject to the judgment and experience of the forecaster or even the settings of the software utilized to produce the forecasts. We argue that tuning model selection processes is critical for improving accuracy and that empirical evidence should be exploited to define which criterion should be considered for the data set and forecasting application at hand. To support our argument, we evaluated some of the most widely used model selection criteria on a large data set of real series with the exponential smoothing family of models, a standard method for time-series forecasting. Our analysis focused on both the precision of the criteria and the forecasting accuracy of the underlying selection approaches, providing evidence about the way that the two measures are correlated. We also investigated the disagreement between the examined criteria and discuss its implications for forecasting practice.
The rest of this paper is organized as follows. Section 2 provides an introduction to the model selection criteria used in our study. Section 3 presents the exponential smoothing family of models, forming the pool of candidate models used in our experiments. Section 4 empirically evaluates the performance of the selection criteria, describes the experimental setup, and discusses the results. Finally, Section 5 concludes the paper.
2. Model Selection Criteria
2.1. Criteria Based on In-Sample Accuracy Measurements
The simplest and fastest approach to selecting a forecasting model from a pool of candidate models is to compare their accuracy on the in-sample data of the series. This is because in-sample accuracy can be directly measured when fitting the models, requiring no further computations. The most common measures used in this direction are the mean squared error (MSE) and the mean absolute error (MAE), defined as follows:
where n is the sample size (number of in-sample observations), is the observed value of the series being forecast at point t, and is the forecast provided by the model given n observations for estimating its parameters. Smaller values of MAE and MSE suggest a better fit.
Although other measures (e.g., measures based on percentage errors, relative errors, relative measures, and measures based on scaled errors) can be used instead of MSE and MAE, given their limitations [19] and the fact that model selection is typically performed in a series-by-series fashion, the aforementioned scale-dependent measures can be considered sufficient for the described task.
In terms of statistical properties, MAE is an appropriate measure for evaluating the ability of a forecasting model to specify the median of the future values of a series [20], while MSE is suitable for measuring the ability of a model to specify its mean [21]. Moreover, since MSE builds on squared errors, it penalizes more large errors than small ones and is therefore more sensitive to outliers than MAE [22]. Therefore, although MSE has long been the standard measure of choice for selecting and optimizing time-series forecasting models, it becomes evident that there may be settings where MAE provides superior results.
Model selection criteria that build on in-sample measurements theoretically come with two major issues. First, since they just focus on how well the model fits the historical observations, they are prone to overfitting. In general, sophisticated models that consist of multiple parameters have the capacity to fit series better than simpler models, although the latter may result in more accurate post-sample forecasts. Second, since in-sample measurements evaluate accuracy across the complete sample of historical observations, they may favor models that do not necessarily perform well in the most recent past. Typically, the latest information available is of higher importance for producing accurate post-sample forecasts, meaning that models should put particular emphasis on the last part of the series, especially when its underlying patterns (e.g., seasonality and trend) have changed.
Although the first issue can be tackled by the criteria presented in the following two subsections, the second one can be mitigated by simply adjusting the time window in which the accuracy measures are computed. For the sake of simplicity, in this study, we considered some variants of the MSE and MAE measures, called MSEh and MAEh, that capture the in-sample accuracy of the examined models in the last h observations of the series, as follows:
where h is the forecasting horizon, i.e., the number of periods the model is tasked to forecast in the post-sample. Although h can in principle be selected based on the particular requirements of the forecasting task at hand (e.g., set equal to a full calendar year or the last observation), we argue that the forecasting horizon is a reasonable and practical alternative for determining the time window. Moreover, by selecting a sufficiently large evaluation window (e.g., greater than 1 observation), the results are expected to be more representative and less sensitive to potential extreme values.
2.2. Information Criteria
Information criteria have become particularly popular for model selection, as they are fast to compute but can also mitigate overfitting [23]. To do so, instead of selecting the model that best fits the series, as measured by an accuracy measure in the in-sample data, they make choices by penalizing the in-sample accuracy of the candidate models according to their complexity, as realized based on the number of parameters that have to be estimated to form each model.
Specifically, information criteria build on complexity-penalized maximum likelihood estimations (as described in Section 3 for the case of exponential smoothing models). The most notable variants of information criteria include AIC, AIC corrected for small sample sizes (AICc), and BIC, defined as follows:
where L is the likelihood, and k is the total number of parameters. In all cases, smaller values imply better performance. As seen in the equations, by definition, BIC assigns larger penalties to more sophisticated models than AIC, thus favoring simpler models of comparable likelihood. The same applies to AICc, provided that the sample size is relatively small (AICc approximates AIC as the sample size increases).
Although there have been theoretical arguments over the use of particular information criteria over others, Burnham and Anderson [24] demonstrate that AIC and AICc can be derived in the same Bayesian framework as BIC, just by using different prior probabilities. As a result, information criterion selection should be based on the assumptions made about reality and models while also taking into consideration empirical evidence about the forecasting performance of each criterion in the application at hand. Simulation studies suggest that AICc tends to outperform BIC and also recommend its use over AIC, even when sample sizes are relatively large [25,26]. This may justify the utilization of AICc in popular model selection software, such as the auto.arima and ets functions of the forecast package for R, which allow the automatic selection of ARIMA and exponential smoothing models, respectively [27].
2.3. Criteria Based on Cross-Validation
Cross-validation is another approach for selecting among forecasting models. The greatest advantage of this approach is that it focuses on the post-sample accuracy of the candidate models, thus selecting models that perform well in their actual tasks, regardless of how well they managed to fit the historical data, while also making no assumptions about how model complexity should be measured or penalized. As a result, cross-validation has become very popular for model selection and optimization, especially in applications that involve sophisticated models (e.g., neural networks), where standard selection criteria are either challenging to compute or sensitive to overfitting. On the negative side, cross-validation is applicable only to series that have enough observations to allow the creation of hold-out samples and is computationally expensive (the more hold-out samples created, the greater the cost becomes).
In time-series forecasting settings, where data are non-stationary and have serial dependencies, cross-validation is typically implemented using the rolling-origin evaluation approach [28]. According to this approach, a period of historical data is first used to fit a forecasting model. Then, the model is used to produce h-step-ahead forecasts, and its accuracy is assessed based on the actual values of the series in the corresponding period using the measure of choice (e.g., MSE or MAE). Subsequently, the forecast origin is shifted by T periods, the model is re-fitted using the new in-sample data (), and new forecasts are produced, contributing another assessment. This process is repeated until there are no data left for testing, and the overall performance of the model is determined based on its average accuracy over the conducted evaluations.
For the sake of simplicity, and to accelerate computations, in this study, we considered a fixed-origin evaluation, i.e., a single evaluation set that consists of the last h observations of the original in-sample data (). In addition, in accordance with the in-sample selection measures used in our study, we used MSE and MAE to assess the post-sample forecasting accuracy. The examined cross-validation approaches, called MSEv and MAEv, are defined as follows:
Note that MSEv/MAEv are computed on the same sample as MSEh/MAEh. The only difference is that the forecasts used with the MSEv/MAEv criteria are computed using observations, while the forecasts used with the MSEh/MAEh criteria use the complete in-sample data (n observations).
3. Forecasting Models
Exponential smoothing, originally introduced by Brown [29], is considered the workhorse of time-series forecasting, being among the oldest and simplest yet one of the most effective and widely used methods for univariate predictions (for an encyclopedic review on exponential smoothing, please refer to Section 2.3.1 of [30]). The key advantage of the method is that it is fast to compute [31], easy to implement in software [32], and results in competitive accuracy compared to more sophisticated methods in various applications, including financial, economic, demographic, and demand data, among others, as demonstrated empirically by recent forecasting competitions [33,34]. In addition, the forecasts are produced based on intuitive models that are closely connected to key time-series features (e.g., trend and seasonality), thus being easy to communicate to managers or adjust based on judgment [12].
The key idea behind exponential smoothing is that more recent observations are more valuable to forecasting. As a result, the method produces forecasts by putting exponentially more weight on the most recent past of the series. The degree to which the weight is decreased as we move further to the past is determined by the smoothing parameters of the model. Moreover, according to its state-space expression [23], typically referred to as ETS, exponential smoothing can be realized as a combination of three components, namely, the error (E), trend (T), and seasonal (S) components. The error component can be either additive (A) or multiplicative (M), while the trend and seasonal components can be none (N), additive (A), or multiplicative (M). In addition, additive and multiplicative trends can be damped (d), if needed. Consequently, the ETS framework involves a total of 30 exponential smoothing models (or model forms) that can be acronymized using the respective symbols of the three components, as shown in Table 1. From these models, some may result in infinite forecast variances for long forecast horizons [35], while others involve a multiplicative trend that is not recommended to use in practice [36]. Therefore, the ets function of the forecast package for R, which was used to implement exponential smoothing in our study, limits the candidate models to 15 for seasonal data and 6 for non-seasonal data.

Table 1.
Exponential smoothing family of models. Applicable models are highlighted in bold face.
As an example, the simplest form of exponential smoothing that accounts just for level variations (simple exponential smoothing or ANN) can be expressed as:
where is the state of the level component at period t, and is the smoothing parameter of that level. Note that calculating the state of the component at () requires the estimation of some initial state values (). Effectively, this is another parameter of the model, and its estimation is part of the fitting process.
As more components are added to the model, more equations and parameters are considered for producing the forecasts. This results in more generic models that can effectively account for more complicated time-series patterns, such as the trend [37] and seasonality [38]. However, as discussed earlier, more sophisticated models involve more parameters and, as a result, higher parameter uncertainty [3], possibly rendering their use less accurate compared to other, simpler model forms. By default, ets uses the likelihood to estimate the parameters of the models and AICc to select the most appropriate model form. Depending on the form of the error component, likelihood is defined as follows:
where and correspond to the likelihood of models that involve additive and multiplicative error components, respectively.
In terms of the parameters k used, all exponential smoothing models involve a minimum of three parameters, namely, , , and , which corresponds to the standard deviation of the residuals. Then, models with a trend component will involve two additional parameters (for smoothing and initializing the trend), and models with a damped trend component will involve three additional parameters (for initializing, smoothing, and damping the trend), while models with a seasonal component will involve additional parameters (s for initializing and one for smoothing seasonality), where s is equal to the seasonal periods of the data (e.g., 12 for monthly and 4 for quarterly series). For the sake of simplicity, and to allow comparisons between series of different seasonal periods, in this study, we categorized ETS models into four categories based on their complexity, namely, “Low”, “Moderate”, “Significant”, and “High” complexity, as presented in Table 2. As can be seen, models of low complexity involve only estimations about the level of the series, models of moderate complexity involve estimations about either the trend or the seasonality of the series, models of significant complexity involve estimations about either a damped trend or seasonality, and models of high complexity are both damped and seasonal.

Table 2.
Categorization of ETS models based on their complexity, i.e., number of estimated components.
4. Empirical Evaluation
4.1. Experimental Setup
To empirically evaluate the performance of the model selection criteria described in Section 2, we considered a subset of the M4 competition data [33]. The M4 data set is frequently used for benchmarking by the forecasting community, as it originally involves 100,000 series from various domains (micro, macro, industry, finance, demographic, and other) and with varying frequencies (yearly, quarterly, monthly, weekly, daily, and hourly) that are very diverse and representative of several real-life applications [39]. Moreover, since it is publicly available, it facilitates the replication of results and allows comparisons with past and future studies [40]. A detailed description of the data set and the structural characteristics of its series, including their length, forecastability, trend, seasonality, linearity, stability, skewness, kurtosis, non-linear autoregressive structure, and self-similarity, is provided by Spiliotis et al. [39].
Specifically, we considered the yearly, quarterly, and monthly series of the M4 data set (95,000 series) but excluded those that are too short in length to perform cross-validation. Therefore, the data set used in our study involves a total of 91,444 series (20,077 yearly, 23,760 quarterly, and 47,607 monthly).
For each series, we fit all the exponential smoothing models that are recommended to use with the forecast package, i.e., a total of 15 models for seasonal and 6 models for non-seasonal series, as presented in Table 1. Then, we employed the examined model selection criteria and, based on their recommendations, we tracked the forecasting accuracy of each approach, as measured by the mean absolute scaled error (MASE), defined as follows:
MASE, originally proposed by Hyndman and Koehler [41], is equal to the mean absolute error scaled by the in-sample one-step-ahead mean absolute error of seasonal Naive. MASE was preferred over other accuracy measures, as it was officially used in M4 to rank the original submissions, and it has better statistical properties (it is independent of the data scale, becomes infinite or undefined only when all the errors of the Naive method are equal to zero, has a defined mean and finite variance, and equally penalizes positive and negative forecast errors [19]).
In addition to MASE, we also tracked the number of series where the criteria successfully identified the most accurate model in terms of out-of-sample MASE accuracy. To that end, it is possible to evaluate both the precision of the criteria (the proportion of selections that were actually the “best”) and the effect of such a precision score on the post-sample accuracy (absolute accuracy, as measured by MASE). This distinction is important since higher precision may not necessarily lead to better accuracy, meaning that a criterion of lower precision that somehow avoids selecting the worst alternatives could perform better overall than an approach that more frequently selects the best option but also often chooses some of the worst possible forecasting models [42].
Finally, in order to add depth to our analysis, and given that M4 considered the symmetric mean absolute percentage error (sMAPE) in addition to MASE to evaluate the forecasting accuracy of the submitted methods, we also utilized sMAPE, which is defined as follows:
4.2. Results and Discussion
Table 3 summarizes the forecasting accuracy of the examined criteria, both per data frequency and in total. As expected, criteria that build on cross-validation (MSEv and MAEv) result in better forecasts overall. However, this result is mostly driven by the superior performance of these criteria in the yearly data. If we focus on the seasonal series, we find that criteria that build on in-sample accuracy measurements (MAE and MSE) lead to more accurate forecasts. In fact, we can see that the average rank of the models selected by MAE is the lowest among the criteria considered for all the examined data frequencies. Interestingly enough, MAEh and MSEh are consistently less accurate approaches than MAE and MSE, respectively, indicating that focusing on the last part of the series does not guarantee better model selection performance.

Table 3.
Forecasting accuracy (MASE) of the examined criteria used for model selection. The average ranks of the selected models are also displayed. The results are presented per data frequency and for the complete data set. The bold numbers highlight the most accurate criterion per case.
When it comes to information criteria, we observe that balancing complexity with in-sample accuracy is critical. Specifically, we find that AIC, which considers a relatively small penalty for complexity, does not improve accuracy over L, being slightly worse overall. This is also the case for BIC, probably because it applies a relatively large penalty to more sophisticated models and, therefore, tends to select models with insufficient learning capacity. This is evident in the seasonal series, where both L and AIC outperform BIC. Thus, our results confirm the superiority of AICc among the information criteria examined, supporting its utilization in popular forecasting software.
Note that, as presented in Appendix A, similar conclusions can be drawn when sMAPE is used instead of MASE to measure the forecasting accuracy.
To validate our previous claims, we proceeded by computing the percentage of series where the examined criteria selected a model of low, moderate, significant, and high complexity in terms of the estimated components, as defined in Table 2. The results are presented in Table 4 along with the proportion of series where the most accurate model truly falls in the respective categories. The results confirm that L and the criteria that build on in-sample accuracy measurements are indeed more likely to select more sophisticated models, especially when they are based on squared errors (MSE, MSEh, and L). Using the most recent historical data (MSEh and MAEh) or considering some penalty for complexity (AIC, AICc, and BIC) can mitigate this issue. However, it is evident that some of the former approaches are more effective in properly balancing the in-sample accuracy with complexity. For example, we find that although all information criteria tend to use low-complexity models more often than is actually required, BIC is clearly more extreme, selecting high-complexity models in just 6% of the cases and low-complexity models in 42% of the series. Overall, the criteria that build on cross-validation and, to some degree, AICc are proven to be the most balanced approaches, following the actual tendencies of the data set more precisely.

Table 4.
Percentage of time series where the examined criteria selected a model of low, moderate, significant, and high complexity in terms of estimated components. The last column displays the percentage of time series where the most accurate model truly falls in the respective categories. The figures are computed based on the complete data set (91,444 series).
Table 5 presents the precision of the examined criteria used for model selection, both per data frequency and in total. In contrast to the results in Table 3, we observe that, on average, the MSEh and MAEh approaches manage to more frequently identify the most accurate model. This finding supports our claim that precision does not always guarantee accuracy and demonstrates the value added by less precise yet more robust model selection approaches, such as cross-validation and information criteria. Moreover, our findings are in agreement with those reported by [43], demonstrating that forecasting models should be able both to fit the historical data well and to result in “representative” forecasts in the sense that the predictions should mimic the most recent patterns of the series. Consequently, future research could focus on the further development of information criteria, expanding their formulas to simultaneously account for in-sample accuracy, forecast representativeness, and model complexity.

Table 5.
Percentage of time series where the examined criteria used for model selection successfully identified the most accurate alternative. The results are presented per data frequency and for the complete data set. The bold numbers highlight the most successful criterion per case.
As the final step in our analysis, we determined the percentage of series where the model being selected based on a particular criterion is the same as that being selected according to another criterion. Our results are visualized in Figure 1. We find that information criteria, especially AIC and AICc, tend to agree significantly with each other, resulting, however, in very different suggestions to those of other criteria. This is particularly true for the criteria that build on cross-validation, displaying less than 16% agreement with the rest of the model selection approaches, on average. Moreover, we observe that, although changing the measure used to evaluate accuracy (MAE versus MSE) can affect the model being selected, the impact of this choice is relatively small compared to the model selection approach itself. Thus, we conclude that the disagreement between existing forecasting model selection criteria can be substantial and that the selection of the most appropriate approach should be primarily based on the data set and application at hand, with additional support provided by empirical investigations.
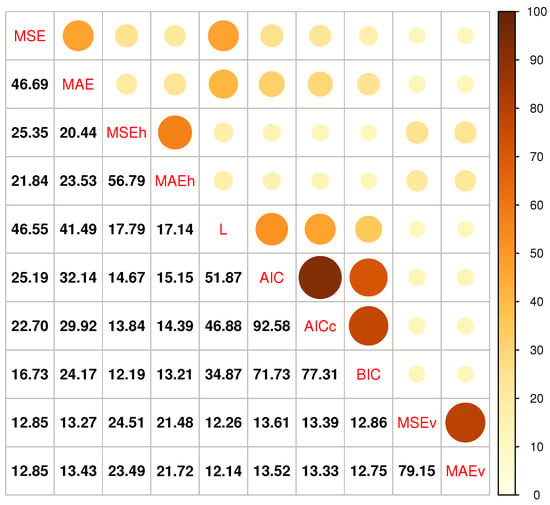
Figure 1.
Percentage of time series where the model being selected based on a particular criterion is the same as that being selected according to another criterion. The percentages are computed in a pairwise fashion by considering the complete data set (91,444 series).
5. Conclusions
We empirically evaluated the forecasting performance of popular model selection criteria using more than 90,000 real-time series and considering 15 models from the exponential smoothing family. We found that criteria that build on cross-validation can result in better forecasts overall but observed cases (seasonal data) where simple in-sample accuracy measurements can produce significantly more accurate results. We also noticed that information criteria offered a fair balance between the approaches that build on either in-sample or post-sample accuracy measurements but identified notable discrepancies among their choices, driven by the different penalties they impose to avoid the use of unnecessarily sophisticated models. Moreover, we concluded that the measure used to assess the forecasting accuracy (e.g., absolute versus squared errors) has a lower impact on forecasting performance compared to the criteria used for model selection per se.
A key finding of our study is that, when it comes to model selection, robustness is probably more important than precision. In other words, in order for a selection criterion to result in accurate forecasts, it is more crucial to systematically avoid choosing the worst forecasting models than to more frequently select the most accurate model. In this respect, it should not be surprising that two criteria with significant disagreement and different precision scores resulted in similar forecasting performance. An interesting direction to improve the robustness of model selection approaches would be to introduce criteria that concurrently balance the in-sample accuracy, forecast representativeness, and model complexity. According to our results, the first component allows the use of sufficiently sophisticated models, the second improves the precision of the selection process, and the third offers a “safety net” against overfitting.
Our findings are relevant to forecasting research and practice. Over the years, some model selection approaches have become so standard that forecasters often ignore the alternatives available and overlook the improvements that more appropriate criteria could offer. This is especially true in large-scale forecasting applications, such as in the retail, energy, and financial industries, where the number of series to be forecast is so great that using automated and off-the-shelf forecasting software has become a necessity. We argue that tuning the model selection options provided by such software is critical, yet practical if based on empirical assessments. Moreover, in some cases, they may even prove to be more computationally efficient with no loss in forecasting accuracy. Therefore, future work could expand the findings of our study by examining the performance of model selection criteria on data sets that are more focused on particular forecasting applications and also extending their examination to different families of models commonly used for automatic batch forecasting, such as ARIMA, regression trees, and neural networks.
Author Contributions
Conceptualization, E.S., F.P., and V.A.; methodology, E.S., F.P., and V.A.; software, E.S.; validation, E.S. and F.P.; formal analysis, E.S. and F.P.; investigation, E.S., F.P., and V.A.; resources, E.S. and V.A.; data curation, E.S.; writing—original draft preparation, E.S., F.P., and V.A.; writing—review and editing, E.S., F.P., and V.A.; visualization, E.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The data used in this research are available at the GitHub repository of the M4 competition https://github.com/Mcompetitions/M4-methods (accessed on 16 May 2023).
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Forecasting Accuracy According to sMAPE
Table A1 summarizes the forecasting accuracy of the examined criteria in terms of sMAPE in a similar fashion to Table 3.

Table A1.
Forecasting accuracy (sMAPE) of the examined criteria used for model selection. The average ranks of the selected models are also displayed. The results are presented per data frequency and for the complete data set. The bold numbers highlight the most accurate criterion per case.
Table A1.
Forecasting accuracy (sMAPE) of the examined criteria used for model selection. The average ranks of the selected models are also displayed. The results are presented per data frequency and for the complete data set. The bold numbers highlight the most accurate criterion per case.
| Criterion | MASE | Average Rank | ||||||
|---|---|---|---|---|---|---|---|---|
| Yearly | Quarterly | Monthly | Total | Yearly | Quarterly | Monthly | Total | |
| MSE | 15.065 | 10.212 | 13.176 | 12.821 | 3.190 | 6.868 | 6.692 | 5.969 |
| MAE | 15.022 | 10.050 | 13.013 | 12.684 | 3.165 | 6.723 | 6.553 | 5.853 |
| MSEh | 15.183 | 10.306 | 13.084 | 12.823 | 3.230 | 6.964 | 6.671 | 5.992 |
| MAEh | 15.258 | 10.256 | 13.025 | 12.796 | 3.206 | 6.957 | 6.665 | 5.981 |
| L | 15.307 | 10.276 | 13.173 | 12.889 | 3.168 | 6.901 | 6.728 | 5.991 |
| AIC | 15.039 | 10.211 | 13.194 | 12.824 | 3.235 | 6.896 | 6.734 | 6.008 |
| AICc | 14.784 | 10.200 | 13.272 | 12.805 | 3.245 | 6.919 | 6.789 | 6.045 |
| BIC | 14.802 | 10.143 | 13.359 | 12.840 | 3.256 | 7.059 | 6.963 | 6.174 |
| MSEv | 14.463 | 10.401 | 13.331 | 12.818 | 3.168 | 7.190 | 6.893 | 6.152 |
| MAEv | 14.543 | 10.399 | 13.309 | 12.824 | 3.177 | 7.188 | 6.886 | 6.150 |
References
- Wolpert, D.; Macready, W. No free lunch theorems for optimization. IEEE Trans. Evol. Comput. 1997, 1, 67–82. [Google Scholar] [CrossRef]
- Fildes, R. Beyond forecasting competitions. Int. J. Forecast. 2001, 17, 556–560. [Google Scholar]
- Petropoulos, F.; Hyndman, R.J.; Bergmeir, C. Exploring the sources of uncertainty: Why does bagging for time series forecasting work? Eur. J. Oper. Res. 2018, 268, 545–554. [Google Scholar] [CrossRef]
- Fildes, R.; Petropoulos, F. Simple versus complex selection rules for forecasting many time series. J. Bus. Res. 2015, 68, 1692–1701. [Google Scholar] [CrossRef]
- Doornik, J.A.; Castle, J.L.; Hendry, D.F. Short-term forecasting of the coronavirus pandemic. Int. J. Forecast. 2022, 38, 453–466. [Google Scholar] [CrossRef] [PubMed]
- Akaike, H. Information Theory and an Extension of the Maximum Likelihood Principle. In Selected Papers of Hirotugu Akaike; Springer: New York, NY, USA, 1998; pp. 199–213. [Google Scholar]
- Schwarz, G. Estimating the Dimension of a Model. Ann. Stat. 1978, 6, 461–464. [Google Scholar] [CrossRef]
- Collopy, F.; Armstrong, J.S. Rule-Based Forecasting: Development and Validation of an Expert Systems Approach to Combining Time Series Extrapolations. Manag. Sci. 1992, 38, 1394–1414. [Google Scholar] [CrossRef]
- Petropoulos, F.; Makridakis, S.; Assimakopoulos, V.; Nikolopoulos, K. ‘Horses for Courses’ in demand forecasting. Eur. J. Oper. Res. 2014, 237, 152–163. [Google Scholar] [CrossRef]
- Montero-Manso, P.; Athanasopoulos, G.; Hyndman, R.J.; Talagala, T.S. FFORMA: Feature-based forecast model averaging. Int. J. Forecast. 2020, 36, 86–92. [Google Scholar] [CrossRef]
- Han, W.; Wang, X.; Petropoulos, F.; Wang, J. Brain imaging and forecasting: Insights from judgmental model selection. Omega 2019, 87, 1–9. [Google Scholar] [CrossRef]
- Petropoulos, F.; Kourentzes, N.; Nikolopoulos, K.; Siemsen, E. Judgmental selection of forecasting models. J. Oper. Manag. 2018, 60, 34–46. [Google Scholar] [CrossRef]
- Kourentzes, N.; Barrow, D.; Petropoulos, F. Another look at forecast selection and combination: Evidence from forecast pooling. Int. J. Prod. Econ. 2019, 209, 226–235. [Google Scholar] [CrossRef]
- Stone, M. Cross-Validatory Choice and Assessment of Statistical Predictions. J. R. Stat. Soc. Ser. (Methodol.) 1974, 36, 111–147. [Google Scholar] [CrossRef]
- Bergmeir, C.; Benítez, J.M. On the use of cross-validation for time series predictor evaluation. Inf. Sci. 2012, 191, 192–213. [Google Scholar] [CrossRef]
- Racine, J. Consistent cross-validatory model-selection for dependent data: hv-block cross-validation. J. Econom. 2000, 99, 39–61. [Google Scholar] [CrossRef]
- Burman, P.; Chow, E.; Nolan, D. A Cross-Validatory Method for Dependent Data. Biometrika 1994, 81, 351–358. [Google Scholar] [CrossRef]
- Bergmeir, C.; Hyndman, R.J.; Koo, B. A note on the validity of cross-validation for evaluating autoregressive time series prediction. Comput. Stat. Data Anal. 2018, 120, 70–83. [Google Scholar] [CrossRef]
- Koutsandreas, D.; Spiliotis, E.; Petropoulos, F.; Assimakopoulos, V. On the selection of forecasting accuracy measures. J. Oper. Res. Soc. 2022, 73, 937–954. [Google Scholar] [CrossRef]
- Schwertman, N.C.; Gilks, A.J.; Cameron, J. A Simple Noncalculus Proof That the Median Minimizes the Sum of the Absolute Deviations. Am. Stat. 1990, 44, 38–39. [Google Scholar]
- Kolassa, S. Evaluating predictive count data distributions in retail sales forecasting. Int. J. Forecast. 2016, 32, 788–803. [Google Scholar] [CrossRef]
- Armstrong, J.S. Standards and practices for forecasting. In Principles of Forecasting; Springer: Berlin/Heidelberg, Germany, 2001; pp. 679–732. [Google Scholar]
- Hyndman, R.J.; Koehler, A.B.; Snyder, R.D.; Grose, S. A state space framework for automatic forecasting using exponential smoothing methods. Int. J. Forecast. 2002, 18, 439–454. [Google Scholar] [CrossRef]
- Burnham, K.P.; Anderson, D.R. Multimodel Inference: Understanding AIC and BIC in Model Selection. Sociol. Methods Res. 2004, 33, 261–304. [Google Scholar] [CrossRef]
- Billah, B.; King, M.L.; Snyder, R.D.; Koehler, A.B. Exponential smoothing model selection for forecasting. Int. J. Forecast. 2006, 22, 239–247. [Google Scholar] [CrossRef]
- Kolassa, S. Combining exponential smoothing forecasts using Akaike weights. Int. J. Forecast. 2011, 27, 238–251. [Google Scholar] [CrossRef]
- Hyndman, R.J.; Khandakar, Y. Automatic Time Series Forecasting: The forecast Package for R. J. Stat. Softw. 2008, 27, 1–22. [Google Scholar] [CrossRef]
- Tashman, L.J. Out-of-sample tests of forecasting accuracy: An analysis and review. Int. J. Forecast. 2000, 16, 437–450. [Google Scholar] [CrossRef]
- Brown, R.G. Exponential Smoothing for Predicting Demand; Little: Cambridge, MA, USA, 1956. [Google Scholar]
- Petropoulos, F.; Apiletti, D.; Assimakopoulos, V.; Babai, M.Z.; Barrow, D.K.; Ben Taieb, S.; Bergmeir, C.; Bessa, R.J.; Bijak, J.; Boylan, J.E.; et al. Forecasting: Theory and practice. Int. J. Forecast. 2022, 38, 705–871. [Google Scholar] [CrossRef]
- Makridakis, S.; Spiliotis, E.; Assimakopoulos, V. Statistical and Machine Learning forecasting methods: Concerns and ways forward. PLoS ONE 2018, 13, e0194889. [Google Scholar] [CrossRef]
- Fildes, R.; Goodwin, P.; Lawrence, M.; Nikolopoulos, K. Effective forecasting and judgmental adjustments: An empirical evaluation and strategies for improvement in supply-chain planning. Int. J. Forecast. 2009, 25, 3–23. [Google Scholar] [CrossRef]
- Makridakis, S.; Spiliotis, E.; Assimakopoulos, V. The M4 Competition: 100,000 time series and 61 forecasting methods. Int. J. Forecast. 2020, 36, 54–74. [Google Scholar] [CrossRef]
- Makridakis, S.; Spiliotis, E.; Assimakopoulos, V. M5 accuracy competition: Results, findings, and conclusions. Int. J. Forecast. 2022, 38, 1346–1364. [Google Scholar] [CrossRef]
- Hyndman, R.J.; Koehler, A.B.; Ord, J.K.; Snyder, R.D. Forecasting with Exponential Smoothing: The State Space Approach; Springer: Berlin, Germany, 2008. [Google Scholar]
- Petropoulos, F.; Grushka-Cockayne, Y.; Siemsen, E.; Spiliotis, E. Wielding Occam’s razor: Fast and frugal retail forecasting. arXiv 2022, arXiv:2102.13209. [Google Scholar]
- Gardner, E.S. Exponential smoothing: The state of the art—Part II. Int. J. Forecast. 2006, 22, 637–666. [Google Scholar] [CrossRef]
- Winters, P.R. Forecasting sales by exponentially weighted moving averages. Manag. Sci. 1960, 6, 324–342. [Google Scholar] [CrossRef]
- Spiliotis, E.; Kouloumos, A.; Assimakopoulos, V.; Makridakis, S. Are forecasting competitions data representative of the reality? Int. J. Forecast. 2020, 36, 37–53. [Google Scholar] [CrossRef]
- Makridakis, S.; Assimakopoulos, V.; Spiliotis, E. Objectivity, reproducibility and replicability in forecasting research. Int. J. Forecast. 2018, 34, 835–838. [Google Scholar] [CrossRef]
- Hyndman, R.J.; Koehler, A.B. Another look at measures of forecast accuracy. Int. J. Forecast. 2006, 22, 679–688. [Google Scholar] [CrossRef]
- Petropoulos, F.; Spiliotis, E.; Panagiotelis, A. Model combinations through revised base rates. Int. J. Forecast. 2023, 39, 1477–1492. [Google Scholar] [CrossRef]
- Petropoulos, F.; Siemsen, E. Forecast Selection and Representativeness. Manag. Sci. 2022, 69, 2672–2690. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).