Day Ahead Electric Load Forecast: A Comprehensive LSTM-EMD Methodology and Several Diverse Case Studies
Abstract
1. Introduction
- Methodology: Data pre-processing, model training and evaluation, and operational forecasting
- Case Studies: Several datasets are studied via the methodology including buildings, an electric vehicle charging station, and transmission networks
- Results: The intermediate and final results are evaluated and contextualized
- Conclusions: A final summary and evaluation of the methodology are discussed
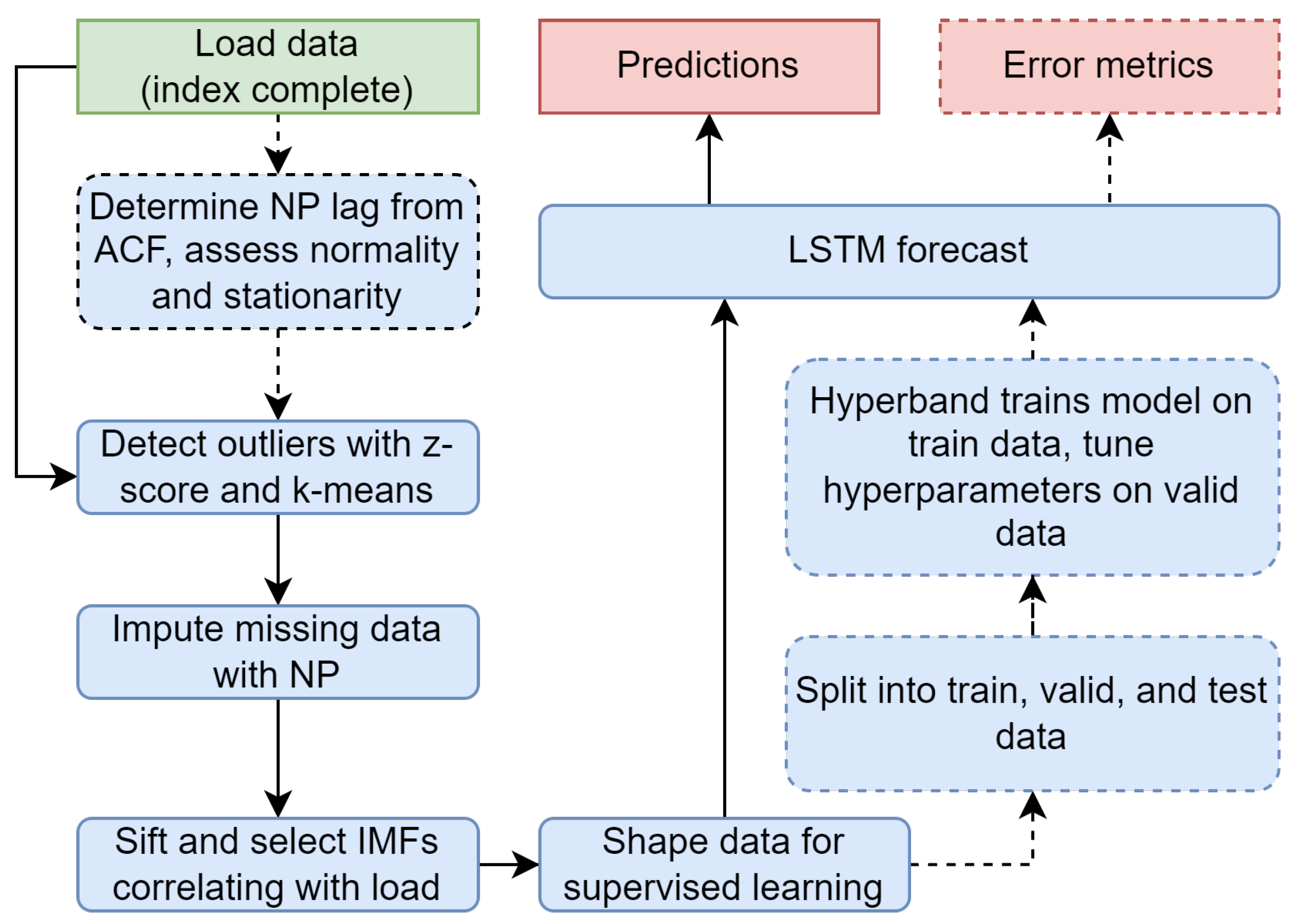
2. Methodology
2.1. Error Metrics
2.2. Data Pre-Processing
2.3. Feature Engineering
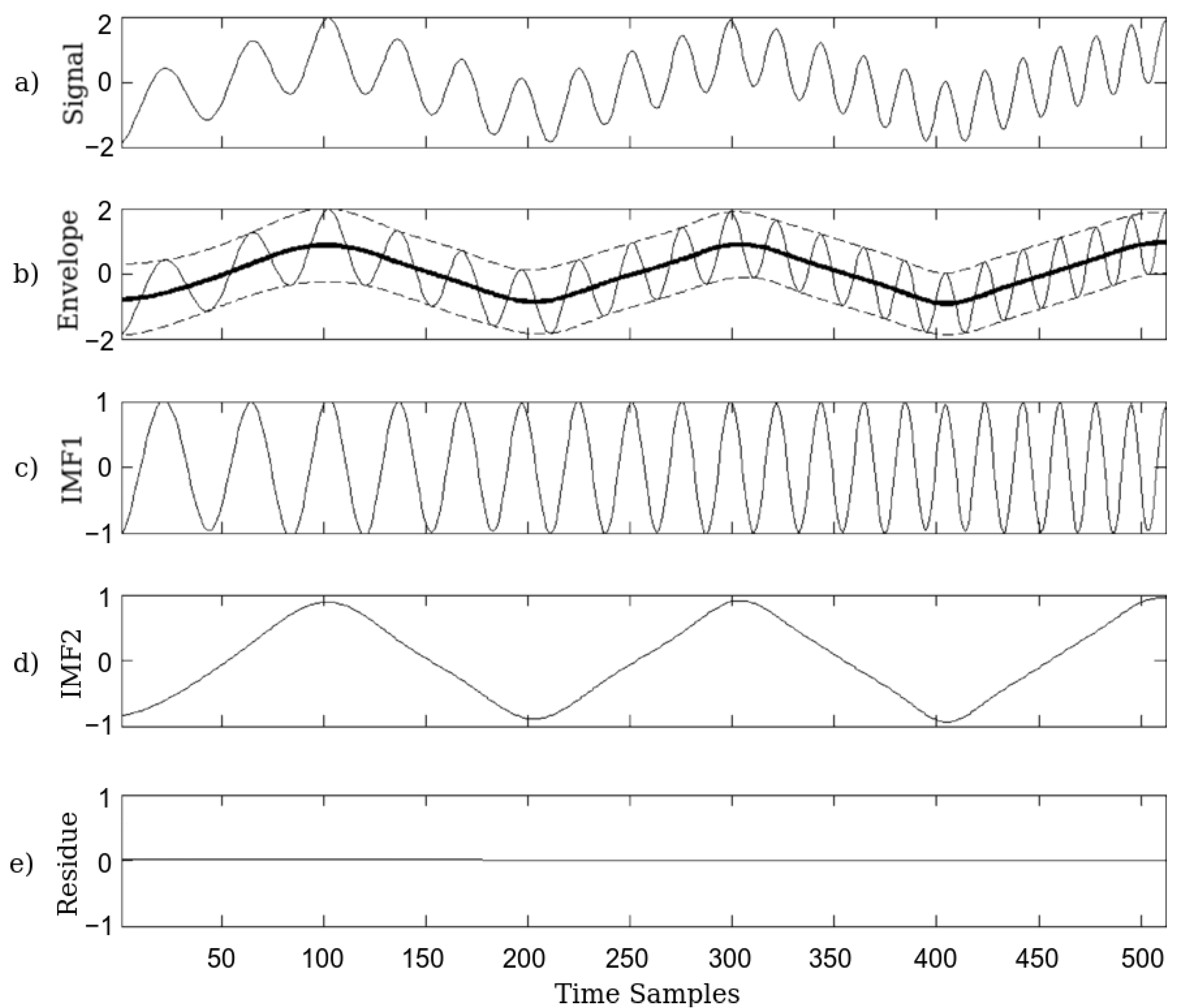
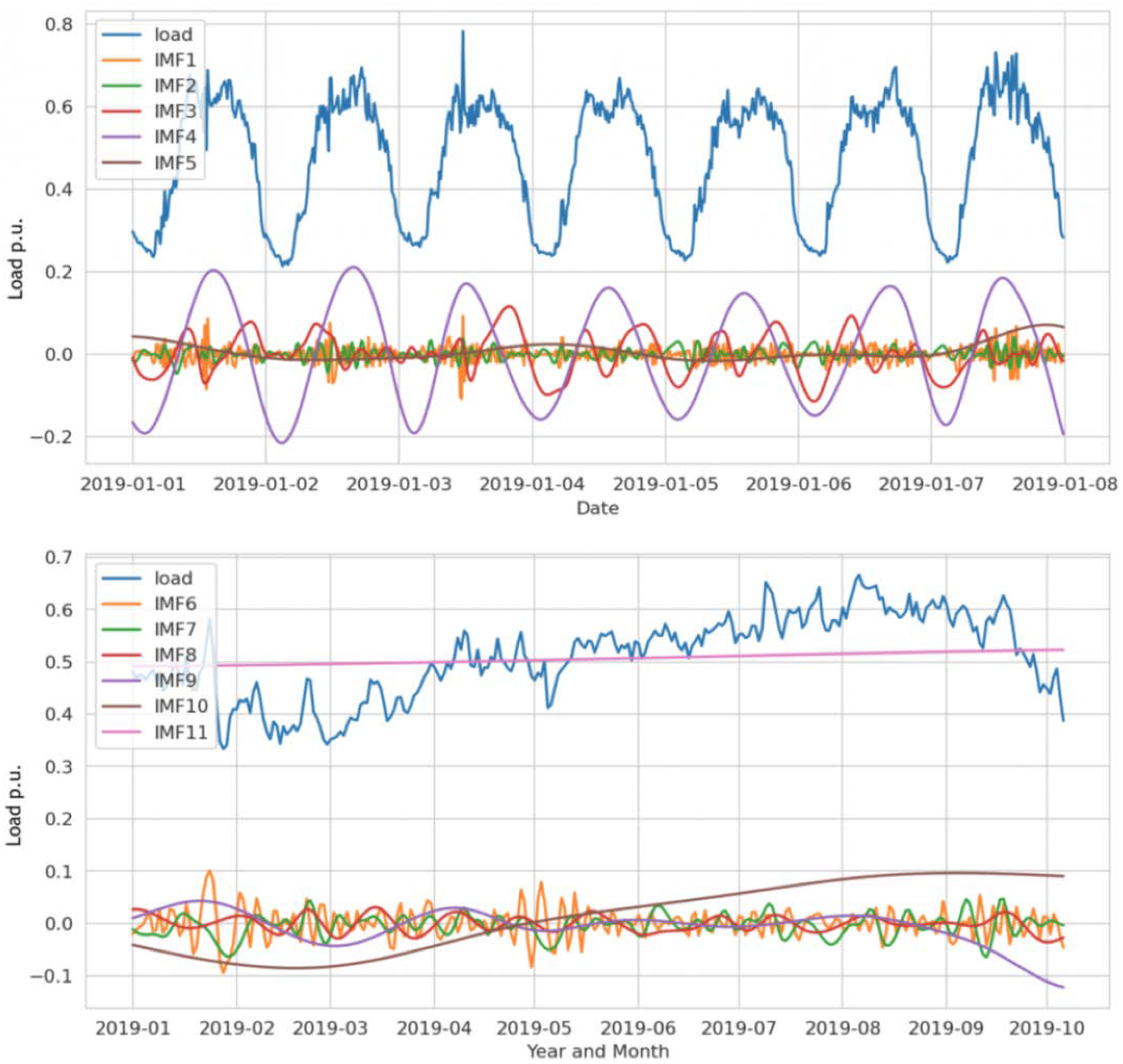
Empirical Mode Decomposition
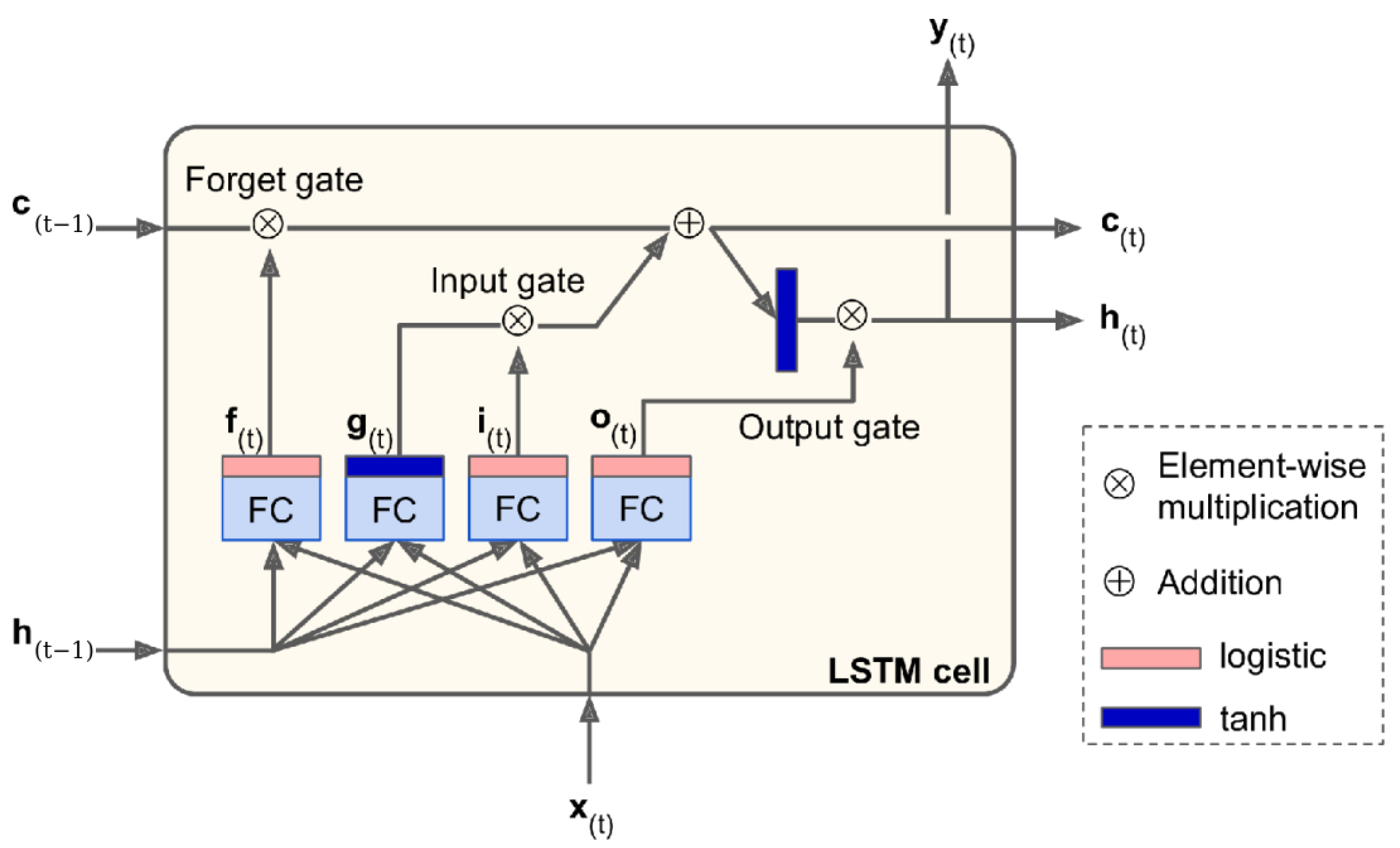
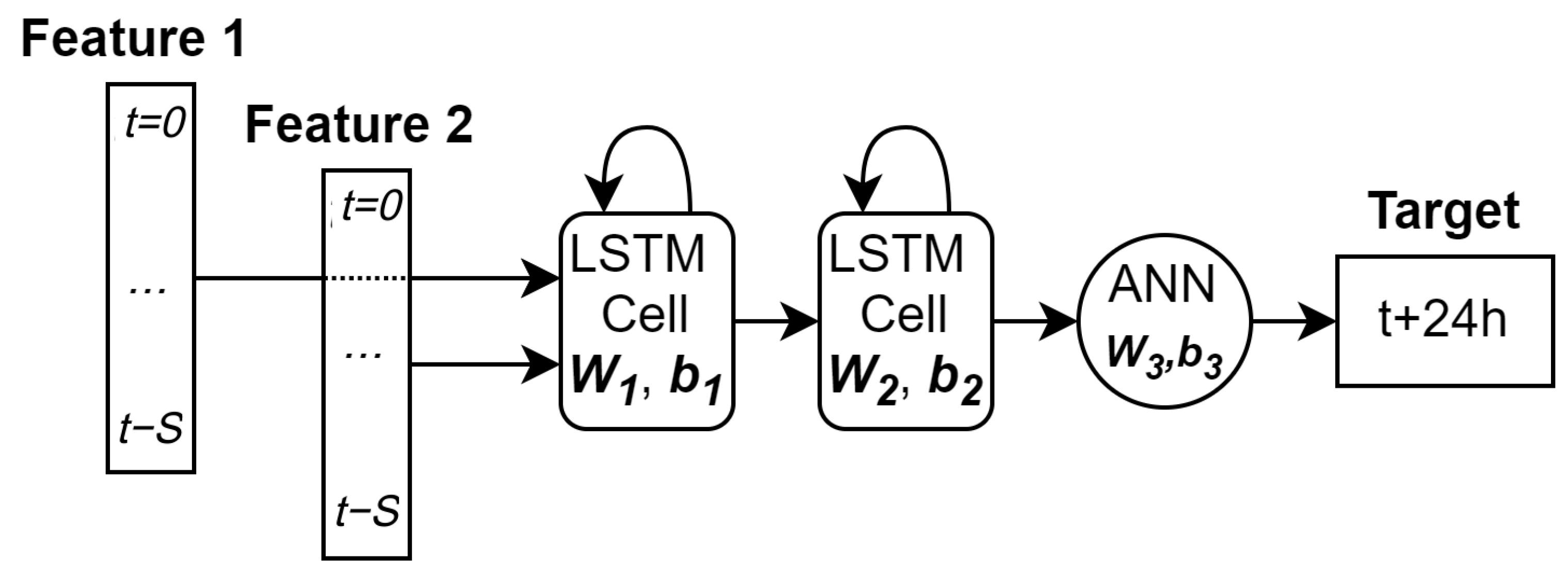
2.4. Long Short-Term Memory Model
2.5. Hyperparameter Tuning
2.6. Computational Burden Estimation
3. Case Studies
4. Results
4.1. Data Pre-Processing
4.2. Forecast
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Phadke, A. 2035: Plummeting Solar, Wind and Battery Costs can Accelerate our Clean Electricity Future; Goldman School of Public Policy; University of California Berkeley: Berkeley, CA, USA, 2020. [Google Scholar]
- Fares, R.L.; Webber, M.E. The impacts of storing solar energy in the home to reduce reliance on the utility. Nat. Energy 2017, 2, 1–10. [Google Scholar] [CrossRef]
- Borghetti, A.; Bosetti, M.; Grillo, S.; Massucco, S.; Nucci, C.A.; Paolone, M.; Silvestro, F. Short-term scheduling and control of active distribution systems with high penetration of renewable resources. IEEE Syst. J. 2010, 4, 313–322. [Google Scholar] [CrossRef]
- Graziano, M.; Gillingham, K. Spatial patterns of solar photovoltaic system adoption: The influence of neighbors and the built environment. J. Econ. Geogr. 2015, 15, 815–839. [Google Scholar] [CrossRef]
- American Society of Mechanical Engineers. REopt: A Platform for Energy System Integration and Optimization; American Society of Mechanical Engineers: New York, NY, USA, 2014; p. V002T03A006. [Google Scholar] [CrossRef]
- Polimeni, S.; Moretti, L.; Manzolini, G.; Leva, S.; Meraldi, L.; Raboni, P. Numerical and experimental testing of predictive EMS algorithms for PV-BESS residential microgrid. In Proceedings of the 2019 IEEE Milan PowerTech, Milan, Italy, 23–27 June 2019; pp. 1–6. [Google Scholar]
- Mellit, A.; Massi Pavan, A.; Ogliari, E.; Leva, S.; Lughi, V. Advanced methods for photovoltaic output power forecasting: A review. Appl. Sci. 2020, 10, 487. [Google Scholar] [CrossRef]
- Voyant, C.; Notton, G.; Kalogirou, S.; Nivet, M.L.; Paoli, C.; Motte, F.; Fouilloy, A. Machine learning methods for solar radiation forecasting: A review. Renew. Energy 2017, 105, 569–582. [Google Scholar] [CrossRef]
- Lindberg, K.B.; Bakker, S.J.; Sartori, I. Modelling electric and heat load profiles of non-residential buildings for use in long-term aggregate load forecasts. Util. Policy 2019, 58. [Google Scholar] [CrossRef]
- Cho, M.Y.; Hwang, J.C.; Chen, C.S. Customer short term load forecasting by using ARIMA transfer function model. In Proceedings of the 1995 International Conference on Energy Management and Power Delivery EMPD ’95, Singapore, 21–23 November 1995; Volume 1, pp. 317–322. [Google Scholar] [CrossRef]
- Amara, F.; Agbossou, K.; Dubé, Y.; Kelouwani, S.; Cardenas, A.; Hosseini, S.S. A residual load modeling approach for household short-term load forecasting application. Energy Build. 2019, 187. [Google Scholar] [CrossRef]
- Amarasinghe, K.; Marino, D.L.; Manic, M. Deep neural networks for energy load forecasting. In Proceedings of the 2017 IEEE 26th International Symposium on Industrial Electronics (ISIE), Edinburgh, UK, 19–21 June 2017; pp. 1483–1488. [Google Scholar] [CrossRef]
- Gajowniczek, K.; Zabkowski, T. Short term electricity forecasting based on user behavior from individual smart meter data. J. Intell. Fuzzy Syst. 2016, 30. [Google Scholar] [CrossRef]
- Ghofrani, M.; Hassanzadeh, M.; Etezadi-Amoli, M.; Fadali, M.S. Smart meter based short-term load forecasting for residential customers. In Proceedings of the NAPS 2011–43rd North American Power Symposium, Boston, MA, USA, 4–6 August 2011. [Google Scholar] [CrossRef]
- Marino, D.L.; Amarasinghe, K.; Manic, M. Building energy load forecasting using Deep Neural Networks. In Proceedings of the IECON Proceedings (Industrial Electronics Conference), Florence, Italy, 23–26 October 2016. [Google Scholar] [CrossRef]
- Wu, H.C.; Lu, C.N. A data mining approach for spatial modeling in small area load forecast. IEEE Trans. Power Syst. 2002, 17, 516–521. [Google Scholar] [CrossRef]
- Javed, F.; Arshad, N.; Wallin, F.; Vassileva, I.; Dahlquist, E. Forecasting for demand response in smart grids: An analysis on use of anthropologic and structural data and short term multiple loads forecasting. Appl. Energy 2012, 96, 150–160. [Google Scholar] [CrossRef]
- Oprea, S.V.; Bara, A. Machine Learning Algorithms for Short-Term Load Forecast in Residential Buildings Using Smart Meters, Sensors and Big Data Solutions. IEEE Access 2019, 7, 177874–177889. [Google Scholar] [CrossRef]
- Lusis, P.; Khalilpour, K.R.; Andrew, L.; Liebman, A. Short-term residential load forecasting: Impact of calendar effects and forecast granularity. Appl. Energy 2017, 205, 654–669. [Google Scholar] [CrossRef]
- Stephen, B.; Tang, X.; Harvey, P.R.; Galloway, S.; Jennett, K.I. Incorporating practice theory in sub-profile models for short term aggregated residential load forecasting. IEEE Trans. Smart Grid 2017, 8, 1591–1598. [Google Scholar] [CrossRef]
- Yao, Q.; Meng, X.; Wang, H.; An, Y. Short-term load forecasting of office building microgrid based on EA-NN. In Proceedings of the 2019 IEEE International Conference on Power, Intelligent Computing and Systems, ICPICS 2019, Shenyang, China, 12–14 July 2019; pp. 408–412. [Google Scholar] [CrossRef]
- Massana, J.; Pous, C.; Burgas, L.; Melendez, J.; Colomer, J. Short-term load forecasting in a non-residential building contrasting models and attributes. Energy Build. 2015, 92, 322–330. [Google Scholar] [CrossRef]
- Ramos, D.; Faria, P.; Vale, Z.; Mourinho, J.; Correia, R. Industrial facility electricity consumption forecast using artificial neural networks and incremental learning. Energies 2020, 13, 4774. [Google Scholar] [CrossRef]
- Ding, N.; Benoit, C.; Foggia, G.; Besanger, Y.; Wurtz, F. Neural network-based model design for short-term load forecast in distribution systems. IEEE Trans. Power Syst. 2016, 31, 72–81. [Google Scholar] [CrossRef]
- Tan, M.; Yuan, S.; Li, S.; Su, Y.; Li, H.; He, F.H. Ultra-Short-Term Industrial Power Demand Forecasting Using LSTM Based Hybrid Ensemble Learning. IEEE Trans. Power Syst. 2020, 35, 2937–2948. [Google Scholar] [CrossRef]
- Chen, Y.; Luh, P.B.; Guan, C.; Zhao, Y.; Michel, L.D.; Coolbeth, M.A.; Friedland, P.B.; Rourke, S.J. Short-term load forecasting: Similar day-based wavelet neural networks. IEEE Trans. Power Syst. 2010, 25, 322–330. [Google Scholar] [CrossRef]
- Hatziargyriou, N. Microgrids: Architectures and Control; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar] [CrossRef]
- Yildiz, B.; Bilbao, J.I.; Sproul, A.B. A review and analysis of regression and machine learning models on commercial building electricity load forecasting. Renew. Sustain. Energy Rev. 2017, 73, 1104–1122. [Google Scholar] [CrossRef]
- Zoha, A.; Gluhak, A.; Imran, M.A.; Rajasegarar, S. Non-intrusive Load Monitoring approaches for disaggregated energy sensing: A survey. Sensors 2012, 12, 16838–16866. [Google Scholar] [CrossRef]
- Amini, M.H.; Kargarian, A.; Karabasoglu, O. ARIMA-based decoupled time series forecasting of electric vehicle charging demand for stochastic power system operation. Electr. Power Syst. Res. 2016, 140, 378–390. [Google Scholar] [CrossRef]
- Nespoli, A.; Ogliari, E.; Pretto, S.; Gavazzeni, M.; Vigani, S.; Paccanelli, F. Data quality analysis in day-ahead load forecast by means of LSTM. In Proceedings of the 2020 IEEE International Conference on Environment and Electrical Engineering and 2020 IEEE Industrial and Commercial Power Systems Europe (EEEIC/I&CPS Europe), Madrid, Spain, 9–12 June 2020. [Google Scholar] [CrossRef]
- Zhang, J.; Verschae, R.; Nobuhara, S.; Lalonde, J.F. Deep photovoltaic nowcasting. Sol. Energy 2018, 176, 267–276. [Google Scholar] [CrossRef]
- Petropoulos, F.; Apiletti, D.; Assimakopoulos, V.; Babai, M.Z.; Barrow, D.K.; Taieb, S.B.; Bergmeir, C.; Bessa, R.J.; Bijak, J.; Boylan, J.E.; et al. Forecasting: Theory and practice. arXiv 2020, arXiv:2012.03854. [Google Scholar] [CrossRef]
- Arif, A.; Wang, Z.; Wang, J.; Mather, B.; Bashualdo, H.; Zhao, D. Load modeling—A review. IEEE Trans. Smart Grid 2018, 9, 5986–5999. [Google Scholar] [CrossRef]
- Ghelardoni, L.; Ghio, A.; Anguita, D. Energy load forecasting using empirical mode decomposition and support vector regression. IEEE Trans. Smart Grid 2013, 4, 549–556. [Google Scholar] [CrossRef]
- Xia, C.; Wang, J.; McMenemy, K. Short, medium and long term load forecasting model and virtual load forecaster based on radial basis function neural networks. Int. J. Electr. Power Energy Syst. 2010, 32, 743–750. [Google Scholar] [CrossRef]
- Kong, W.; Dong, Z.Y.; Jia, Y.; Hill, D.J.; Xu, Y.; Zhang, Y. Short-term residential load forecasting based on LSTM recurrent neural network. IEEE Trans. Smart Grid 2017, 10, 841–851. [Google Scholar] [CrossRef]
- Chen, Q.; Wen, D.; Li, X.; Chen, D.; Lv, H.; Zhang, J.; Gao, P. Empirical mode decomposition based long short-term memory neural network forecasting model for the short-term metro passenger flow. PLoS ONE 2019, 14, e0222365. [Google Scholar] [CrossRef]
- Li, L.; Jamieson, K.; DeSalvo, G.; Rostamizadeh, A.; Talwalkar, A. Hyperband: A novel bandit-based approach to hyperparameter optimization. J. Mach. Learn. Res. 2018, 18, 6765–6816. [Google Scholar]
- Li, T.; Wang, B.; Zhou, M.; Zhang, L.; Zhao, X. Short-Term Load Forecasting Using Optimized LSTM Networks Based on EMD. In Proceedings of the 2018 10th International Conference on Communications, Circuits and Systems (ICCCAS), Chengdu, China, 22–24 December 2018; pp. 84–88. [Google Scholar] [CrossRef]
- Goia, A.; May, C.; Fusai, G. Functional clustering and linear regression for peak load forecasting. Int. J. Forecast. 2010, 26, 700–711. [Google Scholar] [CrossRef]
- Elnozahy, M.S.; Salama, M.M.; Seethapathy, R. A probabilistic load modelling approach using clustering algorithms. In Proceedings of the IEEE Power and Energy Society General Meeting, Vancouver, BC, Canada, 21–25 July 2013. [Google Scholar] [CrossRef]
- Sun, C.; Shrivastava, A.; Singh, S.; Gupta, A. Revisiting unreasonable effectiveness of data in deep learning era. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 843–852. [Google Scholar]
- Banko, M.; Brill, E. Scaling to very very large corpora for natural language disambiguation. In Proceedings of the 39th Annual Meeting of the Association for Computational Linguistics, Toulouse, France, 6–11 July 2001; pp. 26–33. [Google Scholar]
- Géron, A. Hands-On Machine Learning with Scikit-Learn and TensorFlow: Concepts, Tools, and Techniques to Build Intelligent Systems, 1st ed.; O’Reilly Media: Sebastopol, CA, USA, 2017. [Google Scholar]
- Yap, B.W.; Sim, C.H. Comparisons of various types of normality tests. J. Stat. Comput. Simul. 2011, 81, 2141–2155. [Google Scholar] [CrossRef]
- Brockwell, P.J.; Brockwell, P.J.; Davis, R.A.; Davis, R.A. Introduction to Time Series and Forecasting; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Butler, M.; Kazakov, D. The effects of variable stationarity in a financial time-series on artificial neural networks. In Proceedings of the 2011 IEEE Symposium on Computational Intelligence for Financial Engineering and Economics (CIFEr), London, UK, 27–28 March 2011; pp. 1–8. [Google Scholar]
- Hyndman, R.J.; Fan, S. Density forecasting for long-term peak electricity demand. IEEE Trans. Power Syst. 2009, 25, 1142–1153. [Google Scholar] [CrossRef]
- Fabbri, M.; Moro, G. Dow Jones Trading with Deep Learning: The Unreasonable Effectiveness of Recurrent Neural Networks. In Proceedings of the 7th International Conference on Data Science, Technology and Applications (DATA 2018), Porto, Portugal, 26–28 July 2018; pp. 142–153. [Google Scholar]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.C.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. London Ser. A: Math. Phys. Eng. Sci. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Liang, H.; Bressler, S.L.; Buffalo, E.A.; Desimone, R.; Fries, P. Empirical mode decomposition of field potentials from macaque V4 in visual spatial attention. Biol. Cybern. 2005, 92, 380–392. [Google Scholar] [CrossRef]
- Lee, D.; Kim, K. Recurrent neural network-based hourly prediction of photovoltaic power output using meteorological information. Energies 2019, 12, 215. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Stančin, I.; Jović, A. An overview and comparison of free Python libraries for data mining and big data analysis. In Proceedings of the 2019 42nd International Convention on Information and Communication Technology, Electronics and Microelectronics (MIPRO), Opatija, Croatia, 20–24 May 2019; pp. 977–982. [Google Scholar] [CrossRef]
- Lee, Z.J.; Li, T.; Low, S.H. ACN-data: Analysis and applications of an open EV charging dataset. In Proceedings of the Tenth ACM International Conference on Future Energy Systems, Phoenix, AZ, USA, 25–28 June 2019; pp. 139–149. [Google Scholar]





| Sector | Papers (Single Site) | Papers (Multiple Sites) |
|---|---|---|
| Residential | [10,11,12,13,14,15] | [16,17,18,19,20] |
| Commercial | [10,21,22] | [9,16] |
| Industrial | [10,23,24,25] | [16] |
| All Three | [10] | [16] |
| Site | Load | Koppen | Length | Interval | Peak | Autocorr. | ADF |
|---|---|---|---|---|---|---|---|
| Sector 1 | Climate | [y] | [min] | [MW] | 1/7 day | Statistic | |
| Residence 2 | Res. | BSk | 16.4 | 60 | 0.007 | 0.70/0.63 | −17.1 |
| Hotel 1 | Com. | Af | 3.2 | 15 | 1.76 | 0.95/0.92 | −4.9 |
| Hotel 2 | Com. | BSk | 2.0 | 15 | 0.45 | 0.87/0.80 | −5.5 |
| Manufacturing Plant | Ind. | Dfa | 2.9 | 15 | 13.0 | 0.45/0.93 | −20.1 |
| EV Charging Station 3 | Tra. | Cfa | 2.7 | 10 | 0.16 | 0.70/0.84 | −17.4 |
| Distribution Network | Sys. | BSk | 13.8 | 60 | 1.9 | 0.94/0.86 | −10.5 |
| Transmission Network 4 | Sys. | Many | 10.0 | 60 | 59,700 | 0.78/0.89 | −17.7 |
| Case | Site | LSTM | NP | SARIMA | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Hyperparameters | Weights | Test Error | Test Error | Test Error | |||||||
| IMFs | Units | Dropout | Layers | [] | [RMSE] | [RMSE] | [SS] | [RMSE] | [SS] | ||
| 1a | Residence | – | 1024 | 0.1 | 3 | 4.215 | 0.71 kW | 0.73 kW | 2.7% | 0.70 kW | −1.4% |
| 1b | 1,2,3 | 256 | 0 | 3 | 0.280 | 0.63 kW | 14% | 10% | |||
| 2a | Hotel 1 | – | 256 | 0 | 4 | 0.793 | 62.41 kW | 73.05 kW | 15% | 56.5 kW | −11% |
| 2b | 3,4,5 | 256 | 0 | 3 | 0.271 | 60.05 kW | 18% | −6.3% | |||
| 3a | Hotel 2 | – | 128 | 0 | 3 | 0.068 | 25.27 kW | 33.90 kW | 25% | 24.4 kW | −3.6% |
| 3b | 3,4,5 | 512 | 0 | 4 | 3.165 | 24.34 kW | 28% | 0.2% | |||
| 4a | Manufacturing | – | 96 | 0 | 4 | 0.113 | 598.7 kW | 595.1 kW | −0.6% | 1697 kW | 65% |
| 4b | Plant | 3,4,5 | 96 | 0 | 4 | 0.114 | 451.1 kW | 24% | 73% | ||
| 5a | Distribution | – | 128 | 0.1 | 4 | 0.200 | 51.01 MW | 58.18 MW | 12% | 58.1 MW | 12% |
| 5b | Network | 3,4,5 | 96 | 0.1 | 3 | 0.040 | 39.40 MW | 32% | 32% | ||
| 6a | Transmission | – | 512 | 0.1 | 4 | 3.159 | 1952 MW | 3594 MW | 46% | 4236 MW | 54% |
| 6b | Network | 3,4,5 | 512 | 0.1 | 4 | 3.165 | 1580 MW | 56% | 63% | ||
| 7a | EV Charging | – | 96 | 0 | 4 | 0.0039 | 11.23 kW | 24.27 kW | 54% | 19.6 kW | 43% |
| 7b | Station | 3,4,5,6 | 512 | 0.1 | 3 | 1.067 | 8.93 kW | 63% | 54% | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wood, M.; Ogliari, E.; Nespoli, A.; Simpkins, T.; Leva, S. Day Ahead Electric Load Forecast: A Comprehensive LSTM-EMD Methodology and Several Diverse Case Studies. Forecasting 2023, 5, 297-314. https://doi.org/10.3390/forecast5010016
Wood M, Ogliari E, Nespoli A, Simpkins T, Leva S. Day Ahead Electric Load Forecast: A Comprehensive LSTM-EMD Methodology and Several Diverse Case Studies. Forecasting. 2023; 5(1):297-314. https://doi.org/10.3390/forecast5010016
Chicago/Turabian StyleWood, Michael, Emanuele Ogliari, Alfredo Nespoli, Travis Simpkins, and Sonia Leva. 2023. "Day Ahead Electric Load Forecast: A Comprehensive LSTM-EMD Methodology and Several Diverse Case Studies" Forecasting 5, no. 1: 297-314. https://doi.org/10.3390/forecast5010016
APA StyleWood, M., Ogliari, E., Nespoli, A., Simpkins, T., & Leva, S. (2023). Day Ahead Electric Load Forecast: A Comprehensive LSTM-EMD Methodology and Several Diverse Case Studies. Forecasting, 5(1), 297-314. https://doi.org/10.3390/forecast5010016







