A Hybrid Method for the Run-Of-The-River Hydroelectric Power Plant Energy Forecast: HYPE Hydrological Model and Neural Network
Abstract
1. Introduction
2. Materials and Methods
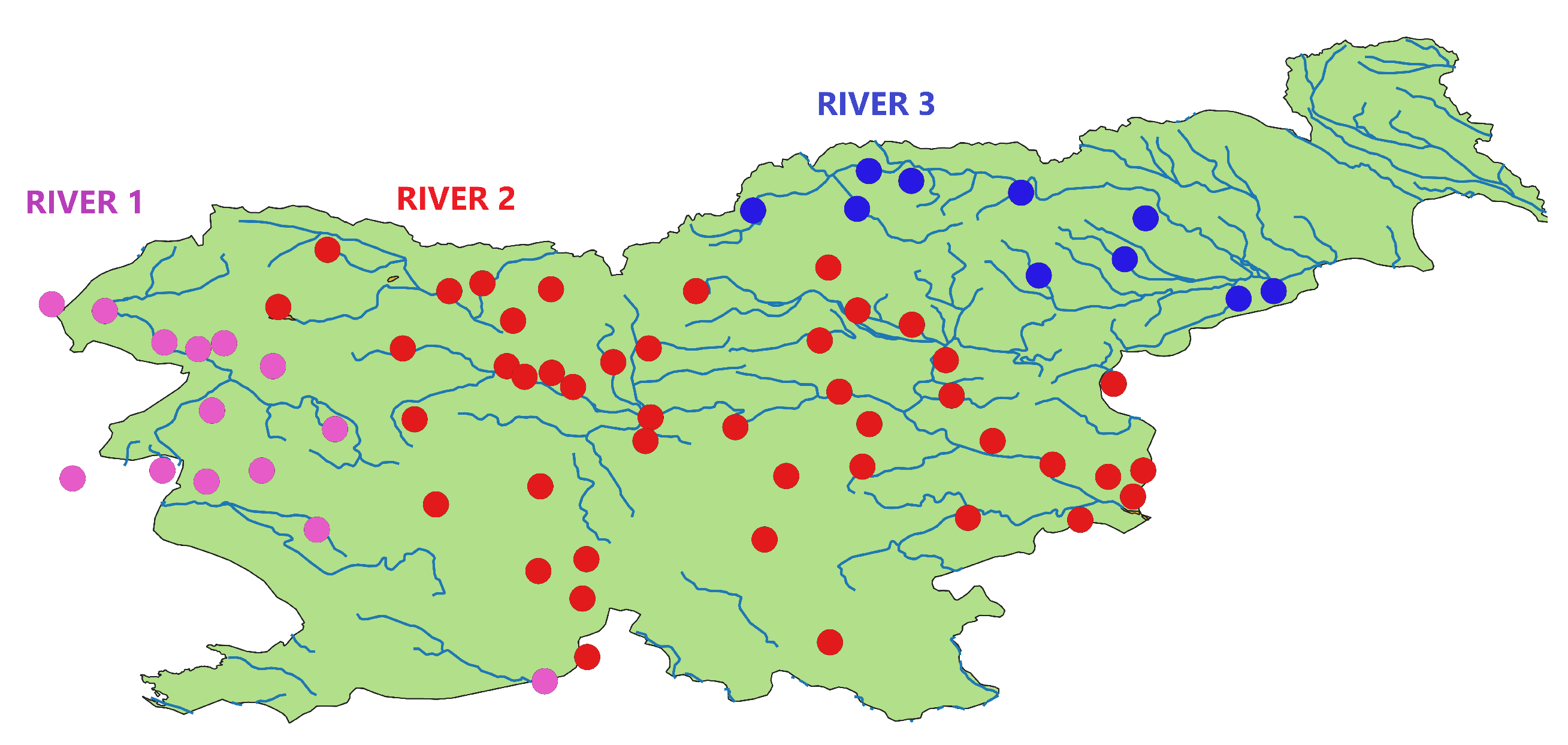
2.1. Available Dataset
2.2. Performance Measurement
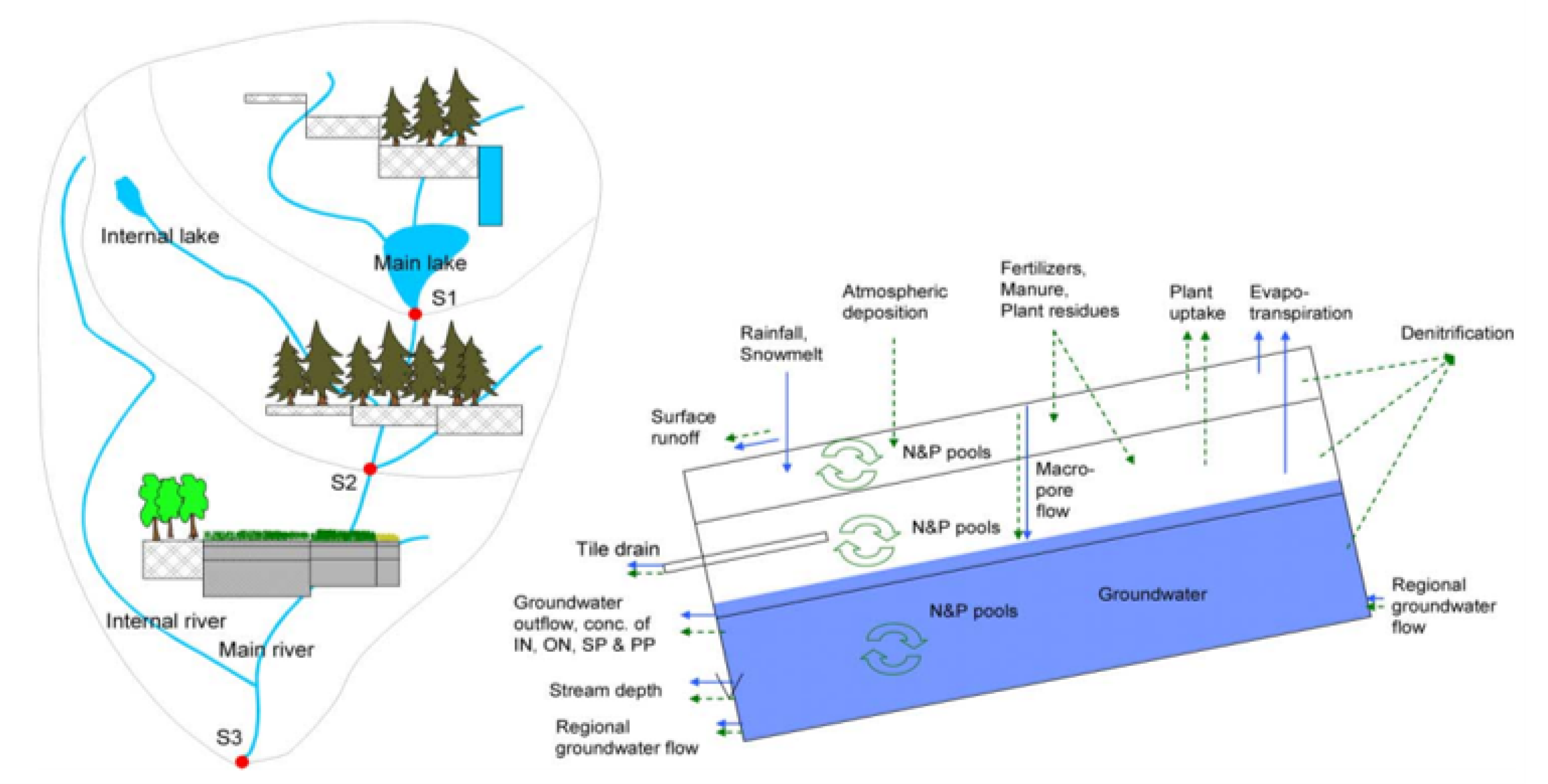
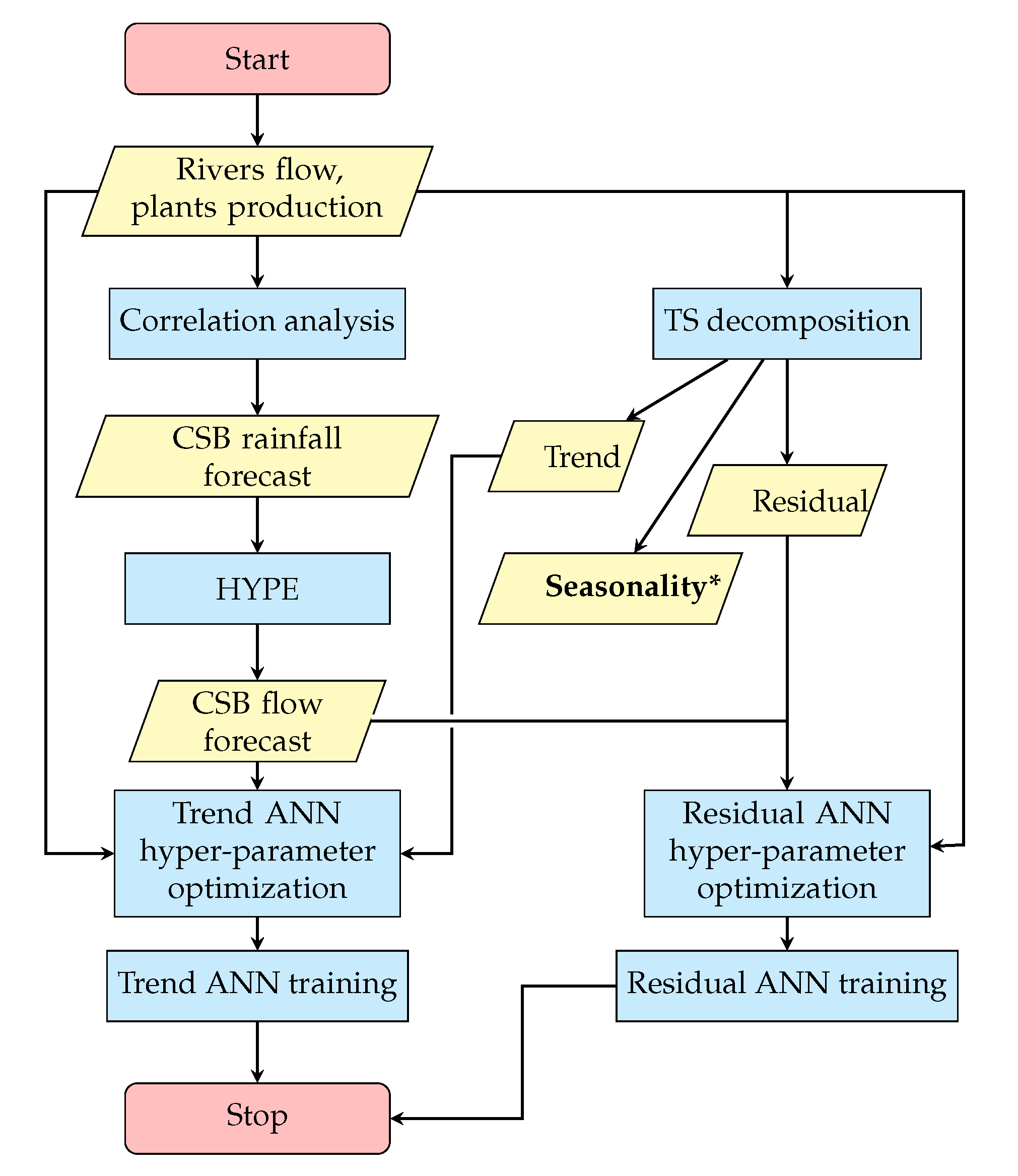
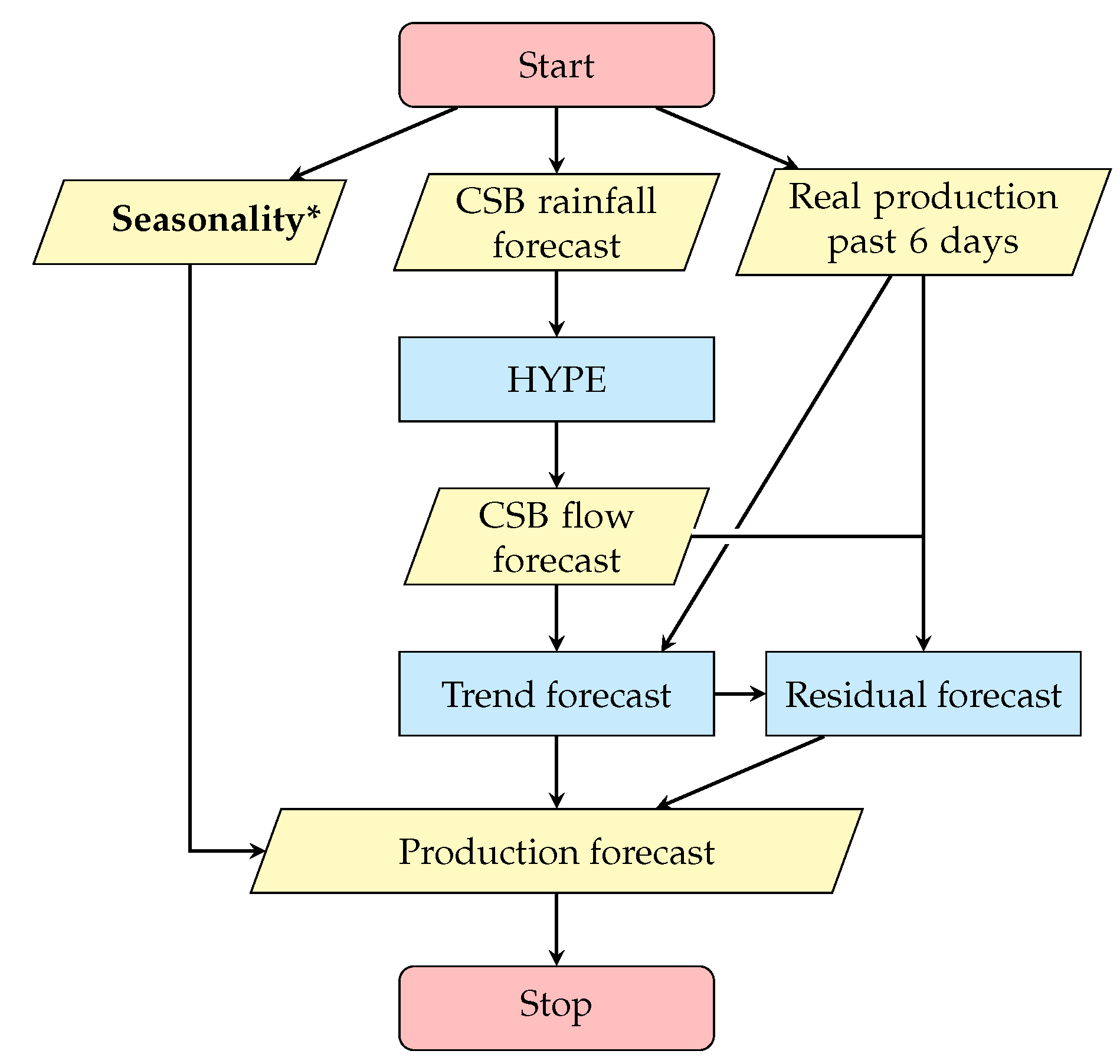
2.3. HYPE model and hybrid forecast method
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| ANN | Artificial Neural Network |
| ARIMA | Auto Regressive Integrated Moving Average |
| CSB | Correlated Sub-Basins |
| ECA | European Climate Assessment |
| E | Nash–Sutcliffe Efficiency Index |
| HYPE | HYdrological Predictions for the Environment |
| MA | Moving Average |
| MAE | Mean Absolute Error |
| MASE | Mean Absolute Scaled Error |
| MBE | Mean Bias Error |
| PSP | Pumped Storage Plant |
| RoR | Run of the River |
| SD | Standard Deviation |
| SHP | Storage Hydro Plants |
| SMAPE | Symmetric Mean Absolute Percentage Error |
| TS | Time Series |
| TSO | Transmission System Operator |
| TSS | Training Set Size |
Appendix A
| (a) Plant 2, River 1. | nMAE | E | MASE |
|---|---|---|---|
| Hybrid + Dec. | 3.62 | 0.94 | 0.44 |
| Hybrid | 3.51 | 0.94 | 0.43 |
| ANN | 8.62 | 0.71 | 1.06 |
| ANN + Dec. | 10.07 | 0.60 | 1.24 |
| (b) Plant 3, River 1. | nMAE | E | MASE |
| Hybrid + Dec. | 5.27 | 0.87 | 0.58 |
| Hybrid | 4.54 | 0.92 | 0.50 |
| ANN | 9.51 | 0.72 | 1.05 |
| ANN + Dec. | 12.99 | 0.44 | 1.43 |
| (c) Plant 2, River 2. | nMAE | E | MASE |
| Hybrid + Dec. | 3.61 | 0.92 | 0.60 |
| Hybrid | 3.23 | 0.94 | 0.54 |
| ANN | 6.50 | 0.74 | 1.09 |
| ANN + Dec. | 8.57 | 0.57 | 1.43 |
| (d) Plant 3, River 2. | nMAE | E | MASE |
| Hybrid + Dec. | 3.74 | 0.93 | 0.61 |
| Hybrid | 3.10 | 0.95 | 0.50 |
| ANN | 6.79 | 0.72 | 1.11 |
| ANN + Dec. | 9.21 | 0.61 | 1.50 |
| (e) Plant 4, River 2. | nMAE | E | MASE |
| Hybrid + Dec. | 4.19 | 0.93 | 0.67 |
| Hybrid | 3.63 | 0.93 | 0.58 |
| ANN | 7.31 | 0.72 | 1.16 |
| ANN + Dec. | 9.19 | 0.66 | 1.46 |
| (f) Plant 5, River 2. | nMAE | E | MASE |
| Hybrid + Dec. | 4.07 | 0.93 | 0.62 |
| Hybrid | 3.79 | 0.94 | 0.58 |
| ANN | 7.11 | 0.76 | 1.09 |
| ANN + Dec. | 9.42 | 0.68 | 1.44 |
| (g) Plant 2, River 3. | nMAE | E | MASE |
| Hybrid + Dec. | 2.62 | 0.96 | 0.33 |
| Hybrid | 2.78 | 0.93 | 0.35 |
| ANN | 7.89 | 0.71 | 1.00 |
| ANN + Dec. | 8.00 | 0.67 | 1.02 |
| (h) Plant 3, River 3. | nMAE | E | MASE |
| Hybrid + Dec. | 2.63 | 0.96 | 0.34 |
| Hybrid | 2.90 | 0.93 | 0.37 |
| ANN | 7.60 | 0.72 | 0.97 |
| ANN + Dec. | 7.59 | 0.68 | 0.97 |
| (i) Plant 4, River 3. | nMAE | E | MASE |
| Hybrid + Dec. | 2.49 | 0.95 | 0.37 |
| Hybrid | 2.70 | 0.94 | 0.40 |
| ANN | 6.60 | 0.79 | 0.98 |
| ANN + Dec. | 6.86 | 0.73 | 1.02 |
| (j) Plant 5, River 3. | nMAE | E | MASE |
| Hybrid + Dec. | 2.55 | 0.96 | 0.41 |
| Hybrid | 2.46 | 0.96 | 0.39 |
| ANN | 6.39 | 0.79 | 1.02 |
| ANN + Dec. | 6.65 | 0.71 | 1.07 |
| (k) Plant 6, River 3. | nMAE | E | MASE |
| Hybrid + Dec. | 2.53 | 0.96 | 0.37 |
| Hybrid | 2.78 | 0.93 | 0.40 |
| ANN | 7.69 | 0.27 | 1.11 |
| ANN + Dec. | 6.93 | 0.70 | 1.00 |
| (l) Plant 7, River 3. | nMAE | E | MASE |
| Hybrid + Dec. | 2.32 | 0.96 | 0.34 |
| Hybrid | 2.67 | 0.95 | 0.39 |
| ANN | 7.01 | 0.71 | 1.03 |
| ANN + Dec. | 7.02 | 0.71 | 1.03 |
References
- Giebel, G.; Al, E. The State of the Art in Short-Term Prediction of Wind Power. ANEMOS.Plus 2011, 1–110. [Google Scholar] [CrossRef]
- Mo, C.; Énergie, N.D.E.L.; Kim, Y.D.; Frei, C. World Energy Resources: Charting the Upsurge in Hydropower Development; World Energy Council: London, UK, 2015; p. 55. [Google Scholar]
- Levine, J.G. Pumped Hydroelectric Energy Storage and Spatial Diversity of Wind Resources as Methods of Improving Utilization of Renewable Energy Sources. Ph.D. Thesis, University of Colorado, Boulder, CO, USA, 2007. [Google Scholar]
- Resgaard, J.C. Hydrological Modelling and River Basin Management. Ph.D. Thesis, University of Copenhagen, Copenhagen, Denmark, 2007. [Google Scholar]
- Bergström, S. Development and Application of a Conceptual Runoff Model for Scandinavian Catchments. In Hydrologi Och Oceanografi, SMHI Reporter; Department of Water Resources Engineering, Lund Institute of Technology, University of Lund: Lund, Sweden, 1976; p. 134. [Google Scholar] [CrossRef]
- Arnold, J.G.; Fohrer, N. SWAT2000: Current capabilities and research opportunities in applied watershed modelling. Hydrol. Process. 2005, 19, 563–572. [Google Scholar] [CrossRef]
- Gupta, K.; Sharma, G.; Jethoo, A.; Tyagi, J.; Gupta, N. A critical review of hydrological models. In Proceedings of the 20th International Conference on Hydraulics, Water Resources and River Engineering, Roorkee, India, 17–19 December 2015; Volume 1, pp. 17–19. [Google Scholar]
- Islam, Z. Literature Review on Physically Based Hydrological Modeling; Technical Report February; University of Alberta: Edmonton, Alberta, 2011. [Google Scholar] [CrossRef]
- Dhami, B.S.; Pandey, A. Comparative Review of Recently Developed Hydrologic Models. J. Indian Water Resour. Soc. 2013, 33, 34–41. [Google Scholar]
- Solomatine, D.; See, L.M.; Abrahart, R.J. Approaches and Experiences. In Practical Hydroinformatics: Computational Intelligence and Technological Developments in Water Applications; Abrahart, R.J., See, L.M., Solomatine, D.P., Eds.; Springer: Berlin/Heidelberg, Germany, 2008; pp. 17–30. [Google Scholar] [CrossRef]
- De Menezes, M.L.; Teixeira Junior, L.A.; Morais De Souza, R.; Mara, C.K.; Moreira Pessanha, J.F.; Castro Souza, R. Hydroelectric energy forecast. Int. J. Energy Stat. 2013. [Google Scholar] [CrossRef]
- Mite-León, M.; Barzola-Monteses, J. Statistical model for the forecast of hydropower production in Ecuador. Int. J. Renew. Energy Res. 2018, 8, 1130–1137. [Google Scholar]
- Das, U.K.; Tey, K.S.; Seyedmahmoudian, M.; Mekhilef, S.; Idris, M.Y.I.; Van Deventer, W.; Horan, B.; Stojcevski, A. Forecasting of photovoltaic power generation and model optimization: A review. Renew. Sustain. Energy Rev. 2018, 81, 912–928. [Google Scholar] [CrossRef]
- Elshorbagy, A.; Corzo, G.; Srinivasulu, S.; Solomatine, D.P. Experimental investigation of the predictive capabilities of data driven modeling techniques in hydrology—Part 1: Concepts and methodology. Hydrol. Earth Syst. Sci. 2010, 14, 1931–1941. [Google Scholar] [CrossRef]
- Hammid, A.T.; Sulaiman, M.H.B.; Abdalla, A.N. Prediction of small hydropower plant power production in Himreen Lake dam (HLD) using artificial neural network. Alex. Eng. J. 2018, 57, 211–221. [Google Scholar] [CrossRef]
- Cobaner, M.; Haktanir, T.; Kisi, O. Prediction of Hydropower Energy Using ANN for the Feasibility of Hydropower Plant Installation to an Existing Irrigation Dam. Water Resour. Manag. 2008, 22, 757–774. [Google Scholar] [CrossRef]
- Beheshti, M.; Heidari, A.; Saghafian, B. Susceptibility of hydropower generation to climate change: Karun III Dam case study. Water 2019, 11, 1025. [Google Scholar] [CrossRef]
- Li, M.; Deng, C.H.; Tan, J.; Yang, W.; Zheng, L. Research on Small Hydropower Generation Forecasting Method Based on Improved BP Neural Network. In 2016 3rd International Conference on Materials Engineering, Manufacturing Technology and Control; Atlantis Press: Paris, France, 2016; pp. 1085–1090. [Google Scholar] [CrossRef][Green Version]
- Monteiro, C.; Ramirez-Rosado, I.J.; Fernandez-Jimenez, L.A. Short-term forecasting model for electric power production of small-hydro power plants. Renew. Energy 2013, 50, 387–394. [Google Scholar] [CrossRef]
- Haykin, S. Neural Networks and Learning Machines, 3th ed.; Pearson: Upper Saddle River, NJ, USA, 2014. Available online: http://xxx.lanl.gov/abs/1312.6199v4 (accessed on 27 August 2020).
- Sobri, S.; Koohi-Kamali, S.; Rahim, N.A. Solar photovoltaic generation forecasting methods: A review. Energy Convers. Manag. 2018, 156, 459–497. [Google Scholar] [CrossRef]
- Escobar, R.; Antonanzas, J.; Antonanzas-Torres, F.; Urraca, R.; Osorio, N.; Martinez-de Pison, F. Review of photovoltaic power forecasting. Sol. Energy 2016, 136, 78–111. [Google Scholar] [CrossRef]
- Hussin, S.N.; Malek, M.A.; Jaddi, N.S.; Hamid, Z.A. Hybrid metaheuristic of artificial neural network-Bat algorithm in forecasting electricity production and water consumption at Sultan Azlan shah Hydropower plant. In Proceedings of the PECON 2016–2016 IEEE 6th International Conference on Power and Energy, Conference Proceeding, Melaka, Malaysia, 28–29 November 2016; pp. 28–31. [Google Scholar] [CrossRef]
- Wang, S.; Yu, L.; Tang, L.; Wang, S. A novel seasonal decomposition based least squares support vector regression ensemble learning approach for hydropower consumption forecasting in China. Energy 2011, 36, 6542–6554. [Google Scholar] [CrossRef]
- Zhang, H.; Singh, V.P.; Wang, B.; Yu, Y. CEREF: A hybrid data-driven model for forecasting annual streamflow from a socio-hydrological system. J. Hydrol. 2016, 540, 246–256. [Google Scholar] [CrossRef]
- Gaudard, L.; Avanzi, F.; De Michele, C. Seasonal aspects of the energy-water nexus: The case of a run-of-the-river hydropower plant. Appl. Energy 2018, 210, 604–612. [Google Scholar] [CrossRef]
- Wang, W.C.; Chau, K.W.; Xu, D.M.; Chen, X.Y. Improving Forecasting Accuracy of Annual Runoff Time Series Using ARIMA Based on EEMD Decomposition. Water Resour. Manag. 2015, 29, 2655–2675. [Google Scholar] [CrossRef]
- Zhang, G.P.; Qi, M. Neural network forecasting for seasonal and trend time series. Eur. J. Oper. Res. 2005, 160, 501–514. [Google Scholar] [CrossRef]
- Miller, D.M.; Williams, D. Shrinkage estimators of time series seasonal factors and their effect on forecasting accuracy. Int. J. Forecast. 2003, 19, 669–684. [Google Scholar] [CrossRef]
- Cleveland, W.P.; Tiao, G.C. Decomposition of Seasonal Time Series: A Model for the Census X-11 Program. J. Am. Stat. Assoc. 1976, 71, 581–587. [Google Scholar] [CrossRef]
- Sala, S.; Amendola, A.; Leva, S.; Mussetta, M.; Niccolai, A.; Ogliari, E. Comparison of Data-Driven Techniques for Nowcasting Applied to an Industrial-Scale Photovoltaic Plant. Energies 2019, 12, 4520. [Google Scholar] [CrossRef]
- Nespoli, A.; Ogliari, E.; Gavazzeni, M.; Vigani, S.; Paccanelli, F. Data quality analysis in day-ahead load forecast by means of LSTM. In Proceedings of the 2020 IEEE International Conference on Environment and Electrical Engineering and 2020 IEEE Industrial and Commercial Power Systems Europe (EEEIC/I&CPS Europe), Madrid, Spain, 9–12 June 2020. [Google Scholar]
- Lindström, G.; Pers, C.; Rosberg, J.; Strömqvist, J.; Arheimer, B. Development and testing of the HYPE (Hydrological Predictions for the Environment) water quality model for different spatial scales. Hydrol. Res. 2010, 41, 295–319. [Google Scholar] [CrossRef]
- Donnelly, C.; Andersson, J.C.M.; Arheimer, B. Using flow signatures and catchment similarities to evaluate the E-HYPE multi-basin model across Europe. Hydrol. Sci. J. 2016, 61, 255–273. [Google Scholar] [CrossRef]
- Strömqvist, J.; Arheimer, B.; Dahné, J.; Donnelly, C.; Lindström, G. Water and nutrient predictions in ungauged basins: Set-up and evaluation of a model at the national scale. Hydrol. Sci. J. 2012, 57, 229–247. [Google Scholar] [CrossRef]
- Arheimer, B.; Wallman, P.; Donnelly, C.; Nyström, K.; Arheimer, B.; Wallman, P.; Donnelly, C.; Nyström, K.; Pers, C. E-HypeWe: Service for Water and Climate Information and Future Hydrological Collaboration across Europe. In International Symposium on Environmental Software Systems; Springer: Berlin/Heidelberg, Germany, 2011; pp. 656–657. [Google Scholar]
- Andersson, J.C.M.; Pechlivanidis, I.G.; Gustafsson, D.; Donnelly, C.; Arheimer, B. Key factors for improving large-scale hydrological model performance. Eur. Water 2015, 49, 77–88. [Google Scholar]
- Montgomery, D.C.; Runger, G.C.; Hubele, N.F. Engineering Statistics, 5th ed.; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Adhikari, R. An Introductory Study on Time Series Modeling and Forecasting. 2013. Available online: http://xxx.lanl.gov/abs/1302.6613 (accessed on 29 August 2020).
- Tawfik, M. Linearity versus non-linearity in forecasting Nile River flows. Adv. Eng. Softw. 2003, 34, 515–524. [Google Scholar] [CrossRef]
- Da’Ar, O.B.; Ahmed, A.E. Underlying trend, seasonality, prediction, forecasting and the contribution of risk factors: An analysis of globally reported cases of Middle East Respiratory Syndrome Coronavirus. Epidemiol. Infect. 2018, 146, 1878. [Google Scholar] [CrossRef]
- Bashiri, M.; Farshbaf Geranmayeh, A. Tuning the parameters of an artificial neural network using central composite design and genetic algorithm. Sci. Iran. 2011, 18, 1600–1608. [Google Scholar] [CrossRef]
- Grimaccia, F.; Leva, S.; Mussetta, M.; Ogliari, E. ANN sizing procedure for the day-ahead output power forecast of a PV plant. Appl. Sci. 2017, 7, 622. [Google Scholar] [CrossRef]
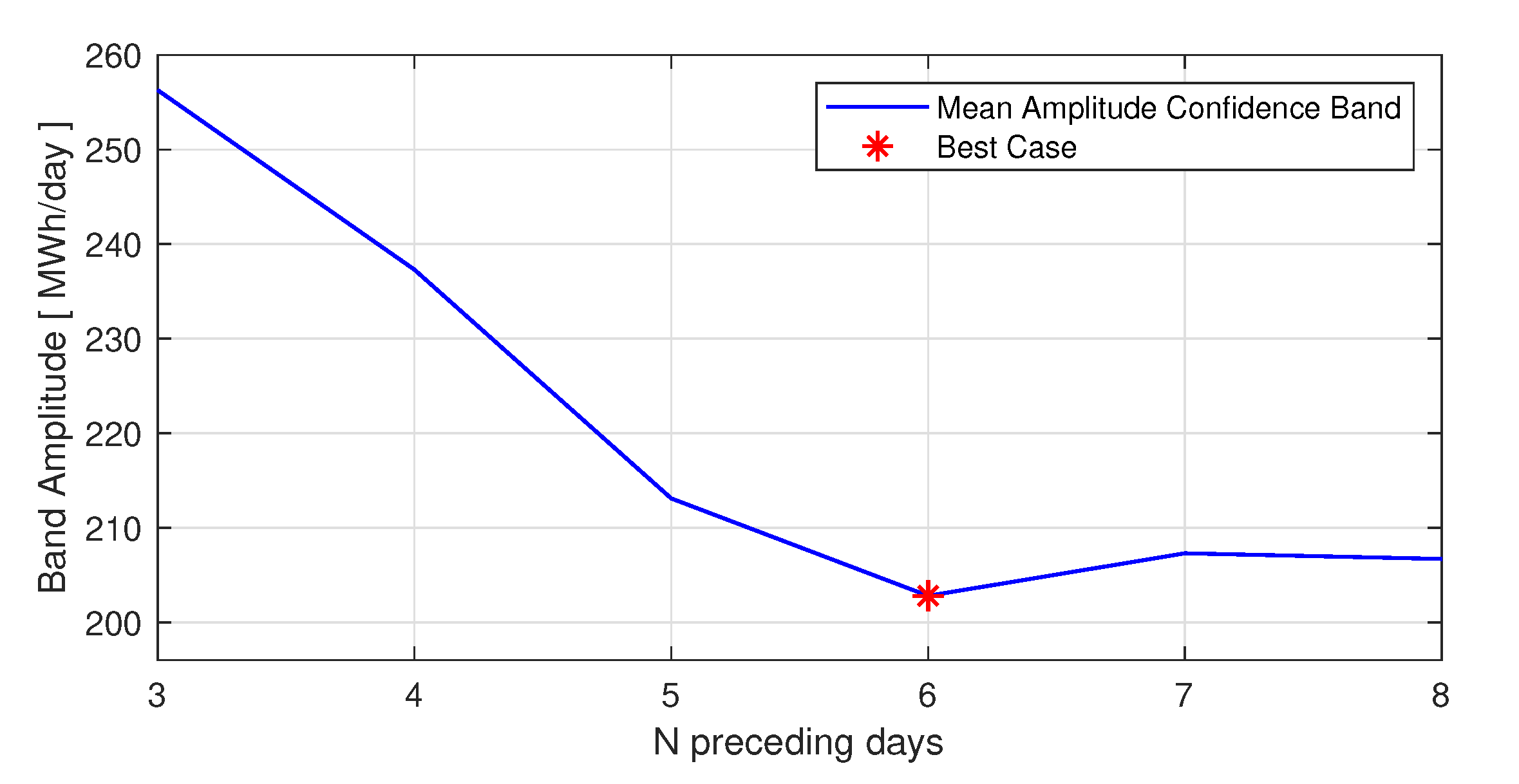
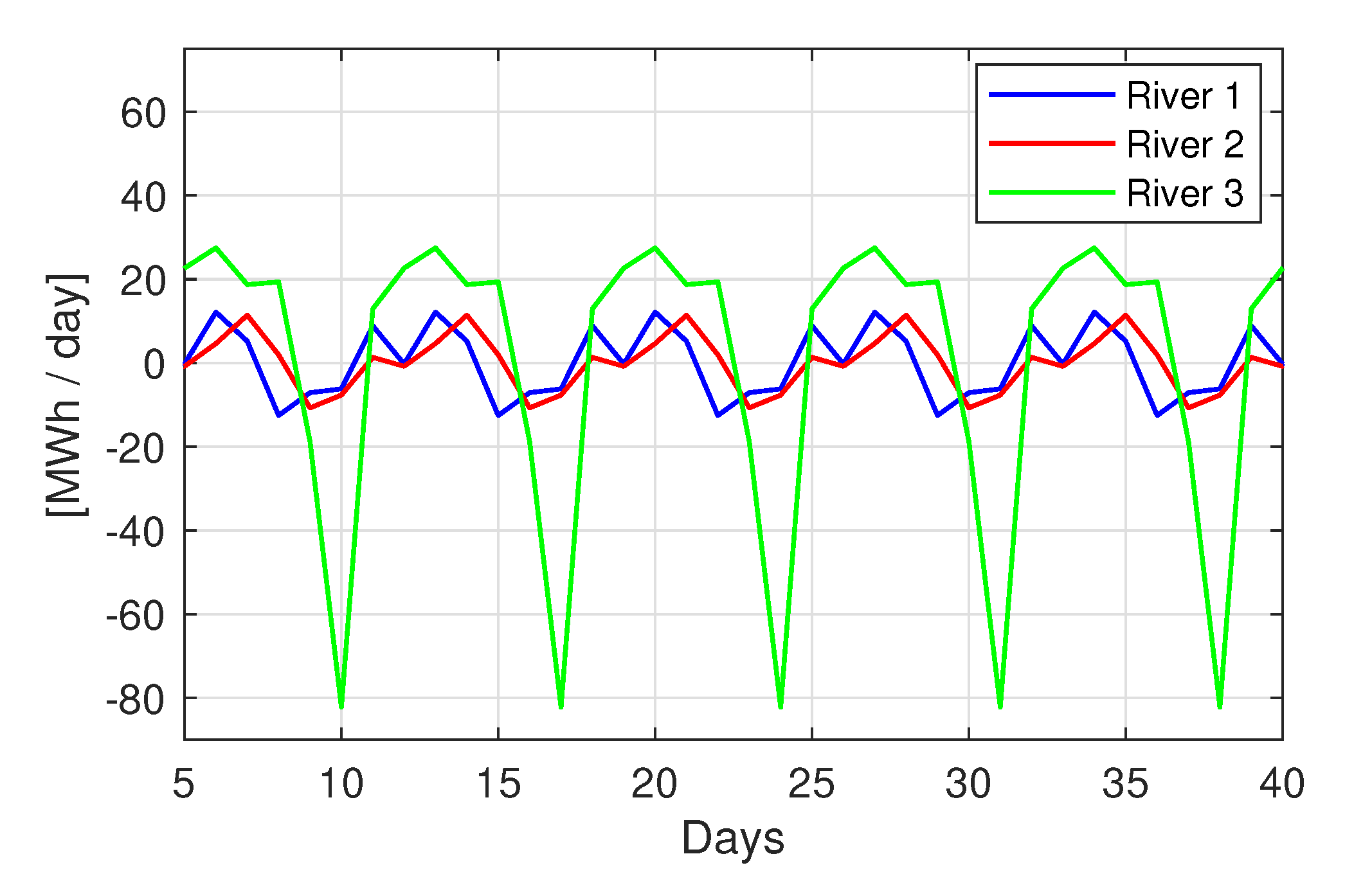
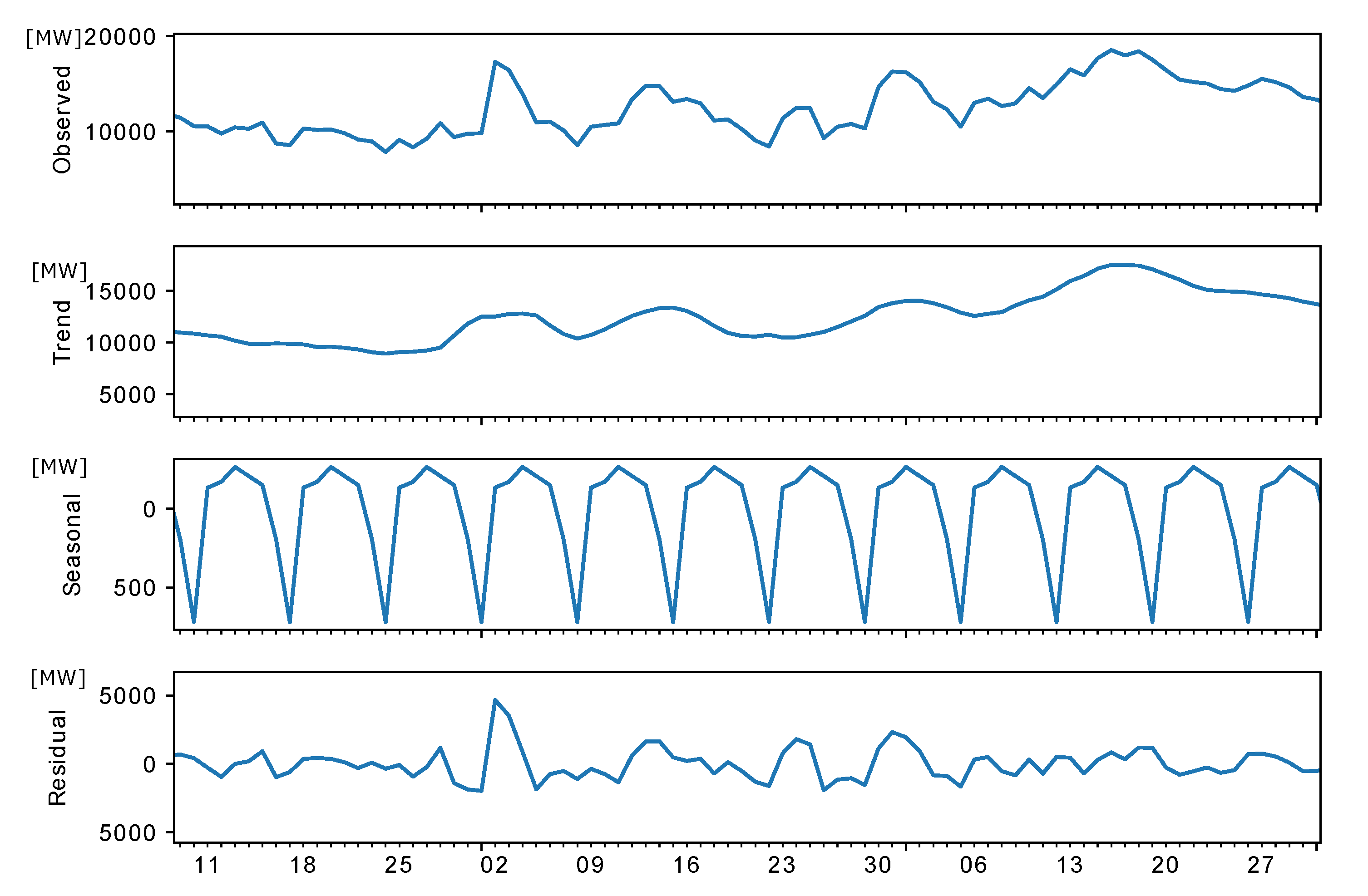
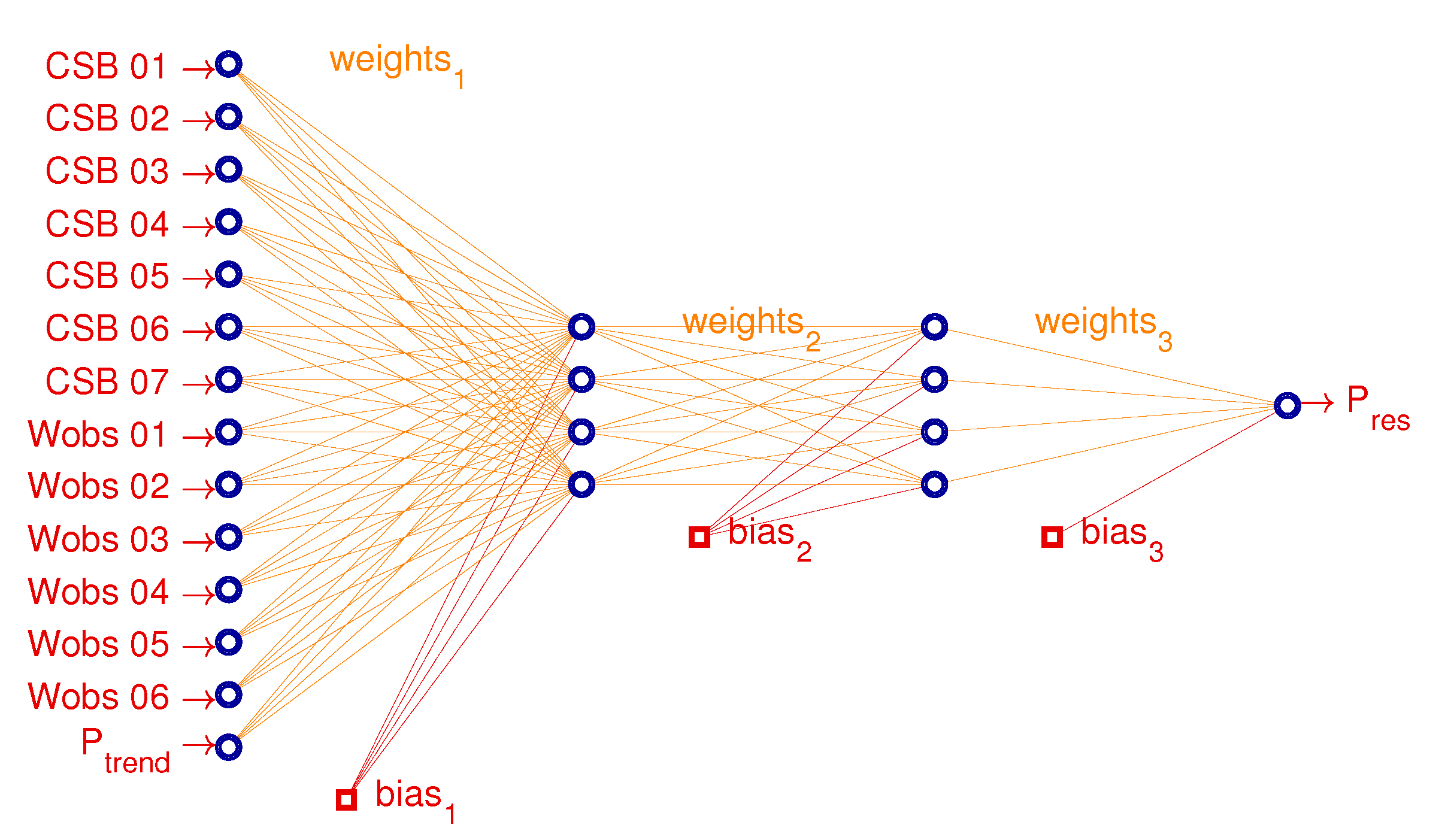
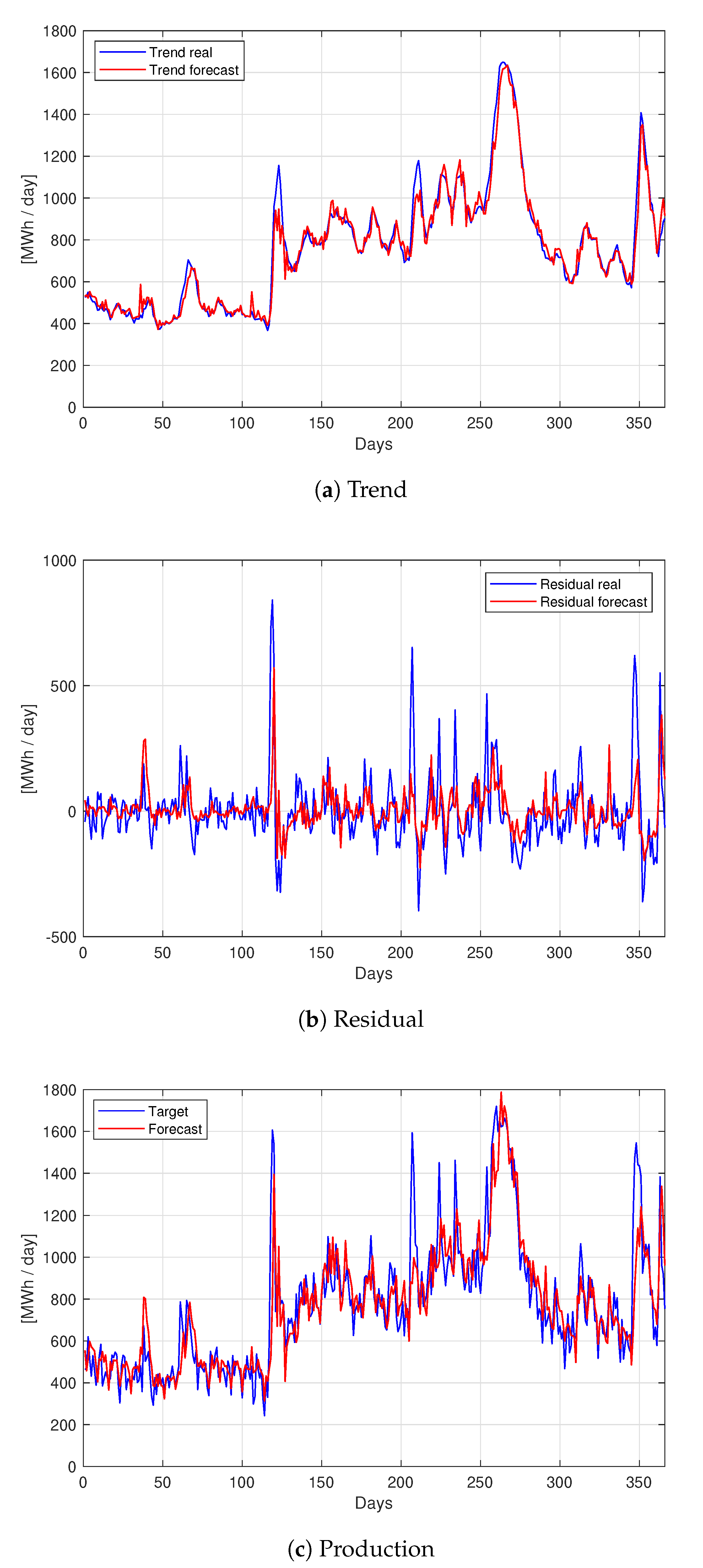
| Decomposition-Trend | Decomposition-Resididual | |
|---|---|---|
| TSS | 50 | 100 |
| N. Layers | 1 | 2 |
| N. Neurons | 8 | 4,4 |
| N. Inputs | 6 + N of CSB | 7 + N of CSB |
| Input Layer | CSB ( > 0.5), | CSB ( > 0.5), |
| past 6 days | past 6 days, trend forecast | |
| Output Layer | trend forecast | residual forecast |
| Hybrid | ANN | ANN + Dec.-Trend | ANN + Dec.-Resididual | |
|---|---|---|---|---|
| TSS | 250 | 250 | 50 | 100 |
| N. Layers | 1 | 1 | 1 | 2 |
| N. Neurons | 12 | 4 | 6 | 6,3 |
| N. Inputs | 6 + N of CSB | 9 | 9 | 10 |
| Input Layer | CSB ( > 0.5), | precipitation [mm], | precipitation [mm], | precipitation [mm], |
| past 6 days | past 6 days | past 6 days | past 6 days, trend forecast | |
| Output Layer | production forecast | production forecast | trend forecast | residual forecast |
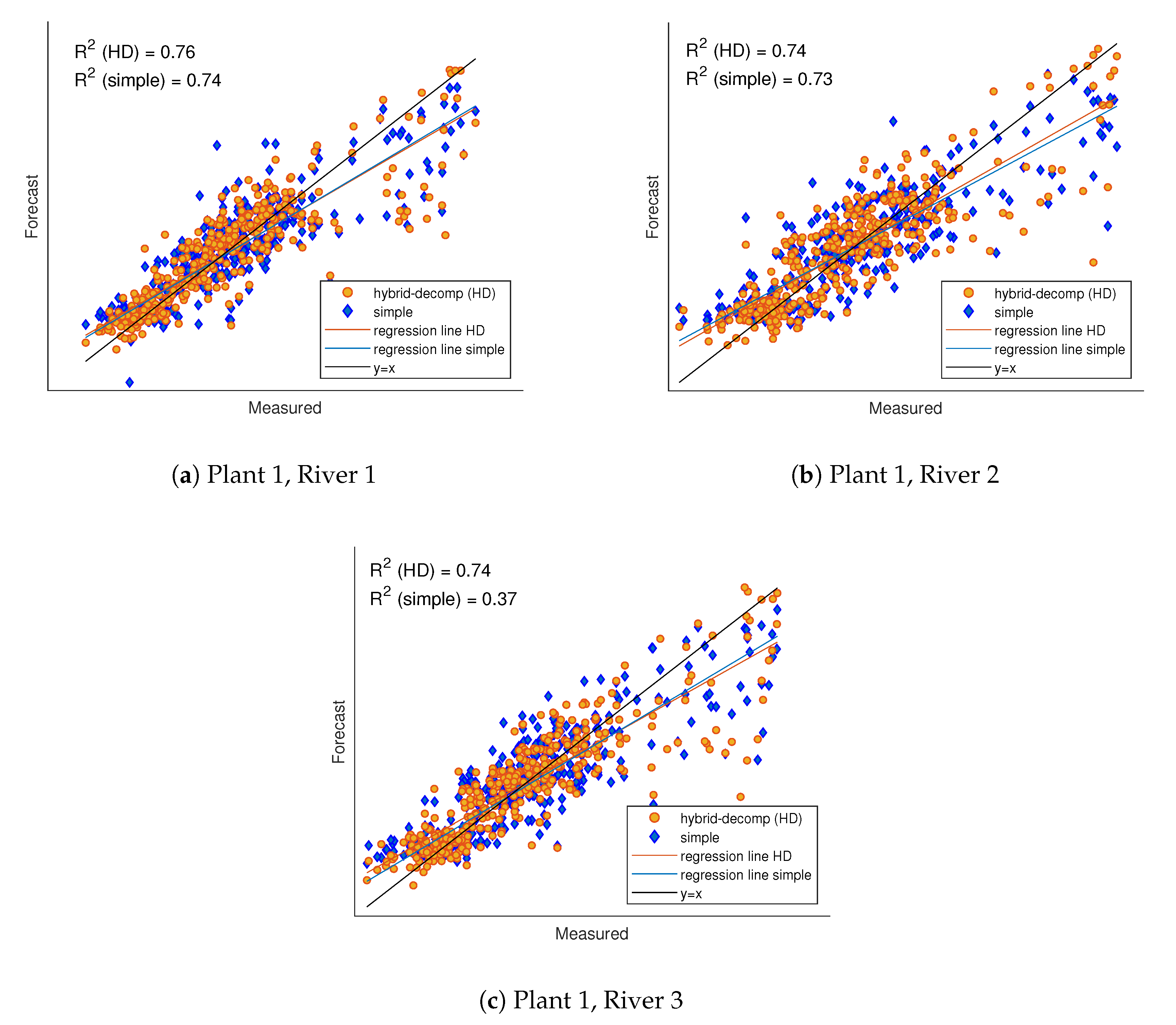
| (a) Plant 1, River 1. | nMAE | E | MASE |
|---|---|---|---|
| Hybrid + Dec. | 4.75 | 0.91 | 0.61 |
| Hybrid | 3.89 | 0.94 | 0.50 |
| ANN | 8.18 | 0.72 | 1.04 |
| ANN + Dec. | 10.94 | 0.57 | 1.40 |
| (b) Plant 1, River 2. | nMAE | E | MASE |
| Hybrid + Dec. | 3.68 | 0.87 | 0.72 |
| Hybrid | 2.97 | 0.92 | 0.58 |
| ANN | 5.53 | 0.71 | 1.08 |
| ANN + Dec. | 7.84 | 0.47 | 1.53 |
| (c) Plant 1, River 3. | nMAE | E | MASE |
| Hybrid + Dec. | 2.52 | 0.96 | 0.39 |
| Hybrid | 2.56 | 0.96 | 0.40 |
| ANN | 6.79 | 0.65 | 1.04 |
| ANN + Dec. | 6.83 | 0.69 | 1.05 |
| (a) Mean Plants on River 1. | nMAE | E | MASE |
|---|---|---|---|
| Hybrid + Dec. | 3.86 | 0.92 | 0.64 |
| Hybrid | 3.34 | 0.94 | 0.56 |
| ANN | 6.65 | 0.73 | 1.10 |
| ANN + Dec. | 8.85 | 0.60 | 1.47 |
| (b) SD Plants on River 1. | nMAE | E | MASE |
| Hybrid + Dec. | 0.25 | 0.03 | 0.05 |
| Hybrid | 0.35 | 0.01 | 0.03 |
| ANN | 0.70 | 0.02 | 0.03 |
| ANN + Dec. | 0.65 | 0.08 | 0.04 |
| (c) Mean Plants on River 2. | nMAE | E | MASE |
| Hybrid + Dec. | 4.55 | 0.91 | 0.54 |
| Hybrid | 3.98 | 0.93 | 0.48 |
| ANN | 8.77 | 0.72 | 1.05 |
| ANN + Dec. | 11.33 | 0.53 | 1.35 |
| (d) SD Plants on River 2. | nMAE | E | MASE |
| Hybrid + Dec. | 0.84 | 0.03 | 0.09 |
| Hybrid | 0.52 | 0.01 | 0.40 |
| ANN | 0.68 | 0.01 | 0.01 |
| ANN + Dec. | 1.50 | 0.08 | 0.11 |
| (e) Mean Plants on River 3. | nMAE | E | MASE |
| Hybrid + Dec. | 2.52 | 0.96 | 0.36 |
| Hybrid | 2.70 | 0.94 | 0.39 |
| ANN | 7.14 | 0.66 | 1.02 |
| ANN + Dec. | 7.13 | 0.70 | 1.02 |
| (f) SD Plants on River 3. | nMAE | E | MASE |
| Hybrid + Dec. | 0.10 | 0.01 | 0.03 |
| Hybrid | 0.14 | 0.01 | 0.02 |
| ANN | 0.59 | 0.18 | 0.05 |
| ANN + Dec. | 0.49 | 0.02 | 0.03 |
| (g) Mean All Plants | nMAE | E | MASE |
| Hybrid + Dec. | 3.37 | 0.93 | 0.49 |
| Hybrid | 3.17 | 0.94 | 0.46 |
| ANN | 7.30 | 0.70 | 1.06 |
| ANN + Dec. | 8.54 | 0.63 | 1.24 |
| (h) SD All Plants. | nMAE | E | MASE |
| Hybrid + Dec. | 0.93 | 0.03 | 0.14 |
| Hybrid | 0.59 | 0.01 | 0.08 |
| ANN | 0.99 | 0.12 | 0.05 |
| ANN + Dec. | 1.80 | 0.09 | 0.22 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ogliari, E.; Nespoli, A.; Mussetta, M.; Pretto, S.; Zimbardo, A.; Bonfanti, N.; Aufiero, M. A Hybrid Method for the Run-Of-The-River Hydroelectric Power Plant Energy Forecast: HYPE Hydrological Model and Neural Network. Forecasting 2020, 2, 410-428. https://doi.org/10.3390/forecast2040022
Ogliari E, Nespoli A, Mussetta M, Pretto S, Zimbardo A, Bonfanti N, Aufiero M. A Hybrid Method for the Run-Of-The-River Hydroelectric Power Plant Energy Forecast: HYPE Hydrological Model and Neural Network. Forecasting. 2020; 2(4):410-428. https://doi.org/10.3390/forecast2040022
Chicago/Turabian StyleOgliari, Emanuele, Alfredo Nespoli, Marco Mussetta, Silvia Pretto, Andrea Zimbardo, Nicholas Bonfanti, and Manuele Aufiero. 2020. "A Hybrid Method for the Run-Of-The-River Hydroelectric Power Plant Energy Forecast: HYPE Hydrological Model and Neural Network" Forecasting 2, no. 4: 410-428. https://doi.org/10.3390/forecast2040022
APA StyleOgliari, E., Nespoli, A., Mussetta, M., Pretto, S., Zimbardo, A., Bonfanti, N., & Aufiero, M. (2020). A Hybrid Method for the Run-Of-The-River Hydroelectric Power Plant Energy Forecast: HYPE Hydrological Model and Neural Network. Forecasting, 2(4), 410-428. https://doi.org/10.3390/forecast2040022






