Cost Estimating Using a New Learning Curve Theory for Non-Constant Production Rates
Abstract
1. Introduction
2. Literature Review and Background
3. Methodology
4. Analysis & Results
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A. Calculation Process for Lot Midpoint Estimation
- Parameter-free lot midpoint approximations (Equation (4)) were calculated for each production lot.
- Crawford’s learning curve parameters A and b were initially estimated using OLS regression.
- Average unit cost was the dependent variable while lot midpoint, calculated in Step 1, was the independent variable.
- These initial learning curve parameter estimates were used as starting values to more precisely estimate Crawford’s learning curve parameters using GRG non-linear solver. This process generated intermediate estimates of Crawford’s learning curve parameters.
- The intermediate estimate of Crawford’s learning curve b parameter was used to calculate a more precise set of lot midpoints using Asher’s approximation (Equation (5)).
- Applying these more precise lot midpoint approximations, Crawford’s learning curve parameters A and b were more accurately estimated using GRG nonlinear solver.
Appendix B. Learning Curve Error Comparisons Using Cumulative Average and Unit Theories
| Program | Number of Lots | Number of Units | Component Estimated | Units | Traditional RMSE | Boone RMSE | RMSE Percentage Difference | Traditional MAPE | Boone MAPE | MAPE Percentage Difference |
|---|---|---|---|---|---|---|---|---|---|---|
| Program 1 | 6 | 483 | PME–Air Vehicle | Dollars | 557.9 | 111.7 | 80.0% | 3.6% | 0.7% | 80.9% |
| Program 1 | 6 | 483 | PME–Air Vehicle | Hours | 15.5 | 0.3 | 98.0% | 27.2% | 0.5% | 98.2% |
| Program 1 | 6 | 483 | Airframe | Dollars | 411.2 | 114.1 | 72.3% | 2.8% | 0.7% | 74.7% |
| Program 1 | 6 | 483 | Airframe | Hours | 21.7 | 1.5 | 93.0% | 31.0% | 1.7% | 94.6% |
| Program 2 | 5 | 638 | PME–Air Vehicle | Dollars | 129.8 | 6.5 | 95.0% | 2.6% | 0.1% | 95.6% |
| Program 3 | 5 | 500 | PME–Air Vehicle | Dollars | 1630.3 | 291.1 | 82.1% | 20.8% | 3.9% | 81.5% |
| Program 4 | 19 | 205 | PME–Air Vehicle | Dollars | 581.7 | 581.8 | 0.0% | 3.1% | 3.1% | 0.0% |
| Program 4 | 19 | 205 | Airframe | Dollars | 546.0 | 546.4 | −0.1% | 3.2% | 3.2% | −0.1% |
| Program 5 | 7 | 459 | PME–Air Vehicle | Dollars | 400.8 | 44.7 | 88.8% | 2.7% | 0.3% | 88.2% |
| Program 5 | 7 | 459 | Electronic Warfare (1) | Dollars | 4.8 | 3.2 | 32.3% | 7.2% | 4.8% | 33.7% |
| Program 6 | 6 | 98 | PME–Air Vehicle | Dollars | 99.3 | 32.2 | 67.6% | 1.1% | 0.3% | 69.4% |
| Program 6 | 6 | 98 | Electronic Warfare (1) | Dollars | 12.7 | 1.7 | 86.8% | 3.6% | 0.6% | 82.4% |
| Program 6 | 6 | 98 | Electronic Warfare (2) | Dollars | 15.0 | 13.3 | 11.4% | 2.3% | 2.0% | 12.9% |
| Program 6 | 6 | 98 | Electronic Warfare (3) | Dollars | 1.8 | 1.1 | 40.3% | 1.3% | 0.8% | 39.6% |
| Program 7 | 7 | 110 | PME–Air Vehicle | Dollars | 145.0 | 98.3 | 32.2% | 1.0% | 0.7% | 32.6% |
| Program 7 | 7 | 110 | Electronic Warfare (1) | Dollars | 8.4 | 3.6 | 57.2% | 2.7% | 1.0% | 61.3% |
| Program 7 | 7 | 110 | Electronic Warfare (2) | Dollars | 140.3 | 107.2 | 23.6% | 1.2% | 0.8% | 27.5% |
| Program 7 | 7 | 110 | Electronic Warfare (3) | Dollars | 0.9 | 0.9 | 0.0% | 0.5% | 0.5% | −0.1% |
| Program 7 | 7 | 110 | Electronic Warfare (4) | Dollars | 140.7 | 111.3 | 20.9% | 1.3% | 1.0% | 24.2% |
| Program 7 | 7 | 110 | Electronic Warfare (5) | Dollars | 21.3 | 21.0 | 1.1% | 2.2% | 2.1% | 5.2% |
| Program 8 | 8 | 3529 | PME–Air Vehicle | Dollars | 27.7 | 23.6 | 14.8% | 1.4% | 1.3% | 7.8% |
| Program 8 | 8 | 3529 | PME–Air Vehicle | Hours | 0.1 | 0.1 | −27.5% | 1.1% | 1.3% | −27.9% |
| Program 9 | 9 | 3798 | PME–Air Vehicle | Dollars | 166.5 | 170.7 | −2.5% | 8.4% | 8.8% | −3.7% |
| Program 10 | 10 | 3803 | PME–Air Vehicle | Dollars | 8.0 | 4.8 | 39.6% | 2.5% | 1.2% | 51.7% |
| Program 10 | 10 | 3803 | PME–Air Vehicle | Hours | 24.4 | 14.0 | 42.7% | 4.3% | 2.0% | 54.0% |
| Program 11 | 6 | 180 | PME–Air Vehicle | Dollars | 514.0 | 508.4 | 1.1% | 0.9% | 0.8% | 4.2% |
| Program 12 | 10 | 20 | PME–Air Vehicle | Dollars | 699.2 | 694.1 | 0.7% | 5.8% | 5.7% | 1.0% |
| Program 12 | 10 | 20 | PME–Air Vehicle | Hours | 1042.5 | 906.5 | 13.1% | 9.5% | 8.4% | 11.8% |
| Program 12 | 7 | 11 | Mission Computer (1) | Dollars | 44.3 | 44.3 | 0.0% | 2.5% | 2.5% | 0.0% |
| Program 13 | 5 | 100 | PME–Air Vehicle | Dollars | 53,386.7 | 21,143.7 | 60.4% | 12.8% | 4.8% | 62.1% |
| Program 13 | 5 | 100 | Airframe | Dollars | 6569.7 | 6578.0 | −0.1% | 3.7% | 3.7% | 0.0% |
| Program 14 | 5 | 275 | PME–Air Vehicle | Dollars | 3114.0 | 145.5 | 95.3% | 3.8% | 0.2% | 95.5% |
| Program 15 | 10 | 77 | PME–Air Vehicle | Dollars | 44,386.0 | 44,390.2 | 0.0% | 9.5% | 9.5% | 0.0% |
| Program 15 | 12 | 83 | PME–Air Vehicle | Hours | 79,242.0 | 79,247.5 | 0.0% | 6.5% | 6.5% | 0.0% |
| Program 15 | 11 | 83 | Airframe | Dollars | 39,624.4 | 39,628.0 | 0.0% | 10.6% | 10.6% | 0.0% |
| Program 15 | 10 | 68 | Mission Computer (1) | Dollars | 1959.3 | 1959.4 | 0.0% | 17.0% | 17.0% | 0.0% |
| Program 16 | 9 | 76 | PME–Air Vehicle | Dollars | 436.3 | 144.4 | 66.9% | 2.6% | 1.0% | 62.9% |
| Program 17 | 5 | 50 | PME–Air Vehicle | Dollars | 13,023.6 | 13,029.8 | 0.0% | 2.8% | 2.8% | −0.1% |
| Program 18 | 9 | 31 | PME–Air Vehicle | Dollars | 2942.5 | 2941.9 | 0.0% | 1.0% | 0.9% | 0.0% |
| Program 19 | 6 | 98 | PME–Air Vehicle | Dollars | 313.3 | 313.4 | 0.0% | 0.5% | 0.5% | −0.1% |
| Program 20 | 11 | 84 | PME–Air Vehicle | Dollars | 1568.7 | 1121.9 | 28.5% | 1.7% | 1.5% | 7.8% |
| Program 20 | 7 | 59 | Electronic Warfare (1) | Dollars | 452.8 | 143.0 | 68.4% | 4.6% | 1.3% | 71.5% |
| Program 20 | 11 | 84 | Electronic Warfare (2) | Dollars | 98.7 | 76.5 | 22.5% | 3.4% | 3.6% | −6.3% |
| Program 20 | 7 | 59 | Electronic Warfare (5) | Dollars | 562.5 | 517.4 | 8.0% | 1.8% | 1.8% | 1.7% |
| Program 21 | 6 | 326 | PME–Air Vehicle | Dollars | 5267.1 | 2408.8 | 54.3% | 8.0% | 4.2% | 47.4% |
| Program 21 | 7 | 344 | Airframe | Dollars | 4819.5 | 2544.3 | 47.2% | 9.1% | 5.4% | 40.4% |
| Program 21 | 7 | 344 | Avionics | Dollars | 763.2 | 429.9 | 43.7% | 6.6% | 3.9% | 40.8% |
| Program 21 | 14 | 453 | PME–Air Vehicle | Hours | 3493.6 | 3495.9 | −0.1% | 4.8% | 4.8% | 0.1% |
| Program 21 | 14 | 453 | Airframe | Hours | 4338.4 | 4339.7 | 0.0% | 6.2% | 6.2% | 0.1% |
| Program 22 | 8 | 538 | PME–Air Vehicle | Hours | 856.7 | 857.7 | −0.1% | 2.5% | 2.6% | −0.1% |
| Program 22 | 8 | 538 | Airframe | Hours | 5608.5 | 5609.7 | 0.0% | 15.8% | 15.9% | −0.1% |
| Program 23 | 5 | 469 | PME–Air Vehicle | Dollars | 637.5 | 339.3 | 46.8% | 5.4% | 2.9% | 47.3% |
| Program 24 | 10 | 59 | PME–Air Vehicle | Dollars | 3032.5 | 3033.0 | 0.0% | 2.2% | 2.2% | 0.0% |
| Program 25 | 9 | 348 | PME–Air Vehicle | Dollars | 117.8 | 118.1 | −0.2% | 0.9% | 0.9% | −0.2% |
| Program 26 | 5 | 109 | PME–Air Vehicle | Dollars | 3247.4 | 1676.8 | 48.4% | 11.0% | 6.0% | 45.7% |
| Program 26 | 5 | 109 | PME–Air Vehicle | Hours | 607.1 | 453.5 | 25.3% | 5.7% | 4.2% | 25.9% |
| Program 27 | 18 | 631 | PME–Air Vehicle | Dollars | 1669.6 | 913.3 | 45.3% | 3.6% | 1.9% | 46.2% |
| Program 28 | 6 | 425 | PME–Air Vehicle | Dollars | 320.0 | 322.0 | −0.6% | 0.9% | 0.9% | −0.6% |
| Program 28 | 7 | 522 | PME–Air Vehicle | Hours | 1776.1 | 1785.6 | −0.5% | 1.8% | 1.8% | −0.1% |
| Program 28 | 7 | 522 | Airframe | Hours | 1389.9 | 1393.9 | −0.3% | 1.2% | 1.2% | −0.2% |
| Program 29 | 9 | 358 | PME–Air Vehicle | Hours | 610.6 | 611.1 | −0.1% | 0.9% | 0.9% | 0.4% |
| Program 29 | 9 | 358 | Airframe | Hours | 4804.8 | 2124.2 | 55.8% | 7.3% | 2.9% | 60.1% |
| Program 30 | 5 | 204 | PME–Air Vehicle | Dollars | 513.5 | 212.7 | 58.6% | 1.2% | 0.5% | 56.1% |
| Program 31 | 5 | 605 | PME–Air Vehicle | Dollars | 1482.6 | 629.1 | 57.6% | 6.1% | 2.9% | 53.1% |
| Program 32 | 5 | 870 | PME–Air Vehicle | Dollars | 61.3 | 61.6 | −0.5% | 0.4% | 0.4% | −0.3% |
| Program 33 | 10 | 178 | PME–Air Vehicle | Dollars | 7093.5 | 7101.1 | −0.1% | 3.5% | 3.5% | −0.1% |
| Program 33 | 10 | 178 | PME–Air Vehicle | Hours | 8131.1 | 8144.1 | −0.2% | 2.9% | 2.9% | −0.1% |
| Program 33 | 10 | 178 | Airframe | Dollars | 1906.9 | 1910.8 | −0.2% | 1.7% | 1.7% | −0.2% |
| Program 33 | 10 | 712 | Body | Dollars | 232.2 | 234.9 | −1.2% | 1.5% | 1.6% | −1.3% |
| Program 33 | 10 | 178 | Alighting Gear | Dollars | 76.6 | 76.6 | 0.0% | 7.9% | 7.9% | 0.0% |
| Program 33 | 10 | 178 | Auxiliary Power Plant | Dollars | 90.7 | 90.7 | −0.1% | 3.9% | 3.9% | −0.1% |
| Program 33 | 10 | 178 | Electronic Warfare (1) | Dollars | 775.5 | 776.1 | −0.1% | 6.5% | 6.5% | −0.1% |
| Program 33 | 10 | 178 | Electronic Warfare (2) | Dollars | 360.1 | 273.4 | 24.1% | 58.3% | 46.0% | 21.2% |
| Program 33 | 10 | 178 | Electronic Warfare (3) | Dollars | 62.5 | 62.4 | 0.2% | 5.7% | 5.7% | 0.1% |
| Program 33 | 10 | 178 | Empennage | Dollars | 352.2 | 352.3 | 0.0% | 5.1% | 5.1% | −0.1% |
| Program 33 | 10 | 178 | Hydraulic | Dollars | 22.7 | 22.7 | −0.1% | 2.2% | 2.2% | −0.1% |
| Program 33 | 10 | 178 | Wing | Dollars | 296.5 | 296.9 | −0.1% | 2.3% | 2.3% | −0.1% |
| Program 34 | 6 | 67 | PME–Air Vehicle | Dollars | 11,059.1 | 11,061.2 | 0.0% | 6.6% | 6.6% | 0.0% |
| Program 34 | 6 | 67 | PME–Air Vehicle | Hours | 9058.6 | 9061.7 | 0.0% | 4.4% | 4.4% | 0.0% |
| Program 34 | 6 | 67 | Airframe | Dollars | 2798.1 | 2004.6 | 28.4% | 2.8% | 1.7% | 37.9% |
| Program 34 | 6 | 201 | Body | Dollars | 1924.5 | 828.9 | 56.9% | 19.0% | 8.7% | 54.0% |
| Program 34 | 6 | 67 | Alighting Gear | Dollars | 316.5 | 166.9 | 47.3% | 17.2% | 8.3% | 51.9% |
| Program 34 | 6 | 67 | Electrical | Dollars | 50.7 | 50.7 | −0.1% | 1.9% | 1.9% | −0.1% |
| Program 34 | 6 | 67 | Electronic Warfare (1) | Dollars | 428.3 | 428.4 | 0.0% | 5.3% | 5.3% | 0.0% |
| Program 34 | 5 | 49 | Empennage | Dollars | 202.2 | 202.2 | 0.0% | 4.1% | 4.1% | 0.0% |
| Program 34 | 6 | 67 | EO/IR | Dollars | 45.6 | 36.6 | 19.7% | 1.2% | 1.1% | 13.1% |
| Program 34 | 6 | 67 | EOTS | Dollars | 347.6 | 347.7 | 0.0% | 6.5% | 6.5% | 0.0% |
| Program 34 | 6 | 67 | Hydraulic | Dollars | 122.3 | 101.5 | 17.0% | 8.4% | 6.2% | 26.8% |
| Program 34 | 6 | 67 | Mission Computer (1) | Dollars | 484.8 | 484.9 | 0.0% | 0.9% | 0.9% | −0.2% |
| Program 34 | 6 | 67 | Surface Controls | Dollars | 196.0 | 196.0 | 0.0% | 4.9% | 4.9% | 0.0% |
| Program 34 | 6 | 67 | Wing | Dollars | 998.4 | 998.6 | 0.0% | 3.3% | 3.3% | −0.1% |
| Program 35 | 5 | 41 | PME–Air Vehicle | Dollars | 3578.6 | 3579.8 | 0.0% | 1.5% | 1.5% | 0.0% |
| Program 35 | 5 | 41 | PME–Air Vehicle | Hours | 2003.7 | 2004.7 | 0.0% | 1.1% | 1.1% | 0.0% |
| Program 35 | 5 | 50 | Airframe | Dollars | 609.3 | 610.4 | −0.2% | 0.6% | 0.6% | −0.3% |
| Program 35 | 5 | 150 | Body | Dollars | 235.8 | 156.5 | 33.6% | 1.9% | 1.4% | 28.0% |
| Program 35 | 5 | 50 | Alighting Gear | Dollars | 13.2 | 13.2 | −0.1% | 0.5% | 0.5% | 0.0% |
| Program 35 | 5 | 50 | Electronic Warfare (1) | Dollars | 259.6 | 259.7 | 0.0% | 3.2% | 3.2% | 0.0% |
| Program 35 | 5 | 50 | EO/IR | Dollars | 121.6 | 121.7 | 0.0% | 1.3% | 1.3% | −0.1% |
| Program 35 | 5 | 50 | EOTS | Dollars | 177.9 | 177.9 | 0.0% | 2.8% | 2.8% | −0.1% |
| Program 35 | 5 | 50 | Hydraulic | Dollars | 58.2 | 58.2 | 0.0% | 3.1% | 3.1% | 0.0% |
| Program 35 | 5 | 50 | Radar | Dollars | 256.8 | 256.9 | 0.0% | 3.2% | 3.2% | 0.0% |
| Program 35 | 5 | 50 | Surface Controls | Dollars | 121.5 | 121.5 | 0.0% | 2.6% | 2.6% | 0.0% |
| Program 35 | 5 | 50 | Wing | Dollars | 1213.5 | 1213.6 | 0.0% | 3.8% | 3.8% | 0.0% |
| Program 36 | 13 | 1285 | PME–Air Vehicle | Dollars | 28.8 | 29.4 | −2.1% | 0.6% | 0.6% | −2.2% |
| Program 37 | 6 | 432 | PME–Air Vehicle | Dollars | 791.3 | 793.8 | −0.3% | 3.4% | 3.4% | −0.4% |
| Program 38 | 6 | 52 | PME–Air Vehicle | Dollars | 253.6 | 154.9 | 38.9% | 1.2% | 0.7% | 41.6% |
| Program 38 | 6 | 44 | PME–Air Vehicle | Hours | 831.5 | 614.2 | 26.1% | 1.3% | 0.8% | 42.8% |
| Program 39 | 19 | 1023 | PME–Air Vehicle | Dollars | 19.3 | 19.3 | −0.2% | 0.7% | 0.7% | −0.2% |
| Program 40 | 5 | 1725 | PME–Air Vehicle | Dollars | 19.2 | 0.6 | 96.7% | 2.0% | 0.1% | 97.0% |
| Program 41 | 10 | 16 | PME–Air Vehicle | Dollars | 14,787.6 | 14,787.8 | 0.0% | 5.2% | 5.2% | 0.0% |
| Program 41 | 10 | 16 | Data Link (1) | Dollars | 138.8 | 138.8 | 0.0% | 3.7% | 3.7% | 0.0% |
| Program 42 | 11 | 203 | PME–Air Vehicle | Dollars | 1000.0 | 1000.1 | 0.0% | 7.0% | 7.0% | 0.0% |
| Program 42 | 11 | 899 | Electronic Warfare (1) | Dollars | 67.5 | 67.7 | −0.2% | 13.9% | 13.9% | −0.5% |
| Program 43 | 11 | 203 | PME–Air Vehicle | Dollars | 1121.7 | 1121.9 | 0.0% | 5.5% | 5.5% | 0.0% |
| Program 43 | 13 | 251 | PME–Air Vehicle | Hours | 1944.2 | 1762.2 | 9.4% | 3.4% | 3.2% | 6.1% |
| Program 44 | 5 | 136 | PME–Air Vehicle | Dollars | 57.1 | 16.3 | 71.4% | 1.1% | 0.3% | 71.4% |
| Program 45 | 9 | 155 | PME–Air Vehicle | Dollars | 149.6 | 149.7 | −0.1% | 0.3% | 0.3% | −0.1% |
| Program 46 | 6 | 68 | PME–Air Vehicle | Dollars | 3435.9 | 3436.0 | 0.0% | 1.7% | 1.7% | 0.1% |
| Program 46 | 6 | 68 | PME–Air Vehicle | Hours | 2286.4 | 2286.6 | 0.0% | 2.6% | 2.6% | 0.0% |
| Program 46 | 6 | 68 | Airframe | Dollars | 539.1 | 527.6 | 2.1% | 2.3% | 2.1% | 10.9% |
| Program 46 | 6 | 68 | Data Link (1) | Dollars | 44.0 | 44.0 | 0.0% | 3.0% | 3.0% | 0.0% |
| Program 46 | 6 | 68 | Electronic Warfare (1) | Dollars | 221.8 | 221.9 | 0.0% | 5.4% | 5.4% | 0.0% |
| Program 46 | 6 | 68 | Electronic Warfare (2) | Dollars | 220.0 | 220.0 | 0.0% | 6.5% | 6.5% | 0.0% |
| Program 46 | 6 | 68 | Electronic Warfare (3) | Dollars | 17.7 | 8.8 | 50.4% | 2.2% | 1.0% | 54.6% |
| Program 46 | 6 | 68 | Electronic Warfare (4) | Dollars | 530.0 | 530.0 | 0.0% | 5.2% | 5.2% | 0.0% |
| Program 46 | 6 | 68 | EO/IR | Dollars | 120.7 | 120.8 | 0.0% | 15.7% | 15.7% | 0.0% |
| Program 46 | 6 | 68 | Mission Computer (1) | Dollars | 477.9 | 478.0 | 0.0% | 4.3% | 4.3% | 0.0% |
| Program 47 | 9 | 36 | PME–Air Vehicle | Dollars | 1039.4 | 1039.4 | 0.0% | 2.5% | 2.5% | 0.0% |
| Program 47 | 9 | 36 | PME–Air Vehicle | Hours | 8278.7 | 8278.6 | 0.0% | 15.5% | 15.5% | 0.0% |
| Program 47 | 9 | 36 | Data Link (1) | Dollars | 170.2 | 170.2 | 0.0% | 17.7% | 17.7% | 0.0% |
| Program 48 | 5 | 179 | PME–Air Vehicle | Dollars | 1858.3 | 391.3 | 78.9% | 3.1% | 0.6% | 79.4% |
| Program 49 | 6 | 180 | PME–Air Vehicle | Dollars | 435.3 | 99.8 | 77.1% | 4.4% | 1.0% | 76.5% |
| Program 50 | 5 | 488 | PME–Air Vehicle | Dollars | 349.3 | 350.7 | −0.4% | 3.3% | 3.4% | −0.8% |
| Program 51 | 6 | 663 | PME–Air Vehicle | Dollars | 5.6 | 3.6 | 36.6% | 0.6% | 0.4% | 24.8% |
| Program 52 | 5 | 380 | PME–Air Vehicle | Dollars | 456.9 | 454.6 | 0.5% | 9.0% | 8.9% | 0.3% |
| Program 53 | 6 | 749 | PME–Air Vehicle | Dollars | 37.2 | 36.6 | 1.7% | 0.5% | 0.5% | 4.3% |
| Program 54 | 8 | 194 | PME–Air Vehicle | Dollars | 28.8 | 28.8 | −0.1% | 0.6% | 0.6% | −0.1% |
| Program 55 | 9 | 677 | PME–Air Vehicle | Dollars | 74.8 | 74.8 | 0.0% | 1.6% | 1.6% | 0.0% |
| Program 56 | 5 | 590 | PME–Air Vehicle | Dollars | 6.6 | 6.6 | 0.5% | 0.2% | 0.2% | 6.3% |
| Program 57 | 5 | 579 | PME–Air Vehicle | Dollars | 22.8 | 22.8 | −0.1% | 0.8% | 0.8% | 0.0% |
| Program | Number of Lots | Number of Units | Component Estimated | Units | Traditional RMSE | Boone RMSE | RMSE Percentage Difference | Traditional MAPE | Boone MAPE | MAPE Percentage Difference |
|---|---|---|---|---|---|---|---|---|---|---|
| Program 1 | 7 | 503 | Airframe | Hours | 4.6 | 3.5 | 23.4% | 7.1% | 5.0% | 28.7% |
| Program 1 | 6 | 483 | PME–Air Vehicle | Hours | 5.4 | 1.5 | 72.5% | 11.3% | 2.9% | 74.0% |
| Program 1 | 7 | 503 | PME–Air Vehicle | Dollars | 2260.6 | 517.0 | 77.1% | 12.9% | 3.2% | 75.2% |
| Program 1 | 7 | 503 | Airframe | Dollars | 2383.2 | 857.9 | 64.0% | 14.6% | 4.9% | 66.4% |
| Program 2 | 5 | 638 | PME–Air Vehicle | Dollars | 315.4 | 195.3 | 38.1% | 5.8% | 4.3% | 26.3% |
| Program 3 | 5 | 500 | PME–Air Vehicle | Dollars | 2984.5 | 1120.2 | 62.5% | 49.4% | 17.6% | 64.4% |
| Program 4 | 7 | 357 | Airframe | Dollars | 2662.2 | 2664.3 | −0.1% | 13.1% | 13.2% | −0.1% |
| Program 4 | 9 | 424 | PME–Air Vehicle | Dollars | 9323.3 | 4999.8 | 46.4% | 37.9% | 14.1% | 62.8% |
| Program 5 | 19 | 205 | Airframe | Dollars | 2446.1 | 2445.8 | 0.0% | 12.6% | 12.6% | −0.3% |
| Program 5 | 19 | 205 | PME–Air Vehicle | Dollars | 3228.6 | 3228.9 | 0.0% | 12.4% | 12.4% | 0.0% |
| Program 6 | 7 | 459 | Electronic Warfare (1) | Dollars | 20.9 | 20.9 | 0.0% | 30.8% | 30.8% | 0.0% |
| Program 6 | 7 | 459 | PME–Air Vehicle | Dollars | 1439.9 | 738.1 | 48.7% | 11.3% | 5.9% | 47.2% |
| Program 7 | 5 | 321 | PME–Air Vehicle | Dollars | 37.9 | 33.3 | 12.2% | 3.8% | 3.8% | 1.1% |
| Program 8 | 6 | 98 | Electronic Warfare (3) | Dollars | 5.2 | 4.9 | 6.1% | 4.8% | 4.8% | 1.4% |
| Program 8 | 6 | 98 | Electronic Warfare (2) | Dollars | 84.2 | 70.3 | 16.5% | 11.1% | 10.6% | 4.7% |
| Program 8 | 6 | 98 | PME–Air Vehicle | Dollars | 375.2 | 339.5 | 9.5% | 4.2% | 3.7% | 13.4% |
| Program 8 | 6 | 98 | Electronic Warfare (1) | Dollars | 27.5 | 18.7 | 31.9% | 10.2% | 5.9% | 42.5% |
| Program 9 | 7 | 110 | Electronic Warfare (5) | Dollars | 102.9 | 99.2 | 3.5% | 9.7% | 10.4% | −6.6% |
| Program 9 | 7 | 110 | Electronic Warfare (3) | Dollars | 6.4 | 6.4 | 0.0% | 4.7% | 4.7% | 0.0% |
| Program 9 | 7 | 110 | Electronic Warfare (4) | Dollars | 653.6 | 653.6 | 0.0% | 6.2% | 6.2% | 0.0% |
| Program 9 | 7 | 110 | Electronic Warfare (2) | Dollars | 709.4 | 709.4 | 0.0% | 6.1% | 6.1% | 0.0% |
| Program 9 | 7 | 110 | PME–Air Vehicle | Dollars | 668.5 | 668.5 | 0.0% | 5.1% | 5.1% | 0.0% |
| Program 9 | 7 | 110 | Electronic Warfare (1) | Dollars | 31.6 | 29.1 | 8.0% | 8.7% | 8.0% | 8.3% |
| Program 10 | 9 | 1586 | PME–Air Vehicle | Dollars | 115.5 | 115.6 | −0.2% | 12.5% | 12.5% | −0.2% |
| Program 10 | 10 | 1796 | PME–Air Vehicle | Hours | 150.8 | 150.9 | 0.0% | 12.5% | 12.5% | −0.1% |
| Program 11 | 8 | 3529 | PME–Air Vehicle | Hours | 0.9 | 0.7 | 21.2% | 27.5% | 44.9% | −63.4% |
| Program 11 | 8 | 3529 | PME–Air Vehicle | Dollars | 97.1 | 97.5 | −0.4% | 10.1% | 10.4% | −2.1% |
| Program 12 | 16 | 7891 | PME–Air Vehicle | Hours | 520.1 | 525.6 | −1.1% | 86.2% | 86.2% | 0.0% |
| Program 12 | 21 | 10035 | PME–Air Vehicle | Dollars | 243.8 | 239.2 | 1.9% | 30.1% | 28.8% | 4.2% |
| Program 13 | 6 | 3385 | EO | Dollars | 12.1 | 9.4 | 22.5% | 10.7% | 9.6% | 10.0% |
| Program 13 | 10 | 3803 | PME–Air Vehicle | Dollars | 33.6 | 24.8 | 26.1% | 10.3% | 7.5% | 27.1% |
| Program 13 | 10 | 3803 | PME–Air Vehicle | Hours | 130.1 | 100.5 | 22.7% | 21.5% | 17.1% | 20.7% |
| Program 14 | 6 | 180 | PME–Air Vehicle | Dollars | 2249.4 | 1008.9 | 55.2% | 6.4% | 2.3% | 64.2% |
| Program 15 | 10 | 20 | PME–Air Vehicle | Hours | 3430.3 | 3430.4 | 0.0% | 41.5% | 41.5% | 0.0% |
| Program 15 | 10 | 20 | PME–Air Vehicle | Dollars | 3013.9 | 3013.9 | 0.0% | 17.4% | 17.4% | 0.0% |
| Program 15 | 7 | 11 | Mission Computer (1) | Dollars | 213.9 | 213.9 | 0.0% | 11.6% | 11.5% | 0.6% |
| Program 16 | 5 | 100 | Airframe | Dollars | 10,807.3 | 7455.4 | 31.0% | 7.0% | 4.1% | 41.8% |
| Program 16 | 5 | 100 | PME–Air Vehicle | Dollars | 137,225.9 | 81,884.9 | 40.3% | 51.7% | 26.9% | 48.0% |
| Program 17 | 5 | 275 | PME–Air Vehicle | Dollars | 8837.5 | 1396.3 | 84.2% | 17.6% | 3.3% | 81.6% |
| Program 18 | 12 | 83 | PME–Air Vehicle | Hours | 266,012.8 | 266,015.3 | 0.0% | 39.3% | 39.3% | 0.0% |
| Program 18 | 11 | 83 | Airframe | Dollars | 89,956.0 | 89,961.1 | 0.0% | 39.1% | 39.1% | 0.0% |
| Program 18 | 10 | 68 | Mission Computer (1) | Dollars | 4143.0 | 4143.2 | 0.0% | 68.2% | 68.2% | 0.0% |
| Program 18 | 11 | 83 | PME–Air Vehicle | Dollars | 82,138.6 | 82,143.3 | 0.0% | 23.2% | 23.2% | 0.0% |
| Program 19 | 5 | 45 | Airframe | Dollars | 501.2 | 501.2 | 0.0% | 53.9% | 53.9% | 0.0% |
| Program 19 | 5 | 45 | PME–Air Vehicle | Dollars | 649.0 | 649.0 | 0.0% | 17.6% | 17.6% | 0.0% |
| Program 19 | 5 | 45 | Mission Computer (1) | Dollars | 61.7 | 59.7 | 3.2% | 9.8% | 9.7% | 1.2% |
| Program 20 | 9 | 76 | PME–Air Vehicle | Dollars | 1108.7 | 522.5 | 52.9% | 7.2% | 3.6% | 49.9% |
| Program 21 | 5 | 50 | PME–Air Vehicle | Dollars | 24,625.3 | 6362.0 | 74.2% | 7.4% | 2.3% | 69.5% |
| Program 22 | 9 | 31 | PME–Air Vehicle | Dollars | 16,636.3 | 16,636.4 | 0.0% | 6.6% | 6.6% | 0.0% |
| Program 23 | 5 | 14 | PME–Air Vehicle | Dollars | 14,475.8 | 14,476.0 | 0.0% | 8.7% | 8.7% | 0.0% |
| Program 24 | 6 | 98 | PME–Air Vehicle | Dollars | 2259.9 | 2260.1 | 0.0% | 3.3% | 3.3% | 0.0% |
| Program 25 | 7 | 59 | Electronic Warfare (5) | Dollars | 2808.4 | 2805.2 | 0.1% | 14.8% | 15.4% | −4.0% |
| Program 25 | 11 | 84 | PME–Air Vehicle | Dollars | 5083.2 | 4228.8 | 16.8% | 8.7% | 9.2% | −5.2% |
| Program 25 | 11 | 84 | Electronic Warfare (2) | Dollars | 248.9 | 248.6 | 0.1% | 13.9% | 14.3% | −2.9% |
| Program 25 | 7 | 59 | Electronic Warfare (1) | Dollars | 1259.1 | 653.3 | 48.1% | 16.1% | 7.1% | 55.6% |
| Program 26 | 7 | 344 | Airframe | Dollars | 11,474.7 | 8294.9 | 27.7% | 22.7% | 21.5% | 5.3% |
| Program 26 | 7 | 344 | Avionics | Dollars | 2218.8 | 2102.8 | 5.2% | 29.5% | 26.9% | 8.8% |
| Program 26 | 7 | 344 | PME–Air Vehicle | Dollars | 12,898.4 | 8742.1 | 32.2% | 20.7% | 16.9% | 18.4% |
| Program 27 | 14 | 453 | PME–Air Vehicle | Hours | 54,142.9 | 53,766.4 | 0.7% | 59.9% | 63.1% | −5.4% |
| Program 27 | 14 | 453 | Airframe | Hours | 70,415.0 | 69,426.8 | 1.4% | 58.8% | 59.1% | −0.5% |
| Program 28 | 8 | 538 | PME–Air Vehicle | Hours | 3828.8 | 3829.8 | 0.0% | 9.8% | 9.9% | 0.0% |
| Program 28 | 8 | 538 | Airframe | Hours | 3865.3 | 3866.2 | 0.0% | 7.6% | 7.6% | 0.0% |
| Program 29 | 8 | 529 | Hydraulic | Dollars | 156.9 | 156.4 | 0.3% | 22.3% | 22.9% | −2.8% |
| Program 29 | 12 | 477 | Airframe | Dollars | 6490.2 | 5974.2 | 7.9% | 14.2% | 14.4% | −1.8% |
| Program 29 | 12 | 477 | Wing | Dollars | 712.3 | 712.7 | −0.1% | 27.8% | 27.8% | −0.1% |
| Program 29 | 11 | 433 | Electronic Warfare (1) | Dollars | 57.5 | 57.5 | 0.0% | 13.5% | 13.5% | −0.1% |
| Program 29 | 8 | 309 | Electrical | Dollars | 230.6 | 230.7 | −0.1% | 8.2% | 8.2% | 0.0% |
| Program 29 | 12 | 1045 | Body | Dollars | 1922.2 | 1826.7 | 5.0% | 26.0% | 25.9% | 0.7% |
| Program 29 | 5 | 177 | Empennage | Dollars | 32.3 | 22.0 | 31.8% | 6.1% | 4.6% | 24.5% |
| Program 29 | 12 | 477 | PME–Air Vehicle | Dollars | 8218.5 | 5525.3 | 32.8% | 15.0% | 10.2% | 32.0% |
| Program 29 | 8 | 309 | Alighting Gear | Dollars | 205.7 | 42.2 | 79.5% | 11.6% | 2.0% | 83.1% |
| Program 30 | 5 | 469 | PME–Air Vehicle | Dollars | 1283.8 | 891.8 | 30.5% | 13.5% | 8.3% | 38.3% |
| Program 31 | 10 | 59 | PME–Air Vehicle | Dollars | 11,978.9 | 11,979.3 | 0.0% | 8.6% | 8.6% | 0.0% |
| Program 32 | 9 | 348 | PME–Air Vehicle | Dollars | 430.6 | 430.8 | 0.0% | 3.5% | 3.5% | −0.1% |
| Program 33 | 5 | 109 | PME–Air Vehicle | Hours | 993.9 | 994.0 | 0.0% | 9.5% | 9.5% | 0.0% |
| Program 33 | 5 | 109 | PME–Air Vehicle | Dollars | 6824.7 | 6824.8 | 0.0% | 28.2% | 28.2% | 0.0% |
| Program 34 | 18 | 631 | PME–Air Vehicle | Dollars | 6926.7 | 2799.9 | 59.6% | 17.0% | 6.6% | 61.0% |
| Program 35 | 6 | 425 | PME–Air Vehicle | Dollars | 1135.8 | 1137.5 | −0.2% | 3.5% | 3.5% | −0.2% |
| Program 35 | 7 | 522 | PME–Air Vehicle | Hours | 4615.3 | 4458.5 | 3.4% | 6.3% | 6.1% | 3.1% |
| Program 35 | 7 | 522 | Airframe | Hours | 6757.0 | 6280.7 | 7.0% | 5.7% | 5.4% | 4.8% |
| Program 36 | 9 | 358 | PME–Air Vehicle | Hours | 5118.7 | 5120.1 | 0.0% | 6.8% | 6.8% | 0.0% |
| Program 36 | 9 | 358 | Airframe | Hours | 12,155.2 | 11,257.1 | 7.4% | 15.5% | 14.3% | 7.6% |
| Program 37 | 5 | 204 | PME–Air Vehicle | Dollars | 1468.7 | 921.0 | 37.3% | 2.9% | 1.9% | 36.4% |
| Program 38 | 5 | 605 | PME–Air Vehicle | Dollars | 2641.9 | 1527.7 | 42.2% | 14.9% | 8.1% | 46.0% |
| Program 39 | 5 | 870 | PME–Air Vehicle | Dollars | 310.9 | 311.5 | −0.2% | 2.3% | 2.3% | −0.2% |
| Program 40 | 10 | 178 | Electronic Warfare (3) | Dollars | 751.2 | 551.9 | 26.5% | 69.7% | 74.7% | −7.1% |
| Program 40 | 10 | 712 | Body | Dollars | 617.6 | 577.6 | 6.5% | 4.8% | 5.1% | −7.6% |
| Program 40 | 10 | 178 | Airframe | Dollars | 4251.9 | 4226.4 | 0.6% | 4.8% | 4.9% | −1.0% |
| Program 40 | 10 | 178 | Electronic Warfare (2) | Dollars | 721.7 | 721.7 | 0.0% | 393.4% | 393.4% | 0.0% |
| Program 40 | 10 | 178 | Electronic Warfare (1) | Dollars | 1642.3 | 1643.0 | 0.0% | 20.7% | 20.7% | 0.0% |
| Program 40 | 10 | 178 | PME–Air Vehicle | Hours | 13,454.5 | 13,466.8 | −0.1% | 6.0% | 6.0% | −0.1% |
| Program 40 | 10 | 178 | Auxiliary Power Plant | Dollars | 385.1 | 385.1 | 0.0% | 24.9% | 24.9% | 0.0% |
| Program 40 | 10 | 178 | PME–Air Vehicle | Dollars | 12,231.7 | 12,236.6 | 0.0% | 7.9% | 7.9% | 0.0% |
| Program 40 | 10 | 178 | Alighting Gear | Dollars | 233.6 | 233.6 | 0.0% | 30.1% | 30.1% | 0.0% |
| Program 40 | 10 | 178 | Wing | Dollars | 607.4 | 607.6 | 0.0% | 6.2% | 6.2% | 0.0% |
| Program 40 | 10 | 178 | Empennage | Dollars | 702.1 | 702.1 | 0.0% | 17.4% | 17.4% | 0.0% |
| Program 40 | 10 | 178 | Hydraulic | Dollars | 72.2 | 70.2 | 2.8% | 9.0% | 8.8% | 2.2% |
| Program 41 | 6 | 67 | PME–Air Vehicle | Hours | 12,741.5 | 12,743.8 | 0.0% | 9.5% | 9.5% | 0.0% |
| Program 41 | 5 | 49 | Empennage | Dollars | 242.2 | 242.2 | 0.0% | 5.8% | 5.9% | 0.0% |
| Program 41 | 6 | 67 | PME–Air Vehicle | Dollars | 16,643.9 | 16,645.6 | 0.0% | 10.7% | 10.7% | 0.0% |
| Program 41 | 6 | 67 | Surface Controls | Dollars | 281.7 | 281.7 | 0.0% | 7.7% | 7.7% | 0.0% |
| Program 41 | 6 | 67 | EOTS | Dollars | 442.3 | 442.4 | 0.0% | 9.5% | 9.5% | 0.0% |
| Program 41 | 6 | 67 | Wing | Dollars | 1927.0 | 1927.3 | 0.0% | 7.4% | 7.4% | 0.0% |
| Program 41 | 6 | 67 | Electrical | Dollars | 57.2 | 57.2 | 0.0% | 2.1% | 2.1% | 0.0% |
| Program 41 | 6 | 67 | Electronic Warfare (1) | Dollars | 547.3 | 547.3 | 0.0% | 8.1% | 8.1% | 0.0% |
| Program 41 | 6 | 67 | Hydraulic | Dollars | 281.5 | 274.6 | 2.4% | 19.4% | 19.0% | 2.0% |
| Program 41 | 6 | 67 | Mission Computer (1) | Dollars | 1698.1 | 1542.4 | 9.2% | 4.6% | 3.7% | 19.5% |
| Program 41 | 6 | 67 | Airframe | Dollars | 6877.8 | 5547.4 | 19.3% | 8.7% | 6.4% | 26.8% |
| Program 41 | 6 | 67 | Alighting Gear | Dollars | 582.3 | 521.1 | 10.5% | 28.3% | 25.0% | 11.6% |
| Program 41 | 6 | 67 | EO/IR | Dollars | 233.0 | 89.4 | 61.6% | 9.3% | 3.1% | 66.8% |
| Program 41 | 6 | 201 | Body | Dollars | 3431.8 | 2343.2 | 31.7% | 42.6% | 29.9% | 29.7% |
| Program 42 | 5 | 41 | PME–Air Vehicle | Dollars | 8498.6 | 8499.6 | 0.0% | 6.2% | 6.2% | 0.0% |
| Program 42 | 5 | 41 | PME–Air Vehicle | Hours | 15,696.5 | 15,696.9 | 0.0% | 10.7% | 10.7% | 0.0% |
| Program 42 | 5 | 50 | EOTS | Dollars | 593.3 | 593.3 | 0.0% | 11.6% | 11.6% | 0.0% |
| Program 42 | 5 | 50 | EO/IR | Dollars | 578.4 | 578.4 | 0.0% | 7.5% | 7.5% | 0.0% |
| Program 42 | 5 | 50 | Hydraulic | Dollars | 297.0 | 297.0 | 0.0% | 15.4% | 15.4% | 0.0% |
| Program 42 | 5 | 50 | Surface Controls | Dollars | 424.9 | 424.9 | 0.0% | 11.0% | 11.0% | 0.0% |
| Program 42 | 5 | 50 | Radar | Dollars | 733.8 | 733.8 | 0.0% | 10.9% | 10.9% | 0.0% |
| Program 42 | 5 | 50 | Airframe | Dollars | 5222.7 | 5222.8 | 0.0% | 5.9% | 5.9% | 0.0% |
| Program 42 | 5 | 50 | Electronic Warfare (1) | Dollars | 746.5 | 746.5 | 0.0% | 10.7% | 10.7% | 0.0% |
| Program 42 | 5 | 50 | Wing | Dollars | 3726.6 | 3726.7 | 0.0% | 16.5% | 16.5% | 0.0% |
| Program 42 | 5 | 50 | Alighting Gear | Dollars | 78.6 | 77.4 | 1.5% | 3.6% | 3.5% | 2.3% |
| Program 42 | 5 | 150 | Body | Dollars | 1588.5 | 892.1 | 43.8% | 12.6% | 8.7% | 30.8% |
| Program 43 | 13 | 1285 | PME–Air Vehicle | Dollars | 88.1 | 88.8 | −0.8% | 1.9% | 1.9% | −1.0% |
| Program 44 | 6 | 432 | PME–Air Vehicle | Dollars | 1621.0 | 1623.3 | −0.1% | 10.0% | 10.0% | −0.2% |
| Program 45 | 9 | 63 | PME–Air Vehicle | Dollars | 2152.3 | 1557.1 | 27.7% | 9.5% | 6.4% | 33.2% |
| Program 46 | 6 | 44 | PME–Air Vehicle | Hours | 7736.9 | 7255.3 | 6.2% | 17.6% | 16.7% | 4.8% |
| Program 46 | 10 | 113 | PME–Air Vehicle | Dollars | 797.9 | 627.0 | 21.4% | 3.8% | 2.9% | 22.7% |
| Program 47 | 19 | 1023 | PME–Air Vehicle | Dollars | 115.2 | 115.2 | 0.0% | 4.3% | 4.2% | 0.2% |
| Program 48 | 5 | 1725 | PME–Air Vehicle | Dollars | 59.8 | 3.1 | 94.9% | 6.8% | 0.3% | 95.4% |
| Program 49 | 10 | 16 | Data Link (1) | Dollars | 470.3 | 470.3 | 0.0% | 20.4% | 20.4% | 0.0% |
| Program 49 | 10 | 16 | PME–Air Vehicle | Dollars | 41,008.9 | 41,009.2 | 0.0% | 14.1% | 14.1% | 0.0% |
| Program 50 | 7 | 577 | PME–Air Vehicle | Dollars | 1674.7 | 1224.7 | 26.9% | 5.5% | 4.6% | 15.7% |
| Program 51 | 12 | 244 | PME–Air Vehicle | Hours | 625.6 | 612.8 | 2.0% | 191.4% | 191.8% | −0.2% |
| Program 52 | 11 | 899 | Electronic Warfare (1) | Dollars | 90.1 | 90.2 | −0.1% | 29.2% | 29.3% | −0.1% |
| Program 52 | 11 | 203 | PME–Air Vehicle | Dollars | 2995.1 | 2992.0 | 0.1% | 24.9% | 23.6% | 5.2% |
| Program 53 | 13 | 251 | PME–Air Vehicle | Hours | 4585.2 | 4585.2 | 0.0% | 6.7% | 6.7% | 0.0% |
| Program 53 | 11 | 203 | PME–Air Vehicle | Dollars | 2459.9 | 2460.0 | 0.0% | 9.6% | 9.6% | 0.0% |
| Program 54 | 11 | 184 | PME–Air Vehicle | Hours | 7010.4 | 7010.7 | 0.0% | 18.0% | 18.0% | 0.0% |
| Program 54 | 9 | 134 | PME–Air Vehicle | Dollars | 1907.3 | 970.0 | 49.1% | 11.8% | 6.5% | 44.9% |
| Program 55 | 5 | 136 | PME–Air Vehicle | Dollars | 321.6 | 277.7 | 13.7% | 5.5% | 4.7% | 14.8% |
| Program 56 | 9 | 155 | PME–Air Vehicle | Dollars | 1356.5 | 1356.6 | 0.0% | 3.9% | 3.9% | 0.0% |
| Program 57 | 6 | 68 | EO/IR | Dollars | 326.0 | 326.0 | 0.0% | 1261.8% | 1261.8% | 0.0% |
| Program 57 | 6 | 68 | PME–Air Vehicle | Dollars | 8574.7 | 8470.9 | 1.2% | 4.3% | 4.3% | −0.5% |
| Program 57 | 6 | 68 | Electronic Warfare (1) | Dollars | 998.8 | 998.9 | 0.0% | 58.9% | 58.9% | 0.0% |
| Program 57 | 6 | 68 | Electronic Warfare (2) | Dollars | 750.2 | 750.2 | 0.0% | 31.3% | 31.3% | 0.0% |
| Program 57 | 6 | 68 | Data Link (1) | Dollars | 94.8 | 94.8 | 0.0% | 7.2% | 7.2% | 0.0% |
| Program 57 | 6 | 68 | Electronic Warfare (4) | Dollars | 1156.3 | 1156.3 | 0.0% | 12.2% | 12.2% | 0.0% |
| Program 57 | 6 | 68 | Mission Computer (1) | Dollars | 1030.6 | 1030.6 | 0.0% | 13.0% | 13.0% | 0.0% |
| Program 57 | 6 | 68 | PME–Air Vehicle | Hours | 6435.9 | 6435.0 | 0.0% | 12.3% | 12.3% | 0.3% |
| Program 57 | 6 | 68 | Airframe | Dollars | 1443.2 | 1285.1 | 11.0% | 6.7% | 5.4% | 18.5% |
| Program 57 | 6 | 68 | Electronic Warfare (3) | Dollars | 53.4 | 21.8 | 59.1% | 7.2% | 3.0% | 58.5% |
| Program 58 | 9 | 36 | PME–Air Vehicle | Hours | 60,347.2 | 60,347.3 | 0.0% | 78.2% | 78.2% | 0.0% |
| Program 58 | 9 | 36 | Data Link (1) | Dollars | 227.8 | 227.8 | 0.0% | 29.3% | 29.3% | 0.0% |
| Program 58 | 9 | 36 | PME–Air Vehicle | Dollars | 4570.2 | 4570.2 | 0.0% | 10.9% | 10.9% | 0.0% |
| Program 58 | 5 | 18 | EO/IR | Dollars | 3488.4 | 3469.8 | 0.5% | 28.8% | 28.7% | 0.3% |
| Program 59 | 5 | 179 | PME–Air Vehicle | Dollars | 4583.3 | 1334.5 | 70.9% | 8.1% | 2.8% | 65.4% |
| Program 60 | 6 | 180 | PME–Air Vehicle | Dollars | 1010.5 | 333.9 | 67.0% | 12.4% | 4.6% | 63.1% |
| Program 61 | 5 | 488 | PME–Air Vehicle | Dollars | 502.3 | 486.5 | 3.1% | 9.2% | 7.7% | 16.3% |
| Program 62 | 6 | 78 | PME–Air Vehicle | Hours | 6027.1 | 5952.3 | 1.2% | 33.8% | 34.3% | −1.6% |
| Program 62 | 6 | 97 | Airframe | Hours | 2648.5 | 2649.0 | 0.0% | 20.5% | 20.5% | 0.0% |
| Program 62 | 9 | 110 | PME–Air Vehicle | Dollars | 13,027.5 | 13,028.9 | 0.0% | 24.0% | 24.0% | 0.0% |
| Program 63 | 6 | 663 | PME–Air Vehicle | Dollars | 23.2 | 21.1 | 9.2% | 2.9% | 2.6% | 11.6% |
| Program 64 | 5 | 380 | PME–Air Vehicle | Dollars | 1520.9 | 1521.2 | 0.0% | 57.4% | 57.4% | 0.0% |
| Program 65 | 6 | 749 | PME–Air Vehicle | Dollars | 116.6 | 115.9 | 0.6% | 1.7% | 1.8% | −5.1% |
| Program 66 | 8 | 194 | PME–Air Vehicle | Dollars | 128.3 | 119.3 | 7.0% | 2.6% | 2.4% | 8.6% |
| Program 67 | 9 | 677 | PME–Air Vehicle | Dollars | 273.5 | 273.5 | 0.0% | 5.1% | 5.1% | 0.0% |
| Program 68 | 5 | 590 | PME–Air Vehicle | Dollars | 87.1 | 87.2 | 0.0% | 2.8% | 2.8% | 0.0% |
| Program 69 | 5 | 579 | PME–Air Vehicle | Dollars | 305.7 | 305.8 | 0.0% | 9.5% | 9.5% | 0.0% |
References
- United States Government Accountability Office; Oakley, S.S. Weapon Systems Annual Assessment: Knowledge Gaps Pose Risks to Sustaining Recent Positive Trends: Report to Congressional Committees; United States Government Accountability Office: Washington, DC, USA, 2018.
- Wright, T.P. Factors Affecting the Cost of Airplanes. J. Aeronaut. Sci. 1936, 3, 122–128. [Google Scholar] [CrossRef]
- Asher, H. Cost-Quantity Relationships in the Airframe Industry. Ph.D. Thesis, The Ohio State University, Columbus, OH, USA, 1956. [Google Scholar]
- Boone, E.R.; Elshaw, J.J.; Koschnick, C.M.; Ritschel, J.D.; Badiru, A.B. A Learning Curve Model Accounting for the Flattening Effect in Production Cycles. Def. Acquis. Res. J. 2021. in-print. [Google Scholar]
- Mislick, G.K.; Nussbaum, D.A. Cost Estimation: Methods and Tools; John Wiley & Sons: Hoboken, NJ, USA, 2015. [Google Scholar]
- Argote, L.; Beckman, S.L.; Epple, D. The Persistence and Transfer of Learning in Industrial Settings. Manag. Sci. 1990, 36, 140–154. [Google Scholar] [CrossRef]
- Argote, L. Group and Organizational Learning Curves: Individual, System and Environmental Components. Br. J. Soc. Psychol. 1993, 32, 31–51. [Google Scholar] [CrossRef]
- Jaber, M.Y. Learning and Forgetting Models and Their Applications. Handb. Ind. Syst. Eng. 2006, 30, 30–127. [Google Scholar]
- Glock, C.H.; Grosse, E.H.; Jaber, M.Y.; Smunt, T.L. Applications of Learning Curves in Production and Operations Management: A Systematic Literature Review. Comput. Ind. Eng. 2019, 131, 422–441. [Google Scholar] [CrossRef]
- Jaber, M.Y.; Bonney, M. Production Breaks and the Learning Curve: The Forgetting Phenomenon. Appl. Math. Model. 1996, 2, 162–169. [Google Scholar] [CrossRef]
- Nembhard, D.A.; Uzumeri, M.V. Experiential Learning and Forgetting for Manual and Cognitive Tasks. Int. J. Ind. Ergon. 2000, 25, 315–326. [Google Scholar] [CrossRef]
- Sikström, S.; Jaber, M.Y. The Depletion–Power–Integration–Latency (DPIL) Model of Spaced and Massed Repetition. Comput. Ind. Eng. 2012, 63, 323–337. [Google Scholar] [CrossRef]
- Anzanello, M.J.; Fogliatto, F.S. Learning Curve Models and Applications: Literature Review and Research Directions. Int. J. Ind. Ergon. 2011, 41, 573–583. [Google Scholar] [CrossRef]
- Crossman, E.R. A Theory of the Acquisition of Speed-Skill∗. Ergonomics 1959, 2, 153–166. [Google Scholar] [CrossRef]
- Moore, J.R.; Elshaw, J.J.; Badiru, A.B.; Ritschel, J.D. Acquisition Challenge: The Importance of Incompressibility in Comparing Learning Curve Models; US Air Force Cost Analysis Agency: Arlington, TX, USA, 2015. [Google Scholar]
- Honious, C.; Johnson, B.; Elshaw, J.; Badiru, A. The Impact of Learning Curve Model Selection and Criteria for Cost Estimation Accuracy in the DoD; Air Force Institute of Technology: Wright Patterson AFB, OH, USA, 2016. [Google Scholar]
- Baloff, N. Startups in Machine-Intensive Production Systems. J. Ind. Eng. 1966, 17, 25. [Google Scholar]
- Baloff, N. Startup Management. IEEE Trans. Eng. Manag. 1970, 4, 132–141. [Google Scholar] [CrossRef]
- Corlett, E.N.; Morecombe, V.J. Straightening Out Learning Curves. Pers. Manag. 1970, 2, 14–19. [Google Scholar]
- Yelle, L.E. The Learning Curve: Historical Review and Comprehensive Survey. Decis. Sci. 1979, 10, 302–328. [Google Scholar] [CrossRef]
- Hirschmann, W.B. Profit from the Learning-Curve. Harv. Bus. Rev. 1964, 42, 125–139. [Google Scholar]
- Li, G.; Rajagopalan, S. A Learning Curve Model with Knowledge Depreciation. Eur. J. Oper. Res. 1998, 105, 143–154. [Google Scholar] [CrossRef]
- Chalmers, G.; DeCarteret, N. Relationship for Determining the Optimum Expansibility of the Elements of a Peacetime Aircraft Procurement Program; Stanford Research Institute: Menlo Park, CA, USA, 1949. [Google Scholar]
- De Jong, J.R. The Effects of Increasing Skill on Cycle Time and Its Consequences for Time Standards. Ergonomics 1957, 1, 51–60. [Google Scholar] [CrossRef]
- Knecht, G.R. Costing, Technological Growth and Generalized Learning Curves. J. Oper. Res. Soc. 1974, 25, 487–491. [Google Scholar] [CrossRef]
- Badiru, A.B. Computational Survey of Univariate and Multivariate Learning Curve Models. IEEE Trans. Eng. Manag. 1992, 39, 176–188. [Google Scholar] [CrossRef]
- Office of the Secretary of Defense. 1921-1 Data Item Description. Available online: https://cade.osd.mil/content/cade/files/csdr/dids/archive/1921-1.DI-FNCL-81566B.pdf (accessed on 29 September 2020).
- Hu, S.-P.; Smith, A. Accuracy Matters: Selecting a Lot-Based Cost Improvement Curve. J. Cost Anal. Parametr. 2013, 6, 23–42. [Google Scholar] [CrossRef]
- Cohen, J. Quantitative Methods in Psychology. Nature 1938, 141, 613. [Google Scholar] [CrossRef]
- Badiru, A.B. Half-Life Learning Curves in the Defense Acquisition Life Cycle. Def. Acquis. Res. J. 2012, 19, 283–308. [Google Scholar]
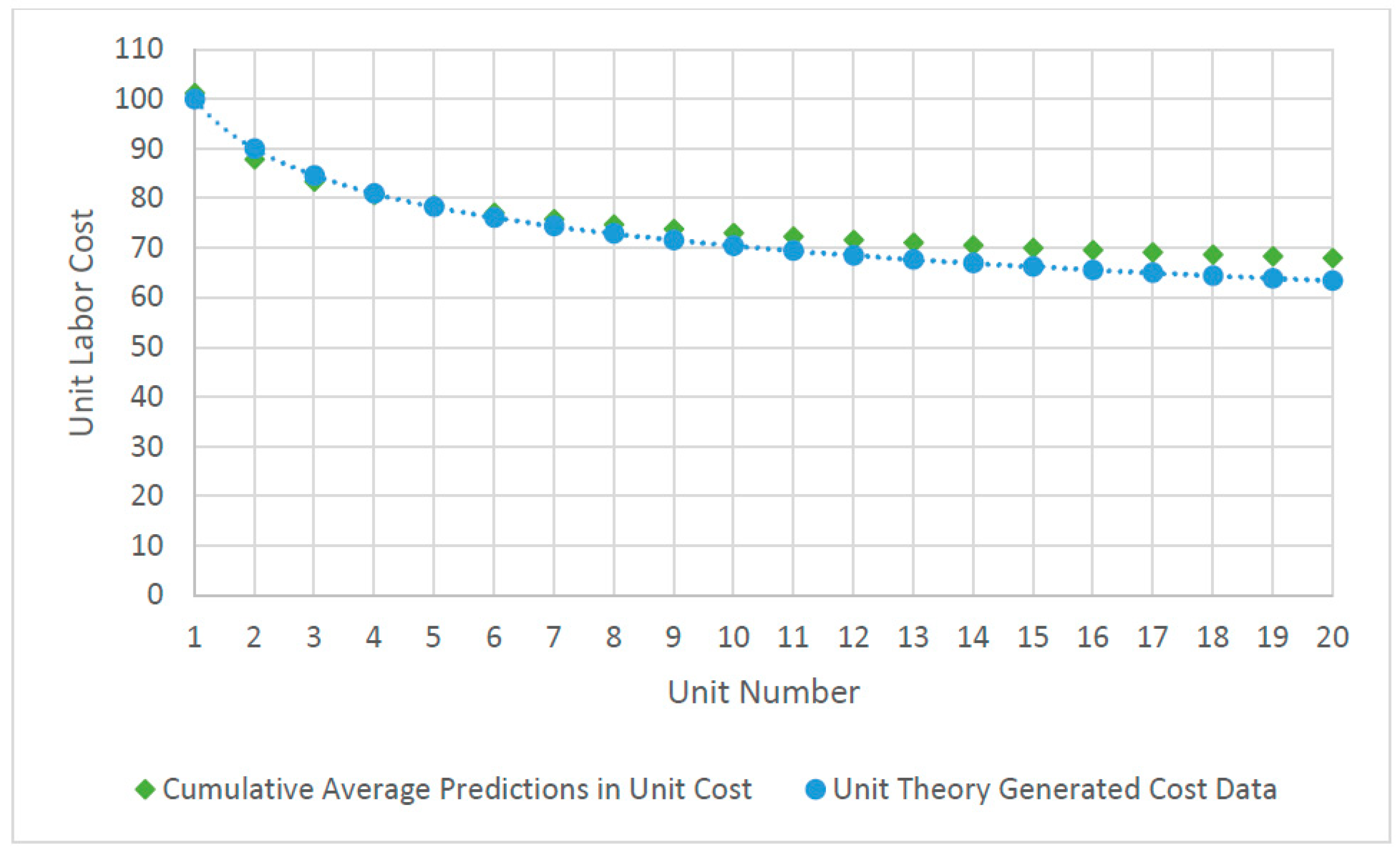

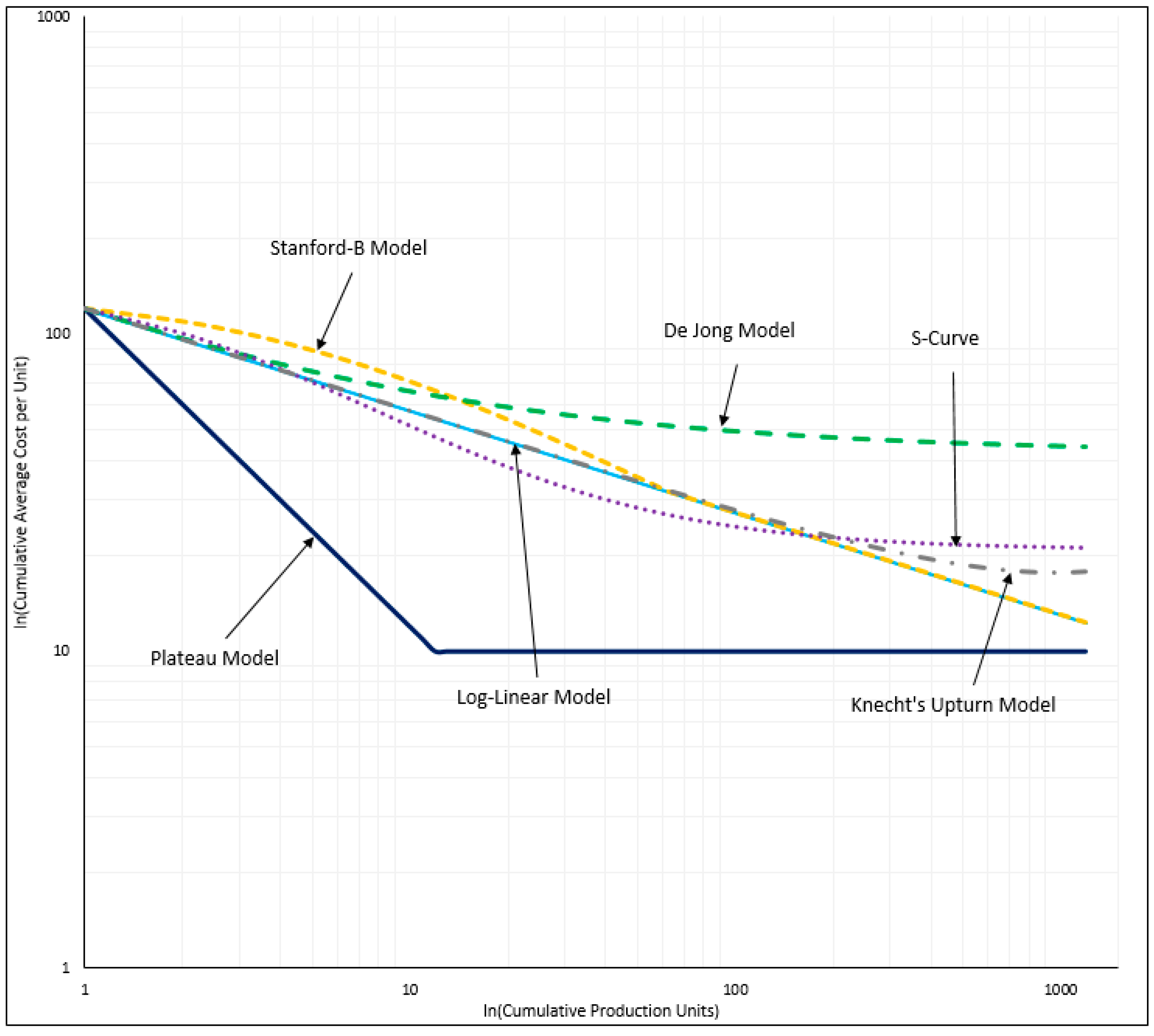
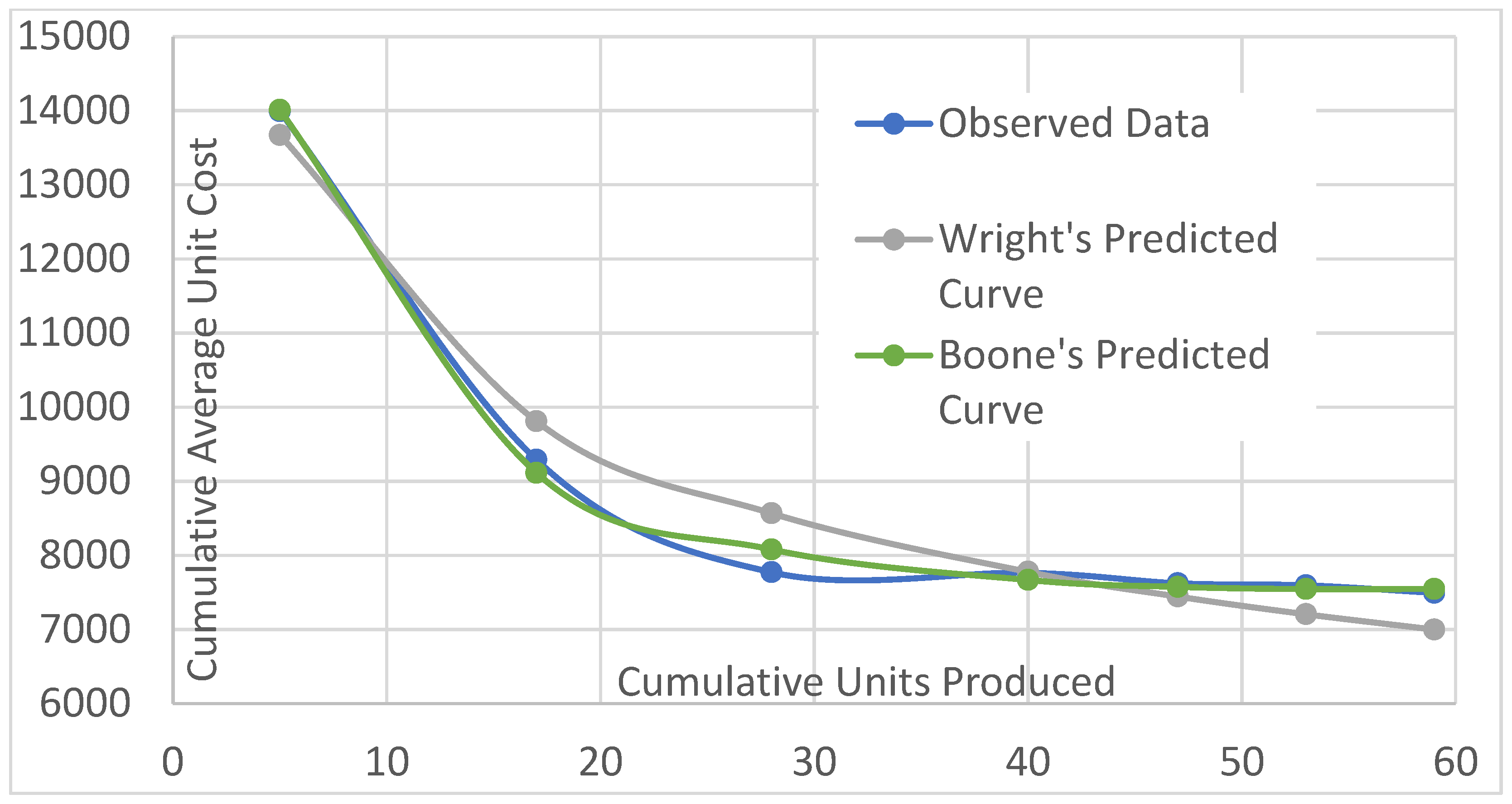

| Learning Curve Theory | Error Measure | Units of Measure |
|---|---|---|
| Cumulative Average Theory | Root Mean Squared Error Percentage Difference | Total Dollars(K) |
| Labor Hours | ||
| Mean Absolute Percent Error Percentage Difference | Total Dollars(K)&Labor Hours Combined | |
| Unit Theory | Root Mean Squared Error Percentage Difference | Total Dollars(K) |
| Mean Absolute Percent Error Percentage Difference | Total Dollars(K)&Labor Hours Combined |
| Hypothesis Test: H0: µ ≤ 0 HA: µ > 0 | ||||||||
|---|---|---|---|---|---|---|---|---|
| Learning Curve Theory | Error Measure | Units of Measure | Sample Mean | Sample Standard Deviation (s) | Number of Observations | Test Statistic | p-Value | Result |
| Cumulative Average Theory | Root Mean Squared Error Percentage Difference | Total Dollars(K) | 19.3% | 28.90% | 118 | 7.23 | <0.001 | Reject H0 |
| Labor Hours | 15.20% | 31.20% | 22 | 18.5 | 0.28 | Fail to reject H0 | ||
| Mean Absolute Percent | Total Dollars(K)&Labor Hours Combined | 18.60% | 29.50% | 140 | 7.45 | <0.001 | Reject H0 | |
| Hypothesis Test: H0: µ ≤ 0 HA: µ > 0 | ||||||||
|---|---|---|---|---|---|---|---|---|
| Learning Curve Theory | Error Measure | Units of Measure | Sample Mean | Sample Standard Deviation (s) | Number of Observations | Test Statistic | p-Value | Result |
| Unit Theory | Root Mean Squared Error Percentage Difference | Total Dollars(K) | 13.80% | 22.70% | 141 | 7.23 | <0.001 | Reject H0 |
| Labor Hours | 6.00% | 14.80% | 28 | 74.00 | 0.046 | Reject H0 | ||
| Mean Absolute Percent Error Percentage Difference | Total Dollars(K)&Labor Hours Combined | 11.30% | 23.10% | 169 | 6.36 | <0.001 | Reject H0 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hogan, D.; Elshaw, J.; Koschnick, C.; Ritschel, J.; Badiru, A.; Valentine, S. Cost Estimating Using a New Learning Curve Theory for Non-Constant Production Rates. Forecasting 2020, 2, 429-451. https://doi.org/10.3390/forecast2040023
Hogan D, Elshaw J, Koschnick C, Ritschel J, Badiru A, Valentine S. Cost Estimating Using a New Learning Curve Theory for Non-Constant Production Rates. Forecasting. 2020; 2(4):429-451. https://doi.org/10.3390/forecast2040023
Chicago/Turabian StyleHogan, Dakotah, John Elshaw, Clay Koschnick, Jonathan Ritschel, Adedeji Badiru, and Shawn Valentine. 2020. "Cost Estimating Using a New Learning Curve Theory for Non-Constant Production Rates" Forecasting 2, no. 4: 429-451. https://doi.org/10.3390/forecast2040023
APA StyleHogan, D., Elshaw, J., Koschnick, C., Ritschel, J., Badiru, A., & Valentine, S. (2020). Cost Estimating Using a New Learning Curve Theory for Non-Constant Production Rates. Forecasting, 2(4), 429-451. https://doi.org/10.3390/forecast2040023






