On Underdispersed Count Kernels for Smoothing Probability Mass Functions

Abstract

Only a few count smoothers are available for the widespread use of discrete associated kernel estimators, and their constructions lack systematic approaches. This paper proposes the mean dispersion technique for building count kernels. It is only applicable to count distributions that exhibit the underdispersion property, which ensures the convergence of the corresponding estimators. In addition to the well-known binomial and recent CoM-Poisson kernels, we introduce two new ones such the double Poisson and gamma-count kernels. Despite the challenging problem of obtaining explicit expressions, these kernels effectively smooth densities. Their good performances are pointed out from both numerical and comparative analyses, particularly for small and moderate sample sizes. The optimal tuning parameter is here investigated by integrated squared errors. Also, the added advantage of faster computation times is really very interesting. Thus, the overall accuracy of two newly suggested kernels appears to be between the two old ones. Finally, an application including a tail probability estimation on a real count data and some concluding remarks are given.

1. Introduction

Nonparametric statistics use (discrete) asymmetric kernel methods to capture and visually represent complex relationships between variables that cannot be effectively captured by symmetric kernels. A common practice now is to employ kernels whose support coincides with the nature or support of the dataset, whether it is count, categorical, bounded, unbounded, continuous, left or right skewed, and so on. See, for example, refs. [1,2,3] for smoothing of probability mass, probability density, and regression functions with environmental, econometric and financial applications, among others. Discrete smoothing of probability mass functions in the case of counts and categoricals has not been studied as extensively as its continuous counterparts, primarily due to the limited options for suitable kernels. There are two main classes of discrete associated kernels. The first, called of the “second order” (with $\delta =0$ in Definition 1), includes kernels whose estimators are consistent and asymptotically tend towards the true function as for the Dirac kernel. Such discrete (asymmetric and symmetric) kernels are, for instance, triangular [4], Aitchison–Aitken or Dirac Uniform [5], Wang and Van Ryzin [6], and the recently proposed CoM-Poisson [7,8]; see also [3]. The second class, so-called of the “first order” (with $\delta \in (0,1)$ in Definition 1), generally contains the binomial kernel [4] appropriate for small and moderate sample sizes for which the corresponding estimators do not converge. The previous discrete kernels are suitable for categorical data, with the exception of the binomial and CoM-Poisson kernels, which are appropriated for count data. Additionally, all these associated kernels are typically underdispersed, i.e., its variance is less than the expectation; on the contrary, the equidispersed Poisson and overdispersed negative binomial kernels are not recommended for count smoothings; see [4], the authors of which make intensive simulations that highlight the superiority of these underdispersed discrete smoothers versus equi-/over-dispersed ones. The reader can also refer to [9,10] for some applications of discrete kernels in survey sampling and the model specification test, respectively, and more generally to Li and Racine [11]. Here is the precise definition of a discrete associated kernel; see, e.g., Esstafa et al. [8].

Definition 1. 

Let $\mathbb{T}\subseteq \mathbb{R}$ be the discrete support of the probability mass function (pmf) f to be estimated, $x\in \mathbb{T}$ a target point and $h>0$ a bandwidth. A parameterized pmf $K_{x,h}(·)$ on the discrete support ${\mathbb{S}}_x\subseteq \mathbb{R}$ is called “discrete associated kernel” if the following conditions are satisfied:

$$x\in {\mathbb{S}}_x,\underset{h\to 0}{lim}\mathbb{E}\left(Z_{x,h}\right)=xand\underset{h\to 0}{lim}\mathrm{Var}\left(Z_{x,h}\right)=\delta \in [0,1),$$

where $Z_{x,h}$ denotes the discrete random variable with pmf $K_{x,h}(·)$.

We suppose $X_1,X_2,\dots ,X_n$ is a sample of independent and identically distributed (iid) discrete random variables with a pmf f defined on $\mathbb{T}\subseteq \mathbb{R}$. The usual discrete associated kernel estimator of f is generally not a pmf. This is particularly true for some discrete associated-kernels such as the binomial, triangular, and CoM-Poisson, where the total mass of the corresponding estimator does not necessarily equal one; see, e.g., [12]. Specifically, one can express both estimators as follows:

$${\widehat{f}}_n\left(x\right)=\frac{{\tilde{f}}_n\left(x\right)}{C_n},x\in \mathbb{T},$$

(1)

with

$${\tilde{f}}_n\left(x\right)=\frac{1}{n}\sum _{i=1}^n{K}_{x,h_n}\left(X_i\right)\mathrm{and}{C}_n=\sum _{x\in \mathbb{T}}{\tilde{f}}_n\left(x\right)>0,$$

(2)

where ${\left(h_n\right)}_{n\ge 1}$ is an arbitrary sequence of positive smoothing (or tuning) parameters that satisfies ${lim}_{n\to \infty }{h}_n=0$, while $K_{x,h_n}(·)$ is a suitably chosen discrete kernel function. For the following three kernels of Dirac, Aitchison and Aitken [5] and Wang and Van Rizin [6], it is easy to check that $C_n=1$, and therefore ${\tilde{f}}_n={\widehat{f}}_n$. Esstafa et al. [8] recently demonstrated the effectiveness of the normalized version (1) compared to the unnormalized one (2) with illustrations using the existing count (convergent or not-convergent) smoothers: binomial and CoM-Poisson, respectively. We here use the standardized version (1) for all. In nonparametric (discrete or continous) kernel estimation, the tuning (smoothing) parameter plays a crucial role in preventing overfitting and underfitting. Bandwidth selection methods can be categorized into three families: global bandwidths for all smoothers, adaptive for continuous kernels, and local ones for discrete (count and categorical) estimators. For example, Chu et al. [13] proposed a rule-of-thumb approach, Harfouche et al. [1] utilized cross-validations, and Somé et al. [2] emploed a local Bayesian method. It is important to note that smoothers using local bandwidths, which vary according to each estimation point, are referred to as “balloon estimators”, while adaptive bandwidths, varying for each data point, are known as “sample-point estimators”.

In this paper, we propose two new count kernels, namely the double Poisson and the gamma-count, derived from their underdispersed distributions parts. These additions enrich the list of existing count kernels, such as binomial and CoM-Poisson. Specifically, they reinforce the roster of “first-order” kernels, which exclusively contains the CoM-Poisson, and whose smoothers are consistent and asymptotically tend towards the Dirac kernel. Their construction is performed through the mean dispersion technique which appears as a variant of the mode dispersion method [12] in continuous cases. The rest of the paper is organized as follows. In Section 2, we recall some underdispersed count distributions including the double Poisson and gamma-count which have some specific properties in their expressions. Section 3 is devoted to building the double Poisson and gamma-count kernels after introducing the mean dispersion method of consruction and despite some approximations in their properties. Section 4 presents the main results from our simulation studies and then an application on a count dataset on development days of insect pests on Hura trees. Final remarks are made in Section 5. Some other underdispersed count distributions and local Bayesian bandwidth selection are mentionned in Appendix A and Appendix B in relation to their feasibility.

2. Some Properties of Underdispersed Count Distributions

In this section we recall three count distributions, namely the double Poisson, the gamma-count and the CoM-Poisson, which are underdispersed according to a part of their parameters. Before building their corresponding associated kernels to satisfy Definition 1, we point out their main properties needed (pmf, mean and variance) even if they are not generally in closed-form expressions. Thus, approximation and computation approaches are used for a better understanding of the parameters.

• The double Poisson pmf is defined by

  $$\begin{array}{c}\hfill p(y;\lambda ,\gamma ):=K_{\lambda ,\gamma }^{DP}\left(y\right)=k(\lambda ,\gamma ){\gamma }^{1/2}{e}^{-\gamma \lambda }\left(\frac{e^{-y}{y}^y}{y!}\right){\left(\frac{e\lambda }{y}\right)}^{\gamma \lambda },y=0,1,2,\dots ,\hfill \end{array}$$

  (3)

  with

  $${\displaystyle \frac{1}{k(\lambda ,\gamma )}=\sum _{y=0}^{\infty }{\gamma }^{1/2}{e}^{-\gamma \lambda }\left(\frac{e^{-y}{y}^y}{y!}\right){\left(\frac{e\lambda }{y}\right)}^{\gamma \lambda }\simeq 1+\frac{1-\gamma }{12\gamma \lambda }\left(1+\frac{1}{\gamma \lambda }\right)}$$

  and where $\gamma >0$ is the dispersion parameter and $\lambda >0$. The mean and variance do not have closed-form expressions but they can be approximated, respectively, by

  $$\mathbb{E}\left(Y\right)\simeq \lambda \mathrm{and}Var\left(Y\right)\simeq \frac{\lambda }{\gamma }.$$
  We note that the values $0<\gamma <1,\gamma =1$ and $\gamma >1$ correspond to overdispersion, equidispersion and underdispersion, respectively. See Efron [14] and Toledo et al. [15] for further details.
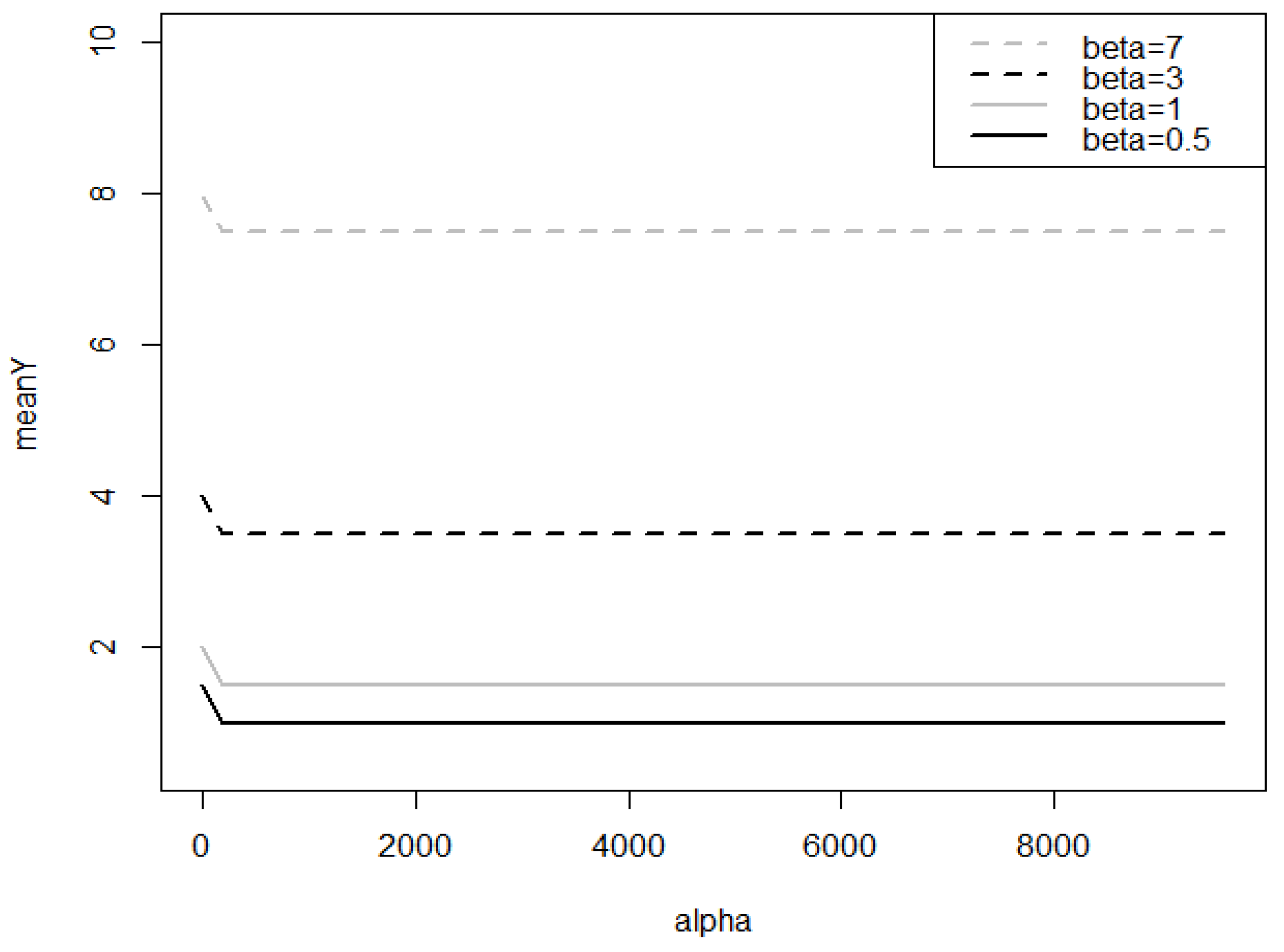
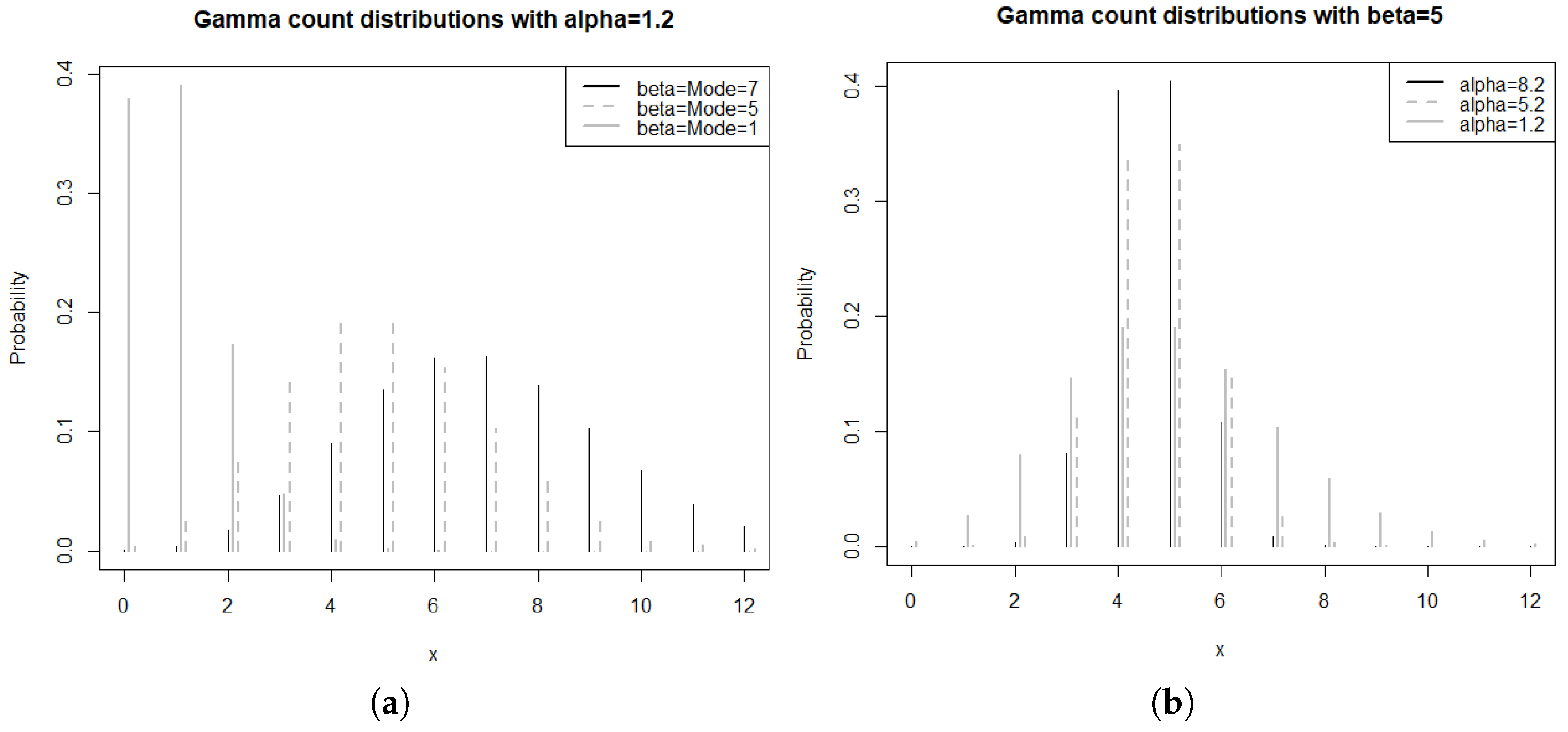
• The gamma-count pmf for the number of events within the time interval $(0,T)$ is given, with $\alpha ,\beta >0$, through

  $$p(y;\alpha ,\beta )=K_{\alpha ,\beta }^{GC}\left(y\right)=G(y\alpha ,\beta T)-G(\alpha (y+1),\beta T)y=0,1,2,\dots ,$$

  (4)

  with the cumulative distribution function

  $$G(y\alpha ,\beta T)=\frac{1}{\mathrm{\Gamma }\left(y\alpha \right)}{\int }_0^{\beta T}{u}^{y\alpha -1}exp(-u)du$$

  and for $y=0,G(0,\beta T)=1$ and T can be set to one, without loss of generality. The parameter $\alpha >0$ is such that $\alpha >1$ and $0<\alpha <1$ refer to underdispersion or overdispersion, respectively. Here, the mean and variance are not available in closed form but they can be computed through

  $$\mathbb{E}\left(Y\right)=\sum _{y=1}^{\infty }G\left(y\alpha ,\beta T\right)\mathrm{and}Var\left(Y\right)=\sum _{y=1}^{\infty }\left[y^2{K}_{\alpha ,\beta }^{GC}\left(y\right)\right]-{\left[\mathbb{E}\left(Y\right)\right]}^2.$$
  See Winkelmann [16] for further details, Zeviani et al. [17] for an application to regression model, and also [15].
  Numerically and from Figure 1, we can observe that the mean $\mathbb{E}\left(Y\right)$ of the gamma-count distribution is almost always a constant around $\beta$; specifically, by zooming in, we notice that the shape of the curve is logarithmic or approximately linear in $\alpha >0$ for fixed $\beta >0$. The same fact is observed for its mode, as shown in Figure 2. We also note that Figure 2 highlights the role of $\beta >0$ as a shape or location parameter and $\alpha >0$ as a scale or dispersion parameter of the gamma-count distribution. Hence, the variance of the gamma-count distribution can be seen as a function of $\alpha >0$.
  

  Figure 1. Computation of the mean of gamma-count distribution according to $\alpha$ and $\beta =0.5,1,3,7$.
  

  Figure 2. Some gamma-count distributions according to (a) $\alpha =1.2$ and also to (b) $\beta =5$ fixed.
• The CoM-Poisson distribution with location parameter $\mu \ge 0$ and dispersion parameter $\nu >0$ ($\nu >1$ for underdispersion) such that its pmf $p(·;\mu ,\nu )$ is defined by

  $$\begin{array}{c}\hfill p(y;\mu ,\nu ):=K_{\mu ,1/\nu }^{CMP}\left(y\right)=\frac{\lambda {(\mu ,\nu )}^y}{{(y!)}^{\nu }}\frac{1}{D\left(\lambda \right(\mu ,\nu ),\nu )},y\in \mathbb{N},\hfill \end{array}$$

  (5)

  where function $\lambda :=\lambda (\mu ,\nu )$ is the solution to equation

  $$\begin{array}{c}\hfill \sum _{z=0}^{\infty }\frac{{\left\{\lambda (\mu ,\nu )\right\}}^z}{{(z!)}^{1/h}}(z-\mu )=0,\hfill \end{array}$$

  and it is used to define the normalizing constant $D(\lambda (\mu ,\nu ),\nu )={\sum }_{y=0}^{\infty }{\left[\lambda (\mu ,\nu )\right]}^y/{(y!)}^{\nu }$. Then,

  $$\mathbb{E}\left(Y\right)=\mu \mathrm{and}\mathrm{Var}\left(Y\right)=\frac{1}{\nu }{\left[\lambda (\mu ,\nu )\right]}^{1/\nu }+\mathcal{O}\left({\left\{\lambda (\mu ,\nu )\right\}}^{-1/\nu }\right),$$

  when ${\left\{\lambda (\mu ,\nu )\right\}}^{1/\nu }\to \infty$ as $\nu \to \infty$. See, for example, ref. [8] for some references.

Also, we can refer to Appendix A for some underdispersed count distributions such as the BerPoi, generalized Poisson, an underdispersed Poisson, the BerG and the hyper-Poisson, for which their corresponding count associated kernels are inconclusive.

3. Associated Kernel Versions

We introduce in this section the notion of the mean dispersion-ready pmf, a new method inspired by the mode dispersion technique (see, for example, [12]) and adapted to the discrete setting. This method allows construction of discrete associated kernels and is applicable to underdispersed count distributions.

Definition 2. 

A mean dispersion-ready pmf $K_{\theta }$ is a underdispersed parametrized pmf with discrete support ${\mathbb{S}}_{\theta }\subseteq \mathbb{R}$, $\theta \in \mathrm{\Theta }\subseteq {\mathbb{R}}^2$, such that $K_{\theta }$ has moments of second order with mode $m\in \mathbb{R}$ and admitting dispersion parameter D.

Remark 1. 

Let $K_{\theta }$ be a mean dispersion-ready pmf on ${\mathbb{S}}_{\theta }\subseteq \mathbb{R}$. The following two assertions are satisfied:

(i) 

the mode m of $K_{\theta }$ always belongs to ${\mathbb{S}}_{\theta }$;

(ii) 

if μ is the mean of $K_{\theta }$, then $K_{\theta }\left(m\right)\ge K_{\theta }\left(\lfloor \mu \rfloor \right)$, where $\lfloor ·\rfloor$ denotes the integer part.

In order to create discrete associated kernels from an underdispersed unimodal mean dispersion-ready pmf $K_{\theta }$ defined on ${\mathbb{S}}_{\theta }$, the mean dispersion method requires, if it exists, an explicit solution of the following system of equations:

$$\left(\theta (m,D)\right)=(x,h).$$

(6)

It should be noted that this construction may not always be possible, and alternative methods can be found in [8,12,18].

Now, we illustrate the use of (6) in four examples such both new double Poisson and gamma-count kernels, as well as the old CoM-Poisson and binomial kernels.

Example 1. 

The double Poisson kernel of the second order and underdispersed for any $h\in (0,1)$ is defined on ${\mathbb{S}}_x=\mathbb{T}=\mathbb{N}$ for each $x\in \mathbb{N}$,

$$K_{x,h}^{DP}\left(z\right)=k(x+h,1/h)h^{-1/2}{e}^{-(x+h)/h}\left(\frac{e^{-z}{z}^z}{z!}\right){\left(\frac{e(x+h)}{z}\right)}^{(x+h)/h},z=0,1,2,\dots ,$$

where $k(x+h,1/h)$ is the normalizing constant. It comes from (3) with the reparametrization of the system $(\lambda ,\gamma )=(x+h,1/h)$ which implies

$$\mathbb{E}\left(Z_{x,h}^{DP}\right)\simeq x+h\to xandVar\left(Z_{x,h}^{DP}\right)\simeq (x+h)h\to 0$$

as $h\to 0$, where $Z:=Z_{x,h}^{DP}$ is the count random variable associated to this double Poisson kernel.

Example 2. 

The gamma-count kernel, which exhibits the underdispersion phenomenon for any $h\in (0,1)$, is derived from (4) with parametrization $(\alpha ,\beta )=(1/h,x+h)$. It is defined on ${\mathbb{S}}_x=\mathbb{T}=\mathbb{N}$ for each $x\in \mathbb{N}$ and any $h\in (0,1)$ by

$$K_{x,h}^{GC}\left(z\right)=G(z/h,(x+h)T)-G((z+1)/h,(x+h)T),z=0,1,2,\dots$$

From the analyses of Figure 1 and Figure 2, the mean and mode of the associated gamma-count random variable $Z:=Z_{x,h}^{GC}$ are around $x+h$, which therefore tend to a neighborhood of x when $h\to 0$. Also, one can observe that $Var\left(Z_{x,h}^{GC}\right)\to 0$ as $h\to 0$.

Example 3. 

The CoM-Poisson kernel of the second order and underdispersed for any $h\in (0,1)$ is defined with ${\mathbb{S}}_x=\mathbb{T}=\mathbb{N}$ for each $x\in \mathbb{N}$,

$$K_{x,h}^{CMP}\left(z\right)=\frac{{\left\{\lambda (x,1/h)\right\}}^z}{{(z!)}^{1/h}}{\left\{D\left(\lambda (x,1/h),1/h\right)\right\}}^{-1},$$

where $D(\lambda (x,1/h),1/h)={\sum }_{z=0}^{\infty }{\left[\lambda (x,1/h)\right]}^z/{(z!)}^{1/h}$ is the normalizing constant and $\lambda :=\lambda (x,1/h)$ represents a function of x and $1/h$ given by the solution of

$$\sum _{z=0}^{\infty }\frac{{\left\{\lambda (x,1/h)\right\}}^z}{{(z!)}^{1/h}}(z-x)=0.$$

One can refer to [7,8] for further details. This construction implies that $\mathbb{E}\left(Z_{x,h}^{CMP}\right)=x$ and

$$\mathrm{Var}\left(Z_{x,h}^{CMP}\right)={\left\{\lambda (x,1/h)\right\}}^{h}h+\mathcal{O}\left({\left\{\lambda (x,1/h)\right\}}^{-h}\right)\to 0\mathrm{as}h\to 0.$$

Example 4. 

The first-order and underdispersed binomial kernel is introduced by Kokonendji and Senga Kiessé [4] as follows: ${\mathbb{S}}_x=\{0,1,\dots ,x+1\}$ for each $x\in \mathbb{N}=\mathbb{T}$ and $h\in (0,1)$,

$$K_{x,h}^B\left(z\right)=\frac{(x+1)!}{z!(x+1-z)!}{\left(\frac{x+h}{x+1}\right)}^z{\left(\frac{1-h}{x+1}\right)}^{x+1-z}$$

with $\mathbb{E}\left(Z_{x,h}^B\right)=x+h\to x$ as $h\to 0$ and

$$\mathrm{Var}\left(Z_{x,h}^B\right)=\frac{(x+h)(1-h)}{x+1}\to \frac{x}{x+1}\in (0,1)\mathrm{as}h\to 0.$$

Figure 3 and Figure 4 show different behaviours of these four underdispersed count kernels at the origin $x=0$ and at $x=5$, respectively, according to three values of the bandwidth $h>0$. Hence, the two newly suggested count kernels appear to be better competitors to the second-order CoM-Poisson kernel compared to the binomial one.

Figure 3. Gamma-count (GC), double Poisson (DP) kernels with parametrization $(x+h,1/h)$ compared to binomial (B) and CoM-Poisson (CMP) at $x=0$ with (a) $h=0.01$; (b) $h=0.1$; (c) $h=0.3$.

Figure 4. Double Poisson and gamma-count kernels with parametrization $(x+h,1/h)$ compared to CoM-Poisson (CMP) and binomial kernels at $x=5$ with (a) $h=0.1$; (b) $h=0.5$; (c) $h=0.9$.

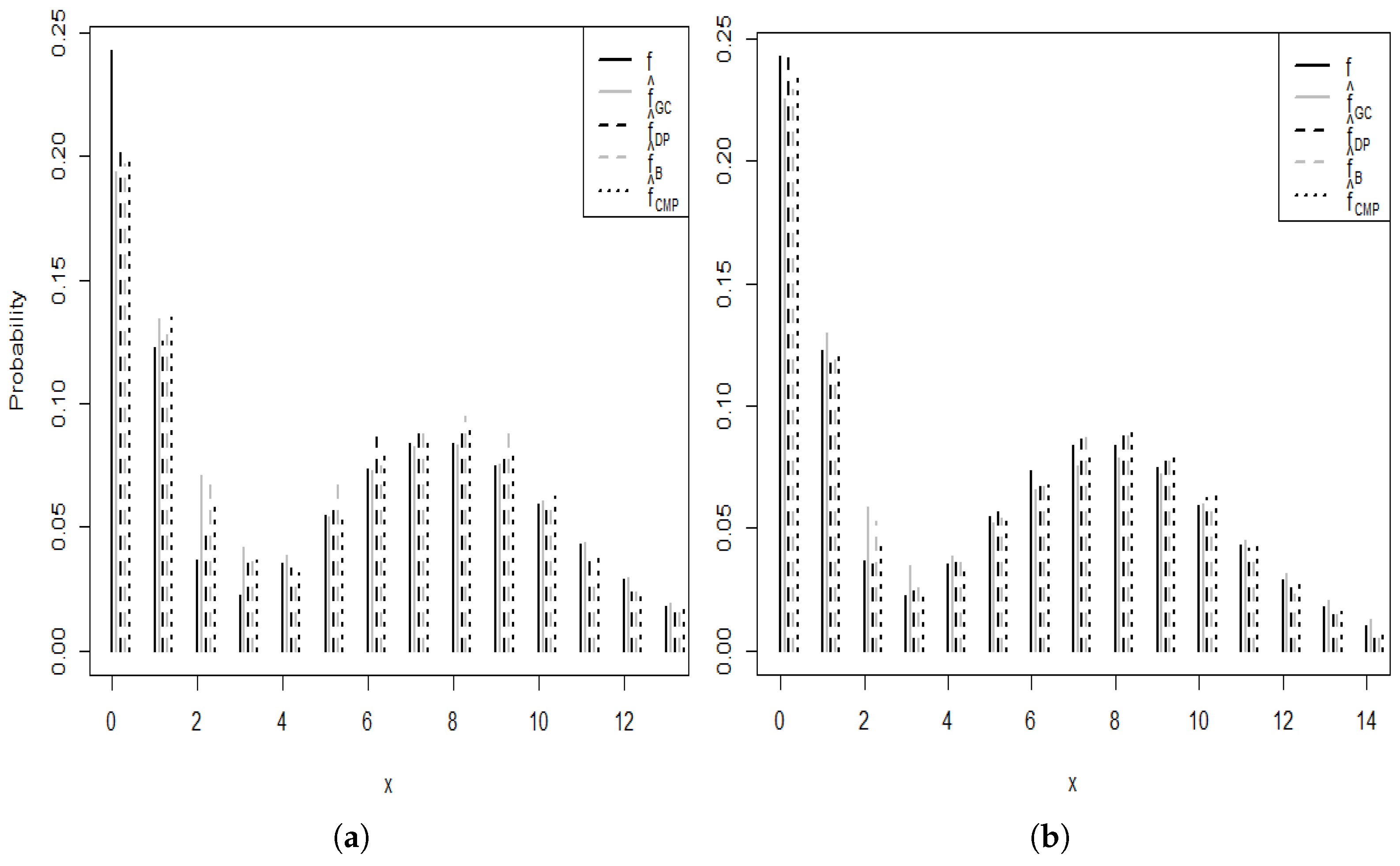
4. Simulation Studies and an Application to Real Data

The purpose of all numerical studies conducted here is to investigate the performances of the two new double Poisson and gamma-count kernels alongside the classical binomial and CoM-Poisson smoothers derived from (1) and (2). Computations are conducted on a 2.30 GHz PC using the R 4.2.1 software [19]. The previous smoothers are fitted using the rmutil, Ake and mpcmp packages [20,21,22], respectively. The corresponding four underdispersed count kernel estimators are assessed by employing integrated squared error (ISE) method to determine the optimal bandwidth parameter

$$h_{ise}=arg\underset{h\in (0,1)}{min}\left[{\displaystyle \sum _{x\in \mathbb{T}}{\left\{{\widehat{f}}_n\left(x\right)-f\left(x\right)\right\}}^2}\right].$$

(7)

In fact, the usual cross-validation (data-driven) technique does not converge in simulations and real data for the proposed kernel estimator: double Poisson and gamma-count. The reader can refer, for others methods, to Chu [13] for the plug-in method, Harfouche et al. [1] for cross-validation and to Kokonendji and Senga Kiéssé [4] for mean integrated squared errors.

In this study, we examine the performances of four count smoothers using count simulated datasets under four different scenarios denoted by A, B, C, and D. These scenarios are chosen to assess how well the estimators handle zero inflation, unimodality and multimodality. We evaluate the effectiveness of the smoothers by analyzing the empirical estimates of the ISE, specifically

$${\displaystyle {\widehat{ISE}}_n:=\frac{1}{N_{sim}}\sum _{t=1}^{N_{sim}}\sum _{x\in \mathbb{T}}{\left\{{\widehat{f}}_n\left(x\right)-f\left(x\right)\right\}}^2,}$$

where $N_{sim}$ is the number of replications and n denotes the sample size.

• Scenario A is generated by using the Poisson distribution

  $$f_A\left(x\right)=\frac{8^x{e}^{-8}}{x!},x\in \mathbb{N};$$
• Scenario B comes from the zero-inflated Poisson distribution

  $$f_B\left(x\right)=\left(\frac{7}{10}{\mathbb{1}}_{\{x=0\}}\right)+\left(\frac{3}{10}\times \frac{{10}^x{e}^{-10}}{x!}\right){\mathbb{1}}_{\mathbb{N}\setminus \left\{0\right\}}\left(x\right);$$
• Scenario C is from a mixture of two Poisson distributions

  $$f_C\left(x\right)=\left(\frac{2}{5}\times \frac{0.5^x{e}^{-0.5}}{x!}\right)+\left(\frac{3}{5}\times \frac{8^x{e}^{-8}}{x!}\right),x\in \mathbb{N};$$
• Scenario D comes from a mixture of three Poisson distributions

  $$f_D\left(x\right)=\left(\frac{3}{5}\times \frac{{10}^x{e}^{-10}}{x!}\right)+\left(\frac{1}{5}\times \frac{{22}^x{e}^{-22}}{x!}\right)+\left(\frac{1}{5}\times \frac{{50}^x{e}^{-50}}{x!}\right),x\in \mathbb{N}.$$

Table 1 presents the computation times required to perform all ISE bandwidth selection techniques (7) for gamma-count, double Poisson, binomial and CoM-Poisson smoothers based on a single replication of sample sizes ranging from $n=20$ to 500 for the target function C. For all sample sizes, the results show that the CoM-Poisson is the most time consuming followed by the double Poisson smoother mainly due to the normalizing constant in their expressions, (5) and (3), respectively. As the sample sizes increase, the binomial kernel outperforms in terms of CPU times due to its support ${\mathbb{S}}_x=\{0,1,\dots ,x\}$, whereas the gamma-count kernel becomes the second quickest due to the integrals in its expression.

Table 1. Comparison of execution times (in seconds) for one replication of Scenario C using gamma-count (gc), double Poisson (dp), binomial (b) and CoM-Poisson (cmp) kernel estimates.

$\mathit{n}$	${\mathit{t}}_{\mathit{gc}}$	${\mathit{t}}_{\mathit{dp}}$	${\mathit{t}}_{\mathit{b}}$	${\mathit{t}}_{\mathit{cmp}}$
20	0.14757	1.37290	0.07343	51.82259
50	0.22256	4.63862	0.14665	126.42510
100	0.42298	10.53522	0.16610	263.30720
250	0.79673	17.08182	0.25914	467.66510
500	1.82560	32.71456	0.49030	945.52740

Figure 5 depicts the true pmf and the smoothing ones using gamma-count, double Poisson, binomial and CoM-Poisson kernels with respect to Scenario C, and for one replication. The graphs show that, in general, the two new underdispersed count kernel estimators are accurate.

Figure 5. True pmf and estimate ones by gamma-count (GC), double Poisson (DP), binomial (B) and CoM-Poisson (CMP) kernels for the bimodal Scenario C with (a) $n=50$; (b) $n=250$.

Table 2 exhibits some empirical values of $IS{E}_n$, obtained through ISE bandwidth selection (7) using $N=500$ as number of replications, according to the four Scenarios A, B, C and D and with respect to sample sizes $n=10,25,50,100,250,500.$ Then, several behaviours emerge. As the sample sizes increase, the smoothings improve for all smoothers. As expected, the binomial kernel is the least efficient since it is of the first order. The three others have comparable performances. The two new count kernels, namely double Poisson and gamma-count, are slightly more precise than the CoM-Poisson one, notably for small and medium sample sizes (i.e., $n\le 100$) while the latter is the best for large sample sizes. Additionally, approximations made for the moments of the gamma-count distribution (4) may help clarify the performance discrepancy between the two new kernels for larger sample sizes. Finally, from a purely practical perspective, Table 1 and Table 2 highlight the following ranking in performances: double Poisson, gamma-count and CoM-Poisson.

Table 2. Empirical mean values $(\times {10}^3)$ of ${\widehat{ISE}}_n$ with their standard deviations in parentheses over $N_{sim}=500$ replications and with different sample sizes $n=10,25,50,100,250,500$ under four Scenarios A, B, C and D by using gamma-count (gc), double Poisson (dp), binomial (b) and CoM-Poisson (cmp) kernel estimators with the $ISE$ bandwidth selection.

	$\mathit{n}$	${\widehat{\mathit{ISE}}}_{\mathit{gc},\mathit{n}}$	${\widehat{\mathit{ISE}}}_{\mathit{dp},\mathit{n}}$	${\widehat{\mathit{ISE}}}_{\mathit{b},\mathit{n}}$	${\widehat{\mathit{ISE}}}_{\mathit{cmp},\mathit{n}}$
A	10	9.2240 (7.9708)	8.2596 (6.9910)	24.5732 (19.0226)	17.7012 (23.1386)
	25	3.4346 (2.2426)	4.0327 (2.5589)	8.5250 (5.8778)	9.3622 (11.2054)
	50	2.9191 (2.0443)	3.5842 (2.7603)	4.5986 (3.0472)	5.4105 (4.0815)
	100	1.8657 (1.2710)	2.0070 (1.6637)	2.2286 (1.3852)	2.7595 (2.2578)
	250	0.9299 (0.7017)	0.9670 (0.7401)	1.2736 (0.8046)	1.2511 (0.9823)
	500	0.5621 (0.3472)	0.5906 (0.3923)	1.2451 (0.6987)	0.3669 (0.3047)
B	10	9.9963 (8.2902)	10.4663 (8.8282)	25.3129 (13.1625)	26.0588 (26.1514)
	25	4.9811 (3.2787)	5.4373 (4.2802)	11.1561 (5.4033)	10.5811 (8.4023)
	50	3.1851 (2.2039)	3.2929 (2.6541)	5.0259 (3.1212)	5.7034 (3.4369)
	100	2.2802 (1.2304)	1.8941 (1.3242)	2.8072 (1.4701)	3.3802 (2.0909)
	250	1.7360 (0.7059)	1.0332 (0.6626)	1.3826 (0.6745)	1.0374 (0.7745)
	500	1.5323 (0.5410)	0.6010 (0.6010)	0.8543 (0.3585)	0.6245 (0.4315)
C	10	10.1931 (7.5874)	11.2862 (7.3767)	20.3614 (10.5060)	23.3991 (20.7747)
	25	5.3461 (3.8926)	5.3975 (3.5143)	8.1700 (4.1344)	10.5258 (8.6422)
	50	4.1610 (2.9936)	4.0950 (2.6204)	4.8990 (3.1218)	5.0903 (4.2856)
	100	2.9958 (2.0992)	2.1094 (1.7659)	2.8961 (2.6908)	3.0479 (2.1213)
	250	2.6143 (1.7647)	1.5706 (1.2562)	2.0777 (2.4729)	0.8465 (0.5463)
	500	2.3825 (1.4641)	1.0457 (1.1703)	1.6664 (2.4254)	0.4847 (0.2213)
D	10	4.8289 (2.9155)	4.9263 (2.9017)	27.3001 (10.7675)	10.7178 (20.0109)
	25	2.3274 (1.5628)	2.5004 (1.5756)	9.4341 (3.6559)	9.8068 (9.6282)
	50	1.6284 (1.0325)	1.8046 (1.2067)	4.8759 (1.9313)	2.1646 (1.8732)
	100	0.9935 (0.4916)	1.0355 (0.6685)	2.4179 (0.9076)	1.1866 (0.7682)
	250	0.5522 (0.5522)	0.5493 (0.3678)	0.9362 (0.4277)	0.4444 (0.3726)
	500	0.4297 (0.2286)	0.3738 (0.2110)	0.5068 (0.1881)	0.3746 (0.2075)

Now, we apply these four underdispersed count kernels for smoothing the real count dataset on development days of insect pests on Hura trees with moderate sample size $n=51$; see also [8]. Practical performances are here examined via the empirical $ISE$ method (7) and the empirical criterion of $ISE$:

$$h_{is{e}_0}=arg\underset{h\in (0,1)}{min}\left[\sum _{x\in \mathbb{T}}{\left\{{\widehat{f}}_n\left(x\right)-f_0\left(x\right)\right\}}^2\right]\mathrm{and}{\widehat{ISE}}_0:=\sum _{x\in \mathbb{T}\subseteq \mathbb{N}}{\left\{{\widehat{f}}_n\left(x\right)-f_0\left(x\right)\right\}}^2,$$

where $f_0(·)$ is the empirical or naive estimator. The double Poisson and the CoM-Poisson kernels are comparable and appear to be the best with $h_{is{e}_0}^{DP}=0.001$, ${\widehat{ISE}}_0^{DP}=0.00031657$ and $h_{is{e}_0}^{CMP}=0.006$, ${\widehat{ISE}}_0^{CMP}=0.00034531$ followed by the binomial smoother with $h_{is{e}_0}^B=0.001$ and ${\widehat{ISE}}_0^B=0.01232621$ and finally the gamma-count smoother with $h_{is{e}_0}^{GC}=0.012$ and ${\widehat{ISE}}_0^{GC}=0.01287723$.

Figure 6 offers their graphical representations. We also evaluate the practical upper tail probability $\mathbb{P}(X\ge 32)$ suitable for applied statisticians. Then, these tail probabilities are estimated to be $0.1569$, $0.1949$, $0.1568$, $0.1510$ and $0.1572$ for the empirical frequency $f_0$, gamma-count, double Poisson, binomial and CoM-Poisson kernel estimations, respectively. Although the double Poisson and the CoM-Poisson have similar performances, we recommend, again, the first one, which is more flexible and much faster; see Table 1.

Figure 6. Empirical frequency with its corresponding gamma-count (GC), double Poisson (DP), binomial (B) and CoM-Poisson (CMP) kernel estimates of count dataset of insect pests on Hura trees with $n=51$.

5. Summary and Final Remarks

We introduced two novel underdispersed count kernels, specifically the double Poisson and gamma-count ones. They were developed using the proposed mean dispersion method. Also, we considered the integrated squared error method (7) to select as quickly and efficiently as possible the bandwidth of their corresponding estimations. Through simulation experiments and real count data analysis, we demonstrated that these kernels perform better than the binomial kernel, while falling between the CoM-Poisson kernel smoothing (which performs the best) and the binomial kernel (which performs the worst). Although the CoM-Poisson and double Poisson kernels have similar performances, we strongly recommend using the latter due to its significantly lower time consumption and its flexibility from some closed-form expressions.

We note that any underdispersed count distribution cannot always lead to its corresponding associated kernel; see Appendix A and also [23,24]. It would also be better to improve the bandwidth selection with data-driven methods; Appendix B mentions the direction for the local Bayesian bandwidth selection. In addition, an important fact for smoothing a pmf on $\mathbb{T}=\{k,k+1,\dots \}$ with $k\ge 1$ is to consider, for instance, the k-shifted version of any underdispersed count kernel. In fact, the two main properties of the associated kernel, as recalled in Definition 1, are first to adapt the support $\mathbb{S}$ of the kernel to $\mathbb{T}$ and second to maintain the variance property which tends to $\delta \in [0,1)$ as $h\to 0$.