Abstract
The two-parameter normal-ogive (2PNO) model is one of the most popular item response theory (IRT) models for analyzing dichotomous items. Consistent parameter estimation of the 2PNO model using marginal maximum likelihood estimation relies on the local independence assumption. However, the assumption of local independence might be violated in practice. Likelihood-based estimation of the local dependence structure is often computationally demanding. Moreover, many IRT models that model local dependence do not have a marginal interpretation of item parameters. In this article, limited information estimation methods are reviewed that allow the convenient and straightforward handling of local dependence in estimating the 2PNO model. In detail, pairwise likelihood, weighted least squares, and normal-ogive harmonic analysis robust method (NOHARM) estimation are compared with marginal maximum likelihood estimation that ignores local dependence. A simulation study revealed that item parameters can be consistently estimated with limited information methods. At the same time, marginal maximum likelihood estimation resulted in biased item parameter estimates in the presence of local dependence. From a practical perspective, there were only minor differences regarding the statistical quality of item parameter estimates of the different estimation methods. Differences between the estimation methods are also compared for two empirical datasets.
1. Introduction
Item response theory (IRT) models [1,2,3] are statistical models for analyzing a vector of binary (i.e., dichotomous) random variables. IRT models represent a high-dimensional contingency table by a low-dimensional latent factor variable (also referred to as a trait or ability variable).
Let be the vector of I dichotomous items . A unidimensional IRT model [3,4] is a statistical model for the probability distribution for the vector of item responses , where
and are item parameters of item . The latent variable with density f in (1) summarizes the vector of item responses. Frequently, the density f is fixed and does not depend on the model parameters to be estimated. For convenience, f is often chosen as the standard normal density . The IRT model is most frequently estimated with marginal maximum likelihood (MML) estimation, in which the latent variable is integrated out [4,5].
The item response functions (IRFs)
in (1) describe the relationship of the dichotomous item with . Let be the model parameter of interest. The two-parameter logistic (2PL) model [6] (also referred to as the two-parameter logit model) uses the IRF
where denotes the logistic distribution function and . The item parameter is often called item discrimination, while is denoted as the item intercept. As an alternative IRT model, the IRF of the two-parameter normal-ogive (2PNO) model [7] (also referred to as the two-parameter probit model) is defined as
where denotes the standard normal distribution function and . There is a close correspondence between the 2PL and the 2PNO model (see [8,9,10,11]) because it holds that
Hence, item parameters from the 2PL model can be converted to item parameters of the 2PNO model and the other way around if one defines
The dimensional reduction of to in the IRT model (1) is accomplished by the property of local independence [3], which means that item responses are independent conditionally on the latent variable . In the IRT model, it is assumed that
In empirical datasets containing item responses, the local independence assumption could be violated. In this case, there could exist items and such that
For example, in a reading comprehension test, students are asked to respond to items that refer to several reading texts. However, items that refer to the same reading text are likely more dependent on each other than items from different reading texts. Hence, the local dependence (i.e., deviation from local independence) of item responses of items within the same reading text can be expected. The item groups that are prone to local dependence are also referred to as testlets [12]. However, local independence holds for item responses to different testlets (i.e., reading texts).
It has been shown that item discriminations are distorted and positively biased in the case of local dependence [13]. Moreover, the neglected local dependence entails inflated reliability estimates [14,15]. Hence, parameter estimation methods must be adapted to allow consistent parameter estimates for of the IRFs.
The literature mainly treats local dependence by means of three alternative strategies. First, in testlet IRT models, additional latent variables are included to model the testlet structure [12,16]. Second, the dependency structure is covered by additional parameters within a testlet [17,18,19,20,21]. In this approach, a polytomous superitem is defined as one that decodes the combination of values of items within a testlet in their categories [22]. For example, if a testlet consists of three items, the superitem possesses categories. The first and the second approaches have the disadvantage that item parameters do not have a marginal interpretation [14,23]. The third approach employs a marginal unidimensional IRT model and models the local dependence structure employing copula models [14,24,25,26,27]. This approach allows a marginal interpretation of item parameters. However, copula models require the specification of the type of copula distribution of the testlets and estimate testlet residual dependence parameters along with item parameters .
In this article, we are interested in estimating item parameters and of the 2PNO model that possess a marginal interpretation but avoid simultaneously estimating local dependence parameters . The 2PNO model can be equivalently formulated using underlying continuous latent variables for dichotomous items . Let the dichotomous variable be defined due to the dichotomization of
where denotes the indicator function. The Gaussian copula 2PNO model with local dependence [14,25,28] relies on a vector of correlated item residuals . Item residuals and the factor variable are uncorrelated. Moreover, each of the components is standard normally distributed. The correlation matrix models deviations from local independence. Define
Due to the definition (9), we obtain
which is the IRF of the 2PNO model. Hence, local dependence can be induced by assuming a non-diagonal correlation matrix . Nevertheless, item parameters and retain their marginal interpretation irrespective of an assumed local dependence structure.
Purpose
This article compares different limited information estimation methods of the 2PNO model with correlated item residuals (i.e., the 2PNO normal copula model). The limited information estimation methods can handle local dependence but do not require the specification and estimation of parameters that refer to deviations from local independence. Previous research considered item response datasets under local independence. It indicated that the different limited information methods provided similar estimates and resulted in only minor efficiency loss compared to full information methods. This research investigates whether the findings also translate to item response data with local dependence. To our knowledge, no simulation studies have previously addressed this topic.
The rest of the article is structured as follows. Section 2 discusses the application of limited information methods to handle local dependence. Section 3 presents findings from a simulation study that compares different limited information methods with MML estimation that ignores local dependence. Differences in estimation methods are illustrated through two empirical datasets in Section 4. Section 5 discusses the main findings of our study. Finally, the paper closes with conclusions in Section 6.
2. Limited Information Methods for Local Dependence
In this section, we describe three limited information methods capable of handling local dependence in item responses.
2.1. Pairwise Maximum Likelihood Estimation (PML)
Pairwise (maximum) likelihood (PML; [29,30,31,32,33]) estimation models first-order or second-order probabilities of items. Hence, in contrast to MML, the dependence among items is only modeled up to probabilities of item responses if they are item pairs. The marginal univariate probabilities are given by
where denotes the density of the standard normal distribution. PML estimation also relies on the evaluation of bivariate probabilities for an item pair
In PML estimation, item parameters are computed by maximizing a weighted sum of likelihood contributions of univariate and bivariate probabilities. In more detail, the optimization function utilized in PML is given by
where denotes the univariate frequency that item takes the value . Furthermore, denotes the bivariate frequency in the sample that item has the value and item has the value . The weights and can be specifically chosen [34]. For example, the choices and ensure that the univariate and bivariate frequencies equally contribute to the optimization function l defined in (14).
PML is particularly useful in avoiding computationally demanding multidimensional integration in multidimensional IRT models or models involving longitudinal data [35,36,37,38]. In these situations, high-dimensional integrals of latent variables in MML are reduced to lower-dimensional integrals in PML estimation.
PML can also be used to estimate IRT models with locally dependent items. In this case, item pairs that are locally dependent have an inflated associated and will bias estimated item discriminations and item intercepts in the 2PNO model. However, these item pairs can be essentially removed from the PML estimation by setting the corresponding weights to zero. This technique has proven successful in estimating the 2PL model [39].
2.2. Weighted Least Squares Estimation (DWLS and ULS)
As an alternative to MML and PML estimation, weighted least squares (WLS) estimation for factor analysis of dichotomous and polytomous item responses have been proposed [40,41,42,43,44]. WLS is a two-step (or three-step) procedure that estimates thresholds and tetrachoric correlations in the first step and computes item parameters in the second step.
Assume that dichotomous items have an underlying normally distributed latent variable defined in the 2PNO model by
where is the item residual, and denotes the normal distribution with mean and variance . The proportion correct of item can be computed as
where is the item threshold. The threshold can be estimated by , where is the proportion correct of item in the sample.
The correlation between the underlying latent variables and (i.e., the tetrachoric correlation) can be determined from the 2PNO model as
The tetrachoric correlation can be estimated with maximum likelihood [43] with fixed item thresholds and . The involved probabilities of item pair in the estimation are given by
where denotes the distribution function of the bivariate standard normal distribution with correlation . Note that and are underlying normally distributed standardized latent variables. More generally, it holds that
The optimization function G in diagonally weighted least squares (DWLS; [30]) relies on estimated tetrachoric correlations and is defined as
The weights are chosen as the inverse of the variances of estimated tetrachoric correlations and must be estimated in the first step (see [41]). If the test contains locally dependent items, the corresponding item pair receives a weight of zero (i.e., ) in the DWLS estimation.
Unweighted least squares (ULS; [45]) estimation is obtained by choosing all weights equal to one. Again, weights of item pairs that are locally dependent can be set to zero.
The minimizer of G defined in (20) provides an estimate of item discriminations. Item intercepts are subsequently estimated by
The IRT approach and the underlying latent variable approach to dichotomous items have been shown to be (essentially) equivalent [46,47,48]. DWLS and ULS estimation showed only a minor efficiency loss compared to MML estimation for dichotomous and polytomous item responses [49,50]. The advantage of WLS estimation is that multidimensionality in latent variables does not pose an issue in the estimation because no multidimensional integrals appear in the estimation function. However, WLS estimation requires the estimation of tetrachoric correlations, which can also be computationally demanding for a large number of items.
2.3. NOHARM Estimation
As an alternative to MML, PML, and WLS estimation, McDonald [51,52,53] proposed an alternative estimation method that relies on approximating the normal-ogive IRF in the 2PNO model by a series of orthogonal Hermite polynomials of order three. This estimation method is referred to as the normal-ogive harmonic analysis robust method (NOHARM) method (see [54,55,56] for overviews). As for WLS estimation, the estimation of item intercepts is separated from the estimation of item discriminations .
Let the item threshold be defined as
Like in WLS estimation, the threshold can be estimated on the sample proportion correct:
The NOHARM estimation method starts with determining the coefficients of the Hermite series for item :
Due to the orthogonality of the Hermite polynomials, the pairwise probabilities passing items and can be approximated by
Using (28), estimates of the item discriminations can be obtained by minimizing
The item intercepts can be obtained in the same way as in (21). The originally proposed NOHARM procedure fixes all weights in (28) equally to one. In the case of the local dependence of item pairs , the corresponding weights can be set to zero. In this article, we also investigate a weighted NOHARM (WNOHARM) estimation method in which we define the weights as the variance of the estimated proportions (i.e., ). To our knowledge, the WNOHARM method has not been investigated previously in the literature. In the literature, it has been demonstrated that NOHARM produces similar results to MML, DWLS, and ULS estimation [57,58,59,60,61].
3. Simulation Study
3.1. Methodology
In this simulation study, item responses under local dependence are simulated according to the 2PNO model with a normal copula model for item residuals [25]. The factor variable is assumed to be standard normally distributed. Two test lengths for the 2PNO model with local dependence are simulated: and items. The item discriminations in the case of items are 1.0, 0.9, 0.8, 0.6, 0.6, 1.1, 0.9, 1.0, 0.8, and 0.7. The item intercepts are chosen as −0.9, −0.7, 1.3, −1.9, −1.0, −1.3, −0.2, −1.3, −0.1, and 0.2. The 10 items are arranged into three testlets containing three items each and a single item. The item residuals are standard normally distributed with a correlation matrix
The local dependence parameter is chosen as 0, 0.4, and 0.8, indicating local independence, moderate local dependence, and strong local dependence, respectively. In the case of items, the item parameters from the case of 10 items are duplicated.
The sample sizes , 1000, and 2000 are employed in this simulation. In smaller sample sizes, estimation issues of the 2PNO model can be expected.
Each simulated dataset is analyzed with the 2PNO model assuming a standard normal distribution for the factor variable . Six different estimation methods are investigated. First, MML estimation ignores the local dependence. Next to MML, five different limited information estimation methods (PML, DWLS, ULS, WNOHARM, NOHARM) are specified that take the local dependence structure into account. In all the approaches, the weights referring to item pairs are set to zero if there is local dependence between and .
In total, 1500 replications in each of the 2 (number of items I) × 3 (extent of local dependence ) × 3 (sample size N) = 18 cells of the simulation study are conducted. We compute the empirical bias and the empirical root mean square error (RMSE) for all estimated item discriminations and item intercepts . For each item parameter, the RMSE of an estimation method is divided by the RMSE of the PML estimation method and multiplied by 100. By doing so, the estimation methods are compared relative to the performance of PML estimation. To summarize the simulation results, we compute the average absolute bias and the average relative RMSE across all item discriminations and item intercepts, respectively.
All estimation methods and the analysis of the findings of this simulation study have been carried out using the statistical software R [62]. MML and PML estimation is specified using the R function sirt::xxirt() in the R package sirt [63]. DWLS and ULS estimation is conducted with the probit_wls() function that can be found at https://osf.io/wxbfn accessed on 27 April 2024. The required tetrachoric correlations and their variances are estimated with the R package lavaan [64]. The WNOHARM and NOHARM estimation methods are specified in the R function sirt::noharm.sirt() in the R package sirt [63]. The functions sirt::xxirt(), probit_wls(), and sirt::noharm.sirt() utilize the R-internal optimizers stats::optim() or stats::nlminb(). Replication material for the simulation study can be found at https://osf.io/wxbfn accessed on 27 April 2024.
3.2. Results
Table 1 reports the average absolute bias and the average relative RMSE for estimated item discriminations and item intercepts in the 2PNO model as a function of the number of items I, the extent of local dependence , and the sample size N.

Table 1.
Simulation Study: Average absolute bias and average relative root mean square error (RMSE) for estimated item discriminations and item intercepts in the two-parameter normal-ogive (2PNO) model as a function of the number of items I, the extent of local dependence , and sample size N.
All six estimation methods are unbiased in large samples if local independence holds (i.e., ). Notably, small biases occur for the sample size . The average relative RMSE indicates an efficiency loss when using PML estimation and omitting some item pairs from estimation compared to MML under local independence. However, the efficiency loss is decreased with a larger number of items.
In the case of local dependence (i.e., and ), MML produces strongly biased results. The biases for MML are larger for item discriminations than for item intercepts. Note that the bias in MML estimation is reduced with an increasing number of items. Across all conditions, PML and DWLS perform similarly regarding the mean (denoted by M) RMSE and slightly outperform ULS, WNOHARM, and NOHARM estimation for item discriminations (PML: M = 100, DWLS: M = 100.5, ULS: M = 103.2, WNOHARM: M = 103.2, NOHARM: M = 103.2). Overall, WNOHARM resulted in similar estimates to NOHARM. However, there are slight advantages of WNOHARM compared to NOHARM only for strong local dependence in the case of . For item intercepts , PML and DWLS have smaller advantages over ULS, WNOHARM, and NOHARM (PML: M = 100, DWLS: M = 100.3, ULS: M = 101.1, WNOHARM: M = 101.6, NOHARM: M = 101.5).
To sum up, all limited information methods could handle locally dependent item responses and result in approximately unbiased item parameter estimates. In applied research, the differences between the estimation methods can be considered negligible.
4. Empirical Examples
In this section, two datasets with item responses with a testlet structure from the R package sirt [63] are analyzed with the 2PNO model. The same estimation methods (i.e., MML, PML, DWLS, ULS, WNOHARM, and NOHARM) as in the simulation study (see Section 4) are utilized. Item pairs that refer to the same testlet receive a zero weight in the limited information estimation methods. We compute the average absolute deviation of estimated item parameters between the estimation methods as a measure of the discrepancy between the methods.
4.1. Dataset data.read
The first dataset data.read contains item responses of subjects on items from a reading comprehension test administered to Austrian students. The twelve items are arranged into three testlets, each testlet containing four items. Table 2 displays estimated item discriminations and item intercepts in the 2PNO model.

Table 2.
Dataset data.read: Estimated item discriminations and item intercepts in the two-parameter normal-ogive (2PNO) model for different estimation methods.
MML substantially differs in the item discriminations from all limited information methods regarding the average absolute deviations (PML: 0.20, DWLS: 0.23, ULS: 0.25, WNOHARM: 0.22, NOHARM: 0.23). The average absolute deviations between the limited information methods are much smaller and range between 0.01 (WNOHARM and NOHARM) and 0.07 (ULS and NOHARM).
We also observe non-negligible differences for item intercepts of MML with the five specified limited information methods (PML: 0.13, DWLS: 0.14, ULS: 0.15, WNOHARM: 0.14, NOHARM: 0.14). The differences in item intercepts between the limited information methods are small, with the largest average absolute deviation of 0.03 between ULS and NOHARM estimation.
Figure 1 presents pairwise scatter plots and correlations of estimated item discriminations for the dataset data.read. The correlation of the MML estimates with the other estimation methods are almost zero. Obviously, one outlying observation (i.e., Item C1 with ) impacts the correlations of the MML estimates with other methods. Moreover, WNOHARM and NOHARM are correlated at 1.00, while the correlation of ULS and NOHARM is relatively small at 0.86, which indicates non-negligible differences in the estimates.
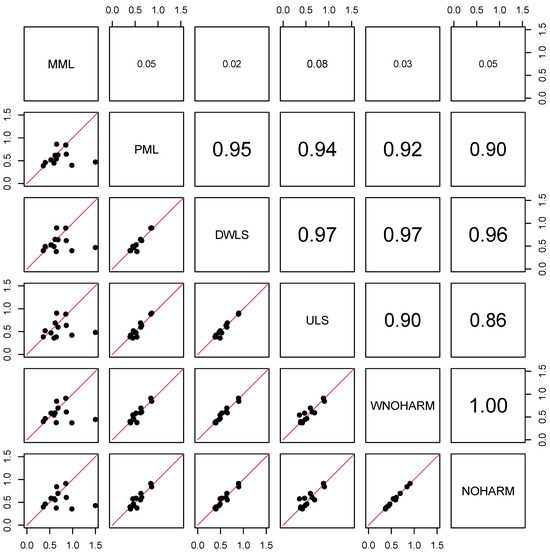
Figure 1.
Dataset data.read: Pairwise scatter plots and correlations of estimated item discriminations for between different estimation methods.
Figure 2 shows pairwise scatter plots and correlations of estimated item intercepts . The correlations of the MML estimates for with the other estimation methods are far from perfect at 0.95. However, the estimates of the alternative estimation methods correlate at 1.00, indicating almost identical estimates.
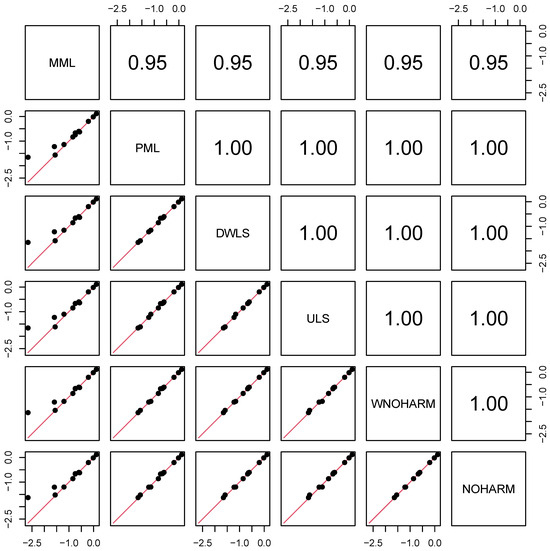
Figure 2.
Dataset data.read: Pairwise scatter plots and correlations of estimated item intercepts for between different estimation methods.
4.2. Dataset data.pisaMath
The second dataset data.pisaMath contains item responses of Austrian students on mathematics items as a subset of students and items from a PISA study [65,66]. The eleven items are arranged into four testlets with two items each. Moreover, the dataset has three single items without a testlet structure.
Table 3 displays estimated item discriminations and item intercepts of the 2PNO model for this dataset. Substantial deviations for item parameters between MML estimation and the limited information estimation methods are observed for items in the testlets M406 and M496. The average absolute deviation of estimated item discriminations of MML estimation with the five limited information methods is always 0.07. However, there are no substantial differences in item discriminations between the limited information methods, and they differ, on average, by no more than 0.01. For item intercepts , the average absolute differences between MML and all limited information methods are smaller and at 0.02. Furthermore, there are no notable differences among the limited information estimation methods, with a maximum absolute difference of 0.002.

Table 3.
Dataset data.pisaMath: Estimated item discriminations and item intercepts in the two-parameter normal-ogive (2PNO) model for different estimation methods.
5. Discussion
5.1. Merits
In this article, we compared MML estimation with limited information estimation methods in the 2PNO model with locally dependent items. It turned out that limited information methods PML, DWLS, ULS, WNOHARM, and NOHARM were effective in handling local dependence and produced approximately unbiased item parameters in the 2PNO model. The employed limited information methods operate on statistical information (i.e., bivariate frequencies) of item pairs. This property allows the exclusion of item pairs prone to local dependence from estimation. By doing so, item parameters from the 2PNO model can be marginally interpreted. Overall, there were only minor differences in the quality of parameter estimates between the different limited information methods. From the perspective of an applied researcher, the different estimation methods can be considered exchangeable, and the availability of software can determine the choice of a particular estimation method. Notably, MML estimation that ignores local dependence will typically provide biased item parameter estimates.
5.2. Limitations
As with any simulation study, our study had several limitations. First, we did not simulate item responses with larger item discriminations. It could be that the performance of the limited information methods more substantially differs with more extreme item parameters. Second, we did not investigate smaller sample sizes such as . In this case, it is more crucial how to handle estimation issues. Third, we did not treat polytomous data. However, the NOHARM procedure must be adapted from dichotomous to polytomous item responses [56]. Fourth, our analyses were restricted to unidimensional IRT models with local dependence. In a similar vein, multidimensional IRT models with locally dependent items can also be handled and investigated in future research. Fifth, the item discriminations used in the simulation study had moderate deviations. We carried out preliminary additional simulation studies in which there was more variation in item discriminations. It turned out that NOHARM (and WNOHARM) estimates performed worse than PML or DWLS (and ULS) in these situations. Sixth, we only considered a normally distributed variable and the probit link function in the 2PNO model. PML estimation has the advantage that it can be generalized to other link functions (such as in the 2PL model) or non-normal distributions [39]. However, DWLS/ULS and NOHARM rely on the probit link function and the normal distribution and cannot be generalized straightforwardly.
5.3. Meaning of Local Dependence
We would like to emphasize that any empirical dataset will necessarily have some deviations from local independence [67]. If a unidimensional IRT model is fitted to a dataset of item responses, positive and negative local dependencies will average out in some way. It is up to the researcher to define whether positive local dependence should only exist. Such a decision would imply that positive local dependence is treated as a nuisance that should be removed from model estimation. However, there might be situations in which local dependence is an in-built feature of a test, and it is not advised to control for such factors in statistical analysis [68].
6. Conclusions
Our study demonstrated that ignoring local dependence in the estimation of the 2PNO model results in biased item parameters, particularly in biases for item discriminations. We have shown in a simulation study and empirical examples that limited information methods can easily be adapted to item responses containing local dependence by only including item pairs in the estimation that are not prone to local dependence. Utilizing this modification in the estimation methods results in unbiased item parameter estimation under local dependence. Importantly, there is no need to model the local dependence structure in the modified limited information estimation methods. In this respect, limited information methods are more robust than the full information maximum likelihood estimation method, which requires a correctly specified distribution to model local dependence.
Author Contributions
Conceptualization, A.R.; methodology, A.R.; software, A.R.; validation, A.R.; formal analysis, A.R.; investigation, A.R.; resources, A.R.; data curation, A.R.; writing—original draft preparation, A.R.; writing—review and editing, A.R.; visualization, A.R.; supervision, A.R.; project administration, A.R.; funding acquisition, A.R. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The empirical datasets used in Section 4 can be extracted from the R package sirt (https://cran.r-project.org/web/packages/sirt; accessed on 27 April 2024).
Conflicts of Interest
The author declares no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| 2PL | two-parameter logistic |
| 2PNO | two-parameter normal-ogive |
| DWLS | diagonally weighted least squares |
| IRF | item response function |
| IRT | item response theory |
| MML | marginal maximum likelihood |
| NOHARM | normal-ogive harmonic analysis robust method |
| PML | pairwise maximum likelihood |
| ULS | unweighted least squares |
| WLS | weighted least squares |
| WNOHARM | weighted normal-ogive harmonic analysis robust method |
References
- Chen, Y.; Li, X.; Liu, J.; Ying, Z. Item Response Theory—A Statistical Framework for Educational and Psychological Measurement. 2023. Epub Ahead of Print. Available online: https://imstat.org/journals-and-publications/statistical-science/statistical-science-future-papers/ (accessed on 27 April 2024).
- van der Linden, W.J. Unidimensional logistic response models. In Handbook of Item Response Theory, Volume 1: Models; van der Linden, W.J., Ed.; CRC Press: Boca Raton, FL, USA, 2016; pp. 11–30. [Google Scholar]
- Yen, W.M.; Fitzpatrick, A.R. Item response theory. In Educational Measurement; Brennan, R.L., Ed.; Praeger Publishers: Westport, CT, USA, 2006; pp. 111–154. [Google Scholar]
- Bock, R.D.; Moustaki, I. Item response theory in a general framework. In Handbook of Statistics, Vol. 26: Psychometrics; Rao, C.R., Sinharay, S., Eds.; Elsevier: Amsterdam, The Netherlands, 2007; pp. 469–513. [Google Scholar] [CrossRef]
- Bock, R.D.; Aitkin, M. Marginal maximum likelihood estimation of item parameters: Application of an EM algorithm. Psychometrika 1981, 46, 443–459. [Google Scholar] [CrossRef]
- Birnbaum, A. Some latent trait models and their use in inferring an examinee’s ability. In Statistical Theories of Mental Test Scores; Lord, F.M., Novick, M.R., Eds.; MIT Press: Reading, MA, USA, 1968; pp. 397–479. [Google Scholar]
- Lord, F.M.; Novick, R. Statistical Theories of Mental Test Scores; Addison-Wesley: Reading, MA, USA, 1968. [Google Scholar]
- Camilli, G. Origin of the scaling constant d = 1.7 in item response theory. J. Educ. Behav. Stat. 1994, 19, 293–295. [Google Scholar] [CrossRef]
- Savalei, V. Logistic approximation to the normal: The KL rationale. Psychometrika 2006, 71, 763–767. [Google Scholar] [CrossRef]
- Camilli, G. The scaling constant D in item response theory. Open J. Stat. 2017, 7, 780–785. [Google Scholar] [CrossRef][Green Version]
- Cho, E. Interchangeability between factor analysis, logistic IRT, and normal ogive IRT. Front. Psychol. 2023, 14, 1267219. [Google Scholar] [CrossRef] [PubMed]
- Bradlow, E.T.; Wainer, H.; Wang, X. A Bayesian random effects model for testlets. Psychometrika 1999, 64, 153–168. [Google Scholar] [CrossRef]
- Tuerlinckx, F.; De Boeck, P. Non-modeled item interactions lead to distorted discrimination parameters: A case study. Methods Psychol. Res. 2001, 6, 2. Available online: http://tinyurl.com/mrydstwz (accessed on 27 April 2024).
- Braeken, J.; Tuerlinckx, F.; De Boeck, P. Copula functions for residual dependency. Psychometrika 2007, 72, 393–411. [Google Scholar] [CrossRef]
- Ip, E.H. Testing for local dependency in dichotomous and polytomous item response models. Psychometrika 2001, 66, 109–132. [Google Scholar] [CrossRef]
- Wang, W.C.; Wilson, M. The Rasch testlet model. Appl. Psychol. Meas. 2005, 29, 126–149. [Google Scholar] [CrossRef]
- Hoskens, M.; De Boeck, P. A parametric model for local dependence among test items. Psychol. Methods 1997, 2, 261–277. [Google Scholar] [CrossRef]
- Marais, I.; Andrich, D. Effects of varying magnitude and patterns of response dependence. J. Appl. Meas. 2008, 9, 105–124. Available online: http://tinyurl.com/yc7mhmkw (accessed on 27 April 2024). [PubMed]
- Noventa, S.; Spoto, A.; Heller, J.; Kelava, A. On a generalization of local independence in item response theory based on knowledge space theory. Psychometrika 2019, 84, 395–421. [Google Scholar] [CrossRef] [PubMed]
- Ye, S.; Kelava, A.; Noventa, S. Parameter estimation of KST-IRT model under local dependence. Psych 2023, 5, 908–927. [Google Scholar] [CrossRef]
- Wilson, M.; Adams, R.J. Rasch models for item bundles. Psychometrika 1995, 60, 181–198. [Google Scholar] [CrossRef]
- Eckes, T. Item banking for C-tests: A polytomous Rasch modeling approach. Psychol. Test Assess. Model. 2011, 53, 414–439. Available online: http://tinyurl.com/bap2z4nh (accessed on 27 April 2024).
- Ip, E.H. Empirically indistinguishable multidimensional IRT and locally dependent unidimensional item response models. Br. J. Math. Stat. Psychol. 2010, 63, 395–416. [Google Scholar] [CrossRef] [PubMed]
- Braeken, J. A boundary mixture approach to violations of conditional independence. Psychometrika 2011, 76, 57–76. [Google Scholar] [CrossRef]
- Braeken, J.; Kuppens, P.; De Boeck, P.; Tuerlinckx, F. Contextualized personality questionnaires: A case for copulas in structural equation models for categorical data. Multivar. Behav. Res. 2013, 48, 845–870. [Google Scholar] [CrossRef]
- Joe, H. Dependence Modeling with Copulas; CRC Press: Boca Raton, FL, USA, 2014. [Google Scholar]
- Schroeders, U.; Robitzsch, A.; Schipolowski, S. A comparison of different psychometric approaches to modeling testlet structures: An example with C-tests. J. Educ. Meas. 2014, 51, 400–418. [Google Scholar] [CrossRef]
- Nikoloulopoulos, A.K.; Joe, H. Factor copula models for item response data. Psychometrika 2015, 80, 126–150. [Google Scholar] [CrossRef]
- Bellio, R.; Varin, C. A pairwise likelihood approach to generalized linear models with crossed random effects. Stat. Model. 2005, 5, 217–227. [Google Scholar] [CrossRef]
- Chen, Y.; Moustaki, I.; Zhang, S. On the estimation of structural equation models with latent variables. In Handbook of Structural Equation Modeling; Hoyle, R.H., Ed.; Guilford Press: New York, NY, USA, 2023; pp. 145–162. [Google Scholar]
- Katsikatsou, M.; Moustaki, I.; Yang-Wallentin, F.; Jöreskog, K.G. Pairwise likelihood estimation for factor analysis models with ordinal data. Comput. Stat. Data Anal. 2012, 56, 4243–4258. [Google Scholar] [CrossRef]
- Renard, D.; Molenberghs, G.; Geys, H. A pairwise likelihood approach to estimation in multilevel probit models. Comput. Stat. Data Anal. 2004, 44, 649–667. [Google Scholar] [CrossRef]
- Varin, C.; Reid, N.; Firth, D. An overview of composite likelihood methods. Stat. Sin. 2011, 21, 5–42. Available online: https://bit.ly/38lbhom (accessed on 27 April 2024).
- Vasdekis, V.G.S.; Rizopoulos, D.; Moustaki, I. Weighted pairwise likelihood estimation for a general class of random effects models. Biostatistics 2014, 15, 677–689. [Google Scholar] [CrossRef]
- Fieuws, S.; Verbeke, G. Pairwise fitting of mixed models for the joint modeling of multivariate longitudinal profiles. Biometrics 2006, 62, 424–431. [Google Scholar] [CrossRef] [PubMed]
- Fieuws, S.; Verbeke, G.; Boen, F.; Delecluse, C. High dimensional multivariate mixed models for binary questionnaire data. J. R. Stat. Soc. Ser. Appl. Stat. 2006, 55, 449–460. [Google Scholar] [CrossRef]
- Mauff, K.; Erler, N.S.; Kardys, I.; Rizopoulos, D. Pairwise estimation of multivariate longitudinal outcomes in a Bayesian setting with extensions to the joint model. Modelling 2021, 21, 115–136. [Google Scholar] [CrossRef]
- Fu, Z.H.; Tao, J.; Shi, N.Z.; Zhang, M.; Lin, N. Analyzing longitudinal item response data via the pairwise fitting method. Multivar. Behav. Res. 2011, 46, 669–690. [Google Scholar] [CrossRef]
- Robitzsch, A. Pairwise likelihood estimation of the 2PL model with locally dependent item responses. Appl. Sci. 2024, 14, 2652. [Google Scholar] [CrossRef]
- Christoffersson, A. Factor analysis of dichotomized variables. Psychometrika 1975, 40, 5–32. [Google Scholar] [CrossRef]
- Christoffersson, A. Two-step weighted least squares factor analysis of dichotomized variables. Psychometrika 1977, 42, 433–438. [Google Scholar] [CrossRef]
- Muthén, B. Contributions to factor analysis of dichotomous variables. Psychometrika 1978, 43, 551–560. [Google Scholar] [CrossRef]
- Muthén, B. A general structural equation model with dichotomous, ordered categorical, and continuous latent variable indicators. Psychometrika 1984, 49, 115–132. [Google Scholar] [CrossRef]
- Muthén, B.O.; Satorra, A. Technical aspects of Muthén’s LISCOMP approach to estimation of latent variable relations with a comprehensive measurement model. Psychometrika 1995, 60, 489–503. [Google Scholar] [CrossRef]
- Huang, P.H. Penalized least squares for structural equation modeling with ordinal responses. Multivar. Behav. Res. 2022, 57, 279–297. [Google Scholar] [CrossRef]
- Takane, Y.; de Leeuw, J. On the relationship between item response theory and factor analysis of discretized variables. Psychometrika 1987, 52, 393–408. [Google Scholar] [CrossRef]
- Kamata, A.; Bauer, D.J. A note on the relation between factor analytic and item response theory models. Struct. Equ. Model. Multidiscip. J. 2008, 15, 136–153. [Google Scholar] [CrossRef]
- Paek, I.; Cui, M.; Öztürk Gübeş, N.; Yang, Y. Estimation of an IRT model by Mplus for dichotomously scored responses under different estimation methods. Educ. Psychol. Meas. 2018, 78, 569–588. [Google Scholar] [CrossRef]
- Forero, C.G.; Maydeu-Olivares, A.; Gallardo-Pujol, D. Factor analysis with ordinal indicators: A Monte Carlo study comparing DWLS and ULS estimation. Struct. Equ. Model. 2009, 16, 625–641. [Google Scholar] [CrossRef]
- Kappenburg-ten Holt, J. A Comparison between Factor Analysis and Item Response Theory Modeling in Scale Analysis. Unpublished Dissertation, University of Groningen, Groningen, The Netherlands, 2014. Available online: https://tinyurl.com/52yewx34 (accessed on 27 April 2024).
- McDonald, R.P. Linear versus non-linear models in item response theory. Appl. Psychol. Meas. 1982, 6, 379–396. [Google Scholar] [CrossRef]
- McDonald, R.P. Test Theory: A Unified Treatment; Lawrence Erlbaum: Mahwah, NJ, USA, 1999. [Google Scholar] [CrossRef]
- Fraser, C.; McDonald, R.P. NOHARM: Least squares item factor analysis. Multivar. Behav. Res. 1988, 23, 267–269. [Google Scholar] [CrossRef] [PubMed]
- McDonald, R.P. Normal-ogive multidimensional model. In Handbook of Modern Item Response Theory; van der Linden, W., Hambleton, R., Eds.; Springer: New York, NY, USA, 1997; pp. 257–269. [Google Scholar] [CrossRef]
- Maydeu-Olivares, A. Multidimensional item response theory modeling of binary data: Large sample properties of NOHARM estimates. J. Educ. Behav. Stat. 2001, 26, 51–71. [Google Scholar] [CrossRef]
- Swaminathan, H.; Rogers, H.J. Normal-ogive multidimensional models. In Handbook of Item Response Theory, Volume 1: Models; van der Linden, W.J., Ed.; CRC Press: Boca Raton, FL, USA, 2016; pp. 167–187. [Google Scholar]
- Finch, H. Item parameter estimation for the MIRT model: Bias and precision of confirmatory factor analysis—Based models. Appl. Psychol. Meas. 2010, 34, 10–26. [Google Scholar] [CrossRef]
- Finch, H. Multidimensional item response theory parameter estimation with nonsimple structure items. Appl. Psychol. Meas. 2011, 35, 67–82. [Google Scholar] [CrossRef]
- Sass, D.A. Factor loading estimation error and stability using exploratory factor analysis. Educ. Psychol. Meas. 2010, 70, 557–577. [Google Scholar] [CrossRef]
- Svetina, D.; Levy, R. An overview of software for conducting dimensionality assessment in multidimensional models. Appl. Psychol. Meas. 2012, 36, 659–669. [Google Scholar] [CrossRef]
- Svetina, D.; Levy, R. Dimensionality in compensatory MIRT when complex structure exists: Evaluation of DETECT and NOHARM. J. Exp. Educ. 2016, 84, 398–420. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Core Team: Vienna, Austria, 2023; Available online: https://www.R-project.org/ (accessed on 15 March 2023).
- Robitzsch, A. sirt: Supplementary Item Response Theory Models. R Package Version 4.2-57. 2024. Available online: https://github.com/alexanderrobitzsch/sirt (accessed on 20 April 2024).
- Rosseel, Y. lavaan: An R package for structural equation modeling. J. Stat. Softw. 2012, 48, 1–36. [Google Scholar] [CrossRef]
- Lietz, P.; Cresswell, J.C.; Rust, K.F.; Adams, R.J. (Eds.) Implementation of Large-scale Education Assessments; Wiley: New York, NY, USA, 2017. [Google Scholar] [CrossRef]
- Rutkowski, L.; von Davier, M.; Rutkowski, D. (Eds.) A Handbook of International Large-scale Assessment: Background, Technical Issues, and Methods of Data Analysis; Chapman Hall; CRC Press: London, UK, 2013. [Google Scholar] [CrossRef]
- Habing, B.; Roussos, L.A. On the need for negative local item dependence. Psychometrika 2003, 68, 435–451. [Google Scholar] [CrossRef]
- Robitzsch, A.; Lüdtke, O. Some thoughts on analytical choices in the scaling model for test scores in international large-scale assessment studies. Meas. Instruments Soc. Sci. 2022, 4, 9. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).