Abstract
In the social sciences, the performance of two groups is frequently compared based on a cognitive test involving binary items. Item response models are often utilized for comparing the two groups. However, the presence of differential item functioning (DIF) can impact group comparisons. In order to avoid the biased estimation of groups, appropriate statistical methods for handling differential item functioning are required. This article compares the performance-regularized estimation and several robust linking approaches in three simulation studies that address the one-parameter logistic (1PL) and two-parameter logistic (2PL) models, respectively. It turned out that robust linking approaches are at least as effective as the regularized estimation approach in most of the conditions in the simulation studies.
1. Introduction
Item response theory (IRT) models [1,2] are an important class of multivariate statistical models for analyzing dichotomous random variables used to model testing data from social science applications. Of vital importance is the application of item response models in educational large-scale assessment (LSA; [3,4]), such as the programme for international student assessment (PISA; [5]) study.
In this article, we only investigate unidimensional IRT models. Let be the vector of I dichotomous random variables (also referred to as test items or items). A unidimensional item response model [6] is a statistical model for the probability distribution for the vector , where
where denotes the density of the normal distribution with mean and standard deviation . The vector contains the distribution parameters of the ability variable . The vector contains all estimated item parameters of item response functions .
Different IRT models emerge by choosing particular item response functions in (1). The one-parameter logistic (1PL) model (also referred to as the Rasch model; [7]) employs the item response function , where denotes the logistic distribution function, and is the item difficulty of item i (i.e., ). The two-parameter logistic (2PL) model [8] additionally includes the item discrimination (i.e., ), and the item response function is given by .
Note that distribution parameters and item parameters cannot be simultaneously identified. For example, in the 2PL model, the mean and the standard deviation must be fixed to 0 or 1, respectively, if all item discriminations and item difficulties were estimated. As an alternative, one could fix at least (or all) item parameters to predefined values to enable the estimation of distribution parameters.
In this article, we investigate the estimation of the 1PL and 2PL models in the presence of two groups. In this case, we are primarily interested in comparing the mean of the second group with the mean of the first group. In order to enable group comparisons, assumptions on item parameters must be imposed in the 1PL and 2PL models. First, one must fix to zero. Second, some assumptions on item parameters must be made to enable the identification of the distribution parameters of the second group. A typical assumption is the measurement invariance assumption [9,10], which says that item parameters do not differ across the two groups. However, in practical applications, some item parameters will almost always differ across groups. This situation is also referred to as differential item functioning (DIF; [11,12]). In this article, we assume that there could be DIF in item difficulties in the 1PL and 2PL models (i.e., uniform DIF; [12]). The classes of techniques of robust linking and regularized estimation are compared through three simulation studies regarding the performance of parameter recovery of the group comparison.
The rest of the article is structured as follows. Different statistical methods for group comparisons in the 1PL and the 2PL models in the presence of uniform DIF are discussed in Section 2. Section 3 presents results from Simulation Study 1, which investigates the group comparison in the 1PL model in the presence of DIF. Section 4 more thoroughly investigates the choice of tuning parameters for regularized estimation in a subset of conditions of Simulation Study 1 in the Focused Simulation Study 1A. Section 5 presents results from Simulation Study 2, which investigates the group comparison in the 2PL model in the presence of uniform DIF effects. Finally, the article closes with a discussion in Section 6.
2. Two-Group Comparison under Sparse DIF
We now present IRT estimation in two groups . Let of person in group . We now define the log-likelihood function for data in group g () as
where and is the 2PL model, and the vectors of item parameters are defined as and .
For reasons of identification, we fix the mean in the first group to zero and the standard deviation to 1. We assume that the 2PL (or the 1PL model as a restricted version) holds in both groups, and there is uniform DIF in item difficulties (i.e., equal item discriminations in the two groups are assumed). That is, we model the difference in item difficulties as
We assume that DIF effects are fixed (see [13] for a random DIF perspective). Throughout this paper, we impose a sparsity assumption on DIF effects . In this case, the majority of items have DIF effects of zero, while only a few DIF effects differ from zero [14,15]. The situation is known as partial invariance [16,17,18,19]. Hence, DIF effects can be regarded as outliers that might bias the estimation of group mean differences [14,20,21,22,23,24].
In the next subsections, we discuss alternative methods for two-group comparisons in the 1PL and 2PL models in the presence of uniform DIF. In Section 2.1, concurrent calibration relying on invariant item parameters is discussed. Section 2.2 investigates regularization approaches to handling DIF in two-group comparisons. Robust linking approaches are treated in Section 2.3. Finally, relationships between regularization and robust linking are highlighted in Section 2.4.
2.1. Concurrent Calibration
Concurrent calibration jointly estimates common (group-invariant) item parameters and distribution parameters in one estimation run. This property is particularly convenient for practitioners because no additional steps or postprocessing of model results is required. We now present concurrent calibration separately for the 1PL and 2PL models.
2.1.1. 1PL Model
We now estimate the distribution parameters of the second group (i.e., and ) with a concurrent calibration approach in the 1PL model. In the 1PL model, item discriminations are set to one and indicate this using the notation of a vector of ones. The distribution parameters and the vector of common item difficulties are estimated by minimizing the negative of the log-likelihood function (see (2))
Note that the minimization in (4) assumes invariant item difficulties across the two groups. In the presence of uniform DIF, the log-likelihood function in (4) is misspecified. However, under certain conditions, it is possible that group differences could nevertheless be unbiasedly estimated [25,26].
2.1.2. 2PL Model
We now weaken the assumption of equal item discriminations in the 2PL model. Common item discriminations and item difficulties are estimated by minimizing the estimation function
Like in the 1PL model, the log-likelihood function in (5) is misspecified in the presence of uniform DIF. Nevertheless, it is interesting to empirically investigate situations in which misspecified concurrent calibration can provide approximately unbiased results.
2.2. Regularization Approaches
In practical applications, all items could be prone to DIF effects. However, modeling all DIF effects without any constraints leads to an unidentified IRT model. To circumvent this issue, regularization techniques have been proposed in statistics to estimate nonidentified models under sparsity assumptions [27,28]. The main idea of using regularization techniques for multiple-group IRT estimation is that by adding an appropriate penalty term to the negative log-likelihood function, some simplified structure on DIF effects is imposed. It can be shown that under sparse DIF effects, regularized estimation provides unbiased group means [20]. Regularized estimation recently became popular in psychometrics, such as item response modeling [29,30], structural equation modeling [31,32,33], structured latent class analysis [34,35,36], and mixture models [37,38]. The investigation of regularization approaches of known demographic groups, such as gender or language groups, is an important topic in educational measurement. Moreover, regularization techniques were recently discussed for manifest DIF detection in the 1PL and 2PL models [19,20,39,40,41,42,43,44].
For a scalar parameter x, lasso penalty is a popular penalty function used in regularization [28], and it is defined as
where is a non-negative regularization parameter that controls the extent of regularization. It is known that the lasso penalty induces bias in estimated parameters. To circumvent this issue, the smoothly clipped absolute deviation (SCAD; [45]) penalty has been proposed. It is defined by
with . In many studies, the recommended value of (see [45]) has been adopted (e.g., [27,36,38,46,47,48]). However, other studies considered the simultaneous selection of both tuning parameters and a [31,49,50,51].
Figure 1 displays the SCAD penalty function for different values of a with a fixed value of 0.2. The SCAD penalty retains the penalization rate and the induced bias of the lasso for model parameters close to zero, but continuously relaxes the rate of penalization as the absolute value of the model parameters increases. Note that has the property of the lasso penalty around zero, but has zero derivatives for x values that strongly differ from zero. In contrast, the derivative of the lasso penalty is 1 or for positive and negative x values, respectively.
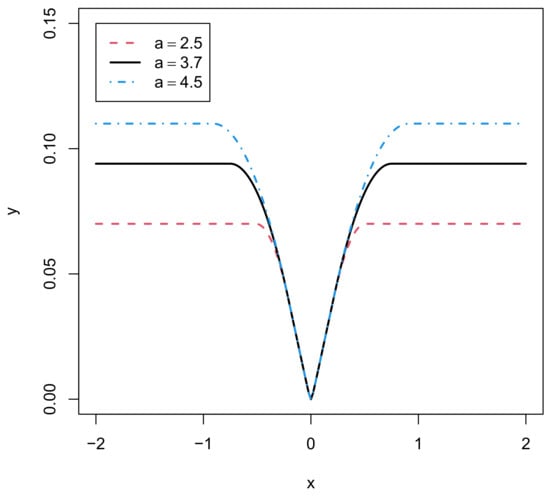
Figure 1.
SCAD penalty function for different values of a for .
We now present regularization estimation under uniform DIF for the 1PL and the 2PL model.
2.2.1. 1PL Model
In regularization, we specify an overidentified IRT model but enable the identification of distribution parameters of the second group (i.e., and ) by adding a penalty function to the negative log-likelihood function. Compared with (4), we additionally introduce the vector of DIF effects and consider the minimization problem
where includes the sample sizes in the penalty term.
In practice, the minimization of (8) for a fixed value of results in a subset of DIF effects that are different from zero, where the rest of the DIF effects has been set to zero. In essence, the group difference is only based on those items whose DIF effects are estimated equal to zero.
Typically, the regularization parameter is an unknown nuisance parameter in (8) that must also be estimated. In practice, the minimization of (8) is carried out on a discrete grid of values, and the optimal regularization parameter is selected that minimizes the Akaike information criterion (AIC) or the Bayesian information criterion (BIC).
The regularized estimation problem (8) can be minimized using marginal maximum likelihood estimation and the expectation maximization (EM) algorithm [30,36,46]. The EM algorithm alternates between the E-step and the M-step. The E-step computation is identical to the estimation in nonregularized item response models. In the M-step, the minimizing of the regularized negative log-likelihood function is carried out using expected counts that are computed in the expected log-likelihood function. The difference between regularized estimation and ordinary maximum likelihood estimation is that the optimization function becomes nondifferentiable, because the SCAD penalty is nondifferentiable. The optimization of nondifferentiable optimization can be performed using gradient descent [28] approaches or by substituting the nondifferentiable optimization functions with differentiable approximating functions [36,52,53,54]. In our experience, the latter approach performs quite satisfactorily in applications.
2.2.2. 2PL Model
We now turn to regularized estimation in the 2PL model. Like in the 1PL model, the overidentified vector of the DIF effects is introduced. In addition, the vector of common item discriminations is estimated. The following estimation function is minimized for determining group differences
In principle, regularized estimation in the 2PL model using common item discriminations is not different from regularized estimation in the 1PL model. The principle of regularization can be extended to modeling DIF effects in item discriminations by introducing additional penalty terms for these DIF effects [44].
2.3. Robust Linking Approaches
Linking methods are typically two-step methods that separately estimate IRT models, such as the 1PL or 2PL models in each of the groups, and compute group distribution parameters (i.e., group means and standard deviations) in a second step [25,55,56,57]. We replace the separate estimation with a simultaneous estimation in a two-group IRT model. We differ from this usual setup in this article for two reasons. First, we want to highlight the notational similarity to regularized estimation. Second, we also want to conduct linking in the 2PL model under the assumption of common item discriminations if there is a strong belief that most of the DIF effects can be attributed to uniform instead of nonuniform DIF effects. Robust linking as a concept refers to the property that group differences can be estimated without bias (or only with small bias) despite the presence of (uniform) DIF [25,58].
2.3.1. 1PL Model
We now present robust linking approaches in the 1PL model. In the first step, we consider the minimization problem
Note that (10) differs from regularized estimation (8) in two aspects. First, it does not involve a penalty function. Second, it does not provide an estimate of the group mean of the second group. We want to point out that the estimates from the minimization (10) are equivalent to the separate estimation of the 1PL model with item difficulties in the first group and difficulties in the second group.
Robust (and nonrobust) linking methods employ estimated DIF effects to determine a group mean estimate .
Robust Linking Using the Loss Function
The first robust linking method uses the loss function for (see [25,59,60]) and determines the group mean estimate as
Mean–mean linking (MM; [55,61]) results with . The case corresponds to median linking [20] and is expected to be more robust than . Finally, the case corresponds to the loss function used in invariance alignment [59,62,63]. In optimization, one can replace the nondifferentiable function with using a sufficiently small , such as [59].
Robust Linking Using the MAD Statistic
Researchers Matthias von Davier and Bezirhan proposed robust outlier detection of items with large DIF effects and removed them from linking [64] (see also [61,65,66]). For each item i, a z statistic is defined by
where denotes the median of the vector of estimated DIF effects, and MAD is the (scaled) median absolute deviation of the DIF effects. An item is declared an outlier (because of possessing a large DIF effect) if exceeds the cutoff of 2.7 [64]. The group mean difference is defined as
Obviously, items with large DIF effects are removed from the computation of the group mean in (13).
2.3.2. 2PL Model
Linking based on the 2PL model can be applied in two variants. The first approach relies on a first simultaneous estimation step in which common item discriminations are estimated. It is well known that the 2PL model gets unstable with small samples, which motivates the estimation of a simplified model with joint item discriminations. In the first step of the linking approach, we determine item parameters and the standard deviation in the second group by
Alternatively, separate estimation of the 2PL model in the two groups can be conducted, which results in estimated item parameters and and and , respectively.
Robust Linking Using Loss Function or MAD Statistic
Joint Haberman Linking Using Common Item Discriminations
We now show how to perform Haberman linking [67,68] if the first linking step is carried out using common item discriminations (see minimization problem (14). The more general loss function is again used for Haberman linking [60]. In this case, common item difficulties are estimated by minimizing
Haberman Linking Based on Separate Calibration
We also compare the performance of joint Haberman linking using common item discriminations with the ordinary Haberman linking that is based on separation calibration [60,68]. In the first step of Haberman linking, common logarithmized item discriminations , and the logarithmized standard deviation of the second group is determined as the minimizer of
Note that the standard deviation of the second group is given by .
In the second step of Haberman linking, the group means of the second group are estimated along with common item difficulties
2.4. On the Relation of Robust Linking and Regularized Estimation
It has been argued that robust linking yields very similar results to regularization approaches for linking two groups [20]. We now sketch a heuristic proof of why this is the case. In the regularization approach, one uses the SCAD penalty, which behaves similarly to the lasso penalty for x values close to zero. We now use the notation of for the penalty function in regularized estimation to indicate that a general loss function can be used in regularized estimation. The optimization function in regularized estimation in the 1PL model is then given by
We demonstrated that robust linking relies on the first minimization step
Importantly, the log-likelihood in (19) does not change under reparametrization by including the redundant group mean . We obtain
for any and . Hence, the overidentified right-hand side of (20) can be made identifiable by adding a penalty function to the log-likelihood function. A condition for unbiased estimation of the group mean is to define DIF effects in such a way that is minimal [20]. This condition can also encode sparsity assumptions on DIF effects using the loss function and . Importantly, robust linking can be defined as
which demonstrates the practical equivalence of robust linking and regularized estimation in sufficiently large samples.
3. Simulation Study 1: DIF Effects in the 1PL Model
In this Simulation Study 1, we compare robust linking and regularized estimation in the 1PL model in the presence of DIF effects. We consider the case of two groups.
3.1. Method
In this simulation study, we fixed the number of items to 20 and fixed item difficulties throughout all replications. Item parameters and DIF effects can be found at https://osf.io/tma3f/ (accessed on 8 December 2022). Item difficulties (see column “b”) ranged between and , with a mean of 0.00 and a standard deviation of 1.20. Items with DIF effects (column “e”) can also be found at https://osf.io/tma3f/ (accessed on 8 December 2022). The DIF effects had values . Only 4 out of 20 items were simulated to have DIF effects different from zero.
Item response data were generated according to the 1PL model using item difficulties in the first group and in the second group. The DIF effect size was either 0.5 (i.e., small DIF effects) or 1.0 (i.e., large DIF effects). Furthermore, DIF was chosen to be balanced or unbalanced. In the balanced DIF condition, two items had DIF effects , and two items had DIF effects . In the unbalanced DIF condition, all items had DIF effects .
The distribution of the ability variable was assumed as standard normal (i.e., ) in the first group and had a mean of and a standard deviation in the second group. Finally, we varied sample sizes per group N as 500, 1000, 2500, and 5000.
The different linking approaches presented for the 1PL model in Section 2 were evaluated in Simulation Study 1. In the scaling models, we used rectangular integration on a discrete quadrature of 41 equidistant points on . In concurrent calibration, we assumed invariant item parameters across groups. Regularized estimation was carried out using the SCAD penalty, and the regularized model was estimated at a grid of regularization parameters between 1.0 and 0.005 (see replication material on https://osf.io/tma3f/(accessed on 8 December 2022) for specification details). In this simulation study, the tuning parameter a was fixed to 3.7. We chose estimates of the regularization approach using the optimal regularization based on AIC, BIC, and fixed values of 0.05, 0.10, and 0.15 (see [38,69] for a similar approach). Moreover, powers (; mean–mean linking), (; median–median linking), and (; invariance alignment) were used in the robust linking approach that utilizes the loss function. Finally, we determined the group mean of the second group on the outlier removal approach using the MAD statistic and a cutoff value of 2.7.
In total, 3000 replications were conducted in each simulation condition. We assessed the bias and root mean square error (RMSE) of the estimated group mean . In each of the R replications in a simulation condition, the group mean () was estimated. The bias was estimated by
The RMSE was estimated by
To ease the comparability of the RMSE between different methods across sample sizes, we used a relative RMSE in which we divided the RMSE of a particular method by the RMSE of the best-performing method in a simulation condition. Hence, a relative RMSE of 100 is the reference value for the best-performing method.
The statistical software R [70] was employed for all parts of the simulation. Concurrent calibration in a multiple-group IRT model was estimated using the TAM package [71]. Regularized estimation was carried out using the xxirt function in the sirt package [72]. Replication material can be found at https://osf.io/tma3f/ (accessed on 8 December 2022).
3.2. Results
In Table 1, the bias of the estimated group mean as a function of the size of the DIF effect and the sample size N is presented. It turned out that all methods performed well in the case of balanced DIF.

Table 1.
Simulation Study 1: Bias of estimated group means for balanced and unbalanced DIF effects as a function of the size of DIF effects and sample size N.
In the case of unbalanced DIF, nonrobust linking methods such as concurrent calibration (CC) and mean–mean linking () were substantially biased. Interestingly, there was also a bias for median–median linking () with unbalanced DIF. However, the bias decreased in larger samples. This can be expected because median–median linking (i.e., linking) recovers the true group difference in infinite sample sizes. In finite samples, estimated DIF effects with a true value of 0 will differ from 0, but have an expected mean of 0. As a consequence, the median of all estimated DIF effects (DIF items and non-DIF items) will be negative in the case of unbalanced DIF, because estimated DIF effects for DIF items are positive, resulting in a negative bias of the estimated group mean of the second group.
The robust linking approach performed well regarding the bias, particularly in larger samples. Overall, the estimated group means tended to be less biased when the BIC instead of the AIC was used in regularized estimation. However, the bias for robust linking and regularization approaches under unbalanced DIF turned out to be larger in conditions with small DIF effects of compared with large DIF effects of .
Table 2 presents the relative RMSE as a function of the size of DIF effects and the sample size N. It can be seen that CC is the frontrunner in terms of RMSE in the condition of unbalanced DIF. Notably, regularized estimation was particularly inefficient in larger samples of or in the condition of a small DIF effect. Furthermore, the robust linking approach based on the MAD statistic that performs outlier removal showed less variability than linking based on the invariance alignment loss function.

Table 2.
Simulation Study 1: Relative root mean sqaure error (RMSE) of estimated group means for balanced and unbalanced DIF effects as a function of the size of DIF effects and sample size N.
The situation changed in the conditions of unbalanced DIF. As expected, nonrobust linking approaches CC and had large RMSE values. In the case of small DIF effects (i.e., ), the performance of the methods depended on the sample size. For moderate sample sizes, and , regularized estimation based on the BIC was satisfactory, while the MAD approach would be preferred in larger sample sizes and . Nevertheless, the robust linking approach was quite competitive across all sample sizes for small DIF effects. For large unbalanced DIF effects (i.e., ), regularized estimation based on BIC and robust linking using the MAD statistic outperformed other methods. Interestingly, regularized estimation using fixed values of 0.10 or 0.15 also yielded satisfactory group mean estimates. Notably, the invariance alignment approach had some efficiency loss but might still be considered a viable alternative to the MAD linking and regularization approach.
4. Focused Simulation Study 1A: Optimal Choice of two Tuning Parameters for the SCAD Penalty
In this Focused Simulation Study 1A, we additionally investigated the impact of different choices of the second tuning parameter a for the SCAD penalty.
4.1. Method
This focused simulation study only considered the impact of the tuning parameter a for the SCAD penalty in regularized estimation. We only investigated selected conditions of Simulation Study 1. We focused on unbalanced DIF and chose sample sizes , 1000, and 2000. Regularized estimation with the SCAD penalty was carried out using different a values of 2.2, 2.5, 3, 3.7, 4.5, 6, and 9. The same grid of values as in Simulation Study 1 was employed (see Section 3.1). For each fixed a value, the optimal value was determined by means AIC or BIC. In addition, we also determined estimated group means by choosing the optimal pair for AIC and BIC.
The performance of the different analytical choices was evaluated by using a relative RMSE. The relative RMSE was obtained by dividing the RMSE of a method by the RMSE of the best-performing method. The best-performing method could either be a regularized estimation with a particular choice of and a or a regularized estimation with an optimal choice of or a using AIC or BIC.
4.2. Results
Table 3 presents the relative RMSE of estimated group means for different choices of a and . Like in Simulation Study 1, the RMSE was smaller for methods that relied on BIC than on AIC. For methods based on AIC, it turned out that using the optimal a parameter across a range of a values resulted in the least RMSE for and . However, this was not the case for . Across different conditions, the choice did not result in estimated group means with the least RMSE values. This finding also occurred for regularized estimation based on BIC. However, differences between different choices of a values turned out to be smaller. For or , the choice of a for the SCAD penalty does not seem to matter. In contrast, using the optimal a value resulted in a substantial RMSE decrease for small DIF effects (i.e., ). On the other hand, using the optimal a value resulted in an RMSE increase for in the presence of large DIF effects (i.e., ) compared with methods that use a fixed a value of the SCAD penalty. Interestingly, the least RMSE values could also be obtained with proper choices of fixed values of a and . In particular, for a large sample size of , relying on a fixed instead of an optimal value can substantially decrease the RMSE.

Table 3.
Focused Simulation Study 1A: Relative root mean square error (RMSE) of estimated group means for unbalanced DIF effects as a function of the size of DIF effects and sample size N for different values a of the SCAD penalty.
As a conclusion of this focused simulation study, one could state that the choice of a for the SCAD penalty can have some impact. However, it is more important whether regularized estimation is carried out using AIC or BIC.
5. Simulation Study 2: Uniform DIF Effects in the 2PL Model
In this Simulation Study 2, robust linking and regularization estimation is compared in the 2PL IRT model in the presence of uniform DIF effects.
5.1. Method
The simulation design of Simulation Study 2 closely follows the design of Simulation Study 1 described in Section 3.1. We now only emphasize the differences between this study and the first one.
Notably, item response data were generated based on the 2PL model using the same invariant item discriminations across the two groups (see https://osf.io/tma3f/ (accessed on 8 December 2022)) for data-generating item parameters; see column “a” for item discriminations. Like in Simulation Study 1, item difficulties ranged between and with a mean of 0.00 and a standard deviation of 1.20. Item discriminations ranged between and with a mean of 1.00 and a standard deviation of 0.30. Item difficulties and item discriminations were essentially uncorrelated (). DIF effects only occurred in item difficulties (i.e., uniform DIF). Like in Simulation Study 1, we set and as data-generating distribution parameters in the second group. Moreover, the number of items (i.e., ) was also fixed throughout all conditions. DIF effects were either small () or large () and either balanced or unbalanced. Finally, we also simulated four different sample sizes N of 500, 1000, 2500, and 5000.
For regularized estimation, the same grid of values like in Simulation Study 1 and Focused Simulation Study 1A was utilized. In this simulation study, the tuning parameter a was fixed to 3.7.
In the linking approaches, we either relied on a simultaneous first estimation step assuming common item discriminations or separate estimation assuming groupwise item discriminations. In contrast to Simulation Study 1, we also applied joint Haberman linking (JHL) to common item discriminations and ordinary Haberman linking (HL) to groupwise estimated item discriminations with powers , 1, and 0.5.
In total, 3000 replications were simulated in each condition. R software [70] was used throughout the whole simulation. The R packages TAM [71] and sirt [72] were employed for estimating the IRT models. Replication material can again be found at https://osf.io/tma3f/ (accessed on 8 December 2022).
5.2. Results
Table 4 presents the bias for the estimated group mean as a function of the size of DIF effects and the sample size N. It turned out that all methods except concurrent calibration (CC) resulted in unbiased estimates of group means. Consistent with other studies, CC resulted in slightly biased estimates in the case of the 2PL model, even in the situation of balanced DIF effects. The reason might be that the presence of DIF negatively impacted the estimation of common item discriminations and the standard deviation of the second group.

Table 4.
Simulation Study 2: Bias of estimated group means for balanced and unbalanced DIF effects as a function of the size of DIF effects and sample size N.
In the case of unbalanced DIF, robust linking approaches based on or MAD, as well as the regularization approach based on BIC, performed satisfactorily in terms of bias. Joint Haberman linking (JHL) and Haberman linking based on separate calibration (HL) resulted in approximately unbiased estimates with .
Table 5 presents the relative RMSE of the estimated group mean as a function of the size of the DIF effect and the sample size N. In the case of unbalanced DIF, mean–mean linking and JHL performed the best across all conditions. It should be emphasized that the RMSE of CC became unacceptable in larger sample sizes due to bias. Moreover, a robust linking approach with powers or resulted in some efficiency losses.

Table 5.
Simulation Study 2: Relative root mean square error (RMSE) of estimated group means for balanced and unbalanced DIF effects as a function of the size of DIF effects and sample size N.
The case of unbalanced DIF in the 2PL model was similar to the 1PL model presented in Simulation Study 1 in Section 3.2. For small DIF effects (i.e., ), regularized estimation using BIC was the frontrunner for moderate sample sizes and , while robust linking based on the MAD statistic performed well in larger sample sizes and . For large DIF effects (i.e., ), robust linking using the MAD statistic performed satisfactorily. Moreover, JHL with and the robust linking also resulted in group mean estimates of acceptable variability.
6. Discussion
In this article, we investigated the performance of robust linking and regularized estimation in the presence of sparse uniform differential item functioning by means of three simulation studies. It turned out that robust linking approaches were competitive or outperformed regularized estimation in most conditions in the simulation studies. In particular, regularized estimation was not quite successful in parameter recovery in conditions with small DIF effects. It was also found that robust linking based on outlier removal using the MAD statistic [64] was often superior to robust linking using the loss function with , which corresponds to invariance alignment. Overall, one could generally conclude that there is probably no need for using the computationally much more demanding regularization approaches instead of employing robust linking.
As in any simulation study, our findings are limited to the studied conditions. First, we only considered a fixed test of 20 items. Additional studies could also involve a larger number of items or balanced incomplete block designs for item response data [73]. Second, only 4 out of 20 items (i.e., 20% of the items) showed uniform DIF effects. Other research indicated that higher DIF rates would also be possible in robust linking, as long as the threshold of 50% of DIF items is not exceeded [21,24]. Third, we simulated uniform DIF under a sparsity condition. The 16 non-DIF items had DIF effects of exactly 0. Future research could also assume that there would also be small DIF effects that could add up to zero [26,74]. Fourth, future research could also investigate the case of nonuniform DIF in item discriminations. It could be that larger sample sizes would be required for robust linking in this situation, and regularized estimation might be advantageous.
In this article, we assumed that DIF effects potentially bias group mean differences. Hence, DIF effects should be essentially removed from group comparisons. However, it could be argued that eliminating items from comparisons poses a threat to validity [74,75,76,77], and statistical criteria should not determine which items enter group comparisons [78].
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| 1PL | one-parameter logistic |
| 2PL | two-parameter logistic |
| AIC | Akaike information criterion |
| BIC | Bayesian information criterion |
| CC | concurrent calibration |
| DIF | differential item functioning |
| DWLS | diagonally weighted least squares |
| FIPC | fixed item parameter calibration |
| IPD | item parameter drift |
| IRT | item response theory |
| JK | jackknife |
| LE | linking error |
| LSA | large-scale assessment studies |
| MAD | median absolute deviation |
| PISA | programme for international student assessment |
| RMSE | root mean square error |
| SCAD | smoothly clipped absolute deviation |
References
- Van der Linden, W.J.; Hambleton, R.K. (Eds.) Handbook of Modern Item Response Theory; Springer: New York, NY, USA, 1997. [Google Scholar] [CrossRef]
- Van der Linden, W.J. (Ed.) Unidimensional logistic response models. In Handbook of Item Response Theory, Volume 1: Models; CRC Press: Boca Raton, FL, USA, 2016; pp. 11–30. [Google Scholar] [CrossRef]
- Lietz, P.; Cresswell, J.C.; Rust, K.F.; Adams, R.J. (Eds.) Implementation of Large-scale Education Assessments; Wiley: New York, NY, USA, 2017. [Google Scholar] [CrossRef]
- Rutkowski, L.; von Davier, M.; Rutkowski, D. (Eds.) A Handbook of International Large-scale Assessment: Background, Technical Issues, and Methods of Data Analysis; Chapman Hall/CRC Press: London, UK, 2013. [Google Scholar] [CrossRef]
- OECD. PISA 2018. Technical Report; OECD: Paris, France, 2020; Available online: https://bit.ly/3zWbidA (accessed on 8 December 2022).
- Yen, W.M.; Fitzpatrick, A.R. Item response theory. In Educational Measurement; Brennan, R.L., Ed.; Praeger Publishers: Westport, CT, USA, 2006; pp. 111–154. [Google Scholar]
- Rasch, G. Probabilistic Models for Some Intelligence and Attainment Tests; Danish Institute for Educational Research: Copenhagen, Denmark, 1960. [Google Scholar]
- Birnbaum, A. Some latent trait models and their use in inferring an examinee’s ability. In Statistical Theories of Mental Test Scores; Lord, F.M., Novick, M.R., Eds.; MIT Press: Reading, MA, USA, 1968; pp. 397–479. [Google Scholar]
- Mellenbergh, G.J. Item bias and item response theory. Int. J. Educ. Res. 1989, 13, 127–143. [Google Scholar] [CrossRef]
- Millsap, R.E. Statistical Approaches to Measurement Invariance; Routledge: New York, NY, USA, 2011; p. 3821961. [Google Scholar] [CrossRef]
- Holland, P.W.; Wainer, H. (Eds.) Differential Item Functioning: Theory and Practice; Lawrence Erlbaum: Hillsdale, NJ, USA, 1993. [Google Scholar] [CrossRef]
- Penfield, R.D.; Camilli, G. Differential item functioning and item bias. In Handbook of Statistics, Vol. 26: Psychometrics; Rao, C.R., Sinharay, S., Eds.; 2007; Elsevier: Amsterdam, The Netherlands pp. 125–167. [CrossRef]
- Robitzsch, A. A comparison of linking methods for two groups for the two-parameter logistic item response model in the presence and absence of random differential item functioning. Foundations 2021, 1, 116–144. [Google Scholar] [CrossRef]
- De Boeck, P. Random item IRT models. Psychometrika 2008, 73, 533–559. [Google Scholar] [CrossRef]
- Frederickx, S.; Tuerlinckx, F.; De Boeck, P.; Magis, D. RIM: A random item mixture model to detect differential item functioning. J. Educ. Meas. 2010, 47, 432–457. [Google Scholar] [CrossRef]
- Byrne, B.M.; Shavelson, R.J.; Muthén, B. Testing for the equivalence of factor covariance and mean structures: The issue of partial measurement invariance. Psychol. Bull. 1989, 105, 456–466. [Google Scholar] [CrossRef]
- Lee, S.S.; von Davier, M. Improving measurement properties of the PISA home possessions scale through partial invariance modeling. Psychol. Test Assess. Model. 2020, 62, 55–83. Available online: https://bit.ly/3FRN6Qf (accessed on 8 December 2022).
- Magis, D.; Tuerlinckx, F.; De Boeck, P. Detection of differential item functioning using the lasso approach. J. Educ. Behav. Stat. 2015, 40, 111–135. [Google Scholar] [CrossRef]
- Tutz, G.; Schauberger, G. A penalty approach to differential item functioning in Rasch models. Psychometrika 2015, 80, 21–43. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Li, C.; Xu, G. DIF statistical inference and detection without knowing anchoring items. arXiv 2021, arXiv:2110.11112. [Google Scholar] [CrossRef]
- Halpin, P.F. Differential item functioning via robust scaling. arXiv 2022, arXiv:2207.04598. [Google Scholar] [CrossRef]
- Magis, D.; De Boeck, P. Identification of differential item functioning in multiple-group settings: A multivariate outlier detection approach. Multivar. Behav. Res. 2011, 46, 733–755. [Google Scholar] [CrossRef]
- Magis, D.; De Boeck, P. A robust outlier approach to prevent type I error inflation in differential item functioning. Educ. Psychol. Meas. 2012, 72, 291–311. [Google Scholar] [CrossRef]
- Wang, W.; Liu, Y.; Liu, H. Testing differential item functioning without predefined anchor items using robust regression. J. Educ. Behav. Stat. 2022, 47, 666–692. [Google Scholar] [CrossRef]
- Robitzsch, A. Robust and nonrobust linking of two groups for the Rasch model with balanced and unbalanced random DIF: A comparative simulation study and the simultaneous assessment of standard errors and linking errors with resampling techniques. Symmetry 2021, 13, 2198. [Google Scholar] [CrossRef]
- Robitzsch, A.; Lüdtke, O. A review of different scaling approaches under full invariance, partial invariance, and noninvariance for cross-sectional country comparisons in large-scale assessments. Psychol. Test Assess. Model. 2020, 62, 233–279. Available online: https://bit.ly/3ezBB05 (accessed on 8 December 2022).
- Fan, J.; Li, R.; Zhang, C.H.; Zou, H. Statistical Foundations of Data Science; Chapman and Hall/CRC: Boca Raton, FL, USA, 2020. [Google Scholar] [CrossRef]
- Hastie, T.; Tibshirani, R.; Wainwright, M. Statistical Learning with Sparsity: The Lasso and Generalizations; CRC Press: Boca Raton, FL, USA, 2015. [Google Scholar] [CrossRef]
- Chen, Y.; Li, X.; Liu, J.; Ying, Z. Robust measurement via a fused latent and graphical item response theory model. Psychometrika 2018, 83, 538–562. [Google Scholar] [CrossRef]
- Sun, J.; Chen, Y.; Liu, J.; Ying, Z.; Xin, T. Latent variable selection for multidimensional item response theory models via L1 regularization. Psychometrika 2016, 81, 921–939. [Google Scholar] [CrossRef] [PubMed]
- Geminiani, E.; Marra, G.; Moustaki, I. Single- and multiple-group penalized factor analysis: A trust-region algorithm approach with integrated automatic multiple tuning parameter selection. Psychometrika 2021, 86, 65–95. [Google Scholar] [CrossRef]
- Huang, P.H.; Chen, H.; Weng, L.J. A penalized likelihood method for structural equation modeling. Psychometrika 2017, 82, 329–354. [Google Scholar] [CrossRef]
- Jacobucci, R.; Grimm, K.J.; McArdle, J.J. Regularized structural equation modeling. Struct. Equ. Modeling 2016, 23, 555–566. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Li, X.; Liu, J.; Ying, Z. Regularized latent class analysis with application in cognitive diagnosis. Psychometrika 2017, 82, 660–692. [Google Scholar] [CrossRef] [PubMed]
- Robitzsch, A.; George, A.C. The R package CDM for diagnostic modeling. In Handbook of Diagnostic Classification Models; von Davier, M., Lee, Y.S., Eds.; Springer: Cham, Switzerland, 2019; pp. 549–572. [Google Scholar] [CrossRef]
- Robitzsch, A. Regularized latent class analysis for polytomous item responses: An application to SPM-LS data. J. Intell. 2020, 8, 30. [Google Scholar] [CrossRef]
- Fop, M.; Murphy, T.B. Variable selection methods for model-based clustering. Stat. Surv. 2018, 12, 18–65. [Google Scholar] [CrossRef]
- Robitzsch, A. Regularized mixture Rasch model. Information 2022, 13, 534. [Google Scholar] [CrossRef]
- Belzak, W.C. The multidimensionality of measurement bias in high-stakes testing: Using machine learning to evaluate complex sources of differential item functioning. Educ. Meas. 2022; epub ahead of print. [Google Scholar] [CrossRef]
- Belzak, W.; Bauer, D.J. Improving the assessment of measurement invariance: Using regularization to select anchor items and identify differential item functioning. Psychol. Methods 2020, 25, 673–690. [Google Scholar] [CrossRef]
- Bauer, D.J.; Belzak, W.C.M.; Cole, V.T. Simplifying the assessment of measurement invariance over multiple background variables: Using regularized moderated nonlinear factor analysis to detect differential item functioning. Struct. Equ. Model. 2020, 27, 43–55. [Google Scholar] [CrossRef] [PubMed]
- Gürer, C.; Draxler, C. Penalization approaches in the conditional maximum likelihood and Rasch modelling context. Brit. J. Math. Stat. Psychol. 2022; epub ahead of print. [Google Scholar] [CrossRef]
- Liang, X.; Jacobucci, R. Regularized structural equation modeling to detect measurement bias: Evaluation of lasso, adaptive lasso, and elastic net. Struct. Equ. Model. 2020, 27, 722–734. [Google Scholar] [CrossRef]
- Schauberger, G.; Mair, P. A regularization approach for the detection of differential item functioning in generalized partial credit models. Behav. Res. Methods 2020, 52, 279–294. [Google Scholar] [CrossRef]
- Fan, J.; Li, R. Variable selection via nonconcave penalized likelihood and its oracle properties. J. Am. Stat. Assoc. 2001, 96, 1348–1360. [Google Scholar] [CrossRef]
- Chen, Y.; Liu, J.; Xu, G.; Ying, Z. Statistical analysis of Q-matrix based diagnostic classification models. J. Am. Stat. Assoc. 2015, 110, 850–866. [Google Scholar] [CrossRef] [PubMed]
- Umezu, Y.; Shimizu, Y.; Masuda, H.; Ninomiya, Y. AIC for the non-concave penalized likelihood method. Ann. Inst. Stat. Math. 2019, 71, 247–274. [Google Scholar] [CrossRef]
- Zhang, H.; Li, S.J.; Zhang, H.; Yang, Z.Y.; Ren, Y.Q.; Xia, L.Y.; Liang, Y. Meta-analysis based on nonconvex regularization. Sci. Rep. 2020, 10, 5755. [Google Scholar] [CrossRef]
- Breheny, P.; Huang, J. Coordinate descent algorithms for nonconvex penalized regression, with applications to biological feature selection. Ann. Appl. Stat. 2011, 5, 232–253. [Google Scholar] [CrossRef] [PubMed]
- Xiao, H.; Sun, Y. On tuning parameter selection in model selection and model averaging: A Monte Carlo study. J. Risk Financ. Manag. 2019, 12, 109. [Google Scholar] [CrossRef]
- Williams, D.R. Beyond lasso: A survey of nonconvex regularization in Gaussian graphical models. PsyArXiv 2020. [Google Scholar] [CrossRef]
- Battauz, M. Regularized estimation of the nominal response model. Multivar. Behav. Res. 2020, 55, 811–824. [Google Scholar] [CrossRef] [PubMed]
- Oelker, M.R.; Tutz, G. A uniform framework for the combination of penalties in generalized structured models. Adv. Data Anal. Classif. 2017, 11, 97–120. [Google Scholar] [CrossRef]
- Tutz, G.; Gertheiss, J. Regularized regression for categorical data. Stat. Model. 2016, 16, 161–200. [Google Scholar] [CrossRef]
- Kolen, M.J.; Brennan, R.L. Test Equating, Scaling, and Linking; Springer: New York, NY, USA, 2014. [Google Scholar] [CrossRef]
- Lee, W.C.; Lee, G. IRT linking and equating. In The Wiley Handbook of Psychometric Testing: A Multidisciplinary Reference on Survey, Scale and Test; Irwing, P., Booth, T., Hughes, D.J., Eds.; Wiley: New York, NY, USA, 2018; pp. 639–673. [Google Scholar] [CrossRef]
- Sansivieri, V.; Wiberg, M.; Matteucci, M. A review of test equating methods with a special focus on IRT-based approaches. Statistica 2017, 77, 329–352. [Google Scholar] [CrossRef]
- Robitzsch, A. Robust Haebara linking for many groups: Performance in the case of uniform DIF. Psych 2020, 2, 155–173. [Google Scholar] [CrossRef]
- Pokropek, A.; Lüdtke, O.; Robitzsch, A. An extension of the invariance alignment method for scale linking. Psychol. Test Assess. Model. 2020, 62, 303–334. Available online: https://bit.ly/2UEp9GH (accessed on 8 December 2022).
- Robitzsch, A. Lp loss functions in invariance alignment and Haberman linking with few or many groups. Stats 2020, 3, 246–283. [Google Scholar] [CrossRef]
- Manna, V.F.; Gu, L. Different Methods of Adjusting for form Difficulty under the Rasch Model: Impact on Consistency of Assessment Results; (Research Report No. RR-19-08); Educational Testing Service: Princeton, NJ, USA, 2019. [Google Scholar] [CrossRef]
- Asparouhov, T.; Muthén, B. Multiple-group factor analysis alignment. Struct. Equ. Model. 2014, 21, 495–508. [Google Scholar] [CrossRef]
- Muthén, B.; Asparouhov, T. IRT studies of many groups: The alignment method. Front. Psychol. 2014, 5, 978. [Google Scholar] [CrossRef] [PubMed]
- von Davier, M.; Bezirhan, U. A robust method for detecting item misfit in large scale assessments. Educ. Psychol. Meas. 2022; epub ahead of print. [Google Scholar] [CrossRef]
- Huynh, H.; Meyer, P. Use of robust z in detecting unstable items in item response theory models. Pract. Assess. Res. Eval. 2010, 15, 2. [Google Scholar] [CrossRef]
- Liu, C.; Jurich, D. Outlier detection using t-test in Rasch IRT equating under NEAT design. Appl. Psychol. Meas. 2022; epub ahead of print. [Google Scholar] [CrossRef]
- Battauz, M. Multiple equating of separate IRT calibrations. Psychometrika 2017, 82, 610–636. [Google Scholar] [CrossRef]
- Haberman, S.J. Linking Parameter Estimates Derived from an Item Response Model through Separate Calibrations; (Research Report No. RR-09-40); Educational Testing Service: Princeton, NJ, USA, 2009. [Google Scholar] [CrossRef]
- Liu, X.; Wallin, G.; Chen, Y.; Moustaki, I. Rotation to sparse loadings using Lp losses and related inference problems. arXiv 2022, arXiv:2206.02263. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Core Team: Vienna, Austria, 2022. Available online: https://www.R-project.org/ (accessed on 11 January 2022).
- Robitzsch, A.; Kiefer, T.; Wu, M. TAM: Test Analysis Modules. R Package Version 4.1-4. 2022. Available online: https://CRAN.R-project.org/package=TAM (accessed on 28 August 2022).
- Robitzsch, A. Sirt: Supplementary Item Response Theory Models. R Package Version 3.12-66. 2022. Available online: https://CRAN.R-project.org/package=sirt (accessed on 17 May 2022).
- Frey, A.; Hartig, J.; Rupp, A.A. An NCME instructional module on booklet designs in large-scale assessments of student achievement: Theory and practice. Educ. Meas. 2009, 28, 39–53. [Google Scholar] [CrossRef]
- Robitzsch, A.; Lüdtke, O. Mean comparisons of many groups in the presence of DIF: An evaluation of linking and concurrent scaling approaches. J. Educ. Behav. Stat. 2022, 47, 36–68. [Google Scholar] [CrossRef]
- Camilli, G. The case against item bias detection techniques based on internal criteria: Do item bias procedures obscure test fairness issues? In Differential Item Functioning: Theory and Practice; Holland, P.W., Wainer, H., Eds.; Erlbaum: Hillsdale, NJ, USA, 1993; pp. 397–417. [Google Scholar]
- El Masri, Y.H.; Andrich, D. The trade-off between model fit, invariance, and validity: The case of PISA science assessments. Appl. Meas. Educ. 2020, 33, 174–188. [Google Scholar] [CrossRef]
- Robitzsch, A.; Lüdtke, O. Some thoughts on analytical choices in the scaling model for test scores in international large-scale assessment studies. Meas. Instrum. Soc. Sci. 2022, 4, 9. [Google Scholar] [CrossRef]
- Brennan, R.L. Misconceptions at the intersection of measurement theory and practice. Educ. Meas. 1998, 17, 5–9. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).