Goodness-of-Fit and Generalized Estimating Equation Methods for Ordinal Responses Based on the Stereotype Model
Abstract
1. Introduction
1.1. Ordinal Responses
1.2. The Ordered Stereotype Model
2. Methods
2.1. OSM: Formulation and Basics
2.2. Recent Advances in the OSM
2.2.1. Goodness-of-Fit Tests
2.2.2. Generalized Estimating Equations
3. Case Study
3.1. Arthritis Clinical Trial
3.2. Goodness-of-Fit Test for the Arthritis Data Set
3.3. GEE Estimator for the Arthritis Data Set
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Arthritis Clinical Trial
| Follow-Up (1-Month) (t1) | Follow-Up (3-Month) (t3) | Follow-Up (5-Month) (t5) | ||||||
|---|---|---|---|---|---|---|---|---|
| 1 | 0 | 0 | 0.116 | −0.107 | −0.107 | 0.221 | −0.047 | −0.047 |
| 0 | 1 | 0 | −0.107 | 0.116 | −0.107 | −0.047 | 0.221 | −0.047 |
| 0 | 0 | 1 | −0.107 | −0.107 | 0.116 | −0.047 | −0.047 | 0.221 |
| 0.191 | −0.078 | −0.078 | 1 | 0 | 0 | 0.236 | −0.078 | −0.078 |
| −0.078 | 0.191 | −0.078 | 0 | 1 | 0 | −0.078 | 0.236 | −0.078 |
| −0.078 | −0.078 | 0.191 | 0 | 0 | 1 | −0.078 | −0.078 | 0.236 |
| 0.191 | −0.078 | −0.078 | 0.191 | −0.078 | −0.078 | 1 | 0 | 0 |
| −0.078 | 0.191 | −0.078 | −0.078 | 0.191 | −0.078 | 0 | 1 | 0 |
| −0.078 | −0.078 | 0.191 | −0.078 | −0.078 | 0.191 | 0 | 1 | 0 |
References
- Ahn, J.; Mukherjee, B.; Banerjee, M.; Cooney, K.A. Bayesian inference for the stereotype regression model: Application to a case–control study of prostate cancer. Stat. Med. 2009, 28, 3139–3157. [Google Scholar] [CrossRef] [PubMed]
- Cupp, M.A.; Owugha, J.; Florschutz, A.; Beckingham, A.; Kisan, V.; Manikam, L.; Lakhanpaul, M. Birthing a better future: A mixed-methods evaluation of multimedia exposition conveying the importance of the first 1001 days of life. Lancet 2018, 392, S27. [Google Scholar] [CrossRef]
- Furman, B.T.; Leone, E.H.; Bell, S.S.; Durako, M.J.; Hall, M.O. Braun-Blanquet data in ANOVA designs: Comparisons with percent cover and transformations using simulated data. Mar. Ecol. Prog. Ser. 2018, 597, 13–22. [Google Scholar] [CrossRef]
- McNellie, M.J.; Dorrough, J.; Oliver, I. Species abundance distributions should underpin ordinal cover-abundance transformations. Appl. Veg. Sci. 2019, 22, 361–372. [Google Scholar] [CrossRef]
- Loda, T.; Löffler, T.; Erschens, R.; Zipfel, S.; Herrmann-Werner, A. Medical education in times of COVID-19: German students’ expectations–A cross-sectional study. PLoS ONE 2020, 15, e0241660. [Google Scholar] [CrossRef]
- Likert, R. A technique for the measurement of attitudes. Arch. Psychol. 1932, 22, 5–55. [Google Scholar]
- Göb, R.; McCollin, C.; Ramalhoto, M. Ordinal Methodology in the Analysis of Likert Scales. Qual. Quant. 2007, 41, 601–626. [Google Scholar] [CrossRef]
- Braun-Blanquet, J. Plant Sociology: The Study of Plant Communities; McGraw Hill: New York, NY, USA, 1932. [Google Scholar]
- Wikum, D.A.; Shanholtzer, G.F. Application of the Braun-Blanquet cover-abundance scale for vegetation analysis in land development studies. Environ. Manag. 1978, 2, 323–329. [Google Scholar] [CrossRef]
- Agresti, A. Analysis of Ordinal Categorical Data, 2nd ed.; Wiley Series in Probability and Statistics; Wiley: Hoboken, NJ, USA, 2010. [Google Scholar]
- Stromberg, U. Collapsing ordered outcome categories: A note of concern. Am. J. Epidemiol. 1996, 144, 421–424. [Google Scholar] [CrossRef]
- Liu, I.; Agresti, A. The analysis of ordered categorical data: An overview and a survey of recent developments. Test 2005, 14, 1–73. [Google Scholar] [CrossRef]
- McCullagh, P. Regression models for ordinal data. J. R. Stat. Soc. 1980, 42, 109–142. [Google Scholar] [CrossRef]
- McCullagh, P.; Nelder, J.A. Generalized Linear Models, 2nd ed.; Chapman & Hall: London, UK, 1989. [Google Scholar]
- Anderson, J.A. Regression and Ordered Categorical Variables. J. R. Stat. Soc. Ser. B 1984, 46, 1–30. [Google Scholar] [CrossRef]
- Greenland, S. Alternative models for ordinal logistic regression. Stat. Med. 1994, 13, 1665–1677. [Google Scholar] [CrossRef] [PubMed]
- Ananth, C.V.; Kleinbaum, D.G. Regression models for ordinal responses: A review of methods and applications. Int. J. Epidemiol. 1997, 26, 1323–1333. [Google Scholar] [CrossRef]
- Johnson, T.R. Discrete choice models for ordinal response variables: A generalization of the stereotype model. Psychometrika 2007, 72, 489–504. [Google Scholar] [CrossRef]
- Fullerton, A.S. A conceptual framework for ordered logistic regression models. Sociol. Methods Res. 2009, 38, 306–347. [Google Scholar] [CrossRef]
- Liu, X. Fitting stereotype logistic regression models for ordinal response variables in educational research (Stata). J. Mod. Appl. Stat. Methods 2014, 13, 31. [Google Scholar] [CrossRef]
- Fernández, D.; Pledger, S. Categorising count data into ordinal responses with application to ecological communities. J. Agric. Biol. Environ. Stat. 2016, 21, 348–362. [Google Scholar] [CrossRef]
- Williams, A.A.; Archer, K.J. Elastic Net Constrained Stereotype Logit Model for Ordered Categorical Data. Biom. Biostat. Int. J. 2015, 2, 00049. [Google Scholar] [CrossRef][Green Version]
- Spiess, M.; Fernández, D.; Nguyen, T.; Liu, I. Generalized estimating equations to estimate the ordered stereotype logit model for panel data. Stat. Med. 2020, 39, 1919–1940. [Google Scholar] [CrossRef]
- Kuss, O. On the estimation of the stereotype regression model. Comput. Stat. Data Anal. 2006, 50, 1877–1890. [Google Scholar] [CrossRef]
- Holtbrugge, W.; Schumacher, M. A comparison of regression models for the analysis of ordered categorical data. J. R. Stat. Soc. Ser. C (Appl. Stat.) 1991, 40, 249–259. [Google Scholar] [CrossRef]
- Preedalikit, K.; Liu, I.; Hirose, Y.; Sibanda, N.; Fernández, D. Joint modeling of survival and longitudinal ordered data using a semiparametric approach. Aust. N. Z. J. Stat. 2016, 58, 153–172. [Google Scholar] [CrossRef]
- Feldmann, U.; König, J. Ordinal classification in medical prognosis. Methods Inf. Med. 2002, 41, 154–163. [Google Scholar] [PubMed]
- Ahn, J.; Mukherjee, B.; Gruber, S.B.; Sinha, S. Missing exposure data in stereotype regression model: Application to matched case–control study with disease subclassification. Biometrics 2011, 67, 546–558. [Google Scholar] [CrossRef]
- Lunt, M.; Unit, A. Stereotype ordinal regression. Stata Tech. Bull. 2001, 61, 1–28. [Google Scholar]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2020. [Google Scholar]
- Turner, H.; Firth, D. Generalized Nonlinear Models in R: An Overview of the gnm Package; Technical Report; ESRC National Centre for Research Methods: Southampton, UK, 2007. [Google Scholar]
- Yee, T.W. The VGAM Package. R News 2008, 8, 28–39. [Google Scholar]
- Archer, K.J.; Hou, J.; Zhou, Q.; Ferber, K.; Layne, J.G.; Gentry, A.E. ordinalgmifs: An R package for ordinal regression in high-dimensional data settings. Cancer Inform. 2014, 13, 187. [Google Scholar] [CrossRef]
- McMillan, L.; Fernandez, D.; Cui, Y.; Matechou, E. Clustord R Package. Available online: https://github.com/vuw-clustering/clustord (accessed on 29 March 2022).
- Fernández, D.; Arnold, R.; Pledger, S. Mixture-based clustering for the ordered stereotype model. Comput. Stat. Data Anal. 2016, 93, 46–75. [Google Scholar] [CrossRef]
- Fagerland, M.W.; Hosmer, D.W. A goodness-of-fit test for the proportional odds regression model. Stat. Med. 2013, 32, 2235–2249. [Google Scholar] [CrossRef]
- Hosmer, D.W.; Lemeshow, S.; Sturdivant, R.X. Applied Logistic Regression; John Wiley & Sons: Hoboken, NJ, USA, 2013; Volume 398. [Google Scholar]
- Pulkstenis, E.; Robinson, T.J. Goodness-of-fit tests for ordinal response regression models. Stat. Med. 2004, 23, 999–1014. [Google Scholar] [CrossRef] [PubMed]
- Lin, K.C.; Chen, Y.J. Assessing ordinal logistic regression models via nonparametric smoothing. Commun. Stat.-Methods 2008, 37, 917–930. [Google Scholar] [CrossRef]
- Liu, I.; Mukherjee, B.; Suesse, T.; Sparrow, D.; Park, S.K. Graphical diagnostics to check model misspecification for the proportional odds regression model. Stat. Med. 2009, 28, 412–429. [Google Scholar] [CrossRef] [PubMed]
- Lipsitz, S.R.; Fitzmaurice, G.M.; Molenberghs, G. Goodness-of-fit tests for ordinal response regression models. Appl. Stat. 1996, 45, 175–190. [Google Scholar] [CrossRef]
- Li, C.; Shepherd, B.E. A new residual for ordinal outcomes. Biometrika 2012, 99, 473–480. [Google Scholar] [CrossRef] [PubMed]
- Liu, D.; Li, S.; Yu, Y.; Moustaki, I. Assessing partial association between ordinal variables: Quantification, visualization, and hypothesis testing. J. Am. Stat. Assoc. 2020, 116, 955–968. [Google Scholar] [CrossRef]
- Fernández, D.; Liu, I. A goodness-of-fit test for the ordered stereotype model. Stat. Med. 2016, 35, 4660–4696. [Google Scholar] [CrossRef]
- Fernández, D.; Liu, I.; Arnold, R.; Nguyen, T.; Spiess, M. Model-based goodness-of-fit tests for the ordered stereotype model. Stat. Methods Med Res. 2020, 29, 1527–1541. [Google Scholar] [CrossRef]
- Liu, I.; Fernández, D. Discussion on “Assessing the goodness of fit of logistic regression models in large samples: A modification of the Hosmer–Lemeshow test” by Giovanni Nattino, Michael L. Pennell, and Stanley Lemeshow. Biometrics 2020, 76, 564–568. [Google Scholar] [CrossRef]
- Nattino, G.; Pennell, M.L.; Lemeshow, S. Assessing the goodness of fit of logistic regression models in large samples: A modification of the Hosmer–Lemeshow test. Biometrics 2020, 76, 549–560. [Google Scholar] [CrossRef]
- Kuss, O. Modelling physicians’ recommendations for optimal medical care by random effects stereotype regression. In Proceedings of the 18th International Workshop on Statistical Modelling, Leuven, Belgium, 7–11 July 2003; Citeseer: University Park, PA, USA, 2003; p. 245. [Google Scholar]
- Liang, K.Y.; Zeger, S.L. Longitudinal data analysis using generalized linear models. Biometrika 1986, 73, 13–22. [Google Scholar] [CrossRef]
- Touloumis, A.; Agresti, A.; Kateri, M. GEE for multinomial responses using a local odds ratios parameterization. Biometrics 2013, 69, 633–640. [Google Scholar] [CrossRef] [PubMed]
- Lipsitz, S.R.; Kim, K.; Zhao, L. Analysis of repeated categorical data using generalized estimating equations. Stat. Med. 1994, 13, 1149–1163. [Google Scholar] [CrossRef] [PubMed]
- Bombardier, C.; Ware, J.; Russell, I.J.; Larson, M.; Chalmers, A.; Read, J.L.; Arnold, W.; Bennett, R.; Caldwell, J.; Hench, P.K.; et al. Auranofin therapy and quality of life in patients with rheumatoid arthritis. Results of a multicenter trial. Am. J. Med. 1986, 81, 565–578. [Google Scholar] [CrossRef]
- Touloumis, A. R package multgee: A generalized estimating equations solver for multinomial responses. J. Stat. Softw. 2015, 64, 1–14. [Google Scholar] [CrossRef]
- Goodman, L.A. The analysis of cross-classified data having ordered and/or unordered categories: Association models, correlation models, and asymmetry models for contingency tables with or without missing entries. Ann. Stat. 1985, 13, 10–69. [Google Scholar] [CrossRef]
- Yee, T.W.; Hastie, T.J. Reduced-rank vector generalized linear models. Stat. Model. 2003, 3, 15–41. [Google Scholar] [CrossRef]
- Fernández, D.; Liu, I.; Costilla, R.; Gu, P.Y. Assigning scores for ordered categorical responses. J. Appl. Stat. 2020, 47, 1261–1281. [Google Scholar] [CrossRef]
- Tsiatis, A.A. A note on a goodness-of-fit test for the logistic regression model. Biometrika 1980, 67, 250–251. [Google Scholar] [CrossRef]
- Pulkstenis, E.; Robinson, T.J. Two goodness-of-fit tests for logistic regression models with continuous covariates. Stat. Med. 2002, 21, 79–93. [Google Scholar] [CrossRef]
- Archer, K.J.; Lemeshow, S.; Hosmer, D.W. Goodness-of-fit tests for logistic regression models when data are collected using a complex sampling design. Comput. Stat. Data Anal. 2007, 51, 4450–4464. [Google Scholar] [CrossRef]
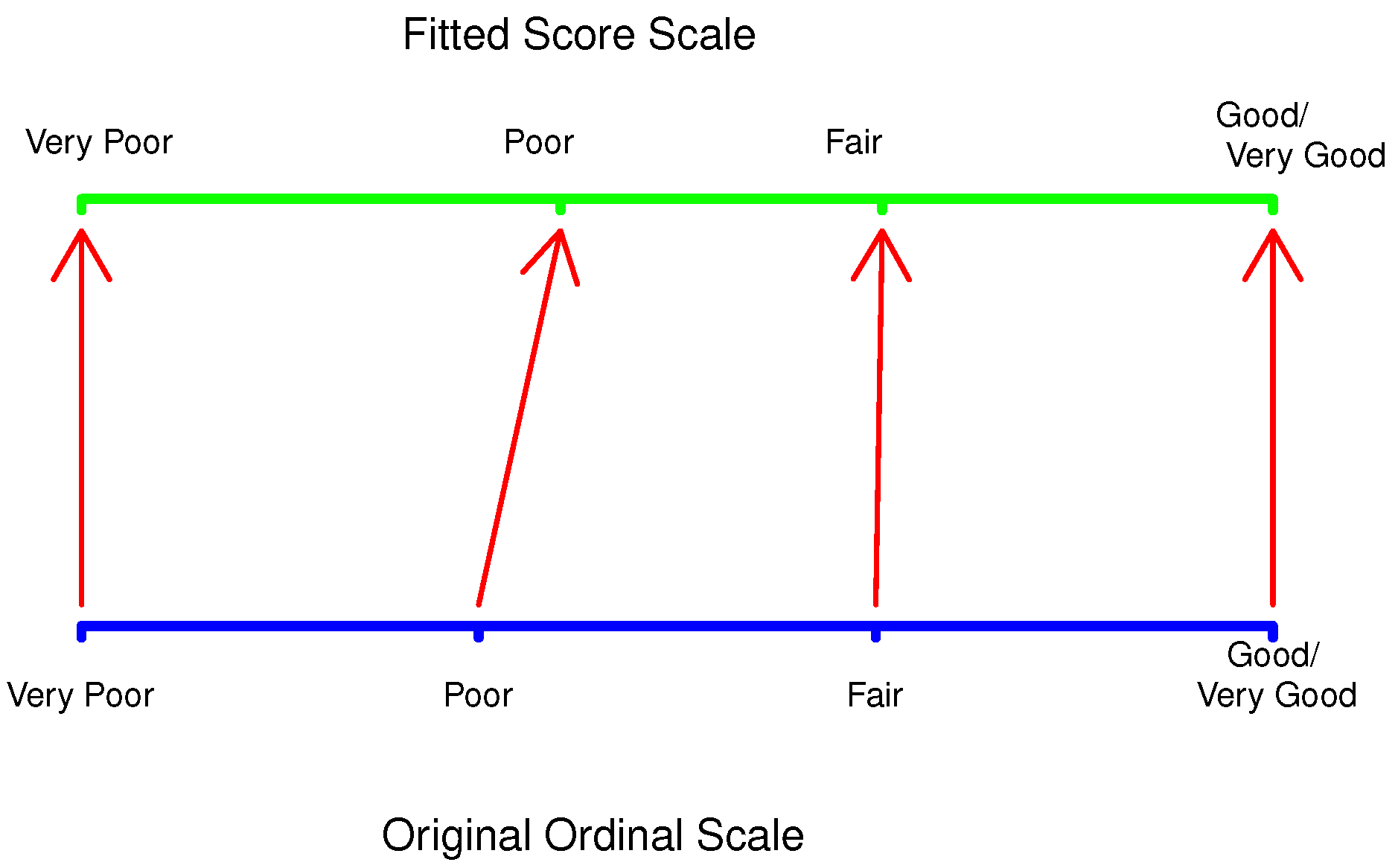
| Variable | Description | Values |
|---|---|---|
| Baseline | Self-assessment before the trial | 1 = very poor |
| 2 = poor | ||
| t1, t3, t5 | and 1, 3, and 5 months follow-up, respectively | 3 = fair |
| 4 = good or very good | ||
| Sex | Gender of the individual | 0 = female |
| 1 = male | ||
| Age | Years. Recorded at the baseline. | Range 21–66 |
| Trt | Treatment | 0 = placebo group |
| 1 = drug group |
| Coefficient | Estimate | S.E. | 95% C.I. |
|---|---|---|---|
| −0.145 | 0.060 | (−0.263, −0.027) | |
| −0.782 | 0.096 | (−0.969, −0.594) | |
| −2.508 | 0.117 | (−2.737, −2.279) | |
| (Sex) | 0.225 | 0.246 | (−0.257, 0.707) |
| (Age) | −0.020 | 0.012 | (−0.044, 0.004) |
| (Trt) | 1.333 | 0.237 | (0.869, 1.797) |
| (Baseline) | 2.304 | 0.260 | (1.795, 2.812) |
| 0.402 | 0.167 | (0.075, 0.729) | |
| 0.672 | 0.142 | (0.394, 0.950) |
| Test | Statistical Value | p-Value |
|---|---|---|
| Fagerland and Hosmer (OSM version) | 21.58 | 0.198 |
| 22.36 | 0.398 | |
| 11.64 | 0.227 | |
| 14.03 | 0.112 |
| Pars. | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| E | S.E. | L | U | E | S.E. | L | U | E | S.E. | L | U | E | S.E. | L | U | |
| 0.800 | 0.552 | −0.283 | 1.883 | 0.746 | 0.453 | −0.141 | 1.633 | 0.788 | 0.451 | −0.095 | 1.672 | 0.742 | 0.451 | −0.143 | 1.626 | |
| 0.824 | 0.674 | −0.496 | 2.145 | 0.755 | 0.543 | −0.310 | 1.820 | 0.804 | 0.542 | −0.258 | 1.865 | 0.748 | 0.544 | −0.318 | 1.814 | |
| −0.485 | 0.852 | −2.156 | 1.185 | −0.654 | 0.723 | −2.070 | 0.762 | 0.615 | 0.730 | −2.045 | 0.815 | −0.668 | 0.727 | −2.092 | 0.757 | |
| 0.349 | 0.167 | 0.021 | 0.677 | 0.349 | 0.169 | 0.018 | 0.680 | 0.339 | 0.170 | 0.005 | 0.672 | 0.349 | 0.167 | 0.021 | 0.677 | |
| 0.623 | 0.102 | 0.422 | 0.823 | 0.612 | 0.122 | 0.373 | 0.851 | 0.605 | 0.123 | 0.365 | 0.846 | 0.612 | 0.122 | 0.373 | 0.850 | |
| −0.130 | 0.269 | −0.656 | 0.397 | −0.114 | 0.260 | −0.624 | 0.397 | 0.113 | 0.258 | −0.619 | 0.393 | −0.119 | 0.261 | −0.629 | 0.392 | |
| 0.505 | 0.254 | 0.007 | 1.004 | 0.538 | 0.266 | 0.017 | 1.059 | 0.526 | 0.263 | 0.012 | 1.041 | 0.530 | 0.264 | 0.012 | 1.047 | |
| 1.191 | 0.471 | 0.267 | 2.115 | 1.240 | 0.410 | 0.437 | 2.043 | 1.216 | 0.409 | 0.415 | 2.017 | 1.239 | 0.412 | 0.430 | 2.047 | |
| 1.271 | 0.900 | −0.494 | 3.036 | 1.458 | 0.765 | −0.042 | 2.957 | 1.467 | 0.768 | −0.037 | 2.972 | 1.494 | 0.767 | −0.009 | 2.998 | |
| 2.449 | 0.937 | 0.613 | 4.285 | 2.602 | 0.751 | 1.130 | 4.075 | 2.552 | 0.755 | 1.072 | 4.033 | 2.616 | 0.755 | 1.136 | 4.095 | |
| 5.331 | 1.637 | 2.123 | 8.538 | 5.356 | 1.482 | 2.451 | 8.262 | 5.312 | 1.458 | 2.454 | 8.171 | 5.375 | 1.473 | 2.487 | 8.262 | |
| Pars. | ||||||||||||||||
| E | S.E. | L | U | E | S.E. | L | U | E | S.E. | L | U | E | S.E. | L | U | |
| 0.791 | 0.460 | −0.111 | 1.693 | 1.063 | 0.493 | 0.096 | 2.030 | 1.067 | 0.498 | 0.092 | 2.042 | 0.833 | 0.458 | −0.065 | 1.731 | |
| 0.773 | 0.557 | −0.319 | 1.865 | 1.142 | 0.593 | −0.020 | 2.305 | 1.153 | 0.591 | −0.004 | 2.311 | 0.831 | 0.548 | −0.244 | 1.906 | |
| −0.566 | 0.731 | −1.999 | 0.867 | −0.172 | 0.793 | −1.726 | 1.382 | −0.191 | 0.797 | −1.754 | 1.372 | −0.623 | 0.754 | −2.102 | 0.855 | |
| 0.342 | 0.178 | −0.007 | 0.692 | 0.269 | 0.208 | −0.139 | 0.677 | 0.269 | 0.208 | −0.138 | 0.676 | 0.320 | 0.174 | −0.020 | 0.660 | |
| 0.624 | 0.126 | 0.377 | 0.870 | 0.563 | 0.139 | 0.290 | 0.835 | 0.557 | 0.139 | 0.285 | 0.829 | 0.590 | 0.124 | 0.346 | 0.834 | |
| −0.125 | 0.262 | −0.638 | 0.388 | −0.118 | 0.245 | −0.597 | 0.362 | −0.111 | 0.243 | −0.587 | 0.365 | −0.101 | 0.253 | −0.597 | 0.394 | |
| 0.514 | 0.265 | −0.005 | 1.033 | 0.458 | 0.242 | −0.016 | 0.932 | 0.458 | 0.242 | −0.016 | 0.932 | 0.529 | 0.255 | 0.030 | 1.029 | |
| 1.231 | 0.412 | 0.423 | 2.038 | 0.986 | 0.399 | 0.203 | 1.768 | 0.976 | 0.396 | 0.199 | 1.752 | 1.148 | 0.397 | 0.371 | 1.926 | |
| 1.348 | 0.767 | −0.156 | 2.852 | 1.072 | 0.801 | −0.497 | 2.641 | 1.144 | 0.809 | −0.442 | 2.729 | 1.471 | 0.792 | −0.081 | 3.024 | |
| 2.526 | 0.762 | 1.032 | 4.019 | 2.082 | 0.820 | 0.474 | 3.689 | 2.090 | 0.822 | 0.479 | 3.702 | 2.537 | 0.775 | 1.018 | 4.057 | |
| 5.341 | 1.579 | 2.247 | 8.436 | 4.841 | 1.542 | 1.819 | 7.863 | 4.863 | 1.521 | 1.883 | 7.844 | 5.321 | 1.450 | 2.479 | 8.163 | |
| Pars. | ||||||||||||||||
| E | S.E. | L | U | |||||||||||||
| 0.811 | 0.456 | −0.084 | 1.705 | |||||||||||||
| 0.806 | 0.538 | −0.249 | 1.861 | |||||||||||||
| −0.686 | 0.749 | −2.155 | 0.783 | |||||||||||||
| 0.322 | 0.169 | −0.010 | 0.654 | |||||||||||||
| 0.589 | 0.120 | 0.353 | 0.824 | |||||||||||||
| −0.064 | 0.252 | −0.559 | 0.430 | |||||||||||||
| 0.533 | 0.253 | 0.036 | 1.029 | |||||||||||||
| 1.165 | 0.395 | 0.391 | 1.939 | |||||||||||||
| 1.565 | 0.792 | 0.013 | 3.117 | |||||||||||||
| 2.594 | 0.771 | 1.083 | 4.105 | |||||||||||||
| 5.351 | 1.400 | 2.607 | 8.096 | |||||||||||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fernández, D.; McMillan, L.; Arnold, R.; Spiess, M.; Liu, I. Goodness-of-Fit and Generalized Estimating Equation Methods for Ordinal Responses Based on the Stereotype Model. Stats 2022, 5, 507-520. https://doi.org/10.3390/stats5020030
Fernández D, McMillan L, Arnold R, Spiess M, Liu I. Goodness-of-Fit and Generalized Estimating Equation Methods for Ordinal Responses Based on the Stereotype Model. Stats. 2022; 5(2):507-520. https://doi.org/10.3390/stats5020030
Chicago/Turabian StyleFernández, Daniel, Louise McMillan, Richard Arnold, Martin Spiess, and Ivy Liu. 2022. "Goodness-of-Fit and Generalized Estimating Equation Methods for Ordinal Responses Based on the Stereotype Model" Stats 5, no. 2: 507-520. https://doi.org/10.3390/stats5020030
APA StyleFernández, D., McMillan, L., Arnold, R., Spiess, M., & Liu, I. (2022). Goodness-of-Fit and Generalized Estimating Equation Methods for Ordinal Responses Based on the Stereotype Model. Stats, 5(2), 507-520. https://doi.org/10.3390/stats5020030






