Abstract
A frequent problem with classic first digit applications of Benford’s law is the law’s inapplicability to clustered data, which becomes especially problematic for analyzing election data. This study offers a novel adaptation of Benford’s law by performing a first digit analysis after converting vote counts from election data to base 3 (referred to throughout the paper as 1-BL 3), spreading out the data and thus rendering the law significantly more useful. We test the efficacy of our approach on synthetic election data using discrete Weibull modeling, finding in many cases that election data often conforms to 1-BL 3. Lastly, we apply 1-BL 3 analysis to selected states from the 2004 US Presidential election to detect potential statistical anomalies.
1. Introduction
Although Benford’s Law (see Section 2 for a review) has successfully detected malfeasance in many settings (flagging, among others, financial records, images, and scientific data that have been modified), the difficulty in determining when one should expect Benfordness severely limits its applications to detect malfeasance or other issues. One popular argument is that data sets that are spread out over several orders of magnitude are often close to Benford. Though this phenomenon is frequently true (see [,] for results on exponential random variables), it can fail; see for example Chapter 2 of [] or [] for issues with the ‘spread’ hypothesis.
Clearly, not all data sets follow Benford’s law, especially in elections [,]. For example, if the data is not spread out sufficiently, the distribution of first digits is unlikely to conform to standard base 10 representations of Benford’s law (hereafter referred to as 1-BL 10); thus, deviations from Benfordness do not suggest malfeasance or other concerns. This issue is the main motivation for this work; specifically, our analysis is intended to address discussions where claims of election malfeasance are made when observed candidate vote counts do not satisfy 1-BL 10 [].
A classic example is precinct by precinct election data. Figure 1 provides such data from three counties from the 2004 US Presidential Election between incumbent President George W. Bush and Senator John F. Kerry. As is apparent in Figure 1, precinct level election data can be clustered thus rendering 1-BL 10 useless. As a result, work by Walter Mebane and others have looked at the second digit (hereafter referred to as 2-BL 10), or the last two digits (which one expects to be the same about 10% of the time base 10). For example, Mebane (2006) applied 2-BL 10 to election data from the state of Florida in 2004 US Presidential Election and the 2006 Mexican Presidential Election []. In subsequent research, Mebane (2009) applied 2-BL 10 to the 2009 Presidential Election in Iran to detect potential instances of malfeasance []. Mebane (2012) applied these techniques to German and American elections, discussing manifestations of coercion as well as effects of strategy and gerrymandering []. Although there have been some criticisms of the usefulness of Benford’s law [], Mebane (2011) responded to these criticisms arguing that 2-BL 10 does indeed have a reasonable degree of potential usefuless depending on the nature of the data analyzed and associated levels of aggregation []. There are many other applications of Benford’s law to election data as well [,,,,,,].
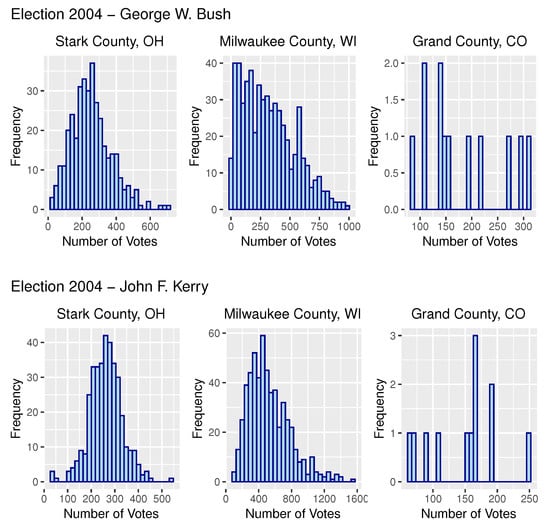
Figure 1.
Vote Distributions Across Precincts in US 2004 Presidential Election for Selected Counties.
In this study, we propose a novel approach for digit-based analysis of concentrated data. Namely, we write the data in terms of base 3 instead of base 10; the advantage of doing so is that our numbers are now spread out over several more magnitudes with two choices for the first digit instead of nine. For example, 81 is a two digit number in base 10, but in base 3 it is , five digits representing four orders of magnitude. The transformation of vote counts to base 3 thus spreads out clumped data. This idea of switching bases was originally proposed by the fourth named author over a decade ago to detect falsified data that passes a Benford test base 10 but might fail it in another base. Other base representations are of course possible; however, higher base representations would cluster the data more than base three, and base two representations would only have a single choice of a leading digit. Base 3 representations in election data were recently applied by the Kossovsky and Miller (2020) in [].
This paper thus contributes to the literature on Benford’s law by performing a first digit analysis of precinct level election data based on base 3 representations (hereafter referred to as 1-BL 3). Specifically, our work is organized as follows. First, we discuss existing forms of Benford’s law used for analyzing data and various generalizations. Subsequently, we fit precinct-level election data from the 2004 US Presidential Election to discrete Weibull distributions and assess the goodness of fit of these distributions in modeling election data. Afterwards, we draw upon this analysis by using a variety of choices of parameters based on this estimation to generate synthetic election data to compare the performance of 1-BL 10 and 1-BL 3. We find that, in many cases, election data generally conforms to 1-BL 3, but does not to 1-BL 10. Lastly, we apply 1-BL 3 analysis to selected states from the 2004 US Presidential election to detect potential statistical anomalies. We emphasize that our work is generalizable to other elections and thus should be a useful tool for researchers to use in analyzing the integrity of elections.
2. Benford’s Law and Generalizations
In the 1880s Simon Newcomb [] observed that the pages of tables of logarithms were not equally worn; there was more wear and tear on the earlier pages (those corresponding to the logarithms of numbers with a small first significant digit, such as 1, 2 or 3) than the later pages (those from numbers with a large first digit (such as 7, 8 or 9). Fifty years later, Frank Benford saw similar biases in many different data sets including population, X-ray volts, and the area of rivers []. Today, it has been found applicable in a broad number of disciplines such as geology, accounting, economics, computer science, and others [,,,,,].
Any positive number x can be written base B as , where is the significand and is an integer. We now say a data set is Benford, or satisfies Benford’s Law, base B if
thus base 10 the probabilities decrease from roughly 30% for a leading digit of 1 down to about 4.6% for a 9.
Sometimes, however, one uses Benford to refer to not just the first digit, but the distribution of the significand (alternatively one often says the system is strongly Benford); thus
Note that the first digit probabilities follow immediately from the significand, as
and we can easily determine the probabilities of the second digits:
We see a set is Benford base B if and only if its logarithms base B are equidistributed modulo 1; thus the digit bias disappears under a logarithmic transformation. For more on the history, theory and applications of Benford’s law see the survey articles [,,,] and the books [,,].
Table 1 provides 1-BL 10 and 2-BL 10 probabilities, namely the probability of a first or second digit being d base 10. Figure 2 provides a visual distribution of the first digits.

Table 1.
Benford probabilities for first and second digit (to four decimal places).
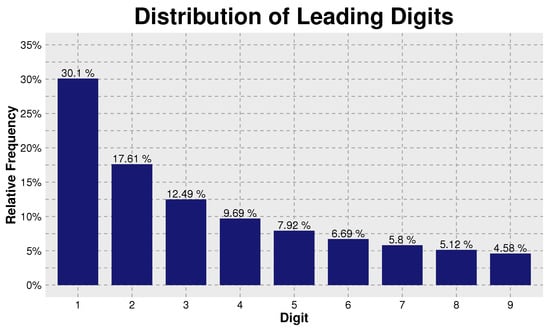
Figure 2.
The distribution of the leading digit base 10 according to Benford’s law.
Table 2 provides analogous probabilities for the distribution of the first and second digits of 1-BL 3 and second digit base 3 (2-BL 3) probabilities, and Figure 3 provides a visual representation of the distribution of the leading digits under base 3 representations.

Table 2.
Benford probabilities for first digit base 3 (to four decimal places).
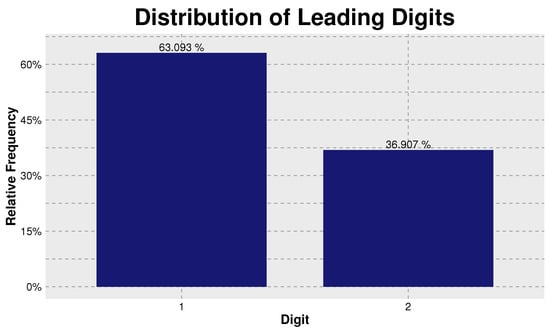
Figure 3.
The distribution of the leading digit base 3 according to Benford’s law.
One of the most utilized tests to see if a set is Benford is to compute the chi-squared statistic, with comparisons of the associated cumulative distribution function to statistical significance levels, usually or 0.05. If is the expected number that have a first digit of d base B, and is the observed number, then the chi-squared statistic is
If we work in base then as we have 9 choices for the first digit and the probabilities sum to 1, we only have 8 degrees of freedom (the probability of the last digit is forced from the other 8, and zero is never a first digit). If the digit distribution is drawn from Benford’s law, then of the time we should have a chi-square value of or less, and of the time it should be or less. To put it another way, if the data follows Benford’s law and we observe a value greater than , there is only a chance of that happening given that the data is Benford; if you observe values larger than the probability falls rapidly.
If we work in base 3, there are only two possibilities for the leading digits. For a set that is Benford we expect to observe a leading digit of 1 approximately 63.093% of the time and of 2 about 36.907%, with the chi-square values (with one degree of freedom) being 3.84 (at the 95% level) and 6.63 (at the 99% level).
In the following section, we modeled the skewed distributions of precinct level election data for the purposes of analyzing these distributions with respect to Benford’s law.
3. Empirical Estimates Using 2004 Election Data
3.1. Modeling with the Discrete Weibull
As is apparent in Figure 1, precinct by precinct election data can be skewed by vote counts heavily occurring in a just a few precincts. The discrete Weibull distribution provides a flexible family of distributions useful for modeling this type of skewed data []. The family, as well as associated variants, have been used to model real-world phenomena including soccer, respiratory capacity, fertility, and levels of microorganisms among others [,,,,]. In this section, we utilize this family to model precinct by precinct election data.
Specifically, in state i and county j consisting of precincts, we can model the vote count for two candidates x and y, and , using a discrete Weibull representation []. We take
and
where is the scale parameter and is the shape parameter.
3.2. Data and Model Estimation
We estimated the discrete Weibull model on data from the 2004 Presidential Election between incumbent President George W. Bush and Senator John F. Kerry available online on Harvard University’s DataVerse repository []. The repository is a comprehensive database providing precinct by precinct vote counts across counties for many states of the 2004 as well as other Presidential, Senatorial, and Congressional elections. Although there were a number of other candidates appearing on the ballot in the general election, we focused our analysis on the two main candidates in several selected states. Specifically, to estimate the model on states with varying political inclinations, we analyzed one “red” state (North Carolina), one “blue” state (Vermont), and three “battleground" states (Colorado, Ohio, and Wisconsin). We verified the data correctly represents vote counts reported by the United States Federal Election Commission for all five states, with the exception of Wisconsin, having an error of less than for each candidate []. In order to ensure a reasonable sample size for our analysis, we restricted our analysis to counties consisting of more than ten election day precincts.
For such counties, we estimated the scale and shape parameters for the distribution of the precinct by precinct vote tallies for each of the two candidates x and y in state i and county j—, , , and —via the method of maximum likelihood (MLE). Subsequently, to assess goodness of fit, we performed a series of two sample Kolmogorov-Smirnov (KS) tests assessing the null hypothesis of distributional equality, comparing the distribution of , or , with a random sample of size K of the associated discrete Weibull distribution using parameter estimates obtained via MLE. We averaged p-values obtained from 100 simulations to obtain a pooled Monte Carlo estimate of the goodness of fit of the estimated distributions. Our estimated shape and scale parameters, as well as pooled p-value estimates, for the battleground states of Ohio, Colorado, and Wisconsin are presented in the scatterplots in Figure 4 for counties having at least ten precincts. Scatterplots of MLE estimates and KS-test results for Vermont and North Carolina are omitted for brevity and are available from the authors upon request.
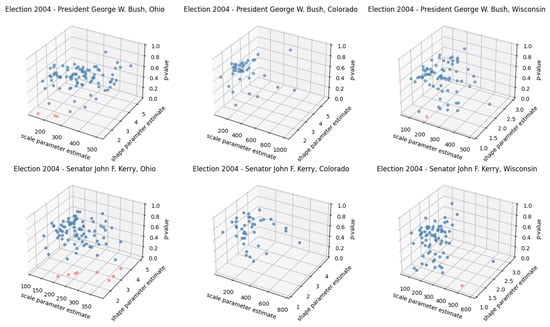
Figure 4.
Discrete Weibull parameter estimation and Kolmogorov Smirnov Goodness of Fit Test Results for Ohio, Colorado, and Wisconsin, US 2004 Presidential Election. p-values above 0.05 (indicate conformance to discrete Weibull distribution.
As Figure 4 illustrates, for all three battleground states, the discrete Weibull distributions fit quite well. Altogether there are three counties in Ohio that have pooled p-values less than 0.05, one county in Wisconsin, and none in Colorado for Bush. For Kerry, there were eight such counties in Ohio, one county in Wisconsin, and none in Colorado. After performing the standard, albeit conservative, Bonferroni corrections there was only one county—Cuyahaga County, Ohio—for Bush, that was statistically significant (). These results demonstrate the efficacy of using discrete Weibull distribution to model precinct level data across counties.
Furthermore, as Figure 4 also illustrates, our estimated parameters vary notably, depending on the county. Table 3 and Table 4 provide MLE parameter estimates and p-values the KS tests, and precinct sizes for the selected counties presented in Figure 1.

Table 3.
Maximum Likelihood Estimates and Goodness of Fit Test Results for Vote Counts for Selected Counties in 2004 US Presidential Election—President George W. Bush. p-values above 0.05 (plotted in blue) indicate conformance to discrete Weibull distribution.

Table 4.
Maximum Likelihood Estimates and Goodness of Fit Test Results for Vote Counts for Selected Counties in 2004 US Presidential Election—Senator John F. Kerry. p-values above 0.05 indicate conformance to discrete Weibull distribution.
Table 3 and Table 4 illustrate the robustness of the discrete Weibull distribution in its ability to model different types of counties across the country. Namely, Milwaukee county, WI has larger scale and smaller shape parameters than the less densely populated Stark County, OH, and Grand County, CO. Regardless, the p-values for all three counties are well above 0.05, demonstrating the robustness of the choice of the discrete Weibull distribution across different counties.
The analysis in this section illustrates the efficacy of using the discrete Weibull distribution at fitting precinct level election data across a wide choice of parameterizations. In the following section, we utilize these facts to examine the usefulness of 1-BL 3 and 1-BL 10 in analyzing election data.
4. Comparisons of 1-BL 3 and 1-BL 10 to Potential Vote Distributions
In the previous section, we demonstrated the usefulness of the discrete Weibull distribution in modeling precinct level election data. In this section, we examine a variety of choices of discrete Weibull parmaeterizations and assess their adherence to 1-BL 3 and 1-BL 10 via Monte Carlo analysis using both chi-squared testing and binomial testing.
4.1. Simulations Using Chi-Squared Testing
Specifically, based on the results presented in Figure 4, we simulated county level data with the number of simulated precincts varying between 50 and 300. We varied the scale parameter between 100 and 600 in increments of 25 and varied the shape parameter between 1 and 6 in increments of 1. After compiling the expected and observed number of first digits under both base 10 and base 3 representations, we performed chi-squared tests for both 1-BL 10 and 1-BL 3 (assuming under the null hypothesis of distributional equality, chi-squared distributions having eight and one degree of freedom respectively as discussed in Section 2) and subsequently computed associated p-values. We averaged these p-values over the course of 25 Monte Carlo simulations. Our results are presented in Figure 5 and Figure 6.
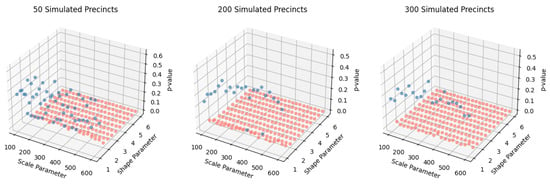
Figure 5.
First Digit Base 10 Monte Carlo Analysis of Simulated Discrete Weibull Distributions with Various Choices of Parameterizations and Precinct Sizes Using Chi Squared Testing. p-values above 0.05 (plotted in blue) indicate conformance to 1-BL 10.
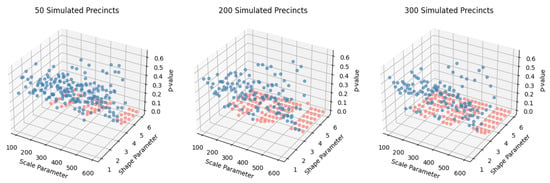
Figure 6.
First Digit Base 3 Monte Carlo Analysis of Simulated Discrete Weibull Distributions with Various Choices of Parameterizations and Precinct Sizes Using Chi-Squared Testing. p-values above 0.05 (plotted in blue) indicate conformance to 1-BL 3.
As is apparent Figure 5, assuming a statistical significance level of = 0.05 the simulated precinct data rarely conforms to 1-BL 10 except for choices of scale parameter between 100 and 200. Upon conversion to base 3, adherence to Benford’s law is considerably more robust, as is illustrated in Figure 6. Even under base 3 representations, however, Benford’s law is not always observed. For example, if the scale parameter exceeds 500 and the shape parameter exceeds 4, the associated p-values are below 0.05 and thus Benford’s behavior is not observed. (This behavior persists even after altering for multiple comparisons via Bonferroni corrections to .)
4.2. Simulations Using Binomial Testing
Although chi-squared testing has been used extensively in Benford’s law analysis of elections [,,,,,,,,,,], some have raised concerns with the use of the chi-squared test in certain situations []. (For example, although it depends on the application, there were nearly half a million observations of some hydrology data in [], the chi-square test was sensitive enough to detect as significant very small deviations from Benford’s law, something that would not happen with essentially pure geometric behavior, such as the Fibonacci numbers, which do pass a chi-square test with this many values). As there are only two possible leading digits, one alternative approach is binomial testing. We performed the same simulations presented in the prior section instead using two-sided binomial testing to test the null hypothesis of adherence to expected frequencies under 1-BL 3. Our results using the same choices of parameterizations used in Figure 5 and Figure 6 are presented in Figure 7.
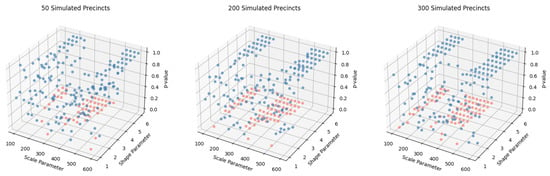
Figure 7.
First Digit Base 3 Monte Carlo Analysis of Simulated Discrete Weibull Distributions with Various Choices of Parameterizations and Precinct Sizes Using Binomial Testing. p-values above 0.05 (plotted in blue) indicate conformance to 1-BL 3.
As Figure 7 illustrates, the binomial test indicates that 1-BL 3 is indeed useful for modeling election data under a variety of paramaterizations. Altogether, our analysis of this synthetic election data using the wide choices of parameters motivated by our MLE estimation in Section 3 illustrates that 1-BL 3 is considerably more effective than 1-BL 10 in fitting election data. Thus, base 3 representations of precinct by precinct data are considerably much more likely to adhere to Benford’s law than standard base 10 representations for most of the choices of parameterizations presented in Figure 5 and Figure 6. For larger sample sizes, however, the chi squared test in some cases does not detect conformity to 1-BL 3, which may be due to the sensitivity of the test itself as well as slight approximation error [,]. Regardless, these results illustrate that for a variety of parameterizations and sample sizes, simulated discrete Weibull data adheres to 1-BL3. As our analysis in Section 3 demonstrates that the American election data analyzed in this study fits these discrete Weibull distributions, our simulations in this section thus provide theoretical justification for applying 1-BL 3 to American election data, which we perform in the following section.
5. Applications of 1-BL 3 to the 2004 US Presidential Election
As a result of our analysis in Section 4, we now have a theoretical justification for applying 1-BL 3 to election data. In this section, we do so by utilizing the data from the 2004 US Presidential Election discussed in Section 3. Specifically, we analyzed counties amongst the states of Colorado, North Carolina, Ohio, Vermont, and Wisconsin to assess adherence to 1-BL 3 on a county by county basis. The electoral outcomes of these states is summarized in Table 5.

Table 5.
States from 2004 US Presidential Election used for Analysis.
5.1. Chi-Square Test Results
As we did in Section 3, we restricted our analysis to counties voting on election day that consisted of at least ten election day precincts. We assumed a statistical significance level and performed comparisons of observed and expected values. Specifically, as discussed in Section 2, we did so by utilizing a chi-squared distribution with one degree of freedom to test the null hypothesis of distributional equality between these observed and expected counts. Afterwards, we computed adjusted p-values using the Benjamni-Hochberg procedure to control for the false discovery rate [] as has been done in other election related work using Benford’s law (see for example [,,]). Our results are presented in Table 6.

Table 6.
First Digit Base 3 Benford’s Analysis on Selected Battleground and Non-Battleground States in the US 2004 Presidential Election.
As Table 6 illustrates, all counties amongst the non-competitive states of North Carolina and Vermont as well as the battleground state of Wisconsin conform to 1-BL3. On the other hand, there are four distributions amongst counties/candidates in Colorado and fifteen distributions in Ohio that are statistically anomalous.
However, as Figure 6 from Section 4 demonstrates, depending on the distribution of votes for either candidate, certain counties may not necessarily conform to 1-BL 3 to begin with. As a result, we performed another series of Monte Carlo simulations for the anomalous counties in Table 6 to assess whether the estimated vote distribution for each county/candidate indeed conforms to Benford’s law. To do so, we again ran 25 Monte Carlo simulations drawing from discrete Weibull distributions using the county’s estimated parameters (presented as part of Figure 4) and reported precinct sizes for the anomalous counties in Table 6 to assess whether these distributions indeed conform to 1-BL 3. We averaged p-values across the 25 simulations and compared these values to those in Table 6. We flagged counties where the estimated distribution conforms to Benford’s law (p-value > 0.05) while the actual data does not (adjusted p-value <0.05). Our results are presented in Table 7.

Table 7.
Analysis of Whether Anomalous Counties from Table 6 Deviate from Benford’s Law.
As Table 7 shows, the vote distribution for Senator John F. Kerry in El Paso county, Colorado should theoretically adhere to 1-BL 3 but does not. There were four additional counties in Ohio for Kerry that should also have conformed to 1-BL 3 that failed (Geuga, Greene, Lorain, and, Muskingum Counties). There was one such county for President George W. Bush—Greene County, Ohio. Furthermore, as Table 7 also illustrates, although several other distributions for both candidates were deemed statistically anomalous in Table 6, their estimated distributions do not either, and thus their non-adherenece to 1-BL 3 may not be unnatural.
5.2. Binomial Test Results
For comparative purposes, we utilize the binomial testing approach analyzed in Section 4.2 in this subsection. For brevity, we present results using these tests for two counties from the state of Colorado, one anomalous and one not, and further analysis of other counties and other states is available from the authors upon request; the analysis shows the tests agreeing on when fits are Benford and when they are not. Using chi-squared testing, Jefferson County, CO has been determined to be statistically anomalous for both candidates (p-value < 0.01). Specifically, for George W. Bush, 1 appears as the first digit 258 times across precincts, whereas 2 appears as the first digit 66 times under base 3 representation. For John F. Kerry, on the other hand, 1 appears as the first digit 295 times and 2 appears as the first digit 29 times. The expected counts for the first digits being 1 or 2 are 204.42 and 119.58 respectively. For Bush and Kerry, the 95% confidence intervals are (242.44, 271.77) and (283.17, 304.31) respectively for 1 being the first digit and (52.23, 81.56) and (19.69, 40.83) for 2 being the second digit. As a result, the digits of neither candidate belong to the associated CIs, and thus for both candidates, the county is statistically anomalous confirming the chi squared test results.
Denver County, CO, however, is not anomalous according to chi-squared testing (p-values 0.48 and 0.79 respectively). For George W. Bush, 1 appears as the first digit 253 times across precincts, whereas 2 appears as the first digit 162 times. For John F. Kerry, on the other hand, 1 appears as the first digit 253 times and 2 appears as the first digit 167 times under base 3 representation. The expected counts for the first digits being 1 or 2 are 264.99 and 155.01 respectively. For the two candidates, the 95% confidence intervals are (239.67, 277.65) and (232.59, 272.69) respectively for 1 being the first digit and (142.35, 182.33) and (147.21, 187.40) respectively for 2 being the second digit. In this instance, both digits for the two candidates belong to their respective CIs, thus confirming the results indicated by the chi squared test.
6. Discussion
The results in Table 7 flag several counties for Senator Kerry and one for President Bush as statistically anomalous in terms of 1-BL 3. Interestingly, Ohio was one of the most contentious states in the 2004 election []. Although our model flags approximately five percent of Ohio’s 88 counties, these statistical anomalies are still detected after corrections due to multiple comparisons. These results, however, neither offer any indication as the cause of potential malfeasance, if present, nor do they shed light on which side was responsible. One goal of Benford tests is to detect malfeasance; however, certain types cannot be observed by these methods. For example, if a fixed percentage of votes were switched from one candidate to another while keeping the number of voters fixed, the net effect is to just change the percentage of support for each candidate. Similarly, if a fixed number of ballots are added in each precinct, the effect would be to both increase the number of voters and adjust the candidates’ support. It is important to remember tests such as these cannot prove malfeasance; the main utility is to highlight situations that are worth additional investigation; for example, in cases where 1-BL 3 fails it might be valuable to check current precinct voting against previous years when 1-BL 3 held.
Again, although malfeasance could constitute one explanation of non-conformance to Benford’s law, associated anomalies do not necessarily prove malfeasance as other explanations are be possible. For example, Mebane (2010, 2012, 2013) has discussed how deviations from 2-BL 10 could be due not only to malfeasance but also may be manifestations of mobilization efforts, last minute changes to voting preference, as well as effects of gerrymandering among others [,,]. The effect of these factors on conformance 1-BL3 has not been studied thus far and is a worthy topic of future research. If 1-BL3 can indeed manifest these effects, it would be useful for future research to differentiate between these effects and malfeasance, to render these techniques more useful for auditing or potential litigation.
7. Conclusions and Future Research
Our study illustrates the usefulness of 1-BL 3 in analyzing elections, flagging a number of counties in the 2004 US Presidential Election. Our analysis in Section 4, suggests that 1-BL 10 analysis would almost surely unnecessarily flag many other counties that may not truly be anomalous. As discussed in Section 6, however, although potential malfeasance could constitute one explanation of 1-BL 3 based anomalies, there may be other potential explanations as well. Future research should look into refining these number theoretic models to differentiate amongst potential explanations. Regardless, if there are concerns about potential malfeasance, 1-BL 3 could indeed be a useful tool to detect for anomalies as a basis for potential auditing.
Although we have analyzed several states from the 2004 US Presidential Election, we hope our work encourages future research to apply our method to other elections of all levels, both American and foreign. However, as noted by Mebane (2011), the appropriate unit of analysis for Benford’s law is precinct level data across counties, as we have utilized in this study []. As a result, Benford’s law is not useful for detecting potential malfeasance with absentee ballots such as in the 2018 Congressional election in North Carolina’s ninth district, but there are other statistical techniques that have been demonstrated to be useful for such absentee ballot analysis []. The number of statistical tools to analyze the integrity of elections is growing [,,,,], and the techniques presented in this paper thus should be viewed as yet another tool in the statistician’s arsenal to analyze election data. Future research should thus include our tool as part of a suite of such tools to comprehensively analyze all aspects of election data.
One potential limitation of this approach is that the data may become so heavily spread out via base three representations that some instances of malfeasance may be rendered undetectable. Other base representations may potentially ameliorate this problem at the expense of clustering the data. Future research should weigh such tradeoffs among different bases.
Moreover, until now, 2-BL 10 was the primary technique used for applying Benford’s law to election data. Future research should compare the efficacy of 1-BL 3 to 2-BL 10. It would be useful to simulate election data as we have done in the study, externally impose malfeasance in the model, and assess what forms of malfeasance are detectable by these techniques. Finally, there is of course no a priori reason to apply these techniques solely to elections, and we hope that this research encourages the use of 1-BL 3 in other applied settings of clustered data where 1-BL 10 is not applicable. Batting averages in baseball, serving speeds in tennis, government-reported statistics, and stock market data are indeed worthy examples of future investigation.
It is always useful to have tools to identify potential anomalies in election data. We hope the techniques presented here provide a useful addition to the applied mathematician/statistician’s toolbox for doing so.
Author Contributions
Conceptualization, K.D. and S.J.M.; Data curation, D.G.; Formal analysis, K.D. and S.J.M.; Investigation, K.D.; Methodology, K.D.; Project administration, S.J.M.; Writing—original draft, K.D. and S.J.M.; Writing—review & editing, K.M.A., K.D., D.G. and S.J.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The data used in this study is publicly available on Harvard University’s DataVerse repository [].
Acknowledgments
We would like to thank the editors and the reviewers for useful comments on this manuscript. Additionally, we would like to thank Parker Sheppard and Hans von Spakovsky for reviewing a prior version of this manuscript as well as Ryan Sotnick, Mary Kolesar, and Mary Catherine Legreid for help with prior analysis.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Engel, H.A.; Leuenberger, C. Benford’s law for exponential random variables. Stat. Probab. Lett. 2003, 63, 361–365. [Google Scholar] [CrossRef]
- Miller, S.J.; Nigrini, M.J. Order statistics and Benford’s law. Int. J. Math. Math. Sci. 2008, 2008, 382948. [Google Scholar] [CrossRef]
- Miller, S.J.; Berger, A.; Hill, T. Theory and Applications of Benford’s Law. 2015. Available online: https://www.researchgate.net/publication/280157559_Benford%27s_Law_Theory_and_Applications (accessed on 29 June 2022).
- Berger, A.; Hill, T.P. Benford’s law strikes back: No simple explanation in sight for mathematical gem. Math. Intell. 2011, 33, 85. [Google Scholar] [CrossRef]
- Deckert, J.; Myagkov, M.; Ordeshook, P.C. Benford’s Law and the detection of election fraud. Political Anal. 2011, 19, 245–268. [Google Scholar] [CrossRef]
- Mebane, W.R. Comment on “Benford’s Law and the detection of election fraud”. Political Anal. 2011, 19, 269–272. [Google Scholar] [CrossRef]
- Mebane, W. Inappropriate Applications of Benford’s Law Regularities to Some Data from the 2020 Presidential Election in the United States. 2020. Available online: http://www.umich.edu/~wmebane/inapB.pdf (accessed on 29 June 2022).
- Mebane, W.R., Jr. Election forensics: Vote counts and Benford’s law. In Proceedings of the Summer Meeting of the Political Methodology Society, UC-Davis, Davis, CA, USA, 20–22 July 2006; Volume 17. [Google Scholar]
- Mebane, W.R.; Larijani, A.; Mehralizadeh, M.; Moeen, M.; Hashemi, A.; These, R. Note on the presidential election in Iran, June 2009. Available online: http://websites.umich.edu/~wmebane/note29jun2009.pdf (accessed on 29 June 2022).
- Mebane, W.R. Second-digit tests for voters’ election strategies and election fraud. In Proceedings of the Annual Meeting of the Midwest Political Science Association, Chicago, IL, USA, 12–15 April 2012. [Google Scholar]
- Kalinin, K.; Mebane, W.R. Understanding electoral frauds through evolution of Russian federalism: From “bargaining loyalty” to “signaling loyalty”. In Proceedings of the Annual Meeting of the Midwest Political Science Association, Chicago, IL, USA, 31 March–2 April 2011; pp. 1–26. [Google Scholar]
- Mebane, W.R. Election fraud or strategic voting? Can second-digit tests tell the difference. In Proceedings of the Summer Meeting of the Political Methodology Society, Iowa, IA, USA, 22–24 July 2010. [Google Scholar]
- Mebane, W.R., Jr. Fraud in the 2009 presidential election in Iran? Chance 2010, 23, 6–15. [Google Scholar] [CrossRef]
- Mebane, W.R., Jr. Election forensics: The meanings of precinct vote counts’ second digits. In Proceedings of the Summer Meeting of the Political Methodology Society, Charlottesville, VA, USA, 18–20 July 2013. [Google Scholar]
- Mebane, W.R., Jr.; Kalinin, K. Electoral falsification in Russia: Complex diagnostics selections 2003–2004, 2007–2008 (in Russian). Elect. Policy REO 2009, 2, 57–70. [Google Scholar]
- Mebane, W.R., Jr.; Kalinin, K. Electoral fraud in Russia: Vote counts analysis using second-digit mean tests. In Proceedings of the Annual Meeting of the Midwest Political Science Association, Chicago, IL, USA, 22–25 April 2010; Volume 20. [Google Scholar]
- Mebane, W.R., Jr.; Kent, T.B. Second Digit Implications of Voters’ Strategies and Mobilizations in the United States during the 2000s. In Proceedings of the Annual Meeting of the Midwest Political Science Association, Chicago, IL, USA, 11–14 April 2013; pp. 11–14. [Google Scholar]
- Kossovsky, A.E.; Miller, S.J. Report on Benford’s Law Analysis of 2020 Presidential Election Data. Available online: https://web.williams.edu/Mathematics/sjmiller/public_html/KossoskyMiller_FinalBenfordAnalysis.pdf (accessed on 29 June 2022).
- Newcomb, S. Note on the frequency of use of the different digits in natural numbers. Am. J. Math. 1881, 4, 39–40. [Google Scholar] [CrossRef]
- Benford, F. The law of anomalous numbers. Proc. Am. Philos. Soc. 1938, 78, 551–572. [Google Scholar]
- Nigrini, M.J.; Miller, S.J. Benford’s law applied to hydrology data—Results and relevance to other geophysical data. Math. Geol. 2007, 39, 469–490. [Google Scholar] [CrossRef]
- Geyer, A.; Martí, J. Applying Benford’s law to volcanology. Geology 2012, 40, 327–330. [Google Scholar] [CrossRef]
- Grammatikos, T.; Papanikolaou, N.I. Applying Benford’s law to detect accounting data manipulation in the banking industry. J. Financ. Serv. Res. 2021, 59, 115–142. [Google Scholar] [CrossRef]
- Jolion, J.M. Images and Benford’s law. J. Math. Imaging Vis. 2001, 14, 73–81. [Google Scholar] [CrossRef]
- Arshadi, L.; Jahangir, A.H. Benford’s law behavior of Internet traffic. J. Netw. Comput. Appl. 2014, 40, 194–205. [Google Scholar] [CrossRef]
- Villas-Boas, S.B.; Fu, Q.; Judge, G. Benford’s law and the FSD distribution of economic behavioral micro data. Phys. A Stat. Mech. Its Appl. 2017, 486, 711–719. [Google Scholar] [CrossRef]
- Hill, T.P. A statistical derivation of the significant-digit law. Stat. Sci. 1995, 10, 354–363. [Google Scholar] [CrossRef]
- Hill, T.P. The first digit phenomenon: A century-old observation about an unexpected pattern in many numerical tables applies to the stock market, census statistics and accounting data. Am. Sci. 1998, 86, 358–363. [Google Scholar] [CrossRef]
- Nigrini, M.J. Benford’s Law: Applications for Forensic Accounting, Auditing, and Fraud Detection; John Wiley & Sons: Hoboken, NJ, USA, 2012; Volume 586. [Google Scholar]
- Raimi, R.A. The first digit problem. Am. Math. Mon. 1976, 83, 521–538. [Google Scholar] [CrossRef]
- Berger, A.; Hill, T.P. An Introduction to Benford’s Law; Princeton University Press: Princeton, NJ, USA, 2015. [Google Scholar]
- Kossovsky, A.E. Benford’s Law: Theory, the General Law of Relative Quantities, and Forensic Fraud Detection Applications; World Scientific: Singapore, 2014; Volume 3. [Google Scholar]
- Nakagawa, T.; Osaki, S. The discrete Weibull distribution. IEEE Trans. Reliab. 1975, 24, 300–301. [Google Scholar] [CrossRef]
- Peluso, A.; Vinciotti, V.; Yu, K. Discrete Weibull generalized additive model: An application to count fertility data. J. R. Stat. Soc. Ser. C (Appl. Stat.) 2019, 68, 565–583. [Google Scholar] [CrossRef]
- El-Morshedy, M.; Eliwa, M.; El-Gohary, A.; Khalil, A. Bivariate exponentiated discrete Weibull distribution: Statistical properties, estimation, simulation and applications. Math. Sci. 2020, 14, 29–42. [Google Scholar] [CrossRef]
- Englehardt, J.D.; Li, R. The discrete Weibull distribution: An alternative for correlated counts with confirmation for microbial counts in water. Risk Anal. Int. J. 2011, 31, 370–381. [Google Scholar] [CrossRef] [PubMed]
- Patriarca, R.; Hu, T.; Costantino, F.; Di Gravio, G.; Tronci, M. A system-approach for recoverable spare parts management using the discrete Weibull distribution. Sustainability 2019, 11, 5180. [Google Scholar] [CrossRef]
- Para, B.A.; Jan, T. Compound of discrete Weibull and Minimax distributions as a new count data model with application in genetics. Appl. Math. Inf. Sci. Lett. 2017, 5, 113–124. [Google Scholar] [CrossRef]
- Ansolabehere, S.; Palmer, M.; Lee, A. Precinct-Level Election Data, 2002–2012. Harvard Dataverse. 2015. Available online: https://dataverse.harvard.edu/ (accessed on 29 June 2022).
- 2004 Election Results. Available online: https://www.fec.gov/resources/cms-content/documents/2004tables.pdf (accessed on 22 June 2022).
- Kossovsky, A.E. On the Mistaken Use of the Chi-Square Test in Benford’s Law. Stats 2021, 4, 419–453. [Google Scholar] [CrossRef]
- Benjamini, Y.; Hochberg, Y. Controlling the false discovery rate: A practical and powerful approach to multiple testing. J. R. Stat. Soc. Ser. B (Methodol.) 1995, 57, 289–300. [Google Scholar] [CrossRef]
- Mebane, W.R.; Alvarez, R.M.; Hall, T.E.; Hyde, S.D. Election forensics: The second-digit Benford’s law test and recent American presidential elections. In Election Fraud: Detecting and Deterring Electoral Manipulation; 2008; pp. 162–181. Available online: https://www.semanticscholar.org/paper/Election-Forensics%3A-The-Second-digit-Benford%27s-Law-Mebane/56ef9eebb429bde1815aed5c49e5fc5157b5f4a8 (accessed on 29 June 2022).
- Mebane, W.R., Jr. Election forensics: Statistics, recounts and fraud. In Proceedings of the Annual Meeting of the Midwest Political Science Association, Chicago, IL, USA, 12–16 April 2007; pp. 12–16. [Google Scholar]
- Dao, J. The 2004 Campaign Battlegrounds; Ohio. The New York Times, 31 October 2004. [Google Scholar]
- Herron, M.C. Mail-In Absentee Ballot Anomalies in North Carolina’s 9th Congressional District. Elect. Law J. Rules Politics Policy 2019, 18, 191–213. [Google Scholar] [CrossRef]
- Zhang, M.; Alvarez, R.M.; Levin, I. Election forensics: Using machine learning and synthetic data for possible election anomaly detection. PLoS ONE 2019, 14, e0223950. [Google Scholar] [CrossRef]
- Lacasa, L.; Fernández-Gracia, J. Election forensics: Quantitative methods for electoral fraud detection. Forensic Sci. Int. 2019, 294, e19–e22. [Google Scholar] [CrossRef] [Green Version]
- Mebane, W.R., Jr. Election forensics: Statistical interventions in election controversies. In Proceedings of the Annual Meeting of the American Political Science Association, Chicago, IL, USA, 30 August–2 September 2007; Volume 13. [Google Scholar]
- Mebane, W.R., Jr.; Klaver, J. Election Forensics: Strategies versus Election Frauds in Germany. In Proceedings of the Annual Conference of the European Political Science Association, Vienna, Austria, 25–27 June 2015. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).