Modeling Secondary Phenotypes Conditional on Genotypes in Case–Control Studies
Abstract
1. Introduction
2. Proposed Method
3. Simulation Study
3.1. General Setup
3.2. Continuous Phenotypes
3.3. Ordinal Phenotypes
- , , , and
- , , , and
- , , , and
- , , , , and .
3.4. Time-to-Event Phenotypes
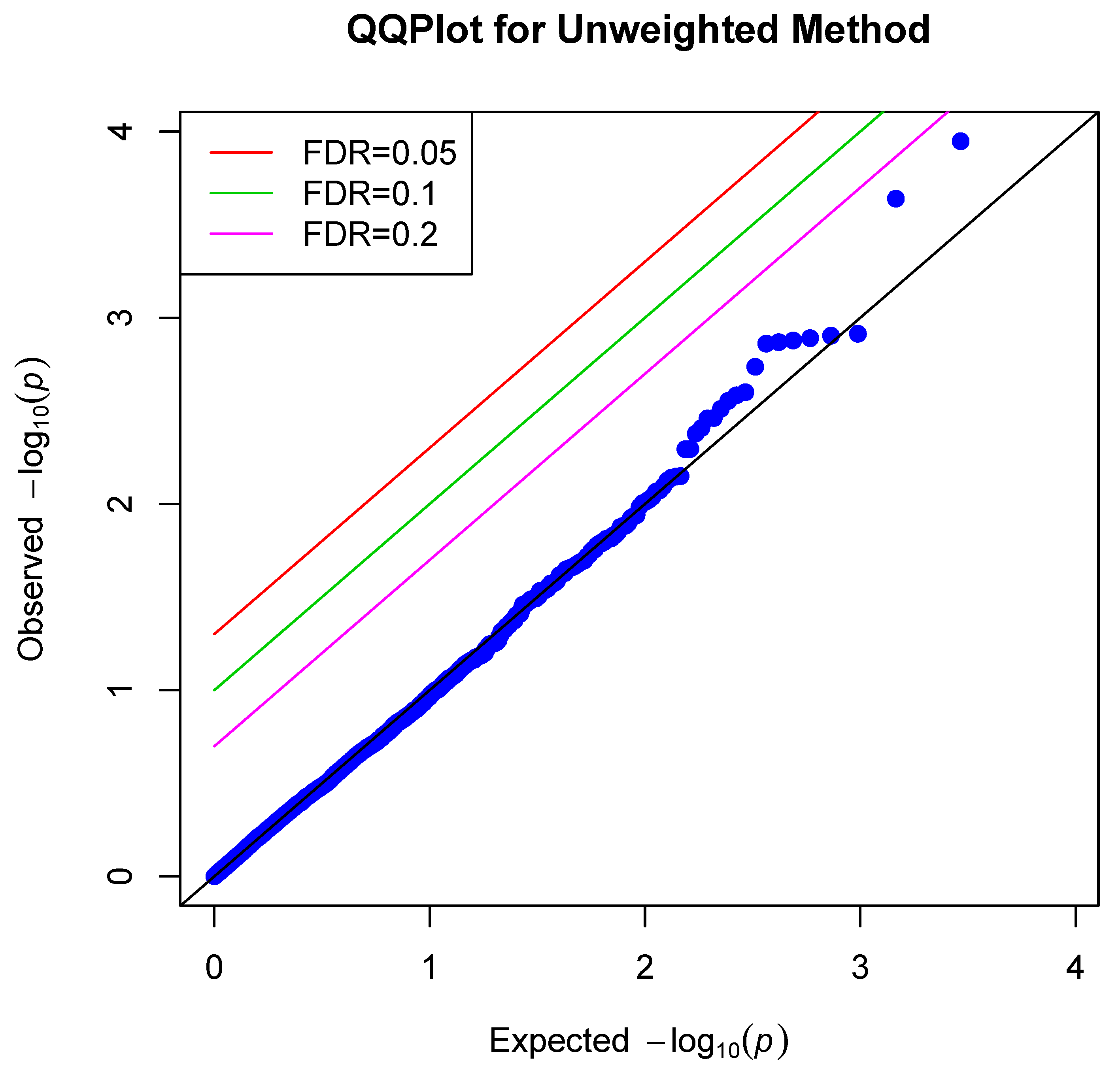
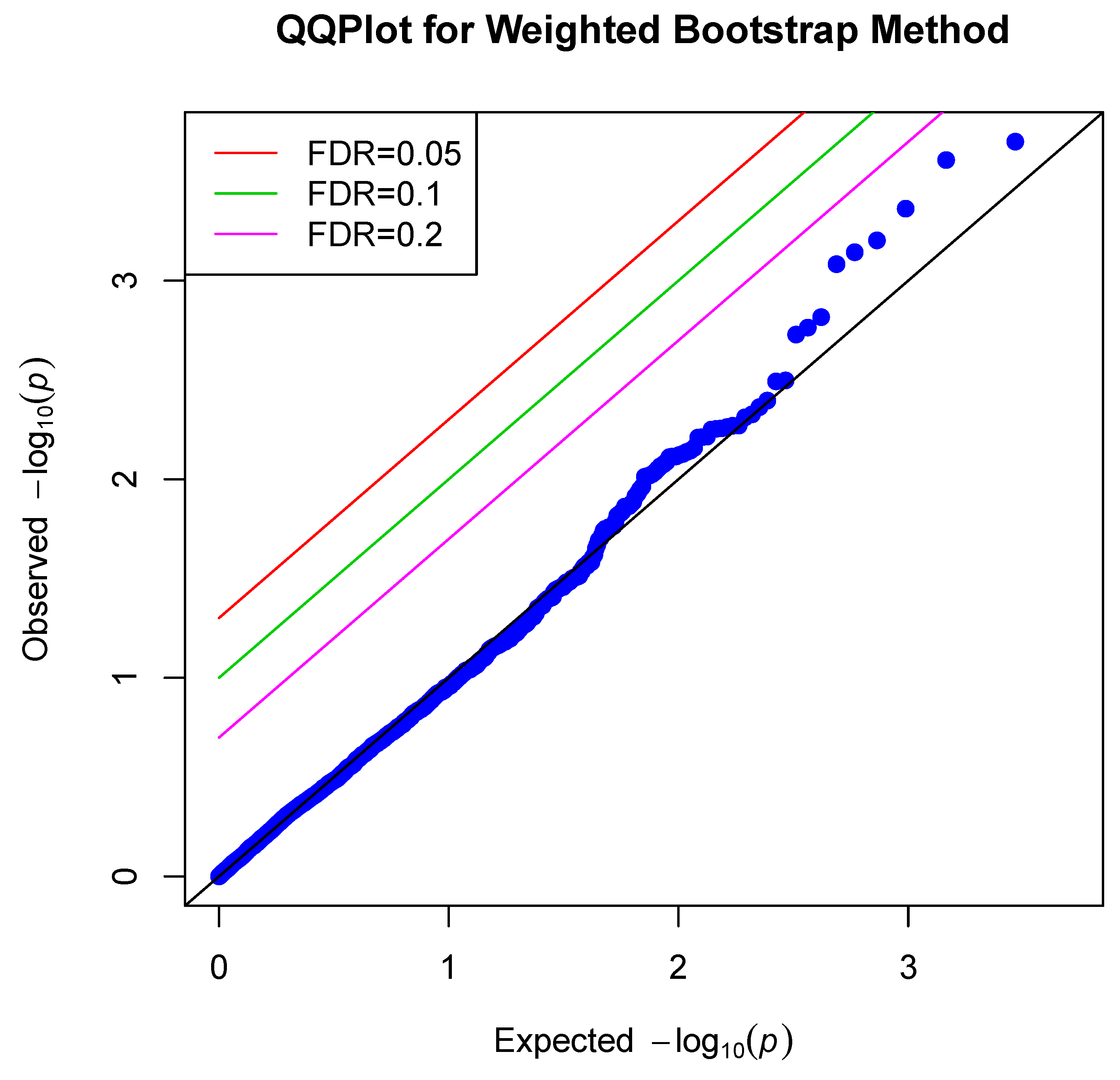
4. Data Application
5. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| OPPERA | Orofacial Pain: Prospective Evaluation and Risk Assessment |
| TMD | Temporomandibular disorders |
| IPW | Inverse probability weighting |
| Q–Q | Quantile–quantile |
References
- Prentice, R.L.; Pyke, R. Logistic Disease Incidence Models and Case-Control Studies. Biometrika 1979, 66, 403–411. [Google Scholar] [CrossRef]
- Monsees, G.M.; Tamimi, R.M.; Kraft, P. Genome-wide association scans for secondary traits using case-control samples. Genet. Epidemiol. 2009, 33, 717–728. [Google Scholar] [CrossRef] [PubMed]
- Slade, G.D.; Bair, E.; By, K.; Mulkey, F.; Baraian, C.; Rothwell, R.; Reynolds, M.; Miller, V.; Gonzalez, Y.; Gordon, S.; et al. Study Methods, Recruitment, Sociodemographic Findings, and Demographic Representativeness in the OPPERA Study. J. Pain 2011, 12, T12–T26. [Google Scholar] [CrossRef]
- Maixner, W.; Diatchenko, L.; Dubner, R.; Fillingim, R.B.; Greenspan, J.D.; Knott, C.; Ohrbach, R.; Weir, B.; Slade, G.D. Orofacial Pain Prospective Evaluation and Risk Assessment Study—The OPPERA Study. J. Pain 2011, 12, T4–T11. [Google Scholar] [CrossRef]
- Richardson, D.B.; Rzehak, P.; Klenk, J.; Weiland, S.K. Analyses of case-control data for additional outcomes. Epidemiology 2007, 18, 441–445. [Google Scholar] [CrossRef] [PubMed]
- Xing, C.; McCarthy, J.M.; Dupuis, J.; Adrienne Cupples, L.; Meigs, J.B.; Lin, X.; Allen, A.S. Robust analysis of secondary phenotypes in case-control genetic association studies. Stat. Med. 2016, 35, 4226–4237. [Google Scholar] [CrossRef]
- Li, F.; Allen, A.S. Secondary analysis of case-control association studies: Insights on weighting-based inference motivate a new specification test. Stat. Med. 2020, 39, 2869–2882. [Google Scholar] [CrossRef]
- Lin, D.Y.; Zeng, D. Proper analysis of secondary phenotype data in case-control association studies. Genet. Epidemiol. 2009, 33, 256–265. [Google Scholar] [CrossRef]
- Ghosh, A.; Wright, F.A.; Zou, F. Unified analysis of secondary traits in case–control association studies. J. Am. Stat. Assoc. 2013, 108, 566–576. [Google Scholar] [CrossRef]
- Li, H.; Gail, M.H.; Berndt, S.; Chatterjee, N. Using cases to strengthen inference on the association between single nucleotide polymorphisms and a secondary phenotype in genome-wide association studies. Genet. Epidemiol. 2010, 34, 427–433. [Google Scholar] [CrossRef]
- He, J.; Li, H.; Edmondson, A.C.; Rader, D.J.; Li, M. A gaussian copula approach for the analysis of secondary phenotypes in case-control genetic association studies. Biostatistics 2011, 13, 497–508. [Google Scholar] [CrossRef] [PubMed]
- Wei, J.; Carroll, R.J.; Müller, U.U.; Keilegom, I.V.; Chatterjee, N. Robust estimation for homoscedastic regression in the secondary analysis of case–control data. J. R. Stat. Soc. Ser. B 2013, 75, 185–206. [Google Scholar] [CrossRef] [PubMed]
- Ma, Y.; Carroll, R.J. Semiparametric estimation in the secondary analysis of case-control studies. J. R. Stat. Soc. Ser. B 2016, 78, 127. [Google Scholar] [CrossRef] [PubMed]
- Schifano, E.D.; Li, L.; Christiani, D.C.; Lin, X. Genome-wide association analysis for multiple continuous secondary phenotypes. Am. J. Hum. Genet. 2013, 92, 744–759. [Google Scholar] [CrossRef]
- Tchetgen Tchetgen, E.J. A general regression framework for a secondary outcome in case–control studies. Biostatistics 2014, 15, 117–128. [Google Scholar] [CrossRef][Green Version]
- Wang, J.; Shete, S. Estimation of odds ratios of genetic variants for the secondary phenotypes associated with primary diseases. Genet. Epidemiol. 2011, 35, 190–200. [Google Scholar] [CrossRef][Green Version]
- Wang, J.; Shete, S. Power and type i error results for a bias-correction approach recently shown to provide accurate odds ratios of genetic variants for the secondary phenotypes associated with primary diseases. Genet. Epidemiol. 2011, 35, 739–743. [Google Scholar] [CrossRef][Green Version]
- Li, H.; Gail, M.H. Efficient adaptively weighted analysis of secondary phenotypes in case-control genome-wide association studies. Hum. Hered. 2012, 73, 159–173. [Google Scholar] [CrossRef]
- Zhou, F.; Zhou, H.; Li, T.; Zhu, H. Analysis of secondary phenotypes in multigroup association studies. Biometrics 2020, 76, 606–618. [Google Scholar] [CrossRef]
- Agresti, A. Categorical Data Analysis; John Wiley & Sons: Hoboken, NJ, USA, 2003; Volume 482. [Google Scholar]
- Cox, D.R. Regression models and life-tables. J. R. Stat. Soc. Ser. B 1972, 34, 187–202. [Google Scholar] [CrossRef]
- DiCiccio, T.J.; Efron, B. Bootstrap confidence intervals. Stat. Sci. 1996, 11, 189–228. [Google Scholar] [CrossRef]
- Davison, A.C.; Hinkley, D.V. Bootstrap Methods and Their Application; Number 1; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2018. [Google Scholar]
- Canty, A.; Ripley, B.D. Boot: Bootstrap R (S-Plus) Functions. 2017. R Package Version 1.3-20. Available online: https://cran.r-project.org/web/packages/boot/index.html (accessed on 30 December 2021).
- Bair, E.; Brownstein, N.C.; Ohrbach, R.; Greenspan, J.D.; Dubner, R.; Fillingim, R.B.; Maixner, W.; Smith, S.B.; Diatchenko, L.; Gonzalez, Y.; et al. Study protocol, sample characteristics, and loss to follow-up: The OPPERA prospective cohort study. J. Pain 2013, 14, T2–T19. [Google Scholar] [CrossRef] [PubMed]
- Bender, R.; Augustin, T.; Blettner, M. Generating survival times to simulate Cox proportional hazards models. Stat. Med. 2005, 24, 1713–1723. [Google Scholar] [CrossRef] [PubMed]
- Smith, S.B.; Maixner, D.W.; Greenspan, J.D.; Dubner, R.; Fillingim, R.B.; Ohrbach, R.; Knott, C.; Slade, G.D.; Bair, E.; Gibson, D.G.; et al. Potential Genetic Risk Factors for Chronic TMD: Genetic Associations from the OPPERA Case Control Study. J. Pain 2011, 12, T92–T101. [Google Scholar] [CrossRef] [PubMed]
- Smith, S.B.; Mir, E.; Bair, E.; Slade, G.D.; Dubner, R.; Fillingim, R.B.; Greenspan, J.D.; Ohrbach, R.; Knott, C.; Weir, B.; et al. Genetic variants associated with development of TMD and its intermediate phenotypes: The genetic architecture of TMD in the OPPERA prospective cohort study. J. Pain 2013, 14, T91–T101. [Google Scholar] [CrossRef] [PubMed]
- Ohrbach, R.; Fillingim, R.B.; Mulkey, F.; Gonzalez, Y.; Gordon, S.; Gremillion, H.; Lim, P.F.; Ribeiro-Dasilva, M.; Greenspan, J.D.; Knott, C.; et al. Clinical Findings and Pain Symptoms as Potential Risk Factors for Chronic TMD: Descriptive Data and Empirically Identified Domains from the OPPERA Case-Control Study. J. Pain 2011, 12, T27–T45. [Google Scholar] [CrossRef] [PubMed]
| Parameters | = −0.12 | = −0.12 | = −0.12 | = −0.12 | = −0.5 | = −1 | = −2 | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Bias | Cover | Bias | Cover | Bias | Cover | Bias | Cover | Bias | Cover | Bias | Cover | Bias | Cover | |
| LM | −0.044 | 0.728 | 0.059 | 0.577 | 0.061 | 0.532 | 0.048 | 0.666 | 0.028 | 0.883 | 0 | 0.944 | −0.058 | 0.643 |
| LM, controls only | −0.039 | 0.875 | −0.073 | 0.698 | −0.108 | 0.444 | −0.151 | 0.206 | −0.022 | 0.926 | −0.002 | 0.939 | 0.037 | 0.892 |
| LM, cases only | −0.056 | 0.761 | −0.099 | 0.394 | −0.166 | 0.06 | −0.256 | 0 | −0.028 | 0.911 | 0.002 | 0.949 | 0.061 | 0.794 |
| LM adjusted for case status | 0.048 | 0.696 | −0.088 | 0.235 | −0.14 | 0.021 | −0.208 | 0 | −0.025 | 0.877 | 0 | 0.945 | 0.047 | 0.736 |
| Monsees | −0.002 | 0.950 | −0.001 | 0.951 | 0.001 | 0.948 | 0.001 | 0.949 | 0.001 | 0.952 | −0.001 | 0.938 | −0.003 | 0.949 |
| Bootstrap | −0.002 | 0.950 | −0.001 | 0.956 | 0.001 | 0.944 | 0.001 | 0.946 | 0.001 | 0.950 | −0.001 | 0.937 | −0.003 | 0.944 |
| CI Width (Valid Methods Only) | ||||||||||||||
| Monsees | 0.164 | 0.160 | 0.155 | 0.148 | 0.166 | 0.167 | 0.168 | |||||||
| Bootstrap | 0.162 | 0.160 | 0.154 | 0.147 | 0.165 | 0.167 | 0.168 | |||||||
| Method | Result | |||||||
|---|---|---|---|---|---|---|---|---|
| Scenario 1 | Scenario 2 | Scenario 3 | Scenario 4 | |||||
| Bias | Coverage | Bias | Coverage | Bias | Coverage | Bias | Coverage | |
| Naive | −0.054 | 0.909 | −0.068 | 0.836 | −0.053 | 0.910 | −0.069 | 0.871 |
| Controls only | 0.075 | 0.937 | 0.051 | 0.937 | 0.063 | 0.948 | 0.093 | 0.933 |
| Cases only | 0.805 | 0 | −0.815 | 0 | 0.226 | 0 | 0.903 | 0 |
| Adjusted for case status | 0.057 | 0.904 | 0.027 | 0.937 | 0.054 | 0.913 | 0.101 | 0.824 |
| Bootstrap | 0.020 | 0.943 | 0.006 | 0.944 | 0.015 | 0.948 | 0.015 | 0.951 |
| CI Width (Valid Methods Only) | ||||||||
| Bootstrap | 0.519 | 0.399 | 0.477 | 0.512 | ||||
| Method | Bias | Coverage |
|---|---|---|
| Naive | −0.457 | 0.006 |
| Controls only | 0.272 | 0.396 |
| Cases only | −0.800 | 0.225 |
| Adjusted for case status | 0.091 | 1.000 |
| Bootstrap | −0.017 | 0.944 |
| CI Width (Valid Methods Only) | ||
| Bootstrap | 0.439 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Brownstein, N.C.; Cai, J.; Smith, S.; Diatchenko, L.; Slade, G.D.; Bair, E. Modeling Secondary Phenotypes Conditional on Genotypes in Case–Control Studies. Stats 2022, 5, 203-214. https://doi.org/10.3390/stats5010014
Brownstein NC, Cai J, Smith S, Diatchenko L, Slade GD, Bair E. Modeling Secondary Phenotypes Conditional on Genotypes in Case–Control Studies. Stats. 2022; 5(1):203-214. https://doi.org/10.3390/stats5010014
Chicago/Turabian StyleBrownstein, Naomi C., Jianwen Cai, Shad Smith, Luda Diatchenko, Gary D. Slade, and Eric Bair. 2022. "Modeling Secondary Phenotypes Conditional on Genotypes in Case–Control Studies" Stats 5, no. 1: 203-214. https://doi.org/10.3390/stats5010014
APA StyleBrownstein, N. C., Cai, J., Smith, S., Diatchenko, L., Slade, G. D., & Bair, E. (2022). Modeling Secondary Phenotypes Conditional on Genotypes in Case–Control Studies. Stats, 5(1), 203-214. https://doi.org/10.3390/stats5010014






