Some New Tests of Conformity with Benford’s Law
Abstract
1. Introduction
2. New Tests of Conformity with Benford’s Law
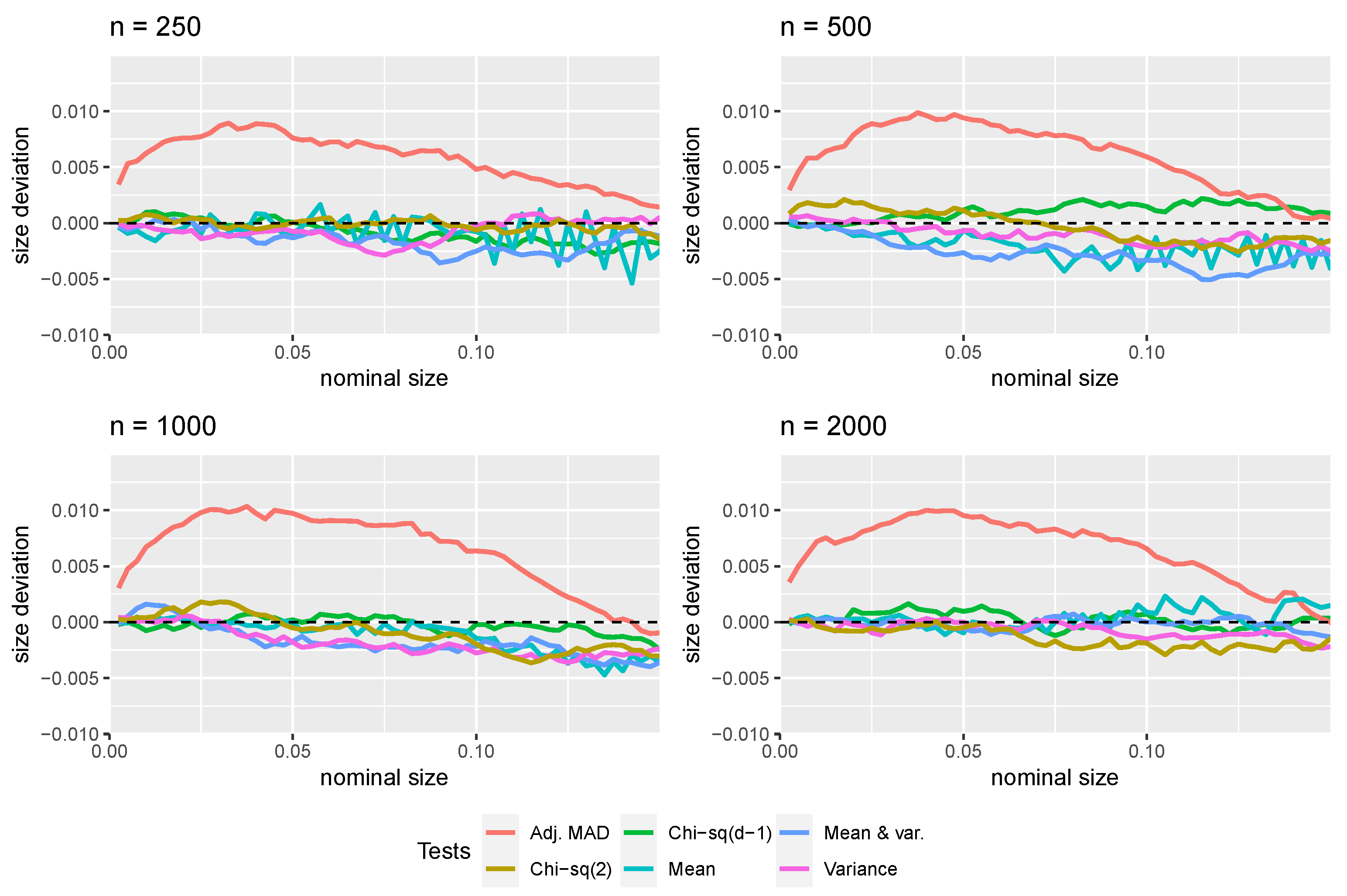
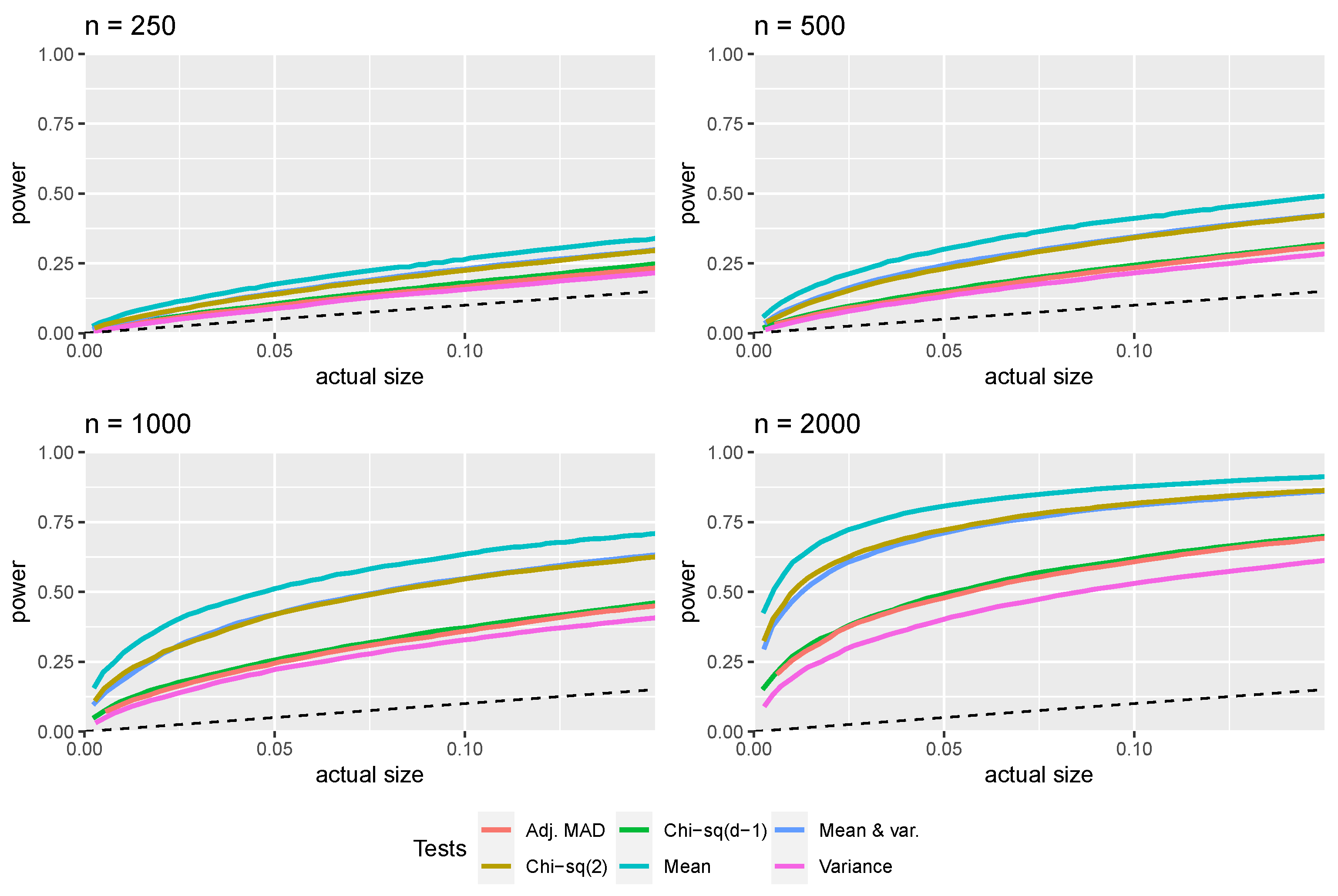
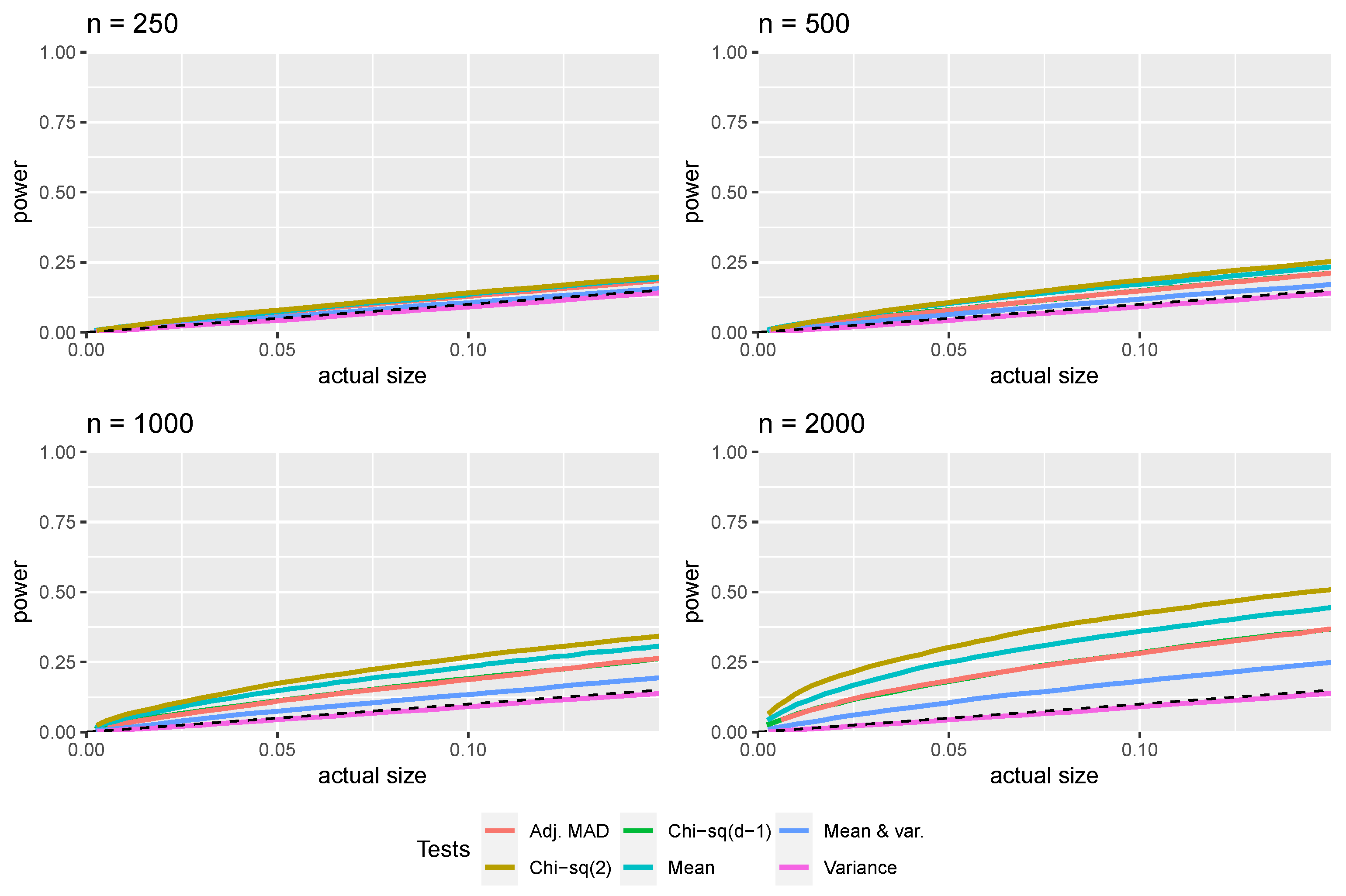
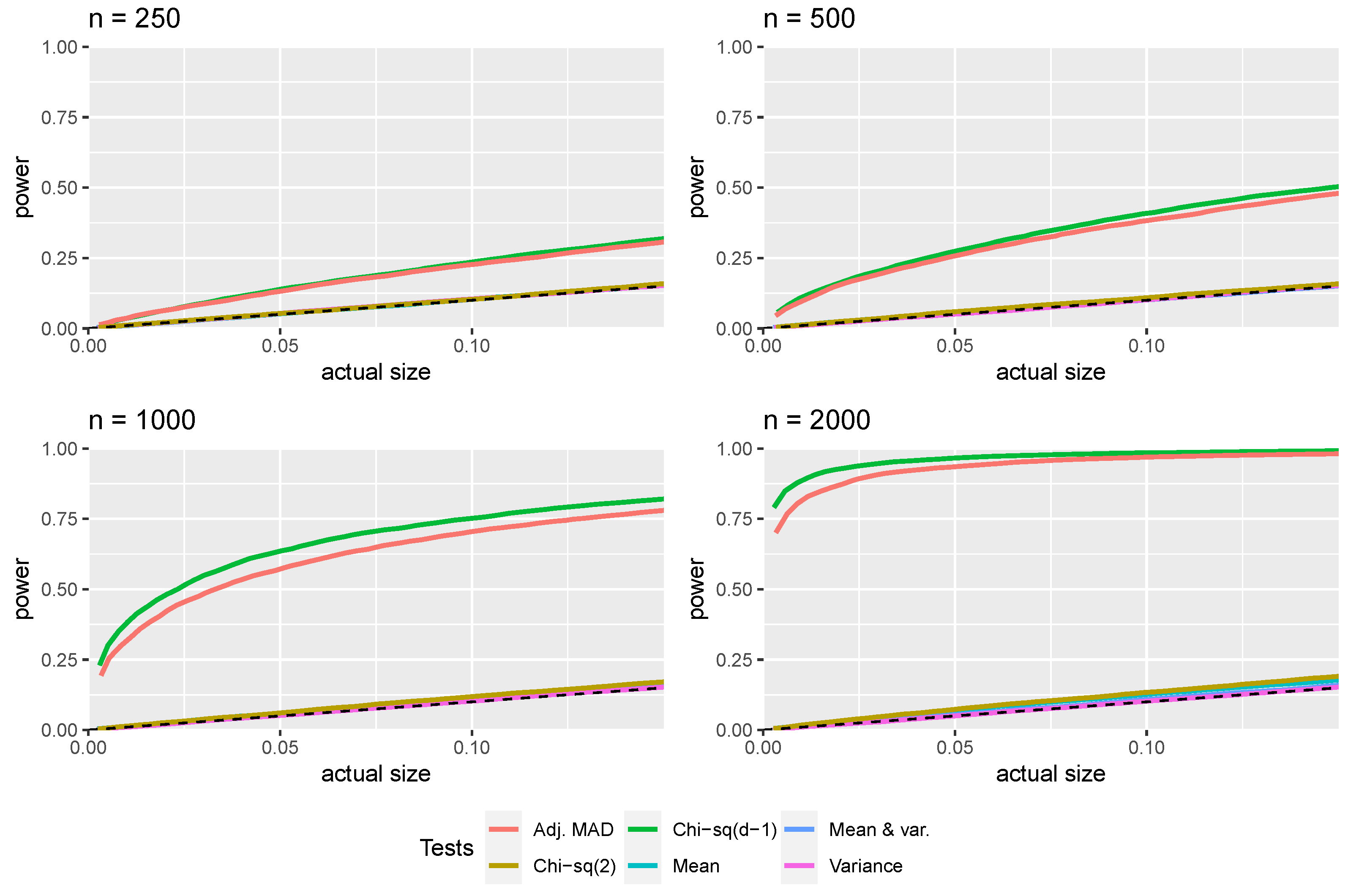
3. Monte Carlo Simulations
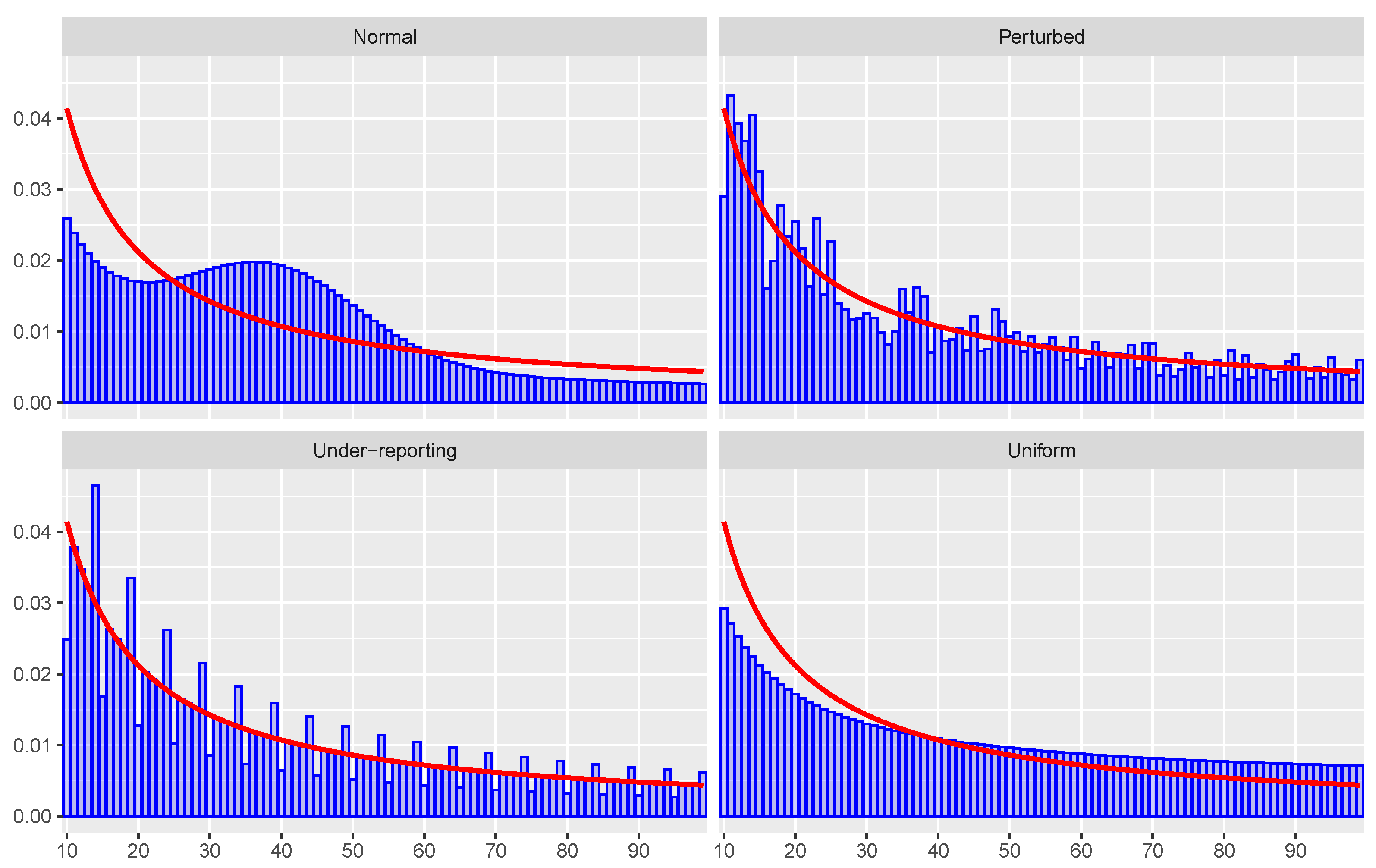
- Uniform mixture: describes the discrete uniform distribution with the same support as the considered Benford’s distribution;
- Normal mixture: are the probabilities of , with the mean of Benford’s distribution and ;
- Randomly perturbed mixture: Benford’s law is perturbed by a random quantity in correspondence to each digit. More precisely, with . Since this mixture contains elements of randomness, each Monte Carlo iteration uses a different mixture. However, the mixtures are the same across all tests;
- Under-reporting mixture: under the alternative, Benford’s distribution is modified by putting to zero the probability of “round” numbers and giving this probability to the preceding number: for example, and . This mixture is only considered with reference to the first two digits case.
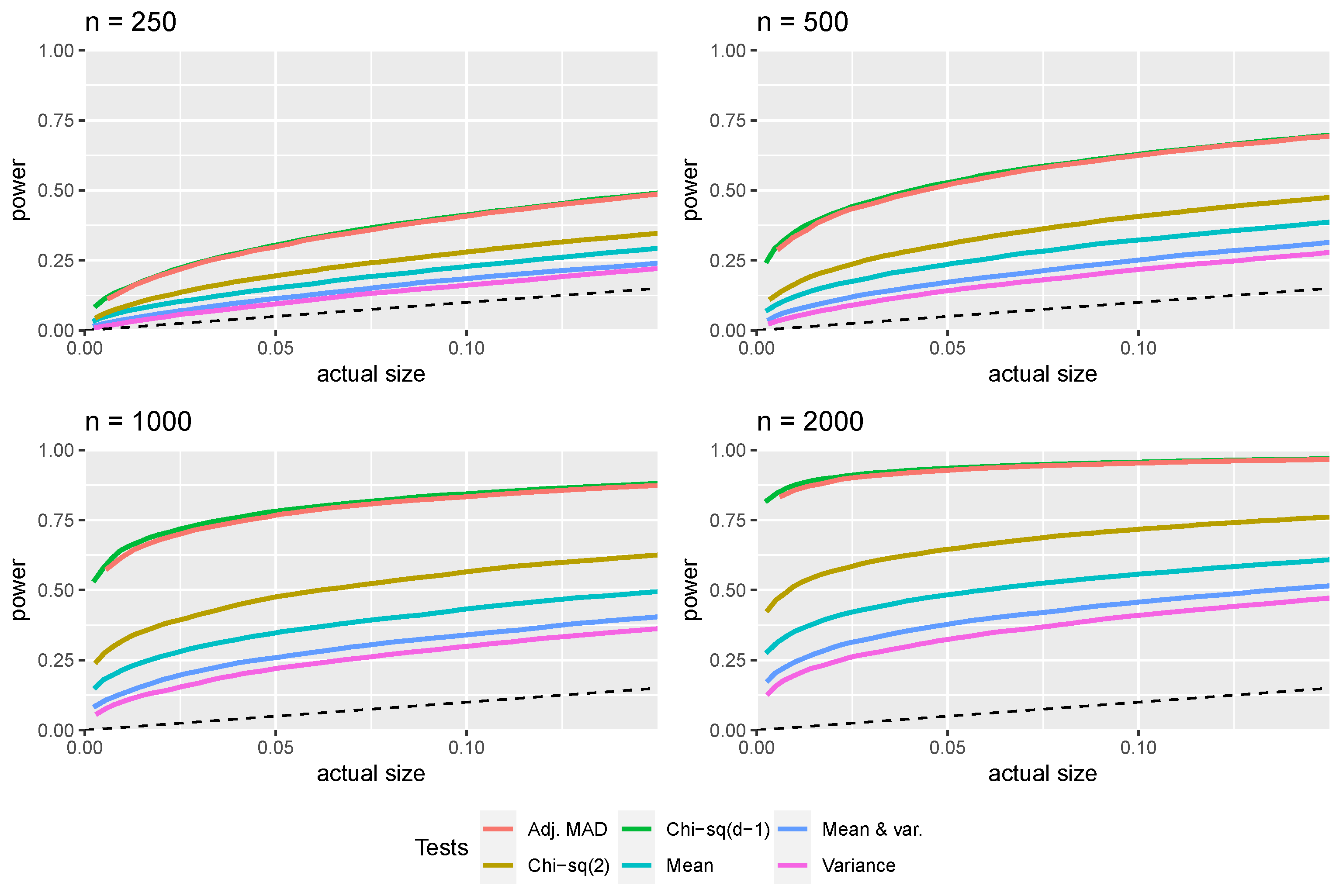
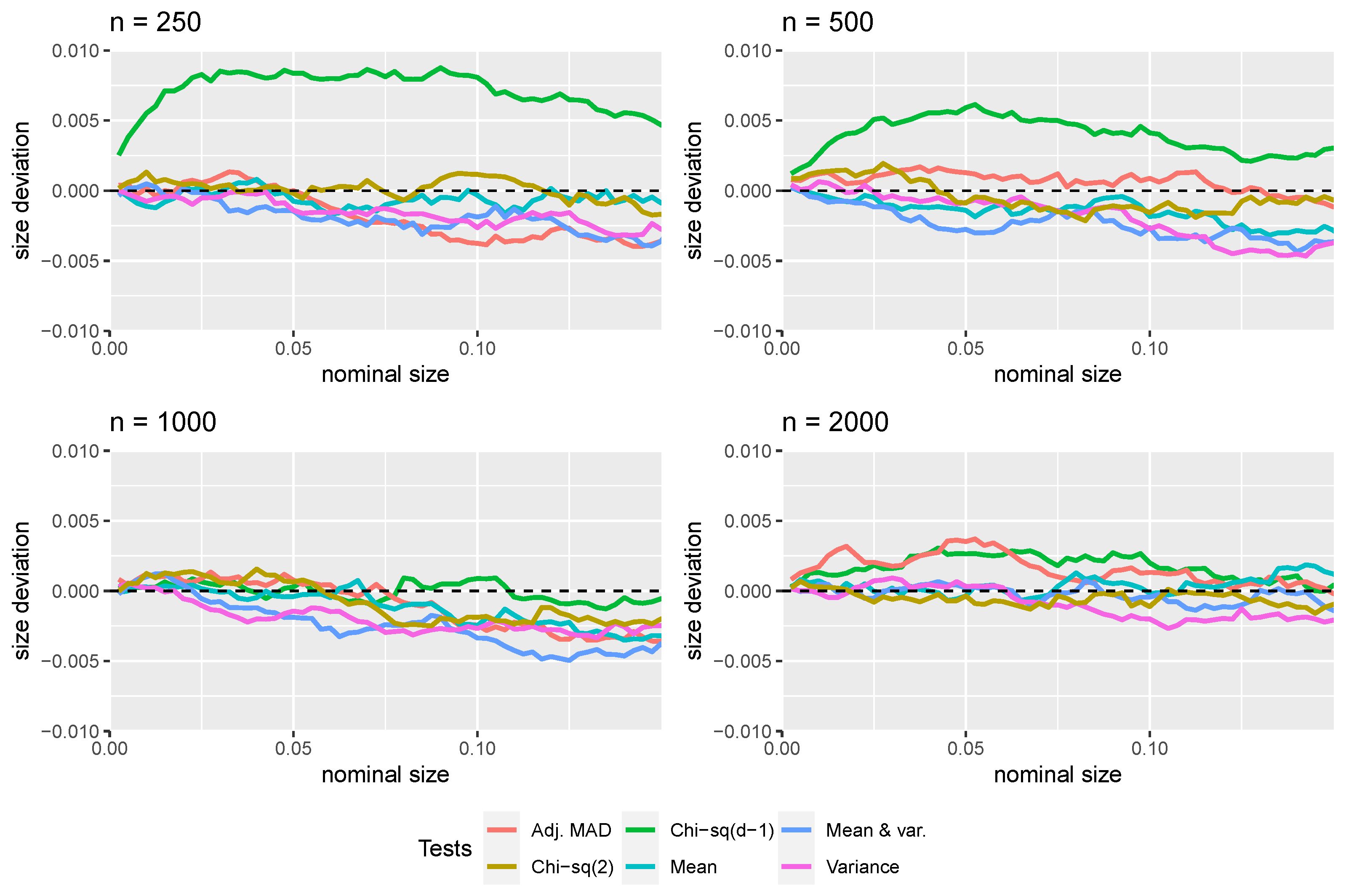
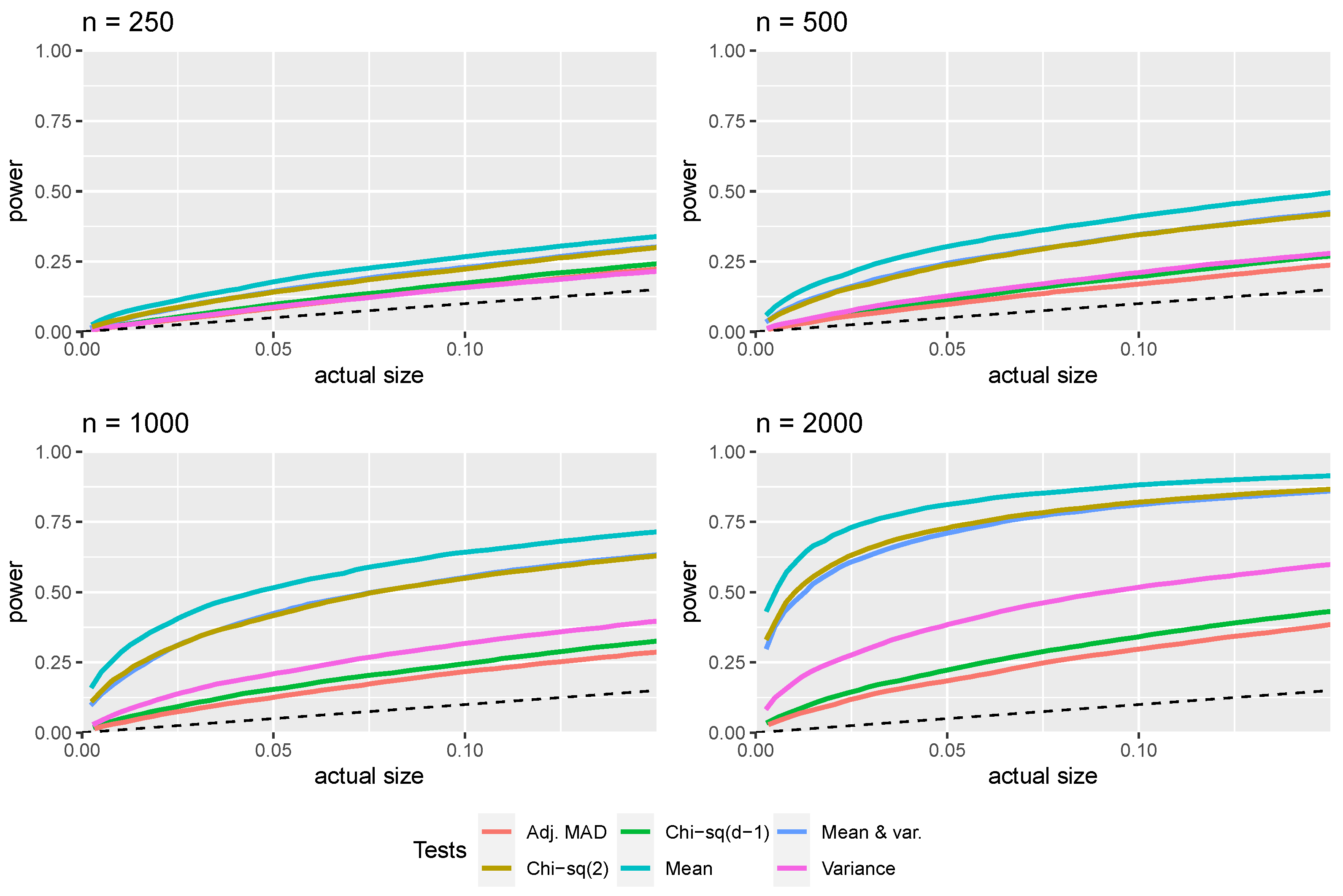
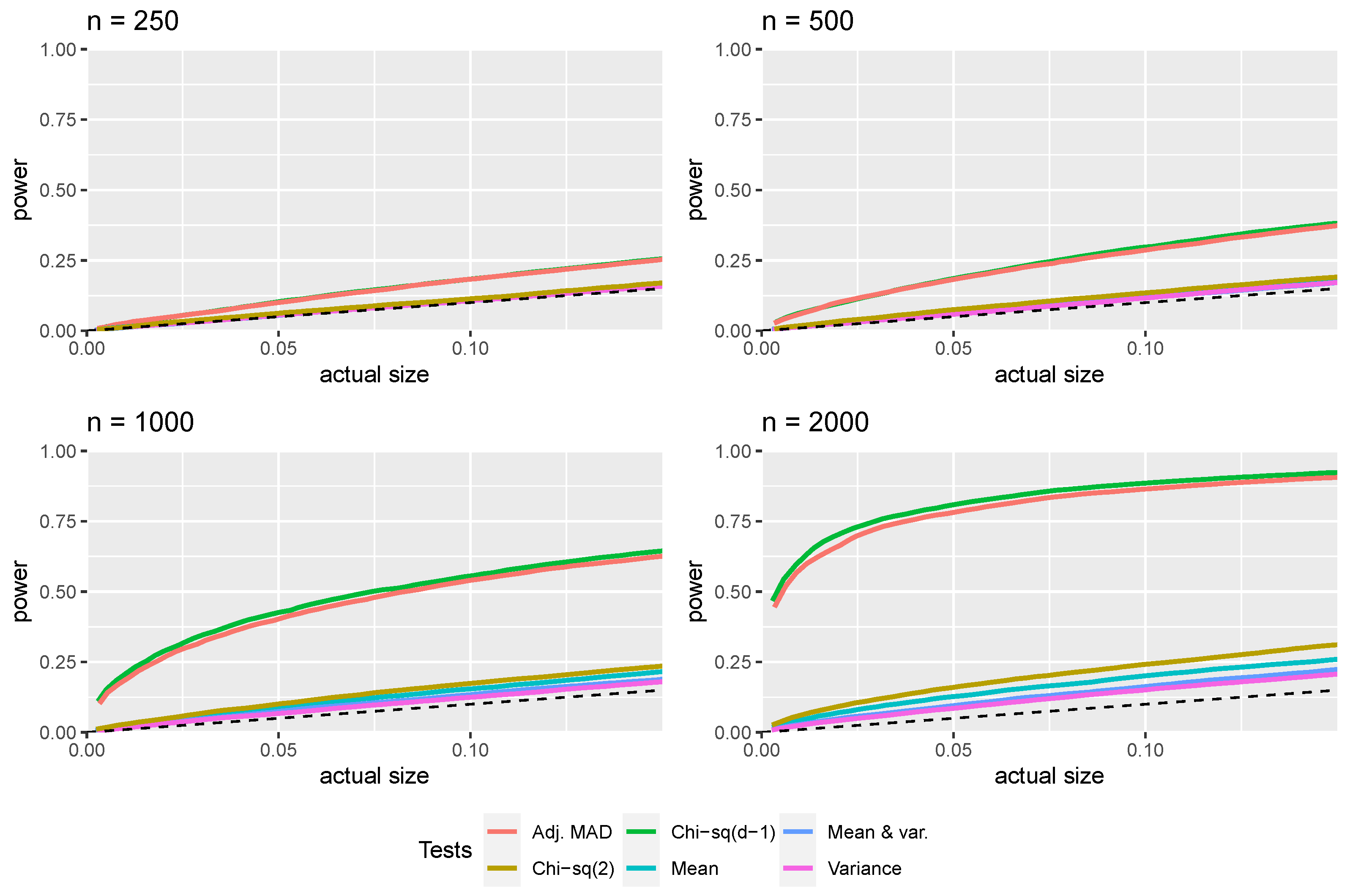
3.1. First-Digit Law
3.2. First Two Digits Law
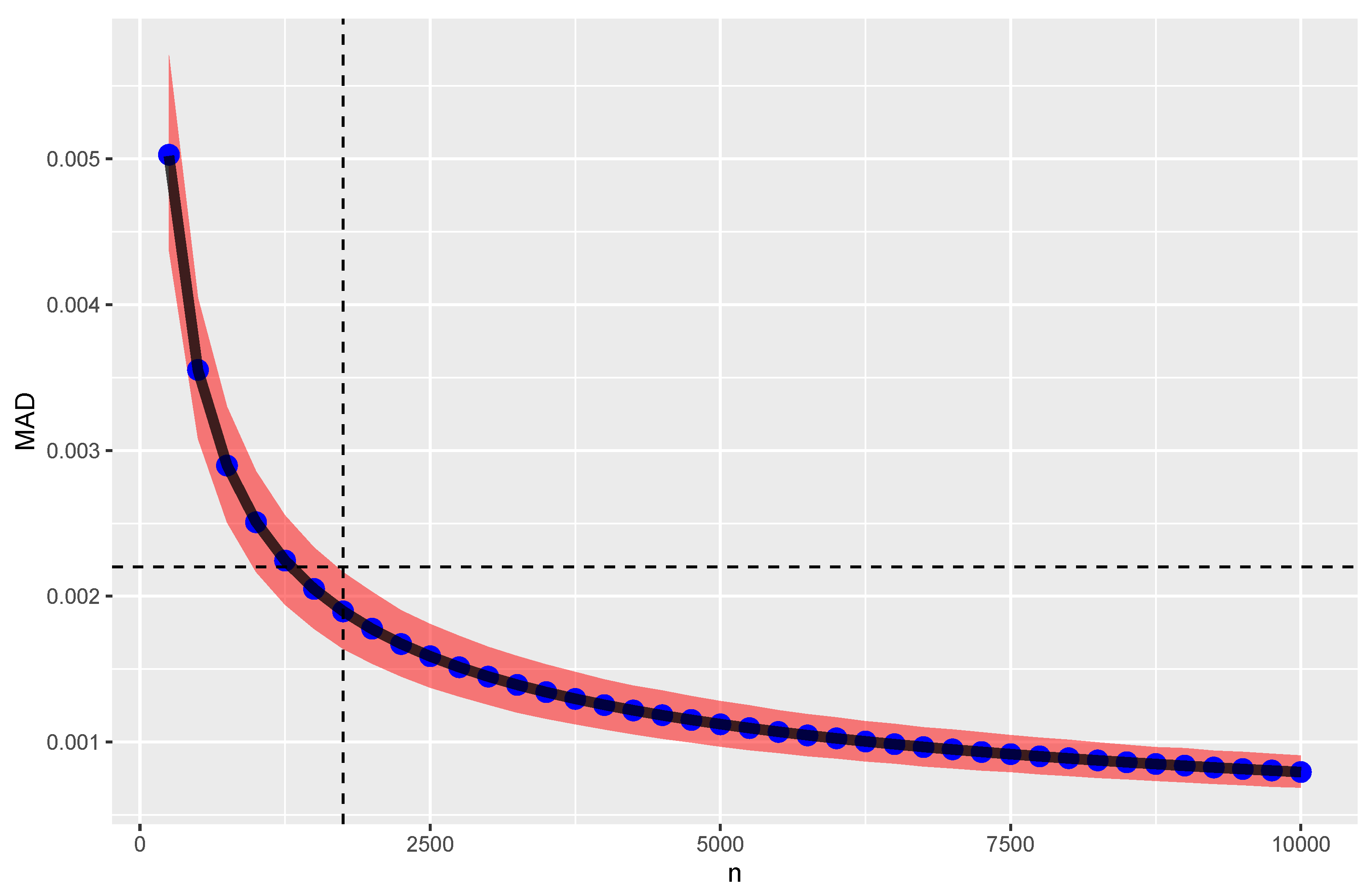
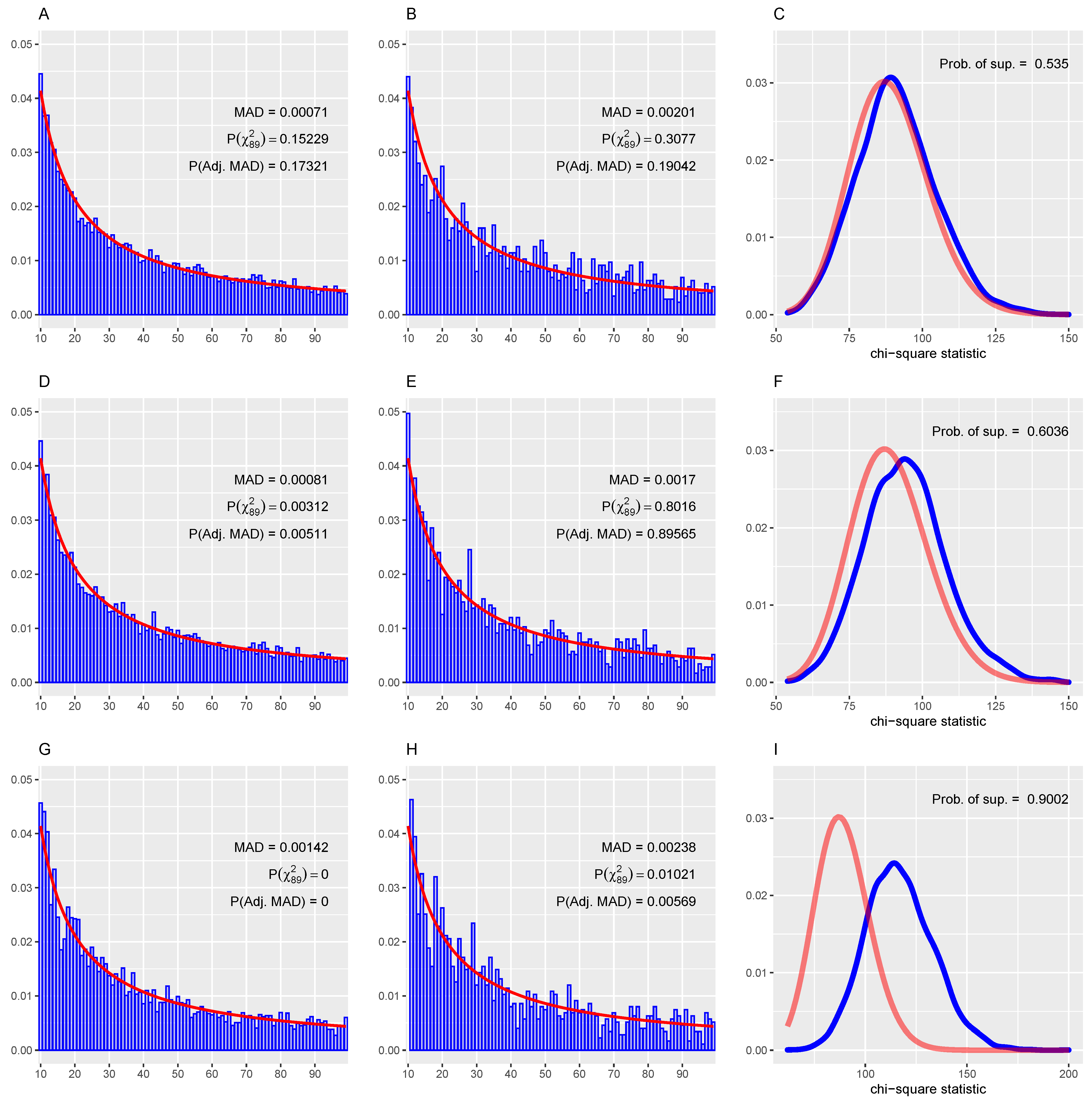
4. Statistical versus Practical Significance
“Virtually all specific null hypotheses will be rejected using present standards. It will probably be necessary to replace the concept of statistical significance with some measure of economic significance.”
“What is needed is a test that ignores the number of records. The mean absolute deviation () test is such a test, and the formula is shown in Equation 7.7. [...] There is no reference to the number of records, N, in Equation 7.7.”
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
References
- Newcomb, S. Note on the frequency of use of the different digits in natural numbers. Am. J. Math. 1881, 4, 39–40. [Google Scholar] [CrossRef]
- Benford, F. The law of anomalous numbers. Proc. Am. Philos. Soc. 1938, 78, 551–572. [Google Scholar]
- Nigrini, M.J. Benford’s Law: Applications for Forensic Accounting, Auditing, and Fraud Detection; John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar] [CrossRef]
- Kossovsky, A.E. Benford’s Law: Theory, the General Law of Relative Quantities, and Forensic Fraud Detection Applications; World Scientific: Singapore, 2014. [Google Scholar]
- Berger, A.; Hill, T.P. An Introduction to Benford’s Law; Princeton University Press: Princeton, NJ, USA, 2015. [Google Scholar]
- Miller, S.J. (Ed.) Benford’s Law: Theory and Applications; Princeton University Press: Princeton, NJ, USA, 2015. [Google Scholar]
- Raimi, R.A. The first digit problem. Am. Math. Mon. 1976, 83, 521–538. [Google Scholar] [CrossRef]
- Hill, T.P. A statistical derivation of the significant-digit law. Stat. Sci. 1995, 10, 354–363. [Google Scholar] [CrossRef]
- Leemis, L. Benford’s Law Geometry. In Benford’s Law: Theory and Applications; Miller, S.J., Ed.; Princeton University Press: Princeton, NJ, USA, 2015; Chapter 4; pp. 109–118. [Google Scholar]
- Miller, S.J. (Ed.) Fourier Analysis and Benford’s Law. In Benford’s Law: Theory and Applications; Princeton University Press: Princeton, NJ, USA, 2015; Chapter 3; pp. 68–105. [Google Scholar]
- Schürger, K. Lévy Processes and Benford’s Law. In Benford’s Law: Theory and Applications; Miller, S.J., Ed.; Princeton University Press: Princeton, NJ, USA, 2015; Chapter 6; pp. 135–173. [Google Scholar]
- Kossovsky, A.E. On the Mistaken Use of the Chi-Square Test in Benford’s Law. Stats 2021, 4, 27. [Google Scholar] [CrossRef]
- Ausloos, M.; Cerqueti, R.; Mir, T.A. Data science for assessing possible tax income manipulation: The case of Italy. Chaos Solitons Fractals 2017, 104, 238–256. [Google Scholar] [CrossRef]
- Mir, T.A.; Ausloos, M.; Cerqueti, R. Benford’s law predicted digit distribution of aggregated income taxes: The surprising conformity of Italian cities and regions. Eur. Phys. J. B 2014, 87, 1–8. [Google Scholar] [CrossRef]
- Nye, J.; Moul, C. The Political Economy of Numbers: On the Application of Benford’s Law to International Macroeconomic Statistics. BE J. Macroecon. 2007, 7, 17. [Google Scholar] [CrossRef]
- Tödter, K.H. Benford’s Law as an Indicator of Fraud in Economics. Ger. Econ. Rev. 2009, 10, 339–351. [Google Scholar] [CrossRef]
- Durtschi, C.; Hillison, W.; Pacini, C. The effective use of Benford’s law to assist in detecting fraud in accounting data. J. Forensic Account. 2004, 5, 17–34. [Google Scholar]
- Nigrini, M.J. I have got your number. J. Account. 1999, 187, 79–83. [Google Scholar]
- Shi, J.; Ausloos, M.; Zhu, T. Benford’s law first significant digit and distribution distances for testing the reliability of financial reports in developing countries. Phys. A Stat. Mech. Appl. 2018, 492, 878–888. [Google Scholar] [CrossRef]
- Ley, E. On the peculiar distribution of the US stock indexes’ digits. Am. Stat. 1996, 50, 311–313. [Google Scholar] [CrossRef]
- Ceuster, M.J.D.; Dhaene, G.; Schatteman, T. On the hypothesis of psychological barriers in stock markets and Benford’s Law. J. Empir. Financ. 1998, 5, 263–279. [Google Scholar] [CrossRef]
- Clippe, P.; Ausloos, M. Benford’s law and Theil transform of financial data. Phys. A Stat. Mech. Appl. 2012, 391, 6556–6567. [Google Scholar] [CrossRef]
- Mir, T.A. The leading digit distribution of the worldwide illicit financial flows. Qual. Quant. 2014, 50, 271–281. [Google Scholar] [CrossRef]
- Ausloos, M.; Castellano, R.; Cerqueti, R. Regularities and discrepancies of credit default swaps: A data science approach through Benford’s law. Chaos Solitons Fractals 2016, 90, 8–17. [Google Scholar] [CrossRef]
- Riccioni, J.; Cerqueti, R. Regular paths in financial markets: Investigating the Benford’s law. Chaos Solitons Fractals 2018, 107, 186–194. [Google Scholar] [CrossRef]
- Sambridge, M.; Tkalčić, H.; Jackson, A. Benford’s law in the natural sciences. Geophys. Res. Lett. 2010, 37. [Google Scholar] [CrossRef]
- Diaz, J.; Gallart, J.; Ruiz, M. On the Ability of the Benford’s Law to Detect Earthquakes and Discriminate Seismic Signals. Seismol. Res. Lett. 2014, 86, 192–201. [Google Scholar] [CrossRef]
- Ausloos, M.; Cerqueti, R.; Lupi, C. Long-range properties and data validity for hydrogeological time series: The case of the Paglia river. Phys. A Stat. Mech. Appl. 2017, 470, 39–50. [Google Scholar] [CrossRef]
- Mir, T. The law of the leading digits and the world religions. Phys. A Stat. Mech. Appl. 2012, 391, 792–798. [Google Scholar] [CrossRef]
- Mir, T. The Benford law behavior of the religious activity data. Phys. A Stat. Mech. Appl. 2014, 408, 1–9. [Google Scholar] [CrossRef]
- Ausloos, M.; Herteliu, C.; Ileanu, B. Breakdown of Benford’s law for birth data. Phys. A Stat. Mech. Appl. 2015, 419, 736–745. [Google Scholar] [CrossRef][Green Version]
- Hassler, U.; Hosseinkouchack, M. Testing the Newcomb-Benford Law: Experimental evidence. Appl. Econ. Lett. 2019, 26, 1762–1769. [Google Scholar] [CrossRef]
- Cerqueti, R.; Maggi, M. Data validity and statistical conformity with Benford’s Law. Chaos Solitons Fractals 2021, 144, 110740. [Google Scholar] [CrossRef]
- Linton, O. Probability, Statistics and Econometrics; Academic Press: London, UK, 2017. [Google Scholar]
- Zhang, L. Sample Mean and Sample Variance: Their Covariance and Their (In)Dependence. Am. Stat. 2007, 61, 159–160. [Google Scholar] [CrossRef]
- Geary, R.C. Moments of the Ratio of the Mean Deviation to the Standard Deviation for Normal Samples. Biometrika 1936, 28, 295. [Google Scholar] [CrossRef]
- Choulakian, V.; Lockhart, R.A.; Stephens, M.A. Cramér-von Mises statistics for discrete distributions. Can. J. Stat. 1994, 22, 125–137. [Google Scholar] [CrossRef]
- White, H. Asymptotic Theory for Econometricians; Economic Theory, Econometrics, and Mathematical Economics; Academic Press: London, UK, 1984. [Google Scholar]
- Wellner, J.A.; Smythe, R.T. Computing the covariance of two Brownian area integrals. Stat. Neerl. 2002, 56, 101–109. [Google Scholar] [CrossRef]
- Drake, P.D.; Nigrini, M.J. Computer assisted analytical procedures using Benford’s Law. J. Account. Educ. 2000, 18, 127–146. [Google Scholar] [CrossRef]
- R Development Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2019. [Google Scholar]
- Wickham, H. ggplot2: Elegant Graphics for Data Analysis; Use R! Springer: New York, NY, USA, 2016. [Google Scholar]
- Davidson, R.; MacKinnon, J.G. Graphical Methods for Investigating The Size and Power of Hypothesis Tests. Manch. Sch. 1998, 66, 1–26. [Google Scholar] [CrossRef]
- Lloyd, C.J. Estimating Test Power Adjusted for Size. J. Stat. Comput. Simul. 2005, 75, 921–934. [Google Scholar] [CrossRef]
- Granger, C.W. Extracting information from mega-panels and high-frequency data. Stat. Neerl. 1998, 52, 258–272. [Google Scholar] [CrossRef]
- Lindley, D.V. A Statistical Paradox. Biometrika 1957, 44, 187–192. [Google Scholar] [CrossRef]
- Bickel, P.J.; Götze, F.; van Zwet, W.R. Resampling Fewer Than n Observations: Gains, Losses, and Remedies for Losses. In Selected Works of Willem van Zwet; Springer: New York, NY, USA, 2011; pp. 267–297. [Google Scholar] [CrossRef]
- Cumming, G. Understanding the New Statistics: Effect Sizes, Confidence Intervals, and Meta-Analysis; Routledge: New York, NY, USA, 2012. [Google Scholar]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cerqueti, R.; Lupi, C. Some New Tests of Conformity with Benford’s Law. Stats 2021, 4, 745-761. https://doi.org/10.3390/stats4030044
Cerqueti R, Lupi C. Some New Tests of Conformity with Benford’s Law. Stats. 2021; 4(3):745-761. https://doi.org/10.3390/stats4030044
Chicago/Turabian StyleCerqueti, Roy, and Claudio Lupi. 2021. "Some New Tests of Conformity with Benford’s Law" Stats 4, no. 3: 745-761. https://doi.org/10.3390/stats4030044
APA StyleCerqueti, R., & Lupi, C. (2021). Some New Tests of Conformity with Benford’s Law. Stats, 4(3), 745-761. https://doi.org/10.3390/stats4030044






