Abstract
In this article, we implement a flexible Gibbs sampler to make inferences for two-parameter Birnbaum–Saunders (BS) distribution in the presence of right-censored data. The Gibbs sampler is applied on the fiducial distributions of the BS parameters derived using the maximum likelihood, methods of moments, and their bias-reduced estimates. A Monte-Carlo study is conducted to make comparisons between these estimates for Type-II right censoring with various parameter settings, sample sizes, and censoring percentages. It is concluded that the bias-reduced estimates outperform the rest with increasing precision. Higher sample sizes improve the overall accuracy of all the estimates while the amount of censoring shows a negative effect. Further comparisons are made with existing methods using two real-world examples.
1. Introduction
The Birnbaum–Saunders (BS) distribution [1] was originally introduced to model failure time due to the growth of a dominant crack that is subject to cyclic stress that causes a failure when it reaches a threshold level. As the distribution was originally derived to model the fatigue life of metals that are subject to periodic stress, it is sometimes referred to as the fatigue-life distribution. However, it is becoming increasingly popular in life testing applications. Reference [2] indicated that the BS distribution can be used as an approximation of the inverse Gaussian (IG) distribution and [3] pointed out that the BS distribution can be viewed as an equal mixture of an IG distribution and its reciprocal. Reference [4] provides a detailed review of various developments and applications of the BS distribution.
The probability density function (pdf) of the BS failure time T with parameters and , denoted by , is given by
where and are the shape and scale parameters, respectively, and and .
The distribution function of the BS failure time T is given by
where represents the distribution function of the standard normal distribution. Since , the scale parameter is the median of the BS distribution.
Classical parameter estimation of the BS distribution such as the maximum likelihood estimation (MLE) is introduced at the early stage of the literature. For instance, MLEs of the BS parameters for complete data were introduced in [5,6], which discussed their asymptotic distributions. Reference [7] introduced the MLE under both Type-I and Type-II censored BS data. However, reference [8] introduced modified moment estimators (MMEs) and a bias reduction method, as well as the Jackknife technique to reduce the bias of both MMEs and MLEs. Reference [9] introduced modified MLEs that are bias-free to second-order and also considered bootstrap bias correction. In addition, they derived a Bartlett correction that improves the finite-sample performance of the likelihood ratio test in finite samples. Point and interval estimations of the BS parameters under Type-II censoring are discussed in [10]. Reference [11] introduced a simple method of modified censored moment estimation (MCME) method to estimate its parameters under random censoring and bias reduced versions of these estimators are also considered. Reference [12] introduced alternative estimators with smaller bias compared to that for [8]. Reference [13] suggested a Bayesian estimation method for Type-II censored BS data in the simple step stress accelerated life test with power law accelerated form. They applied a Gibbs sampling procedure to get the Bayesian estimates for shape parameter of BS distribution and parameters of power law–accelerated model.
Life-time experiments often result in censored data, and the nature of the censoring plays a vital role in its analysis. Right censored data occurs when the test start time of each unit is known but the test end time is unknown. This includes random right censoring that can occur if the units fail to follow up the testing during the testing period due to reasons other than the main cause of interest and the Type-II censored data that can occur only if the experiment continues until a fixed number of units failed.
In this work, we focus on estimating both BS parameters in the presence of random right and Type-II censored units. In addition, we estimate the average remaining test time of the censored units. For instance, assume that we put n non-repairable units with lifetimes in a lifetime test and observe only r failures and rest of the observations are right censored. That is, is the set of censored values. Assume that the experiment were to continue so that all censored values could be observed and would be the set of true observed values such that the remaining test times for censored elements are . Then, the estimate for the average remaining test time becomes
where 1 is a column vector of 1’s of length .
The rest of the article is organized as follows. In Section 2, we discuss the parameter estimation of the BS distribution using the maximum likelihood method, methods of moments, and their biased reduced alternatives. In Section 3, we present our major contribution, where we discuss the Gibbs sampling procedure that relies on fiducial distributions to handle censored data. In Section 4, we report Monte-Carlo simulation results and compare the performance of the estimation methods. We illustrate the Gibbs sampler with analysis of real data and make some comparisons with the existing methods in Section 5. We make some remarks and recommendations in Section 6.
2. Parameter Estimation
This section summarizes both point and interval estimators of the BS parameters. That includes the maximum likelihood and the methods of moments estimates and their bias-reduced counterparts.
2.1. The Maximum Likelihood Approach
The maximum likelihood estimation of the BS parameters, and , was originally proposed by [5]. Some variations and improvements were later reported in many works under different life testing conditions. A complete summary of BS parameter estimations can be found in the monograph by [4]. For a random sample of failure times = {} the log-likelihood function, without the additive constant, can be written as
By taking the partial derivative of Equation (4) with respect to and solving it for zero, we can obtain
where and are the sample arithmetic and harmonic means of the observed data.
Then, by taking the partial derivative of Equation (4) with respect to and using the result given in Equation (5), the following can be obtained.
where . The MLE of is the unique positive root of Equation (6) that lies at the interval . As a result, the MLE of becomes .
The Fisher information matrix of the BS distribution with parameters and is given by
where and is the standard normal distribution function. Then, asymptotic normal property of the MLEs indicates that, for large n,
It can be noticed that from Equation (8) the MLEs and are asymptotically independent. Therefore, the asymptotic confidence intervals for and can easily be constructed (see [8,9]).
That is, confidence intervals for and become
and
respectively. As [9] indicated, these intervals rely on asymptotic properties, and therefore they may display poor performance in smaller sample size cases.
2.2. Modified Moment Estimators
Generally, the moment estimators are obtained by equating population moments with corresponding sample moments. For the BS distribution, the standard moments do not exist when the sample coefficient of variance is greater than [8]. Therefore, [8] introduced the modified moment estimators (MMEs) that rely on the parameters of both the BS and its reciprocal distributions. That led to the following moment equations.
Solving these equations, one can obtain the following MMEs for and , denoted by and .
and
As for the MLE cases, the asymptotic joint distribution of and becomes
Then, confidence intervals for and based on MMEs become
and
respectively.
2.3. Bias-Reduced Estimators
The study by [8] indicated that both MLEs and MMEs perform equally well in terms of both the bias and mean square errors. However, for smaller sample sizes the bias of MLE of increases. Therefore, reference [8] suggested improved estimators that reduced the bias of both MLEs and MMEs. That is, using a standard bias reduction method, they reported that for almost unbiased maximum likelihood estimators (UMLEs)
and for almost unbiased modified moment estimators (UMMEs)
3. Application of Gibbs Sampler
Parameter estimation for the BS distribution in the presence of complete data is well established, but it becomes challenging when the data are censored. Gibbs sampling is a Markov Chain Monte Carlo method and is commonly used to generate samples from the posterior distributions in Bayesian by sweeping through each variable to sample from its conditional distribution with the remaining variables fixed to their current values. However, in this work, we adopt the Fiducial inferential suggested by [14] that has some resemblance to the Bayesian framework, though it has no reliance on prior knowledge of the distribution for parameters involved.
We propose the BS parameters and to be sampled from their sampling distributions given in Equations (8) and (13). In the Fiducial distributions, the parameters are replaced with their corresponding biased and bias-reduced MLEs and MMEs. For instance, MLE based fiducial distributions for and are
respectively.
To start the Gibbs sampler, it is required to identify suitable initial values for and . However, often their maximum likelihood estimates or method of moments estimates from the observed data given censoring are preferred for this purpose.
The BS likelihood function for an ordered Type-II censored sample with the largest observations being censored is written as [15]
where and . The MLEs, and , can be obtained by differentiating the log of this likelihood function with respect to and and equating them to zero. Reference [10] explained that there is no closed-form solution to likelihood estimates but the MLEs can be obtained by solving a derived non-linear equation using their EM algorithm. However, in this work, we use the R function [16] “fitdistcens” available in R-package “fitdistrplus” by [17] to fit the BS distribution with censored data to obtain MLEs of and (see Supplementary Materials for the R exhibit of this function). Then, the Gibbs sampler is used to generate synthetic BS data samples to replace the censored portion of the observed dataset [18]. The steps of our Gibbs sampling algorithm are summarized as follows.
- Calculate the maximum likelihood estimates and from the available right censored dataset. Set and .
- Generate a random variate from a uniform distribution bounded by the BS CDF value of the respective censored observation and 1. Then, use the inverse CDF () value of the newly sampled random variate to replace the censored value as follows:
- Generate: , where .
- Then, set:
- Repeat this process for all censored units as in Step 2; the censored data will be replaced by the the simulated data such that .
- Using the updated sample in Step 3, sample and from their respective fiducial distributions.
- Repeat Steps 2–4 starting with the new sampled parameters, and . This procedure will continue with k total iterations and concluding with the results for and . A new set of simulated BS observations should be picked in the same manner as in Step 3 using the and as newly updated parameters.
- At the conclusion of Step 5, the average remaining life of censored units defined in Equation (3) is calculated using the newly sampled data in Step 3 with and as the as newly updated parameters and is designated .
- Repeat Steps 2–6 a number of times, say m total iterations. This results in a collection of m Fiducial samples of and as well as m samples of :
In the Gibbs sampler, we guarantee the convergence of the sampled data using both numerical and graphical summaries. That includes monitoring the scalar summary and the scale reduction statistic defined in [19]. As suggested in [20], we confirm that the statistic is well below 1.1 and the trace plots behave appropriately to make sure of the convergence of the Gibbs samples in all situations considered. After confirming the convergence, we report both point and interval estimates. That includes means and their stand error estimates as well as the 95% equal-tailed confidence intervals for all the parameters including .
4. Monte-Carlo Simulation
We conduct a simulation study to compare the performance of the discussed methods under the Type-II right censoring scheme. We generate data from the distribution with sample sizes and censoring percentages (CEP) at 10%(10%)40%. The simulation is repeated for while keeping the scale parameter fixed at 1.0. Each experimental condition is repeated for 2000 generated BS datasets. The Gibbs sampler converges adequately in iterations and the scale reduction factor for both parameters is less than 1.1. In this simulation, we obtained both point and interval estimates with total replications. Final Fiducial samples for and are shown in Figure 1 and Figure 2 and their coverage probabilities are shown in Figure 3 and Figure 4, respectively. Average point estimates (PE), their standard errors (SE), and coverage probabilities (CP) are reported Table A1, Table A2, Table A3 in Appendix A.
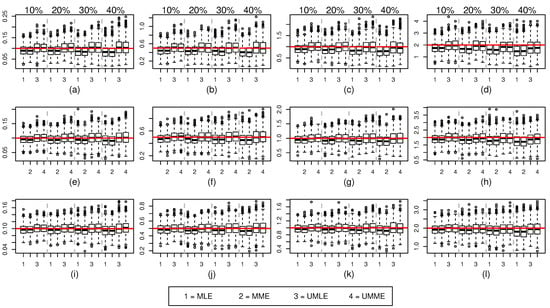
Figure 1.
Sampled values for (top panel), (middle panel), and (bottom panel) for various censoring percentages. The true value of is denoted by red colored solid line. in (a,e,i), in (b,f,j), in (c,g,k), and in (d,h,l).
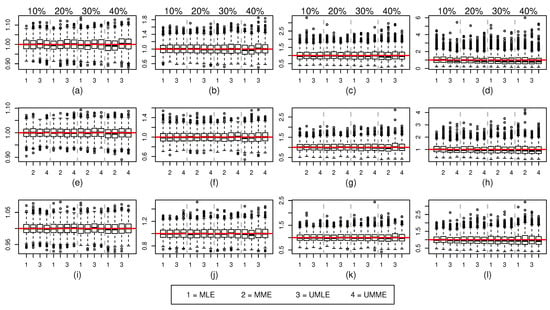
Figure 2.
Sampled values for (top panel), (middle panel), and (bottom panel) for various censoring percentages and values. The true value of is denoted by red colored solid line. in (a,e,i), in (b,f,j), in (c,g,k), and in (d,h,l).
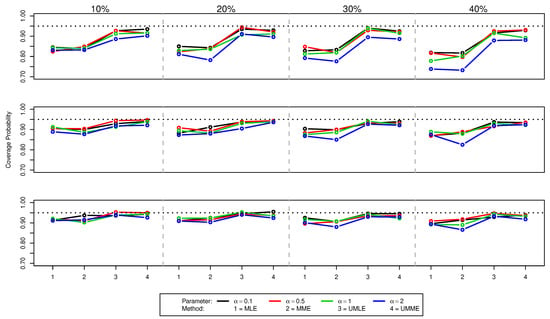
Figure 3.
Coverage probabilities of values for (top panel), (middle panel), and (bottom panel) for various censoring percentages.Dotted black line indicates the nominal 95% confidence level.
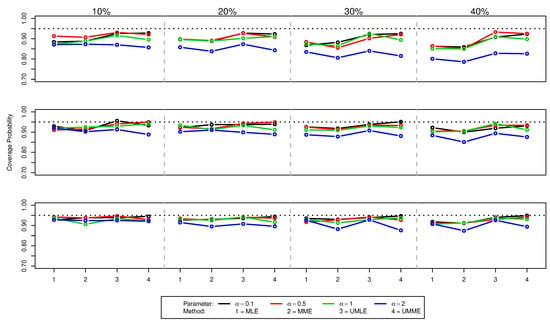
Figure 4.
Coverage probabilities of values for (top panel), (middle panel), and (bottom panel) for various censoring percentages. Dotted black line indicates the nominal 95% confidence level.
As shown in Figure 1 and Table A1, for , both the median and mean of MLE and MME methods underestimate the true value of and the size of the bias increases as the amount of censoring increases. A similar behaviour is noticed for increasing value of true . Interestingly, both mean and median point estimates for UMLE and UMME methods show better precision and outperform both MLE and MME methods in all the situations. However, estimated standard errors of these unbiased methods are slightly higher because UMLE and UMME samples disperse more than that of the MLE and MME samples (Figure 1). As can be seen in Figure 3, both UMLE and UMME show increasingly better coverage probability while MLE and MME are very liberal. Interestingly, on average the overall precision of the coverage probability decreases as and censoring percentages increase. All methods provide somewhat similar point estimates for values (Figure 2). The coverage probability comparison for the estimates (Figure 4) is quite similar to that of the cases. On average, the average remaining times (see Table A1) for both MLE and MME methods are slightly lower than the UMLE and UMME. As far as the standard error is concerned, the results are similar to those of the cases except the MLE method provides unusually higher standard errors and point estimates in the case for higher censoring percentages. The coverage probability comparison is quite similar to that of the and comparisons.
When sample size increases, all the methods improve their precisions and the coverage probabilities show a uniform improvement. However, the comparisons we made in the case are still valid for and cases (see Figure 1 and Figure 2, and Table A2 and Table A3). As expected, the differences between estimates and the effects of high censoring are not as pronounced as in cases and their standard errors are also now lower. We also note that the simulation results discussed here show some overall improvement when compared to the simulation results reported in [10].
5. Illustrative Examples
In this section, we consider two examples to illustrate the Gibbs sampler procedure described in Section 3. These examples exhibit parameter estimation in randomly right and Type-II censored data.
Example 1
(Cancer Patient Data). This dataset consists of lifetimes (in months) of 20 cancer patients who received a new treatment [21]. It was reported that only 17 out of 20 cancer patients completed the study while the rest of the three patients were randomly right censored and those lifetimes are denoted by “+” in the following dataset.
| 3 | 5 | 6 | 7 | 8 | 9 | 10 | 10 | 12 | 15 |
| 15 | 18 | 19 | 20 | 22 | 25 | 28 | 30 | 40 | 45 |
The Kolmogorov–Smirnov goodness-of-fit test indicates that these data adequately follow a BS distribution and its initial MLEs are and . For these data, represents the average remaining lifetime for the three patients censored during the experiment until they die. With only three observations out of 20 being censored, the number of iterations was found to be sufficient to ensure the convergence, and Gibbs sample chains were used for parameter estimation. The resulting estimates are shown in the upper portion of Table 1. Reference [22] used the same dataset to exhibit the performance of their Bayesian approach on analyzing parameter estimates from the generalized Birnbaum–Saunders distribution, , where the additional parameter is a shape-type parameter in which is the regular distribution. For comparison purposes we included their Bayesian and MLE results (SN MLE and SN Bayesian) along with the results from [21] Bayesian work (AM 2010) in the lower portion of Table 1.

Table 1.
Parameter estimates on cancer data.
We note that both MLE and MME compare favorably to one another, and their unbiased counterparts, UMLE and UMME, provide slightly higher point estimates except for MME estimates. Interestingly, our and estimates are lower than the SN (2017) and AM (2010) estimates and our confidence intervals are noticeably narrower though they overlap with SN (2017) and AM (2010) intervals. Among all the estimates, MLE and MME provide the shortest intervals and UMLE and UMME provide slightly wider intervals. This finding is consistent with what we observed in the Monte-Carlo simulation study, and therefore one may prefer biased reduced estimates though they are slightly wider than biased intervals if one desires to maintain the coverage probability at the nominal level.
The estimated average remaining lifetime for the censored patients ranged from 16 to 18 months after their observation period was completed. Besides, the knowledge obtained from the results for the average remaining lifetime confidence bounds will be useful if another experiment of this type is conducted again. The scientist will know approximately how long to run the test to ensure that all patients exhibit the event of interest.
Example 2
(Fatigue Life). This example consists of the fatigue life of 6061-T6 aluminum coupons cut parallel to the direction of rolling and oscillated at 18 cycles per second with maximum stress per cycle 31,000 psi reported in [5]. Using goodness-of-fit tests, we justified that the data shown below adequately follow a BS distribution.
| 70 | 90 | 96 | 97 | 99 | 100 | 103 | 104 | 104 | 105 | 107 | 108 | 108 | 108 | 109 | 109 | 112 |
| 112 | 113 | 114 | 114 | 114 | 116 | 119 | 120 | 120 | 120 | 121 | 121 | 123 | 124 | 124 | 124 | 124 |
| 124 | 128 | 128 | 129 | 129 | 130 | 130 | 130 | 131 | 131 | 131 | 131 | 131 | 132 | 132 | 132 | 133 |
| 134 | 134 | 134 | 134 | 134 | 136 | 136 | 137 | 138 | 138 | 138 | 139 | 139 | 141 | 141 | 142 | 142 |
| 142 | 142 | 142 | 142 | 144 | 144 | 145 | 146 | 148 | 148 | 149 | 151 | 151 | 152 | 155 | 156 | 157 |
| 157 | 157 | 157 | 158 | 159 | 162 | 163 | 163 | 164 | 166 | 166 | 168 | 170 | 174 | 196 | 212 |
Both point and interval estimates for complete data with 101 observations are reported in Table 2. Interestingly, MLE and MME estimates are quite similar, and their unbiased versions are also compared favorably to each other.

Table 2.
Parameter estimates for complete Fatigue Life data.
Reference [10] used this dataset to exhibit the performance of their Monte Carlo EM algorithm based maximum likelihood estimates for Type-II right censored data. A similar application to these data can be found in [23] where they applied reference priors with partial information based Bayesian method. Reference [24] used these data to exhibit a Bayesian approach that relies on proper inverse gamma priors with known hyperparameters. However, they mentioned that as the marginal posterior of becomes intractable and standard sampling methods such as random-walk Metropolis, Metropolis-Hastings, and slice sampler show poor performances, they preferred an efficient sampling algorithm via the generalized ratio-of-uniforms method to compute Bayesian estimates. For comparison purposes, we applied a similar censoring scheme as that applied in aforementioned works, that is, Type-II right censoring with CEP at 10%, 20%, and 30%.
The MLE based initial values of and for the censored data are shown in Table 3. For these data, the Gibbs sampler adequately converged with iterations and Gibbs sample chains were used to get final estimates. The resulting point estimates along with the widths of the 95% confidence intervals for all parameters are reported in Table 4. In addition, the table reports the corresponding Ng (2006), XT (2011) and Wang (2016) estimates for and . Interestingly, our MLE and MME based , and point estimates are quite closer to their corresponding estimates reported for complete data (Table 2) and the increasing censoring percentage seems to have only a slight effect on those estimates. UMLE and UMME estimates are slightly higher than that of the biased estimates and get closer to both Ng (2006) and XT (2011) estimates. However, Wang (2016) point estimates seem to be affected by the higher censoring percentages but with regards to the length of the confidence intervals this method outperforms the rest.

Table 3.
Initial parameter estimates on Type-II censored Fatigue Life data.

Table 4.
Point estimates (, , and ) and widths of the corresponding confidence intervals for different censoring percentages.
As expected, the average remaining time was also increased with respect to the censoring percentages. Further, we noticed that all values overestimated the true average remaining time reported in Table 3 and the increments are proportional to the true values for increasing censoring percentages. Widths of the confidence intervals of exhibit a curved linear trend for increasing censoring percentages.
Overall, these analyses indicate that our Fiducial estimates preform well in both of the examples. Given the conclusions we made in the simulation study, we may prefer the unbiased estimates when compared to the biased estimates. As we noticed in the second example, higher sample sizes could improve the precision of the biased estimators.
6. Concluding Remarks
In this study, we made Fiducial inferences via a flexible Gibbs sampler for right censored BS data. Our simulation study indicates that the biased reduced MLE and MME estimates are robust against higher censoring percentages and lower sample sizes. The amount of censoring and sample size has a direct impact on the performance of the MLE and MME methods and therefore one may cautiously apply them for smaller to moderate sample size problems. The simulation study further reveals that the suggested procedure shows some improvements when compared to the results reported in [10] and the illustrative examples indicate that the suggested procedures provide better performance when compared to the alternative methods we considered in this study.
This study reveals that the Fiducial inference can play a vital role in distribution theory and is a strong alternative for Frequentist and Bayesian paradigms. The MCMC methods such as Gibbs sampler may play a key role in Fiducial methods when analyzing survival data as there is less restriction regarding the type of the Fiducial distribution that may be chosen. Moreover, the Gibbs sampling procedure can easily be altered to adopt other forms of censoring schemes. Undoubtedly the Gibbs sampler has a place in developing complex models, especially when dealing with censored data.
Supplementary Materials
The following are available at https://www.mdpi.com/article/10.3390/stats4020025/s1.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Acknowledgments
The authors thank three anonymous referees and the academic editor for their constructive and very useful comments and suggestions on an earlier manuscript which led to a substantial improvement.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Simulation Results

Table A1.
Mean and standard error of the point estimates and probability coverages of 95% confidence intervals based on Monte-Carlo simulation ().
Table A1.
Mean and standard error of the point estimates and probability coverages of 95% confidence intervals based on Monte-Carlo simulation ().
| Param | CEP% | MLE | MME | UMLE | UMME | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| PE | SE | CP | PE | SE | CP | PE | SE | CP | PE | SE | CP | |||
| 0.1 | 10 | 0.091 | 0.024 | 0.845 | 0.090 | 0.023 | 0.839 | 0.103 | 0.027 | 0.927 | 0.103 | 0.026 | 0.935 | |
| 20 | 0.089 | 0.025 | 0.850 | 0.090 | 0.026 | 0.843 | 0.103 | 0.029 | 0.935 | 0.104 | 0.029 | 0.929 | ||
| 30 | 0.087 | 0.027 | 0.828 | 0.087 | 0.027 | 0.833 | 0.106 | 0.033 | 0.940 | 0.105 | 0.033 | 0.925 | ||
| 40 | 0.085 | 0.030 | 0.819 | 0.084 | 0.030 | 0.817 | 0.106 | 0.038 | 0.916 | 0.106 | 0.037 | 0.929 | ||
| 0.5 | 10 | 0.451 | 0.121 | 0.824 | 0.450 | 0.116 | 0.849 | 0.519 | 0.134 | 0.927 | 0.511 | 0.131 | 0.915 | |
| 20 | 0.438 | 0.125 | 0.823 | 0.445 | 0.125 | 0.839 | 0.520 | 0.143 | 0.944 | 0.510 | 0.148 | 0.921 | ||
| 30 | 0.443 | 0.137 | 0.848 | 0.428 | 0.135 | 0.819 | 0.511 | 0.163 | 0.929 | 0.516 | 0.158 | 0.922 | ||
| 40 | 0.417 | 0.141 | 0.817 | 0.414 | 0.146 | 0.797 | 0.516 | 0.180 | 0.925 | 0.508 | 0.172 | 0.931 | ||
| 1 | 10 | 0.901 | 0.225 | 0.842 | 0.908 | 0.237 | 0.840 | 1.020 | 0.269 | 0.912 | 1.013 | 0.258 | 0.916 | |
| 20 | 0.874 | 0.258 | 0.829 | 0.886 | 0.248 | 0.836 | 0.994 | 0.287 | 0.907 | 1.012 | 0.285 | 0.911 | ||
| 30 | 0.842 | 0.263 | 0.812 | 0.859 | 0.280 | 0.819 | 1.003 | 0.307 | 0.939 | 0.995 | 0.321 | 0.915 | ||
| 40 | 0.812 | 0.286 | 0.778 | 0.819 | 0.287 | 0.802 | 0.989 | 0.350 | 0.915 | 0.966 | 0.348 | 0.892 | ||
| 2 | 10 | 1.762 | 0.446 | 0.831 | 1.761 | 0.454 | 0.832 | 1.974 | 0.532 | 0.886 | 1.980 | 0.518 | 0.902 | |
| 20 | 1.693 | 0.493 | 0.811 | 1.690 | 0.512 | 0.782 | 1.955 | 0.547 | 0.911 | 1.935 | 0.560 | 0.896 | ||
| 30 | 1.657 | 0.562 | 0.792 | 1.633 | 0.544 | 0.776 | 1.865 | 0.565 | 0.895 | 1.859 | 0.582 | 0.886 | ||
| 40 | 1.533 | 0.595 | 0.738 | 1.549 | 0.594 | 0.732 | 1.783 | 0.632 | 0.879 | 1.805 | 0.637 | 0.881 | ||
| 0.1 | 10 | 1.000 | 0.033 | 0.884 | 1.000 | 0.032 | 0.888 | 1.003 | 0.032 | 0.926 | 0.998 | 0.032 | 0.928 | |
| 20 | 0.997 | 0.031 | 0.898 | 0.999 | 0.031 | 0.888 | 1.003 | 0.033 | 0.928 | 1.001 | 0.033 | 0.923 | ||
| 30 | 0.998 | 0.034 | 0.868 | 0.996 | 0.033 | 0.882 | 1.001 | 0.034 | 0.921 | 1.000 | 0.035 | 0.925 | ||
| 40 | 0.994 | 0.037 | 0.863 | 0.995 | 0.036 | 0.859 | 1.004 | 0.037 | 0.908 | 1.002 | 0.038 | 0.923 | ||
| 0.5 | 10 | 1.008 | 0.155 | 0.913 | 1.015 | 0.158 | 0.907 | 1.013 | 0.159 | 0.931 | 1.011 | 0.158 | 0.921 | |
| 20 | 1.015 | 0.159 | 0.898 | 1.009 | 0.162 | 0.891 | 1.010 | 0.163 | 0.927 | 1.002 | 0.160 | 0.909 | ||
| 30 | 1.008 | 0.173 | 0.884 | 1.001 | 0.173 | 0.855 | 1.019 | 0.181 | 0.902 | 1.014 | 0.172 | 0.921 | ||
| 40 | 0.988 | 0.175 | 0.864 | 0.984 | 0.173 | 0.851 | 1.025 | 0.185 | 0.933 | 1.013 | 0.175 | 0.925 | ||
| 1 | 10 | 1.007 | 0.295 | 0.873 | 1.034 | 0.317 | 0.888 | 1.009 | 0.291 | 0.916 | 1.024 | 0.318 | 0.895 | |
| 20 | 1.034 | 0.315 | 0.896 | 1.041 | 0.318 | 0.889 | 1.008 | 0.302 | 0.902 | 1.026 | 0.316 | 0.911 | ||
| 30 | 1.011 | 0.321 | 0.874 | 1.025 | 0.332 | 0.866 | 1.022 | 0.326 | 0.926 | 1.030 | 0.331 | 0.894 | ||
| 40 | 1.007 | 0.351 | 0.851 | 0.990 | 0.349 | 0.850 | 1.027 | 0.345 | 0.910 | 1.019 | 0.341 | 0.898 | ||
| 2 | 10 | 1.106 | 0.597 | 0.871 | 1.096 | 0.521 | 0.873 | 1.014 | 0.508 | 0.870 | 0.992 | 0.499 | 0.857 | |
| 20 | 1.076 | 0.564 | 0.858 | 1.072 | 0.561 | 0.838 | 0.980 | 0.498 | 0.873 | 0.976 | 0.532 | 0.843 | ||
| 30 | 1.063 | 0.638 | 0.835 | 1.015 | 0.600 | 0.806 | 0.941 | 0.533 | 0.840 | 0.976 | 0.568 | 0.815 | ||
| 40 | 0.990 | 0.610 | 0.801 | 0.993 | 0.619 | 0.786 | 0.942 | 0.603 | 0.828 | 0.980 | 0.603 | 0.826 | ||
| 0.1 | 10 | 0.055 | 0.016 | 0.926 | 0.054 | 0.016 | 0.913 | 0.066 | 0.021 | 0.941 | 0.065 | 0.020 | 0.952 | |
| 20 | 0.060 | 0.019 | 0.907 | 0.060 | 0.020 | 0.896 | 0.074 | 0.024 | 0.948 | 0.074 | 0.024 | 0.948 | ||
| 30 | 0.064 | 0.022 | 0.883 | 0.064 | 0.023 | 0.891 | 0.083 | 0.030 | 0.944 | 0.082 | 0.029 | 0.932 | ||
| 40 | 0.068 | 0.027 | 0.866 | 0.068 | 0.027 | 0.864 | 0.092 | 0.037 | 0.921 | 0.091 | 0.037 | 0.927 | ||
| 0.5 | 10 | 0.462 | 0.211 | 0.916 | 0.468 | 0.211 | 0.906 | 0.588 | 0.271 | 0.934 | 0.575 | 0.253 | 0.925 | |
| 20 | 0.465 | 0.225 | 0.900 | 0.479 | 0.230 | 0.905 | 0.612 | 0.297 | 0.953 | 0.590 | 0.291 | 0.942 | ||
| 30 | 0.497 | 0.267 | 0.905 | 0.472 | 0.251 | 0.877 | 0.639 | 0.356 | 0.926 | 0.640 | 0.353 | 0.939 | ||
| 40 | 0.472 | 0.264 | 0.871 | 0.468 | 0.275 | 0.845 | 0.707 | 0.451 | 0.939 | 0.665 | 0.392 | 0.938 | ||
| 1 | 10 | 1.422 | 0.786 | 0.901 | 1.447 | 0.866 | 0.913 | 1.688 | 0.923 | 0.947 | 1.690 | 0.930 | 0.935 | |
| 20 | 1.379 | 0.888 | 0.878 | 1.423 | 0.895 | 0.887 | 1.708 | 1.105 | 0.900 | 1.809 | 1.141 | 0.932 | ||
| 30 | 1.364 | 0.987 | 0.862 | 1.368 | 0.996 | 0.874 | 1.855 | 1.356 | 0.925 | 1.806 | 1.357 | 0.915 | ||
| 40 | 1.401 | 1.336 | 0.847 | 1.334 | 1.142 | 0.859 | 1.977 | 1.612 | 0.916 | 1.819 | 1.449 | 0.916 | ||
| 2 | 10 | 4.529 | 3.937 | 0.849 | 4.475 | 3.442 | 0.838 | 4.709 | 3.943 | 0.872 | 4.647 | 3.266 | 0.912 | |
| 20 | 4.423 | 4.472 | 0.795 | 4.153 | 3.925 | 0.783 | 5.323 | 4.221 | 0.881 | 5.044 | 4.392 | 0.844 | ||
| 30 | 4.940 | 6.075 | 0.778 | 4.144 | 5.038 | 0.785 | 4.790 | 4.133 | 0.841 | 4.867 | 4.814 | 0.861 | ||
| 40 | 5.124 | 10.325 | 0.754 | 4.309 | 5.681 | 0.753 | 5.058 | 5.362 | 0.858 | 5.046 | 5.347 | 0.848 | ||

Table A2.
Mean and standard error of the point estimates and probability coverages of 95% confidence intervals based on Monte-Carlo simulation ().
Table A2.
Mean and standard error of the point estimates and probability coverages of 95% confidence intervals based on Monte-Carlo simulation ().
| Param | CEP% | MLE | MME | UMLE | UMME | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| PE | SE | CP | PE | SE | CP | PE | SE | CP | PE | SE | CP | |||
| 0.1 | 10 | 0.096 | 0.016 | 0.905 | 0.095 | 0.016 | 0.900 | 0.100 | 0.017 | 0.929 | 0.101 | 0.018 | 0.940 | |
| 20 | 0.094 | 0.018 | 0.882 | 0.095 | 0.018 | 0.912 | 0.101 | 0.020 | 0.937 | 0.102 | 0.020 | 0.938 | ||
| 30 | 0.095 | 0.019 | 0.904 | 0.094 | 0.020 | 0.899 | 0.102 | 0.022 | 0.930 | 0.102 | 0.022 | 0.939 | ||
| 40 | 0.092 | 0.022 | 0.870 | 0.091 | 0.022 | 0.882 | 0.102 | 0.024 | 0.937 | 0.103 | 0.025 | 0.934 | ||
| 0.5 | 10 | 0.475 | 0.083 | 0.905 | 0.479 | 0.082 | 0.904 | 0.508 | 0.089 | 0.944 | 0.511 | 0.086 | 0.947 | |
| 20 | 0.473 | 0.087 | 0.909 | 0.466 | 0.090 | 0.892 | 0.505 | 0.098 | 0.939 | 0.506 | 0.098 | 0.943 | ||
| 30 | 0.468 | 0.104 | 0.883 | 0.466 | 0.096 | 0.900 | 0.506 | 0.108 | 0.934 | 0.511 | 0.107 | 0.930 | ||
| 40 | 0.459 | 0.112 | 0.869 | 0.461 | 0.107 | 0.889 | 0.503 | 0.125 | 0.916 | 0.507 | 0.119 | 0.935 | ||
| 1 | 10 | 0.956 | 0.166 | 0.913 | 0.955 | 0.173 | 0.886 | 1.001 | 0.186 | 0.913 | 1.009 | 0.174 | 0.938 | |
| 20 | 0.930 | 0.178 | 0.894 | 0.942 | 0.189 | 0.883 | 1.005 | 0.193 | 0.931 | 1.000 | 0.191 | 0.938 | ||
| 30 | 0.927 | 0.206 | 0.875 | 0.928 | 0.199 | 0.886 | 1.008 | 0.214 | 0.941 | 1.007 | 0.221 | 0.924 | ||
| 40 | 0.916 | 0.227 | 0.889 | 0.906 | 0.208 | 0.879 | 0.996 | 0.247 | 0.930 | 1.007 | 0.250 | 0.922 | ||
| 2 | 10 | 1.893 | 0.339 | 0.889 | 1.889 | 0.340 | 0.877 | 2.015 | 0.366 | 0.918 | 2.003 | 0.364 | 0.921 | |
| 20 | 1.845 | 0.370 | 0.873 | 1.853 | 0.364 | 0.880 | 1.939 | 0.385 | 0.905 | 1.975 | 0.385 | 0.936 | ||
| 30 | 1.808 | 0.423 | 0.868 | 1.813 | 0.422 | 0.850 | 1.965 | 0.431 | 0.927 | 1.951 | 0.424 | 0.921 | ||
| 40 | 1.771 | 0.455 | 0.875 | 1.758 | 0.467 | 0.825 | 1.879 | 0.452 | 0.919 | 1.914 | 0.459 | 0.924 | ||
| 0.1 | 10 | 1.000 | 0.023 | 0.929 | 1.001 | 0.024 | 0.908 | 0.999 | 0.021 | 0.956 | 1.001 | 0.023 | 0.933 | |
| 20 | 0.999 | 0.023 | 0.922 | 1.000 | 0.022 | 0.937 | 0.999 | 0.023 | 0.937 | 1.000 | 0.023 | 0.939 | ||
| 30 | 1.000 | 0.024 | 0.926 | 0.999 | 0.024 | 0.918 | 1.002 | 0.024 | 0.938 | 1.001 | 0.024 | 0.951 | ||
| 40 | 0.996 | 0.024 | 0.922 | 0.997 | 0.026 | 0.900 | 1.000 | 0.026 | 0.919 | 0.999 | 0.025 | 0.931 | ||
| 0.5 | 10 | 1.000 | 0.116 | 0.910 | 0.999 | 0.112 | 0.916 | 1.000 | 0.111 | 0.940 | 1.004 | 0.109 | 0.950 | |
| 20 | 1.003 | 0.111 | 0.924 | 0.997 | 0.110 | 0.916 | 1.004 | 0.112 | 0.943 | 1.004 | 0.111 | 0.949 | ||
| 30 | 1.000 | 0.116 | 0.925 | 0.996 | 0.117 | 0.913 | 1.011 | 0.120 | 0.934 | 1.009 | 0.118 | 0.933 | ||
| 40 | 0.988 | 0.124 | 0.905 | 0.997 | 0.127 | 0.906 | 1.004 | 0.128 | 0.934 | 1.011 | 0.127 | 0.934 | ||
| 1 | 10 | 1.023 | 0.218 | 0.919 | 1.023 | 0.205 | 0.925 | 1.012 | 0.206 | 0.929 | 1.014 | 0.209 | 0.941 | |
| 20 | 1.011 | 0.215 | 0.934 | 1.010 | 0.221 | 0.913 | 1.021 | 0.222 | 0.933 | 1.017 | 0.226 | 0.911 | ||
| 30 | 1.015 | 0.228 | 0.911 | 1.001 | 0.225 | 0.909 | 1.019 | 0.237 | 0.930 | 1.012 | 0.231 | 0.923 | ||
| 40 | 1.001 | 0.248 | 0.902 | 0.986 | 0.236 | 0.904 | 1.035 | 0.263 | 0.942 | 1.014 | 0.256 | 0.911 | ||
| 2 | 10 | 1.051 | 0.328 | 0.920 | 1.053 | 0.364 | 0.902 | 0.994 | 0.332 | 0.913 | 0.995 | 0.338 | 0.888 | |
| 20 | 1.026 | 0.385 | 0.902 | 1.045 | 0.363 | 0.910 | 0.973 | 0.344 | 0.899 | 0.992 | 0.356 | 0.889 | ||
| 30 | 1.009 | 0.414 | 0.887 | 1.019 | 0.400 | 0.878 | 1.007 | 0.390 | 0.908 | 0.984 | 0.380 | 0.881 | ||
| 40 | 1.032 | 0.470 | 0.884 | 0.997 | 0.453 | 0.851 | 0.967 | 0.404 | 0.894 | 0.986 | 0.430 | 0.876 | ||
| 0.1 | 10 | 0.056 | 0.011 | 0.931 | 0.055 | 0.011 | 0.933 | 0.060 | 0.012 | 0.949 | 0.061 | 0.013 | 0.940 | |
| 20 | 0.061 | 0.014 | 0.926 | 0.062 | 0.014 | 0.952 | 0.068 | 0.016 | 0.943 | 0.069 | 0.015 | 0.943 | ||
| 30 | 0.068 | 0.016 | 0.935 | 0.068 | 0.016 | 0.916 | 0.075 | 0.019 | 0.938 | 0.076 | 0.018 | 0.947 | ||
| 40 | 0.073 | 0.020 | 0.906 | 0.072 | 0.019 | 0.905 | 0.083 | 0.022 | 0.939 | 0.084 | 0.023 | 0.932 | ||
| 0.5 | 10 | 0.482 | 0.151 | 0.935 | 0.487 | 0.149 | 0.930 | 0.537 | 0.170 | 0.929 | 0.542 | 0.161 | 0.937 | |
| 20 | 0.492 | 0.155 | 0.934 | 0.479 | 0.156 | 0.932 | 0.548 | 0.181 | 0.951 | 0.551 | 0.182 | 0.947 | ||
| 30 | 0.503 | 0.189 | 0.911 | 0.496 | 0.174 | 0.911 | 0.572 | 0.207 | 0.940 | 0.579 | 0.203 | 0.947 | ||
| 40 | 0.506 | 0.208 | 0.888 | 0.510 | 0.203 | 0.903 | 0.591 | 0.246 | 0.925 | 0.597 | 0.235 | 0.948 | ||
| 1 | 10 | 1.660 | 0.661 | 0.926 | 1.661 | 0.667 | 0.926 | 1.788 | 0.753 | 0.939 | 1.811 | 0.718 | 0.931 | |
| 20 | 1.544 | 0.691 | 0.933 | 1.573 | 0.727 | 0.910 | 1.780 | 0.790 | 0.946 | 1.748 | 0.767 | 0.936 | ||
| 30 | 1.546 | 0.787 | 0.899 | 1.521 | 0.773 | 0.917 | 1.787 | 0.901 | 0.943 | 1.768 | 0.897 | 0.944 | ||
| 40 | 1.531 | 0.941 | 0.897 | 1.442 | 0.777 | 0.909 | 1.849 | 1.171 | 0.924 | 1.806 | 1.061 | 0.936 | ||
| 2 | 10 | 6.313 | 3.321 | 0.929 | 6.235 | 3.176 | 0.938 | 6.605 | 3.131 | 0.944 | 6.571 | 3.375 | 0.930 | |
| 20 | 5.727 | 3.445 | 0.909 | 5.773 | 3.329 | 0.907 | 5.902 | 3.365 | 0.933 | 6.209 | 3.600 | 0.923 | ||
| 30 | 5.700 | 4.576 | 0.888 | 5.514 | 4.100 | 0.876 | 6.328 | 3.981 | 0.928 | 5.963 | 3.706 | 0.919 | ||
| 40 | 6.940 | 12.364 | 0.887 | 5.349 | 4.811 | 0.859 | 5.756 | 4.303 | 0.929 | 5.817 | 4.313 | 0.916 | ||

Table A3.
Mean and standard error of the point estimates and probability coverages of 95% confidence intervals based on Monte-Carlo simulation ().
Table A3.
Mean and standard error of the point estimates and probability coverages of 95% confidence intervals based on Monte-Carlo simulation ().
| Param | CEP% | MLE | MME | UMLE | UMME | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| PE | SE | CP | PE | SE | CP | PE | SE | CP | PE | SE | CP | |||
| 0.1 | 10 | 0.097 | 0.014 | 0.913 | 0.097 | 0.013 | 0.937 | 0.101 | 0.014 | 0.936 | 0.101 | 0.014 | 0.942 | |
| 20 | 0.096 | 0.015 | 0.910 | 0.097 | 0.015 | 0.925 | 0.101 | 0.015 | 0.945 | 0.102 | 0.016 | 0.955 | ||
| 30 | 0.097 | 0.016 | 0.925 | 0.096 | 0.016 | 0.907 | 0.101 | 0.017 | 0.946 | 0.101 | 0.017 | 0.945 | ||
| 40 | 0.094 | 0.018 | 0.896 | 0.095 | 0.017 | 0.914 | 0.100 | 0.019 | 0.929 | 0.102 | 0.019 | 0.938 | ||
| 0.5 | 10 | 0.486 | 0.070 | 0.919 | 0.485 | 0.070 | 0.910 | 0.504 | 0.069 | 0.953 | 0.503 | 0.071 | 0.950 | |
| 20 | 0.476 | 0.073 | 0.911 | 0.479 | 0.073 | 0.915 | 0.502 | 0.079 | 0.944 | 0.506 | 0.080 | 0.936 | ||
| 30 | 0.478 | 0.085 | 0.896 | 0.479 | 0.083 | 0.906 | 0.506 | 0.088 | 0.935 | 0.504 | 0.087 | 0.936 | ||
| 40 | 0.471 | 0.087 | 0.909 | 0.474 | 0.091 | 0.918 | 0.509 | 0.095 | 0.947 | 0.507 | 0.098 | 0.936 | ||
| 1 | 10 | 0.975 | 0.140 | 0.921 | 0.961 | 0.140 | 0.902 | 1.004 | 0.143 | 0.939 | 1.008 | 0.146 | 0.943 | |
| 20 | 0.959 | 0.146 | 0.923 | 0.958 | 0.149 | 0.924 | 1.009 | 0.154 | 0.953 | 1.000 | 0.160 | 0.934 | ||
| 30 | 0.951 | 0.164 | 0.917 | 0.945 | 0.163 | 0.908 | 0.996 | 0.172 | 0.942 | 1.007 | 0.180 | 0.922 | ||
| 40 | 0.937 | 0.184 | 0.892 | 0.925 | 0.183 | 0.890 | 1.005 | 0.202 | 0.943 | 0.988 | 0.192 | 0.932 | ||
| 2 | 10 | 1.922 | 0.275 | 0.911 | 1.939 | 0.281 | 0.915 | 1.999 | 0.275 | 0.939 | 1.989 | 0.296 | 0.926 | |
| 20 | 1.916 | 0.311 | 0.909 | 1.902 | 0.302 | 0.903 | 1.980 | 0.320 | 0.940 | 1.970 | 0.322 | 0.924 | ||
| 30 | 1.888 | 0.351 | 0.901 | 1.874 | 0.354 | 0.880 | 1.963 | 0.361 | 0.930 | 1.970 | 0.356 | 0.929 | ||
| 40 | 1.842 | 0.394 | 0.894 | 1.835 | 0.421 | 0.866 | 1.959 | 0.398 | 0.933 | 1.959 | 0.410 | 0.918 | ||
| 0.1 | 10 | 1.000 | 0.019 | 0.928 | 1.000 | 0.018 | 0.938 | 1.001 | 0.018 | 0.939 | 0.998 | 0.018 | 0.945 | |
| 20 | 1.000 | 0.019 | 0.927 | 0.999 | 0.020 | 0.930 | 1.000 | 0.019 | 0.936 | 1.001 | 0.019 | 0.944 | ||
| 30 | 0.999 | 0.020 | 0.935 | 0.999 | 0.020 | 0.930 | 1.002 | 0.020 | 0.939 | 1.000 | 0.019 | 0.947 | ||
| 40 | 0.998 | 0.021 | 0.918 | 0.998 | 0.021 | 0.911 | 1.000 | 0.021 | 0.940 | 1.000 | 0.020 | 0.949 | ||
| 0.5 | 10 | 1.001 | 0.089 | 0.942 | 0.997 | 0.088 | 0.937 | 1.004 | 0.089 | 0.947 | 1.003 | 0.092 | 0.929 | |
| 20 | 0.998 | 0.092 | 0.935 | 0.998 | 0.092 | 0.925 | 1.004 | 0.093 | 0.941 | 1.004 | 0.092 | 0.936 | ||
| 30 | 1.000 | 0.098 | 0.917 | 1.001 | 0.093 | 0.928 | 1.006 | 0.095 | 0.942 | 1.001 | 0.100 | 0.927 | ||
| 40 | 0.997 | 0.104 | 0.911 | 0.988 | 0.104 | 0.912 | 1.005 | 0.106 | 0.930 | 1.006 | 0.105 | 0.941 | ||
| 1 | 10 | 1.005 | 0.163 | 0.937 | 1.007 | 0.180 | 0.906 | 1.008 | 0.166 | 0.934 | 1.012 | 0.174 | 0.923 | |
| 20 | 1.004 | 0.176 | 0.932 | 1.000 | 0.173 | 0.926 | 1.014 | 0.176 | 0.942 | 1.010 | 0.182 | 0.916 | ||
| 30 | 1.006 | 0.188 | 0.930 | 1.005 | 0.184 | 0.913 | 1.010 | 0.198 | 0.929 | 1.016 | 0.195 | 0.938 | ||
| 40 | 0.997 | 0.199 | 0.906 | 0.995 | 0.203 | 0.913 | 1.025 | 0.212 | 0.936 | 1.007 | 0.198 | 0.931 | ||
| 2 | 10 | 1.016 | 0.259 | 0.928 | 1.039 | 0.279 | 0.924 | 0.995 | 0.265 | 0.925 | 0.991 | 0.257 | 0.921 | |
| 20 | 1.002 | 0.296 | 0.915 | 1.013 | 0.308 | 0.895 | 0.999 | 0.302 | 0.908 | 0.987 | 0.286 | 0.896 | ||
| 30 | 1.008 | 0.322 | 0.926 | 0.995 | 0.326 | 0.882 | 1.001 | 0.324 | 0.928 | 0.975 | 0.316 | 0.876 | ||
| 40 | 0.993 | 0.352 | 0.908 | 1.003 | 0.372 | 0.874 | 1.013 | 0.362 | 0.926 | 0.991 | 0.355 | 0.894 | ||
| 0.1 | 10 | 0.056 | 0.010 | 0.938 | 0.056 | 0.009 | 0.926 | 0.059 | 0.010 | 0.938 | 0.059 | 0.010 | 0.950 | |
| 20 | 0.062 | 0.012 | 0.930 | 0.063 | 0.011 | 0.949 | 0.066 | 0.012 | 0.953 | 0.067 | 0.012 | 0.944 | ||
| 30 | 0.069 | 0.013 | 0.938 | 0.068 | 0.014 | 0.926 | 0.074 | 0.014 | 0.942 | 0.074 | 0.014 | 0.943 | ||
| 40 | 0.074 | 0.016 | 0.930 | 0.074 | 0.015 | 0.923 | 0.080 | 0.017 | 0.939 | 0.082 | 0.017 | 0.939 | ||
| 0.5 | 10 | 0.491 | 0.123 | 0.950 | 0.488 | 0.126 | 0.923 | 0.524 | 0.131 | 0.949 | 0.522 | 0.132 | 0.953 | |
| 20 | 0.488 | 0.130 | 0.928 | 0.492 | 0.129 | 0.929 | 0.535 | 0.147 | 0.953 | 0.540 | 0.146 | 0.950 | ||
| 30 | 0.508 | 0.150 | 0.922 | 0.510 | 0.148 | 0.926 | 0.558 | 0.164 | 0.946 | 0.552 | 0.164 | 0.931 | ||
| 40 | 0.513 | 0.161 | 0.924 | 0.513 | 0.164 | 0.921 | 0.580 | 0.184 | 0.941 | 0.577 | 0.191 | 0.941 | ||
| 1 | 10 | 1.670 | 0.542 | 0.939 | 1.631 | 0.545 | 0.925 | 1.764 | 0.575 | 0.947 | 1.786 | 0.591 | 0.943 | |
| 20 | 1.577 | 0.555 | 0.919 | 1.568 | 0.560 | 0.932 | 1.741 | 0.622 | 0.945 | 1.709 | 0.645 | 0.936 | ||
| 30 | 1.539 | 0.613 | 0.930 | 1.524 | 0.623 | 0.917 | 1.671 | 0.680 | 0.940 | 1.715 | 0.716 | 0.939 | ||
| 40 | 1.494 | 0.695 | 0.918 | 1.457 | 0.689 | 0.906 | 1.734 | 0.824 | 0.934 | 1.633 | 0.736 | 0.922 | ||
| 2 | 10 | 6.272 | 2.518 | 0.929 | 6.486 | 2.625 | 0.929 | 6.616 | 2.603 | 0.940 | 6.477 | 2.496 | 0.938 | |
| 20 | 5.945 | 2.914 | 0.915 | 5.884 | 2.853 | 0.926 | 6.284 | 3.034 | 0.933 | 6.088 | 2.812 | 0.931 | ||
| 30 | 5.728 | 3.360 | 0.930 | 5.529 | 3.306 | 0.894 | 6.086 | 3.540 | 0.928 | 5.840 | 3.247 | 0.917 | ||
| 40 | 5.674 | 4.504 | 0.896 | 5.424 | 4.267 | 0.882 | 6.150 | 4.113 | 0.940 | 5.846 | 3.952 | 0.912 | ||
References
- Birnbaum, Z.W.; Saunders, S.C. A new family of life distributions. J. Appl. Probab. 1969, 6, 319–327. [Google Scholar] [CrossRef]
- Bhattacharyya, G.; Fries, A. Fatigue Failure Models—Birnbaum—Saunders vs. Inverse Gaussian. IEEE Trans. Reliab. 1982, 31, 439–441. [Google Scholar] [CrossRef]
- Desmond, A.F. On the relationship between two fatigue-life models. IEEE Trans. Reliab. 1986, 35, 167–169. [Google Scholar] [CrossRef]
- Balakrishnan, N.; Kundu, D. Birnbaum–Saunders distribution: A review of models, analysis, and applications. Appl. Stoch. Model. Bus. Ind. 2019, 35, 4–49. [Google Scholar] [CrossRef]
- Birnbaum, Z.W.; Saunders, S.C. Estimation for a family of life distributions with applications to fatigue. J. Appl. Probab. 1969, 6, 328–347. [Google Scholar] [CrossRef]
- Engelhardt, M.; Bain, L.J.; Wright, F. Inferences on the parameters of the Birnbaum–Saunders fatigue life distribution based on maximum likelihood estimation. Technometrics 1981, 23, 251–256. [Google Scholar] [CrossRef]
- Desmond, F.A. Local Maxima of Stationary Stochastic Processes and Stochastic Modelling of Fatigue. Ph.D. Thesis, University of Waterloo, Waterloo, ON, Canada, 1982. Unpublished. [Google Scholar]
- Ng, H.; Kundu, D.; Balakrishnan, N. Modified moment estimation for the two-parameter Birnbaum–Saunders distribution. Comput. Stat. Data Anal. 2003, 43, 283–298. [Google Scholar] [CrossRef]
- Lemonte, A.J.; Cribari-Neto, F.; Vasconcellos, K.L. Improved statistical inference for the two-parameter Birnbaum–Saunders distribution. Comput. Stat. Data Anal. 2007, 51, 4656–4681. [Google Scholar] [CrossRef]
- Ng, H.; Kundu, D.; Balakrishnan, N. Point and interval estimation for the two-parameter Birnbaum–Saunders distribution based on Type-II censored samples. Comput. Stat. Data Anal. 2006, 50, 3222–3242. [Google Scholar] [CrossRef]
- Wang, Z.; Desmond, A.F.; Lu, X. Modified censored moment estimation for the two-parameter Birnbaum–Saunders distribution. Comput. Stat. Data Anal. 2006, 50, 1033–1051. [Google Scholar] [CrossRef]
- Balakrishnan, N.; Zhu, X. An improved method of estimation for the parameters of the Birnbaum–Saunders distribution. J. Stat. Comput. Simul. 2014, 84, 2285–2294. [Google Scholar] [CrossRef]
- Sun, T.; Shi, Y. Estimation for Birnbaum–Saunders Distribution in Simple Step Stress–accelerated Life Test with Type-II Censoring. Commun. Stat.-Simul. Comput. 2016, 45, 880–901. [Google Scholar] [CrossRef]
- Fisher, R.A. Statistical Methods and Scientific Inference; Hafner Publishing Co.: New York, NY, USA, 1973. [Google Scholar]
- Balakrishnan, N.; Cohen, A.C. Order Statistics & Inference: Estimation Methods; Academic Press: San Diego, CA, USA, 1991. [Google Scholar]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2019. [Google Scholar]
- Delignette-Muller, M.L.; Dutang, C. fitdistrplus: An R package for fitting distributions. J. Stat. Softw. 2015, 64, 1–34. [Google Scholar] [CrossRef]
- Jayalath, K.P.; Chhikara, R.S. Survival analysis for the inverse Gaussian distribution with the Gibbs sampler. J. Appl. Stat. 2020, 1–20. [Google Scholar] [CrossRef]
- Brooks, S.P.; Gelman, A. General methods for monitoring convergence of iterative simulations. J. Comput. Graph. Stat. 1998, 7, 434–455. [Google Scholar]
- Gelman, A.; Carlin, J.B.; Stern, H.S.; Dunson, D.B.; Vehtari, A.; Rubin, D.B. Bayesian Data Analysis; Chapman and Hall/CRC: Boca Raton, FL, USA, 2013. [Google Scholar]
- Achcar, J.A.; Moala, F.A. Use of MCMC methods to obtain Bayesian inferences for the Birnbaum–Saunders distribution in the presence of censored data and covariates. Adv. Appl. Stat. 2010, 17, 1–27. [Google Scholar]
- Sha, N.; Ng, T.L. Bayesian inference for Birnbaum–Saunders distribution and its generalization. J. Stat. Comput. Simul. 2017, 87, 2411–2429. [Google Scholar] [CrossRef]
- Xu, A.; Tang, Y. Bayesian analysis of Birnbaum–Saunders distribution with partial information. Comput. Stat. Data Anal. 2011, 55, 2324–2333. [Google Scholar] [CrossRef]
- Wang, M.; Sun, X.; Park, C. Bayesian analysis of Birnbaum–Saunders distribution via the generalized ratio-of-uniforms method. Comput. Stat. 2016, 31, 207–225. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).