Weighted Log-Rank Statistics for Accelerated Failure Time Model
Abstract
:1. Introduction
2. Procedures
2.1. Accelerated Failure Time Model
2.2. Weighted Log-Rank Test
2.3. Adaptive Weight Function
2.4. Confidence Interval and Test
3. Numerical Studies
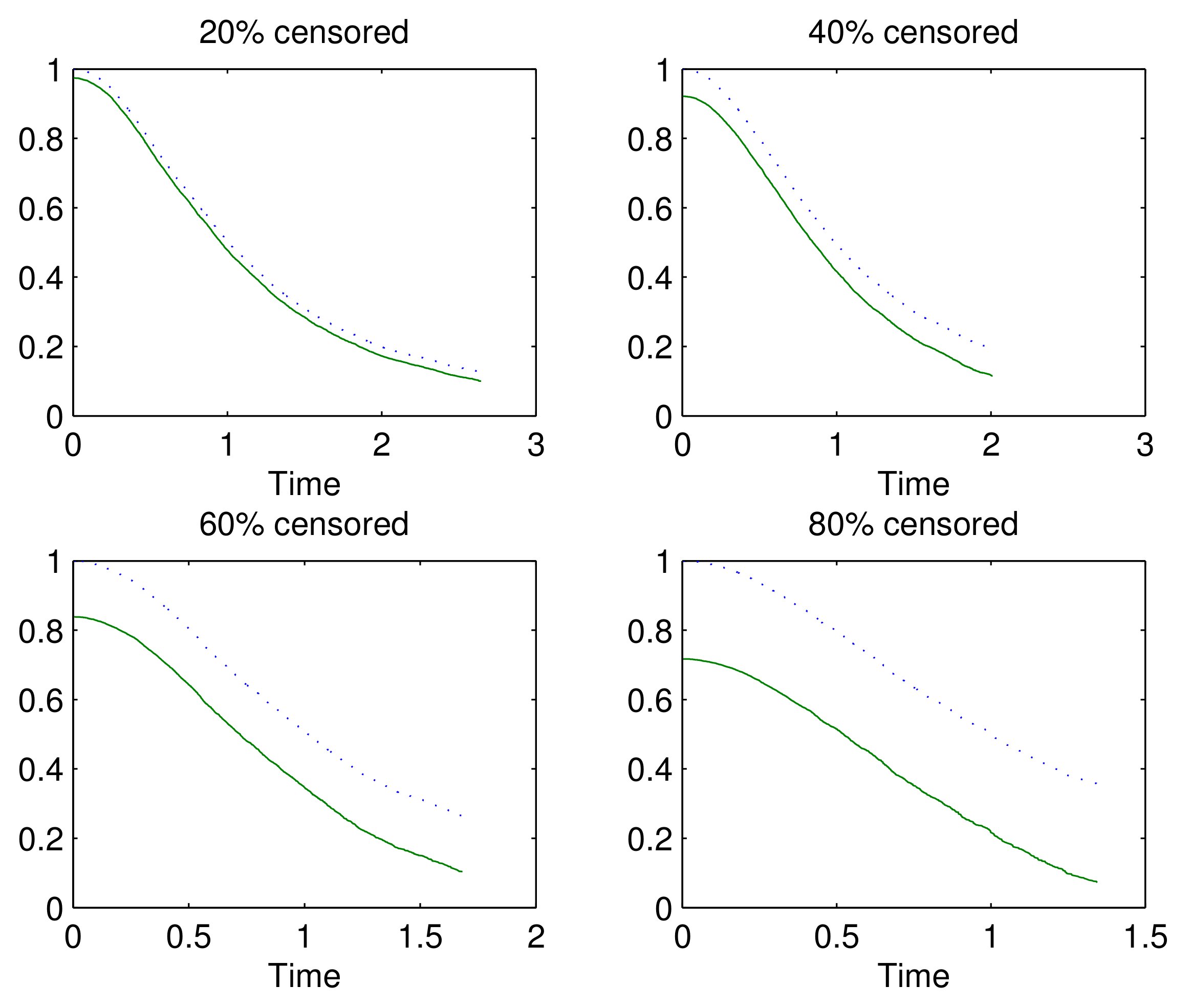
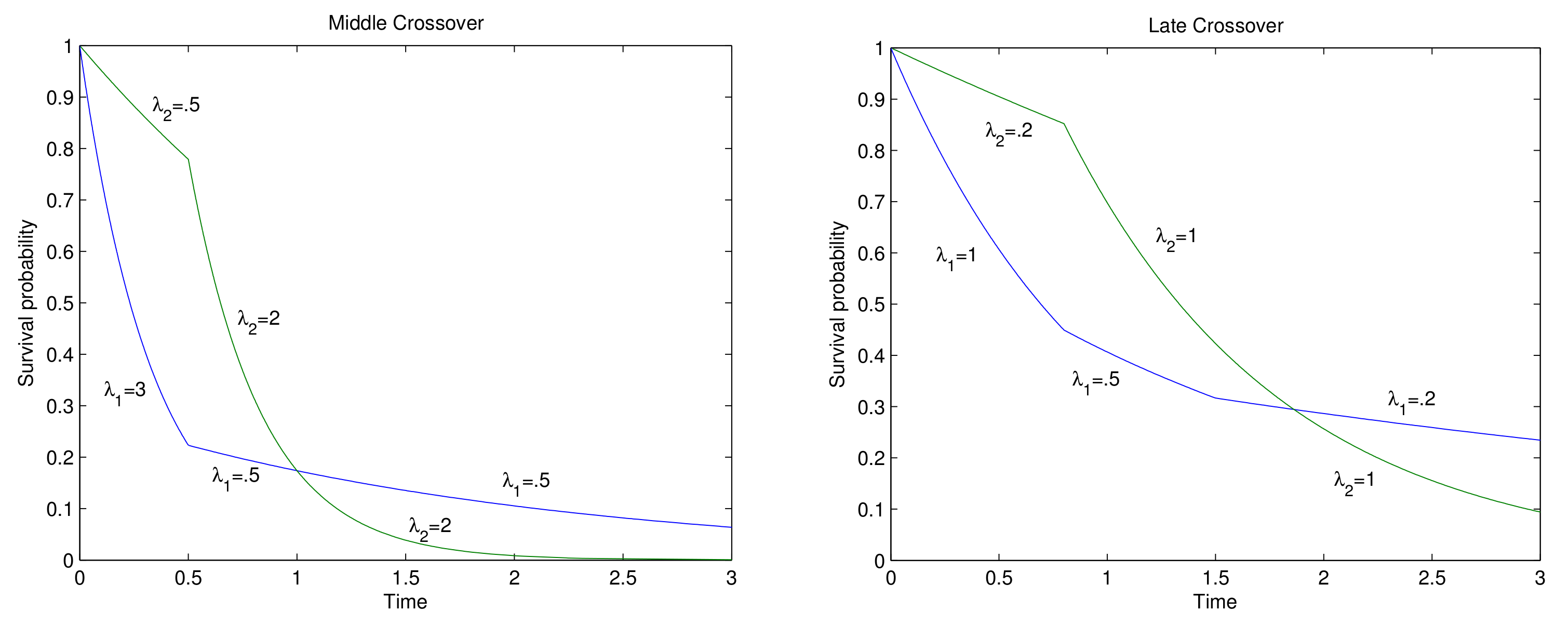
3.1. Simulation
- C1.
- has density , , and has density , , for some constant h.
- C2.
- has density , , and is normal with mean h and standard deviation 1.
- C3.
- is standard normal, and is uniform () for some constant h.
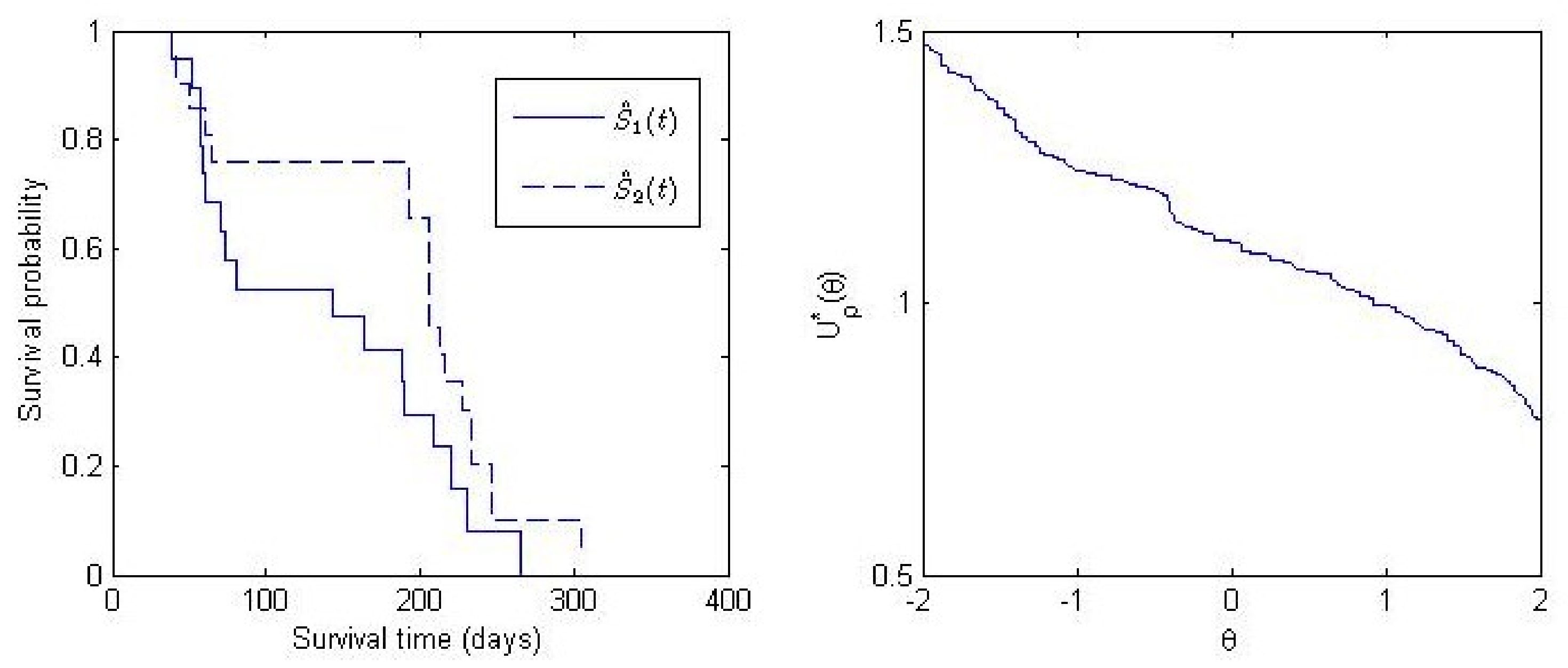
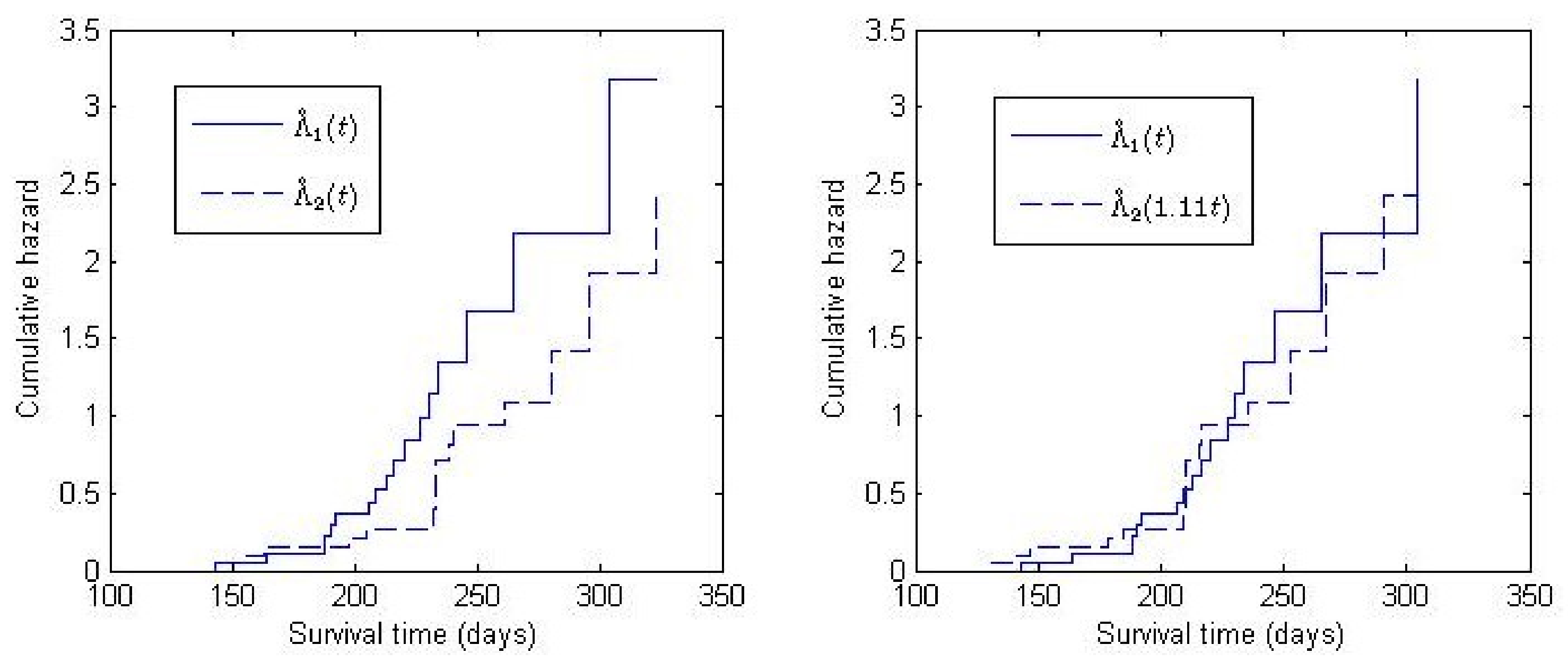
3.2. Application
4. Concluding Remarks
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Louis, T.A. Non-parametric analysis of an accelerated failure time model. Biometrika 1981, 68, 381–390. [Google Scholar] [CrossRef]
- Prentice, R.L. Linear rank tests with right censored data. Biometrika 1978, 65, 167–179. [Google Scholar] [CrossRef]
- Wei, L.J.; Gail, M.H. Nonparametric estimation for a scale-change with censored observations. J. Am. Stat. Assoc. 1983, 78, 312–318. [Google Scholar] [CrossRef]
- Fleming, T.R.; Harrington, D.P. A Class of Hypothesis Tests for One and Two Samples of Censored Survival Data. Commun. Stat. Theory Methods 1981, 13, 2469–2486. [Google Scholar] [CrossRef]
- Fleming, T.R.; Harrington, D.P.; O’Sullivan, M. Supremum versions of the Log-Rank and Generalized Wilcoxon Statistics. J. Am. Stat. Assoc. 1987, 82, 312–320. [Google Scholar] [CrossRef]
- Harrington, D.P.; Fleming, T.R. A class of rank test procedures for censored survival data. Biometrika 1982, 69, 133–143. [Google Scholar] [CrossRef]
- Kaplan, E.; Meier, P. Nonparametric Estimation from Incomplete Observations. J. Am. Assoc. 1958, 53, 457–481. [Google Scholar] [CrossRef]
- Buyske, S.; Fagerstrom, R.; Ying, Z. A class of weighted log-rank tests for survival data when the event is rare. J. Am. Stat. Assoc. 2000, 95, 249–258. [Google Scholar] [CrossRef]
- Lee, S.H.; Lee, E.J. On testing equality of two censored samples. J. Stat. Comput. Simul. 2009, 81, 1017–1026. [Google Scholar] [CrossRef]
- Shen, Y.; Cai, J. Maximum of the Weighted Kaplan–Meier Tests with Applications to Cancer Prevention and Screening Trials. Biometrics 2001, 57, 837–843. [Google Scholar] [CrossRef]
- Wu, L.; Gilbert, P.B. Flexible Weighted Log-Rank Tests Optimal for Detecting Early and/or Late Survival Differences. Biometrics 2002, 58, 997–1004. [Google Scholar] [CrossRef]
- Aalen, D.D. Nonparametric inference for a family of counting processes. Ann. Stat. 1978, 6, 701–726. [Google Scholar] [CrossRef]
- Nelson, W. Hazard plotting for incomplete failure data. J. Qual. Technol. 1969, 1, 27–52. [Google Scholar] [CrossRef]
- Hodges, J.L.; Lehmann, E.L. Estimation of location based on ranks. Ann. Math. Stat. 1963, 34, 598–611. [Google Scholar] [CrossRef]
- Gill, R.D. Censoring and Stochastic Integrals; MC Tract 124; Mathematical Centre: Amsterdam, The Netherlands, 1980. [Google Scholar]
- Cox, D.R. Regression models and life tables (with discussion). J. R. Stat. Soc. 1972, 34, 187–220. [Google Scholar]
- Mantel, N. Evaluation of Survival Data and Two New Rank Order Statistics Arising in Its Consideration. Cancer Chemother. Rep. 1966, 50, 163–170. [Google Scholar]
- Peto, R.; Peto, J. Asymptotically efficient rank invariant test procedures (with discussion). J. R. Stat. Soc. Ser. A 1972, 135, 185–207. [Google Scholar] [CrossRef]
- Lee, S.H.; Yang, S. Checking the censored two-sample accelerated life model using integrated cumulative hazard difference. Lifetime Data Anal. 2007, 13, 371–380. [Google Scholar] [CrossRef]
- Yang, S.; Prentice, R. Semiparametric analysis of short-term and long-term and hazard ratios with two-sample survival data. Biometrika 2005, 92, 1–17. [Google Scholar] [CrossRef]
- Creasman, W.T.; Phillips, J.L.; Menck, H.R. The National Cancer Data Base report on cancer of the vagina. Cancer 1998, 83, 1033–1040. [Google Scholar] [CrossRef]
- Pike, M.C. A method of analysis of a certain class of experiments in carcinogensis. Biometrika 1966, 18, 303–328. [Google Scholar]
- Kalbfleisch, J.D.; Prentice, R.L. The Statistical Analysis of Failure Time Data; Wiley: New York, NY, USA, 1980. [Google Scholar]
| Censoring % | Log-Rank | |||||
|---|---|---|---|---|---|---|
| C1 | ||||||
| (25, 25) | 20 | 94.8 (2.0616) † | 95.5 (2.1151) | 94.9 (2.0620) | 95.5 (2.1205) | 94.5 (2.1326) |
| 40 | 95.2 (2.1329) | 94.7 (2.1851) | 95.3 (2.1380) | 94.8 (2.2025) | 93.8 (2.1557) | |
| 60 | 95.9 (2.3495) | 95.9 (2.3825) | 96.2 (2.3586) | 96.1 (2.4074) | 95.8 (2.3583) | |
| (25, 50) | 20 | 94.6 (1.8030) | 94.6 (1.8568) | 94.6 (1.8038) | 94.7 (1.8629) | 94.6 (1.9095) |
| 40 | 95.2 (1.9196) | 96.1 (1.9778) | 95.2 (1.9234) | 96.5 (1.9910) | 94.2 (1.9641) | |
| 60 | 95.0 (2.1359) | 94.7 (2.1710) | 95.1 (2.1442) | 94.8 (2.1974) | 94.6 (2.1568) | |
| (50, 50) | 20 | 95.9 (1.4851) | 95.4 (1.5312) | 95.8 (1.4858) | 95.5 (1.5365) | 95.5 (1.5861) |
| 40 | 93.9 (1.6014) | 95.0 (1.6459) | 94.1 (1.6045) | 95.0 (1.6607) | 94.0 (1.6591) | |
| 60 | 96.6 (1.8615) | 96.2 (1.8991) | 96.2 (1.8700) | 96.0 (1.9245) | 95.5 (1.8859) | |
| C2 | ||||||
| (25, 25) | 20 | 96.3 (1.5116) | 95.4 (1.6989) | 96.3 (1.5183) | 95.4 (1.7093) | 94.9 (1.3485) |
| 40 | 94.2 (1.7866) | 95.4 (1.9407) | 94.3 (1.8003) | 95.5 (1.9607) | 94.3 (1.6406) | |
| 60 | 94.8 (2.0684) | 94.4 (2.1258) | 94.7 (2.0901) | 94.5 (2.1978) | 94.4 (1.9845) | |
| (25, 50) | 20 | 94.4 (1.3042) | 94.5 (1.4993) | 94.5 (1.3111) | 94.7 (1.5095) | 94.3 (1.1393) |
| 40 | 93.8 (1.4782) | 94.0 (1.6497) | 93.7 (1.4931) | 94.1 (1.6734) | 93.0 (1.3364) | |
| 60 | 94.9 (1.7854) | 94.6 (1.9165) | 94.7 (1.8073) | 94.7 (1.9526) | 94.7 (1.6711) | |
| (50, 50) | 20 | 94.3 (1.0434) | 94.6 (1.1927) | 94.3 (1.0484) | 94.5 (1.2000) | 93.9 (0.9226) |
| 40 | 95.3 (1.2081) | 94.6 (1.3440) | 95.3 (1.2204) | 94.6 (1.3621) | 95.2 (1.1028) | |
| 60 | 94.5 (1.5267) | 94.7 (1.6326) | 94.6 (1.5465) | 94.5 (1.6551) | 94.9 (1.4419) | |
| C3 | ||||||
| (25, 25) | 20 | 94.8 (2.2620) | 94.7 (2.2907) | 94.7 (2.2621) | 94.5 (2.2974) | 94.9 (2.3131) |
| 40 | 94.9 (2.3852) | 95.2 (2.3995) | 95.0 (2.3876) | 95.4 (2.4144) | 94.9 (2.4076) | |
| 60 | 94.6 (2.4918) | 94.9 (2.4981) | 94.5 (2.4944) | 95.2 (2.5185) | 94.5 (2.5072) | |
| (25, 50) | 20 | 94.7 (2.0501) | 94.5 (2.0954) | 94.6 (2.0520) | 94.9 (2.1034) | 95.0 (2.0993) |
| 40 | 96.3 (2.1733) | 96.0 (2.1848) | 96.1 (2.1747) | 96.0 (2.1971) | 96.5 (2.2082) | |
| 60 | 95.6 (2.3492) | 95.7 (2.3517) | 95.5 (2.3486) | 95.6 (2.3662) | 95.4 (2.3694) | |
| (50, 50) | 20 | 95.2 (1.7322) | 95.7 (1.7552) | 95.3 (1.7321) | 95.7 (1.7613) | 94.9 (1.8090) |
| 40 | 95.3 (1.8365) | 95.4 (1.8388) | 95.2 (1.8356) | 95.7 (1.8496) | 95.5 (1.8846) | |
| 60 | 95.0 (2.0581) | 95.0 (2.0573) | 95.4 (2.0575) | 95.0 (2.0693) | 94.8 (2.0763) | |
| Censoring % | Log-Rank | |||||
|---|---|---|---|---|---|---|
| C1 | ||||||
| (25, 25) | 20 | 6.2 | 6.9 | 6.1 | 7.0 | 7.4 |
| 40 | 9.1 | 9.5 | 9.2 | 9.5 | 8.5 | |
| 60 | 9.9 | 10.0 | 9.9 | 10.5 | 9.7 | |
| (25, 50) | 20 | 6.8 | 7.3 | 6.6 | 7.3 | 7.5 |
| 40 | 7.8 | 7.8 | 7.2 | 7.9 | 7.4 | |
| 60 | 9.2 | 9.2 | 9.4 | 9.9 | 9.3 | |
| (50, 50) | 20 | 4.4 | 4.9 | 4.4 | 5.0 | 5.9 |
| 40 | 6.7 | 7.4 | 6.8 | 7.5 | 6.6 | |
| 60 | 9.3 | 9.7 | 9.8 | 6.6 | 9.1 | |
| C2 | ||||||
| (25, 25) | 20 | 3.8 | 5.4 | 4.0 | 5.4 | 2.7 |
| 40 | 4.6 | 6.1 | 5.0 | 6.5 | 4.2 | |
| 60 | 8.1 | 9.5 | 8.8 | 9.8 | 7.1 | |
| (25, 50) | 20 | 4.1 | 5.0 | 4.1 | 5.1 | 3.0 |
| 40 | 3.8 | 5.5 | 4.2 | 5.7 | 3.9 | |
| 60 | 6.5 | 7.5 | 6.6 | 7.6 | 5.8 | |
| (50, 50) | 20 | 2.2 | 3.3 | 2.2 | 3.5 | 1.9 |
| 40 | 3.4 | 4.1 | 3.5 | 4.5 | 2.4 | |
| 60 | 6.2 | 5.7 | 5.3 | 6.8 | 5.9 | |
| C3 | ||||||
| (25, 25) | 20 | 8.1 | 8.1 | 7.9 | 8.5 | 7.6 |
| 40 | 8.2 | 9.5 | 8.7 | 9.8 | 6.9 | |
| 60 | 7.8 | 8.1 | 8 | 9.5 | 6.6 | |
| (25, 50) | 20 | 7.5 | 7.8 | 7.9 | 7.9 | 7.0 |
| 40 | 8.0 | 8.5 | 8.2 | 9.0 | 6.7 | |
| 60 | 7.5 | 7.9 | 8.2 | 9.5 | 7.1 | |
| (50, 50) | 20 | 6.5 | 7.5 | 6.5 | 8.0 | 6.0 |
| 40 | 6.6 | 7.3 | 7.0 | 8.1 | 6.5 | |
| 60 | 7.2 | 7.8 | 7.5 | 8.2 | 6.8 | |
| Censoring % | Log-Rank | |||||
|---|---|---|---|---|---|---|
| S1 | ||||||
| (25, 25) | 20 | 15.8 | 21.2 | 16.5 | 22.1 | 10.3 |
| 40 | 20.5 | 23.8 | 22.6 | 26.2 | 16.2 | |
| 60 | 18.9 | 21.7 | 23.2 | 27.5 | 18.1 | |
| (25, 50) | 20 | 17.6 | 23.1 | 19.6 | 24.0 | 11.2 |
| 40 | 20.3 | 23.7 | 22.9 | 27.0 | 16.2 | |
| 60 | 25.1 | 27.4 | 30.0 | 32.4 | 21.5 | |
| (50, 50) | 20 | 14.9 | 22.9 | 19.6 | 23.7 | 8.1 |
| 40 | 22.0 | 28.1 | 25.0 | 30.2 | 16.1 | |
| 60 | 26.1 | 28.9 | 29.1 | 32.2 | 24.0 | |
| S2 | ||||||
| (25, 25) | 20 | 46.5 | 67.0 | 48.7 | 68.7 | 11.5 |
| 40 | 57.0 | 69.1 | 59.9 | 72.1 | 32.0 | |
| 60 | 70.8 | 74.9 | 74.5 | 76.8 | 60.8 | |
| (25, 50) | 20 | 51.0 | 72.7 | 52.3 | 73.9 | 14.2 |
| 40 | 63.2 | 77.6 | 67.1 | 81.2 | 32.5 | |
| 60 | 77.4 | 81.6 | 80.6 | 83.2 | 67.3 | |
| (50, 50) | 20 | 60.8 | 85.2 | 63.5 | 87.0 | 10.4 |
| 40 | 71.6 | 86.8 | 76.6 | 89.5 | 35.0 | |
| 60 | 88.2 | 90.2 | 90.2 | 91.5 | 81.6 | |
| S3 | ||||||
| (25, 25) | 20 | 8.4 | 26.2 | 9.2 | 28.4 | 1.2 |
| 40 | 20.8 | 30.8 | 22.6 | 36.0 | 8.0 | |
| 60 | 31.2 | 39.4 | 36.8 | 48.6 | 22.6 | |
| (25, 50) | 20 | 11.0 | 28.4 | 11.6 | 29.6 | 0.8 |
| 40 | 18.6 | 35.2 | 21.2 | 40.2 | 5.2 | |
| 60 | 35.2 | 44.4 | 41.6 | 57.4 | 23.6 | |
| (50, 50) | 20 | 7.4 | 27.2 | 8.6 | 28.8 | 0.1 |
| 40 | 14.8 | 34.0 | 20.4 | 41.0 | 1.8 | |
| 60 | 42.0 | 53.0 | 50.2 | 66.2 | 28.4 | |
| Log-Rank | |||||
|---|---|---|---|---|---|
| p-value | 0.49 | 0.48 | 0.49 | 0.48 | 0.49 |
| 1.11 | 1.10 | 1.11 | 1.10 | 1.13 | |
| 95% C.I. | (0.99, 1.25) | (0.96, 1.24) | (0.99, 1.25) | (0.96, 1.24) | (0.98, 1.30) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, S.-H. Weighted Log-Rank Statistics for Accelerated Failure Time Model. Stats 2021, 4, 348-358. https://doi.org/10.3390/stats4020023
Lee S-H. Weighted Log-Rank Statistics for Accelerated Failure Time Model. Stats. 2021; 4(2):348-358. https://doi.org/10.3390/stats4020023
Chicago/Turabian StyleLee, Seung-Hwan. 2021. "Weighted Log-Rank Statistics for Accelerated Failure Time Model" Stats 4, no. 2: 348-358. https://doi.org/10.3390/stats4020023
APA StyleLee, S.-H. (2021). Weighted Log-Rank Statistics for Accelerated Failure Time Model. Stats, 4(2), 348-358. https://doi.org/10.3390/stats4020023





