Unsupervised Feature Selection for Histogram-Valued Symbolic Data Using Hierarchical Conceptual Clustering

Abstract

This paper presents an unsupervised feature selection method for multi-dimensional histogram-valued data. We define a multi-role measure, called the compactness, based on the concept size of given objects and/or clusters described using a fixed number of equal probability bin-rectangles. In each step of clustering, we agglomerate objects and/or clusters so as to minimize the compactness for the generated cluster. This means that the compactness plays the role of a similarity measure between objects and/or clusters to be merged. Minimizing the compactness is equivalent to maximizing the dis-similarity of the generated cluster, i.e., concept, against the whole concept in each step. In this sense, the compactness plays the role of cluster quality. We also show that the average compactness of each feature with respect to objects and/or clusters in several clustering steps is useful as a feature effectiveness criterion. Features having small average compactness are mutually covariate and are able to detect a geometrically thin structure embedded in the given multi-dimensional histogram-valued data. We obtain thorough understandings of the given data via visualization using dendrograms and scatter diagrams with respect to the selected informative features. We illustrate the effectiveness of the proposed method by using an artificial data set and real histogram-valued data sets.

1. Introduction

Unsupervised feature selection is important in pattern recognition, data mining, and generally in data science (e.g., [1,2,3,4]). Solorio-Fernández et al. [4] evaluated and discussed many filter, wrapper, and hybrid methods, and they showed a detail classification of unsupervised feature selection methods. They also pointed out the challenge for complex data models is one of the important themes in unsupervised feature selection. Bock and Diday [5] and Billard and Diday [6] include methods of Symbolic Data Analysis (SDA) for complex data models. Diday [7] presents an overview of SDA in data science, and Billard and Diday [8] present various methods to analyze symbolic data including histogram-valued data.

In unsupervised feature selection, we need a mechanism to detect meaningful structures organized by the data set under the given feature set. Geometrically thin structures such as functional structures and multi-cluster structures are examples of meaningful structures of the data set. Many unsupervised feature selection methods use clustering to search feature subspaces including meaningful structures. Therefore, we have to solve the following four problems:

(1)

How to evaluate the similarity between objects and/or clusters under the given feature subset;

(2)

How to evaluate the quality of clusters under the given feature subset;

(3)

How to evaluate the effectiveness of the given feature subset; and

(4)

How to search the most robustly informative feature subset from the whole feature set.

In hierarchical agglomerative methods, as noted in Billard and Diday [8], we select a (dis)similarity measure between objects and we obtain a dendrogram by merging objects and/or clusters based on the selected criterion, e.g., nearest neighbor, furthest neighbor, Ward’s minimum variance, or other criteria. For histogram-valued data, Irpino and Verde [9] defined the Wasserstein distance and proposed a hierarchical clustering method based on Ward’s criterion. As a non-hierarchical clustering method, De Carvarho and De Souza [10] proposed the dynamical clustering method optimizing an adequacy criterion. By combining these methods with an appropriate wrapper method, for example, we can realize unsupervised feature selection methods for histogram-valued data.

This paper presents an unsupervised feature selection method for mixed-type histogram-valued data by using hierarchical conceptual clustering based on the compactness. The compactness defines the concept size of rectangles describing objects and/or clusters in the given feature space.

In the proposed method, the compactness plays not only the role of similarity measure between objects and/or clusters, but also the roles of cluster quality criterion and feature effectiveness criterion. Therefore, we can greatly simplify to realize the unsupervised feature selection method for complex, histogram-valued symbolic data.

The structure of this paper is as follows: Section 2 describes the quantile method to represent multi-dimensional distributional data. When the given p distributional features describe each of N objects, we use histogram representations for various feature types including categorical multi-value and modal multi-value types. We transform each feature value of each object to the predetermined common number m of bins and their bin probabilities. We define m + 1 quantile vectors ordered from the minimum quantile vector to the maximum quantile vector in order to describe each object in the p dimensional histogram-valued feature space. We define m series of p dimensional bin-rectangles spanned by the successive quantile vectors to have common descriptions for the given objects. Then, we define the concept size of each of m bin-rectangles using the arithmetic average of p normalized bin-widths, respectively. Section 3 describes the measure of compactness for the merged objects and/or clusters. For an arbitrary pair of objects and for each histogram-valued feature, we define the average cumulative distribution function based on the two histogram values, and we find m + 1 quantile values including the minimum and the maximum values from the obtained cumulative distribution function for each of p features. Then, we obtain m series of p-dimensional bin rectangles with predetermined bin probabilities in order to define the Cartesian join of the pair of objects in the p-dimensional feature space. Under the assumption of equal bin probabilities, we define a new similarity measure, the compactness, of a pair of objects and/or clusters as the average of m concept sizes of bin-rectangles obtained for the pair. Section 4 describes the proposed method of hierarchical conceptual clustering (HCC) and exploratory method of feature selection, and then we show the effectiveness of the proposed method using artificial data and using four real data sets, including comparisons with the results by Irpino and Verde [9] and De Carvalho and De Souza [10]. Section 5 is a discussion of the obtained results.

2. Representation of Objects by Bin-Rectangles

Let U = {ω_i, i = 1, 2,…, N} be the set of given objects, and let features F_j, j = 1, 2,…, p, describe each object. Let D_j be the domain of feature F_j, j =1, 2, …, p. Then, the feature space is defined by

D^(p) = D₁ × D₂ ×⋅⋅⋅× D_p

(1)

Since we permit the simultaneous use of various feature types, we use the notation D^(p) for the feature space in order to distinguish it from usual p-dimensional Euclidean space R^p. Each element of D^(p)is represented by

E = E₁ × E₂ ×⋅⋅⋅× E_p,

(2)

where E_j, j = 1, 2, …, p, is the feature value taken by the feature F_j.

2.1. Histogram-Valued Feature

For each object ω_i, let each feature F_j be represented by histogram value:

E_ij = {[a_ijk, a_ij(k+1)), p_ijk; k = 1, 2,…, n_ij},

(3)

where p_ij1 + p_ij2 + … + p_ijnij = 1 and n_ij is the number of bins that compose the histogram E_ij.

Therefore, the Cartesian product of p histogram values represents an object ω_i:

E_i = E_i1 × E_i2 ×⋯× E_ip.

(4)

Since the interval-valued feature is a special case of histogram feature with n_ij = 1 and p_ij1 = 1, the representation of (3) is reduced to an interval:

E_ij = [a_ij1, a_ij2).

(5)

2.2. Histogram Representation of Other Feature Types

2.2.1. Categorical Multi-Valued Feature

Let F_j be a categorical multi-valued feature, and let E_ij be a value of F_j for an object ω_i. The value E_ij contains one or more categorical values taken from the domain D_j that is composed of finite possible categorical values. For example, E_ij = {“white”, “green”} is a value taken from the domain D_j = {“white”, “red”, “blue”, “green”, “black”}. For this kind feature value, we can again use a histogram. For each value in domain D_j, we assign an interval with equal width. Then, assuming uniform probability for values in a multi-valued feature, we assign probabilities to each interval associated with a specific value in D_j according to its presence in E_ij. Therefore, the feature value E_ij = {“white”, “green”}, for example, is now represented by the histogram E_ij = {[0, 1)0.5, [1, 2)0, [2, 3)0, [3, 4)0.5, [4, 5)0}.

2.2.2. Modal Multi-Valued Feature

Let D_j = {ν₁, ν₂,…, ν_n} be a finite list of possible outcomes and be the domain of a modal multi-valued feature F_j. A feature value E_ij for object ω_i is a subset of D_j with a nonnegative measure attached to each of the values in that subset, and the sum of those nonnegative measures is one:

E_ij = {ν_ij1, p_ij1; ν_ij2, p_ij2;…; ν_ijnij, p_ijnij},

(6)

where {ν_ij1, ν_ij2,…, ν_ijnij}⊆D_j, ν_ijk occurs with the nonnegative weight p_ijk, k = 1, 2, …, n_ij, and with p_ij1 + p_ij2 +… + p_ijnij = 1.

For example, E_ij = {“white”, 0.8; “green”, 0.2} is a value of the modal multi-valued feature defined on the domain D_j = {“white”, “red”, “blue”, “green”, “black”}. We assign again a same sized interval to each possible feature value from the domain D_j. The probabilities assigned to a specific feature value of the modal multi-valued feature are used as the bin probabilities of the corresponding histogram with the same bin width. Therefore, in the above example, we have a histogram representation: E_ij = {[0, 1)0.8, [1, 2)0, [2, 3)0, [3, 4)0.2, [4, 5)0}.

2.3. Representation of Histograms by Common Number of Quantiles

Let ω_i∈U be the given object, and let E_ij in (7) be the histogram value for a feature F_j:

E_ij = {[a_ijk, a_ij(k+1)), p_ijk; k = 1, 2,…, n_ij}.

(7)

Then, under the assumption that n_ij bins have uniform distributions, we define the cumulative distribution function F_ij(x) of the histogram (7) as:

F_ij(x) = 0 for x ≤ a_ij1
F_ij(x) = p_ij1(x − a_ij1)/(a_ij2 − a_ij1) for a_ij1 ≤ x < a_ij2
F_ij(x) = F(a_ij1) + p_ij2(x − a_ij2)/(a_ij3 − a_ij2) for a_ij2 ≤ x < a_ij3
⋯⋯
F_ij(x) = F(a_nij−1) + p_ijnij(x − a_nij)/(a_nij+1 − a_nij) for a_nij ≤ x < a_nij+1
F_ij(x) = 1 for a_nij+1 ≤ x.

Figure 1 illustrates such a cumulative distribution function for a histogram feature value.

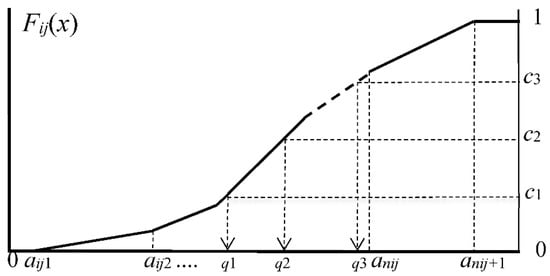
Figure 1. Cumulative distribution function and cut point probabilities.

If we select the number m = 4 and three cut points, c₁ = 1/4, c₂ = 2/4, and c₃ = 3/4, we can obtain three quantile values from the equations c₁ = F_ij(q₁), c₂ = F_ij(q₂), and c₃ = F_ij(q₃). Finally, we obtain four bins [a_ij1, q₁), [q₁, q₂), [q₂, q₃), and [q₃, a_nij+1) and their bin probabilities (c₁ − 0), (c₂ − c₁), (c₃ − c₂), and (1 − c₃) with the same value 1/4.

Our general procedure to have common representation for histogram-valued data is as follows.

(1)

We choose common number m of quantiles.

(2)

Let c₁, c₂,…, c_m−1 be preselected cut points dividing the range of the distribution function F_ij(x) into continuous intervals, i.e., bins, with preselected probabilities associated with m cut points. For example, in the quartile case we use three cut points, c₁ = 1/4, c₂ = 2/4, and c₃ = 3/4, to have four bins with the same probability 1/4. However, we can choose different cut points, for example, c₁ = 1/10, c₂ = 5/10, and c₃ = 9/10, to have four bins with probabilities 1/10, 4/10, 4/10, and 1/10, respectively.

(3)

For the given cut points c₁, c₂,…, c_m−1, we have the corresponding quantiles by solving the following equations:

F_ij(x_ij0) = 0, (i.e., x_ij0 = a_ij1)
F_ij(x_ij1) = c₁, F_ij(x_ij2) = c₂,…, F_ij(x_ij(m−1)) = c_m−1, and
F_ij(x_ijm) = 1, (i.e., x_ijm = a_ijnij+1).

Therefore, we describe each object ω_i∈U for each feature F_j using a (m + 1) tuple:

(x_ij0, x_ij1, x_ij2, …, x_ij(m−1), x_ijm), j = 1, 2, …, p,

(8)

and the corresponding histogram using:

E_ij = {[x_ijk, x_{ij( )}), (c_k+1 − c_k); k = 0, 1,…, m − 1}, j = 1, 2,…, p,

(9)

where we assume that c₀ = 0 and c_m = 1. In (9), (c_k+1 − c_k), k = 0, 1,…, m−1, denote bin probabilities using the preselected cut point probabilities c₁, c₂,…, c_m−1. In the quartile case again, m = 4 and c₁ = 1/4, c₂ = 2/4, and c₃ = 3/4, and four bins, [x_ij0, x_ij1), [x_ij1, x_ij2), [x_ij2, x_ij3), and [x_ij3, x_ij4), have the same probability 1/4.

It should be noted that the number of bins of the given histograms are mutually different in general. However, we can obtain (m + 1)-tuples as the common representation for all histograms by selecting an integer m and a set of cut points.

2.4. Quantile Vectors and Bin-Rectangles

For each object ω_i∈U, we define (m + 1) p-dimensional numerical vectors, called the quantile vectors, as follows.

x_ik = (x_i1k, x_i2k, …, x_ipk), k = 0, 1,…, m.

(10)

We call x_i0 and x_im the minimum quantile vector and the maximum quantile vector for ω_i∈U, respectively. Therefore, m + 1 quantile vectors {x_i0, x_i1,…, x_im} in R^p describe each object ω_i∈U together with cut point probabilities.

The components of m + 1 quantile vectors in (10) for object ω_i∈U satisfy the inequalities:

x_ij0 ≤ x_ij1 ≤ x_ij2 ≤⋯≤ x_ij(m−1) ≤ x_ijm, j = 1, 2, …, p.

(11)

Therefore, m + 1 quantile vectors in (10) for object ω_i∈U satisfy the monotone property:

x_i0 ≤ x_i1 ≤⋯⋯≤ x_im.

(12)

For the series of quantile vectors x_i0, x_i1,…, x_im of object ω_i∈U, we define m series of p dimensional rectangles spanned by adjacent quantile vectors x_ik and x_i(k+1), k = 0, 1,…, m−1, as follows:

B(x_ik, x_i(k+1)) = x_ik⊕x_i(k+1) = (x_i1k⊕x_i1(k+1)) × (x_i2k⊕x_i2(k+1)) ×⋯× (x_ipk⊕x_ip(k+1))
= [x_i1k, x_i1(k+1)] × [x_i2k, x_i2(k+1)] × ⋅⋅⋅ × [x_ipk, x_ip(k+1)], k = 0, 1,…, m−1,

(13)

where x_ik⊕x_i(k+1) is the Cartesian join (Ichino and Yaguchi [11]) of x_ik and x_i(k+1) obtained using the Cartesian join x_ijk⊕x_ij(k+1) = [x_ijk, x_ij(k+1)], j = 1, 2,…, p, and we call B(x_ik, x_i(k+1)), k = 0, 1,…, m−1, the bin-rectangles.

Figure 2 illustrates two objects, ω_i and ω_l, by quartile representations in two-dimensional Euclidean space. Since a p-dimensional rectangle in R^p is equivalent to a conjunctive logical expression, we also use the term concept for a rectangular expression in the space R^p. In other words, m bin-rectangles describe each of the objects ω_i and ω_l as concepts. We should note that the selection of a larger value m yields smaller rectangles as possible descriptions. In this sense, the selection of the integer number m controls the granularity of concept descriptions.

Figure 2. Representations of objects by bin-rectangles in the quartile case.

2.5. Concept Size of Bin-Rectangles

For each feature F_j, j = 1, 2, …, p, let the domain D_j of feature values be the following interval:

D_j = [x_jmin, x_jmax], j = 1, 2, …, p,

where

x_jmin = min(x_1j0, x_2j0, …, x_Nj0) and x_jmax = max(x_1jm, x_2jm, …, x_Njm).

Definition 1.

Let object ω_i∈U be described using the set of histograms for E_ij in (9). We define the average concept size P(E_ij) of m bins for histogram E_ij by

P(E_ij) = {c₁(x_ij1 − x_ij0) + (c_{2 −} c₁)(x_ij2 − x_ij1) + ⋯ + (c_k + c_(k−1))(x_ijk − x_ij(k−1)) + ⋯
+ (c_m−1 − c_m−2)(x_ij(m−1) − x_ij(m−2)) + (1 − c_m−1)(x_ijm − x_ij(m−1))}/|D_j|,
= {c₁|x_ij0⊕x_ij1| + (c₂ − c₁)|x_ij1⊕x_ij2| + ⋅⋅⋅ + (c_k + c_(k−1))|x_ij(k−1)⊕x_ijk| + ⋯
+ (c_m−1 − c_m−2)|x_ij(m−1)⊕x_ij(m−2)| + (1 − c_m−1)|x_ijm⊕x_ij(m−1)|}/|D_j|, j = 1, 2,…, p,

(14)

wherex_ij(k−1)⊕x_ijkdefines the Cartesian join ofx_ij(k−1)andx_ijkas the interval spanned by them, and where |D_j| and |x_ij(k−1)⊕x_ijk| are the lengths of the domain and the k-th bin, respectively.

The average concept size P(E_ij) satisfies the inequality:

0 ≤ P(E_ij) ≤ 1, j = 1, 2,…, p.

(15)

Example 1.

(1)

When E_ij is a histogram with a single bin, the concept size is P(E_ij) = (x_ij1 − x_ij0)/|D_j|

(2)

When E_ij is a histogram with four bins with equal probabilities, i.e., a quartile case, the average concept size of four bins is P(E_ij) = (x_ij4 − x_ij0)/(4|D_j|).

(3)

When E_ij is a histogram with four bins with cut points c₁ = 1/10, c₂ = 5/10, and c₃ = 9/10, the average concept size of four bins is

P(E_ij) = {(x_ij1 − x_ij0)/10 + 4(x_ij2 − x_ij1)/10 + 4(x_ij3 − x_ij2)/10 + (x_ij4 − x_ij3)/10}/|D_j|

= (x_ij4 + 3x_ij3 − 3x_ij1 − x_ij0)/(10|D_j|)

(4)

In the Hardwood data (seeSection 4.4), seven quantile values for five cut point probabilities, c₁ = 1/10, c₂ = 1/4, c₃ = 1/2, c₄ = 3/4, and c₅ = 9/10, describe each histogram for E_ij. Then, the average concept size of six bins becomes:

P(E_ij) = {(10(x_ij1 − x_ij0)/100 + 15(x_ij2 − x_ij1)/100 + 25(x_ij3 − x_ij2)/100 + 25(x_ij4 − x_ij3)/100
+ 15(x_ij5 − x_ij4)/100 + 10(x_ij6 − x_ij5)/100}/|D_j|
= {10x_ij6 + 5x_ij5 + 10x_ij4 − 10x_ij2 − 5x_ij1 −10x_ij0}/(100|D_j|)
= {2x_ij6 + x_ij5 + 2x_ij4 − 2x_ij2 − x_ij1 − 2x_ij0}/(20|D_j|)

This example asserts the simplicity of concept size in the case of equal bin probabilities.

Proposition 1.

(1) 

When m bin probabilities are the same, the average concept size of m bins is reduced to the form:

P(E_ij) = (x_ijm − x_ij0)/(m|D_j|), j = 1, 2,…, p

(16)

(2) 

When m bin-widths are the same size w_ij, we have:

P(E_ij) = w_ij/|D_j|, j = 1, 2,…, p,

(17)

(3) 

It is clear that:

w_ij = (x_ijm − x_ij0)/m.

(18)

Proof of Proposition 1.

Since m bin probabilities are the same, we have

c₁ = (c₂ − c₁) = ⋅⋅⋅ = (c_m−1 − c_m−2) = (1 − c_m−1) = 1/m.

Then, (14) leads to (16). On the other hand, when m bin-widths are the same size w_ij, we have

c₁w_ij + (c₂ − c₁)w_ij + ⋅⋅⋅ + (c_m−1 − c_m−2)w_ij + (1 − c_m−1)w_ij = w_ij.

Then, (14) leads to (17), and (18) is clear, since mw_ij equals the span (x_ijm − x_ij0). □

This proposition asserts that the both extremes yield the same conclusion.

Definition 2.

Let E_i = E_i1× E_i2×⋅⋅⋅× E_ip be the description by p histograms in R^p for ω_i∈U. Then, we define the concept size P(E_i) of E_i using the arithmetic mean

P(E_i) = (P(E_i1) + P(E_i2) + ⋅⋅⋅ + P(E_ip))/p.

(19)

From (15), It is clear that:

0 ≤ P(E_i) ≤ 1.

(20)

Definition 3.

Let P(B(x_ik, x_i(k+1))), k = 0, 1,…, m−1, be the concept size of m bin-rectangles defined by the average of p normalized bin-widths:

P(B(x_ik, x_i(k+1))) = {|x_i1k⊕x_i1(k+1)|/|D₁| + |x_i2k⊕x_i2(k+1)|/|D₂|+⋯+|x_ipk⊕x_ip(k+1)|/|D_p|}/p, k = 0,1,…, m−1.

(21)

Then (14) and (21) lead to the following proposition.

Proposition 2.

The concept size P(E_i) is equivalent to the average value of m concept sizes of bin-rectangles:

P(E_i) = (c₁ − c₀)P(B(x_i0, x_i1)) + (c₂ − c₁)P(B(x_i1, x_i2)) + ⋯ + (c_m-c_(m−1))P(B(x_i(m−1),x_im)),

(22)

where c₀ = 0 and c_m = 1.

In Figure 2, two objects ω_i and ω_l are represented by four bin-rectangles with the same probability 1/4. Hence, smaller sized bin-rectangles mean that they have higher probability densities with respect to the features under consideration. In this sense, object ω_i has a sharp probability distribution compared to that of object ω_l. By the virtue of equiprobability assumption, we can easily compare the object descriptions using a series of bin-rectangles under the selected feature sub-space. If we use the descriptions of objects under the assumption of equal bin-widths, we can no longer compare between objects in such a simple way.

3. Concept Size of the Cartesian Join of Objects and the Compactness

3.1. Concept Size of the Cartesian Join of Objects

A major merit of the quantile representation is that we are able to have a common numerical representation for various types of histogram data. We select a common integer number m, then we obtain a common form of histograms with m bins and the predetermined bin probabilities for each of p features describing each object.

Let E_ij and E_lj be two histogram values of objects ω_i, ω_l∈U with respect to the j-th feature. We represent a generalized histogram value of E_ij and E_lj, called the Cartesian join of E_ij and E_lj, using E_ij⊕E_lj. Let F_Eij(x) and F_Elj(x) be the cumulative distribution functions associated with histograms E_ij and E_lj, respectively.

Definition 4.

We define the cumulative distribution function for the Cartesian join E_ij⊕E_lj by

F_Eij⊕Elj(x) = (F_Eij(x)+ F_Elj(x))/2, j = 1, 2,…, p.

(23)

Then, by applying the same integer number m and the set of cut point probabilities, c₁, c₂,…, c_m−1, used for E_ij and E_lj, we define the histogram of the Cartesian join E_ij ⊕E_lj for the j-th feature as:

E_ij⊕E_lj = {[x_(i+l)jk, x_(i+l)j(k+1)), (c_k+1-c_k); k = 0, 1,…, m−1}, j = 1, 2,…, p,

(24)

where we assume that c₀ = 0 and c_m = 1 and that the suffix (i + l) denotes the quantile values for the Cartesian join E_ij⊕E_lj. We should note that x_(i+l)j0 = min(x_ij0, x_lj0) and x_(i+l)jm = max(x_ijm, x_ljm).

Definition 5.

We define the average concept size P(E_ij⊕E_lj) of m bins for the Cartesian join E_ij and E_lj under the j-th feature as follows.

P(E_ij⊕E_lj) = {c₁(x_(i+l)j1 − x_(i+l)j0) + (c₂ − c₁)(x_(i+l)j2 − x_(i+l)j1) + …
+ (c_m−1 − c_m−2)(x_{(i+l)j(m−1)} − x_{(i+l)j(m−2)}) + (1 − c_m−1)(x_(i+l)jm − x_{(i+l)j(m−1)})}/|D_j|,
= {c₁|x_(i+l)j0⊕x_(i+l)j1| + (c₂ − c₁)|x_(i+l)j1⊕x_(i+l)j2| + …
+ (c_m−1 − c_m−2)|x_(i+l)j(m−2)⊕x_{(i+l)j(m−1)}| + (1 − c_m−1)|x_{(i+l)j(m−1)}⊕x_(i+l)jm|}/|D_j|, j = 1, 2,…, p.

(25)

The average concept size P(E_ij⊕E_lj) satisfies the inequality:

0 ≤ P(E_ij⊕E_lj) ≤ 1, j = 1, 2,…, p.

(26)

Proposition 3.

When m bin probabilities are the same or m bin-widths are the same, we have the following monotone property.

P(E_ij), P(E_lj) ≤ P(E_ij⊕E_lj), j = 1, 2,…, p.

(27)

Proof of Proposition 3.

If the bin probabilities are the same with the value 1/m, (25) becomes simply

P(E_ij⊕E_lj) = (x_(i+l)jm − x_(i+l)j0)/(m|D_j|), j = 1, 2,…, p.

Then, the following inequality leads to the result (27).

(x_ijm − x_ij0)/(m|D_j|), (x_ljm − x_lj0)/(m|D_j|) ≤ (max(x_ijm, x_ljm) − min(x_ij0, x_lj0))/(m|D_j|).

(28)

On the other hand, from Proposition 1, (28) is equivalent to w_ij/|D_j|, w_lj/|D_j| ≤ w_(i+l)j/|D_j|. Hence, we have (27). □

Definition 6.

Let E_i = E_i1× E_i2×⋯× E_ip and E_l = E_l1× E_l2×⋯× E_lp be the descriptions by p histograms in R^p for ω_i and ω_l, respectively. Then, we define the concept size P(E_i ⊕E_l) for the Cartesian join of E_i and E_l using the arithmetic mean

P(E_i⊕E_l) = (P(E_i1⊕E_l1) + P(E_i2⊕E_l2) + ⋯ + P(E_ip⊕E_lp))/p.

(29)

From (26), it is clear that:

0 ≤ P(E_i⊕E_l) ≤ 1.

(30)

Definition 7.

Let x_(i+l)k, k = 0, 1,…, m, be the quantile vectors for the Cartesian join E_i ⊕E_l, and let P(B(x_(i+l)k, x_(i+l)(k+1))), k = 0, 1,…, m−1, be the concept sizes of m bin-rectangles defined by the average of p normalized bin-widths:

P(B(x_ik, x_i(k+1))) = {|x_i1k⊕x_i1(k+1)|/|D₁| + |x_i2k⊕x_i2(k+1)|/|D₂|+ ⋅⋅⋅ + |x_ipk⊕x_ip(k+1)|/|D_p|}/p, k = 0,1,…, m−1.

(31)

Then, we have the following result.

Proposition 4.

The concept size P(E_i ⊕E_l) is equivalent to the average value of m concept sizes of bin-rectangles:

P(E_i⊕E_l) = (c₁ − c₀)P(B(x_(i+l)0, x_(i+l)1)) + (c₂ − c₁)P(B(x_(i+l)1, x_(i+l)2)) + ⋯ + (c_m-c_(m−1))P(B(x_(i+l)(m−1), x_(i+l)m)),

(32)

where c₀ = 0 and c_m = 1.

We have the following monotone property from Proposition 3 and Definition 6.

Proposition 5.

When m bin probabilities are the same or m bin-widths are the same for all features, we have the monotone property:

P(E_i), P(E_l) ≤ P(E_i⊕E_l).

(33)

This property plays a very important role in our hierarchical conceptual clustering.

Example 2.

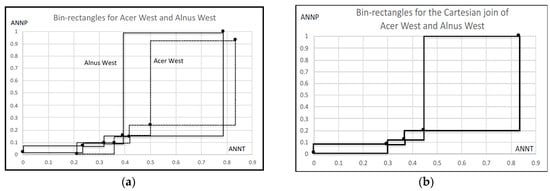
Table 1 shows two hardwoods, Acer West and Alnus West, under quartile descriptions for two features, Anual Temerature (ANNT) and Anual Precipitation (ANNP), using zero-one normalized feature values under the selected ten hardwoods used in Section 4.4. Figure 3a shows the descriptions of Acer West and Alnus West using four series of bin-rectangles. The fourth bin-rectangles for both hardwoods are very large. Hence, they have very low probability density compared to other bin-rectangles. Figure 3b is the description using bin-rectangles for the Cartesian join of Acer West and Alnus West.

Table 1. Two hardwoods using quartile representations.

Quantiles	ANNT	ANNP
Acer West 0	0.211	0.004
1	0.358	0.091
2	0.416	0.145
3	0.500	0.237
4	0.832	0.932
Alnus West 0	0.000	0.018
1	0.234	0.071
2	0.317	0.092
3	0.391	0.153
4	0.784	1.000

Figure 3. Bin-rectangles for two hardwoods and their Cartesian join.

Table 2 shows the average concept sizes for each hardwood and for each feature by Definition 1 and shows also the average concept sizes by Definitions 2 and 3. We can confirm the monotone properties in Propositions 3 and 5. The Cartesian join of two hardwoods for ANNP achieves almost the maximum concept size 1/4. Therefore, four bin-intervals of the Cartesian join for ANNP almost span the whole interval [0, 1].

Table 2. The average concept sizes for two hardwoods and their Cartesian join.

Concept Size	ANNT	ANNP	Average
Acer West	0.155	0.232	0.194
Alnus West	0.196	0.245	0.221
Cartesian join	0.208	0.249	0.229

3.2. Compactness and Its Properties

In the following, we assume that the given distributional data having the same representation using m quantile values with the same bin probabilities, since we can confirm the monotone property in Propositions 3 and 5 and we can easily visualize objects and their Cartesian joins using bin-rectangles under the selected features as in Figure 2.

Definition 8.

Under the assumption of equal bin probabilities, we define the compactness of the generalized concept by ω_i and ω_l as:

C(ω_i, ω_l) = P(E_i⊕E_l) = (P(B(x_(i+l)0, x_(i+l)1)) + P(B(x_(i+l)1, x_(i+l)2)) + ⋅⋅⋅ + P(B(x_(i+l)(m−1), x_(i+l)m))/m.

(34)

For Acer West and Alnus West in Figure 3a, their Cartesian join becomes the series of four bin-rectangles in Figure 3b. The compactness of Acer West and Alnus West is the average value of the concept sizes of four bin-rectangles. Therefore, in this example, the fourth bin rectangle predominates the concept size.

The compactness satisfies the following properties.

Proposition 6.

(1) 

0 ≤ C(ω_i, ω_l) ≤ 1

(2) 

C(ω_i, ω_l) = 0 iff E_i≡E_l and has null size (P(E_i) = 0)

(3) 

C(ω_i, ω_i), C(ω_l, ω_l) ≤ C(ω_i, ω_l)

(4) 

C(ω_i, ω_l) = C(ω_l, ω_i)

(5) 

C(ω_i, ω_r) ≤ C(ω_i, ω_l) + C(ω_l, ω_r) may not hold in general.

Proof of Proposition 6.

(1)~(4) are clear from Definitions 6 and 7 and Propositions 4 and 5. Figure 4a is a counter example for (5). □

Figure 4. Examples for compactness.

Figure 4b illustrates the Cartesian join for interval valued objects. We should note that the compactness C(ω₁, ω₂) = P(E₁⊕E₂) and C(ω₃, ω₄) = P(E₃⊕E₄) take the same value as the concept size. On the other hand, we usually expect that any (dis)similarity measures for distributional data should take different values for the pairs (E₁, E₂) and (E₃, E₄). Therefore, a small value compactness requires that the pair of objects under consideration should be similar to each other, but the converse is not true.

In hierarchical conceptual clustering, the compactness is useful as the measure of similarity between objects and/or clusters. We merge objects and/or clusters so as to minimize the compactness. This means also to maximize the dissimilarity against the whole concept. Therefore, the compactness plays dual roles as a similarity measure and a measure of cluster quality.

4. Exploratory Hierarchical Concept Analysis

This section describes our algorithm of hierarchical conceptual clustering and an exploratory method for unsupervised feature selection based on the compactness. Then, we analyze five data sets in order to show the usefulness of the proposed method.

4.1. Hierarchical Conceptual Clustering

Let U = {ω₁, ω₂, …, ω_N} be the given set of objects, and let each object ω_i be described using a set of histograms E_i = E_i1 × E_i2 ×⋯× E_ip in the feature space R^p. We assume that all histogram values for all objects have the same number m of quantiles and the same bin probabilities.

• Algorithm (Hierarchical Conceptual Clustering (HCC)
• Step 1: For each pair of objects ω_i and ω_l in U, evaluate the compactness C(ω_i, ω_l) and find the pair ω_q and ω_r that minimizes the compactness.
• Step 2: Add the merged concept ω_qr = {ω_q, ω_r} to U and delete ω_q and ω_r from U, where the representation of ω_qr follows to the Cartesian join in Definition 4 under the assumption of m quantiles and the equal bin probabilities.
• Step 3: Repeat Step 1 and Step 2 until U includes only one concept, i.e., the whole concept.

4.2. An Exploratory Method of Feature Selection

We use an artificial data and Oils data (Ichino and Yaguchi [11]) to illustrate feature selection capability to extract a covariate feature subset in which the given data sets take “geometrically thin structures” (Ono and Ichino [12]).

4.2.1. Artificial Data

Sixteen small rectangles organize an oval structure in the first two features, F1 and F2, as shown in Figure 5. For each of the sixteen objects, we transform the feature values of F1 and F2 to 0−1 normalized interval values. Then, we select an additional three randomly selected interval values in the unit interval [0, 1] for features F3, F4, and F5. Table 3 summarizes sixteen objects described using five 0−1 normalized interval valued features. It should be noted that usual numerical data is regarded as a special type of interval data, i.e., null interval.

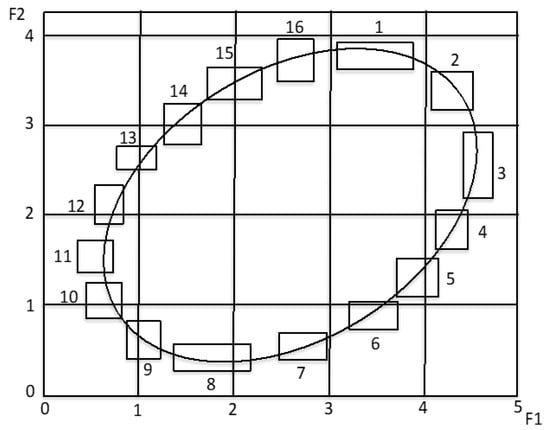
Figure 5. Oval data.

Table 3. Oval artificial data.

		F1	F2	F3	F4	F5	Concept Size
1		[0.629, 0.798]	[0.905, 0.986]	[0.000, 0.982]	[0.002, 0.883]	[0.360, 0.380]	0.427
2		[0.854, 0.955]	[0.797, 0.905]	[0.002, 0.421]	[0.573, 1.000]	[0.754, 0.761]	0.212
3		[0.921, 1.000]	[0.527, 0.716]	[0.193, 0.934]	[0.035, 0.477]	[0.406, 0.587]	0.326
4		[0.865, 0.933]	[0.378, 0.500]	[0.452, 0.854]	[0.213, 0.604]	[0.000, 0.074]	0.211
5		[0.775, 0.876]	[0.257, 0.338]	[0.300, 0.614]	[0.425, 0.979]	[0.217, 0.568]	0.280
6		[0.663, 0.764]	[0.135, 0.216]	[0.712, 1.000]	[0.904, 0.968]	[0.103, 0.950]	0.276
7		[0.494, 0.596]	[0.041, 0.122]	[0.293, 0.470]	[0.023, 0.086]	[0.765, 0.902]	0.112
8		[0.225, 0.427]	[0.000, 0.081]	[0.633, 0.872]	[0.000, 0.582]	[0.719, 0.852]	0.247
9		[0.112, 0.213]	[0.041, 0.149]	[0.167, 0.802]	[0.056, 0.129]	[0.124, 0.642]	0.287
10		[0.022, 0.112]	[0.162, 0.270]	[0.026, 0.718]	[0.418, 0.851]	[0.549, 0.853]	0.325
11		[0.000, 0.090]	[0.297, 0.392]	[0.096, 0.759]	[0.438, 0.938]	[0.495, 0.760]	0.323
12		[0.045,0.112]	[0.446, 0.554]	[0.826, 0.962]	[0.230, 0.755]	[0.104, 0.189]	0.184
13		[0.101, 0.202]	[0.608, 0.676]	[0.367, 0.570]	[0.236, 0.684]	[0.683, 0.930]	0.213
14		[0.213, 0.292]	[0.676, 0.811]	[0.371, 0.381]	[0.086, 0.305]	[0.009, 1.000]	0.287
15		[0.315, 0.438]	[0.811, 0.919]	[0.049, 0.585]	[0.056, 0.891]	[0.528, 0.881]	0.391
16		[0.483, 0.562]	[0.878, 1.000]	[0.402, 0.609]	[0.150, 0.769]	[0.207, 0.732]	0.310
Average CS		0.103	0.105	0.415	0.441	0.315	0.276

Figure 6 shows the result using the quantile method of PCA (Ichino [13]). Each numbered arrow line connects the minimum and the maximum quantile vectors and describes the corresponding rectangular object. The oval structure embedded in the first two features cannot be reproduced in the factor plane. Any well-known correlation criterion fails to capture the embedded oval structure.

Figure 6. PCA result for oval artificial data.

Figure 7 is the dendrogram based on the compactness for the first two features. It is clear that each cluster grows up along the oval structure of Figure 5. Our HCC generates eight comparably sized rectangles along the oval structure, then generates four rectangles, and so on. On the other hand, Figure 8 is the dendrogram for the given five features. We can also recognize the fact that each cluster grows up again along the oval structure of Figure 5 in spite of the addition of three useless features.

Figure 7. Dendrogram using the HCC for the first two features.

Figure 8. Dendrogram using the HCC for five features.

Table 4 summarizes the average compactness for each feature in each step of hierarchical clustering. For example, in Step 1, our HCC generates a larger rectangle using objects 10 and 11. Then, for each feature, we recalculate the average side lengths of 15 rectangles including an enlarged rectangle. The result is the second row in Table 4. We repeat the same procedure for succeeding clustering steps. Until step 13, i.e., the number of clusters are three, the importance of the first two features are valid. We clarify this fact by bold format numbers. In many steps, the values of average compactness of features F1 and F2 are sufficiently small compared to the middle point value 0.5. On the other hand, the values of average compactness for the other three features increases rapidly exceeding the middle point 0.5. Thus, we conclude that the first two features are robustly informative through the clustering process. The proposed method could detect our oval structure embedded in five dimensional interval-valued data as a geometrically thin structure. In the following, we use the middle point 0.5 as a criterion whether the average compactness is small or large.

Table 4. Average compactness of each feature in each clustering step.

Clustering Step	Average Compactness
	F1	F2	F3	F4	F5
0	0.103	0.105	0.415	0.441	0.315
1	0.115	0.109	0.454	0.466	0.330
2	0.118	0.119	0.442	0.470	0.338
3	0.128	0.128	0.475	0.501	0.345
4	0.138	0.142	0.501	0.528	0.386
5	0.154	0.151	0.530	0.519	0.403
6	0.171	0.158	0.532	0.564	0.451
7	0.186	0.185	0.566	0.637	0.519
8	0.208	0.215	0.669	0.660	0.574
9	0.239	0.251	0.744	0.744	0.589
10	0.288	0.293	0.712	0.727	0.692
11	0.346	0.354	0.736	0.839	0.759
12	0.438	0.443	0.860	0.882	0.780
13	0.494	0.599	0.919	0.924	0.906
14	0.483	0.926	0.967	0.968	0.971
15	1.000	1.000	1.000	1.000	1.000

4.2.2. Oils Data

The data in Table 5 describes six plant oils, linseed, perilla, cotton, sesame, camellia, and olive, and two fats, beef and hog, using five interval valued features: specific gravity, freezing point, iodine value, saponification value, and major acids.

Table 5. Oils data.

		Specific Gravity	Freezing Point	Iodine Value	Saponification v.	Major Acids
Linseed		[0.930, 0.935]	[−27, −18]	[170, 204]	[118, 196]	[1.75, 4.81]
Perilla		[0.930, 0.937]	[−5, −4]	[192, 208]	[188, 197]	[0.77, 4.85]
Cotton		[0.916, 0.918]	[−6, −1]	[99, 113]	[189, 198]	[0.42, 3.84]
Sesame		[0.920, 0.926]	[−6,−4]	[104, 116]	[187, 193]	[0.91, 3.77]
Camellia		[0.916, 0.917]	[−21, −15]	[80, 82]	[189, 193]	[2.00, 2.98]
Olive		[0.914, 0.919]	[0, 6]	[79, 90]	[187, 196]	[0.83, 4.02]
Beef		[0.860, 0.870]	[30, 38]	[40, 48]	[190, 199]	[0.31, 2.89]
Hog		[0.858, 0.864]	[22, 32]	[53, 77]	[190, 202]	[0.37, 3.65]

The result of PCA in Figure 9 and the dendrogram in Figure 10 show three explicit clusters (linseed, perilla), (cotton, sesame, olive, camellia), and (beef, hog). Table 6 summarizes the values of the average compactness for each feature in each clustering step. As clarified by bold format numbers, the most robustly informative feature is Specific gravity and then Iodine value until Step 5 obtaining three clusters. In the initial step, major acids exceeds our basic criterion 0.5.

Figure 9. PCA result for Oils data.

Figure 10. Dendrogram using HCC for five features.

Table 6. Average compactness of each feature in each clustering step.

Feature	Average Compactness for Each Clustering Step
	0	1	2	3	4	5	6	7
Specific gravity	0.066	0.080	0.091	0.099	0.114	0.131	0.475	1.000
Freezing point	0.090	0.099	0.154	0.178	0.204	0.338	0.631	1.000
Iodine value	0.090	0.095	0.109	0.137	0.185	0.222	0.339	1.000
Saponification value	0.202	0.224	0.254	0.283	0.327	0.405	0.560	1.000
Major acids	0.646	0.648	0.720	0.753	0.775	0.809	0.856	1.000

Figure 11 is the scatter diagram of the oils data for the selected two robustly informative features. This figure shows again three distinct clusters (linseed, perilla) and (cotton, sesame, camellia, olive), and (beef, hog). They exist in locally limited regions and they organize again a geometrically thin structure with respect to the selected features. Figure 12 shows the dendrogram with concept descriptions of clusters with respect to Specific gravity and Iodine value. This dendrogram clarifies two major clusters, Plant oils and Fats, addition to three distinct clusters, and the compactness takes smaller values compared to the dendrogram in Figure 10.

Figure 11. Scatter diagram using two informative features.

Figure 12. Descriptions using specific gravity and iodine value.

We should note that our exploratory method to analyze distributional data depends only on the compactness for each feature and combined features. In other words, the measure of feature effectiveness, the measure of similarity between objects and/or clusters, and the measure of cluster quality are based on the same simple notion of the concept size.

4.3. Analysis of City Temperature Data

De Carvalho and De Souza [10] used this temperature data in their dynamical clustering methods. In this data, 12 interval-valued features describe 37 selected cities. The minimum and the maximum temperatures in degree centigrade determine the interval value for each month. We use 0−1 normalized temperatures for each month, and we obtained the PCA result in Figure 13. In this figure, each arrow line connects from the minimum to the maximum quantile vectors and its length shows the concept size. The first principal component has a large contribution ratio and 37 cities line up from cold (left) to hot (right) in the limited zone between Tehran and Sydney. In this data, we should note that Frankfurt and Zurich have very large concept sizes while Tehran has a very small size compared to other cities.

Figure 13. PCA result for city temperature data.

In Figure 14, we can recognize 6 clusters at cut-point 0.5 except Frankfurt and Zurich. De Carvalho and De Souza [10] obtained four clusters using their dynamical clustering methods. We can find exactly the same clusters by cutting our dendrogram as the dotted line in the figure.

Figure 14. Dendrogram for 12 months.

Table 7 shows the average values of the compactness for 12 months at selected clustering steps: 25, 29, 31, 33, and 35. As clarified by bold format numbers, the most informative features are February, then January and May. The feature May is important to recognize Cluster 1, 2, and 3. The scatter diagram of Figure 15a shows this fact explicitly, where we used the sum of the minimum and the maximum temperatures as feature values. Figure 15b is the scatter diagram for January and February. This figure describes well the mutual relations of Cluster 4, 5, and 6, while the distinctions between Cluster 1, 2, and 3 disappear. We should note that we can reproduce essential structures appearing in the dendrogram by using only three selected informative features.

Table 7. Average compactness of each feature in selected clustering steps.

Steps	Average Compactness for Several Clustering Steps
	Jan.	Feb.	Mar.	Apr.	May	Jun.	Jul.	Aug.	Sept.	Oct.	Nov.	Dec.
0	0.195	0.194	0.224	0.265	0.217	0.281	0.305	0.286	0.289	0.266	0.233	0.194
25	0.360	0.345	0.363	0.406	0.361	0.461	0.519	0.484	0.466	0.422	0.410	0.375
29	0.409	0.389	0.426	0.490	0.414	0.544	0.609	0.555	0.516	0.456	0.443	0.429
31	0.466	0.443	0.476	0.500	0.451	0.593	0.667	0.609	0.568	0.515	0.486	0.476
33	0.489	0.477	0.476	0.500	0.464	0.618	0.694	0.664	0.586	0.522	0.500	0.512
35	0.580	0.568	0.583	0.645	0.656	0.853	0.984	0.969	0.797	0.662	0.608	0.583

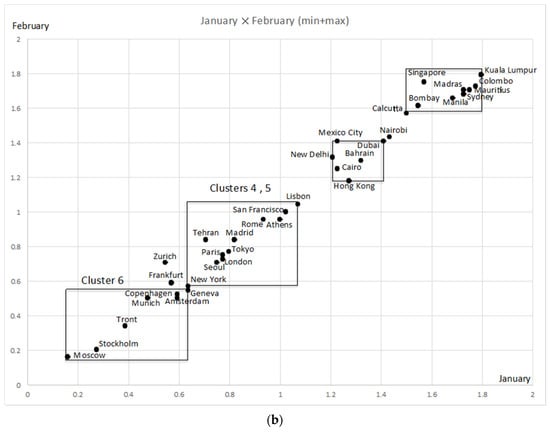
Figure 15. (a) Cluster descriptions for February and May. (b) Cluster descriptions for January and February.

4.4. Analysis of the Hardwood Data

The data is selected from the US Geological Survey (Climate—Vegetation Atlas of North America) [14]. The number of objects is ten and the number of features is eight. Table 8 shows quantile values for the selected ten hardwoods under the feature: (Mean) Annual Temperature (ANNT). We selected the following eight features to describe objects (hardwoods). The data formats for other features F₂~F₈ are the same as in Table 8.

Table 8. The original quantile values for ANNT.

Taxon Name	Mean Annual Temperature (℃)
	0%	10%	25%	50%	75%	90%	100%
ACER EAST	−2.3	0.6	3.8	9.2	14.4	17.9	24
ACER WEST	−3.9	0.2	1.9	4.2	7.5	10.3	21
ALNUS EAST	−10	−4.4	−2.3	0.6	6.1	15.0	21
ALNUS WEST	−12	−4.6	−3.0	0.3	3.2	7.6	19
FRAXINUS EAST	−2.3	1.4	4.3	8.6	14.1	17.9	23
FRAXINUS WEST	2.6	9.4	11.5	17.2	21.2	22.7	24
JAGLANS EAST	1.3	6.9	9.1	12.4	15.5	17.6	21
JAGLANS WEST	7.3	12.6	14.1	16.3	19.4	22.7	27
QUERCUS EAST	−1.5	3.4	6.3	11.2	16.4	19.1	24
QUERCUS WEST	−1.5	6.0	9.5	14.6	17.9	19.9	27

• F₁: Annual Temperature (ANNT) (°C);
• F₂: January Temperature (JANT) (°C);
• F₃: July Temperature (JULT) (°C);
• F₄: Annual Precipitation (ANNP) (mm);
• F₅: January Precipitation (JANP) (mm);
• F₆: July Precipitation (JULP) (mm);
• F₇: Growing Degree Days on 5 °C base ×1000 (GDC5);
• F₈: Moisture Index (MITM).

We use quartile representation by omitting 10% and 90% quantiles from each feature in order to assure the monotone property of our compactness measure. As a result, our hardwood data is histogram data of the size (10 objects) × (8 features) × (5 quantile values). Table 9 shows a part of our 0−1 normalized hardwood data, where five 8-dimensional quantile vectors describe each hardwood.

Table 9. A part of the hardwood data using quantile representation.

Taxon Name	F1	F2	F3	F4	F5	F6	F7	F8
ACER EAST 0	0.251	0.110	0.165	0.072	0.014	0.124	0.048	0.587
1	0.406	0.326	0.416	0.163	0.059	0.197	0.167	0.935
2	0.543	0.452	0.566	0.201	0.102	0.221	0.286	0.967
3	0.675	0.581	0.700	0.242	0.143	0.250	0.417	0.989
4	0.914	0.872	0.813	0.336	0.248	0.491	0.798	1.000
ACER WEST 0	0.211	0.124	0.000	0.004	0.006	0.000	0.000	0.065
1	0.358	0.364	0.213	0.091	0.080	0.051	0.071	0.576
2	0.416	0.420	0.292	0.145	0.137	0.084	0.119	0.728
3	0.500	0.518	0.393	0.237	0.263	0.115	0.179	0.902
4	0.832	0.734	0.828	0.932	0.923	0.354	0.655	1.000

Figure 16 is the result of PCA using the quantile method. Four line segments connecting from 0% to 100% quantile vectors in the factor plane represent each hardwood. East hardwoods have similar shapes, while west hardwoods show significant differences in the last line segments connecting from 75% to 100% quantile vectors. We can recognize three clusters, (Acer West, Alnus West), (five east hardwoods), and (Fraxinus West, Juglans West, Quercus West), in this factor plane.

Figure 16. PCA result for hardwood data.

Figure 17 is the result of our HCC for eight features represented by four equiprobability bins. Ten hardwoods, especially AcW and AlW, have very large concept sizes exceeding our simple criterion 0.5. As a result, we have two major chaining clusters:

Figure 17. Results of clustering for hardwoods data (eight features).

((((((AcE, JE)FE)QE)AlE)AcW)AlW) and ((FW, JW)QW).

Table 10 shows the average compactness of each feature in each clustering step. As clarified by bold format numbers, the most informative feature is ANNP then JULP. Figure 18a shows the nesting structure of rectangles spanned by ten hardwoods with respect to the minimum and the maximum values of ANNP. Another representation of the structure is:

Table 10. Average compactness of each feature in each clustering step.

Step	Average Compactness of Each Feature
	ANNT	JANT	JULT	ANNP	JANP	JULP	GDC5	MITM
0	0.161	0.160	0.178	0.115	0.113	0.133	0.180	0.196
1	0.220	0.228	0.239	0.144	0.140	0.172	0.246	0.242
2	0.229	0.234	0.268	0.186	0.197	0.191	0.256	0.323
3	0.238	0.243	0.282	0.202	0.217	0.203	0.268	0.338
4	0.279	0.269	0.322	0.223	0.243	0.220	0.292	0.358
5	0.404	0.395	0.475	0.337	0.372	0.350	0.455	0.541
6	0.490	0.472	0.570	0.388	0.428	0.401	0.525	0.614
7	0.601	0.578	0.692	0.571	0.595	0.505	0.646	0.739
8	0.829	0.777	0.938	0.768	0.810	0.887	0.899	1.000

Figure 18. Scatter diagrams for the selected informative features.

((((((((JE,AcE)FE)QE)JW)AlE)(FW,QW))AcW)AlW).

Juglans West is merged to the cluster of east hardwoods. From step 8 of Table 10 and Figure 17, we see that JANT is important to separate the cluster (FW, JW, QW) from the other cluster. In fact, we have the scatter diagram of Figure 18b with respect to ANNP and JANT. This scatter diagram is very similar to the PCA result in Figure 16. Figure 18b suggests also the cluster descriptions using three rectangles A, B, and C. Rectangles A and C include the maximum quantile vectors of (AcW, AlW) and five east hardwoods, respectively. Rectangle B includes 25%, 50%, and 75% quantile vectors of (FW, JW, QW). They clarify the distinctions between three clusters.

4.5. Analysis of the US Weather Data

We analyze a climate data set [National Data Center (2014)]. The dataset contains sequential monthly “time bias corrected” average temperature data for 48 states of USA (Alaska and Hawaii are not represented in the data set). Years from 1895 to 2009 are used for comparison purposes. We use 0, 25, 50, 75, and 100% quantiles to describe the temperature each month for each of the 48 states. Therefore, five 12-dimensional quantile vectors describe each state.

In the PCA result of Figure 19, each line graph connecting five quantile vectors describes the corresponding state weather. The first principal component has a very large contribution ratio and 48 distributions line up in a narrow zone of the factor plane. Figure 20 is the dendrogram for 12 months. By cutting the dendrogram at the compactness 0.65, we recognize five major clusters except Arizona, California, and Nevada. These clusters include the following sub-clusters having small compactness less than 0.5.

Figure 19. PCA result for US state weather data.

Figure 20. Dendrogram for 12 months.

(1)

Alabama, Mississippi, Georgia, and Louisiana;

(2)

Connecticut, Rhode Island, Massachusetts, Pennsylvania, Delaware, New Jersey, and Ohio;

(3)

Indiana, West Virginia, and Virginia:

(4)

Kentucky, Tennessee, and Missouri;

(5)

Arkansas and South Carolina;

(6)

Maine, New Hampshire, and Vermont.

Irpino and Verde [9] applied the Ward’s method using their Wasserstein-based distance to the US state weather data and found five clusters. As noted in Section 3.2, dissimilarity between objects and/or clusters and the compactness of objects and/or clusters are different notions. Nevertheless, sub-clusters (1) and (6), for example, appear in both methods. Furthermore, (North Dakota, Minnesota) and (Oregon, Washington) have very similar distributions. Then, in a distance-based approach, these pairs are merged in very early stages. On the other hand, their compactness is larger than many other states, and thus, the compactness delayed their merging steps until later. However, two different methods show similar behavior for (Oregon, Washington) but different behavior for (North Dakota, Minnesota) in the dendrograms.

Table 11 is the average compactness for each feature in selected clustering steps. As clarified by bold format numbers, February and November are the most robustly informative features. Figure 21 is the scatter diagram of 48 states and is similar to the PCA result in Figure 19. All line graphs exist in a narrow region from “cold” to “warm” with respect to February and November. Many states share the minimum and/or the maximum quantile vectors. For example, Alabama, Georgia, and Louisiana share the maximum quantile vector as noted in box C, and the minimum quantile vector as box J, etc. The value of compactness is directly linked to the span of the minimum and the maximum quantile vectors under the assumption of equal bin probabilities. As a result, we have the dendrogram of Figure 22.

Table 11. The average compactness in selected clustering steps.

Step	Average Compactness of Each Feature in Selected Clustering Steps
	Jan	Feb	Mar	Apr	May	June	July	Aug	Sept	Oct	Nov	Dec
0	0.460	0.396	0.516	0.452	0.528	0.486	0.558	0.571	0.500	0.455	0.384	0.447
5	0.470	0.404	0.529	0.462	0.543	0.500	0.581	0.591	0.512	0.468	0.395	0.455
10	0.482	0.411	0.539	0.477	0.561	0.518	0.600	0.605	0.522	0.477	0.404	0.462
15	0.494	0.433	0.545	0.489	0.576	0.530	0.624	0.618	0.535	0.485	0.418	0.471
20	0.507	0.445	0.554	0.495	0.589	0.548	0.643	0.621	0.548	0.495	0.433	0.476
25	0.526	0.462	0.571	0.516	0.616	0.551	0.661	0.635	0.565	0.509	0.449	0.488
30	0.544	0.480	0.576	0.516	0.630	0.574	0.689	0.644	0.583	0.524	0.457	0.500
35	0.562	0.503	0.596	0.527	0.654	0.590	0.723	0.662	0.615	0.549	0.479	0.513
40	0.612	0.545	0.641	0.607	0.750	0.667	0.775	0.750	0.688	0.589	0.528	0.542
41	0.629	0.545	0.643	0.612	0.762	0.667	0.800	0.771	0.714	0.612	0.540	0.556
42	0.650	0.576	0.646	0.619	0.778	0.667	0.833	0.767	0.722	0.619	0.537	0.574
43	0.660	0.600	0.650	0.629	0.800	0.700	0.880	0.800	0.767	0.629	0.556	0.600
44	0.700	0.614	0.688	0.643	0.833	0.708	0.900	0.800	0.792	0.679	0.583	0.639
45	0.733	0.667	0.708	0.667	0.889	0.722	0.867	0.800	0.778	0.667	0.630	0.667
46	0.800	0.682	0.750	0.786	0.917	0.750	0.900	0.900	0.833	0.786	0.722	0.722

Figure 21. The scatter diagram of 48 distributions for February and November.

Figure 22. Clustering result of the US state weather data for February and November.

Under the cut point 0.5, four major clusters, C1~C4, are obtained. Six sub-clusters found in Figure 20 are reproduced in the dendrogram using two features. Sub-cluster (2) obtained in Figure 20 was divided into two smaller sub-clusters (Connecticut, Pennsylvania, Rhode Island, and Massachusetts) and (Delaware, New Jersey, and Ohio). Each of them was merged into different major clusters C4 and C2, respectively. (Illinois, Washington, Kansas, New York, and Iowa) is newly generated cluster C3. Minnesota, Montana, North Dakota, and South Dakota have very small minimum quantile vectors in Figure 19 and Figure 21. They organized a single cluster in Figure 20, while they organized two isolated clusters (Montana, North Dakota) and (Minnesota, South Dakota) with the compactness exceeding 0.5 in Figure 22. We should note that the values of compactness of sub-clusters in Figure 22 are less than those values of the same sub-clusters in Figure 20.

Figure 23 is the scatter diagram of eleven distributions including four major clusters and seven outliers. Each bin-rectangle for a cluster is overlapped with bin-rectangles of other clusters and with remaining states. However, the distinctions between clusters and other states are clear from the maximum quantile vectors and/or the minimum quantile vectors. In other words, we can explain the relationships between eleven distributions by using their mutual positions of the maximum and/or the minimum quantile vectors.

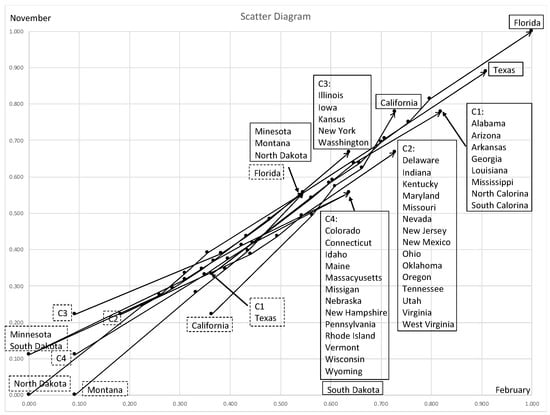
Figure 23. Scatter diagram of four major clusters and seven outliers.

5. Discussion

This paper presented an exploratory hierarchical method to analyze histogram-valued symbolic data using unsupervised feature selection. We described each histogram value of each object and/or cluster using a predetermined number of equiprobability bins. We defined the notion of the concept size and then the compactness for objects and/or clusters as the measure of similarity for our hierarchical clustering method. The compactness is a multi-role measure to evaluate the similarity between objects and/or clusters, to evaluate the dissimilarity of a cluster against the whole concept in each clustering step, and to evaluate the effectiveness of features in the selected clustering steps. We showed the usefulness of the proposed method using five distributional data sets. In each example, we could have two or three robustly informative features. The scatter diagram and the dendrogram for the selected features reproduced well the essential structures embedded in the given distributional data.

In supervised feature selection for histogram-valued symbolic data, we can use class-conditional hierarchical conceptual clustering in addition to our unsupervised feature selection method.